Software piracy and outsourcing in two-sided markets

Abstract

This paper examines the role of software piracy in digital platforms where a platform provider makes a decision of how much software to produce in-house and how much to outsource from a third-party software provider. Using a vertical differentiation model, we theoretically investigate how piracy influences the software outsourcing decision. We find that when piracy is intermediate, the loss in in-house software profits due to piracy outweighs the loss in licensing fee profits. As a result, an increase in piracy leads to more outsourcing. However, when piracy is high, it becomes too expensive for the platform provider to subsidize the software provider, resulting in a decrease in outsourcing. Moreover, when software variety is also endogenously chosen by firms, the platform provider’s incentive to develop software variety in-house depends not only on the return from software profits but also on the return from hardware profits. Under such a situation, an increase in piracy always leads to less outsourcing and less total software variety. To provide additional insights on the outsourcing decision, we conduct empirical analyses using data from the U.S. handheld video game market between 2004 and 2012. This market is a classical two-sided market, dominated by two handheld platforms (Nintendo DS and Sony PlayStation Portable) and is known to have suffered from software piracy significantly. Our regression results show that in this market, piracy increases outsourcing but has no effect on the total software variety.

Appendix A

1.1 A.1 Proof of Proposition 1

The hardware firm’s problem is formulated as

$$ \max_{p_{h},p_{s}}\ p_{h}Q_{h}(p_{h}) + p_{s}Q_{s}(p_{s}) - \frac{C_{h}}{2}, $$

subject to (1) Q_h(p_h) ≥ Q_s(p_s), and (2) $Q_{h}(p_{h})\le \bar {\alpha }$.²⁵ The Lagrangian is then given by

$$ \begin{array}{@{}rcl@{}} L(p_{h},p_{s},\lambda) &=& p_{h}Q_{h}(p_{h})+p_{h}Q_{h}(p_{h}) + p_{s}Q_{s}(p_{s})\\ &&+\lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(p_{s})\right)+\lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right), \end{array} $$

and the Kuhn-Tucker conditions are

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& Q_{h}(p_{h})+p_{h}Q_{h}^{\prime}(p_{h})+\lambda_{1}Q_{h}^{\prime}(p_{h})-\lambda_{2}Q_{h}^{\prime}(p_{h}) = 0\\ \frac{\partial L}{\partial p_{s}} &=& Q_{s}(p_{s})+p_{s}Q_{s}^{\prime}(p_{s})-\lambda_{1}Q_{s}^{\prime}(p_{s}) = 0\\ Q_{h}(p_{h}) &\ge& Q_{s}(p_{s}), \quad \lambda_{1}\ge0,\quad \lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(p_{s})\right)=0\\ Q_{h}(p_{h}) &\le& \bar{\alpha},\quad \lambda_{2}\ge0,\quad \lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right)=0 \end{array} $$

We solve this set of inequalities and equations. Below we examine every possible case.

• 1. When both constraints (1) and (2) are not binding (λ₁ = λ₂ = 0): This is the case with an interior solution. We have

  $$ \begin{array}{@{}rcl@{}} p_{h} &=& \frac{\bar{\alpha}\gamma+v}{2}, p_{s}=\frac{\bar{\alpha}(1-\gamma)}{2}\\ Q_{h} &=& \frac{\bar{\alpha}\gamma+v}{2\gamma}, Q_{s}=\frac{\bar{\alpha}}{4}. \end{array} $$

  Constraint (1) is satisfied for any γ because v > 0. Constraint (2) implies that $\gamma \ge \frac {v}{\bar {\alpha }}$, and Assumption 1 (i.e., $\bar {\alpha }>\sqrt {2}v$) implies that the range of γ that supports this scenario is non-empty.

  With the optimal p_h and p_s, the hardware firm’s profit is

  $$ \pi_{h} = \frac{(\bar{\alpha}\gamma+v)^{2}}{4\gamma}+\frac{\bar{\alpha}^{2}(1-\gamma)}{4}-\frac{C_{h}}{2}. $$

  Now we check the condition for $\pi _{h}\ge \bar {\alpha }v$, i.e., the hardware firm prefers to have software. This condition is equivalent to

  $$ (\bar{\alpha}^{2}-2\bar{\alpha}v-2C_{h})\gamma + v^{2} \ge 0. $$

  When $C_{h}\le \frac {\bar {\alpha }(\bar {\alpha }-2v)}{2}$, $\pi _{h}>\bar {\alpha }v$ for any γ because v > 0. When $C_{h}>\frac {\bar {\alpha }(\bar {\alpha }-2v)}{2}$, $\pi _{h}\ge \bar {\alpha }v$ for $\gamma \le \frac {v^{2}}{2C_{h}-\bar {\alpha }(\bar {\alpha }-2v)}$. For the latter case to be non-empty, we need $\frac {v}{\bar {\alpha }}\le \frac {v^{2}}{2C_{h}-\bar {\alpha }(\bar {\alpha }-2v)}$, or $C_{h}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$.

  In summary, this scenario is supported under the following conditions: (i) $C_{h}\le \frac {\bar {\alpha }(\bar {\alpha }-2v)}{2}$ and $\gamma \in \left [\frac {v}{\bar {\alpha }},1\right )$; (ii) $C_{h}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-2v)}{2},\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}\right ]$ and $\gamma \in \left [\frac {v}{\bar {\alpha }},\frac {v^{2}}{2C_{h}-\bar {\alpha }(\bar {\alpha }-2v)}\right ]$.

• 2. When only constraint (2) is binding (λ₁ = 0 and λ₂ ≥ 0): This is the case with $Q_{s}(p_{s})<Q_{h}(p_{h})=\bar {\alpha }$ (everyone buys hardware). We have

  $$ \begin{array}{@{}rcl@{}} p_{h} &=& v, p_{s}=\frac{\bar{\alpha}(1-\gamma)}{2}\\ Q_{h} &=& \bar{\alpha}, Q_{s}=\frac{\bar{\alpha}}{4}. \end{array} $$

  Constraint (1) is satisfied for any γ. Since constraint (2) is binding, we need λ₁ ≥ 0, which is equivalent to $\gamma \le \frac {v}{\bar {\alpha }}$. Assumption 1 implies that the range of γ that supports this scenario is non-empty.

  With the optimal p_h and p_s, the hardware firm’s profit is

  $$ \pi_{h} = \bar{\alpha}v+\frac{\bar{\alpha}^{2}(1-\gamma)}{4} - \frac{C_{h}}{2}, $$

  and it is easy to check that $\pi _{h}\ge \bar {\alpha }v$ for $\gamma \le 1-\frac {2C_{h}}{\bar {\alpha }^{2}}$. In order for the range of γ that supports this scenario to be non-empty, we need $1-\frac {2C_{h}}{\bar {\alpha }^{2}}>0$, or $C_{h}<\frac {\bar {\alpha }^{2}}{2}$.

  In summary, the following conditions support this scenario: (i) $C_{h}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$ and $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right ]$; (ii) $C_{h}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},\frac {\bar {\alpha }^{2}}{2}\right )$ and $\gamma \in \left (0,1-\frac {2C_{h}}{\bar {\alpha }^{2}}\right )$.

• 3. When only constraint (1) is binding (λ₁ ≥ 0 and λ₂ = 0): This is the case with $Q_{h}(p_{h})=Q_{s}(p_{s})<\bar {\alpha }$. This constraint gives the following relationship between p_s and p_h:

  $$ p_{s} = \frac{(1-\gamma)(p_{h}-v)}{\gamma}. $$

  Substituting this into the first-order conditions, we get $\lambda _{1}=-\frac {v}{\gamma }<0$ for any γ. Thus this scenario is not supported.

• 4. When both constraints are binding (λ₁ ≥ 0 and λ₂ ≥ 0): This is the case with $Q_{h}(p_{h})=Q_{s}(p_{s})=\bar {\alpha }$. From the discussion above, we can obtain

  $$ \begin{array}{@{}rcl@{}} p_{h} &=& v, p_{s}=0\\ Q_{h} &=& Q_{s} = \bar{\alpha}. \end{array} $$

  Constraint (1) requires λ₁ ≥ 0. However, substituting the above optimal prices into the first-order conditions, we can show that $\lambda _{1}=-\bar {\alpha }(1-\gamma )<0$. Thus, this scenario is not supported.

Combining the results, we have:

• 1. When $C_{h}\le \frac {\bar {\alpha }(\bar {\alpha }-2v)}{2}$, the hardware firm will develop software for γ ∈ (0, 1).

  • For $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right ]$, the optimal strategy is characterized by scenario 2.

  • For $\gamma \in \left (\frac {v}{\bar {\alpha }},1\right )$, the optimal strategy is characterized by scenario 1.

• 2. When $C_{h}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-2v)}{2},\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}\right ]$, the hardware firm will develop software if $\gamma \in \left (0,\frac {v^{2}}{2C_{h}-\bar {\alpha }(\bar {\alpha }-2v)}\right ]$. Otherwise, it will only sell hardware.

  • For $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right ]$, the optimal strategy is characterized by scenario 2.

  • For $\gamma \in \left (\frac {v}{\bar {\alpha }},\frac {v^{2}}{2C_{h}-\bar {\alpha }(\bar {\alpha }-2v)}\right )$, the optimal strategy is characterized by scenario 1.

• 3. When $C_{h}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},\frac {\bar {\alpha }^{2}}{2}\right )$, the hardware firm will develop software if $\gamma \in \left (0,1-\frac {2C_{h}}{\bar {\alpha }^{2}}\right )$. Otherwise, it will only sell hardware.

  • The optimal strategy is characterized by scenario 2.

• 4. When $C_{h}\ge \frac {\bar {\alpha }^{2}}{2}$, the hardware firm will not develop software for γ ∈ (0, 1).

In summary, when C_h is sufficiently low, regardless of γ’s value, software is supplied. When γ is small, all consumers buy hardware. When C_h is intermediate, the hardware firm does not supply software if γ is large. This is because the negative effect of software piracy on in-house software is so large that it would not make sense to pay C_h and sell software. When C_h is large, it is too costly to supply software so the hardware firm just sells hardware.

1.2 A.2 Proof of Proposition 2

The software provider’s problem given the licensing fee f is given by

$$ \pi_{s}(f) = \max_{p_{s}}\ (p_{s}-f)\left( \bar{\alpha}-\frac{p_{s}}{1-\gamma}\right)-\frac{C_{s}}{2}. $$

The first-order condition with respect to p_s yields

$$ \begin{array}{@{}rcl@{}} p_{s}(f) &=& \frac{\bar{\alpha}(1-\gamma)+f}{2}\\ Q_{s}(f) &\equiv& \bar{\alpha}-\frac{p_{s}(f)}{1-\gamma} = \frac{\bar{\alpha}}{2} - \frac{f}{2(1-\gamma)}\\ \pi_{s}(f) &=& \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)} - \frac{C_{s}}{2}. \end{array} $$

The hardware provider’s problem is then given by

$$ \begin{array}{@{}rcl@{}} \max_{p_{h},f}\ p_{h}Q_{h}(p_{h}) + f Q_{s}(f) \end{array} $$

subject to (1) Q_h(p_h) ≥ Q_s(f), (2) $Q_{h}(p_{h})\le \bar {\alpha }$, and (3) π_s(f) ≥ 0. The Lagrangian is

$$ \begin{array}{@{}rcl@{}} L(p_{h},f,\lambda) &=& p_{h}Q_{h}(p_{h})+fQ_{s}(f)+\lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(f)\right)\\ &&+\lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right)+\lambda_{3}\pi_{s}(f). \end{array} $$

The Kuhn-Tucker conditions are

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& Q_{h}(p_{h})+p_{h}Q_{h}^{\prime}(p_{h})+\lambda_{1}Q_{h}^{\prime}(p_{h})-\lambda_{2}Q_{h}^{\prime}(p_{h}) = 0\\ \frac{\partial L}{\partial f} &=& Q_{s}(f)+fQ_{s}^{\prime}(f)-\lambda_{1}Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s}^{\prime}(f) = 0\\ Q_{h}(p_{h}) &\ge& Q_{s}(f),\quad \lambda_{1}\ge0,\quad \lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(f)\right)=0\\ Q_{h}(p_{h}) &\le& \bar{\alpha},\quad \lambda_{2}\ge0,\quad \lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right)=0\\ \pi_{s}(f) &\ge& 0,\quad \lambda_{3}\ge0,\quad \lambda_{3}\pi_{s}(f)=0 \end{array} $$

We solve this set of inequalities and equations. Below we examine every possible case.

• 1. When all constraints are not binding (λ₁ = λ₂ = λ₃ = 0): This is the case with interior solutions. We have

  $$ \begin{array}{@{}rcl@{}} p_{h} &=& \frac{\bar{\alpha}\gamma+v}{2}, f=\frac{\bar{\alpha}(1-\gamma)}{2}\\ Q_{h} &=& \frac{\bar{\alpha}\gamma+v}{2\gamma}, Q_{s}=\frac{\bar{\alpha}}{4}. \end{array} $$

  Constraint (1) is satisfied for any γ. Non-binding constraint (2) implies that $\gamma \ge \frac {v}{\bar {\alpha }}$. Finally, non-binding constraint (3) implies that $\gamma \le 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$. The range of γ that supports this scenario is non-empty if $\frac {v}{\bar {\alpha }}\le 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$ or $C_{s}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$.

  With the optimal p_h and f, the hardware firm’s profit is

  $$ \pi_{h} = \frac{(\bar{\alpha}\gamma+v)^{2}}{4\gamma}+\frac{\bar{\alpha}^{2}(1-\gamma)}{8}, $$

  and it is easy to check that $\pi _{h}>\bar {\alpha }v$ for any γ in the range. Thus, the hardware firm prefers to have software developed. Moreover,

  $$ \frac{\partial \pi_{h}}{\partial \gamma} = \frac{\bar{\alpha}^{2}}{8}-\frac{v^{2}}{4\gamma^{2}}. $$

  Thus, $\frac {\partial \pi _{h}}{\partial \gamma }>0$ for $\gamma >\frac {\sqrt {2}v}{\bar {\alpha }}$.

  In summary, this scenario is supported under the following conditions: $C_{h}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$ and $\gamma \in \left [\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right ]$. Moreover, if $C_{h}<\frac {\bar {\alpha }(\bar {\alpha }-\sqrt {2}v)}{8}$, then $\frac {\partial \pi _{h}}{\partial \gamma }\le 0$ for $\gamma \in \left [\frac {v}{\bar {\alpha }},\frac {\sqrt {2}v}{\bar {\alpha }}\right ]$ and $\frac {\partial \pi _{h}}{\partial \gamma }>0$ for $\gamma \in \left (\frac {\sqrt {2}v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right ]$. If $C_{h}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-\sqrt {2}v)}{8},\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}\right )$, $\frac {\partial \pi _{h}}{\partial \gamma }\le 0$ for all $\gamma \in \left [\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right ]$.

• 2. When only constraint (3) is binding (λ₁ = λ₂ = 0 and λ₃ ≥ 0): This is the case where π_s(f) = 0. We have

  $$ \begin{array}{@{}rcl@{}} p_{h} &=&\frac{\bar{\alpha}\gamma+v}{2}, f = \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}\\ Q_{h} &=& \frac{\bar{\alpha}\gamma+v}{2\gamma}, Q_{s}=\sqrt{\frac{C_{s}}{2(1-\gamma)}}. \end{array} $$

  Constraint (1) requires $\frac {\bar {\alpha }\gamma +v}{2\gamma }\ge \sqrt {\frac {C_{s}}{2(1-\gamma )}}$. Let $g(\gamma ) = \frac {\bar {\alpha }\gamma +v}{2\gamma }- \sqrt {\frac {C_{s}}{2(1-\gamma )}}$. It is easy to check that $\frac {\partial g(\gamma )}{\partial \gamma }<0\ \forall \gamma$, $\lim _{\gamma \rightarrow 0}g(\gamma )=+\infty$, and $\lim _{\gamma \rightarrow 1}g(\gamma )=-\infty$. Thus, there exist a unique threshold, say, γ₁ ∈ (0, 1) such that g(γ) ≥ 0 for all γ ≤ γ₁. Constraint (2) implies that $\gamma \ge \frac {v}{\bar {\alpha }}$. Constraint (3) is binding thus we need λ₃ ≥ 0, which is equivalent to $\gamma \ge 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$. The range of γ that supports this scenario is non-empty if g(γ) > 0 at $\gamma =\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \}$. Suppose that $\frac {v}{\bar {\alpha }}<1-\frac {8C_{s}}{\bar {\alpha }^{2}}$ (or $C_{s}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$). Then, it is easy to check $g(\gamma =1-\frac {8C_{s}}{\bar {\alpha }^{2}})>0$, so $\gamma _{1}>1-\frac {8C_{s}}{\bar {\alpha }^{2}}$. If $\frac {v}{\bar {\alpha }}\ge 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$ (or $C_{s}\ge \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$), then $g(\gamma =\frac {v}{\bar {\alpha }})\ge 0$ (i.e., $\frac {v}{\bar {\alpha }}\le \gamma _{1}$) if $C_{s}\le 2\bar {\alpha }(\bar {\alpha }-v)$. Together, the range of γ is non-empty if $C_{s}\le 2\bar {\alpha }(\bar {\alpha }-v)$.

  With the optimal p_h and f, the hardware firm’s profit is

  $$ \pi_{h} = \frac{(\bar{\alpha}\gamma+v)^{2}}{4\gamma}+\left( \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}\right)\sqrt{\frac{C_{s}}{2(1-\gamma)}}. $$

  When $\gamma \ge \frac {v}{\bar {\alpha }}$, not everyone buys hardware and $p_{h}Q_{h} = \frac {(\bar {\alpha }\gamma +v)^{2}}{4\gamma }\ge \bar {\alpha }v$. Thus, the above equation for π_h suggests that π_h can be lower than $\bar {\alpha }v$ only when the optimal licensing fee is negative:

  $$ \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}<0 \Leftrightarrow \gamma > 1-\frac{2C_{s}}{\bar{\alpha}^{2}}. $$

  We first check if a negative licensing fee could actually happen within the above range of γ. When $\frac {v}{\bar {\alpha }}>1-\frac {2C_{s}}{\bar {\alpha }^{2}}$ (or $C_{s}>\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$), then the condition for this scenario to be non-empty ($C_{s}\le 2\bar {\alpha }(\bar {\alpha }-v)$) implies that $1-\frac {2C_{s}}{\bar {\alpha }^{2}}<\gamma _{1}$. If $\frac {v}{\bar {\alpha }}\le 1-\frac {2C_{s}}{\bar {\alpha }^{2}}$, then it can be shown that $g(\gamma =1-\frac {2C_{s}}{\bar {\alpha }^{2}})=\frac {\bar {\alpha }^{2}v}{2(\bar {\alpha }^{2}-2C_{s})}>0$. Thus, the negative licensing fee could indeed happen. Below, we focus on $\gamma \in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right ]$.

  First, note that

  $$ \frac{\partial \pi_{h}}{\partial \gamma} = \frac{\bar{\alpha}^{2}}{4} - \frac{v^{2}}{4\gamma^{2}} - \frac{\bar{\alpha}}{2}\sqrt{\frac{C_{s}}{2(1-\gamma)}}. $$

  We can show that for $\gamma > 1-\frac {2C_{s}}{\bar {\alpha }^{2}}$, $\sqrt {\frac {C_{s}}{2(1-\gamma )}}>\frac {\bar {\alpha }}{2}$. Thus, we have $\frac {\partial \pi _{h}}{\partial \gamma }<0$ for $\gamma \in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right ]$. Given this, if $1-\frac {2C_{s}}{\bar {\alpha }^{2}}<\frac {v}{\bar {\alpha }}$ (or $C_{s}>\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$), then we have $\pi _{h}<\bar {\alpha }v$ for $\gamma \in \left [\frac {v}{\bar {\alpha }},\gamma _{1}\right ]$ because $\pi _{h}<\bar {\alpha }v$ at $\gamma =\frac {v}{\bar {\alpha }}$. For $C_{s}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$, since $\pi >\bar {\alpha }v$ at $\gamma =1-\frac {2C_{s}}{\bar {\alpha }^{2}}$, we can possibly have a unique threshold,say, $\gamma _{2}\in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{2}\right ]$ such that $\pi _{h}<\bar {\alpha }v$ for γ ∈ (γ₂, γ₁]. For example, we can numerically check that for $(\bar {\alpha },v,C_{s})=(1.0,0.5,0.2)$, there exists such γ₂ < γ₁, but for $(\bar {\alpha },v,C_{s})=(1.5,0.5,0.2)$, $\pi _{h}>\bar {\alpha }v$ at γ = γ₁. Since we cannot derive a closed form for the thresholds, let us define ${\Theta }\equiv \{\theta =(\bar {\alpha },v,C_{s}):0<v<\bar {\alpha },0<C_{s}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},\pi _{h}(\gamma =\gamma _{1})\ge \bar {\alpha }v\}$.

  We can now summarize the range of γ that supports this scenario. When $C_{h}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$, $\gamma \in \left [1-\frac {8C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right ]$ for $(\bar {\alpha },v,C_{s})\in {\Theta }$. For $(\bar {\alpha },v,C_{s})\notin {\Theta }$, there exists a unique $\gamma _{2}(\theta )\in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right )$ such that $\pi _{h}<\bar {\alpha }v$ for all γ ∈ (γ₂(θ), γ₁]. When $C_{h}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-v)}{8},\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}\right ]$, $\gamma \in \left [\frac {v}{\bar {\alpha }},\gamma _{1}\right ]$ for $(\bar {\alpha },v,C_{s})\in {\Theta }$. For $(\bar {\alpha },v,C_{s})\notin {\Theta }$, there exists a unique $\gamma _{2}(\theta )\in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right )$ such that $\pi _{h}<\bar {\alpha }v$ for all γ ∈ (γ₂(θ), γ₁]. When $C_{h}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},2\bar {\alpha }(\bar {\alpha }-v)\right ]$, $\gamma \in \left [\frac {v}{\bar {\alpha }},\gamma _{1}\right ]$. But as we saw, $\pi _{h}<\bar {\alpha }v$ for this range of γ and the hardware firm prefers not to have software.

  Finally, we examine the effect of γ on π_h. We saw that for $\gamma \in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right ]$, we have $\frac {\partial \pi _{h}}{\partial \gamma }<0$. We thus consider $\gamma \in \left [\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$. Note that

  $$ \begin{array}{@{}rcl@{}} \frac{\partial^{2} \pi_{h}}{\partial^{2} \gamma} &=& \frac{v^{2}}{2\gamma^{3}}-\frac{\bar{\alpha}}{4(1-\gamma)}\sqrt{\frac{C_{s}}{2(1-\gamma)}}\\ &=& \frac{v^{2}}{2(1-\gamma)\sqrt{1-\gamma}}\left( \frac{(1-\gamma)\sqrt{1-\gamma}}{\gamma^{3}}-\frac{\bar{\alpha}\sqrt{C_{s}}}{2\sqrt{2}v^{2}}\right). \end{array} $$

  It is easy to check that $\lim _{\gamma \rightarrow 0}\frac {\partial ^{2} \pi _{h}}{\partial ^{2} \gamma }=\infty$ and $\lim _{\gamma \rightarrow 1}\frac {\partial ^{2} \pi _{h}}{\partial ^{2} \gamma }=-\infty$. Let $h(\gamma )=\frac {(1-\gamma )\sqrt {1-\gamma }}{\gamma ^{3}}-\frac {\bar {\alpha }\sqrt {C_{s}}}{2\sqrt {2}v^{2}}$. We can show that $\frac {\partial h(\gamma )}{\partial \gamma }<0$ for all γ, and thus, there exists a unique threshold, say, γ₃ such that $\left .\frac {\partial ^{2} \pi _{h}}{\partial ^{2} \gamma }\right |_{\gamma =\gamma _{3}}=0$. We can then consider three possibilities in terms of where γ₃ falls into the range of γ above. Suppose $\gamma _{3}>1-\frac {2C_{s}}{\bar {\alpha }^{2}}$. Then $\frac {\partial ^{2} \pi _{h}}{\partial ^{2} \gamma }>0$ for $\gamma \in \left [\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$. Since $\frac {\partial \pi _{h}}{\partial \gamma }<0$ at $\gamma =1-\frac {2C_{s}}{\bar {\alpha }^{2}}$, we have $\frac {\partial \pi _{h}}{\partial \gamma }<0$ for $\forall \gamma \in \left [\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$. For this to happen, we need $h(\gamma =1-\frac {2C_{s}}{\bar {\alpha }^{2}})>0$. Next, if $\gamma _{3}<\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \}$, then $\frac {\partial ^{2} \pi _{h}}{\partial ^{2} \gamma }<0$ for $\gamma \in \left [\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$. Thus the sign of $\frac {\partial \pi _{h}}{\partial \gamma }$ depends on whether $\frac {\partial \pi _{h}}{\partial \gamma }$ is positive or negative at $\gamma =\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \}$. First, when $\frac {v}{\bar {\alpha }}<1-\frac {8C_{s}}{\bar {\alpha }^{2}}$ (or $C_{s}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$), we have

  $$ \left.\frac{\partial \pi_{h}}{\partial \gamma}\right|_{\gamma=1-\frac{8C_{s}}{\bar{\alpha}^{2}}} = \frac{\bar{\alpha}^{2}}{4}\left[\frac{1}{2}-\left( \frac{\bar{\alpha}v}{\bar{\alpha}^{2}-8C_{s}}\right)^{2}\right], $$

  which is positive if $C_{s}<\frac {\bar {\alpha }(\bar {\alpha }-\sqrt {2}v)}{8}$. Thus, when $C_{s}<\frac {\bar {\alpha }(\bar {\alpha }-\sqrt {2}v)}{8}$, there exists a unique threshold, say, γ₄ such that $\frac {\partial \pi _{h}}{\partial \gamma }>0$ for $\gamma \in \left (1-\frac {8C_{s}}{\bar {\alpha }^{2}},\gamma _{4}\right )$ and $\frac {\partial \pi _{h}}{\partial \gamma }\le 0$ otherwise. If $C_{s}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-\sqrt {2}v)}{8},\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}\right )$, then $\frac {\partial \pi _{h}}{\partial \gamma }<0$ for all $\gamma \in \left (1-\frac {8C_{s}}{\bar {\alpha }^{2}},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right )$. When $\frac {v}{\bar {\alpha }}<1-\frac {8C_{s}}{\bar {\alpha }^{2}}$, it is easy to check

  $$ \left.\frac{\partial \pi_{h}}{\partial \gamma}\right|_{\gamma=\frac{v}{\bar{\alpha}}} = -\frac{\bar{\alpha}}{2}\sqrt{\frac{\bar{\alpha}C_{s}}{2(\bar{\alpha}-v)}}<0\ \ \forall \gamma\in\left( \frac{v}{\bar{\alpha}},1-\frac{2C_{s}}{\bar{\alpha}^{2}}\right). $$

  Finally, if $\gamma _{3}\in \left [\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$, then $\frac {\partial \pi _{h}}{\partial \gamma }$ is a parabola with a maximum at γ = γ₃. Thus, we can check if the maximum attained can be positive. Analytically, it is cumbersome to show. However, our numerical analysis shows that there exists a set of $(\bar {\alpha },v,C_{s})$ such that the maximum is positive (e.g., $(\bar {\alpha },v,C_{s})=(1,0.2,0.1)$). Under such a condition, there exist $\gamma _{4},\gamma _{5}\in \left [\max \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$ such that $\frac {\partial \pi _{h}}{\partial \gamma }>0$ for γ ∈ (γ₄, γ₅) and $\frac {\partial \pi _{h}}{\partial \gamma }\le 0$ otherwise.

• 3. When only constraint (2) is binding (λ₁ = 0, λ₂ ≥ 0, and λ₃ = 0): This is the case where $Q_{h}(p_{h})=\bar {\alpha }$. We have

  $$ \begin{array}{@{}rcl@{}} p_{h} &=& v, f = \frac{\bar{\alpha}(1-\gamma)}{2}\\ Q_{h} &=& \bar{\alpha}, Q_{s}=\frac{\bar{\alpha}}{4}. \end{array} $$

  Constraint (1) is satisfied for any γ. Constraint (2) is binding thus we need λ₂ ≥ 0, which results in $\gamma \le \frac {v}{\bar {\alpha }}$. Constraint (3) implies $\gamma \le 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$. The range of γ that supports this scenario is non-empty if $1-\frac {8C_{s}}{\bar {\alpha }^{2}}>0$, or $C_{s}<\frac {\bar {\alpha }^{2}}{8}$.

  The hardware firm’s profit is $\pi _{h}=\bar {\alpha }v+\frac {\bar {\alpha }^{2}(1-\gamma )}{8}$, which is greater than $\bar {\alpha }v$ for any $\gamma \le \min \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \}$. Moreover, $\frac {\partial \pi _{h}}{\partial \gamma }<0$.

  In summary, this scenario is supported under the following conditions: (i) $C_{s}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$ and $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right ]$; (ii) $C_{s}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-v)}{8},\frac {\bar {\alpha }^{2}}{8}\right ]$ and $\gamma \in \left (0,1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right )$. In both cases, $\frac {\partial \pi _{h}}{\partial \gamma }<0$.

• 4. When constraints (2) and (3) are binding (λ₁ = 0, λ₂ ≥ 0, and λ₃ ≥ 0): This is the case where $Q_{s}(f)\le Q_{h}(p_{h})=\bar {\alpha }$ and π_s(f) = 0. We have

  $$ \begin{array}{@{}rcl@{}} p_{h} &=&v, f = \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}\\ Q_{h} &=& \bar{\alpha}, Q_{s}=\sqrt{\frac{C_{s}}{2(1-\gamma)}}. \end{array} $$

  Constraint (1) requires $\bar {\alpha }\ge \sqrt {\frac {C_{s}}{2(1-\gamma )}}$, which is equivalent to $\gamma \le 1-\frac {C_{s}}{2\bar {\alpha }^{2}}$. Constraint (2) is binding thus we need λ₂ ≥ 0, or $\gamma \le \frac {v}{\bar {\alpha }}$. Constraint (3) is also binding thus we need λ₃ ≥ 0, or $\gamma \ge 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$. The range of γ that supports this scenario is $\gamma \in \left [1-\frac {8C_{s}}{\bar {\alpha }^{2}},\min \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {C_{s}}{2\bar {\alpha }^{2}}\right \}\right ]$. In order for this range to be non-empty, we need the following conditions. When $\frac {v}{\bar {\alpha }}\le 1-\frac {C_{s}}{2\bar {\alpha }^{2}}$ (or $C_{s}\le 2\bar {\alpha }(\bar {\alpha }-v)$), we need $1-\frac {8C_{s}}{\bar {\alpha }^{2}}\le \frac {v}{\bar {\alpha }}$, or $C_{s}\ge \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$. When $\frac {v}{\bar {\alpha }}>1-\frac {C_{s}}{2\bar {\alpha }^{2}}$, we need $1-\frac {C_{s}}{2\bar {\alpha }^{2}}>0$, or $C_{s}<2\bar {\alpha }^{2}$. Thus, the range of γ is non-empty if $C_{s}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-v)}{8},2\bar {\alpha }^{2}\right )$.

  With the optimal p_h and f, the hardware firm’s profit is

  $$ \pi_{h} = \bar{\alpha}v+\left( \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}\right)\sqrt{\frac{C_{s}}{2(1-\gamma)}}. $$

  This is greater than or equal to $\bar {\alpha }v$ as long as the licensing fee is non-negative, which implies $\gamma \le 1- \frac {2C_{s}}{\bar {\alpha }^{2}}$. Since $1- \frac {2C_{s}}{\bar {\alpha }^{2}}<1- \frac {C_{s}}{2\bar {\alpha }^{2}}$, the range of γ that supports this scenario becomes $\gamma \in \left [1-\frac {8C_{s}}{\bar {\alpha }^{2}},\min \limits \left \{\frac {v}{\bar {\alpha }},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right \}\right ]$. When $\frac {v}{\bar {\alpha }}\le 1-\frac {2C_{s}}{\bar {\alpha }^{2}}$ (or $C_{s}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$), we need $1-\frac {8C_{s}}{\bar {\alpha }^{2}}\le \frac {v}{\bar {\alpha }}$, or $C_{s}\ge \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$. When $\frac {v}{\bar {\alpha }}>1-\frac {2C_{s}}{\bar {\alpha }^{2}}$, we need $1-\frac {2C_{s}}{\bar {\alpha }^{2}}>0$, or $C_{s}<\frac {\bar {\alpha }^{2}}{2}$. Thus, the range of γ is non-empty if $C_{s}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-v)}{8},\frac {\bar {\alpha }^{2}}{2}\right )$. Moreover, note that

  $$ \frac{\partial \pi_{h}}{\partial \gamma} = -\frac{\bar{\alpha}}{2}\sqrt{\frac{C_{s}}{2(1-\gamma)}}. $$

  Thus $\frac {\partial \pi _{h}}{\partial \gamma }<0$.

  In summary, this scenario is supported under the following conditions: (i) $C_{s}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-v)}{8}, \frac {\bar {\alpha }(\bar {\alpha }-v)}{2}\right ]$ and $\gamma \in \left (\max \limits \left \{0,1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},\frac {v}{\bar {\alpha }}\right ]$; (ii) $C_{s}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},\frac {\bar {\alpha }^{2}}{2}\right ]$, $\gamma \in \left (\max \limits \left \{0,1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right \},1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$. For $C_{s}\in \left (\frac {\bar {\alpha }^{2}}{2},2\bar {\alpha }^{2}\right ]$, the optimal strategy is supported, but the hardware firm’s profits are lower than $\bar {\alpha }v$. Moreover, we have $\frac {\partial \pi _{h}}{\partial \gamma }<0$ under these conditions.

• 5. When only constraint (1) is binding (λ₁ ≥ 0 and λ₂ = λ₃ = 0): This is the case with Q_h(p_h) = Q_s(f). Intuitively, this scenario will not be supported because when π_s(f) > 0, the optimal licensing fee will be high enough to make Q_s(f) smaller than Q_h(p_h). We can compute

  $$ \begin{array}{@{}rcl@{}} p_{h} &= \frac{\bar{\alpha}(3-2\gamma)\gamma+(4-3\gamma)v}{2(2-\gamma)}, f=\frac{(\bar{\alpha}(1-\gamma)-v)(1-\gamma)}{2-\gamma}. \end{array} $$

  The first-order condition with respect to f gives $\lambda _{1}=\frac {f}{\gamma (1-\gamma )}-\frac {\bar {\alpha }}{2\gamma }$. Substituting the optimal f into this, we can show that λ₁ < 0 for any γ. Thus, this scenario is not supported.

• 6. When constraints (1) and (3) are binding (λ₁ ≥ 0, λ₂ = 0, and λ₃ ≥ 0): This is the case with $Q_{h}(p_{h})=Q_{s}(f)<\bar {\alpha }$ and π_s(f) = 0. This could happen when C_s is large and γ is also large so that the hardware firm needs to lower f sufficiently, which makes the software demand equal to the hardware demand. We can compute

  $$ \begin{array}{@{}rcl@{}} p_{h} &=&\bar{\alpha}\gamma+v-\gamma\sqrt{\frac{C_{s}}{2(1-\gamma)}}, f = \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}\\ Q_{h} &=& Q_{s} = \sqrt{\frac{C_{s}}{2(1-\gamma)}}. \end{array} $$

  Constraint (1) is binding thus we need λ₁ ≥ 0. From the first-order condition with respect to p_h, we get

  $$ \lambda_{1} = -\bar{\alpha}\gamma-v+2\gamma\sqrt{\frac{C_{s}}{2(1-\gamma)}} = 2\gamma\left( \sqrt{\frac{C_{s}}{2(1-\gamma)}}-\frac{\bar{\alpha}\gamma+v}{2\gamma}\right), $$

  which is greater than or equal to zero when γ ≥ γ₁, where $\tilde {\gamma }$ is defined in scenario 2 above. Constraint (2) requires $Q_{h}\le \bar {\alpha }$, or $\gamma \le 1-\frac {C_{s}}{2\bar {\alpha }^{2}}$. Constraint (3) is binding thus we need λ₃ ≥ 0, which can be shown to be satisfied when γ ≥ γ₁. To see this, note that the first-order condition with respect to f gives

  $$ \lambda_{3}\ge 0 \Leftrightarrow \bar{\alpha}(1-\gamma)-2f+\lambda_{1}\ge 0. $$

  First, note that $\bar {\alpha }(1-\gamma )-2f\ge 0$ for $\gamma \ge 1-\frac {8C_{s}}{\bar {\alpha }^{2}}$ and that $\gamma _{1}>1-\frac {8C_{s}}{\bar {\alpha }^{2}}$ (we have proven this in scenario 2 above, but it is easy to check that because $\lambda _{1}(\gamma =1-\frac {8C_{s}}{\bar {\alpha }^{2}})<0$ and $\frac {\partial \lambda _{1}}{\partial \gamma }>0$, it must be $1-\frac {8C_{s}}{\bar {\alpha }^{2}}<\gamma _{1}$). Thus, at γ = γ₁, λ₃ > 0. Overall, the range of γ that supports this scenario is $\gamma \in \left [\gamma _{1},1-\frac {C_{s}}{2\bar {\alpha }^{2}}\right ]$. For this range of γ to be non-empty, we need $\lambda _{1}(\gamma =1-\frac {C_{s}}{2\bar {\alpha }^{2}})\le 0$, which is equivalent to $C_{s}\le 2\bar {\alpha }(\bar {\alpha }-v)$.

  With the optimal p_h and f, the hardware firm’s profit is

  $$ \begin{array}{@{}rcl@{}} \pi_{h} &=& \left( \bar{\alpha}\gamma+v-\gamma\sqrt{\frac{C_{s}}{2(1-\gamma)}}\right)\sqrt{\frac{C_{s}}{2(1-\gamma)}}\\ &&+ \left( \bar{\alpha}(1-\gamma)-\sqrt{2(1-\gamma)C_{s}}\right)\sqrt{\frac{C_{s}}{2(1-\gamma)}}\\ &=&\left( \bar{\alpha}+v-(2-\gamma)\sqrt{\frac{C_{s}}{2(1-\gamma)}}\right)\sqrt{\frac{C_{s}}{2(1-\gamma)}}. \end{array} $$

  We note that at $\gamma =1-\frac {C_{s}}{2\bar {\alpha }^{2}}$, we have p_h = v, $f=-\frac {C_{s}}{2\bar {\alpha }}$, $Q_{h}=Q_{s}=\bar {\alpha }$. Thus,

  $$ \pi_{h} = \left( v-\frac{C_{s}}{2\bar{\alpha}}\right)\bar{\alpha} = \bar{\alpha}v - \frac{C_{s}}{2}, $$

  which is clearly less than $\bar {\alpha }v$. For $\gamma \in \left [\gamma _{1},1-\frac {C_{s}}{2\bar {\alpha }}\right )$, note that

  $$ \frac{\partial \pi_{h}}{\partial \gamma} = \frac{1}{1-\gamma}\sqrt{\frac{C_{s}}{2(1-\gamma)}}\left( \frac{\bar{\alpha}+v}{2}-\sqrt{\frac{C_{s}}{2(1-\gamma)}}\right). $$

  We know that $\frac {\bar {\alpha }+v}{2}<\frac {\bar {\alpha }\gamma +v}{2\gamma }$ for γ < 1. Also, for γ > γ₁, $\frac {\bar {\alpha }\gamma +v}{2\gamma }<\sqrt {\frac {C_{s}}{2(1-\gamma )}}$. Thus, $\frac {\partial \pi _{h}}{\partial \gamma }<0$ for $\gamma \in \left [\gamma _{1},1-\frac {C_{s}}{2\bar {\alpha }^{2}}\right )$. As we saw in scenario 2, we can show that $\pi _{h}-\bar {\alpha }v$ at γ = γ₁ can be positive or negative under some values of $(\bar {\alpha },v,C_{s})$. Note that the hardware firm’s profit function in this scenario is identical to that in scenario 2 at γ = γ₁. Thus, we can use the same set of Θ we defined in scenario 2, and summarize the results as follows.

  When $C_{h}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$ and $(\bar {\alpha },v,C_{s})\in {\Theta }$, there exists a unique threshold, say, $\gamma _{6}(\theta )\in \left (\gamma _{1},1-\frac {C_{s}}{2\bar {\alpha }^{2}}\right )$ such that the hardware firm prefers to have software for γ ∈ [γ₁, γ₆(θ)]. When $C_{h}<\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}$ and $(\bar {\alpha },v,C_{s})\notin {\Theta }$ or $C_{h}\in \left [\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},2\bar {\alpha }(\bar {\alpha }-v)\right ]$, the hardware firm prefers not to have software. Moreover, $\frac {\partial \pi _{h}}{\partial \gamma }<0$.

• 7. When constraints (1) and (2) are binding (λ₁ ≥ 0, λ₂ ≥ 0, and λ₃ = 0): This is the case with $Q_{h}(p_{h})=Q_{s}(f)=\bar {\alpha }$. Once again, intuitively, this scenario will not be supported because when π_s(f) > 0, the optimal licensing fee will be high enough to make Q_s(f) smaller than Q_h(p_h). We can compute

  $$ \begin{array}{@{}rcl@{}} p_{h} &= v f=-\bar{\alpha}(1-\gamma). \end{array} $$

  The first-order condition with respect to f gives $\lambda _{1}=\frac {f}{\gamma (1-\gamma )}-\frac {\bar {\alpha }}{2\gamma }$. Substituting the optimal f into this, we can show that λ₁ < 0 for any γ.

• 8. When all constraints are binding (λ₁ ≥ 0, λ₂ ≥ 0, and λ₃ ≥ 0): This is the case with $Q_{h}(p_{h})=Q_{s}(f)=\bar {\alpha }$ and π_s(f) = 0. We can compute

  $$ \begin{array}{@{}rcl@{}} p_{h} &=& v f=-\bar{\alpha}(1-\gamma)\\ Q_{h} &=& Q_{s} = \bar{\alpha} \end{array} $$

  From the three constraints, we can show that this scenario is supported only at $\gamma =1-\frac {C_{s}}{2\bar {\alpha }^{2}}$. At this γ, the first-order conditions give

  $$ \lambda_{3} = \frac{\bar{\alpha}}{C_{s}}\lambda_{1} + 1, \lambda_{2} = \lambda_{1} + v + \frac{C_{s}}{2\bar{\alpha}}-\bar{\alpha}. $$

  First, for any λ₁ ≥, λ₃ > 0, but λ₂ ≥ 0 if $v + \frac {C_{s}}{2\bar {\alpha }}-\bar {\alpha }\ge 0$, or $C_{s}\ge 2\bar {\alpha }(\bar {\alpha }-v)$.

  Note that the hardware firm’s profits under the above optimal strategy are then

  $$ \pi_{h} = \bar{\alpha}v - \bar{\alpha}(1-\gamma)\bar{\alpha} < \bar{\alpha}v. $$

  Thus, the hardware firm prefers not to have software.

Combining the results from supported scenarios, we have:

• 1. When $C_{s}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$ and $\theta =(\bar {\alpha },v,C_{s})\in {\Theta }$, there exists a unique $\gamma _{6}(\theta )\in \left (\gamma _{1},1-\frac {C_{s}}{2\bar {\alpha }^{2}}\right )$ such that the optimal strategy is characterized as follows.

  • For $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right ]$, the optimal strategy is characterized by scenario 3.

  • For $\gamma \in \left (\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right )$, the optimal strategy is characterized by scenario 1.

  • For $\gamma \in \left (1-\frac {8C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right )$, the optimal strategy is characterized by scenario 2.

  • For $\gamma \in \left (\gamma _{1},\gamma _{6}(\theta )\right ]$, the optimal strategy is characterized by scenario 6.

  • For $\gamma \in \left (\gamma _{6}(\theta ),1\right )$, the hardware firm chooses not to have software.

• 2. When $C_{s}\le \frac {\bar {\alpha }(\bar {\alpha }-v)}{8}$ and $\theta =(\bar {\alpha },v,C_{s})\notin {\Theta }$, there exists a unique $\gamma _{2}(\theta )\in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right )$ such that the optimal strategy is characterized as follows.

  • For $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right ]$, the optimal strategy is characterized by scenario 3.

  • For $\gamma \in \left (\frac {v}{\bar {\alpha }},1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right )$, the optimal strategy is characterized by scenario 1.

  • For $\gamma \in \left (1-\frac {8C_{s}}{\bar {\alpha }^{2}},\gamma _{2}(\theta )\right ]$, the optimal strategy is characterized by scenario 2.

  • For $\gamma \in \left (\gamma _{2}(\theta ),1\right )$, the hardware firm chooses not to have software.

• 3. When $C_{s}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{8},\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}\right ]$ and $\theta =(\bar {\alpha },v,C_{s})\in {\Theta }$, there exists a unique $\gamma _{6}(\theta )\in \left (\gamma _{1},1-\frac {C_{s}}{2\bar {\alpha }^{2}}\right )$ such that the optimal strategy is characterized as follows.

  • For $C_{s}\le \frac {\bar {\alpha }^{2}}{8}$:

    • For $\gamma \in \left (0,1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right ]$, the optimal strategy is characterized by scenario 3.

    • For $\gamma \in \left (1-\frac {8C_{s}}{\bar {\alpha }^{2}},\frac {v}{\bar {\alpha }}\right )$, the optimal strategy is characterized by scenario 4.

    • For $\gamma \in \left (\frac {v}{\bar {\alpha }},\gamma _{1}\right )$, the optimal strategy is characterized by scenario 2.

    • For $\gamma \in \left (\gamma _{1},\gamma _{6}(\theta )\right ]$, the optimal strategy is characterized by scenario 6.

    • For $\gamma \in \left (\gamma _{6}(\theta ),1\right )$, the hardware firm chooses not to have software.

  • For $C_{s}>\frac {\bar {\alpha }^{2}}{8}$:

    • For $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right )$, the optimal strategy is characterized by scenario 4.

    • For $\gamma \in \left (\frac {v}{\bar {\alpha }},\gamma _{1}\right )$, the optimal strategy is characterized by scenario 2.

    • For $\gamma \in \left (\gamma _{1},\gamma _{6}(\theta )\right ]$, the optimal strategy is characterized by scenario 6.

    • For $\gamma \in \left (\gamma _{6}(\theta ),1\right )$, the hardware firm chooses not to have software.

• 4. When $C_{s}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{8},\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}\right ]$ and $\theta =(\bar {\alpha },v,C_{s})\notin {\Theta }$, there exists a unique $\gamma _{2}(\theta )\in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},\gamma _{1}\right )$ such that the optimal strategy is characterized as follows.

  • For $C_{s}\le \frac {\bar {\alpha }^{2}}{8}$:

    • For $\gamma \in \left (0,1-\frac {8C_{s}}{\bar {\alpha }^{2}}\right ]$, the optimal strategy is characterized by scenario 3.

    • For $\gamma \in \left (1-\frac {8C_{s}}{\bar {\alpha }^{2}},\frac {v}{\bar {\alpha }}\right )$, the optimal strategy is characterized by scenario 4.

    • For $\gamma \in \left (\frac {v}{\bar {\alpha }},\gamma _{2}(\theta )\right ]$, the optimal strategy is characterized by scenario 2.

    • For $\gamma \in \left (\gamma _{2}(\theta ),1\right )$, the hardware firm chooses not to have software.

  • For $C_{s}>\frac {\bar {\alpha }^{2}}{8}$:

    • For $\gamma \in \left (0,\frac {v}{\bar {\alpha }}\right )$, the optimal strategy is characterized by scenario 4.

    • For $\gamma \in \left (\frac {v}{\bar {\alpha }},\gamma _{2}(\theta )\right ]$, the optimal strategy is characterized by scenario 2.

    • For $\gamma \in \left (\gamma _{2}(\theta ),1\right )$, the hardware firm chooses not to have software.

• 5. When $C_{s}\in \left (\frac {\bar {\alpha }(\bar {\alpha }-v)}{2},\frac {\bar {\alpha }^{2}}{2}\right ]$, the optimal strategy is characterized as follows. Note that Assumption 1 implies that $\frac {\bar {\alpha }(\bar {\alpha }-v)}{2}>\frac {\bar {\alpha }^{2}}{8}$, thus $C_{s}>\frac {\bar {\alpha }^{2}}{8}$ in this region of C_s.

  • For $\gamma \in \left (0,1-\frac {2C_{s}}{\bar {\alpha }^{2}}\right ]$, the optimal strategy is characterized by scenario 4.

  • For $\gamma \in \left (1-\frac {2C_{s}}{\bar {\alpha }^{2}},1\right )$, the hardware firm chooses not to have software.

• 6. When $C_{s}>\frac {\bar {\alpha }^{2}}{2}$, the hardware firm prefers not to have software for γ ∈ (0, 1).

1.3 A.3 Proof of Proposition 3a

The software provider’s problem given the licensing fee f is given by

$$ \pi_{s}(f,\delta) = \max_{p_{s}}\ (1-\delta)(p_{s}-f)\left( \bar{\alpha}-\frac{p_{s}}{1-\gamma}\right)-\frac{C_{s}}{2}(1-\delta)^{2}. $$

The first-order condition with respect to p_s yields

$$ \begin{array}{@{}rcl@{}} p_{s}(f) &=& \frac{\bar{\alpha}(1-\gamma)+f}{2}\\ Q_{s}(f) &\equiv& \bar{\alpha}-\frac{p_{s}(f)}{1-\gamma} = \frac{\bar{\alpha}}{2} - \frac{f}{2(1-\gamma)}\\ \pi_{s}(f,\delta) &=& (1-\delta)\frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)} - \frac{C_{s}}{2}(1-\delta)^{2}. \end{array} $$

The hardware provider’s problem is then given by

$$ \begin{array}{@{}rcl@{}} \max_{p_{h},f,\delta}\ p_{h}Q_{h}(p_{h}) + \left( \delta p_{s}(f)+(1-\delta)f\right)Q_{s}(f) - \frac{C_{h}}{2}\delta^{2} \end{array} $$

subject to (1) Q_h(p_h) ≥ Q_s(f), (2) $Q_{h}(p_{h})\le \bar {\alpha }$, and (3) π_s(f) ≥ 0. The Lagrangian is

$$ \begin{array}{@{}rcl@{}} L(p_{h},f,\lambda) &=& p_{h}Q_{h}(p_{h}) + \left( \delta p_{s}(f)+(1-\delta)f\right)Q_{s}(f) - \frac{C_{h}}{2}\delta^{2}\\ & &+\lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(f)\right)+\lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right)+\lambda_{3}\pi_{s}(f,\delta). \end{array} $$

The Kuhn-Tucker conditions are

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& Q_{h}(p_{h})+p_{h}Q_{h}^{\prime}(p_{h})+\lambda_{1}Q_{h}^{\prime}(p_{h})-\lambda_{2}Q_{h}^{\prime}(p_{h}) = 0\\ \frac{\partial L}{\partial f} &=& \left( \delta p_{s}^{\prime}(f)+(1-\delta)\right)Q_{s}(f)+\left( \delta p_{s}(f)+(1-\delta)f\right)Q_{s}^{\prime}(f)\\&&-\lambda_{1}Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ \frac{\partial L}{\partial \delta} &=& (p_{s}(f)-f)Q_{s}(f)-C_{h}\delta +\lambda_{3}\pi_{s,\delta}^{\prime}(f,\delta) = 0\\ Q_{h}(p_{h}) &\ge& Q_{s}(f),\quad \lambda_{1}\ge0,\quad \lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(f)\right)=0\\ Q_{h}(p_{h}) &\le& \bar{\alpha},\quad \lambda_{2}\ge0,\quad \lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right)=0\\ \pi_{s}(f,\delta) &\ge& 0,\quad \lambda_{3}\ge0, \quad\lambda_{3}\pi_{s}(f,\delta)=0 \end{array} $$

We solve this set of inequalities and equations by restricting our attention to the interior solution case (λ₁ = λ₂ = λ₃ = 0).

The first-order conditions with respect to p_h and f give:

$$ \begin{array}{@{}rcl@{}} p_{h} &=& \frac{\bar{\alpha}\gamma+v}{2},\quad f=\frac{\bar{\alpha}(1-\gamma)(1-\delta)}{2-\delta}\\ Q_{h} &=& \frac{\bar{\alpha}\gamma+v}{2\gamma},\quad Q_{s}=\frac{\bar{\alpha}}{2(2-\delta)}. \end{array} $$

Note that $Q_{h}>\frac {\bar {\alpha }}{2}$ and $Q_{s}\le \frac {\bar {\alpha }}{2}$. Thus, constraint (1) is satisfied. The first-order condition with respect to δ then gives

$$ \frac{\bar{\alpha}^{2}(1-\gamma)}{4(2-\delta)^{2}} = C_{h}\delta. $$

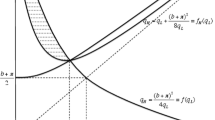
As in Fig. 2, the solution does not exist (i.e., the marginal return on δ is strictly positive for any δ) if the LHS is strictly greater than the RHS for all δ. It is easy to check that this is the case for $\gamma <1-\frac {128C_{h}}{27\bar {\alpha }^{2}}$. In other words, when γ is very small, we expect a corner solution in which δ = 1.

Now consider $\gamma \ge 1-\frac {128C_{h}}{27\bar {\alpha }^{2}}$. As γ increases, the RHS shifts down. Also, the RHS is equivalent to the software firm’s per-software profit ((p_s(f) − f)Q_s(f)). Thus, in order to satisfy constraint (3) (i.e., the software firm’s participation constraint), we need

$$ \frac{\bar{\alpha}^{2}(1-\gamma)}{4(2-\delta)^{2}}\ge \frac{C_{s}}{2}(1-\delta). $$

The LHS is independent of γ, so there is a lower bound of γ that satisfies the first-order conditions and constraint (3). At the lower bound, we have $\frac {\bar {\alpha }^{2}(1-\gamma )}{4(2-\delta )^{2}} = C_{h}\delta =\frac {C_{s}}{2}(1-\delta )$. Thus, the lower bound of δ is obtained as $\delta = \frac {C_{s}}{2C_{h}+C_{s}}$. Substituting this into constraint (3), we get

$$ \frac{\bar{\alpha}^{2}(1-\gamma)}{4(2-\frac{C_{s}}{2C_{h}+C_{s}})^{2}}\ge \frac{C_{s}}{2}(1-\frac{C_{s}}{2C_{h}+C_{s}})\Leftrightarrow\gamma\le 1-\frac{4(4C_{h}+C_{s})^{2}C_{h}C_{s}}{(2C_{h}+C_{s})^{3}\bar{\alpha}^{2}} $$

Constraint (2) requires $\gamma \ge \frac {v}{\bar {\alpha }}$. Because we focus on $\gamma \ge 1-\frac {128C_{h}}{27\bar {\alpha }^{2}}$, constraint (2) is satisfied on this range as long as $\frac {v}{\bar {\alpha }}\le 1-\frac {128C_{h}}{27\bar {\alpha }^{2}}$. This implies that $C_{h}\le \frac {27\bar {\alpha }(\bar {\alpha }-v)}{128}$. Assumption 1 guarantees that the RHS is strictly positive. Thus, constraint (2) is satisfied as long as C_h is sufficiently low.

Next, we discuss the sufficient conditions. Recall that when $\gamma \in \left (1-\frac {128C_{h}}{27\bar {\alpha }^{2}},1-\frac {4C_{h}}{\bar {\alpha }^{2}}\right ]$, two δ’s satisfy the first-order condition.²⁶ However, we can show that one of the δ’s that is greater than $\frac {2}{3}$ is a saddle point (i.e., the point b in Fig. 2).

To see this, we check the second-order condition of the hardware firm’s problem. First note that $\frac {\partial ^{2} \pi _{h}}{\partial p_{h} \partial f}=\frac {\partial ^{2} \pi _{h}}{\partial p_{h} \partial \delta }=0$ and $\frac {\partial ^{2} \pi _{h}}{\partial ^{2} p_{h}}<0$. Thus, we only need to examine the condition for (f, δ). The Hessian is given by

$$ H = \left( \begin{array}{cc} \frac{\partial^{2} \pi_{h}}{\partial^{2} f} & \frac{\partial^{2} \pi_{h}}{\partial f \partial \delta} \\ \frac{\partial^{2} \pi_{h}}{\partial \delta \partial f} & \frac{\partial^{2} \pi_{h}}{\partial^{2} \delta} \end{array} \right) = \left( \begin{array}{cc} -\frac{2-\delta}{2(1-\gamma)} & -\frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)} \\ -\frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)} & -C_{h} \end{array} \right). $$

We know that $-\frac {2-\delta }{2(1-\gamma )}<0$, and

$$ \begin{array}{@{}rcl@{}} |H| &=& \frac{(2-\delta)C_{h}}{2(1-\gamma)}-\frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)^{2}}\\ &=& \frac{2(1-\gamma)(2-\delta)C_{h}-(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)^{2}}. \end{array} $$

Since the denominator is positive, we only need to check the sign of the numerator. In order for H to be negative semidefinite, we need

$$ \frac{2-\delta}{2\delta}-1 \ge 0 \Leftrightarrow \delta \le \frac{2}{3}. $$

Thus, we conclude that when $\gamma \in \left (1-\frac {128C_{h}}{27\bar {\alpha }^{2}},1-\frac {4C_{h}}{\bar {\alpha }^{2}}\right ]$, one of the solutions for δ that is greater than $\frac {2}{3}$ is a saddle point.

Finally, since the licensing fee is positive, it is easy to show that the hardware firm’s profits are larger than $\bar {\alpha }v$.

1.4 A.4 Proof of Proposition 3b

First, it is easy to show that when $\gamma <1-\frac {128C_{h}}{27\bar {\alpha }^{2}}$, the marginal return on δ becomes strictly positive for any δ. As a result, we have a corner solution with δ = 1. This is equivalent to the Full Integration case, and we have provided details in Appendix 1.

Now consider $\gamma >1-\frac {4(4C_{h}+C_{s})^{2}C_{h}C_{s}}{(2C_{h}+C_{s})^{3}\bar {\alpha }^{2}}$, and recall the first-order conditions from Appendix 3a:

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& Q_{h}(p_{h})+p_{h}Q_{h}^{\prime}(p_{h})+\lambda_{1}Q_{h}^{\prime}(p_{h})-\lambda_{2}Q_{h}^{\prime}(p_{h}) = 0\\ \frac{\partial L}{\partial f} &=& \left( \delta p_{s}^{\prime}(f)+(1-\delta)\right)Q_{s}(f)+\left( \delta p_{s}(f)+(1-\delta)f\right)Q_{s}^{\prime}(f)-\lambda_{1}Q_{s}^{\prime}(f)\\&&+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ \frac{\partial L}{\partial \delta} &=& (p_{s}(f)-f)Q_{s}(f)-C_{h}\delta +\lambda_{3}\pi_{s,\delta}^{\prime}(f,\delta) = 0 \end{array} $$

Since the constraint π_s ≥ 0 is now binding, we have λ₃ ≥ 0. Also, we know from Appendix 2 that when γ is even higher, the constraint Q_h ≥ Q_s binds. So for now, consider the case where λ₂ = 0. Also, we know that we can satisfy $Q_{h}\le \bar {\alpha }$ for sufficiently low C_h. The constraint π_s = 0 gives:

$$ (p_{s}(f)-f)Q_{s}(f) = \frac{C_{s}}{2}(1-\delta)\Leftrightarrow 1 - \delta = \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{2(1-\gamma)C_{s}}. $$

This condition characterizes the relationship between δ and f and implies that δ increases monotonically as f increases. Moreover,

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial f} \!&=&\! \left( \delta p_{s}^{\prime}(f)+(1-\delta)\right)Q_{s}(f)+\left( \delta p_{s}(f)+(1-\delta)f\right)Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ \!&\Leftrightarrow&\! \lambda_{3} = \frac{\bar{\alpha}(1-\gamma)(1-\delta)-(2-\delta)f}{\bar{\alpha}(1-\gamma)-f} = \frac{(\bar{\alpha}(1-\gamma)-f)^{3}-2(1-\gamma)C_{s}f}{2(1-\gamma)C_{s}(\bar{\alpha}(1-\gamma)-f)}. \end{array} $$

It is easy to check $\frac {\partial \lambda _{3}}{\partial f}<0$, and thus λ₃ is uniquely determined given f. The first-order condition with respect to δ is

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial \delta} &=& \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)} - C_{h}\delta + \lambda_{3}\frac{C_{s}}{2} = 0\\ &\Leftrightarrow& \frac{(C_{h}+C_{s})(\bar{\alpha}(1-\gamma)-f)^{3}-(1-\gamma){C_{s}^{2}}f}{2(1-\gamma)C_{s}(\bar{\alpha}(1-\gamma)-f)}-C_{h}=0 \end{array} $$

It is easy to check that the LHS is monotonically decreasing in f. Thus, there is a unique f that satisfies the first-order condition. Since δ and λ₃ are uniquely determined given f, there is a unique optimal strategy $(p_{h}^{*},f^{*},\delta ^{*})$ (note that $p_{h}^{*}$ is the same as the interior solution).

Now consider the case where λ₂, λ₃ ≥ 0. We now have another constraint:

$$ \bar{\alpha}-\frac{p_{h}-v}{\gamma} = \bar{\alpha}-\frac{p_{s}}{1-\gamma}\Leftrightarrow p_{h}= v + \frac{\gamma}{1-\gamma}p_{s} = v + \frac{(\bar{\alpha}(1-\gamma)+f)\gamma}{2(1-\gamma)} $$

The first-order condition with respect to p_h is now

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& \bar{\alpha}-\frac{2p_{h}-v}{\gamma} - \lambda_{1}\frac{1}{\gamma} =0\\ &\Leftrightarrow& \lambda_{1} = -v-\frac{\gamma f}{1-\gamma} \end{array} $$

Since λ₂ ≥ 0, $f<-\frac {(1-\gamma )v}{\gamma }$. The first-order condition with respect to f gives

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial f} &=& \left( \delta p_{s}^{\prime}(f)+(1-\delta)\right)Q_{s}(f)+\left( \delta p_{s}(f)+(1-\delta)f\right)Q_{s}^{\prime}(f)\\&&-\lambda_{1}Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ &\Leftrightarrow& \lambda_{3} = \frac{\bar{\alpha}(1-\gamma)(1-\delta)-(2-\delta)f-(1-\gamma)v-\gamma f}{(1-\gamma)(\bar{\alpha}(1-\gamma)-f)}\\ &=& \frac{(\bar{\alpha}(1-\gamma)-f)^{3}-2C_{s}f-2(1-\gamma)vC_{s}}{2(1-\gamma)C_{s}(\bar{\alpha}(1-\gamma)-f)}. \end{array} $$

We can check that λ₃ monotonically decreases in f. The first-order condition with respect to δ is

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial \delta} &=& \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)} - C_{h}\delta + \lambda_{3}\frac{C_{s}}{2} = 0\\ &\Leftrightarrow& \frac{(C_{h}+C_{s})(\bar{\alpha}(1-\gamma)-f)^{3}-{C_{s}^{2}}f-(1-\gamma)v{C_{s}^{2}}}{2(1-\gamma)C_{s}(\bar{\alpha}(1-\gamma)-f)}-C_{h}=0 \end{array} $$

We can also check that the LHS monotonically decreases in f. Thus, there is a unique f that satisfies the first-order condition. Since p_h, δ, λ₂ and δ₃ are uniquely determined given f, there is a unique optimal strategy $(p_{h}^{*},f^{*},\delta ^{*})$.

Now we are interested in the sign of $\frac {\partial \delta ^{*}}{\partial \gamma }$. It is difficult to analytically derive the sign. However, the optimal strategy is unique, so we can numerically solve for $(p_{h}^{*},f^{*},\delta ^{*})$ and examine how δ^∗ changes with γ. Specifically, given $(\bar {\alpha },C_{h},C_{s})$, we solve for the optimal strategy $(p_{h}^{*},f^{*},\delta ^{*})$ over γ ∈ (0, 1). We use 10,000 evenly spaced grid points over (0, 1). We have tested extensive sets of $(\bar {\alpha },C_{h},C_{s})$, and consistently found that $\frac {\partial \delta ^{*}}{\partial \gamma }>0$ for $\gamma >1-\frac {4(4C_{h}+C_{s})^{2}C_{h}C_{s}}{(2C_{h}+C_{s})^{3}\bar {\alpha }^{2}}$.

1.5 A.5 Proof of Proposition 4a

Let p_i and p_s be the price of in-house and outsourced software, respectively, and p_i is set by the hardware firm and p_s is set by the software firm. We consider a case where we take our main analysis in Section 2.4 as the basis (except that we now assume v = 0) and allow p_i to be set by the hardware firm.

We first derive the demand for in-house and outsourced software. As before, let p_h be the price of hardware, δ be the proportion of in-house software, and α be the benefit from software. Consumers now have the following four options regarding software acquisition:

$$ u(\alpha) = \left\{\begin{array}{ll} - p_{h} + \delta(\alpha-p_{i}) + (1-\delta)(\alpha-p_{s}) & \text{if buying both types of software, (b,b)}\\ - p_{h} + \delta(\alpha-p_{i}) + (1-\delta)\gamma\alpha & \text{if buying in-house and pirating outsourced software, (b,p)}\\ - p_{h} + \delta\gamma\alpha + (1-\delta)(\alpha-p_{s}) & \text{if buying outsourced and pirating in-house software, (p,b)}\\ - p_{h} + \delta\gamma\alpha + (1-\delta)\gamma\alpha & \text{if pirating both types of software, (p,p)} \end{array}\right. $$

We show that regardless of whether p_i is higher or lower than p_s, the marginal consumer who is indifferent between buying and pirating in-house software depends only on p_i, not p_s, and the marginal consumer who is indifferent between buying and pirating outsourced software depends only on p_s. To see this, first notice that the slope on α is the highest for (b,b) (the slope is 1), the lowest for (p,p) (the slope is γ). The slope on (b,p) (i.e., δ + (1 − δ)γ) is larger than the slope on (p,b) (i.e., δγ + (1 − δ)) if $\delta >\frac {1}{2}$. Notice that the marginal consumer who is indifferent between (b,b) and (b,p) is given by $\alpha =\frac {p_{s}}{1-\gamma }$. But the marginal consumer who is indifferent between (p,b) and (p,p) is also given by $\frac {p_{s}}{1-\gamma }$. Consider the utility for each buying/pirating behavior at $\alpha =\frac {p_{s}}{1-\gamma }$. Then, we know that the utility for (b,b) is equal to that for (b,p), and the utility for (p,b) is equal to that for (p,p). Comparing the utilities for (b,b) and (p,b) at $\alpha =\frac {p_{s}}{1-\gamma }$, we know that the utility for (b,b) is higher than that for (p,b) when

$$ \frac{p_{s}}{1-\gamma}-p_{i}>\gamma\frac{p_{s}}{1-\gamma} \Leftrightarrow p_{s}>p_{i}. $$

Suppose p_s > p_i. Then, we know that $\alpha \in \left [\frac {p_{s}}{1-\gamma },\bar {\alpha }\right ]$ will choose (b,b). Also, we know that for $\alpha <\frac {p_{s}}{1-\gamma }$, the utility for (p,p) is higher than that for (p,b). Thus, no one chooses (p,b), and there is a marginal consumer who is indifferent between (b,p) and (p,p), which is given by $\alpha =\frac {p_{i}}{1-\gamma }$. Thus, the segments will be: (b,b) for $\alpha \in \left [\frac {p_{s}}{1-\gamma },\bar {\alpha }\right ]$, (b,p) for $\alpha \in \left [\frac {p_{i}}{1-\gamma },\frac {p_{s}}{1-\gamma }\right ]$, and (p,p) for the rest who buys hardware.

Now suppose p_s < p_i. Then, we know that $\alpha <\frac {p_{s}}{1-\gamma }$ will choose (p,p). Also, we know that for $\alpha >\frac {p_{s}}{1-\gamma }$, the utility for (b,b) is higher than that for (b,p). Thus, no one chooses (b,p), and there is a marginal consumer who is indifferent between (p,b) and (b,b), which is given by $\alpha =\frac {p_{i}}{1-\gamma }$. Thus, the segments will be: (b,b) for $\alpha \in \left [\frac {p_{i}}{1-\gamma },\bar {\alpha }\right ]$, (p,b) for $\alpha \in \left [\frac {p_{s}}{1-\gamma },\frac {p_{i}}{1-\gamma }\right ]$, and (p,p) for the rest who buys hardware.

The same logic applies when $\delta <\frac {1}{2}$. In this case, the slope on α for (p,b) is larger than that for (b,p). But then the indifferent consumer for (b,b) and (p,b) $\left (\frac {p_{i}}{1-\gamma }\right )$ is the same as that for (b,p) and (p,p). Thus, we just swap p_s and p_i and get the same result.

Thus, regardless of whether p_i < p_s or not and $\delta >\frac {1}{2}$ or not, the per-unit demand for in-house and outsourced software will be given by

$$ Q_{i}(p_{i})=\bar{\alpha}-\frac{p_{i}}{1-\gamma}\text{and}Q_{s}(p_{s})=\bar{\alpha}-\frac{p_{s}}{1-\gamma}. $$

The software firm’s problem given (f, δ) is

$$ \pi_{s}(f,\delta) = \max_{p_{s}} (1-\delta)(p_{s}-f)\left( \bar{\alpha}-\frac{p_{s}}{1-\gamma}\right)-\frac{C_{s}}{2}(1-\delta)^{2}. $$

The first-order condition with respect to p_s gives

$$ \begin{array}{@{}rcl@{}} p_{s}(f) &=& \frac{\bar{\alpha}(1-\gamma)+f}{2}\\ Q_{s}(f) &=& \bar{\alpha}-\frac{p_{s}(f)}{1-\gamma} = \frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)}\\ \pi_{s}(f,\delta) &=& (1-\delta)\frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)} - \frac{C_{s}}{2}(1-\delta)^{2}. \end{array} $$

The hardware firm’s problem is now

$$ \begin{array}{@{}rcl@{}} \max_{p_{h},p_{i},f,\delta} \pi_{h}(p_{h},p_{i},f,\delta) &=& p_{h}Q_{h}(p_{h}) + (1-\delta) f Q_{s}(f) + \delta p_{i} Q_{i}(p_{i}) - \frac{C_{h}}{2}\delta^{2}\\ &=& p_{h}\left( \bar{\alpha}-\frac{p_{h}}{\gamma}\right) + (1-\delta) f \frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)}\\ &&+ \delta p_{i}\left( \bar{\alpha}-\frac{p_{i}}{1-\gamma}\right) - \frac{C_{h}}{2}\delta^{2} \end{array} $$

subject to (1) Q_h(p_h) ≥ Q_s(f), (2) $Q_{h}(p_{h})\le \bar {\alpha }$, and (3) π_s(f, δ) ≥ 0.²⁷ The Lagrangian is then given by

$$ \begin{array}{@{}rcl@{}} L(p_{h},p_{i},f,\delta) &=& p_{h}Q_{h}(p_{h}) + (1-\delta)fQ_{s}(f) +\delta p_{i}Q_{i}(p_{i}) - \frac{C_{h}}{2}\delta^{2}\\ &&+ \lambda_{1} \left( Q_{h}(p_{h})-Q_{s}(f)\right) + \lambda_{2} \left( \bar{\alpha}-Q_{h}(p_{h})\right) + \lambda_{3} \pi_{s}(f,\delta). \end{array} $$

The Kuhn-Tucker conditions are

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& Q_{h}(p_{h})+p_{h}Q_{h}^{\prime}(p_{h}) + \lambda_{1} Q_{h}^{\prime}(p_{h}) - \lambda_{2} Q_{h}^{\prime}(p_{h}) = 0\\ \frac{\partial L}{\partial p_{i}} &=& \delta Q_{i}(p_{i})+\delta p_{i}Q_{i}^{\prime}(p_{i}) = 0\\ \frac{\partial L}{\partial f} &=& (1-\delta)Q_{s}(f)+(1-\delta)fQ_{s}^{\prime}(f)-\lambda_{1}Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ \frac{\partial L}{\partial \delta} &=& p_{i}Q_{i}(p_{i})-fQ_{s}(f)-C_{h}\delta+\lambda_{3}\pi_{s,\delta}^{\prime}(f,\delta) = 0\\ Q_{h}(p_{h}) &\ge& Q_{s}(f),\quad \lambda_{1}\ge 0,\quad \lambda_{1}\left( Q_{h}(p_{h})-Q_{s}(f)\right)=0\\ Q_{h}(p_{h}) &\le& \bar{\alpha}, \lambda_{2}\ge 0,\quad \lambda_{2}\left( \bar{\alpha}-Q_{h}(p_{h})\right)=0\\ \pi_{s}(f,\delta) &\ge& 0,\quad \lambda_{3}\ge 0,\quad \lambda_{3}\pi_{s}(f,\delta)=0 \end{array} $$

We first note that the FOC for p_i is not influenced by the constraints. Solving the FOC gives

$$ p_{i} = \frac{\bar{\alpha}(1-\gamma)}{2}, Q_{i}(p_{i}) = \frac{\bar{\alpha}}{2}, p_{i}Q_{i}(p_{i}) = \frac{\bar{\alpha}^{2}(1-\gamma)}{4}. $$

The per-unit gross profit of in-house software decreases in γ through a lower price. We solve this set of inequalities and equations.

We restrict our attention to the interior solution case (λ₁ = λ₂ = λ₃ = 0). The FOC for p_h gives:

$$ p_{h} = \frac{\bar{\alpha}\gamma}{2}, Q_{h}(p_{h})=\frac{\bar{\alpha}}{2}, p_{h}Q_{h}(p_{h})=\frac{\bar{\alpha}^{2}\gamma}{4}. $$

The profit from hardware is increasing in γ. Next, the first-order condition with respect to f gives

$$ f = \frac{\bar{\alpha}(1-\gamma)}{2}, Q_{s}(f)=\frac{\bar{\alpha}}{4}, fQ_{s}(f)=\frac{\bar{\alpha}^{2}(1-\gamma)}{8}. $$

We thus have

$$ p_{s} = \frac{3\bar{\alpha}^{2}(1-\gamma)}{4}, (p_{s}-f)Q_{s}(f)=\frac{\bar{\alpha}^{2}(1-\gamma)}{16}. $$

We note that $\frac {\partial p_{i}Q_{i}}{\partial \gamma }<\frac {\partial fQ_{s}}{\partial \gamma }$. This is one driving force to push software development to the software firm when γ increases. This can be seen in the first-order condition for δ, which gives

$$ \delta = \frac{p_{i}Q_{i}-fQ_{s}}{C_{h}} = \frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}. $$

Thus, we have $\frac {\partial \delta }{\partial \gamma }<0$. Given δ ≤ 1, we require $\gamma \ge 1-\frac {8C_{h}}{\bar {\alpha }^{2}}$.

With the optimal strategy, the software firm’s profit is

$$ \begin{array}{@{}rcl@{}} \pi_{s} &=& (1-\delta)(p_{s}-f)Q_{s}(f)-\frac{C_{s}(1-\delta)^{2}}{2}\\ &=& \left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)\frac{\bar{\alpha}^{2}(1-\gamma)}{16}-\frac{C_{s}}{2}\left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)^{2}\\ &=& \left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)\left[\frac{\bar{\alpha}^{2}(1-\gamma)}{16} - \frac{C_{s}}{2}\left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)\right]\\ &=&\left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)\frac{1}{16C_{h}}\left( \bar{\alpha}^{2}(1-\gamma)(C_{h}+C_{s})-8C_{h}C_{s}\right)\\ &=&\frac{(C_{h}+C_{s})}{16C_{h}}\left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)\left( \bar{\alpha}^{2}(1-\gamma)-\frac{8C_{h}C_{s}}{C_{h}+C_{s}}\right). \end{array} $$

Thus π_s ≥ 0 if and only if

$$ \bar{\alpha}^{2}(1-\gamma)-\frac{8C_{h}C_{s}}{C_{h}+C_{s}}\ge 0 \Longleftrightarrow \gamma \le 1- \frac{8C_{h}C_{s}}{\bar{\alpha}^{2}(C_{h}+C_{s})}. $$

Finally, hardware firm’s profit is

$$ \begin{array}{@{}rcl@{}} \pi_{h} &=& \frac{\bar{\alpha}^{2}\gamma}{4} + \delta\frac{\bar{\alpha}^{2}(1-\gamma)}{4} + (1-\delta)\frac{\bar{\alpha}^{2}(1-\gamma)}{8}-\frac{C_{h}}{2}\delta^{2}\\ &=& \frac{\bar{\alpha}^{2}\gamma}{4} + \frac{\bar{\alpha}^{2}(1-\gamma)}{8} + \frac{\bar{\alpha}^{2}(1-\gamma)}{8}\delta - \frac{C_{h}}{2}\delta^{2}\\ &=&\frac{\bar{\alpha}^{2}(1+\gamma)}{8} + \frac{\bar{\alpha}^{2}(1-\gamma)}{8}\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}-\frac{C_{h}}{2}\frac{\bar{\alpha}^{4}(1-\gamma)^{2}}{64{C_{h}^{2}}}\\ &=&\frac{\bar{\alpha}^{2}(1+\gamma)}{8} + \frac{\bar{\alpha}^{4}(1-\gamma)^{2}}{128C_{h}}>0. \end{array} $$

Also,

$$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial \gamma} &=& \frac{\bar{\alpha}^{2}}{8} - \frac{\bar{\alpha}^{4}(1-\gamma)}{64C_{h}} = \frac{\bar{\alpha}^{2}}{8}\left( 1-\frac{\bar{\alpha}^{2}(1-\gamma)}{8C_{h}}\right)\\ &=& \frac{\bar{\alpha}^{2}}{8}(1-\delta) > 0. \end{array} $$

Thus, hardware firm benefits from piracy.

1.6 A.6 Proof of Proposition 4b

The proof here is similar to Appendix A.4. First, it is easy to show that when $\gamma <1-\frac {8C_{h}}{\bar {\alpha }^{2}}$, the marginal return on δ becomes strictly positive for any δ. As a result, we have a corner solution with δ = 1. This is equivalent to the Full Integration case, and we have provided details in Appendix 1.

Now consider $\gamma >1-\frac {8C_{h}C_{s}}{\bar {\alpha }^{2}(C_{h}+C_{s})}$, and recall the first-order conditions from Appendix A.5:

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& Q_{h}(p_{h})+p_{h}Q_{h}^{\prime}(p_{h}) + \lambda_{1} Q_{h}^{\prime}(p_{h}) - \lambda_{2} Q_{h}^{\prime}(p_{h}) = 0\\ \frac{\partial L}{\partial f} &=& (1-\delta)Q_{s}(f)+(1-\delta)fQ_{s}^{\prime}(f)-\lambda_{1}Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ \frac{\partial L}{\partial \delta} &=& p_{i}Q_{i}(p_{i})-fQ_{s}(f)-C_{h}\delta+\lambda_{3}\pi_{s,\delta}^{\prime}(f,\delta) = 0 \end{array} $$

Since the constraint π_s ≥ 0 is now binding, we have λ₃ ≥ 0. Also, we know from Appendix 2 that when γ is even higher, the constraint Q_h ≥ Q_s binds. So for now, consider the case where λ₂ = 0. Also, we know that we can satisfy $Q_{h}\le \bar {\alpha }$ for sufficiently low C_h. The constraint π_s = 0 gives:

$$ (p_{s}(f)-f)Q_{s}(f) = \frac{C_{h}}{2}(1-\delta)\Leftrightarrow 1 - \delta = \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{2(1-\gamma)C_{s}}. $$

This condition characterizes the relationship between δ and f and implies that δ increases monotonically as f increases. Moreover,

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial f} &=& (1-\delta)Q_{s}(f)+(1-\delta)fQ_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ &\Leftrightarrow& \lambda_{3} = \frac{(\bar{\alpha}(1-\gamma)-f)(\bar{\alpha}(1-\gamma)-2f)}{2(1-\gamma)C_{s}}. \end{array} $$

Since λ₃ ≥ 0, $f\le \frac {\bar {\alpha }(1-\gamma )}{2}$. It is easy to check $\frac {\partial \lambda _{3}}{\partial f}<0$, and thus λ₃ is uniquely determined given f. The first-order condition with respect to δ is

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial \delta} \!&=&\! p_{i}Q_{i}(p_{i})-fQ_{s}(f)-C_{h}\delta+\lambda_{3}\pi_{s,\delta}^{\prime}(f,\delta) = 0\\ \!&\Leftrightarrow&\! \frac{\bar{\alpha}^{2}(1-\gamma)}{4}-C_{h} + \frac{(\bar{\alpha}(1-\gamma)-f)((2C_{h}+C_{s})\bar{\alpha}(1-\gamma)-2(C_{h}+2C_{s})f)}{4(1-\gamma)C_{s}}=0 \end{array} $$

It is easy to check that the LHS is monotonically decreasing in f. Thus, there is a unique f that satisfies the first-order condition. Since δ and λ₃ are uniquely determined given f, there is a unique optimal strategy $(p_{h}^{*},f^{*},\delta ^{*})$ (note that $p_{h}^{*}$ is the same as the interior solution).

Now consider the case where λ₂, λ₃ ≥ 0. We now have another constraint:

$$ \bar{\alpha}-\frac{p_{h}}{\gamma} = \bar{\alpha}-\frac{p_{s}}{1-\gamma}\Leftrightarrow p_{h}= \frac{\gamma}{1-\gamma}p_{s} = \frac{(\bar{\alpha}(1-\gamma)+f)\gamma}{2(1-\gamma)} $$

The first-order condition with respect to p_h is now

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial p_{h}} &=& \bar{\alpha}-\frac{2p_{h}}{\gamma} - \lambda_{1}\frac{1}{\gamma} =0\\ &\Leftrightarrow& \lambda_{1} = -\frac{\gamma f}{1-\gamma} \end{array} $$

Since λ₂ ≥ 0, f < 0. The first-order condition with respect to f gives

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial f} &=& (1-\delta)Q_{s}(f)+(1-\delta)fQ_{s}^{\prime}(f)-\lambda_{1}Q_{s}^{\prime}(f)+\lambda_{3}\pi_{s,f}^{\prime}(f,\delta) = 0\\ &\Leftrightarrow& \lambda_{3} = \frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)-2f)-2C_{s}\gamma f}{2(1-\gamma)C_{s}(\bar{\alpha}(1-\gamma)-f)}. \end{array} $$

We can check that λ₃ monotonically decreases in f. The first-order condition with respect to δ is

$$ \begin{array}{@{}rcl@{}} \frac{\partial L}{\partial \delta} &=& p_{i}Q_{i}(p_{i})-fQ_{s}(f)-C_{h}\delta+\lambda_{3}\pi_{s,\delta}^{\prime}(f,\delta) = 0\\ &\Leftrightarrow& \frac{\bar{\alpha}^{2}(1-\gamma)}{4}-C_{h}\\ &&+ \frac{((2C_{h}+C_{s})(\bar{\alpha}(1-\gamma)-f)^{3}-3C_{s}(\bar{\alpha}(1-\gamma)-f)^{2}f-2{C_{s}^{2}}\gamma f}{4(1-\gamma)C_{s}}=0 \end{array} $$

We can also check that the LHS monotonically decreases in f. Thus, there is a unique f that satisfies the first-order condition. Since δ, p_h, λ₂ and δ₃ are uniquely determined given f, there is a unique optimal strategy $(p_{h}^{*},f^{*},\delta ^{*})$.

We are interested in the sign of $\frac {\partial \delta ^{*}}{\partial \gamma }$. Similar to Appendix app4A.4, it is difficult to analytically derive the sign. Thus we numerically examine it using a similar approach described there. Again, we consistently found that $\frac {\partial \delta ^{*}}{\partial \gamma }>0$ for $\gamma >1-\frac {8C_{h}C_{s}}{\bar {\alpha }^{2}(C_{h}+C_{s})}$.

1.7 A.7 Proof of Proposition 5

The software firm’s profit is

$$ \pi_{s} = n_{s}(p_{s}-f)Q_{s}-\frac{C_{s}{n_{s}^{2}}}{2}, $$

The first-order conditions with respect to p_s and n_s give:

$$ \begin{array}{@{}rcl@{}} p_{s}&=&\frac{\bar{\alpha}(1-\gamma)+f}{2}, Q_{s}=\frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)}, (p_{s}-f)Q_{s} = \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)}\\ n_{s}&=& \frac{(p_{s}-f)Q_{s}}{C_{s}} = \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)C_{s}} \end{array} $$

Given p_s and n_s(f), the hardware firm’s problem is

$$ \pi_{h}(p_{h},p_{i},n_{i},f) = p_{h}Q_{h}(p_{h},n_{i},f)+n_{i}p_{i}Q_{i}(p_{i})+n_{s}(f) f Q_{s}(f) - \frac{C_{h}{n_{i}^{2}}}{2}, $$

where p_h is the price of hardware, Q_h is the demand for hardware ($Q_{h}=\bar {\alpha }-\frac {p_{h}}{(n_{i}+n_{s}(f))\gamma })$, p_i is the price of in-house software, Q_i is the demand for in-house software ($Q_{i}(p_{i})=\bar {\alpha }-\frac {p_{i}}{1-\gamma }$).

First, p_i influences only the in-house software profit, so can be simply determined by $\frac {\partial \pi _{h}}{\partial p_{i}}=0$:

$$ \begin{array}{@{}rcl@{}} p_{i} = \frac{\bar{\alpha}(1-\gamma)}{2}, Q_{i} = \frac{\bar{\alpha}}{2}, p_{i}Q_{i} = \frac{\bar{\alpha}^{2}(1-\gamma)}{4} \end{array} $$

Thus the problem now is

$$ \pi_{h}(p_{h},n_{i},f) = p_{h}Q_{h}(p_{h},n_{i},f)+n_{i}\frac{\bar{\alpha}^{2}(1-\gamma)}{4}+n_{s}(f) f Q_{s}(f) - \frac{C_{h}{n_{i}^{2}}}{2}. $$

The hardware firm maximizes the profit subject to Q_h(p_h, n_i, f) ≥ Q_s(f) and π_s(f) ≥ 0. However, the latter is always satisfied because the software firm can choose n_s optimally. Thus, we consider two scenarios based on the first constraint.

• 1. Q_h ≥ Q_s is not binding:

  $$ \pi_{h}(p_{h},n_{i},f) = p_{h}Q_{h}(p_{h},n_{i},f)+n_{i}\frac{\bar{\alpha}^{2}(1-\gamma)}{4}+n_{s}(f) f Q_{s}(f) - \frac{C_{h}{n_{i}^{2}}}{2}. $$

  The first-order conditions are:

  $$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial p_{h}} &=& \bar{\alpha}-\frac{2p_{h}}{\gamma(n_{i}+n_{s})} = 0 \Longleftrightarrow p_{h}=\frac{\bar{\alpha}\gamma(n_{i}+n_{s})}{2},\ Q_{h}=\frac{\bar{\alpha}}{2}\\ \frac{\partial \pi_{h}}{\partial n_{i}} &=& \frac{\bar{\alpha}^{2}\gamma}{4} + \frac{\bar{\alpha}^{2}(1-\gamma)}{4} - C_{h} n_{i}=0 \Longleftrightarrow n_{i}=\frac{\bar{\alpha}^{2}}{4C_{h}}\\ \frac{\partial \pi_{h}}{\partial f} &=&\frac{\bar{\alpha}^{2}\gamma}{4}n_{s}^{\prime} + n_{s}^{\prime}(fQ_{s})+n_{s}(fQ_{s})'=0 \end{array} $$

  Note that f influences π_h in two channels: via n_s and via fQ_s:

  $$ \frac{\partial \pi_{h}}{\partial f} =\left[\frac{\bar{\alpha}^{2}\gamma}{4}+fQ_{s}\right]n_{s}^{\prime} + n_{s}(fQ_{s})' $$

  The first term captures the return on f via n_s and the second term is the direct return on f. Solving the FOC, we get

  $$ f = \frac{5\bar{\alpha}(1-\gamma)\pm\bar{\alpha}\sqrt{(1-\gamma)(9+7\gamma)}}{8}. $$

  Note that $(1-\gamma )(9+7\gamma )=9(1-\gamma )(1+\frac {7}{9}\gamma )>9(1-\gamma )^{2}$. Thus,

  $$ \frac{5\bar{\alpha}(1-\gamma)+\bar{\alpha}\sqrt{(1-\gamma)(9+7\gamma)}}{8}> \frac{5\bar{\alpha}(1-\gamma)+3\bar{\alpha}(1-\gamma)}{8}=\bar{\alpha}(1-\gamma). $$

  Since $f\le \bar {\alpha }(1-\gamma )$, the optimal f is

  $$ f = \frac{5\bar{\alpha}(1-\gamma)-\bar{\alpha}\sqrt{(1-\gamma)(9+7\gamma)}}{8}. $$

  We thus have

  $$ \begin{array}{@{}rcl@{}} p_{s} = \frac{\bar{\alpha}(1-\gamma)\left( 13-\sqrt{\frac{9+7\gamma}{1-\gamma}}\right)}{16}, Q_{s} = \frac{\bar{\alpha}\left( 3+\sqrt{\frac{9+7\gamma}{1-\gamma}}\right)}{16} \end{array} $$

  Since we require $Q_{s}\le Q_{h}=\frac {\bar {\alpha }}{2}$,

  $$ \begin{array}{@{}rcl@{}} \frac{\bar{\alpha}\left( 3+\sqrt{\frac{9+7\gamma}{1-\gamma}}\right)}{16} \le \frac{\bar{\alpha}}{2} \Longleftrightarrow \gamma \le \frac{1}{2}. \end{array} $$

  For $\gamma \le \frac {1}{2}$, $\frac {\partial f}{\partial \gamma }<0$. Also, note that

  $$ \begin{array}{@{}rcl@{}} p_{s}-f =\frac{\bar{\alpha}(1-\gamma)\left( 3+\sqrt{\frac{9+7\gamma}{1-\gamma}}\right)}{16} \end{array} $$

  Thus,

  $$ \begin{array}{@{}rcl@{}} n_{s} = \frac{(p_{s}-f)Q_{s}}{C_{s}}=\frac{K\bar{\alpha}^{2}}{256}\left( 3\sqrt{1-\gamma}+\sqrt{9+7\gamma}\right)^{2} \end{array} $$

  and

  $$ \begin{array}{@{}rcl@{}} \frac{\partial n_{s}}{\partial \gamma} = \frac{\bar{\alpha}^{2}}{128C_{s}}\left( 3\sqrt{1-\gamma}+\sqrt{9+7\gamma}\right)\left( -\frac{3}{2\sqrt{1-\gamma}}+\frac{7}{2\sqrt{9+7\gamma}}\right). \end{array} $$

  It is straightforward to show that $\frac {\partial n_{s}}{\partial \gamma }<0$.

  Finally, we check π_h:

  $$ \begin{array}{@{}rcl@{}} \pi_{h} &=& p_{h}Q_{h} + n_{i}p_{i}Q_{i} + n_{s}fQ_{s} - \frac{C_{h}{n_{i}^{2}}}{2}\\ &=&\frac{\bar{\alpha}^{2}\gamma(n_{i}+n_{s})}{4} + n_{i}\frac{\bar{\alpha}^{2}(1-\gamma)}{4} + n_{s} fQ_{s} - \frac{C_{h}{n_{i}^{2}}}{2}\\ &=&\left[\frac{\bar{\alpha}^{2}\gamma}{4}+fQ_{s}\right]n_{s} + \frac{\bar{\alpha}^{2}}{4}n_{i}-\frac{C_{h}}{2}{n_{i}^{2}}\\ &=&\left[\frac{\bar{\alpha}^{2}\gamma}{4}+fQ_{s}\right]n_{s} + \frac{\bar{\alpha}^{4}}{32C_{h}}>0. \end{array} $$

  Thus hardware firm is in business. Also, we check how γ influences π_h. Note that

  $$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial \gamma} = \left[\frac{\bar{\alpha}^{2}}{4}+\frac{\partial (fQ_{s})}{\partial \gamma}\right]n_{s} + \left[\frac{\bar{\alpha}^{2}\gamma}{4}+fQ_{s}\right]\frac{\partial n_{s}}{\partial \gamma} \end{array} $$

  where a change in γ influences (1) the marginal return on n_s (i.e., first bracket) and (2) n_s (i.e., $\frac {\partial n_{s}}{\partial \gamma }$). First,

  $$ \begin{array}{@{}rcl@{}} fQ_{s} &=& \frac{\bar{\alpha}^{2}(5\sqrt{1-\gamma}-\sqrt{9+7\gamma})(3\sqrt{1-\gamma}+\sqrt{9+7\gamma})}{128}>0\ \forall \gamma\le\frac{1}{2}\\ \frac{\partial (fQ_{s})}{\partial \gamma} &=& \frac{\bar{\alpha}^{2}\left( 7(1-\gamma)-(9+7\gamma)-22\sqrt{(1-\gamma)(9+7\gamma)}\right)}{64\sqrt{(1-\gamma)(9+7\gamma)}} <0\ \forall \gamma \end{array} $$

  It can be shown that the change in marginal return on n_s due to an increase in γ is negative:

  $$ \left[\frac{\bar{\alpha}^{2}}{4}+\frac{\partial (fQ_{s})}{\partial \gamma}\right]=\frac{\bar{\alpha}^{2}}{64AB}(7A+B)(A-B)<0 $$

  where $A=\sqrt {1-\gamma }$ and $B=\sqrt {9+7\gamma }$. Then

  $$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial \gamma} &=& \left[\frac{\bar{\alpha}^{2}}{4}+\frac{\bar{\alpha}^{2}(7A^{2}-B^{2}-22AB)}{64AB}\right]\frac{K\bar{\alpha}^{2}(3A+B)^{2}}{256}\\ &&+\left[\frac{\bar{\alpha}^{2}\gamma}{4} + \frac{\bar{\alpha}^{2}(5A-B)(3A+B)}{128}\right]\frac{K\bar{\alpha}^{2}(3A+B)(7A-3B)}{256AB}\\ &=&\frac{\bar{\alpha}^{2}(16AB+7A^{2}-B^{2}-22AB)}{64AB}\frac{K\bar{\alpha}^{2}(3A+B)^{2}}{256}\\ &&+\frac{\bar{\alpha}^{2}(32\gamma+(5A-B)(3A+B)}{128}\frac{K\bar{\alpha}^{2}(3A+B)(7A-3B)}{256AB}\\ &=&\frac{K\bar{\alpha}^{4}(3A+B)}{128\cdot256AB}\left[2(7A+B)(A-B)(3A+B)\right.\\ &&\left.-[32\gamma+(5A-B)(3A+B)](7A-3B)\right] \end{array} $$

  Note $\frac {K\bar {\alpha }^{4}(3A+B)}{128\cdot 256AB}>0$. Thus, we drop it and focus on

  $$ S\equiv 2(7A+B)(A-B)(3A+B)-[32\gamma+(5A-B)(3A+B)](7A-3B) $$

  First, we note that when $\gamma \le \frac {1}{2}$,

  $$ S = 2\underbrace{(7A+B)}_{+}\underbrace{(A-B)}_{-}\underbrace{(3A+B)}_{+} -[32\gamma+\underbrace{(5A-B)}_{+}\underbrace{(3A+B)}_{+}]\underbrace{(7A-3B)}_{-} $$

  Thus, its sign could depend on γ. This expression can be simplified as

  $$ S = -108A-196\gamma A - 36B + 52\gamma B < 0\ \forall \gamma\le\frac{1}{2} $$

  because $(-36 + 52\gamma )<0\ \forall \gamma \le \frac {1}{2}$. Thus, $\frac {\partial \pi _{h}}{\partial \gamma }<0$ in this scenario.

• 2. Q_h = Q_s:

  This happens when γ is high (i.e., $\gamma >\frac {1}{2}$) and f < 0. Recall that the constraint implies

  $$ \bar{\alpha}-\frac{p_{h}}{(n_{i}+n_{s})\gamma)} = \bar{\alpha} - \frac{p_{s}}{1-\gamma}\ \Longleftrightarrow\ p_{h} = \frac{\gamma(n_{i}+n_{s})}{1-\gamma}p_{s} $$

  Thus the profit from hardware can be written as

  $$ p_{h}Q_{h}=\frac{\gamma(n_{i}+n_{s})}{1-\gamma}p_{s}Q_{s}=\frac{\bar{\alpha}^{2}(1-\gamma)^{2}-f^{2}}{4(1-\gamma)} $$

  The hardware firm’s profit is now

  $$ \begin{array}{@{}rcl@{}} \pi_{h}(n_{i},f) &=& \frac{\gamma(n_{i}+n_{s}(f))}{1-\gamma}\frac{\bar{\alpha}^{2}(1-\gamma)^{2}-f^{2}}{4(1-\gamma)}+n_{i}\frac{\bar{\alpha}^{2}(1-\gamma)}{4}\\ &&+n_{s}(f) f Q_{s}(f) - \frac{C_{h}{n_{i}^{2}}}{2}. \end{array} $$

  First, the FOC with respect to n_i is

  $$ \frac{\partial \pi_{h}}{\partial n_{i}} = \frac{\gamma}{1-\gamma}\frac{\bar{\alpha}^{2}(1-\gamma)^{2}-f^{2}}{4(1-\gamma)} + \frac{\bar{\alpha}^{2}(1-\gamma)}{4}-C_{h} n_{i}=0 $$

  We then get

  $$ n_{i} = \frac{\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2}}{4C_{h}(1-\gamma)^{2}}. $$

  Note that this is less than $\frac {\bar {\alpha }^{2}}{4C_{h}}$ (optimal n_i when $\gamma \le \frac {1}{2}$). Next, the FOC with respect to f is

  $$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial f} &= \frac{\gamma}{1-\gamma}n_{s}^{\prime}(p_{s}Q_{s})+\frac{\gamma(n_{i}+n_{s})}{1-\gamma}(p_{s}Q_{s})' + n_{s}^{\prime}(fQ_{s})+n_{s}(fQ_{s})'=0, \end{array} $$

  where

  $$ \begin{array}{@{}rcl@{}} \frac{\gamma}{1-\gamma}n_{s}^{\prime}(p_{s}Q_{s})&=&\frac{\gamma}{1-\gamma}\left( -\frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)C_{s}}\right)\left( \frac{\bar{\alpha}^{2}(1-\gamma)^{2}-f^{2}}{4(1-\gamma)}\right)\\ &=& -\frac{\gamma(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)+f)}{8(1-\gamma)^{3}C_{s}}\\ \frac{\gamma(n_{i}+n_{s})}{1-\gamma}(p_{s}Q_{s})^{\prime}\!&=&\!\frac{\gamma}{1-\gamma}\left[\frac{\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2}}{4(1-\gamma)^{2}C_{h}}+\frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)C_{s}}\right]\\ &&\!\times \left( -\frac{f}{2(1-\gamma)}\right)\frac{\gamma}{1-\gamma}n_{s}^{\prime}(p_{s}Q_{s}) + \frac{\gamma(n_{i}+n_{s})}{1-\gamma}(p_{s}Q_{s})^{\prime}\\ \!&=&\!-\frac{\gamma(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)+2f)}{8(1-\gamma)^{3}C_{s}}\\ &&- \frac{\gamma(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})f}{8(1-\gamma)^{4}C_{h}} \end{array} $$

  and

  $$ \begin{array}{@{}rcl@{}} n_{s}^{\prime}(fQ_{s})&=&\left( -\frac{\bar{\alpha}(1-\gamma)-f}{2(1-\gamma)C_{s}}\right)\left( \frac{\bar{\alpha}(1-\gamma)-f)f}{2(1-\gamma)}\right)\\ &=& -\frac{(\bar{\alpha}(1-\gamma)-f)^{2}f}{4(1-\gamma)^{2}C_{s}}\\ n_{s}(fQ_{s})^{\prime}&=&\left( \frac{(\bar{\alpha}(1-\gamma)-f)^{2}}{4(1-\gamma)C_{s}}\right)\left( \frac{\bar{\alpha}(1-\gamma)-2f}{2(1-\gamma)}\right)\\ &=& \frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)-2f)}{8(1-\gamma)^{2}C_{s}}\\ n_{s}^{\prime}(fQ_{s})+n_{s}(fQ_{s})^{\prime}&=&\frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)-4f)}{8(1-\gamma)^{2}C_{s}} \end{array} $$

  Thus,

  $$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial f} &=&-\frac{\gamma(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)+2f)}{8(1-\gamma)^{3}C_{s}} - \frac{\gamma(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})f}{8(1-\gamma)^{4}C_{h}}\\ &&+ \frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)-4f)}{8(1-\gamma)^{2}C_{s}}\\ &=&\frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f)}{8(1-\gamma)^{3}C_{s}}\\ &&- \frac{\gamma(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})f}{8(1-\gamma)^{4}C_{h}} \end{array} $$

  We note that since $f\in [-\bar {\alpha }(1-\gamma ),0]$ (otherwise, we have Q_s < Q_h or $Q_{s}>\bar {\alpha }$), we have $\bar {\alpha }^{2}(1-\gamma )^{2}-\gamma f^{2}>0$. Thus, the second component is positive

  $$ -\frac{\gamma(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})f}{8(1-\gamma)^{4}C_{h}} >0 $$

  and zero only when f = 0. Thus the first component needs to be negative, or zero (when f = 0). First, the first component under f = 0 becomes zero only when $\gamma =\frac {1}{2}$. Thus, this is one solution, and consistent with the previous case where Q_h ≥ Q_s. For $\gamma >\frac {1}{2}$ and f < 0, the first component is negative if

  $$ \bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f<0\Leftrightarrow f>\frac{\bar{\alpha}(1-\gamma)(1-2\gamma)}{2(2-\gamma)}. $$

  So when $\gamma >\frac {1}{2}$, $f\in (\frac {\bar {\alpha }(1-\gamma )(1-2\gamma )}{2(2-\gamma )},0)$. Now rewrite the FOC as

  $$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial f} \!&=&\!\frac{(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})}{8(1-\gamma)^{3}C_{s}}\\ &&\!\times \left( \frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f)}{(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})}-\frac{\gamma C_{s}f}{(1-\gamma)C_{h}}\right) \end{array} $$

  Let

  $$ \begin{array}{@{}rcl@{}} A(f) &\equiv& \frac{(\bar{\alpha}(1-\gamma)-f)^{2}(\bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f)}{(\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})}\\ B(f) &\equiv& \frac{\gamma C_{s}f}{(1-\gamma)C_{h}} \end{array} $$

  and consider their values on $f\in (\frac {\bar {\alpha }(1-\gamma )(1-2\gamma )}{2(2-\gamma )},0)$. First, B(f) increases monotonically in f and

  $$ B(f=\frac{\bar{\alpha}(1-\gamma)(1-2\gamma)}{2(2-\gamma)})<0\text{and} B(f=0)=0 $$

  Also, we can show

  $$ A(f=\frac{\bar{\alpha}(1-\gamma)(1-2\gamma)}{2(2-\gamma)}) = 0\text{and} A(f=0)<0 $$

  Thus, if A(f) decreases monotonically in f, we have a unique f that satisfies the FOC. Now let

  $$ \begin{array}{@{}rcl@{}} C(f)&=&\bar{\alpha}(1-\gamma)-f,\quad D(f)=\bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f, \\ E(f) &=&\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2} \end{array} $$

  and note that for $f\in (\frac {\bar {\alpha }(1-\gamma )(1-2\gamma )}{2(2-\gamma )},0)$, C(f) > 0, D(f) < 0, E(f) > 0, and

  $$ C(f)'=-1,\ D(f)'=-2(2-\gamma),\ E(f)'=-2\gamma f $$

  Then $A(f)=\frac {C(f)^{2}D(f)}{E(f)}$ and

  $$ \begin{array}{@{}rcl@{}} \frac{\partial A(f)}{\partial f} &=& \frac{[2C(f)C(f)'D(f)+C(f)^{2}D(f)']E(f)-C(f)^{2}D(f)E(f)'}{E(f)^{2}}\\ &=&\frac{[-2D(f)-2(2-\gamma)C(f)]C(f)E(f)+2\gamma fC(f)^{2}D(f)}{E(f)^{2}}\\ &=&-\frac{2C(f)}{E(f)^{2}}\left( \left[D(f)+(2-\gamma)C(f)\right]E(f)-\gamma fC(f)D(f)\right) \end{array} $$

  Since $\frac {C(f)}{E(f)^{2}}>0$, the sign of $\frac {\partial A(f)}{\partial f}$ depends on $\left [D(f)+(2-\gamma )C(f)\right ]E(f)-\gamma fC(f)D(f)$. Let this be F and note that

  $$ \begin{array}{@{}rcl@{}} F \!&=&\! \left[(\bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f)+(2-\gamma)(\bar{\alpha}(1-\gamma)-f)\right] \\ &&\times (\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})-\gamma f (\bar{\alpha}(1-\gamma)-f)(\bar{\alpha}(1-\gamma)(1-2\gamma)-2(2-\gamma)f)\\ \!&=&\! 3\left[\bar{\alpha}(1-\gamma)^{2}-(2-\gamma)f\right] (\bar{\alpha}^{2}(1-\gamma)^{2}-\gamma f^{2})\\ &&-\gamma f\left[\bar{\alpha}^{2}(1-\gamma)^{2}(1-2\gamma)-2\bar{\alpha}(1-\gamma)(2-\gamma)f\right.\\&&\left.-\bar{\alpha}(1-\gamma)(1-2\gamma)f+2(2-\gamma)f\vphantom{\bar{\alpha}^{2}}\right]\\ \!&=&\! 3\bar{\alpha}^{3}(1-\gamma)^{4}-3\bar{\alpha}(1-\gamma)^{2}\gamma f^{2}-3(2-\gamma)f\bar{\alpha}^{2}(1-\gamma)^{2}+3(2-\gamma)\gamma f^{3}\\ &&-\bar{\alpha}^{2}(1\!-\gamma)^{2}(1\!-2\gamma)\gamma f+\bar{\alpha}(1\!-\gamma)\gamma f^{2} (4\!-2\gamma+1\!-2\gamma)- 2(2\!-\gamma)\gamma f^{3}\\ \!&=&\! 3\bar{\alpha}^{3}(1-\gamma)^{4} - f\bar{\alpha}^{2}(1-\gamma)^{2}[6-3\gamma+\gamma-2\gamma^{2}] + f^{2}\bar{\alpha}(1-\gamma)\\ &&\times \gamma[5-4\gamma-3+3\gamma] - (2-\gamma)\gamma f^{3}\\ \!&=&\!\underbrace{3\bar{\alpha}^{3}(1-\gamma)^{4}}_{+} - \underbrace{2f\bar{\alpha}^{2}(1-\gamma)^{2}[3-\gamma-\gamma^{2}]}_{-} + \underbrace{f^{2}\bar{\alpha}(1-\gamma)(2-\gamma)\gamma}_{+}\\ &&- \underbrace{(2-\gamma)\gamma f^{3}}_{-}\\ &>&0 \end{array} $$

  Thus $\frac {\partial A(f)}{\partial f}<0$ and the solution of f is unique and lies on $(\frac {\bar {\alpha }(1-\gamma )(1-2\gamma )}{2(2-\gamma )},0)$. We can also show that for a given δ, an increase in $\frac {C_{s}}{C_{h}}$ increases the optimal f (i.e., less negative). This is due to the fact that as it costs less to develop in-house software (relative to outsourced software), the hardware firm increases in-house production (relative to outsourced production) so it can lower the “subsidy” to the software firm.

  Since the optimal strategy is unique, we use numerical analyses to examine: (1) $\frac {\partial f}{\partial \gamma }$, (2) $\frac {\partial n_{i}}{\partial \gamma }$, $\frac {\partial n_{s}}{\partial \gamma }$, and (3) $\frac {\partial \pi _{h}}{\partial \gamma }$ and $\frac {\partial \pi _{s}}{\partial \gamma }$. As before, for extensive sets of $(\bar {\alpha },C_{h},C_{s})$, we observe the following:

  • There exists $\gamma _{1}\in \left (\frac {1}{2},1\right )$ such that $\frac {\partial f}{\partial \gamma }<0$ for $\gamma \in \left (\frac {1}{2},\gamma _{1}\right )$ and $\frac {\partial f}{\partial \gamma }>0$ for γ ∈ (γ₁, 1).

  • $\frac {\partial n_{i}}{\partial \gamma }<0$ and $\frac {\partial n_{s}}{\partial \gamma }<0$ for all $\gamma >\frac {1}{2}$. Also, the proportion of outsourced software $\left (\frac {n_{s}}{n_{i}+n_{s}}\right )$ is decreasing in γ.

  • $\frac {\partial \pi _{h}}{\partial \gamma }<0$ and $\frac {\partial \pi _{s}}{\partial \gamma }<0$ for all $\gamma >\frac {1}{2}$.

1.8 A.8 Proof of Proposition 6

Let f ∈ [0, 1] be the proportion of the outsourced software revenue taken by the hardware firm. Then the software firm’s profit is

$$ \pi_{s} = n_{s}(1-f)p_{s}\left( \bar{\alpha}-\frac{p_{s}}{1-\gamma}\right)-\frac{C_{s}}{2}{n_{s}^{2}}. $$

The first-order conditions with respect to p_s and n_s give:

$$ p_{s}=\frac{\bar{\alpha}(1-\gamma)}{2}, n_{s}(f)=\frac{\bar{\alpha}^{2}(1-\gamma)(1-f)}{4C_{s}}. $$

The hardware firm’s profit is then

$$ \pi_{h} = p_{h}\left( \bar{\alpha}-\frac{p_{h}}{(n_{i}+n_{s}(f))\gamma}\right) + n_{s}(f)fp_{s}Q_{s} + n_{i} p_{i}Q_{i} -\frac{C_{h}}{2}{n_{i}^{2}} $$

The first-order conditions with respect to p_h, p_i, n_i give

$$ p_{h}=\frac{\bar{\alpha}(n_{i}+n_{s}(f))\gamma}{2}, p_{i}=\frac{\bar{\alpha}(1-\gamma)}{2}, n_{i}=\frac{\bar{\alpha}^{2}}{4C_{h}} $$

The first-order condition with respect to f is

$$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial f} &=& \frac{\bar{\alpha}^{2}\gamma}{4}n_{s}^{\prime}(f) + n_{s}^{\prime}(f)f\frac{\bar{\alpha}^{2}(1-\gamma)}{4} + n_{s}(f) \frac{\bar{\alpha}^{2}(1-\gamma)}{4} = 0\\ &\Leftrightarrow& \left[\frac{\bar{\alpha}^{2}}{4}\left( \gamma+f(1-\gamma)\right)\right]n_{s}^{\prime}(f) + n_{s}(f)\frac{\bar{\alpha}^{2}(1-\gamma)}{4} = 0\\ &\Leftrightarrow& f = \frac{1-2\gamma}{2(1-\gamma)} \end{array} $$

Since we require f ∈ [0, 1], the above result is supported when $\gamma \le \frac {1}{2}$. Given f, we have

$$ n_{s} = \frac{\bar{\alpha}^{2}}{8C_{s}}. $$

When $\gamma >\frac {1}{2}$ (i.e., f = 0 is binding), the optimal quantity of outsourced software is $n_{s}=\frac {\bar {\alpha }^{2}(1-\gamma )}{4C_{s}}$. Other strategies will remain the same as above.

Now we consider a case in which the total software variety is fixed at one and the hardware firm chooses the proportion of in-house software. The software firm’s profit in this case is

$$ \pi_{s} = (1-\delta)(1-f)p_{s}\left( \bar{\alpha}-\frac{p_{s}}{1-\gamma}\right)-\frac{C_{s}}{2}(1-\delta)^{2} $$

The first-order condition with respect to p_s gives

$$ p_{s}=\frac{\bar{\alpha}(1-\gamma)}{2}, Q_{s}=\frac{\bar{\alpha}}{2}, \pi_{s} = (1-\delta)\left( (1-f)\frac{\bar{\alpha}^{2}(1-\gamma)}{4}-\frac{C_{s}}{2}(1-\delta)\right) $$

The hardware firm’s profit is

$$ \pi_{h} = p_{h}\left( \bar{\alpha}-\frac{p_{h}}{\gamma}\right) + (1-\delta)fp_{s}Q_{s} + \delta p_{i}Q_{i} - \frac{C_{h}}{2}\delta^{2} $$

We first note that $\frac {\partial \pi _{h}}{\partial f}=(1-\delta )p_{s}Q_{s}>0$ when δ < 1. Thus, we only have a corner solution where the hardware firm will choose f based on the condition that π_s = 0, which gives

$$ f = 1-\frac{2(1-\delta)C_{s}}{\bar{\alpha}^{2}(1-\gamma)}. $$

Thus, we can re-write the hardware firm’s profit as

$$ \pi_{h} = p_{h}\left( \bar{\alpha}-\frac{p_{h}}{\gamma}\right) + (1-\delta)\left( 1-\frac{2(1-\delta)C_{s}}{\bar{\alpha}^{2}(1-\gamma)}\right)p_{s}Q_{s} + \delta p_{i}Q_{i} - \frac{C_{h}}{2}\delta^{2} $$

The first-order conditions with respect to p_h and p_i give

$$ p_{h}=\frac{\bar{\alpha}\gamma}{2},p_{i}=\frac{\bar{\alpha}(1-\gamma)}{2} $$

The first-order condition with respect to δ is

$$ \begin{array}{@{}rcl@{}} \frac{\partial \pi_{h}}{\partial \delta} &=& -\left( 1-\frac{2(1-\delta)C_{s}}{\bar{\alpha}^{2}(1-\gamma)}\right)\frac{\bar{\alpha}^{2}(1-\gamma)}{4}+(1-\delta)\left( \frac{2C_{s}}{\bar{\alpha}^{2}(1-\gamma)}\right)\frac{\bar{\alpha}^{2}(1-\gamma)}{4}\\ &&+ \frac{\bar{\alpha}^{2}(1-\gamma)}{4} - C_{h}\delta = 0\\ &\Leftrightarrow& (1-\delta)C_{s} - C_{h}\delta = 0\\ &\Leftrightarrow& \delta = \frac{C_{s}}{C_{h}+C_{s}} \end{array} $$

Thus we have

$$ f = \frac{\bar{\alpha}^{2}(1-\gamma)(C_{h}+C_{s})-2C_{h}C_{s}}{\bar{\alpha}^{2}(1-\gamma)(C_{h}+C_{s})} $$

Since we require f ≥ 0, the above is valid when

$$ \gamma \le 1-\frac{2C_{h}C_{s}}{(C_{h}+C_{s})\bar{\alpha}^{2}}. $$

Note that under the optimal δ and f, the hardware firm’s profits are given by

$$ \pi_{h} = \frac{\bar{\alpha}^{2}}{4} - \frac{C_{h}C_{s}}{2(C_{h}+C_{s})}, $$

which is greater than the profits under Full Integration $\frac {\bar {\alpha }^{2}}{4}-\frac {C_{h}}{2}$ for all C_h, C_s > 0.

When $\gamma \ge 1-\frac {2C_{h}C_{s}}{(C_{h}+C_{s})\bar {\alpha }^{2}}$, we have f = 0 and π_s = 0. These constraints give $\delta = 1-\frac {\bar {\alpha }^{2}(1-\gamma )}{2C_{s}}$. We also note than under the optimal δ and f, the hardware firm’s profits are given by

$$ \pi_{h} = \frac{\bar{\alpha}^{2}}{4} - \frac{C_{h}}{2} + \frac{\bar{\alpha}^{4}(1-\gamma)(C_{h}+C_{s})}{8{C_{s}^{2}}}\left( \frac{4C_{h}C_{s}}{(C_{h}+C_{s})\bar{\alpha}^{2}} - (1-\gamma)\right). $$

This is higher than the profits under Full Integration if $\gamma \ge 1- \frac {4C_{h}C_{s}}{(C_{h}+C_{s})\bar {\alpha }^{2}}$. This condition is satisfied because $1-\frac {2C_{h}C_{s}}{(C_{h}+C_{s})\bar {\alpha }^{2}}>1- \frac {4C_{h}C_{s}}{(C_{h}+C_{s})\bar {\alpha }^{2}}$.

In summary, the results under the proportional licensing fee are weakly consistent with those under the per-unit licensing fee.