Modelling of Transportation Process in Plane Flows with Stagnation Points

Abstract

We study transport of passive tracers by plane laminar flows with stagnation points. This setup serves as a simple model of transport in porous media. Close to stagnation points, the flow velocity is much lower than on the average. Many experimental data disclose that transport through porous media is slower than predictions of the standard advection-diffusion model. Commonly, in descriptions of flows through porous media the heterogeneity of flow is disregarded, and some average velocity is adopted. To model regular arrays of flow patterns with stagnation points, we employ the construction of special flow: a combination of mapping and a sort of ceiling function with singularity. We show that, depending on the type of stagnation points, many experimentally established effects can be reproduced. This includes the linear sorption, usually described by the standard MIM model, as well as subdiffusion, described by the fractional MIM model. We also show that slow molecular diffusion does not eliminate the effects of the transport slowdown.

Appendices

Appendices

Appendix A: Conditions for Existence of Stagnation Points in the Flow

Here we derive for the flow in the form (6) the critical value (8) of external force f, at which stagnation points come into existence. The condition of stagnation $\mathbf {v}=0$ in terms of shifted coordinates $\overline{x}_s$ and $\overline{y}_s$ reads

$$\begin{aligned} \begin{aligned} \alpha -\frac{f}{k\sqrt{\beta ^2+k^2\nu ^2}}\cos {k\overline{y}_s}=0,\\ \beta -\frac{f}{k\sqrt{\alpha ^2+k^2\nu ^2}}\cos {k\overline{x}_s}=0. \end{aligned} \end{aligned}$$

(26)

Combining the solution of these equations

$$\begin{aligned} \cos {k \overline{y}_s}= & {} \frac{\alpha k \sqrt{\beta ^2+k^2\nu ^2}}{f}\nonumber \\ \cos {k \overline{x}_s}= & {} \frac{\beta k \sqrt{\alpha ^2+k^2\nu ^2}}{f} \end{aligned}$$

(27)

with obvious inequality $|\cos \varphi |\le 1\;\forall \varphi$, we arrive at

$$\begin{aligned} |f|\ge k \max \left( \alpha \sqrt{\beta ^2+k^2\nu ^2},\beta \sqrt{\alpha ^2+k^2\nu ^2}\right) = k \sqrt{\alpha ^2\beta ^2+k^2\nu ^2\max (\alpha ^2,\beta ^2)}\,. \end{aligned}$$

(28)

Appendix B: Flow Evolution Near Stagnation Point at $f>f_\mathrm{cr}$

In the parameter range $f>f_\mathrm{cr}$, stagnation points in the flow pattern are structurally stable.

Evolution of infinitesimal deviations $\delta _x=x-\overline{x}_s$ and $\delta _y=y-\overline{y}_s$ from the hyperbolic stagnation point is governed by the linearization of Eq. (7) near this point:

$$\begin{aligned} \frac{\text {d} \delta _x}{\text {d} t} =G\delta _y,\quad \frac{\text {d} \delta _y}{\text {d} t} =H\delta _x, \end{aligned}$$

(29)

with $G=\displaystyle \sqrt{\frac{f^2-k^2\alpha ^2(\beta ^2+k^2\nu ^2)}{\beta ^2+k^2\nu ^2}}$ and $H=\displaystyle \sqrt{\frac{f^2-k^2\beta ^2(\alpha ^2+k^2\nu ^2)}{\alpha ^2+k^2\nu ^2}}$. For $f>f_\mathrm{cr}$, both G and H are positive.

On the phase plane, solutions of Eq. (29) build a family of hyperbolas $G\delta _y^2-H\delta _x^2=\text{ const }$. The case of $\text{ const }=0$ delivers separatrices of the stagnation point: two straight lines $\delta _y=\pm \sqrt{H/G}\,\delta _x$; the sign $+\ (-)$ corresponds to the unstable (stable) separatrix. Tracers approach the stagnation point along the stable separatrix and depart from it along the unstable one. Choose a streamline with positive $\hbox {const}=C$ that, as a whole, lies in the half-plane $\delta _y>0$ (other cases are treated similarly). The motion along it is governed by

$$\begin{aligned} \frac{\text {d} \delta _x}{\text {d} t}=\sqrt{G\,(H\delta _x^2+C)}. \end{aligned}$$

(30)

Take on this streamline a segment containing $\delta _x=0$, with endpoints $x_\mathrm{L}<0$ and $x_\mathrm{R}>0$. At the left end of this segment, the coordinate y of the streamline is $y_0=\sqrt{(H\,x_\mathrm{L}^2+C)/G}$, whereas for the stable separatrix this coordinate is $y_\mathrm{s}=\sqrt{H/G}\,|x_\mathrm{L}|$. At $x_\mathrm{L}$, the deviation of the streamline from the stable separatrix is

$$y_0-y_\mathrm{s}=\sqrt{\frac{H\,x_\mathrm{L}^2+C}{G}}+ \sqrt{\frac{H}{G}}\,x_\mathrm{L}$$

Passage time along this segment of the streamline is

$$\begin{aligned} t=\frac{1}{\sqrt{G}}\int _{x_\mathrm{L}}^{x_\mathrm{R}} \frac{\text {d}x}{Hx^2+C}\,=\,\frac{1}{\sqrt{GH}}\ln \left| \frac{Hx_\mathrm{R}+\sqrt{H(C+H x_\mathrm{R}^2})}{Hx_\mathrm{L}+\sqrt{H(C+H x_\mathrm{L}^2})}\right| . \end{aligned}$$

(31)

For small values of C (and keeping in mind $x_L<0$) we obtain

$$y_0-y_\mathrm{s}\approx \frac{C}{2|x_\mathrm{L}|\sqrt{G\,H}},$$

and

$$\begin{aligned} t\approx \frac{1}{\sqrt{GH}}\ln \frac{4 x_\mathrm{R}|x_\mathrm{L}|H}{C}=\frac{1}{\sqrt{GH}}\ln \left( 2 x_\mathrm{R}\sqrt{\frac{H}{G}}\cdot \frac{1}{y_0-y_\mathrm{s}}\right) \, . \end{aligned}$$

(32)

Thereby, for small deviations from the separatrix at the entrance to the cell, the time of passage through this cell is asymptotically proportional to the logarithm of the deviation.

Appendix C: Dynamics Near the Stagnation Point at $f=f_\mathrm{cr}$

Analysis from the preceding section is not valid for structurally unstable newborn stagnation points. Indeed, for $\alpha >\beta$, the coefficient G can be rewritten as $G= \sqrt{(f^2-f_\mathrm{cr}^2)/(\beta ^2+k^2\nu ^2)}$; it vanishes at $f=f_\mathrm{cr}$. [In the complementary case $\beta >\alpha$, the coefficient H vanishes.] This makes linearization insufficient: higher order terms should be taken into account. Below, we consider the case $\alpha >\beta$ and restrict ourselves to the basic periodic cell ($m=n=0$). Here, at $f=f_\mathrm{cr}$, Eqs. (7) become

$$\begin{aligned} \frac{\text {d} \overline{x}}{\text {d} t}= & {} \alpha \,(1-\cos k\overline{y}),\nonumber \\ \frac{\text {d} \overline{y}}{\text {d} t}= & {} \beta -\frac{f_\mathrm{cr}}{k\sqrt{\alpha ^2+k^2\nu ^2}} \cos k\overline{x} \end{aligned}$$

(33)

with $\overline{y}_s=0$. Accordingly, equations for the evolution of small disturbances $\delta _x,\,\delta _y$ turn from (29) into

$$\begin{aligned} \frac{\text {d} \delta _x}{\text {d} t} =\frac{\alpha }{2}\delta _y^2,\quad \frac{\text {d} \delta _y}{\text {d} t} =H\delta _x. \end{aligned}$$

(34)

Equation for streamlines in this case is

$$\begin{aligned} \displaystyle \frac{\alpha \delta _y^3}{3}-H\delta _x^2 =\text{ const }, \end{aligned}$$

(35)

and the zero value of const renders the separatrix of the fixed point at the origin: two branches of the semicubical parabola:

$$\begin{aligned} \delta _y= \left( \frac{3H}{\alpha }\right) ^{1/3} \delta _x^{2/3} \end{aligned}$$

(36)

(recall the cuspoidal shape of red curves in the left panel of Fig. 2).

We choose a segment of the streamline with positive $\text {const}=C$ between $x_\mathrm{L}<0$ and $x_\mathrm{R}>0$. At the entrance $x_\mathrm{L}$, the streamline has the coordinate $y_0=\left( \frac{3Hx_\mathrm{L}^2+3C}{\alpha }\right) ^{1/3}$ whereas the coordinate y of the separatrix is $y_s=\left( \frac{3Hx_\mathrm{L}^2}{\alpha }\right) ^{1/3}$. At small values of C the initial deviation $y_0-y_s$ is proportional to C.

The time of passage along this segment of the streamline is

$$t=2\alpha ^{-1/3}\int _{x_\mathrm{L}}^{x_\mathrm{R}} \frac{\text {d}x}{(3Hx^2+3C)^{2/3}}.$$

For small values of C the integral is dominated by the segment adjacent to $x=0$, and its value is well approximated by $\int _{-\infty }^{+\infty }(3Hx^2+C)^{-2/3}\text {d}x=R C^{-1/6}H^{-1/2}$ with the constant $R=3^{-2/3}\sqrt{\pi }\,\varGamma (1/6)/\varGamma (2/3)$. Since C is proportional to the initial deviation, we conclude that the passage time asymptotically scales as $|y_0-y_s|^{-1/6}$.

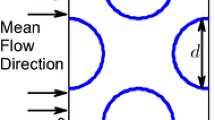
Appendix D: Calculation of Porous Media Properties

The main transport properties of porous media are porosity and permeability. Porosity $\varphi$ is the geometrical characteristics of the medium, and the effect of its variation upon transport is usually indirect: variation of porosity invokes variation of permeability which affects the transport process. Porosity is defined as the ratio of the volume (area in the case of two-dimensional flows), accessible for the motion of the tracers, to the entire volume (area) of the cavity. For the square array of solid circular obstacles (cf. Fig. 5) with radius R and distance H between the centers, porosity is $\varphi =1-\pi R^2/H^2$. For the forced flow from Sect. 2.1, porosity depends on the amplitude f of the driving force. The eddies behave like liquid obstacles: in absence of molecular diffusion their borders are impenetrable for the flow, and their core stays inaccessible to the drifting tracers. For $f<f_{\text{ cr }}$, when the eddies are absent, the whole area is available for the global motion, and $\varphi =1$. When the force f is raised, the size of the eddies grows, the accessible area lowers, and, hence, the porosity monotonically decreases; this effect is pictured in the left panel of Fig. 11.

Fig. 11

Transport characteristics for the flow governed by Eq. (5) as functions of the amplitude f of the driving force. Parameter values: $\nu =1,\,\alpha =1,\,\beta =(\sqrt{5}-1)/2$. Left panel: Porosity. Middle panel: Components of mean velocity. Right panel: Permeability, estimated by Eq. (38). Break points of curves at $f\approx 123.5$ correspond to the secondary heteroclinic bifurcation in the flow pattern

Permeability is the dynamic property of porous media which directly affects the transport processes. Traditionally, it is introduced in the context of fluid motions, driven by the inhomogeneities of pressure. The celebrated Darcy’s law (see Darcy 1856; Muskat 1946) postulates that the mean velocity of the motion through the medium is proportional to the mean pressure gradient. Within this law, compressibility is the coefficient of proportionality, divided by the dynamical viscosity of the fluid.

For the flows, discussed in the preceding sections, this definition should be modified: there, velocity owes not to the pressure gradient, but to the imposed mean drift condition. For example, for the forced flow of Eq. (5), the pressure, reconstructed from the Navier–Stokes equations (1), has the form:

$$\begin{aligned} p(\overline{x},\overline{y})=\frac{\rho _d f^2}{k^2}\frac{\sin (k\overline{x})\sin (k\overline{y})}{\sqrt{\alpha ^2+k^2\nu ^2}\sqrt{\beta ^2+k^2\nu ^2}}. \end{aligned}$$

(37)

Since $p(\overline{x},\overline{y})$ is periodic in both arguments, the pressure difference between the points, arbitrarily distant from each other, remains bounded, and the mean pressure gradient is zero. Without forcing, at $f=0$, the pressure vanishes identically, whereas the velocity, ensured by the imposed mean drift, is $\mathbf { v_0}=(\alpha ,\beta )$. In presence of the force, as long as there are no eddies, the mean velocity does not change: $\langle \mathbf {v}\rangle =\mathbf {v_ 0}$. Beyond $f_{\text{ cr }}$, when eddies appear in the flow pattern, the inner part of the eddies does not contribute to the drift (thereby the effective porosity decreases); this leads to the growth of the mean values for both components of the velocity, as seen in the middle panel of Fig. 11. The break points on the curves at $f\approx 123.5$ indicate a further transition in the flow pattern: formation of heteroclinic streamlines that connect the hyperbolic stagnation points.

To accommodate the Darcy-like reasoning within this setup, we introduce the permeability $\kappa$ as the coefficient of proportionality between the surplus mean velocity $\mathbf {\langle v \rangle -v_0}$ and the amplitude of the external force f:

$$\begin{aligned} |\mathbf {\langle v \rangle -v_0}|=\frac{\kappa }{\nu }\, f\;\;\Rightarrow \; \kappa =\frac{\nu \,|\mathbf {\langle v \rangle -v_0}|}{f} \end{aligned}$$

(38)

(recall that $\nu$ denotes the kinematic viscosity of the fluid, and that f is force per mass unit, so that $\kappa$, like the canonical permeability, has a dimension of squared length). The dependence $\kappa (f)$ is plotted in the right panel of Fig. 11: $\kappa$ remains zero below $f_{\text{ cr }}$, monotonically grows between $f_{\text{ cr }}$ and the heteroclinic transition, and slowly decreases beyond the latter.

Another widely used transport characteristics, the diffusion coefficient, formally vanishes for the discussed flow patterns: since transport is subdiffusive, variance in the ensemble of tracers grows as a sublinear function of time.

Appendix E: Calculation of passage time for flows with random fluctuations

Here we explain how to calculate the passage time function for the special flow, taking into account random diffusive jumps of passive tracers.

Since standard molecular diffusion is additive random process, fluctuations of position and time possess the same distributions all over the considered array of cells. Further, at weak noise, diffusion and regular advection by the flow can be treated as independent processes. Recall that the approach of special flow is based on assigning duration to iterations of the mapping; thereby the discrete time of the map turns into the continuous time variable of the flow. In the deterministic special flow, the value of the mapping variable x remains frozen within the duration of the iteration: the time interval of length T(x). When noise is switched on, the value of x fluctuates. To capture the microscopic stochastic evolution of x between the mapping iterations, we introduce the “inner” time variable $\tau$, and view the process $x(\tau )$ as a discretized random walk with small time increments of length $\delta t\ll T(x)$. During this random motion, the instantaneous coordinate $x(\tau )$ obeys the discrete recurrence

$$\begin{aligned} x(\tau +\delta t)= & {} x(\tau )+\varepsilon \, \xi (\tau ) \sqrt{2\,\delta t},\nonumber \\ \tau= & {} \tau +\delta t \end{aligned}$$

(39)

where $\varepsilon$ is the intensity of noise and $\xi (\tau )$ is a random variable with zero mean and standard normal distribution.

Then, iterations of the circle mapping are replaced by the following algorithm:

• (a) At the start of the $(n+1)$th iteration, $\tau$ is set at zero, and $x(\tau =0)$ assumes the current value of the mapping variable $x_n$.

• (b) Recurrence (39) is iterated until the step at which the value of $\tau$ exceeds the deterministic passage time $T\big (x(\tau )\big )$.

• (c) On reaching this point, we perform the next iteration of the circle mapping, taking for it not $x_n$ but the latest value of $x(\tau )$:

  $$x_{n+1}=\big (x(\tau )+\rho \big )_{\mathrm{mod}\, 1},$$

  and return to the step (a).

As a result we obtain the passage time in which the diffusive process is incorporated. Since sticking to the value of x with infinite duration of iteration is disabled, diffusion eliminates the singularity in the passage time distribution, making the latter continuous. The level of smoothness depends on the noise intensity $\varepsilon$.