Rate-optimal fair power allocation in complex field network coded relay communications

Abstract

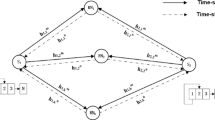
In this paper, we consider the complex field network coded relay assisted communication (CFNC-RAC) channel. Although CFNC-RAC is spectrally efficient, its bit error rate performance is degraded by multi-access interference, which can be improved by appropriately allocating the user and relay powers. Since the fairness is an important factor for a practical multi-user communication system, we have proposed a rate-optimal fair power adaptation (ROFPA) technique in this work. The proposed ROFPA policy not only aims to maximize the average achievable sum-rate of CFNC-RAC under the use of the decode and forward relaying but also intends to satisfy the average rate-fairness restriction while taking the total power constraint and the network topology into account. We formulate the ROFPA as a non-convex optimization program and then derive an analytical solution for it. Extensive performance evaluation and numerical simulations validate that ROFPA method can provide significant sum-rate with considerable user fairness when compared to symbol-error-rate optimized (SER-OPT) policy proposed by Eritmen et al. (Wirel Netw, 2015. doi:10.1007/s11276-015-0924-1).

Appendices

Appendix 1: Proof of monotonicity of the objective in partition 1

Within this partition, the following inequalities hold

$$\begin{aligned} & \gamma_{1} + g_{r} \alpha \le g_{1} \\ & \gamma_{2} + g_{r} \alpha \le g_{2} \\ & (\gamma_{1} + g_{r} \alpha )P_{1} + (\gamma_{2} + g_{r} \alpha )P_{2} \le g_{1} P_{1} + g_{2} P_{2} \\ \end{aligned}$$

(31)

Therefore, the objective function and the fairness constraint in Eq. (19) can be re-written as:

$$\begin{aligned} w_{0} (P_{1} ,P_{2} ,\alpha ) & = \gamma_{1} P_{1} + \gamma_{2} P_{2} + g_{r} \alpha \left( {P_{1} + P_{2} } \right) \\ w_{5} (P_{1} ,P_{2} ,\alpha ) & = (\gamma_{1} + g_{r} \alpha )P_{1} - (\gamma_{2} + g_{r} \alpha )P_{2} = 0 \\ \end{aligned}$$

(32)

The users powers for this partition can be determined using the total power constraint and fairness constraint as:

$$\begin{aligned} P_{1} & = \frac{{\left( {\gamma_{2} + g_{r} \alpha } \right)P_{T} }}{{\left( {1 + \alpha } \right)\left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right)}} \\ P_{2} & = \frac{{\left( {\gamma_{1} + g_{r} \alpha } \right)P_{T} }}{{\left( {1 + \alpha } \right)\left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right)}} \\ \end{aligned}$$

(33)

The derivative of the objective function with respect to α becomes:

$$\begin{aligned} \frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } & = \left( {\gamma_{1} - \gamma_{2} } \right)\frac{{g_{r} P_{T} \left( {1 + \alpha } \right)\left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right) - \left( {\gamma_{2} + g_{r} \alpha } \right)P_{T} \left( {\left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right) + \left( {1 + \alpha } \right)2g_{r} } \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right)^{2} }} \\ & \quad + \frac{{\left( {g_{r} - \gamma_{2} } \right)P_{T} \left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right)^{2} }}{{\left( {1 + \alpha } \right)^{2} \left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right)^{2} }} \\ \end{aligned}$$

(34)

After some manipulations, the derivative in Eq. (34) can be put into the following form

$$\begin{aligned} & \frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = \frac{{P_{T} \left( {A\alpha^{2} + B\alpha + C} \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {\gamma_{1} + 2g_{r} \alpha + \gamma_{2} } \right)^{2} }} \\ & {\text{where}} \\ & A = 2g_{r}^{2} \left( {2g_{r} - \gamma_{1} - \gamma_{2} } \right) \\ & B = 4g_{r} \left( {g_{r} (\gamma_{1} + \gamma_{2} ) - 2\gamma_{1} \gamma_{2} } \right) \\ & C = g_{r} (\gamma_{1} - \gamma_{2} )^{2} + (\gamma_{1} + \gamma_{2} )\left( {g_{r} (\gamma_{1} + \gamma_{2} ) - 2\gamma_{1} \gamma_{2} } \right) \\ \end{aligned}$$

(35)

Since γ ₁ < g _r and γ ₂ < g _r hold, A in Eq. (35) is clearly positive. To prove the positivity of B and C, we need to use the result of the following claim.

Claim

For γ ₁ < g _r and γ ₂ < g _r , (g _r (γ ₁ + γ ₂) − 2γ ₁ γ ₂) is strictly greater than zero.

Proof

Assume γ ₁ ≤ γ ₂ is true. Then this implies 2γ ₁ ≤ γ ₁ + γ ₂, and since γ ₂ < g _r , g _r (γ ₁ + γ ₂) > 2γ ₁ γ ₂ holds. By proceeding similarly for the case of γ ₂ ≤ γ ₁, we end up with the same result.

Therefore, the coefficients B and C in Eq. (35) are also strictly positive, and w ₀(P ₁, P ₂, α) is an increasing function of α.

Appendix 2: Proof of monotonicity of the objective in partition 2

For this interval, the objective function is w ₀(P ₁, P ₂, α) = γ ₁ P ₁ + γ ₂ P ₂ + g _r α(P ₁ + P ₂) since the value of α is less than α ₀, at which sum-rate bounds at the relay and destination become the same under fairness constraint. The value of α ₀ is determined as follows.

Assume g ₁ − γ ₁ ≤ g ₂ − γ ₂. Then the following inequalities are valid:

$$\begin{aligned} g_{1} \le \gamma_{1} + g_{r} \alpha \hfill \\ \gamma_{2} + g_{r} \alpha \le g_{2} \hfill \\ \end{aligned}$$

(36)

Therefore, the fairness constraint becomes

$$w_{5} (P_{1} ,P_{2} ,\alpha ) = g_{1} P_{1} - \left( {\gamma_{2} + g_{r} \alpha } \right)P_{2} = 0$$

(37)

Hence, the following expression is valid at α = α ₀.

$$\gamma_{1} P_{1} + \gamma_{2} P_{2} + g_{r} \alpha_{0} \left( {P_{1} + P_{2} } \right) - \left( {g_{1} P_{1} + g_{2} P_{2} } \right) = 0$$

(38)

By combining Eq. (37) with Eq. (38), α ₀ should satisfy

$$g_{r}^{2} \alpha_{0}^{2} + \left( {\gamma_{1} g_{r} + \gamma_{2} g_{r} } \right)\alpha_{0} - g_{1} g_{2} + \gamma_{1} \gamma_{2} = 0$$

(39)

The positive root of this equation can be found as:

$$\alpha_{0} = \frac{{ - \left( {\gamma_{1} + \gamma_{2} } \right) + \sqrt {\left( {\gamma_{1} + \gamma_{2} } \right)^{2} - 4\left( {\gamma_{1} \gamma_{2} - g_{1} g_{2} } \right)} }}{{2g_{r} }}$$

(40)

For g ₂ − γ ₂ ≤ g ₁ − γ ₁, we end up with the same quadratic relation as in Eq. (39), and therefore, the same root in Eq. (40) is obtained.

After finding the value of α ₀, we are now ready to show the monotonicity of the objective function over this interval.

For g ₁ − γ ₁ ≤ g ₂ − γ ₂, the user powers can be derived as:

$$\begin{aligned} P_{1} & = \frac{{\left( {\gamma_{2} + g_{r} \alpha } \right)P_{T} }}{{\left( {1 + \alpha } \right)\left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)}} \\ P_{2} & = \frac{{g_{1} P_{T} }}{{\left( {1 + \alpha } \right)\left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)}} \\ \end{aligned}$$

(41)

By using Eq. (41), the derivative of the objective function can be determined as:

$$\frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = \left( {\gamma_{1} - \gamma_{2} } \right)\frac{{g_{r} P_{T} \left( {1 + \alpha } \right)\left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right) - \left( {\gamma_{2} + g_{r} \alpha } \right)P_{T} \left( {\left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right) + \left( {1 + \alpha } \right)g_{r} } \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)^{2} }} + \frac{{\left( {g_{r} - \gamma_{2} } \right)P_{T} }}{{\left( {1 + \alpha } \right)^{2} }}$$

(42)

After some manipulations, Eq. (42) can be put into the following form:

$$\begin{aligned} & \frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = \frac{{P_{T} \left( {A\alpha^{2} + B\alpha + C} \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)^{2} }} \\ & {\text{where}} \\ & A = g_{r}^{2} \left( {g_{r} - \gamma_{1} } \right) \\ & B = 2g_{r} \left( {\gamma_{2} (g_{r} - \gamma_{1} ) + g_{1} (g_{r} - \gamma_{2} )} \right) \\ & C = \left( {\gamma_{1} - \gamma_{2} } \right)\left( {g_{r} g_{1} - g_{1} \gamma_{2} - \gamma_{2}^{2} } \right) + \left( {g_{r} - \gamma_{2} } \right)\left( {g_{1} + \gamma_{2} } \right)^{2} \\ \end{aligned}$$

(43)

It is clear that A, B > 0 because of γ ₁ < g _r and γ ₂ < g _r . The positivity of the coefficient C is not obvious at first glance. After some manipulations, C can be obtained as:

$$\begin{aligned} C & = \left( {\gamma_{1} - \gamma_{2} } \right)\left( {g_{r} g_{1} - g_{1} \gamma_{2} - \gamma_{2}^{2} } \right) + \left( {g_{r} - \gamma_{2} } \right)\left( {g_{1} + \gamma_{2} } \right)^{2} \\ & = (g_{r} - \gamma_{2} )\left( {g_{1} \left( {\gamma_{1} - \gamma_{2} } \right) + \left( {g_{1} + \gamma_{2} } \right)^{2} } \right) - \gamma_{2}^{2} \left( {\gamma_{1} - \gamma_{2} } \right) \\ & = (g_{r} - \gamma_{2} )(g_{1} \gamma_{1} + g_{1} \gamma_{2} + g_{1}^{2} + \gamma_{2}^{2} ) - \gamma_{2}^{2} \left( {\gamma_{1} - \gamma_{2} } \right) \\ & = (g_{r} - \gamma_{2} )g_{1} (\gamma_{1} + \gamma_{2} + g_{1} ) + \gamma_{2}^{2} \left( {g_{r} - \gamma_{2} - \left( {\gamma_{1} - \gamma_{2} } \right)} \right) \\ & = (g_{r} - \gamma_{2} )g_{1} (\gamma_{1} + \gamma_{2} + g_{1} ) + \gamma_{2}^{2} (g_{r} - \gamma_{1} ) \\ \end{aligned}$$

(44)

Each term in Eq. (44) is positive, so is the coefficient C. For g ₂ − γ ₂ ≤ g ₁ − γ ₁, the fairness constraint becomes w ₅(P ₁, P ₂, α) = γ ₁ P ₁ + g _r αP ₁ − g ₂ P ₂ = 0, and we perform the same analysis as we did in the case of g ₁ − γ ₁ ≤ g ₂ − γ ₂. Then the user powers can be obtained as:

$$\begin{aligned} P_{1} & = \frac{{g_{2} P_{T} }}{{\left( {1 + \alpha } \right)\left( {\gamma_{1} + g_{r} \alpha + g_{2} } \right)}} \\ P_{2} & = \frac{{\left( {\gamma_{1} + g_{r} \alpha } \right)P_{T} }}{{\left( {1 + \alpha } \right)\left( {\gamma_{1} + g_{r} \alpha + g_{2} } \right)}} \\ \end{aligned}$$

(45)

Hence, the derivative of the objective function can be derived as:

$$\begin{aligned} & \frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = \frac{{P_{T} \left( {A\alpha^{2} + B\alpha + C} \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {\gamma_{1} + g_{r} \alpha + g_{2} } \right)^{2} }} \\ & {\text{where}} \\ & A = g_{r}^{2} \left( {g_{r} - \gamma_{2} } \right) \\ & B = 2g_{r} \left( {\gamma_{1} (g_{r} - \gamma_{2} ) + g_{2} (g_{r} - \gamma_{1} )} \right) \\ & C = \left( {\gamma_{2} - \gamma_{1} } \right)\left( {g_{r} g_{2} - g_{2} \gamma_{1} - \gamma_{1}^{2} } \right) + \left( {g_{r} - \gamma_{1} } \right)\left( {g_{2} + \gamma_{1} } \right)^{2} \\ & = (g_{r} - \gamma_{1} )g_{2} (\gamma_{1} + \gamma_{2} + g_{2} ) + \gamma_{1}^{2} (g_{r} - \gamma_{2} ) \\ \end{aligned}$$

(46)

Hence, we have shown that the objective function is an increasing function of the variable α within Partition 2.

Appendix 3: Proof of monotonicity of the objective in partition 3

In this interval, the objective function becomes w ₀(P ₁, P ₂, α) = g ₁ P ₁ + g ₂ P ₂. For g ₁ − γ ₁ ≤ g ₂ − γ ₂, the fairness constraint and user powers are the same as in Eqs. (37) and (41), respectively. Hence, the derivative of the objective function can be written as:

$$\begin{aligned} & \frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = \left( {g_{2} - g_{1} } \right)\frac{{ - g_{1} P_{T} \left( {\left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right) + \left( {1 + \alpha } \right)\left( {g_{r} \alpha } \right)} \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)^{2} }} - \frac{{g_{1} P_{T} \left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)^{2} }}{{\left( {1 + \alpha } \right)^{2} \left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)^{2} }} \\ & = \frac{{P_{T} \left( {A\alpha^{2} + B\alpha + C} \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {g_{1} + g_{r} \alpha + \gamma_{2} } \right)^{2} }} \\ & {\text{where}} \\ & A = - g_{1} g_{r}^{2} \\ & B = - 2g_{1} g_{r} \left( {g_{2} + \gamma_{2} } \right) \\ & C = - g_{1} g_{r} \left( {g_{2} - g_{1} } \right) - g_{1} \left( {\gamma_{2} + g_{2} } \right)\left( {\gamma_{2} + g_{1} } \right) \\ & = - g_{1} \left( {g_{r} - g_{2} - \gamma_{2} } \right)\left( {g_{2} - g_{1} } \right) \\ \end{aligned}$$

(47)

It is obvious that A, B < 0, and therefore, the polynomial Aα ² + Bα + C does not have any real positive root when C ≤ 0. Hence, the positive root of Aα ² + Bα + C may exist only when C > 0 (i.e. (g ₁ − g ₂)(g _r  − g ₂ − γ ₂) > 0), for which the root can be derived as:

$$\alpha_{1} = \frac{{ - \left( {g_{2} + \gamma_{2} } \right) + \sqrt {\left( {g_{1} - g_{2} } \right)\left( {g_{r} - g_{2} - \gamma_{2} } \right)} }}{{g_{r} }}$$

(48)

Since A < 0, the sign of the derivative in Eq. (47) is positive for α ≤ α ₁. Otherwise, it is negative. Hence, when there exists a real positive $\alpha_{1} \in [\alpha_{0} ,\frac{{\hbox{max} \left( {g_{1} - \gamma_{1} ,g_{2} - \gamma_{2} } \right)}}{{g_{r} }}]$, the objective function is an increasing function for α ∊ [α ₀, α ₁] and is decreasing monotonically over $[\alpha_{1} ,\frac{{\hbox{max} \left( {g_{1} - \gamma_{1} ,g_{2} - \gamma_{2} } \right)}}{{g_{r} }}]$. Therefore, when such α ₁ does not exist, the objective function decreases monotonically. The existence of a real positive α ₁, which is greater than α ₀, requires the following conditions (assuming g ₁ − γ ₁ ≤ g ₂ − γ ₂) to be met:

$$\begin{aligned} g_{2} + \gamma_{2} + \frac{1}{{g_{1} - g_{2} }}\left( {g_{2} + \gamma_{2} + \frac{{ - \left( {\gamma_{1} + \gamma_{2} } \right) + \sqrt {\left( {\gamma_{1} + \gamma_{2} } \right)^{2} - 4\left( {\gamma_{1} \gamma_{2} - g_{1} g_{2} } \right)} }}{2}} \right)^{2} \le g_{r} \le\, \frac{{4g_{2}^{2} }}{{g_{1} - g_{2} }} + g_{2} + \gamma_{2} \\ g_{2} < g_{1} \\ \end{aligned}$$

(49)

For g ₂ − γ ₂ ≤ g ₁ − γ ₁, the fairness constraint is w ₅(P ₁, P ₂, α) = γ ₁ P ₁ + g _r αP ₁ − g ₂ P ₂ = 0, where user powers are stated in Eq. (41). The derivative of the objective function can be derived as:

$$\begin{aligned} & \frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = \frac{{P_{T} \left( {A\alpha^{2} + B\alpha + C} \right)}}{{\left( {1 + \alpha } \right)^{2} \left( {\gamma_{1} + g_{r} \alpha + g_{2} } \right)^{2} }} \\ & {\text{where}} \\ & A = - g_{2} g_{r}^{2} \\ & B = - 2g_{2} g_{r} \left( {g_{1} + \gamma_{1} } \right) \\ & C = - g_{2} g_{r} \left( {g_{1} - g_{2} } \right) - g_{2} \left( {\gamma_{1} + g_{1} } \right)\left( {\gamma_{1} + g_{2} } \right) \\ &\quad = - g_{2} \left( {g_{r} - g_{1} - \gamma_{1} } \right)\left( {g_{1} - g_{2} } \right) \\ \end{aligned}$$

(50)

The real positive root of Aα ² + Bα + C exists only when (g ₂ − g ₁)(g _r  − g ₁ − γ ₁) > 0, for which the root can be expressed as:

$$\alpha_{1} = \frac{{ - \left( {g_{1} + \gamma_{1} } \right) + \sqrt {\left( {g_{2} - g_{1} } \right)\left( {g_{r} - g_{1} - \gamma_{1} } \right)} }}{{g_{r} }}$$

(51)

Again, when there exists a real positive $\alpha_{1} \in [\alpha_{0} ,\frac{{\hbox{max} \left( {g_{1} - \gamma_{1} ,g_{2} - \gamma_{2} } \right)}}{{g_{r} }}]$, the objective function is an increasing function over the interval [α ₀, α ₁] and decreases monotonically over $[\alpha_{1} ,\frac{{\hbox{max} \left( {g_{1} - \gamma_{1} ,g_{2} - \gamma_{2} } \right)}}{{g_{r} }}]$. Such α ₁, which is greater than α ₀ and less than $\frac{{\hbox{max} \left( {g_{1} - \gamma_{1} ,g_{2} - \gamma_{2} } \right)}}{{g_{r} }}$, does exist only when the following conditions are satisfied:

$$\begin{aligned} g_{1} + \gamma_{1} + \frac{1}{{g_{2} - g_{1} }}\left( {g_{1} + \gamma_{1} + \frac{{ - \left( {\gamma_{1} + \gamma_{2} } \right) + \sqrt {\left( {\gamma_{1} + \gamma_{2} } \right)^{2} - 4\left( {\gamma_{1} \gamma_{2} - g_{1} g_{2} } \right)} }}{2}} \right)^{2} \le g_{r} \le \frac{{4g_{1}^{2} }}{{g_{2} - g_{1} }} + g_{1} + \gamma_{1} \\ g_{1} < g_{2} \\ \end{aligned}$$

(52)

Appendix 4: Proof of monotonicity of the objective in partition 4

When $\alpha \ge \frac{{\hbox{max} \left( {g_{1} - \gamma_{1} ,g_{2} - \gamma_{2} } \right)}}{{g_{r} }}$ is valid, the objective function and fairness constraint can be expressed as:

$$\begin{aligned} w_{0} (P_{1} ,P_{2} ,\alpha ) = g_{1} P_{1} + g_{2} P_{2} \hfill \\ w_{5} (P_{1} ,P_{2} ,\alpha ) = g_{1} P_{1} - g_{2} P_{2} = 0 \hfill \\ \end{aligned}$$

(53)

Using these constraints, the user powers can be written as:

$$\begin{aligned} P_{1} = \frac{{P_{T} }}{{\left( {1 + \alpha } \right)}}\frac{{g_{2} }}{{g_{1} + g_{2} }} \hfill \\ P_{2} = \frac{{P_{T} }}{{\left( {1 + \alpha } \right)}}\frac{{g_{1} }}{{g_{1} + g_{2} }} \hfill \\ \end{aligned}$$

(54)

The derivative of objective function w ₀(P ₁, P ₂, α)can be given as:

$$\frac{{\partial w_{0} (P_{1} ,P_{2} ,\alpha )}}{\partial \alpha } = - 2g_{1} g_{2} \frac{{P_{T} }}{{\left( {1 + \alpha } \right)^{2} \left( {g_{2} + g_{1} } \right)}} < 0$$

(55)

Hence, the objective function in Eq. (53) decreases monotonically over Partition 4.

Appendix 5: Justification of the negligibility of the cross-term

In the previous section, we assumed that the cross-term $P_{1} P_{2} \left( {\sqrt {\gamma_{2} } - \sqrt {\gamma_{1} } } \right)^{2}$ is negligible compared to P ₁ + P ₂ and came up with analytical results for Eq. (19). In this section, we shall justify this assumption over each of these partitions.It is clear that the cross-term gets close to zero for all segments for γ ₂ ≈ γ ₁ due to its third component (i.e., $(\sqrt {\gamma_{2} } - \sqrt {\gamma_{1} } )^{2}$). We shall show below that the cross-term becomes approximately zero for γ ₁ ≪ γ ₂ or γ ₁ ≫ γ ₂ due to fact that the multiplication of user powers P ₁ P ₂ is almost zero for these values of γ ₁ and γ ₂.Over the Partition 1, the multiplication of user powers can be written as:

$$P_{1} P_{2} = \frac{{\left( {\gamma_{2} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + \gamma_{2} + 2g_{r} \alpha } \right)}}\frac{{\left( {\gamma_{1} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + \gamma_{2} + 2g_{r} \alpha } \right)}}\frac{{P_{T}^{2} }}{{\left( {1 + \alpha } \right)^{2} }}$$

(56)

The first and second term in the RHS of Eq. (56) get close to zero for γ ₁ ≫ γ ₂ andγ ₂ ≫ γ ₁, respectively.Over the Partitions 2 and 3, the multiplication of user powers can be expressed as:

$$P_{1} P_{2} = \left\{ {\begin{array}{*{20}c} {\frac{{\left( {\gamma_{2} + g_{r} \alpha } \right)}}{{\left( {g_{1} + \gamma_{2} + g_{r} \alpha } \right)}}\frac{{g_{1} }}{{\left( {g_{1} + \gamma_{2} + g_{r} \alpha } \right)}}\frac{{P_{T}^{2} }}{{\left( {1 + \alpha } \right)^{2} }}{\text{ for }}g_{1} - \gamma_{1} \le g_{2} - \gamma_{2} \, } \\ {\frac{{g_{2} }}{{\left( {\gamma_{1} + g_{r} \alpha + g_{2} } \right)}}\frac{{\left( {\gamma_{1} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + g_{r} \alpha + g_{2} } \right)}}\frac{{P_{T}^{2} }}{{\left( {1 + \alpha } \right)^{2} }}{\text{ for }}g_{2} - \gamma_{2} \le g_{1} - \gamma_{1} \, } \\ \end{array} } \right.$$

(57)

Note that the following inequality holds for these partitions:

$$\begin{array}{*{20}c} {g_{1} \le \gamma_{1} + g_{r} \alpha {\text{ for }}g_{1} - \gamma_{1} \le g_{2} - \gamma_{2} \, } \\ {g_{2} \le \gamma_{2} + g_{r} \alpha {\text{ for }}g_{2} - \gamma_{2} \le g_{1} - \gamma_{1} \, } \\ \end{array}$$

(58)

Also, the conditions of γ ₁ ≤ g ₁ and γ ₂ ≤ g ₂ are always valid. Hence, the expressions in Eq. (57) are bounded above as follows:

$$P_{1} P_{2} \le \left\{ {\begin{array}{*{20}c} {\frac{{\left( {\gamma_{2} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + \gamma_{2} + g_{r} \alpha } \right)}}\frac{{\left( {\gamma_{1} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + \gamma_{2} + g_{r} \alpha } \right)}}\frac{{P_{T}^{2} }}{{\left( {1 + \alpha } \right)^{2} }}{\text{ for }}g_{1} - \gamma_{1} \le g_{2} - \gamma_{2} \, } \\ {\frac{{\left( {\gamma_{2} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + g_{r} \alpha + \gamma_{2} } \right)}}\frac{{\left( {\gamma_{1} + g_{r} \alpha } \right)}}{{\left( {\gamma_{1} + g_{r} \alpha + \gamma_{2} } \right)}}\frac{{P_{T}^{2} }}{{\left( {1 + \alpha } \right)^{2} }}{\text{ for }}g_{2} - \gamma_{2} \le g_{1} - \gamma_{1} \, } \\ \end{array} } \right.$$

(59)

A similar analysis performed for Partition 1 reveals that the first and second terms in the RHS of Eq. (59) get close to zero for γ ₁ ≫ γ ₂ and γ ₂ ≫ γ ₁, respectively.

For the Partition 4, adding or removing does not change the objective since it is independent from the cross-term. Hence, we can do our calculations as if there is no cross-term

In short, these analyses show that ignoring the cross-term can be accurately justified for most of the time. Also, our simulations show that the numerical difference between the optimal solution for Eq. (18) and that for Eq. (19) is negligibly small. Therefore, our analytical results can be considered as accurate and consistent with the true optimal solution of Eq. (18), which is numerically found.