Multi-scale modeling of the human cardiovascular system with applications to aortic valvular and arterial stenoses

Abstract

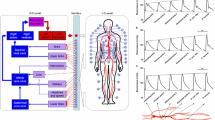
A computational model of the entire cardiovascular system is established based on multi-scale modeling, where the arterial tree is described by a one-dimensional model coupled with a lumped parameter description of the remainder. The resultant multi-scale model forms a closed loop, thus placing arterial wave propagation into a global hemodynamic environment. The model is applied to study the global hemodynamic influences of aortic valvular and arterial stenoses located in various regions. Obtained results show that the global hemodynamic influences of the stenoses depend strongly on their locations in the arterial system, particularly, the characteristics of hemodynamic changes induced by the aortic valvular and aortic stenoses are pronounced, which imply the possibility of noninvasively detecting the presence of the stenoses from peripheral pressure pulses. The variations in aortic pressure/flow pulses with the stenoses play testimony to the significance of modeling the entire cardiovascular system in the study of arterial diseases.

Appendices

Appendix 1: Numerical methods for bifurcation conditions

The system of Eqs. 4 and 5 describing the bifurcation conditions contains six unknowns, requiring another three equations to complete the system. We adopt a ‘ghost-point’ method [11] in which a “ghost” point is assumed to exist between the last two grid points of the mother tube and the first two grid points of the daughter tubes. When the current time is (n + 1)∆t, the index of the last grid-point of the mother tube is m, and that of the first grid point of the daughter tubes is 0, an algebraic equation can be obtained by discretizing the mass conservation equation at each of the three ghost-points.

For the mother tube:

$$ \frac{{\frac{{A_{m - 1}^{n + 1} + A_{m}^{n + 1} }}{2} - \frac{{A_{m - 1}^{n} + A_{m}^{n} }}{2}}}{\Updelta t} + \frac{{\left( {UA} \right)_{m}^{n + 1} - \left( {UA} \right)_{m - 1}^{n + 1} }}{\Updelta x} = 0, $$

(15)

and for the daughter tubes:

$$ \frac{{\frac{{A_{0}^{n + 1} + A_{1}^{n + 1} }}{2} - \frac{{A_{0}^{n} + A_{1}^{n} }}{2}}}{\Updelta t} + \frac{{\left( {UA} \right)_{1}^{n + 1} - \left( {UA} \right)_{0}^{n + 1} }}{\Updelta x} = 0. $$

(16)

Substituting Eqs. 15 and 16 into Eqs. 4 and 5 yields a set of nonlinear coupled algebraic equations which may be solved by using an iterative Newton–Raphson method.

Appendix 2: Numerical methods for 0–1-D coupling

Several numerical methods have been proposed to handle 0–1-D coupling problems [6, 7, 22]. We developed a new 0–1-D coupling method better fitting the current model system. Our method starts by extrapolating Riemann invariants [7] on the 1-D model side.

Riemann invariants are the characteristic variables of a hyperbolic system (Eq. 17) transformed from Eq. 1.

$$ \frac{\partial }{\partial t}\left( \begin{gathered} W_{1} \hfill \\ W_{2} \hfill \\ \end{gathered} \right) + \left( \begin{gathered} \lambda_{1} \hfill \\ \lambda_{2} \hfill \\ \end{gathered} \right)\frac{\partial }{\partial z}\left( \begin{gathered} W_{1} \hfill \\ W_{2} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} 0 \\ 0 \\ \end{gathered} \right), $$

(17)

where (W ₁, W ₂) are the Riemann invariants which represent, respectively, a forward-and a backward-traveling wave at speed, λ ₁, λ ₂. By choosing the reference conditions (A = A ₀, U = 0), we can obtain the solutions of system (Eq. 17) as [7]

$$ W_{ 1 , 2} = U \pm 4\sqrt {\frac{\beta }{{2\rho A_{0} }}} \left( {A^{{\frac{1}{4}}} - A_{0}^{{\frac{1}{4}}} } \right) = U \pm 4\left( {c - c_{0} } \right), $$

(18)

where c is the wave speed when A = A, and c ₀ the wave speed when A = A ₀.

From Eq. 18, we may rewrite (A, U) in terms of (W ₁, W ₂):

$$ A = \left( {\frac{{2\rho A_{0} }}{\beta }} \right)^{2} \left( {\frac{{W_{ 1} - W_{ 2} }}{8} + c_{0} } \right)^{4} ,\quad U = \frac{{W_{ 1} + W_{ 2} }}{2}. $$

(19)

Since W ₁, W ₂ represent waves traveling at certain speeds, at a certain time step (t ⁿ⁺¹), we may derive the values of W ₁ (t ⁿ⁺¹, L) and W ₂ (t ⁿ⁺¹, 0) from values at the previous time step (t ⁿ) at the distal end (denoted by L) and proximal end (denoted by 0) of an artery by extrapolating the outgoing Riemann invariants along the characteristic lines [7]

$$ W_{ 1} (t^{n + 1} ,L) = W_{ 1} \left( {t^{n} ,L - \lambda_{1}^{n} \Updelta t} \right),\quad W_{ 2} (t^{n + 1} ,0) = W_{ 2} \left( {t^{n} ,\lambda_{2}^{n} \Updelta t} \right), $$

(20)

where ∆t is the time step.

Based on the extrapolated Riemann invariants, other unknowns can be derived from the interface conditions. Because analytical solutions to the interface conditions are not obtainable, numerical iteration is required to approximate the solutions. Taking the interface at the distal end of a peripheral artery as an example, the procedure of numerical iteration is described in Fig. 7, where t ⁿ⁺¹ denotes the current time step, and t ⁿ⁺² the next time step; W ₁ (t ⁿ⁺¹, L) is the extrapolated Riemann invariant; Q* and P* are the intermediate variables belonging commonly to the 0-D model and the 1-D model, and W ₂*, U* and A* the intermediate variables of the 1-D model. The residual error is calculated based on Q*. All the intermediate variables will approximate the true solutions after the coupling computation converges.

Fig. 7

Schematic representation of 0–1-D coupling computation at a peripheral arterial distal end interface