A New Family of Topp and Leone Geometric Distribution with Reliability Applications

Abstract

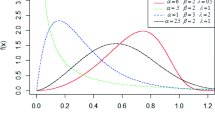
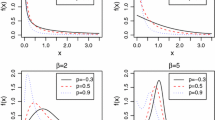
In this paper, a new class of lifetime distribution, which is called Topp–Leone (J-shaped) geometric distribution, is obtained by compound of the Topp–Leone and geometric distributions. Reliability and statistical properties of the new distribution such as quantiles, moment, hazard rate, reversed hazard rate, mean residual life, mean inactivity time, entropies, moment generating function, order statistics and their stochastic orderings are obtained. Estimation of the model parameters by least squares, weighted least squares, maximum likelihood and the observed information matrix are derived. Finally, a real data set is analyzed for illustrative purposes.

Appendices

Appendix 1: The Values of First Derivatives of the Log-Likelihood Function of the TLG Distribution

Differentiating Eq 39 with respect to $\alpha ,$ $\beta ,$ and p respectively, and equating to zero gives:

$$\begin{aligned} \frac{\partial L}{\partial \alpha }&= -\frac{2n\beta }{\alpha }+\sum\limits _{i=1}^{n}\frac{1}{\alpha -x_i}+(\beta -1)\sum\limits _{i=1}^{n}\frac{2}{2\alpha -x_i}+ 2\sum\limits _{i=1}^{n}\frac{(x_i-\alpha )(\dot{v_i})_{\alpha }}{v_i} =0, \end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial L}{\partial \beta }&= \frac{n}{\beta }-2n\log \alpha +\sum\limits _{i=1}^{n}\log x_i+\sum\limits _{i=1}^{n}\log (2\alpha -x_i)-2\sum\limits _{i=1}^{n}\frac{(\dot{v_i})_{\beta }}{v_i}=0,\end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial L}{\partial p}&= \frac{-n}{(1-p)}-2\sum\limits _{i=1}^{n}\frac{(\dot{v_i})_{p}}{v_i}=0. \end{aligned}$$

(44)

Appendix 2

The second derivatives of the log-likelihood function of TLG distribution with respect to $\alpha ,$ $\beta ,$ p are given by:

$$\begin{aligned}&\frac{\partial ^{2}L}{\partial \alpha ^{2}}= \frac{2n\beta }{\alpha ^2}-\sum\limits _{i=1}^{n}\frac{1}{(\alpha -x_i)^2}+(1-\beta )\sum\limits _{i=1}^{n}\frac{4}{(2\alpha -x_i)^2}+2\sum\limits _{i=1}^{n}\left[ \frac{3\alpha -x_i}{\alpha -x_i}\right] ^2\left[ \frac{(\dot{v_i})_{\alpha }}{v_i}\right] ^2-2\sum\limits _{i=1}^{n}\frac{(\dot{v_i})_{\alpha \alpha }}{v_i}, \\&\frac{ \partial ^{2}L}{\partial \beta ^{2}}=-\frac{n}{\beta ^2}-2\sum\limits _{i=1}^{n}\frac{(1-p)(\dot{v_i})_{\beta \beta }}{v_i^2}=0, \\&\frac{\partial ^{2}L}{\partial p ^{2}}=-\frac{n}{(1-p)^2}+2 \sum\limits _{i=1}^n\left( \frac{v_i-1}{pv_i}\right) ^2=0, \\&\frac{\partial ^{2}L}{\partial \alpha \partial \beta }=-\frac{2n}{\alpha }+\sum\limits _{i=1}^{n}\frac{2}{2\alpha -x_i}-\frac{2}{\beta }\sum\limits _{i=1}^{n} \frac{(1-p)\beta (\dot{v_i})_{\alpha \beta }+\alpha ^{2\beta }(\dot{v_i})_{\alpha }(v_i+p-1)}{v_i^2},\\&\frac{\partial ^{2}L}{\partial \alpha \partial p} =-2 \sum\limits _{i=1}^{n}\frac{(v_i+p)(\dot{v_i})_{\alpha p}-[(\dot{v_i})_{p}+1](\dot{v_i})_{\alpha }}{v_i^2}, \\&\frac{\partial ^{2}L}{\partial \beta \partial p}=-2 \sum\limits _{i=1}^{n}\frac{(\dot{v_i})_{\beta p}}{v_i^2}, \end{aligned}$$

where

$$\begin{aligned} v_{i}&= v_{i}(\alpha , \beta , p)= 1 - p + p\alpha ^{-2 \beta }(2 \alpha - x_i)^{\beta } x_i^{\beta }, \quad (\dot{ v_{i}})_{\alpha }= -2 p \beta \alpha ^{-(2 \beta +1)}(\alpha - x_i) (2 \alpha - x_i)^{\beta -1} x_i^{\beta }, \\ (\dot{ v_{i}})_{\beta }&= -p \alpha ^{-2\beta } \left( 2 \log (\alpha ) - \log (2\alpha - x_i) -\log (x_i)\right) (2\alpha - x_i)^{\beta } x_i^{\beta }, \quad (\dot{ v_{i}})_{p}=-1 + \alpha ^{-2 \beta }(2 \alpha - x_i)^{\beta } x_i^{\beta }, \\ (\dot{ v_{i}})_{\alpha \alpha }&= 2p\beta \alpha ^{-2(1+\beta )}(2\alpha - x_i)^{-2+\beta }x_i^{\beta } (2\alpha ^2(1+\beta )-4\alpha (1+\beta )x_i+(1+2\beta )x_i^2), \\ (\dot{ v_{i}})_{\beta \beta }&= p\alpha ^{-2\beta }(-2\log \alpha +\log (2\alpha -x_i)+\log x_i)^2 (2\alpha - x_i)^{\beta }x_i^{\beta }, \\ (\dot{ v_{i}})_{\alpha \beta }&= 2p\alpha ^{-1-2\beta }\left( -1+2\beta \log \alpha -\beta \left( \log (2\alpha -x_i)+\log x_i\right) \right) (\alpha - x_i)(2\alpha - x_i)^{-1+\beta }x_i^{\beta }, \\ (\dot{ v_{i}})_{\beta p}&= \alpha ^{-2\beta }(-2\log \alpha +\log (2\alpha -x_i)+\log x_i) (2\alpha - x_i)^{\beta }x_i^{\beta }, \\ (\dot{ v_{i}})_{\alpha p}&= -2\alpha ^{-(2\beta +1)}\beta (\alpha - x_i)(2\alpha - x_i)^{\beta -1}x_i^{\beta }. \end{aligned}$$