Cross-Permeability of the Semisolid Region in Directional Solidification: A Combined Phase-Field and Lattice-Boltzmann Simulation Approach

Abstract

Based on the results of microstructure simulations, fluid flow through the semisolid region during directional solidification of the technical Ni-base alloy 718 has been studied. Three-dimensional microstructures at different positions in the semisolid region were obtained by using a multicomponent multiphase-field model that was online coupled to a commercial thermodynamic database. For the range of five different primary dendrite distances λ ₁ between 50 µm and 250 µm, the flow velocity and the permeability perpendicular to the dendrite growth direction was evaluated by using a proprietary Lattice-Boltzmann model. The commercial CFD software ANSYS FLUENT was alternatively applied for reference. Consistent values of the average flow velocity along the dendrites were obtained for both methods. From the results of the fluid flow simulations, the cross-permeability was evaluated as a function of temperature and fraction liquid for each of the five different primary dendrite distances λ ₁. The obtained permeability values can be approximated by a single analytical function of the fraction liquid and λ ₁ and are discussed and compared with known relations from the literature.

Introduction

In simulation of solidification processes, fluid flow phenomena play a crucial role. Numerous types of defects arise during solidification as the formation of dendritic structures in the mushy zone causes specific fluid flow patterns. Although most of these defects are located at the micro- or meso-scale, they can be linked to the macro-scale by the melt permeability of the mushy zone. As stated by several authors, the specific permeability is a determining parameter in fluid flow phenomena like freckles, as well as in defects like porosity and hot cracking among others.1–4

Improvements of simulation techniques and the combination of multiple tools working on different length scales through Integrated Computational Materials Engineering (ICME)5 open up new possibilities of investigations on the impact of permeability on casting defects. Phase-field models have become very popular for the simulation of the microstructure evolution during solidification processes of alloys. To describe their thermodynamic properties, idealized descriptions of the phase diagrams (ideal solution approximation6 and linear phase diagrams7) have been used for binary and pseudo-binary alloys. But this approximation is not suitable for use in multicomponent multiphase systems. Instead, using Gibbs energy descriptions assessed from experimental data via the Calphad approach,8 together with software tools for Gibbs energy minimization,9 seems to be most promising.

MICRESS^® 10 has been developed by Access11 at Aachen Technical University (RWTH). It is based on a phase-field concept for multiphase systems that has been consequently extended to multicomponent systems12–14 by direct coupling to thermodynamic databases via the TQ Fortran interface to Thermo-Calc.9 Since then the software has been developed further and applied to different alloy systems and to Ni-based super alloys.15,16

Although numerous phase-field studies on directional dendritic solidification have been published, the three-dimensional (3D) simulation of representative parts of the mushy zone for technical multicomponent alloys, which are needed for a reliable evaluation of the liquid permeability, is still a challenge. The present paper reports phase field simulations carried out with MICRESS^® that allowed subsequent investigations concerning the permeability during the solidification process. The results of the 3D dendrite simulations were subjected to further calculations by using the Lattice-Boltzmann method and the commercial CFD software ANSYS FLUENT. This allowed for assessment of the relation between temperature, fraction liquid and cross permeability for isothermal fluid flow, which plays a crucial role for freckle formation in technical remelting processes (e.g., of alloy 718).2 The obtained results are compared with empirical relations provided by Poirier17 and Madison.18

Phase-Field Simulation

The multiphase-field theory describes the evolution of multiple phase-field parameters $\phi_{\alpha } (\vec{x},t)$ in time and space. The phase-field parameters reflect the spatial distribution of different grains of different orientation and/or of several phases with different thermodynamic properties. At the interfaces, the phase-field variables change continuously over an interface thickness η that can be defined as being large compared with the atomic interface thickness but small compared with the microstructure length scale. The time evolution of the phases is calculated by a set of phase-field equations deduced by minimization of the free energy functional:13

$$ \dot{\phi }_{\alpha } = \sum\limits_{\beta } {M_{\alpha \beta } \left( {\vec{n}} \right)\,\,\left( {\sigma_{\alpha \beta }^{*} \left( {\vec{n}} \right)\,\,K_{\alpha \beta } + \frac{\pi }{\eta }\sqrt {\phi_{\alpha } \phi_{\beta } } \,\,\Delta G_{\alpha \beta } \left( {\vec{c},T} \right)} \right)} $$

(1)

$$ K_{\alpha \beta } = \phi_{\beta } \nabla^{2} \phi_{\alpha } - \phi_{\alpha } \nabla^{2} \phi_{\beta } + \frac{{\pi^{2} }}{{\eta^{2} }}\left( {\phi_{\alpha } - \phi_{\beta } } \right). $$

(2)

In Eq. 1, M _αβ is the mobility of the interface as a function of the interface orientation, described by the normal vector $\vec{n}$. σ* _αβ is the anisotropic surface stiffness, and K _αβ is related to the local curvature of the interface. The interface, on the one hand, is driven by the curvature contribution σ* _αβ K _αβ and, on the other hand, by the thermodynamic driving force ΔG _αβ . The thermodynamic driving force, which is a function of temperature T and local composition $\vec{c} = \left( {c^{1} ,c^{2} , \ldots ,c^{k} } \right)$, couples the phase-field equations to the multiphase diffusion equations for the k alloying elements:

$$ \dot{\vec{c}} = \nabla \sum\limits_{\alpha = 1}^{N} {\phi_{\alpha } \vec{D}_{\alpha } \nabla \vec{c}_{\alpha } } \,{\text{with}}\,\vec{c}\,{\text{defined by}}\,\vec{c} = \sum\limits_{\alpha = 1}^{N} {\phi_{\alpha } \vec{c}_{\alpha } } $$

(3)

and $\vec{D}_{\alpha }$ being the multicomponent diffusion coefficient matrix for phase α. $\vec{D}_{\alpha }$ is calculated online from databases for the given concentration and temperature.

These equations are implemented in the software package MICRESS^® 10 being used for the simulations throughout this paper. Direct coupling to thermodynamic and mobility databases is accomplished via the TQ-interface of Thermo-Calc Software.9 The thermodynamic driving force ΔG _αβ and the solute partitioning are calculated separately by using the quasi-equilibrium approach,13 and they are introduced into the equation for the multiple phase-fields Eq. 1. This allows the software package to be highly flexible with respect to thermodynamic data of a variety of alloy systems and not to be restricted by the number of elements or phases being considered. Various extrapolation schemes14 have been implemented to minimize the thermodynamic data handling, especially for complex alloy systems.

Simulation Conditions

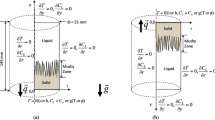
For simulation of 3D dendritic microstructures, the smallest representative domain was chosen by taking advantage of the fourfolded mirror symmetry of the dendrites (Fig. 1). Correspondingly, symmetric boundary conditions (Neumann condition with symmetry plane through the centers of the boundary FD grid cells) have been used on the four sides of the domain for the phase field and the concentration fields. For the top concentration boundary, a fixed condition was used to ensure that the far-field concentration remains constant (and equal to the average alloy composition). At the bottom, an isolation (Neumann) boundary condition was used.

Fig. 1

Growth of an alloy 718 dendrite at a primary spacing λ ₁ = 250 µm

Simulation started with a temperature of 1733 K at the bottom of the domain. A constant temperature gradient of G = 40 K/cm and cooling rate of V = 0.40 K/s were applied in all cases, ensuring a constant secondary arm spacing,19 the average of which has been determined as 31.2 µm. TiN particles were nucleated at the beginning according to a seed-density model by using an arbitrary density-radius distribution20,21 and were given time to grow and ripen before the primary dendrite appeared. To reach stationary growth conditions as quickly as possible, nucleation of the initial seed of fcc phase was performed exactly at the stationary tip temperature of 1618.8 K at the lower left corner of the simulation domain. Due to the high composition of alloying elements in alloy 718, stationary growth is achieved almost immediately, and the tip temperature remained at this value until the dendrite reached the top boundary.

To reduce the required calculation time, spatial resolution was reduced to a minimum and a grid spacing of Δx = 1.0 µm was chosen. The total height of the domain was 1000 grid cells or 1 mm, and the width varied from 25 to 150 cells, according to a primary dendrite spacing of 50 µm to 300 µm. The interface mobility value for the liquid/fcc boundary was calibrated such that the tip temperature stayed constant during the period of free dendrite tip growth, as will be discussed. This value of 0.058 cm⁴ J⁻¹ s⁻¹ was applied for all simulations. For other interfaces (TiN-liquid, TiN-fcc), the mobility values were estimated. Respective numerical parameters are given in Table I.

Table I Numerical parameters

In the phase-field simulations, the elements Ni, Cr, Fe, Nb, Mo, Ti, Al, C, N, and B and the phases LIQUID, FCC_A1, and FCC_A1#2 (Ti(N,C)) were taken into account. Thermodynamic data were obtained directly by coupling to the thermodynamic database TTNI7. Diffusion coefficients for the solid phases were taken from the mobility database MOBNI1;9 for the liquid phase, they were estimated to 1 × 10⁻⁵ cm² s⁻¹ for all elements.

Calibration of Interface Kinetics

It is well known that phase-field models suffer from numerical artifacts if spatial resolution is not sufficiently high.22 If the interface thickness is not much smaller than the diffusion length of all elements, the interface kinetics deviate from the sharp interface solution due to artificial solute trapping. As an additional problem, the interface even may get instable if the driving force varies too much over the length of the diffuse interface. For the case of solidification, there have been attempts to correct for these artifacts by introducing an anti-trapping current to the diffusion equations and by applying a suitable correction to the interface mobility (the so-called thin interface limit).23 Those approaches are often referred to as quantitative phase-field models. But even when rigorous thin interface corrections are considered, the interface thickness has to be on the order of the capillary length, and the required grid would still be too fine for 3D application of the phase-field method to multicomponent and multiphase technical alloys.

A typical approach is to compensate the artificial trapping effect by the choice of suitable interface mobility values. This has been done recently by calibration against a representative high-resolution reference simulation.21 In the present case, however, the high computational effort makes such a calibration impossible, particularly as no substantial reduction of the domain size is possible without affecting the selection of the correct stationary tip temperature. Therefore, in this work, another approach has been used to obtain quantitative interface kinetics: A numerical approach based on KGT theory24 was used to estimate the stationary tip temperature for the given temperature gradient and cooling rate. A pseudo-binary phase diagram description in the form

$$ c_{s}^{*} = \sum\limits_{i} {c_{s}^{i} } ,\,c_{l}^{*} = c_{s}^{*} + \sqrt {\sum\nolimits_{i} {\left( {c_{l}^{i} - c_{s}^{i} } \right)^{2} } } $$

(4)

$$ m_{s}^{*} = \frac{{\sum\nolimits_{i} {\left( {c_{l}^{i} - c_{s}^{i} } \right)\,\,m_{s}^{i} } }}{{\sqrt {\sum\nolimits_{i} {\left( {c_{l}^{i} - c_{s}^{i} } \right)^{2} } } }},\,m_{l}^{*} = \frac{{\sum\nolimits_{i} {\left( {c_{l}^{i} - c_{s}^{i} } \right)\,\,m_{l}^{i} } }}{{\sqrt {\sum\nolimits_{i} {\left( {c_{l}^{i} - c_{s}^{i} } \right)^{2} } } }} $$

(5)

was used for the KGT model, leading to a value of 9.6 K for the dendrite tip undercooling. By systematic variation of the interface mobility of the liquid-fcc interface, a calibrated value of 0.058 cm⁴ J⁻¹ s⁻¹ was obtained that guaranteed a correct tip temperature despite the relatively coarse grid resolution.

Furthermore, an averaging of the driving force ΔG along the normal vector of the interface was performed to reduce “artificial solute trapping” and to stabilize the interface profile, and a small interface thickness (η = 3Δx = 3 µm) was used that further helps reducing trapping artifacts. Artifacts originating from the small number of interface grid points were minimized by using a correction scheme for numerical discretization errors.25

Results of 3D Dendrite Simulations

Figure 1 shows the shape of the growing dendrite as an iso-surface with $\phi = 0.5$ at three different times (t = 3, 9, and 37 s). Small spherical TiN particles can be observed in front of the dendrite tip, which have formed at a much higher temperature. The dendrite emerges and overgrows tertiary arms that compete with the primary trunk. After hitting the top boundary, dendrite coarsening is the main phenomenon that can be observed. Due to the immense calculation time, only in the case of the smaller simulation domains (lower primary spacing), an overall fraction of solid above 0.5 could be reached.

It is well known that for given G/V ratio, λ ₁ is history dependent and may adopt different values within a certain stability range.26 A comparison of the simulated growth morphologies of alloy 718 dendrites for different values of the primary dendrite spacing λ ₁ is shown in Fig. 2. For the smallest spacing of 50 µm, only small side branches can form, leading to a cellular-dendritic growth mode. With an increasing value of λ ₁, the side branches evolve more and more and eventually show tertiary branching.

Fig. 2

Comparison of growth morphology for six different values of the primary dendrite spacing

Furthermore, these tertiary branches that grow in the direction of the temperature gradient compete with the primary dendrite. When a primary distance of λ ₁ = 300 µm is reached, those tertiary arms cannot be blocked any more. This indicates that the upper limit of the stability range has been passed. Hence, this simulation set has been discarded from further evaluation.

Simulation of Permeability

In the process of solidification, the mushy zone is a domain of solid phases with emerging dendritic structures and an interconnected void phase filled with liquid. It has been proven to be consistent to model the mushy zone as a porous medium showing a spatially varying permeability.27

As the criteria of a large area of porous medium and negligible boundary effects are fulfilled, the interdendritic flow follows Darcy’s law.28 Therefore, the pressure gradient $\nabla p$ is proportional to the flow velocity vector $\bar{v}$:

$$ \nabla p = \frac{\mu }{K}\bar{v}. $$

(6)

Here, μ is the (dynamic) viscosity and K is the permeability. The dendritic structure determined by phase-field simulations follows the assumption of a symmetric array of dendrites. Therefore, a periodic boundary condition can be used to calculate numerically the fluid flow in a specific symmetric volume.

The calculations are carried out by using the Lattice-Boltzmann method29 or alternatively the CFD software ANSYS FLUENT. As the velocities and characteristic lengths are very small, in the order of 10⁻⁸ m/s and 10⁻⁵ m, respectively, a laminar, steady flow can be assumed in both models.

ANSYS FLUENT solves continuity Eq. 7 and momentum Eq. 8 equations on a finite volume grid:

$$ \frac{\partial \rho }{\partial t} + \nabla \left( {\rho \bar{v}} \right) = 0 $$

(7)

$$ \bar{\bar{\tau }} = \mu_{D} \left( {\left( {\nabla \bar{v} + \nabla \bar{v}^{T} } \right) - \frac{2}{3}\nabla \left( {\bar{v}\bar{\bar{e}}} \right)} \right). $$

(8)

Here, ρ is the melt density, $\bar{\bar{\tau }}$ the stress tensor, μ _D the dynamic viscosity, and $\bar{\bar{e}}$ the unity tensor. Solving these equations numerically has been proven valid in many cases, especially considering a laminar, steady fluid flow. Analogous to the Lattice-Boltzmann model, a periodic flow perpendicular to the primary dendrites is being assumed. Due to the high geometric complexity of the dendritic structure, a stair step grid is generated including only cells above a specific fraction liquid. This specific fraction liquid has been chosen in a manner in which the average fraction liquid is being conserved.

The Lattice-Boltzmann method, however, is founded on particle interaction on a microscopic and a mesoscopic level. It can be derived from the lattice gas automata (LGA) on the approach of fluid or gas as a big number of randomly moving particles that allows the use of Navier–Stokes equations on a macroscopic scale.30 A transformation of the particles into a single-particle distribution function results in the lattice Boltzmann equation (LBE). Several different LBE models denoted as DdQq exist, where d refers to the dimension and q to the amount of velocity directions.31 The following study uses the LBE model D3Q19, a 3D space with 19 orthogonal velocity vectors shown in Fig. 3. Between the several existing cubic models, it is considered to combine both a high computational reliability and efficiency, thereby promising consistent results.30

Fig. 3

Lattice structure of the D3Q19 (Ref. 29)

For athermal fluids, the equilibrium distribution function introduced by He and Luo can be applied for D3Q19:29

$$ f_{i}^{eq} = \rho w_{i} \left( {1 + \frac{3}{{c^{2} }}e_{i} \cdot u + \frac{9}{{2c^{4} }}\left( {e_{i} \cdot u} \right)^{2} - \frac{3}{{2c^{2} }}\left( {u \cdot u} \right)} \right) $$

(9)

The function depends on the weighting factor w _i , the discrete velocity e _i , and the lattice speed c. Hereby is lattice speed, the quotient of the lattice constant and the time step: $c = {{\delta x} \mathord{\left/ {\vphantom {{\delta x} {\delta t}}} \right. \kern-0pt} {\delta t}}$. The weighting factor and the set of discrete velocities vary with the respective model; in the case of D3Q19, they are defined as follows. The lattice structures with the discrete velocity vectors e _i are shown in Fig. 3.30

$$ e_{i} = \left\{ {\begin{array}{*{20}l} {(0, \, 0, \, 0)} \hfill & {\text{i = 0}} \hfill & {\text{rest particle}} \hfill \\ {( \pm 1, \, 0, \, 0)c,\,(0, \, \pm 1, \, 0)c,\,(0, \, 0, \, \pm 1)c} \hfill & {{\text{i = 1,2,}} \ldots 6 ,} \hfill & {\text{group I}} \hfill \\ {( \pm 1, \, \pm 1, \, 0)c,\,(0, \, \pm 1, \, \pm 1)c,\,( \pm 1, \, 0, \, \pm 1)c} \hfill & {{\text{i = 7,8}}, \ldots 1 8 ,} \hfill & {\text{group II}} \hfill \\ \end{array} } \right. $$

(10)

$$ w_{i} = \left\{ {\begin{array}{*{20}l} {1/3} \hfill & {\text{i = 0}} \hfill & {\text{rest particle}} \hfill \\ {1/18} \hfill & {{\text{i = 1,2,}} \ldots 6 ,} \hfill & {\text{group I}} \hfill \\ {1/36} \hfill & {{\text{i = 7,8}}, \ldots 1 8 ,} \hfill & {\text{group II}} \hfill \\ \end{array} }. \right. $$

(11)

This LBG model does not require a scattered matrix but uses a quasi-linear LBE variation. This implies a change from a multi-to a single-time relaxation that gives a fixed time scale for all modes. The individual particle motion is neglected; the particles instead follow an ensemble average.27,32 As the requirements of mass and momentum conservation are no longer guaranteed through sum rules of the formerly scattered matrix, local equilibrium has to be imposed by the definition of the local density $\rho$ (12) and momentum $\rho \bar{u}$ (13) as particle velocity moments of the distribution function f _i .27 Eq. 12 enables us to step back from a discrete microscopic velocity to a continuous macroscopic velocity, such as the fluid motion.33

$$ \rho = \sum\limits_{i = 0}^{N} {f_{i} } $$

(12)

$$ \rho \bar{u} = \sum\limits_{i = 0}^{N} {f_{i} } e_{i} . $$

(13)

The discretization in space and time allows the fitting of the LBEs in the collision model of Bhatnagar-Gross-Krook (BGK), resulting in the lattice Bhatnagar-Gross-Krook (LBGK) approximation for the contribution function f _i :

$$ f_{i} \left( {x + e_{i} ,t + 1} \right) - f_{i} \left( {x,t} \right) = - \frac{1}{\tau }\left[ {f_{i} \left( {x,t} \right) - f_{i}^{eq} \left( {x,t} \right)} \right]. $$

(14)

Hereby, f ^eq _i is the equilibrium value and the characteristic time $\tau = {\lambda \mathord{\left/ {\vphantom {\lambda {\delta t}}} \right. \kern-0pt} {\delta t}}$, with λ the relaxation time. The LBGK model has become widely used due to its easy implementation and numerical effectiveness. In Eq. 14, two steps are implemented, equating streaming with collision. While in the streaming step the distribution function f _i moves to the next lattice place, the collision step relaxes f _i toward f ^eq _i . Both the step of streaming and the collision of the fluid particles have to be separately approached to solve the LBGK Eq. 14.33 Although the collision step is entirely local, the streaming step is consistent. The simulation of solid boundaries follows the bounce back condition where particles are reversely bounced back from the wall points. The bounce back boundary condition is integrated in the collision step.

Results

The original results from the MICRESS^® simulations comprise precise fraction liquid data for all grid cells. For simulation of fluid flow, the fraction liquid information had to be reduced to zero or one in each cell. This was achieved by using a threshold value for the fraction liquid close to 0.5 below which the cell was assumed to be completely solid and otherwise completely liquid. This threshold value was chosen such that the total fraction liquid in the whole simulation domain was conserved. During this procedure, all TiN particles that were not in contact with the fcc dendrite were converted into liquid phase because they moved with the melt flow and such did not contribute to the pressure drop.

Figure 4 illustrates the smallest representative domain for simulation of fluid flow across the mushy zone when a symmetric structure of the dendrite network is assumed. Accordingly, the computational domain of the phase-field simulations had to be doubled by mirroring in the x-direction.

Fig. 4

Symmetry of the dendrite array assumed for fluid flow simulation

With the described procedures, according to the value of λ ₁ in the phase-field simulation, cubic domains with a height of 1000 cells and base areas between 50 × 25 and 250 × 125 cells with a cell size of 1 µm³ were obtained that comprise a sharp interface between solid and liquid. These were directly used as representative domains for CFD calculation of the permeability of the mushy zone for different temperature and primary spacing.

The presented equations and considerations lead to the velocities in x-, y-, and z-direction. As the general stream direction is assumed normal to the primary dendrite arms (Fig. 5), the velocity in the x-direction is the decisive factor. The permeability coefficient represents a characteristic value that does not require additional information of the internal structure of the porous media; only the velocity’s x-component on the periodic faces of the computational domain is crucial. The velocities increase near the dendritic solidified structure as the flow cross section becomes smaller.

Fig. 5

Representation of the 3D flow field around the dendrite arms

To check the accuracy of the results, some of the CFD calculations were done by using both ANSYS FLUENT and the Lattice-Boltzmann method. Furthermore, the grid resolution was doubled (“fine” resolution, Δx = 0.5 µm) to reduce discretization errors. A very high conformity of the results proved evidence of correctness and applicability of both approaches. Figure 6 shows the average flow velocities obtained with the different methods and resolutions.

Fig. 6

Comparison between left: ANSYS FLUENT and the Lattice-Boltzmann method, right: normal and double grid resolutions for a simulation time of 20 s and λ ₁ = 150 µm

Therefore, for the further simulation, the average velocities (v) at the left border of the mesh grid obtained by using the Lattice-Boltzmann method and the coarse grid were identified as representative for the velocity trend. With a viscosity of $\mu { = 0} . 0 0 9 {\text{ Pa}} \cdot {\text{s}}$ and a pressure gradient of $\nabla p \, = \, 200 \, {\raise0.7ex\hbox{${Pa}$} \!\mathord{\left/ {\vphantom {{Pa} m}}\right.\kern-0pt} \!\lower0.7ex\hbox{$m$}}$, the permeability is presented in Eq. 15:

$$ k_{x} = \frac{{\mu \cdot v_{mw} }}{\nabla p} \, \left[ {m^{2} } \right]. $$

(15)

Due to the dendritic structure including the secondary arms, the fraction liquid presents a strong fluctuation along the z-coordinate. Therefore, the liquid fractions as well as the velocity are averaged over the distance of two secondary dendrite arm spacings (λ ₂).

Calculation of fluid flow was done for the five phase-field simulations for λ ₁ = 50, 100, 150, 200, and 250 µm which are shown in Fig. 2. For each case, the results at 4–12 different intermediate output times were selected to span the temperature range between the dendrite tip and the lowest temperature reached in each phase-field simulation (Fig. 7). Note that for large values of λ ₁, only information for higher temperatures could be obtained due to the high computation times of the corresponding phase-field simulations.

Fig. 7

Averaged permeability for different primary spacings λ ₁ as a function of temperature

To allow for a comparison of the findings to existing empirical relations, the simulated permeability values also have been plotted as a function of the liquid fraction (Fig. 8). Although for d ₂ = 100 µm, d ₃ = 150 µm, d ₄ = 200 µm, and d ₅ = 250 µm, the differences are only small, for the lowest value of λ ₁ (d ₁ = 50 µm), considerably higher values of the permeability are obtained. This can be explained with the mostly cellular morphology obtained under these conditions (Fig. 2).

Fig. 8

Averaged permeability for different primary spacings λ ₁ as a function of liquid fraction. Approximation curves according to Eq.  16 have been included

The permeability as a function of fraction solid can be approximated by the following relation, which has been obtained empirically (Fig. 8):

$$ k_{x} = \left\{ {\begin{array}{*{20}ll} {10^{ - 10.3} \cdot f_{L} \cdot d_{i}^{{0.6 \cdot (0.9 - f_{L} )}} } & {0.3 \le f_{L} \le tv} \\ {10^{ - 5.8} \cdot \left( {\frac{{f_{L} }}{{1 - f_{L} }}^{0.7} - 4} \right) \cdot \left( {10^{ - 4} + \frac{{d_{i} }}{10}} \right)} & {tv \le f_{L} \le 1} \\ \end{array} } \right.. $$

(16)

The transition between the steep curve at high fraction liquid values and the continuous descent in the lower fraction liquid region can be related to the transition between the free growth of the dendrite tip and a restricted growth once the dendrite side branches interact with the neighboring dendrite. Not only the temperature for this transition (as can be clearly seen in Fig. 2) but also the corresponding fraction liquid value tv is found to vary with the primary dendrite arm spacing:

$$ tv = 3194 \cdot d_{i}^{2} - 7.481 \cdot d_{i} + 0.888. $$

(17)

Discussion

It is interesting to compare the results of the current study with well-established empirical relations that are frequently used for mesoscopic or macroscopic simulation of fluid flow in semisolid regions (e.g., for predicting freckles, microporosity, or hot cracking in different types of casting). Figure 9 puts our results in contrast with the equations presented by Madison et al.18 and Poirier et al.17 For all three cases, the curves are shown for λ ₁ = 100, 150, 200, and 250 µm (d ₂–d ₅), plotted as a function of the fraction liquid f _L .

Fig. 9

Permeability curves comparing Madison et al.,18 Poirier,17 and the current study (inside each series, the top curve is for d ₅ (λ ₁ = 250 µm), followed by d ₄ (λ ₁ = 200 µm), d ₃ (λ ₁ = 150 µm), and d ₂ (λ ₁ = 100 µm))

Although there is very good agreement for the cross-permeability curves for intermediate values of λ ₁ (150–200 µm) and the fraction liquid range below 0.65, there are strong deviations otherwise. Most striking is the steep decay of the cross-permeability curve in the current results occurring already at high values of f _L (>0.85), whereas it was predicted by Poirier for the range 0.65 < f _L  < 0.75.17 The decay is attributed to the transition between free growth in the dendrite tip region and restricted growth below and (at least under these conditions) is wrongly predicted by the empirical relation of Poirier by up to a factor of 100 for high fraction liquid values. For prediction of fluid-flow phenomena in the upper part of the mushy zone (e.g., the initiation of freckles during electro-slag remelting (ESR)),2 this can have significant consequences.

The second strong difference is the much smaller dependency of the cross-permeability on λ ₁ in our study. This can be easily explained by the fact that in our phase-field simulations, the primary dendrite distance λ ₁ was modified “artificially” without changing the local thermal parameters (temperature gradient and cooling rate). To the contrary, the formulae by Poirier17 and Madison18 assume the change of λ ₁ to be attributed to a change of the local thermal condition (i.e., they assume that the dendrites have selected their primary distance according to the local conditions). Thus, no similarity should be expected with respect to the λ ₁-dependency of the cross-permeability because the main effect, which is the change of λ ₂ due to an altered local solidification time, has not been included in our study. Direct comparisons of the datasets should only be made for average (stable) values of the primary distance (λ ₁ = 150–200 µm).

Although for application a representation as a function of temperature (Fig. 7) may be most practical, plotting permeability in terms of the interfacial surface area (ISA) has been proposed as a more comprehensive description.34 Whether the ISA, which can be easily evaluated from simulated microstructures, provides a suitable metric for prediction of permeability will be the subject of future research.

Conclusion and Outlook

The coupling between the 3D phase-field simulation of multicomponent alloy microstructures by using MICRESS^® and fluid-flow simulations carried out with ANSYS FLUENT or the Lattice-Boltzmann method presents an important contribution to the still developing and improving field of computational simulation of casting processes in an ICME framework. Besides the methodological aspects, the study also gives new knowledge and insight into the cross-permeability of the interdendritic zone and points out the opportunities offered by simulation approaches. By direct simulation of the dendrite morphology and its change downward through the mushy zone and by a systematic variation of the primary dendrite distance in the phase-field simulations, the dependency of the effective cross-permeability on the fraction liquid and the effect of the primary dendrite distance could be quantitatively evaluated for the technical Ni-base alloy 718 and compared with empirical relations from the literature.

The study not only presents a methodology to link different software tools and exchange data between them but also proposes a way to aggregate detailed results on the microscale and transform them by systematic variation and averaging into empirical laws that can be applied on the macroscale. The path is now open, and more dimensions can be included by variation of other parameters like cooling rate, temperature gradient, or alloy composition to obtain more comprehensive description of the permeability and other properties of the mushy zone.