Multiscale models for movement in oriented environments and their application to hilltopping in butterflies

Abstract

Hilltopping butterflies direct their movement in response to topography, facilitating mating encounters via accumulation at summits. In this paper, we take hilltopping as a case study to explore the impact of complex orienteering cues on population dynamics. The modelling employs a standard multiscale framework, in which an individual’s movement path is described as a stochastic ‘velocity-jump’ process and scaling applied to generate a macroscopic model capable of simulating large populations in landscapes. In this manner, the terms and parameters of the macroscopic model directly relate to statistical inputs of the individual-level model (mean speeds, turning rates and turning distributions). Applied to hilltopping in butterflies, we demonstrate how hilltopping acts to aggregate populations at summits, optimising mating for low-density species. However, for abundant populations, hilltopping is not only less effective but also possibly disadvantageous, with hilltopping males recording a lower mating rate than their non-hilltopping competitors.

Appendix: Numerical methods

Stochastic individual-based model

Each individual starts at t = 0 with position and velocity according to the given initial distributions. A movement path is generated through direct simulation of the stochastic velocity-jump process in Matlab. If t _i represents a time at which a turn is made, x _i is the location of the individual at this time and v _{i − 1} is its previous velocity:

• 1. The new velocity v _i is chosen according to the proposed velocity distribution q;

• 2. The new runtime τ _i is selected from a Poisson distribution, with turning rate parameter λ ( = 1/τ, where τ is the mean runtime).

• 3. The individual is moved to position x _{i + 1} = x _i + τ _i v _i , time is incremented to t _{i + 1} = t _i + τ _i and the process is repeated.

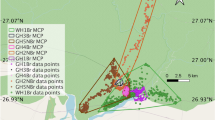
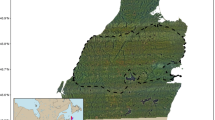
For velocity distributions based on the von Mises distribution, we employ code (circ _vmrnd.m) from the circular statistics toolbox (Berens 2009). Selecting an orientation according to this distribution requires a concentration parameter (κ) and dominant angle (ϕ), drawn from the local gradient of an underlying orienteering cue E(x). For landscapes such as Arthur’s seat, where terrain data is only available at discrete points, local gradients of E are approximated via a central difference scheme.

Mesoscopic velocity-jump model

Equation (3) is solved using a method of lines (MOL) approach: we discretise in position and velocity space to create a large system of ordinary differential equations (ODEs) to be solved with an appropriate time integration method. In two dimensions, with fixed speed s, positional coordinates (x, y) ∈ A = 0, L _x × 0, L _y are discretised onto a regular lattice $x_{1} = \frac {\Delta _{x}}{2}, x_{2} = \frac {3 \Delta _{x}}{2} \hdots , x_{M} = L_{x} - \frac {\Delta _{x}}{2}$, $y_{1} = \frac {\Delta _{y}}{2}, y_{2} = \frac {3 \Delta _{y}}{2} \hdots , y_{N} = L_{y} - \frac {\Delta _{y}}{2}$ for Δ _x = L _x / M, Δ _y = L _y / N, while velocity v = s(cosθ, sinθ) is discretised according to its angular coordinate θ ∈ ( − π, π such that θ ₁ = − π + Δ _θ , θ ₂ = − π + 2Δ _θ , … , θ _P = π, where Δ _θ = 2π / P,

Spatial terms consist of the advective term representing movement: this is discretised in conservative form via a third-order upwinding scheme, augmented with a flux-limiting scheme to ensure positivity of solutions. The righthand side terms of (3) are treated as kinetic-type terms. Integration of the ODEs has been performed with both explicit and implicit schemes: the former a forward Euler method with sufficiently small time step, the latter with the rowmap stiff systems integrator (Weiner et al. 1997). Tests using the two time iteration methods yield equivalent results and simulations have been performed across a range of discretisation steps. Default discretisations for the simulations employ N = M = 200 and P = 100.

Macroscopic model

We also employ a MOL scheme to solve the macroscopic Eq. (5). The spatial region A is discretised using the same regular lattice as above for the transport model. In 2D, assuming the drift vector and diffusion tensor are of the form

$${\mathbf{a}}\left( {x,\,y} \right) = \left( {\begin{array}{*{20}{c}} {\mu \left( {x,\,y} \right)} \\ {v\left( {x,\,y} \right)} \end{array}} \right)\,{\text{and}}\,\overline D \left( {x,\,y} \right) = \left( {\begin{array}{*{20}{c}} {\alpha \left( {x,\,y} \right)\,\gamma \left( {x,\,y} \right)} \\ {\gamma (x,\,y)\,\beta \left( {x,\,y} \right)} \end{array}} \right),$$

we can expand the spatial terms of (5) as follows

$$\begin{array}{@{}rcl@{}} - \nabla (\mathbf{a} u) \,+\, \nabla \nabla ( \bar{D} u ) {} & = & {} (\alpha u_{x})_{x} + (\gamma u_{x})_{y} + (\gamma u_{y})_{x} + (\beta u_{y})_{y} \\ & + & ( ( \mu \,+\, \alpha_{x} \,+\, \beta_{y} ) u)_{x} \,+\, ((\nu \,+\, \beta_{x} \,+\, \gamma_{y} ) u)_{y} \,. \end{array} $$

The above reveals a combination of diffusive (first line) and advective (second line)-type terms, with the diffusive terms in the first line identical to those generated for standard anisotropic diffusion.

The choice of finite difference discretisation for diffusive terms is crucial: naive discretisations can lead to numerical instability for large and negative γ, see Mosayebi et al. (2010). The possibility of numerical instability can be reduced using the method in Weickert (1998): finite difference derivatives are calculated not only along the ‘standard’ axes of the lattice, but combined with those in an appropriately chosen new direction. Advective terms are discretised in conservative form, employing a first-order upwinding scheme. Time integration involves a forward Euler method with a suitably small time step Δt. To verify the numerical method, simulations have been performed for varying time-step and mesh-discretisations. The validity of the various numerical methods is further substantiated by convergence of the models within relevant regimes.