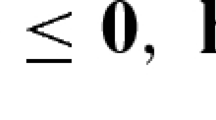Skip to main content
SpringerLink
Log in

Solving linear programs with complementarity constraints using branch-and-cut

  • Full Length Paper
  • Published:
Mathematical Programming Computation Aims and scope Submit manuscript

Abstract

A linear program with linear complementarity constraints (LPCC) requires the minimization of a linear objective over a set of linear constraints together with additional linear complementarity constraints. This class has emerged as a modeling paradigm for a broad collection of problems, including bilevel programs, Stackelberg games, inverse quadratic programs, and problems involving equilibrium constraints. The presence of the complementarity constraints results in a nonconvex optimization problem. We develop a branch-and-cut algorithm to find a global optimum for this class of optimization problems, where we branch directly on complementarities. We develop branching rules and feasibility recovery procedures and demonstrate their computational effectiveness in a comparison with CPLEX. The implementation builds on CPLEX through the use of callback routines. The computational results show that our approach is a strong alternative to constructing an integer programming formulation using big-M terms to represent bounds for variables, with testing conducted on general LPCCs as well as on instances generated from bilevel programs with convex quadratic lower level problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Achterberg, T.: Constraint integer programming. Ph.D. thesis, Technische University Berlin (2007)

  2. Achterberg, T., Koch, T., Martin, A.: Branching rules revisited. Oper. Res. Lett. 33(1), 42–54 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  3. Applegate, D., Bixby, R., Chvátal, V., Cook, W.: The Traveling Salesman Problem: A Computational Study. Princeton University Press, Princeton (2006)

    MATH  Google Scholar 

  4. Audet, C., Haddad, J., Savard, G.: Disjunctive cuts for continuous bilevel programming. Optim. Lett. 1(3), 259–267 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  5. Audet, C., Hansen, P., Jaumard, B., Savard, G.: A symmetrical linear maxmin approach to disjoint bilinear programming. Math. Program. 85(3), 573–592 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  6. Audet, C., Savard, G., Zghal, W.: New branch-and-cut algorithm for bilevel linear programming. J. Optim. Theory Appl. 38(2), 353–370 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bai, L., Mitchell, J.E., Pang, J.: On convex quadratic programs with linear complementarity constraints. Comput. Optim. Appl. 54(3), 517–554 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Bai, L., Mitchell, J.E., Pang, J.: On conic QPCCs, conic QCQPs and completely positive programs. Math. Program. 159(1–2), 109–136 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  9. Balas, E.: Disjunctive programming. Ann. Discrete Math. 5, 3–51 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  10. Bard, J.F., Moore, J.T.: A branch and bound algorithm for the bilevel programming program. SIAM J. Sci. Stat. Comput. 11(2), 281–292 (1990)

    Article  MATH  Google Scholar 

  11. Beale, E.M.L., Tomlin, J.A.: Special facilities in a general mathematical programming system for non-convex problems using ordered sets of variables. In: Lawrence, J. (ed.) Proceedings of the Fifth International Conference on Operational Research, pp. 447–454. Travistock Publications, London (1970)

  12. Benichou, M., Gauthier, J.M., Girodet, P., Hentges, G., Ribiere, G., Vincent, O.: Experiments in mixed-integer linear programming. Math. Program. 1(1), 76–94 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  13. Burdakov, O., Kanzow, C., Schwartz, A.: Mathematical programs with cardinality constraints: reformulation by complementarity-type conditions and a regularization method. SIAM J. Optim. 26(1), 397–425 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Cottle, R.W., Pang, J., Stone, R.S.: The Linear Complementarity Problem. Academic Press, Cambridge (1992)

    MATH  Google Scholar 

  15. Dolan, E., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91, 201–213 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  16. de Farias Jr., I.R., Johnson, E.L., Nemhauser, G.L.: A generalized assignment problem with special ordered sets: a polyhedral approach. Math. Program. 89(1), 187–203 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  17. de Farias Jr., I.R., Johnson, E.L., Nemhauser, G.L.: Branch-and-cut for combinatorial optimisation problems without auxiliary binary variables. Knowl. Eng. Rev. 16(1), 25–39 (2001)

    Article  MATH  Google Scholar 

  18. de Farias Jr., I.R., Kozyreff, E., Zhao, M.: Branch-and-cut for complementarity-constrained optimization. Math. Program. Comput. 6(4), 365–403 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Facchinei, F., Pang, J.: Finite-Dimensional Variational Inequalities and Complementarity Problems, vol. I,II. Springer, New York (2003)

    MATH  Google Scholar 

  20. Fang, H., Leyffer, S., Munson, T.S.: A pivoting algorithm for linear programs with complementarity constraints. Optim. Methods Softw. 27(1), 89–114 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  21. Feng, M., Mitchell, J.E., Pang, J., Shen, X., Wächter, A.: Complementarity formulations of $\ell _0$-norm optimization problems. Pac. J. Optim. 14(2), 273–305 (2018)

    MathSciNet  Google Scholar 

  22. Fischer, T., Pfetsch, M.E.: Branch-and-cut for linear programs with overlapping SOS1 constraints. Math. Program. Comput. 10(1), 33–68 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  23. Fischetti, M., Salvagnin, D.: Feasibility pump 2.0. Math. Program. Comput. 1(2–3), 201–222 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Fomeni, F.D., Gabriel, S.A., Anjos, M.F.: An RLT approach for solving the binary-constrained mixed linear complementarity problem. Tech. Rep. G-2015-60, GERAD, HEC Montréal, Canada (2015). https://www.gerad.ca/en/papers/G-2015-60

  25. Fügenschuh, A., Martin, A.: Computational integer programming and cutting planes. In: Handbooks in Operations Research and Management, vol. 12, chapter. 2, pp. 69–122. Elsevier (2005)

  26. Fukushima, M., Tseng, P.: An implementable active-set algorithm for computing a B-stationary point of a mathematical program with linear complementarity constraints. SIAM J. Optim. 12(3), 724–739 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Giannessi, F., Tomasin, E.: Nonconvex quadratic programs, linear complementarity problems, and integer linear programs. In: Conti, R., Ruberti, A. (eds.) Fifth Conference on Optimization Techniques (Rome 1973), Part I, Lecture Notes in Computer Science, vol. 3, pp. 437–449. Springer, Berlin (1973)

  28. Gleixner, A.M., Berthold, T., Müller, B., Weltge, S.: Three enhancements for optimization-based bound tightening. J. Glob. Optim. 67, 731–757 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  29. Hansen, P., Jaumard, B., Savard, G.: New branch-and-bound rules for linear bilevel programming. SIAM J. Sci. Stat. Comput. 13(5), 1194–1217 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  30. Hooker, J.N., Osorio, M.A.: Mixed logical-linear progrmaming. Discrete Appl. Math. 96–97, 395–442 (1999)

    Article  MATH  Google Scholar 

  31. Hu, J., Mitchell, J.E., Pang, J.: An LPCC approach to nonconvex quadratic programs. Math. Program. 133(1–2), 243–277 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  32. Hu, J., Mitchell, J.E., Pang, J., Bennett, K.P., Kunapuli, G.: On the global solution of linear programs with linear complementarity constraints. SIAM J. Optim. 19(1), 445–471 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  33. Hu, J., Mitchell, J.E., Pang, J., Yu, B.: On linear programs with linear complementarity constraints. J. Glob. Optim. 53(1), 29–51 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  34. Ibaraki, T.: The use of cuts in complementary programming. Oper. Res. 21, 353–359 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  35. ILOG Inc, Mountain View, California: ILOG CPLEX Callable Library C API 11.0 Reference Manual (2007)

  36. Izmailov, A.F., Solodov, M.V.: An active-set Newton method for mathematical programs with complementarity constraints. SIAM J. Optim. 19(3), 1003–1027 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  37. Jara-Moroni, F., Pang, J.S., Wächter, A.: A study of the difference-of-convex approach for solving linear programs with complementarity constraints. Math. Program. 169(1), 221–254 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  38. Jeroslow, R.G.: Cutting-planes for complementarity constraints. SIAM J. Control Optim. 16(1), 56–62 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  39. Júdice, J.J.: Algorithms for linear programming with linear complementarity constraints. TOP 20(1), 4–25 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  40. Júdice, J.J., Faustino, A.M.: A sequential LCP method for bilevel linear programming. Ann. Oper. Res. 34, 89–106 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  41. Keha, A.B., de Farias Jr, I.R., Nemhauser, G.L.: A branch-and-cut algorithm without binary variables for nonconvex piecewise linear optimization. Oper. Res. 54(5), 847–858 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  42. Kunapuli, G., Pang, J., Bennett, K.P.: Bilevel cross-validation-based model selection. In: Guyon, I., Crawley, G., Dror, G., Saffari, A. (eds.) Hands-On Pattern Recognition: Challenges in Machine Learning, vol. 1, chapter. 15, pp. 345–370. Mikrotone Publishing, Brookline, MA (2011)

  43. Lee, Y., Pang, J., Mitchell, J.E.: Global resolution of the support vector machine regression parameters selection problem with LPCC. EURO J. Comput. Optim. 3(1), 197–261 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  44. Leyffer, S., Lopez-Calva, G., Nocedal, J.: Interior methods for mathematical programs with complementarity constraints. SIAM J. Optim. 17(1), 52–77 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  45. Linderoth, J.T., Savelsbergh, M.W.P.: A computational study of strategies for mixed integer programming. INFORMS J. Comput. 11, 173–187 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  46. Luo, Z.Q., Pang, J., Ralph, D.: Mathematical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge (1996)

    Book  MATH  Google Scholar 

  47. Maranas, C.D., Floudas, C.A.: Global optimization in generalized geometric programming. Comput. Chem. Eng. 21, 351–569 (1997)

    Article  Google Scholar 

  48. McCormick, G.P.: Computability of global solutions to factorable nonconvex programs: part I—convex underestimating problems. Math. Program. 10, 147–175 (1976)

    Article  MATH  Google Scholar 

  49. Mitchell, J.E., Pang, J., Yu, B.: Obtaining tighter relaxations of mathematical programs with complementarity constraints. In: Terlaky, T., Curtis, F. (eds.) Modeling and Optimization: Theory and Applications, Springer Proceedings in Mathematics and Statistics, vol. 21, chapter. 1, pp. 1–23. Springer, New York (2012)

  50. Mitchell, J.E., Pang, J., Yu, B.: Convex quadratic relaxations of nonconvex quadratically constrained quadratic programs. Optim. Methods Softw. 29(1), 120–136 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  51. Pang, J.: Three modeling paradigms in mathematical programming. Math. Program. 125(2), 297–323 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  52. Pang, J., Fukushima, M.: Some feasibility issues in mathematical programs with equilibrium constraints. SIAM J. Optim. 8, 673–681 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  53. Pang, J., Leyffer, S.: On the global minimization of the Value-at-Risk. Optim. Methods Softw. 19(5), 611–631 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  54. Scholtes, S.: Convergence properties of a regularisation scheme for mathematical programs with complementarity constraints. SIAM J. Optim. 11(4), 918–936 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  55. Stackelberg, H.V.: The Theory of the Market Economy. Oxford University Press, Oxford (1952)

    Google Scholar 

  56. Vandenbussche, D., Nemhauser, G.L.: A branch-and-cut algorithm for nonconvex quadratic programs with box constraints. Math. Program. 102(3), 559–575 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  57. Watson, L.T., Billups, S.C., Mitchell, J.E., Easterling, D.R.: A globally convergent probability-one homotopy for linear programs with linear complementarity constraints. SIAM J. Optim. 23(2), 1167–1188 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  58. Zamora, J.M., Grossmann, I.E.: A branch and contract algorithm for problems with concave univariate, bilinear and linear fractional terms. J. Glob. Optim. 14(3), 217–249 (1999)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. JD.com, 675 E Middlefield Rd, Mountain View, CA, 94043, USA

    Bin Yu

  2. Department of Mathematical Sciences, Rensselaer Polytechnic Institute, Troy, NY, 12180, USA

    John E. Mitchell

  3. Department of Industrial and Systems Engineering, University of Southern California, Los Angeles, CA, 90089, USA

    Jong-Shi Pang

Authors
  1. Bin Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. John E. Mitchell
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jong-Shi Pang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to John E. Mitchell.

Additional information

Yu and Mitchell were supported in part by the Air Force Office of Sponsored Research under Grants FA9550-08-1-0081 and FA9550-11-1-0260 and by the National Science Foundation under Grant Numbers CMMI-1334327 and DMS-1736326. Pang was supported in part by the National Science Foundation under Grant Number CMMI-1333902 and by the Air Force Office of Scientific Research under Grant Number FA9550-11-1-0151.

The software that was reviewed as part of this submission was given in https://doi.org/10.5281/zenodo.1419515

Appendices

A LPCC test instances

See Tables 5 and 6.

Table 5 Objective function data for the 60 instances. All instances have \(n=2\) and \(k=20\). The number of complementarities is m. The rank of M and the density of each matrix are indicated. Three relative gaps are given as percentages: (1) the gap between the upper and lower bounds obtained through preprocessing, (2) the gap between the upper bound obtained from feasibility recovery and the optimal value of the LPCC, and (3) the improvement in the gap between upper and lower bound effected by the improvement in the LP relaxation obtained through preprocessing
Full size table
Table 6 Performance data for the 60 instances. The final gap obtained by default CPLEX is indicated for the 18 instances it didn’t solve (DNF) within the time limit of 3600 s
Full size table

In order to test the effectiveness of different type of valid constraints, a series of LPCC instances was randomly generated, and Procedure 4 gives a detailed description of the generator.

figure d

Remark 1

In the initialization step of the procedure, n is the dimension of x variable; m is the dimension of y variable; k is the dimension of b; rankM is the rank of matrix M; dense is the density of generated matrices; we assume all instances have the non-negativity constraint \(x\ge 0\) which are not included in the constraint \(Ax+By\ge b\); step 1 and step 2 are used to generate a feasible LPCC solution; step 8 is to generate matrix M to be a non-symmetric positive semidefinite matrix with rank rankM.

We generated 60 LPCC instances with 100, 150, 200 complementaries, 20 instances of each size, and with the same parameter, we randomly generated 5 instances. For CPLEX solving LPCC instances, we used indicator constraints in CPLEX C callable library [35] to formulate the complementarity constraints, and the CPLEX setting is default. The time limit for CPLEX is 3600 s. Notice that default CPLEX is unable to solve most of our LPCC instances when \(m=200\) within 3600 s.

Table 5 contains objective function value information for the 60 instances, including the effectiveness of the preprocessing routines. Table 6 contains performance data.

B Bilevel test instances

See Tables 7, 8, 9, and 10.

Table 7 Values of bilevel instances with dimension of v equal to 50
Full size table
Table 8 Values of bilevel instances with larger dimensions of v. The final gaps obtained by each code are indicated for the instances it did not solve
Full size table
Table 9 Performance on bilevel instances with dimension of v equal to 50
Full size table
Table 10 Performance on bilevel instances with larger dimensions of v
Full size table

Our code solved all 63 of the instances with dimension of v equal to 50 and 18 / 35 of the larger instances. With extended time, default CPLEX was able to solve all but one problem with \(n=50\); it still has a gap of 16.56% for problem 60 after more than 7200 s of wall clock time and 47304 s of processor time. It solved just 6 / 35 of the larger instances. Run time information can be found in Tables 9 and 10.

C Inverse QP instances

See Table 11.

Computational results on 25 inverse QP instances can be found in Table 11. For each set of 5 instances, the average CPU time is listed if all the instances were solved or the number of solved instances is noted.

Table 11 Performance on 25 inverse quadratic programs. Mean solution time is listed for each set of five problems solved successfully by a code; otherwise, the number of solved instances is given. The number of cutting planes added by CPLEX MIP is also reported; GF are Gomory fractional cuts, MIR are mixed integer rounding cuts, L&P are lift-and-project cuts, and IB are implicit bound cuts
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, B., Mitchell, J.E. & Pang, JS. Solving linear programs with complementarity constraints using branch-and-cut. Math. Prog. Comp. 11, 267–310 (2019). https://doi.org/10.1007/s12532-018-0149-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12532-018-0149-2

Keywords

Mathematics Subject Classification

Search

Navigation