Abstract
In 1886 Giuseppe Peano presents the first proof of the existence of a solution of an initial value problem \(y^\prime =f(x,y)\), \(y(a)=b\), under the assumption of the continuity of the function f. The present paper gives a detailed description of Peano’s original statements and proofs, filling gaps, clarifying obscure points and avoiding ambiguous use of mathematical symbols. Peano’s 1886 work is compared with later papers of Peano himself as well as of Mie (Math Ann 43:553–568, 1893), Osgood (Monatsh Math Phys 9:331–345, 1898) and Perron (Math. Ann. 76:471–484, 1915).
Similar content being viewed by others
Notes
Among the huge literature on differential equations, we have analyzed the work of a restricted number of authors. Our choice is based on the particular topic under study and cannot be exhaustive.
We believe that our proposal to fill gaps in 1886 original proof is not the only possibility. The reader can try alternative ways.
Here and in the sequel, we quote passages of Peano’s paper from the English translation in Kennedy [15] and, for a typographical convenience, we replace the symbols of derivative of the form \(\frac{d y}{d x}\), used by Peano, with \(y^\prime \).
It is worth noticing that the family of the continuous piecewise linear functions \(y_{1}\) (resp. \(y_{2}\)), verifying the inequality \(y_{1}^\prime >f(x,y_{1})\) (resp. \(y_{2}^\prime <f(x,y_{2})\)) on each closed interval where are linear, is the minimum we need to support and to validate Peano’s 1886 arguments.
In fact this convention relative to the definition of sub- and super-solution is rather natural and it is adopted also in the modern mathematical literature on differential equations [13].
Observe that it is implicitly assumed that the inequality “\(D_{\pm }\gamma (x)>t\)” should be understood as “\(D_{+}\gamma (x)>t\)” (resp. “\(D_{-}\gamma (x)>t\)”), whenever x is the lower extremum (resp. upper extremum) of the domain of \(\gamma \). A similar convention holds for the other inequalities \(D_{\pm }\gamma (x)\ge t\), \(D_{\pm }\gamma (x)< t\), \(D_{\pm }\gamma (x)\le t\).
In proving Theorem 3 it is necessary only the existence of at least one strict sub-solution and one strict super-solution. In Peano’s original proof of (2.3) strict sub- and super-solutions are constructed as continuous piecewise linear functions. In this way the interval where the related differential inequalities (2.2) are valid can be enlarged. This technique allows Peano to assert (2.3), i.e., there are infinitely many strict super- and sub-solutions.
Kennedy [14] has misunderstood this point of Peano’s proof and thus considered it wrong.
Proof of the existence of \(\bar{\nu }_{n}\). Let \(\hat{b}\) and M be real numbers verifying the following four inequalities: (i)
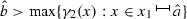 , (ii) \(\hat{b}>\nu _{n}(x_{1})\), (iii)
, (ii) \(\hat{b}>\nu _{n}(x_{1})\), (iii) 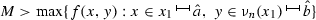 and (iv) \(M(\hat{a}-x_{1})>\hat{b}-\nu _{n}(x_{1})\). Define the linear function \(\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) by \(\psi (x):=\nu _{n}(x_{1})+M(x-x_{1})\) and consider the real number \(\hat{x}:=x_{1}+ \frac{\hat{b}-\nu _{n}(x_{1})}{M}\). Clearly, \(x_{1}<\hat{x}<x_{1}+\frac{M(\hat{a} -x_{1})}{M}=\hat{a}\) and \(\nu _{n}(x_{1})=\psi (x_{1})\le \psi (x)\le \psi (\hat{x})=\hat{b}\) for every
and (iv) \(M(\hat{a}-x_{1})>\hat{b}-\nu _{n}(x_{1})\). Define the linear function \(\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) by \(\psi (x):=\nu _{n}(x_{1})+M(x-x_{1})\) and consider the real number \(\hat{x}:=x_{1}+ \frac{\hat{b}-\nu _{n}(x_{1})}{M}\). Clearly, \(x_{1}<\hat{x}<x_{1}+\frac{M(\hat{a} -x_{1})}{M}=\hat{a}\) and \(\nu _{n}(x_{1})=\psi (x_{1})\le \psi (x)\le \psi (\hat{x})=\hat{b}\) for every 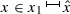 ; hence, by (iii) we have that \(\psi \) is a strict super-solution of (ODE) on
; hence, by (iii) we have that \(\psi \) is a strict super-solution of (ODE) on 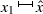 . Thus, the required strict super-solution function \(\bar{\nu }_{n}\) is defined by \(\bar{\nu }_{n}(x):=\inf \{\nu _{n}(x),\gamma _{2}(x)\}\) for
. Thus, the required strict super-solution function \(\bar{\nu }_{n}\) is defined by \(\bar{\nu }_{n}(x):=\inf \{\nu _{n}(x),\gamma _{2}(x)\}\) for  , \(\bar{\nu }_{n}(x):=\inf \{\psi (x),\gamma _{2}(x)\}\) for
, \(\bar{\nu }_{n}(x):=\inf \{\psi (x),\gamma _{2}(x)\}\) for 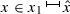 and \(\bar{\nu }_{n}(x):=\gamma _{2}(x)\) for
and \(\bar{\nu }_{n}(x):=\gamma _{2}(x)\) for 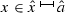 .
.Proof of the left-continuity of \(\Phi \) at \(x_0\). By (3.18) one can deduce the inequality \(\limsup _{x\rightarrow x_{0}^{-}}\Phi (x)\le \Phi (x_{0})\). To prove the remaining inequality \(\Phi (x_{0})\le \liminf _{x\rightarrow x_{0}^{-}}\Phi (x)\), choose \(b_{1},b_{2},M,\delta \in {\mathbb {R}}\) such that \(0<\delta <x_{0}-a\) and
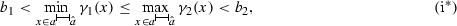
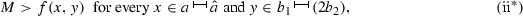

Let
 , \(\mu \in {{\mathop {\mathrm {Sol}}}}_{>}(b;a,\hat{a})\) and let us define the linear function \(\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) by \(\psi (x):=\bar{\mu }(\tilde{x})+M(x-\tilde{x})\), where \(\bar{\mu }\) is a strict super-solution of (ODE) on
, \(\mu \in {{\mathop {\mathrm {Sol}}}}_{>}(b;a,\hat{a})\) and let us define the linear function \(\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) by \(\psi (x):=\bar{\mu }(\tilde{x})+M(x-\tilde{x})\), where \(\bar{\mu }\) is a strict super-solution of (ODE) on  , defined by \(\bar{\mu }:=\inf \{\mu ,\gamma _{2}\}\). From (i\(^*\)) and (iii\(^*\)) it follows that the solution \(\hat{x}:=\tilde{x}+\frac{2b_{2}-\bar{\mu }(\tilde{x})}{M}\) of the equation \(\psi (x)=2b_{2}\) satisfies:
, defined by \(\bar{\mu }:=\inf \{\mu ,\gamma _{2}\}\). From (i\(^*\)) and (iii\(^*\)) it follows that the solution \(\hat{x}:=\tilde{x}+\frac{2b_{2}-\bar{\mu }(\tilde{x})}{M}\) of the equation \(\psi (x)=2b_{2}\) satisfies: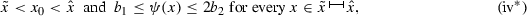
since \(\gamma _{1}\le \bar{\mu }\le \gamma _{2}\), \(\hat{x}> \tilde{x}+\frac{b_{2}}{M}> \tilde{x}+\frac{M\delta }{M}=x_{0}+\delta >x_{0}\), and
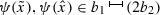 . On the other hand, from (ii\(^*\)) and (iv\(^*\)) it follows that
. On the other hand, from (ii\(^*\)) and (iv\(^*\)) it follows that
Now define a function
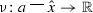 by
byFootnote 11 continued
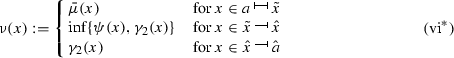
in the case where \(\hat{x}<\hat{a}\); otherwise
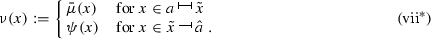
Consequently, since \(\bar{\mu }\) is a strict super-solution of (ODE) on
 , by (v\(^*\)) we have that \(\nu \) is a strict super-solution of (ODE) on
, by (v\(^*\)) we have that \(\nu \) is a strict super-solution of (ODE) on  . Then from the definition (3.8) of \(\Phi \) follows that \(\Phi (x_{0})\le \nu (x_{0})\le \psi (x_{0})=\bar{\mu }(\tilde{x})+M(x_{0}-\tilde{x})\le \mu (\tilde{x})+M(x_{0}-\tilde{x})\). Therefore, by the arbitrariness of
. Then from the definition (3.8) of \(\Phi \) follows that \(\Phi (x_{0})\le \nu (x_{0})\le \psi (x_{0})=\bar{\mu }(\tilde{x})+M(x_{0}-\tilde{x})\le \mu (\tilde{x})+M(x_{0}-\tilde{x})\). Therefore, by the arbitrariness of  and \(\mu \in {\mathop {\mathrm {Sol}}}(b;a,\hat{a})\), we have \(\Phi (x_{0})\le \Phi (\tilde{x})+M(x_{0}-\tilde{x})\) for every
and \(\mu \in {\mathop {\mathrm {Sol}}}(b;a,\hat{a})\), we have \(\Phi (x_{0})\le \Phi (\tilde{x})+M(x_{0}-\tilde{x})\) for every 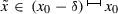 ; hence, \(\Phi (x_{0})\le \liminf _{\tilde{x}\rightarrow x_{0}^{-}}\Phi (\tilde{x})\). This concludes the proof of the left-continuity of \(\Phi \) at \(x_{0}\).
; hence, \(\Phi (x_{0})\le \liminf _{\tilde{x}\rightarrow x_{0}^{-}}\Phi (\tilde{x})\). This concludes the proof of the left-continuity of \(\Phi \) at \(x_{0}\).I.e., the set \(\{y\in {\mathbb {R}}:(x,y)\in \mathrm {dom} (f)\}\) is a non-empty interval for every
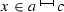 .
.
References
Arzelà, C.: Sull’integrabilità delle equazioni differenziali ordinarie. R. Accad. Sci. Istit. Bologna Mem. 5, 257–270 (1895–96)
Birkhoff, G., Merzbach, U.: A Source Book in Classical Analysis. Harvard University Press, Massachusetts (1973)
de La Vallée Poussin, Ch.-J.: Mémoire sur l’intégration des équations différentielles. Mémoires. Acad. R. Belgique 47, 1–82 (1893) [de La Vallée Poussin, Ch.-J.: Collected Works, Oeuvres Scientifiques. In: Butzer, P., Mawhin, J., Vetro, P. (eds) Académie Royale de Belgique and Circolo Matematico di Palermo, vol. 2, pp. 405–486 (2001)]
de La Vallée Poussin, Ch.-J.: Sur l’intégration des équations différentielles. Ann. Soc. Sci. Bruxelles 17 (1e partie), 8–12 (1893) [de La Vallée Poussin, Ch.-J.: Collected Works, Oeuvres Scientifiques. In: Butzer, P., Mawhin, J., Vetro, P. (eds.) Académie Royale de Belgique and Circolo Matematico di Palermo, vol. 2, pp. 487–491 (2001)]
Dow, M.A., Výborný, R.: Elementary proofs of Peano’s existence theorem. J. Aust. Math. Soc. 15, 366–372 (1973)
Flett, T.M.: Differential Analysis. Cambridge University Press, Cambridge (1980)
Fukuhara, M.: Sur les systèmes des équations differentielles ordinaires. Jpn. J. Math. 5, 345–350 (1928)
Fukuhara, M.: Sur le théorème d’existence des intégrales des équations différentielles ordinaires du premier ordre. Jpn. J. Math. 5, 239–251 (1928)
Gardner, C.: Another elementary proof of Peano’s existence theorem. Am. Math. Monthly 83, 556–560 (1976)
Gilain, C.: Introduction to A. L. Cauchy: Équations différentielles ordinaires. Cours inédit. Fragment. Études Vivantes, Paris (1981)
Greco, G.H., Mazzucchi, S.: The originality of Peano’s 1886 existence theorem for scalar differential equations. J. Convex Anal. 23 (2016) (to appear)
Greco, G.H., Mazzucchi, S.: Peano’s 1890 proof of existence theorem for systems of differential equations: a celebrated unknown (forthcoming, 2016)
Hubbard, J.H., West, B.H.: Differential Equations: A Dynamical Systems Approach Ordinary Differential Equations. Springer, New York (1991)
Kennedy, H.C.: Is there an elementary proof of Peano’s existence theorem for first order differential equations? Am. Math. Monthly 76, 1043–1045 (1969)
Kennedy, H.C.: Selected works of Giuseppe Peano. Allen & Unwin Ltd, Sydney (1973)
Kennedy, H.C.: Life and Works of Giuseppe Peano, Peremptory Edition (2nd edn.) (2006)
Kneser, H.: Uber die Lösungen eine system gewöhnlicher differential Gleichungen, das der lipschitzschen Bedingung nicht genügt S. B. Preuss Akad. Wiss. Phys. Math. Kl. 4, 171–174 (1923)
López Pouso, R.: Peano’s Existence Theorem Revisited. arXiv:1202.1152 (2012)
López Pouso, R.: Greatest solutions and differential inequalities: a journey in two directions. arXiv:1304.3576 (2013)
Mawhin, J.: Integration and the fundamental theory of ordinary differential equations : a historical sketch. In: Rassias, T.M. (ed.) Constantin Carathéodory, an International Tribute, vol. 2, pp. 828–849. World Scientific Publishing, Singapore (1991)
Mie, G.: Beweis der Integribarkeit gewöhnlicher Differentialgleichungssysteme nach Peano. Math. Ann. 43, 553–568 (1893)
Osgood, W.F.: Beweis der Existenz einer Lösung der Differentialgleichung \(\frac{dy}{dx}=f(x, y)\) ohne Hinzunahme der Cauchy-Lipschitzchen Bedingung. Monatsh. Math. Phys. 9, 331–345 (1898)
Painlevé, P.: Existence de l’intégrale générale. In: Molk, J. (ed.) Encyclopédie des Sciences Mathématiques pures et appliquées, vol. 2.3, pp. 1–57. Gauthiers-Villars, Paris (1910)
Peano, G.: Sull’integrabilità delle equazioni differenziali di primo ordine. Atti Reale Accad. Sci. Torino 21, 677–685 (1885–86)
Peano, G.: Applicazioni geometriche del calcolo infinitesimale. Fratelli Bocca Editori, Torino (1887)
Peano, G.: Démonstration de l’intégrabilité des équations différentielles ordinaires. Math. Ann. 37, 182–228 (1890)
Peano, G.: Sur la définition de la dérivée. Mathesis 12, 12–14 (1892)
Peano, G.: Sulla definizione di integrale. Ann. Mat. Pura Appl. 23, 153–157 (1895)
Peano, G.: Formulario Mathematico, 5th edn. Fratres Bocca, Torino (1908) (reprinted by Cremonese, Roma, 1960)
Perron, O.: Ein neuer Existenzbeweis für die Integrale der Differentialgleichung \(y = f (x, y)\). Math. Ann. 76, 471–484 (1915)
Perron, O.: Eine neue behandlung der ersten randwertaufgabe für \(\Delta u=0\). Math. Z. 18, 42–54 (1923)
Volterra, V.: Sui principi del calcolo integrale. G. Mat. (Battaglini) 19, 333–372 (1881)
Walter, J.: On elementary proofs of Peano’s existence theorems. Am. Math. Monthly 80, 282–286 (1973)
Walter, W.: There is an elementary proof of Peano’s existence theorem. Am. Math. Monthly 78, 170–173 (1971)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Greco, G.H., Mazzucchi, S. Peano’s 1886 existence theorem on first-order scalar differential equations: a review. Boll Unione Mat Ital 9, 375–389 (2016). https://doi.org/10.1007/s40574-016-0052-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40574-016-0052-6



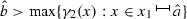 , (ii)
, (ii) 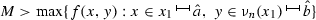 and (iv)
and (iv) 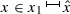 ; hence, by (iii) we have that
; hence, by (iii) we have that 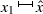 . Thus, the required strict super-solution function
. Thus, the required strict super-solution function  ,
, 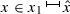 and
and 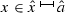 .
.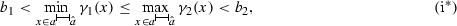
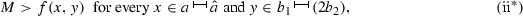

 ,
,  , defined by
, defined by 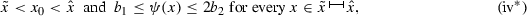
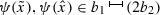 . On the other hand, from (ii
. On the other hand, from (ii
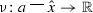 by
by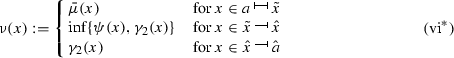
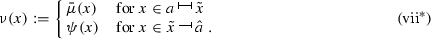
 , by (v
, by (v . Then from the definition (3.8) of
. Then from the definition (3.8) of  and
and 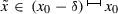 ; hence,
; hence, 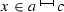 .
.