The invariant-based shortcut to adiabaticity for qubit heat engine operates under quantum Otto cycle

Abstract

In this paper, we study the role and relevance of the cost for an invariant-based shortcut to adiabaticity enabled qubit heat engine operates in a quantum Otto cycle. We consider a qubit heat engine with Landau-Zener Hamiltonian and improve its performance using the Lewis–Riesenfeld invariant-based shortcut to adiabaticity method. Addressing the importance of cost for better performance, the paper explores its relationship with the work and efficiency of the heat engine. We analyze the cost variation with the time duration of non-adiabatic unitary processes involved in the heat engine cycle. The cost required to attain the quasi-static performance of the qubit heat engine is also discussed. We found the efficiency lost due to non-adiabaticity of the engine can be revived using the shortcut method and it is even possible to attain quasi-static performance under finite time with higher cost.

Appendices

Appendix A: Time-dependent Schrodinger Equation; Numerical Approach

Fig. 9

Splitting the total time duration in to ‘n’ equal intervals gives F(t) and the time evolution operators in a sequence. Algorithm to find the time evolution of $\tilde{\Psi }(t)$ should not change this sequence as the operator F(t) at different instants of time do not commute in general $\left( \left[ F(t_{a}),F(t_{b})\right] \ne 0; a,b\in \left\{ 0,n\right\} \right)$

Consider in general, this paper deals with the time evolution of some state $\tilde{\Psi }(t)$ corresponding to the Schrodinger equation $i\frac{\partial \tilde{\Psi }(t)}{\partial t}=F(t)\tilde{\Psi }(t)$. F(t) is the generator of time evolution, which represents any of the Hermitian operators $\mathcal {\hat{H}}_{S}(t),\mathcal {\hat{H}}_{LZ}(t)$ and $\mathcal {\hat{I}}(t)$. Analytical solution might be existing for some particular F(t). However, a numerical solution is the general possibility for any operator F(t). Calculating the evolution of $\tilde{\Psi }(t)$ requires enormous computational power. The non-commuting F(t) at different instants of time further restricts the algorithms to follow the F(t) sequentially in time space. In other words, splitting the total time duration ($\tau$) in to ‘n’ equal intervals gives a sequence of time evolution operators as explained in Fig. 9. We can define $F(t_{i})$ at any instant of time $t_{i}$, where $i\in \left\{ 0,n\right\}$, the initial time $t_{0}=0$ and the final time $t_{n}=\tau$. By defining a step by step evolution operator $U(t_{i};t_{i+1})$, we can construct the total evolution operator as [51]

$$\begin{aligned} U(0;\tau )=\prod _{i=0}^{n-1}U(t_{i};t_{i+1}), \end{aligned}$$

(40)

where

$$\begin{aligned} U(t_{i};t_{i+1})=exp\left( -i\int _{t_{i}}^{t_{i+1}}F(t)dt\right) . \end{aligned}$$

(41)

For a very large value of ‘n’, we can approximate that the operator $F(t)=F\left( \frac{t_{i}+t_{i+1}}{2}\right)$ is fixed in between $t_{i}$ and $t_{i+1}$ for all $i\in \left\{ 0,n-1\right\}$ [62, 63]. The approximation of fixed generator for smaller intervals of time reduces the time evolution operator to

$$\begin{aligned} U(t_{i}:t_{i+1})=exp\left( -i\cdot F\left( \frac{t_{i}+t_{i+1}}{2}\right) \cdot (t_{i+1}-t_{i})\right) . \end{aligned}$$

(42)

Iteratively finding $U\left( t_{i};t_{i+1}\right)$ gives the time evolution operator for the total duration, $U(0;\tau )$, which gives the final state $\tilde{\Psi }(\tau )$ from $\tilde{\Psi }(0)$ using the equation, $\tilde{\Psi }(\tau )=U(0;\tau )\tilde{\Psi }(0)$. The step by step algorithm is as follows,

• Step 1: Initialize the variables $n,t_{0}$ and $t_{n}$

• Step 2: Define the set of $n+1$ values in between $t_{0}$ and $t_{n}$

• Step 3: Iteratively find the values of $F\left( \frac{t_{i}+t_{i+1}}{2}\right)$ and $U(t_{i};t_{i+1})$ by looping over all the values of ’i’.

• Step 4: Find $U(0;\tau )$, using Eq. (40).

• Stap 5: Find $\tilde{\Psi }(\tau )$ from $\tilde{\Psi }(0)$ by applying $U(0;\tau )$.

We have executed the above algorithm for $F(t)=\mathcal {\hat{H}}_{S}(t), \mathcal {\hat{H}}_{LZ}(t)$ and $\mathcal {\hat{I}}$. The initial time is set to 0 setting $\tau$ as the total duration of the process. Also, the algorithm is implemented for various $\tau$ values. We split the total time duration to 10000 small intervals ($n=10001$), which gave the precision up to three decimal points. This iterative approach always preserve the sequence of time evolution operator necessary for the non-commuting generators of time evolution. This method is partially inspired from the numerical approach explained in the Ref. [52], which update the evolved state using the fourth-order Runge-Kutta iteration method. Instead of updating the evolved state, we update the evolution operator, which reduces the computational complexity by avoiding the use of fourth-order Runge-Kutta method for each loop of iteration.

Appendix B: Fidelity analysis for two more z(t) protocols

Fig. 10

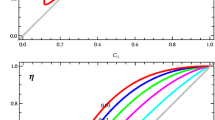
Fidelity of the unitary processes using LR invariant is plotted against the cost ratio, $\frac{C_{I}}{C_{LZ}}$ for time duration, $\tau =1.0$. The corresponding fidelity of the QHE with LZ Hamiltonian is included in each plot for comparison. The change in the energy gap is fixed corresponding to the ratio, a $\frac{\epsilon _{2}}{\epsilon _{1}}=0.4$ and b $\frac{\epsilon _{2}}{\epsilon _{1}}=0.6$. $C_{I}$ is changed by the parametric variation of x(t), y(t) and z(t) (i.e., $z_{1}(t)$ or $z_{2}(t)$) with constant X given by Eqs. (28), (29), (43), (44) and (21) respectively

We have been using the protocol given in Eq. (35) to analyze the cost and performance of invariant-based STA enabled QHE. A natural question arises is the variation in efficiency and work for some other protocol for z(t). The dependence of performance on the selection of z(t) is completely arbitrary resulting from the random path of evolution. However, we can analyze such variations in performance by constituting different protocols for z(t) obeying the conditions given in Eqs. (32),(33) and (34). In this appendix, we consider two more feasible protocols for z(t),

$$\begin{aligned} z_{1}(t)= & {} z(0)+\left( z(\tau )-z(0)\right) sin^{2}\left[ \frac{\pi }{2}sin^{2}\left( \frac{\pi t}{2\tau }\right) \right] , \end{aligned}$$

(43)

$$\begin{aligned} z_{2}(t)= & {} z(0)+30\left( z(\tau )-z(0)\right) \left( \frac{t}{\tau }\right) ^{4}-54\left( z(\tau )-z(0)\right) \left( \frac{t}{\tau }\right) ^{5}+25\left( z(\tau )-z(0)\right) \left( \frac{t}{\tau }\right) ^{6}, \end{aligned}$$

(44)

where, $z_{1}(t)$ is inspired from Ref. [64] and we have constructed $z_{2}(t)$ by our own. Although it is labeled as $z_{1}(t)$ and $z_{2}(t)$ for distinguishability, but it follows all the necessary conditions for z(t) and can replace z(t) in Sect. (4) to analyze the performance of the engine.

The performance analysis in Sect. 4, shows the linear dependence of work and efficiency on the fidelity of unitary process (i.e., the heat exchanged, that characterizing the heat engine is a linear function of fidelity). Thus, the comparison of fidelity among LZ dynamics and Invariant dynamics of the engine gives intuitive conclusion regarding the performance of the engine. Figure 10 shows the fidelity of invariant-based STA engine with protocol $z_{1}(t)$ and $z_{2}(t)$ along with fidelity of LZ Hamiltonian for comparison. By analyzing the fidelity plots and comparing with Fig. 5, we can conclude that, the both the protocols $z_{1}(t)$ and $z_{2}(t)$ cost more than that of the protocol in Eq. (35) to outperform the LZ dynamics. Also, the arbitrariness in dependence of fidelity (equivalently performance) on different protocol is evident from the plot.