A Novel Bayesian Model Incorporating Deep Neural Network and Statistical Shape Model for Pancreas Segmentation

Abstract

Deep neural networks have achieved significant success in medical image segmentation in recent years. However, poor contrast to surrounding tissues and high flexibility of anatomical structure of the interest object are still challenges. On the other hand, statistical shape model based approaches have demonstrated promising performance on exploiting complex shape variabilities but they are sensitive to localization and initialization. This motivates us to leverage the rich shape priors learned from statistical shape models to improve the segmentation of deep neural networks. In this work, we propose a novel Bayesian model incorporating the segmentation results from both deep neural network and statistical shape model for segmentation. In evaluation, experiments are performed on 82 CT datasets of the challenging public NIH pancreas dataset. We report 85.32 % of the mean DSC that outperforms the state-of-the-art and approximately 12 % improvement from the predicted segment of deep neural network.

1 Introduction

With the rapid development of Convolutional Neural Networks (CNNs) in semantic segmentation, deep neural networks like U-Net [1], SegNet [2] have become a popular trend in medical image segmentation and achieved remarkable success in segmentation of many organs, e.g. liver, lung and spleen. However, segmentation of challenging organs such as pancreas still remains difficulties due to the relatively small region in the whole volume, highly complex anatomical structure and significantly ambiguous boundary. On the other hand, usually the amount of labeled medical image data is limited which inhibits the segmentation from achieving considerable accuracy. To tackle these challenges, we aim to propose a robust segmentation approach for pancreas, which is one of the most challenging organs.

Numerous works focus on pancreas segmentation in literature, and the majority of them adopt deep neural networks with various refinement methods. In [3, 4], a coarse-to-fine framework is designed where the coarse network is trained to obtain the rough segment and remove the background regions, afterwards the shrunken region is passed to the fine network for precise segmentation. In [5], a Recurrent Neural Network (RNN) combining with CNN layers is employed to exploit spatial relations among successive slices. On the other hand, traditional machine learning approaches are demonstrated to be useful in segmentation framework for locally fine-tuning, e.g., random forests are utilized in feature extraction and classification following the deep neural networks in [6, 7] and Gaussian Mixture Model is employed to refine the U-Net in [8].

Considering of the ambiguities on boundary, it is well worth to leverage the 3D shape variabilities to distinguish the non-visible boundary, this motivates us to employ statistical shape models in segmentation framework. Through back projection onto the shape model, the corruptness on input shape is supposed to be corrected. Owing to the high variability of pancreas shape, we adopt the robust kernel statistical shape model presented in [9] as it has compelling advantages in handling corrupted and highly deformable training data than conventional PCA models. However, the model based approaches are sensitive to initialization, thus a deep neural network plays an important role in providing a rough segmentation for shape model initialization. With this motivation, we integrate the segmentation from deep neural network and statistical shape model within a Bayesian model for pancreas segmentation. A novel optimization principle joint with image feature and shape prior is proposed to guide segmentation. Our approach is demonstrated to be promising and efficient in terms of evaluation.

2 Method

In this section, we elaborate our segmentation approach starting with the deep neural network architecture, followed by the Bayesian model. Let us assume we have a set of 3D CT volumes $I = \{I_1, \dots , I_N\}$ and corresponding ground truth mask $Y= \{ Y_1, \dots Y_N\}$ for training. We extract shapes $S= \{S_1, \dots , S_N\}$ from the ground truth mask to train the robust kernel statistical shape model [9], defined as $RKSSM(S |\mathrm {\Phi }; \mathrm {V} ; \mathrm {K})$, where $\mathrm {\Phi }$ represents the implicit feature space, $\mathrm {V}$ decides the eigenvectors in kernel space, $\mathrm {K}$ is the robust kernel matrix with elements $\mathrm {K}_{ij} = \kappa (S_i,S_j ) = \mathrm {\Phi }(S_i)^T\mathrm {\Phi }(S_j)$ and $\kappa$ is the kernel trick function.

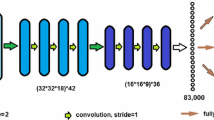
2.1 Dense-UNet Segmentation Network

DenseNet [10] has advantages in narrowing the network width, reusing features and significantly alleviating the problem of gradient vanishing. Therefore, we adopt the DenseNet in U-Net architecture by simply replacing the stacked $Conv-Relu$ and a following max pooling operation at each downsampling step with a 3-layer dense block with the growth rate of 4, meanwhile, keeping the upsampling path and concatenation unchanged. We use the Dice coefficient loss with a smooth value according to the most of related works that $\mathcal {L}(Z, Y) = 1 - \frac{2 \times \sum _{i} z_i y_i + 0.1}{\sum _{i} (z_i^2 + \sum _{i} y_i^2) + 0.1}$, where Z represents the predicted mask. Our Dense-UNet is trained with 2D slices extracted from 3D training images from Axial view, Sagittal view and Coronal view respectively, resulting in three predicted segment $Z^A$, $Z^S$ and $Z^C$. Due to the ReLu activation in the output layer, the intensity range in predicted segment is in [0, 255]. To make use of the predicted segments in further Bayesian model, we generate probability maps $\varPi = \{\varPi _1, \dots , \varPi _N\}$ by merging the three predicted segments and feeding into a sigmoid logistic function:

$$\begin{aligned} \varPi _i = \frac{1}{1 + \exp (- \frac{S^A_i + S^Z_i + S^C_i}{255} )}, \end{aligned}$$

(1)

where $\varPi _i$ indicates the probability map of the $i^{th}$ image. Using the sigmoid function to compute probability map is because (1) this is a binary segmentation task with 2 classes in total, and (2) considering the uncertain accuracy of Dense U-Net, we make the probability for each pixel in range [0.5, 1] that “1” indicates the pixel has a considerable probability of being ROI (Region of Interest) and “0.5” indicates the pixel is unsure to be ROI or NOI (Non of Interest). Apparently, the intersection region of $Z^A$, $Z^S$ and $Z^C$ is assigned higher probabilities, and uncertain or corrupted areas receive lower probabilities.

2.2 Bayesian Model

Let the shape model RKSSM fed into $\varPi$ for initialization (cf. Fig. 1(b)), we have an initial shape of segmentation $C = \{x_1, \dots , x_{n_P}\}$, where landmark $x_i$ represents the $i^{th}$ pixel in the test image. Given the test image I, probability map $\varPi$ and the shape model RKSSM, assume the optimal shape C can be derived using Bayes’ rule as follows:

$$\begin{aligned} p(C | I, \varPi ) \propto p(I, \varPi | C) \ p(C) , \end{aligned}$$

(2)

term $p(I, \varPi | C)$ is maximum likelihood estimation of C based on image and probability map and term p(C) is considered as the prior distribution of the shape model. Shape C is guided towards the most probable mode by maximizing the posteriori in Eq. 2, which is equivalent to simply minimizing its negative logarithm leading to the energy function:

$$\begin{aligned} E(C) = -\log (p(I, \varPi | C)) - \log (p(C)), \end{aligned}$$

(3)

the first term related to the intensity feature is solved via a Gaussian Mixture Model and the second term related to the shape prior is solved with the shape model. The optimal solution is reached by adapting the gradient descent to the energy. The overall procedure of segmentation algorithm is summarized in Algorithm 1.

Fig. 1.

This figure illustrates the pipeline of segmentation approach: given the test image with probability map (a), the shape model is initialized to fit the detected region (b); considering the neighborhood region around each landmark (c), a Gaussian Mixture Model is trained (d) to guide shape adaption (e); afterwards, project the shape onto statistical shape model (f); we obtain the segmentation output (g) when the convergence is reached.

Gaussian Mixture Model Joint with Probability Map. To find the maximum likelihood of $p(I, \varPi | C)$, we train a Gaussian Mixture Model (GMM) based on the image intensity as the pixels are statistically independent from each other. In contrast to conventional mixture models, the probability map $\varPi$ is adopted as prior weights of different components in the model. Let $X = \{x_1, \dots , x_{n_K}\}$ be a D-dimension image with $n_K$ pixels, the probability density function of GMM is defined as:

$$\begin{aligned} \mathcal {P}(X | \varPi , \varTheta ) = \prod _{i = 1}^{n_K} \{ \pi _i \varPsi (x_i | \varTheta _R) + (1 - \pi _i) \varPsi (x_i | \varTheta _N ) \} , \end{aligned}$$

(4)

given that $\varPsi (X|\varTheta _R)$ follows Gaussian distribution where the parameters $\varTheta _R$ consists of mean value and standard deviation of image intensity, $\varPsi (X|\varTheta _N)$ is defined in the same way. This GMM contains two independent components $\varPsi (X|\varTheta _R)$ and $\varPsi (X|\varTheta _N)$ representing ROI and NOI. As a result, the probability of pixel $x_i$ being each component can be estimated from GMM in Eq. 4, we define $w_R(x_i)$ and $w_N(x_i)$ as the probability of pixel $x_i$ being ROI and NOI:

$$\begin{aligned} \begin{aligned} w_R(x_i)&= \frac{ \pi _i \varPsi (x_i | \varTheta _R) }{\pi _i \varPsi (x_i | \varTheta _R) + (1 - \pi _i) \varPsi (x_i | \varTheta _N)} \\ w_N(x_i)&= \frac{ (1 - \pi _i) \varPsi (x_i | \varTheta _N) }{\pi _i \varPsi (x_i | \varTheta _R) + (1 - \pi _i) \varPsi (x_i | \varTheta _N)}. \end{aligned} \end{aligned}$$

(5)

To release the non-related pixels’ influence on GMM, only the neighborhood around each landmark is considered in training (cf. Fig. 1(c)). Let $\varOmega (x_i)$ donate the cubic neighborhood around the center $x_i$ with radius r, thus each neighborhood contains $(2r+1)^3$ pixels. Let $\varOmega ^+(x_i)$ be the region inside the shape within $\varOmega (x_i)$ and $\varOmega ^-(x_i) = \varOmega (x_i) - \varOmega ^+(x_i)$ be the outside region (cf. Fig. 1(c)). Therefore, the parameters $\varTheta _R$, $\varTheta _N$ are trained within $\int _{x_i \in C} \varOmega ^+(x_i) dx$ and $\int _{x_i \in C} \varOmega ^-(x_i) dx$ respectively. Similarly, we obtain the mean probability $\mu _{wR}$ and $\mu _{wN}$ of being ROI and NOI by only considering the pixels in region $\int _{i=1}^{n_P} \varOmega (x_i) dx$. In this way, more precise probabilities can be obtained by shrinking the region of neighborhood, leading to finer segmentation.

Theoretically, it would be ideal that the pixels inside shape C have the highest probability of being ROI and the pixels outside shape C have the highest probability of being NOI. Inspired by the popular Mumford-Shah function [11], we form the energy function term:

$$\begin{aligned} \begin{aligned} -\log (p(I, \varPi |C)) =&\int _{i=1}^{n_P} \int _{j \in \varOmega (x_i)} \big ( w_R(x_j) - \mu _{wR}\big )^2 + \big (w_N(x_j) - \mu _{wN}\big )^2 \\&+ \big (w_R(x_j) - \mu _{wR}\big )\big (w_N(x_j) - \mu _{wN}\big ) dx , \end{aligned} \end{aligned}$$

(6)

at this stage, the landmarks are fitting to superior positions automatically in terms of the probability rules in Eq. 5. Since the pixels are statistically independent without global constraint, assume the landmark $x_i$ will move along the outward curvature normal with direction $\overrightarrow{\mathbf {\jmath }}(x_i)$ to reach the optimal, we compute $\frac{\partial (p(I, \varPi |C))}{\partial (C)} = 0$ to obtain the movement direction $\overrightarrow{\mathbf {\jmath }}^*(x_i)$ for each landmark that:

$$\begin{aligned} \overrightarrow{\mathbf {\jmath }}^*(x_i) = \frac{(w_R(x_i) - \mu _{wR})^2 - (w_N(x_i) - \mu _{wN})^2}{(w_R(x_i) - \mu _{wR})(w_N(x_i) - \mu _{wN})} , \end{aligned}$$

(7)

note that for pixels $x_j \in \varOmega ^+(x_i)$, $\overrightarrow{\mathbf {\jmath }}^*(x_j) < 0$, otherwise for pixels $x_j \in \varOmega ^-(x_i)$, $\overrightarrow{\mathbf {\jmath }}^*(x_j) > 0$. Namely, $\overrightarrow{\mathbf {\jmath }}^*(x_i) > 0$ indicates $x_i$ moves along the normal to exterior and $\overrightarrow{\mathbf {\jmath }}^*(x_i) < 0$ indicates $x_i$ moves along the inverse direction of outward normal to interior.

Shape Prior. Statistical shape models are demonstrated to have a strong ability in global shape constraint. In this work, we employ the RKPCA method in [9] to train such a robust kernel model $RKSSM(S |\mathrm {\Phi }; \mathrm {V} ;\mathrm {K})$. Differently, we use the model statistics to correct the erroneous modes and estimate the uncertain pieces (cf. Fig. 1(e) to (f)), which means we only focus on the back projection process. Subject to the nonlinearity of kernel space, it is sensitive to initialization of clusters. Furthermore, the shape to be projected onto the model at this stage already contains certain pieces that are supposed to be preserved. Consequently, we improve the back projection of kernel model by assigning a supervised initialization to project onto the optimal cluster. Namely, finding the $j^{th}$ shape in training datasets $S_j$ satisfying $\kappa (C, S_j) = \max ( \kappa (C, S_i): i = 1, \dots , N )$. Employing the shape model in Bayesian model, we consider the prior as:

(8)

the first term is the objective function employed in [9] and we add an additional term with a balance $\lambda$. $\mathbb {P}_n \mathrm {\Phi }(x)$ denotes the projection of $\mathrm {\Phi }(x)$ onto the principal subspace of $\mathrm {\Phi }$. Afterwards, the shape projection is solved by taking gradient $\frac{\partial ( -\log (p(C)))}{\partial (\hat{C})} = 0$ and the reconstructed shape vector is derived by:

$$\begin{aligned} \hat{C} = \frac{\sum _{i=1}^{N} \gamma _i \kappa (C, S_i)S_i - \lambda S_j}{\sum _{i=1}^{N}\gamma _i \kappa (C, S_i) - \lambda } , ~~~ \gamma _i = \sum _{k=1}^{N} \mathrm {V}_i^j \mathrm {K}_j \mathrm {V}_i^k. \end{aligned}$$

(9)

3 Evaluation

Datasets and Experiments Experiments are conducted on the public NIH pancreas datasets [12], containing 82 abdominal contrast-enhanced 3D CT volumes with size $512 \times 512 \times D$ ($D \in [181, 146]$) under 4-fold cross validation. We take the measures Dice Similarity Coefficient $DSC = 2(|Y_+ \cap \hat{Y}_+|) / (|Y_+| + |\hat{Y}_+|)$ and Jaccard Index $JI = (|Y_+ \cap \hat{Y}_+|) / (|Y_+| \cup |\hat{Y}_+|)$. For statistical shape modeling, we define the kernel trick $\kappa (x_i, x_j) = \exp (- (x_i - x_j)^2 / 2 \sigma ^2)$, where the kernel width $\sigma = 150$. In the shape projection, we set the balance term $\lambda = \frac{1}{2\sigma ^2}$. We set $r=2$ at the beginning in shape adaption with GMM. The convergence condition value for shape adaption is $\epsilon = 0.0001$.

Table 1. Pancreas segmentation results comparing with the state-of-the-art. ‘−’ indicates the item is not presented.

Segmentation Results. We compare the segmentation results with related works using the same datasets in Table 1. In terms of the segmentation results, we report the highest 85.32% average DSC with smallest deviation 4.19, and the DSC for the worse case reaches 71.04%. That is to say, our proposed method is robust to extremely challenging cases. We can also find an improvement of JI. More importantly, we can come to the conclusion that the proposed Bayesian model is efficient and robust in terms of the significant improvement (approximately 12% in DSC) from the neural network segmentation. For an intuitive view, the segmentation procedure of Bayesian model is shown in Fig. 2, where we compare the segmentation at every stage with the ground truth (in red). The DSC for probability map in Fig. 2(b) is 57.30%, and DSC for the final segmentation in Fig. 2(f) is 82.92%. Obviously, we find that the segmentation leads more precise by shrinking the radius of neighborhood.

Fig. 2.

Figure shows the segmentation procedure of NIH case $\#4$: (a) test image I; (b) probability map $\varPi$; (c) initialization for shape model (ground truth mask is in red); (d)–(f) shape adaption with neighborhood radius $r=2, 1, 0$ respectively.

4 Discussion

Motivated by tackling difficulties in challenging organ segmentation, we integrate deep neural network and statistical shape model within a Bayesian model in this work. A novel optimization principle is proposed to guide segmentation. We conduct experiments on the public NIH pancreas datasets and report the average $DSC=85.34\%$ that outperforms the state-of-the-art. In future work, we will focus on more challenging segmentation tasks such as the tumor and lesion segmentation.