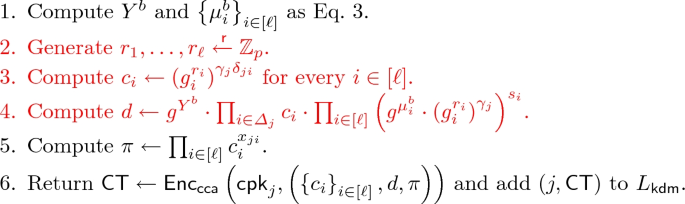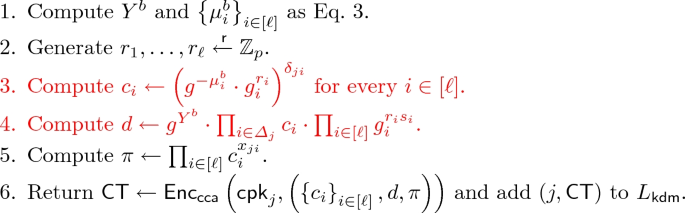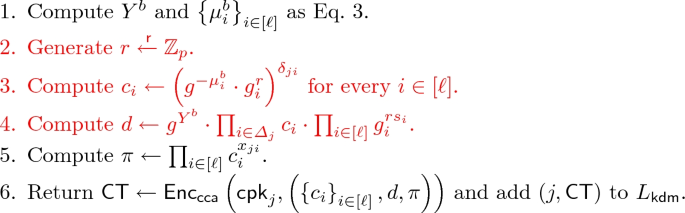A Framework for Achieving KDM-CCA Secure Public-Key Encryption

Abstract

We propose a framework for achieving a public-key encryption (PKE) scheme that satisfies key dependent message security against chosen ciphertext attacks (KDM-CCA security) based on projective hash function. Our framework can be instantiated under the decisional diffie-hellman (DDH), quadratic residuosity (QR), and decisional composite residuosity (DCR) assumptions. The constructed schemes are KDM-CCA secure with respect to affine functions and compatible with the amplification method shown by Applebaum (EUROCRYPT 2011). Thus, they lead to PKE schemes satisfying KDM-CCA security for all functions computable by a-priori bounded size circuits. They are the first PKE schemes satisfying such a security notion in the standard model using neither non-interactive zero knowledge proof nor bilinear pairing. The above framework based on projective hash function captures only KDM-CCA security in the single user setting. However, we can prove the KDM-CCA security in the multi user setting of our concrete instantiations by using their algebraic structures explicitly. Especially, we prove that our DDH based scheme satisfies KDM-CCA security in the multi user setting with the same parameter setting as in the single user setting.

1 Introduction

1.1 Backgrounds

Key dependent message (KDM) security, introduced by Black, Rogaway and Shrimpton [3], guarantees confidentiality of communication even if an adversary can get a ciphertext of secret keys. KDM security is useful for many practical applications including anonymous credential systems [7] and hard disk encryption systems (e.g., BitLocker [4]). KDM security is defined with respect to a function family $\mathcal {F}$. Let n denote the number of keys and $\mathbf {sk}=(\mathsf {sk}_1, \cdots , \mathsf {sk}_n)$ be secret keys. Informally, a PKE scheme is said to be $\mathcal {F}$-KDM secure if confidentiality of messages is protected even when an adversary can see a ciphertext of $f(\mathbf {sk})$ under the k-th public key for any $f \in \mathcal {F}$ and $k \in \{1, \cdots , n\}$. In this paper, we focus on constructing PKE schemes that satisfy KDM security against chosen ciphertext attacks, namely KDM-CCA security in the standard model.

Camenisch, Chandran and Shoup [6] proposed the first $\text {KDM}\text {-}\text {CCA}$ secure PKE based on the Naor-Yung paradigm [16]. They showed that for any function class $\mathcal {F}$, ${\mathcal {F}}\text {-}\text {KDM}\text {-}\text {CPA}$ secure PKE can be transformed into ${\mathcal {F}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure one assuming non-interactive zero knowledge (NIZK) proof. They also showed a concrete instantiation based on the decisional diffie-hellman (DDH) assumption on a bilinear pairing. Subsequently, Hofheinz [10] showed more efficient $\text {KDM}\text {-}\text {CCA}$ secure PKE. His scheme is circular secure (KDM-CCA secure with respect to selection functions) relying on both the DDH and decisional composite residuosity (DCR) assumptions on a bilinear pairing.

The first $\text {KDM}\text {-}\text {CCA}$ secure PKE using neither NIZK proof nor bilinear pairing was proposed by Lu, Li and Jia [14]. They claimed their scheme is $\text {KDM}\text {-}\text {CCA}$ secure with respect to affine functions (${\mathcal {F}_{\mathsf {aff}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure) relying on both the DDH and DCR assumptions. However, a flow on their security proof was later discovered by Han, Liu and Lyu [9]. Han et al. also showed a new ${\mathcal {F}_{\mathsf {aff}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure PKE scheme based on the construction methodology of Lu et al. In addition, they constructed $\text {KDM}\text {-}\text {CCA}$ secure PKE with respect to bounded degree polynomial functions. Their schemes are efficient and secure relying on both the DDH and DCR assumptions.

Despite the above previous efforts, it is still open whether we can construct $\text {KDM}\text {-}\text {CCA}$ secure PKE based on a single computational assumption using neither NIZK proof nor bilinear pairing. All existing $\text {KDM}\text {-}\text {CCA}$ secure PKE schemes without NIZK proof were proved to be secure relying on both the DDH and DCR assumptions. These schemes are proposed based on a specific algebraic structure and it is crucial to assume the hardness of both the DDH and DCR problems on the specific algebraic structure. Thus, it seems difficult to construct $\text {KDM}\text {-}\text {CCA}$ secure PKE based on a single computational assumption using their techniques.

Moreover, it is also an open question whether we can construct $\text {KDM}\text {-}\text {CCA}$ secure PKE with respect to all functions computable by bounded size circuits (${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure) using neither NIZK proof nor bilinear pairing. The only existing way to construct ${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure PKE is to utilize the amplification method shown by Applebaum [2]. Applebaum showed if a PKE scheme is $\text {KDM}\text {-}\text {CCA}$ secure with respect to projection functions, we can transform it into a ${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure one, where projection function is a function whose each output bit depends on only a single bit of an input. Kitagawa, Matsuda, Hanaoka and Tanaka [12] later showed we can perform such a transformation even if the underlying PKE is only $\text {KDM}\text {-}\text {CCA}$ secure with respect to projection functions whose output is one bit.

Among existing $\text {KDM}\text {-}\text {CCA}$ secure schemes, only Camenisch et al.’s scheme is compatible with those transformations. Thus, a construction of ${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure PKE using neither NIZK proof nor bilinear pairing is not known so far.

1.2 Our Results

Based on the above back ground, we show the following results.

A framework achieving $\text {KDM}\text {-}\text {CCA}$ security in the single user setting. First, we propose a framework to construct PKE that is ${\mathcal {F}_{\mathsf {aff}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure in the single user setting based on projective hash function. Our framework can be instantiated based on the DDH, quadratic residuosity (QR), and DCR assumptions. More specifically, we obtain the following theorem.

Theorem 1

(Informal). Under each of the DDH, QR, and DCR assumptions, there exists PKE that is ${\mathcal {F}_{\mathsf {aff}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure in the single user setting.

These schemes are also $\text {KDM}\text {-}\text {CCA}$ secure with respect to projection functions of single-bit output thus compatible with the amplification method of Applebaum [2] and Kitagawa et al. [12]. Thus, we obtain the following corollary.

Corollary 1

(Informal). Under each of the DDH, QR, and DCR assumptions, there exists PKE that is ${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure in the single user setting.

$KDM\text {-}CCA$ secure PKE in the multi user setting. Then, we focus on $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting. Although the above framework based on projective hash function captures only $\text {KDM}\text {-}\text {CCA}$ security in the single user setting, we can prove the $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of our concrete instantiations by using their algebraic structures explicitly.

Our DDH based construction is an extension of the $\text {KDM}\text {-}\text {CPA}$ secure scheme proposed by Boneh, Halevi, Hamburg and Ostrovsky [4]. Similarly to Boneh et al., using the self-reducibility of the DDH problem, we can prove the $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of our DDH based construction with the same parameter setting as in the single user setting. Especially, we formally prove the following theorem.

Theorem 2

(Informal). Under the DDH assumption, there exists PKE that is ${\mathcal {F}_{\mathsf {aff}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure in the multi user setting.

Since the DDH based construction is compatible with the results by Applebaum [2] and Kitagawa et al. [12], we obtain the following corollary.

Corollary 2

(Informal). Under the DDH assumption, there exists PKE that is ${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure in the multi user setting.

Our QR and DCR based constructions are extensions of the $\text {KDM}\text {-}\text {CPA}$ secure scheme proposed by Brakerski and Goldwasser [5]. If we allow the length of a secret key to depend on the number of users, we can also prove the $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of our DCR and QR based schemes using a technique similar to Brakerski and Goldwasser. We briefly explain how to prove it after the proof of multi user security of the DDH based scheme.

We summarize our results and previous results in Fig. 1.

Fig. 1.

Comparison of $\text {KDM}\text {-}\text {CCA}$ secure PKE schemes. “Amplification” indicates whether we can transform the scheme into ${\mathcal {F}_{\mathsf {all}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure one using the results of Applebaum [2] and Kitagawa et al. [12]. “Flexible parameter” indicates whether we can prove $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of the scheme without making the length of a secret key depend on the number of users.

1.3 Technical Overview

Our starting point is the constructions of PKE proposed by Wee [19] that is KDM secure in the single user setting (hereafter, $\text {KDM}^{(1)}$ security). He showed how to construct $\text {KDM}^{(1)}\text {-}\text {CPA}$ secure PKE based on homomorphic projective hash function. His framework captures the previous constructions proposed by Boneh et al. [4] and Brakerski and Goldwasser [5].

Projective hash function was originally introduced by Cramer and Shoup [8] to construct PKE satisfying indistinguishability against chosen ciphertext attacks (IND-CCA security). Thus, we have a natural question whether we can construct $\text {KDM}^{(1)}\text {-}\text {CCA}$ secure PKE based on projective hash function.

We answer the above question affirmatively with a simple construction. Below, we first review the construction proposed by Wee [19].

$\mathbf{KDM }^\mathbf{(1) }\text {-}\mathbf{CPA }$ Secure PKE Based on Homomorphic Projective Hash Function. We consider a group $\mathcal {C}$ and its subgroup $\mathcal {V}$ satisfying the subgroup indistinguishability, that is, uniform distributions over $\mathcal {C}$ and $\mathcal {V}$ are computationally indistinguishable. Based on $\mathcal {C}$ and $\mathcal {V}$, we define projective hash function as follows. A projective hash function is a family $\mathcal {H}$ of hash functions $\varLambda _\mathsf {sk}:\mathcal {C}\rightarrow \mathcal {K}$ indexed by a key $\mathsf {sk}\in \mathcal {SK}$, where $\mathcal {K}$ is a group. Let $\mu$ be a projection map defined over $\mathcal {SK}$. We require $\varLambda _\mathsf {sk}$ be projective, that is, for every $c\in \mathcal {V}$, the value of $\varLambda _\mathsf {sk}(c)$ is determined by only c and $\mathsf {pk}=\mu (\mathsf {sk})$. In addition, we require that there exist a public evaluation algorithm $\mathsf {Pub}$ that given $\mathsf {pk}$, $c\in \mathcal {V}$, and a witness w of $c\in \mathcal {V}$, outputs $\varLambda _\mathsf {sk}(c)$. Below, we denote group operations of $\mathcal {C}$ and $\mathcal {K}$ by “$\cdot$” and “$+$”, respectively.

Using a projective hash function $\mathcal {H}$, we can naturally construct a PKE scheme $\mathsf {\Pi }$ as follows. When generating a key pair $(\mathsf {pk},\mathsf {sk})$, we sample random $\mathsf {sk}$ and compute $\mathsf {pk}=\mu (\mathsf {sk})$. When encrypting a message $m\in \mathcal {K}$, we first sample $c\xleftarrow {\mathsf {r}}\mathcal {V}$ with a witness w of $c\in \mathcal {V}$. Then, we compute $d\leftarrow \mathsf {Pub}(\mathsf {pk},c,w) + m$ and set (c, d) as a ciphertext. When decrypting (c, d), we compute $m \leftarrow d - \varLambda _\mathsf {sk}(c)$.

$\mathsf {\Pi }$ is $\text {IND}\text {-}\text {CPA}$ secure if $\mathcal {H}$ is smooth, that is, the value of $\varLambda _\mathsf {sk}(c)$ is statistically chose to uniform given $\mathsf {pk}=\mu (\mathsf {sk})$ and c, where $\mathsf {sk}\xleftarrow {\mathsf {r}}\mathcal {SK}$ and $c\xleftarrow {\mathsf {r}}\mathcal {C}$.¹ We prove the $\text {IND}\text {-}\text {CPA}$ security of $\mathsf {\Pi }$ as follows. We first switch ${c^*}$ used to encrypt the challenge message to ${c^*}\xleftarrow {\mathsf {r}}\mathcal {C}$ by using the subgroup indistinguishability. Then, the distribution of the resulting ciphertext is close to uniform due to the smoothness and thus $\text {IND}\text {-}\text {CPA}$ security follows.

KDM security from homomorphism. Wee [19] showed $\mathsf {\Pi }$ is also $\text {KDM}^{(1)}\text {-}\text {CPA}$ secure if $\mathcal {H}$ is homomorphic, that is, for every $c_0,c_1\in \mathcal {C}$, it holds that $\varLambda _\mathsf {sk}(c_0\cdot c_1)=\varLambda _\mathsf {sk}(c_0)+\varLambda _\mathsf {sk}(c_1)$. More precisely, $\mathsf {\Pi }$ is $\text {KDM}^{(1)}\text {-}\text {CPA}$ secure with respect to functions defined as $f_e(\mathsf {sk})=\varLambda _\mathsf {sk}(e)$, where $e\in \mathcal {C}$. Note that this function class corresponds to the set of affine functions in his instantiations.

If $\mathcal {H}$ is homomorphic, we can change the distribution of an encryption of $f_e(\mathsf {sk})$, that is $\left( c, \mathsf {Pub}(\mathsf {pk},c,w)+\varLambda _\mathsf {sk}(e)\right)$ as

where w denotes a witness of $c\in \mathcal {V}$, and $\approx _\mathsf {c}$ and $\approx _\mathsf {s}$ denote computational indistinguishability and statistical indistinguishability, respectively. This means that we can simulate an encryption of $f_e(\mathsf {sk})$ without $\mathsf {sk}$. Then, based on the standard hybrid argument, we can prove the $\text {KDM}^{(1)}\text {-}\text {CPA}$ security of $\mathsf {\Pi }$ using the smoothness of $\mathcal {H}$ similarly to the proof for the $\text {IND}\text {-}\text {CPA}$ security of $\mathsf {\Pi }$.

Extension to $\mathbf{KDM }^\mathbf{(1) }\text {-}\mathbf{CCA\,Secure\,PKE. }$ We can construct $\text {IND}\text {-}\text {CCA}$ secure PKE by adding 2-universal projective hash function to the construction of $\mathsf {\Pi }$. More precisely, we use a projective hash function $\hat{\mathcal {H}}$ consisting of hash functions $\hat{\varLambda }_{\hat{\mathsf {sk}}}$ indexed by ${\hat{\mathsf {sk}}}\in \hat{\mathcal {SK}}$ defined on $\mathcal {C}$ and $\mathcal {V}$.² Let $\hat{\mu }$ and $\hat{\mathsf {Pub}}$ be the projection map and public evaluation algorithm of $\hat{\mathcal {H}}$. We require that $\hat{\mathcal {H}}$ be 2-universal, that is, for every ${\hat{\mathsf {pk}}}$, $c, c^*\in \mathcal {C}\setminus \mathcal {V}$, and $\mathsf {K},\mathsf {K}^*\in \mathcal {K}$, $\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)=\mathsf {K}$ holds with only negligible probability under the condition that ${\hat{\mathsf {pk}}}=\hat{\mu }\left( {\hat{\mathsf {sk}}}\right)$ and $\hat{\varLambda }_{\hat{\mathsf {sk}}}(c^*)=\mathsf {K}^*$, where ${\hat{\mathsf {sk}}}\xleftarrow {\mathsf {r}}\hat{\mathcal {SK}}$.

We modify $\mathsf {\Pi }$ into $\text {IND}\text {-}\text {CCA}$ secure $\mathsf {\Pi }'$ as follows. When generating a key pair, in addition to $(\mathsf {pk},\mathsf {sk})$, we sample ${\hat{\mathsf {sk}}}\xleftarrow {\mathsf {r}}\hat{\mathcal {SK}}$ and compute ${\hat{\mathsf {pk}}}=\hat{\mu }\left( {\hat{\mathsf {sk}}}\right)$. A public key and secret key of $\mathsf {\Pi }'$ are $\left( \mathsf {pk},{\hat{\mathsf {pk}}}\right)$ and $\left( \mathsf {sk},{\hat{\mathsf {sk}}}\right)$, respectively. When encrypting a message, we first compute c and d in the same way as $\mathsf {\Pi }$ using $\mathsf {pk}$. Then, we compute $\pi \leftarrow \hat{\mathsf {Pub}}\left( {\hat{\mathsf {pk}}},c,w\right)$ and set $(c,d,\pi )$ as the resulting ciphertext. When decrypting $(c,d,\pi )$, we first check whether $\pi =\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ holds and if so decrypt a message in the same way as $\mathsf {\Pi }$ using $\mathsf {sk}$. Otherwise, we output $\bot$.

Since $\hat{\mathcal {H}}$ is 2-universal, an adversary cannot compute $\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ correctly for $c\in \mathcal {C}\setminus \mathcal {V}$ even if he obtain a single hash value $\hat{\varLambda }_{\hat{\mathsf {sk}}}\left( {c^*}\right)$ for ${c^*}\in \mathcal {C}\setminus \mathcal {V}$ in the challenge ciphertext. In other words, the adversary cannot make a valid decryption query $(c,d,\pi )$ for $c\in \mathcal {C}\setminus \mathcal {V}$. Then, from the projective property of $\mathcal {H}$, the adversary cannot obtain information of $\mathsf {sk}$ other than $\mathsf {pk}$ through decryption queries. Thus, we can reduce the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi }'$ to the smoothness of $\mathcal {H}$.

Problems for proving $KDM^\mathrm{(1)}\text {-}CCA$ security. Even if $\mathcal {H}$ is homomorphic, we cannot prove the $\text {KDM}^{(1)}\text {-}\text {CCA}$ security of $\mathsf {\Pi }'$ straightforwardly. In the security game of $\text {KDM}^{(1)}\text {-}\text {CCA}$ security, an adversary can obtain an encryption of ${\hat{\mathsf {sk}}}$ in addition to that of $\mathsf {sk}$. Thus, we need to eliminate ${\hat{\mathsf {sk}}}$ from the view of the adversary to use the 2-universal property of $\hat{\mathcal {H}}$.

Moreover, if we can do that, there is another problem. Consider functions of the form $f_e\left( \mathsf {sk},{\hat{\mathsf {sk}}}\right) =\varLambda _\mathsf {sk}(e)+f\left( {\hat{\mathsf {sk}}}\right)$, where $e\in \mathcal {C}$ and $f:\hat{\mathcal {SK}}\rightarrow \mathcal {K}$ is a function. If $\mathcal {H}$ is homomorphic, using a similar argument as Wee [19], we can simulate an encryption of $f_e\left( \mathsf {sk},{\hat{\mathsf {sk}}}\right)$ by

$$\begin{aligned} \left( c\cdot e^{-1}, \mathsf {Pub}(\mathsf {pk},c,w)+f\left( {\hat{\mathsf {sk}}}\right) , \hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c\cdot e^{-1}\right) \right) , \end{aligned}$$

where $c\in \mathcal {V}$ and w is an witness of $c\in \mathcal {V}$. Even if we can eliminate $f\left( {\hat{\mathsf {sk}}}\right)$ from the second component, the third component $\hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c\cdot e^{-1}\right)$ incurs another problem. e is an element chosen by an adversary in the security game, and thus $c\cdot e^{-1}$ might not be included in $\mathcal {V}$. Thus, the adversary can obtain a hash value $\hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c\cdot e^{-1}\right)$ for $c\cdot e^{-1} \notin \mathcal {V}$ through each KDM query $f_e$. In this case, we cannot rely on the 2-universal property of $\hat{\mathcal {H}}$ to argue about decryption queries made by the adversary if he makes multiple KDM queries. Therefore, we also need to eliminate $\hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c\cdot e^{-1}\right)$ from the view of the adversary.

Our solution: Double layered encryption. We solve the above two problems at once by extending double layered encryption techniques originally used to expand the plaintext space of an $\text {IND}\text {-}\text {CCA}$ secure PKE scheme [11, 15]. More precisely, by adding an outer encryption layer, we put the estimation of the probability that an adversary makes an “illegal” decryption query off till the end of the sequence of games where all information about the inner layer is eliminated from the challenge ciphertexts. We use an $\text {IND}\text {-}\text {CCA}$ secure PKE scheme $\mathsf {\Pi _{cca}}$ as the outer layer encryption scheme. When encrypting a message, we first generate $(c,d,\pi )$ in the same way as $\mathsf {\Pi }'$ and then encrypt them by $\mathsf {\Pi _{cca}}$. We call the resulting PKE scheme $\mathsf {\Pi _{kdm}}$.

Of course, if we just maintain a secret key $\mathsf {csk}$ of $\mathsf {\Pi _{cca}}$ as a part of a secret-key of $\mathsf {\Pi _{kdm}}$, we cannot use the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$. Thus, we add a modification. We maintain $\mathsf {csk}$ after encrypting by $\mathcal {H}$. More precisely, we modify the key generation procedure of $\mathsf {\Pi _{kdm}}$ as follows. We first generate $\left( \mathsf {pk},\mathsf {sk}\right)$ and $\left( {\hat{\mathsf {pk}}},{\hat{\mathsf {sk}}}\right)$ in the same way as $\mathsf {\Pi }'$ and generate a key pair $(\mathsf {cpk},\mathsf {csk})$ of $\mathsf {\Pi _{cca}}$. Moreover, we sample ${c^*}\xleftarrow {\mathsf {r}}\mathcal {C}$ and compute ${d^*}\xleftarrow {\mathsf {r}}\varLambda _\mathsf {sk}({c^*})+\mathsf {csk}$.³ The resulting public key and secret key of $\mathsf {\Pi _{kdm}}$ are $\left( \mathsf {pk},{\hat{\mathsf {pk}}},\mathsf {cpk}\right)$ and $\left( \mathsf {sk},{\hat{\mathsf {sk}}},{c^*},{d^*}\right)$, respectively.

The overview of the security proof is as follows. Let $\mathcal {A}$ be an adversary for the $\text {KDM}^{(1)}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{kdm}}$. We consider functions of the form

$$\begin{aligned} f_e\left( \mathsf {sk},{\hat{\mathsf {sk}}},{c^*},{d^*}\right) =\varLambda _\mathsf {sk}(e)+f\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) , \end{aligned}$$

where $e\in \mathcal {C}$ and $f:\hat{\mathcal {SK}}\times \mathcal {C}\times \mathcal {K}\rightarrow \mathcal {K}$ is a function. This set of functions includes affine functions in the actual instantiations.

• 1. We first change the security game so that we do not need $\mathsf {sk}$ to simulate KDM queries using the projective property and homomorphism of $\mathcal {H}$ and subgroup indistinguishability. Note that we do not need the smoothness of $\mathcal {H}$ to make this change as explained before.

  After this change, the answer to a KDM query $f_e$ is of the form

  $$\begin{aligned} \mathsf {Enc}_{\mathsf {cpk}}\left( c\cdot e^{-1}, \mathsf {Pub}(\mathsf {pk},c,w)+f\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) , \hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c\cdot e^{-1}\right) \right) . \end{aligned}$$

• 2. Then, we change the security game so that a decryption query $\mathsf {CT}$ made by $\mathcal {A}$ is replied with $\bot$ if $c\notin \mathcal {V}$, where $(c,d,\pi )\leftarrow \mathsf {Dec}_{\mathsf {csk}}(\mathsf {CT})$. The probability that this change affects the behavior of $\mathcal {A}$ is bounded by the probability that $\mathcal {A}$ makes a decryption query $\mathsf {CT}$ such that $c\notin \mathcal {V}$ and $\pi =\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$, where $(c,d,\pi )\leftarrow \mathsf {Dec}_{\mathsf {csk}}(\mathsf {CT})$. We call such a decryption query a bad decryption query. Since ${\hat{\mathsf {sk}}}$ is contained in answers to KDM queries, we cannot estimate the probability at this point. However, as noted above, we can put the estimation off till the end of the sequence of games, and thus we continue the sequence.

• 3. By the previous change on how decryption queries are replied, we can use the smoothness of $\mathcal {H}$. We eliminate $\mathsf {csk}$ encrypted in $({c^*},{d^*})$ using the smoothness of $\mathcal {H}$.

• 4. Then, we can use $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$. We change the security game so that a KDM query made by $\mathcal {A}$ is replied with $\mathsf {CT}\leftarrow \mathsf {Enc}_{\mathsf {cpk}}\left( 0\right)$. In this game, the advantage of $\mathcal {A}$ is 0.

To complete the security proof, we need to estimate the probability that $\mathcal {A}$ makes a bad decryption query. In the final game, ${\hat{\mathsf {sk}}}$ is hidden from the view of $\mathcal {A}$ and he cannot obtain any hash value $\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ for $c\notin \mathcal {V}$. Thus, the probability is negligible in the final game if $\hat{\mathcal {H}}$ is 2-universal. In fact, since the universal property of $\hat{\mathcal {H}}$ is sufficient for this argument, we use a universal projective hash function instead of a 2-universal one in the actual construction. Then, the remaining problem is whether the probability that $\mathcal {A}$ makes a bad decryption query changes during the sequence of games.

The probability does not change by the third step since the view of $\mathcal {A}$ before the third step is statistically close to that after the third step from the smoothness of $\mathcal {H}$. In addition, if we can efficiently detect a bad decryption query made by $\mathcal {A}$, we can prove that the probability does not change by the fourth step based on the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$. For the purpose, in this work, we require there exist a trapdoor that enables us to efficiently check the membership of $\mathcal {V}$ for projective hash function. We can complete the security proof under the existence of such a trapdoor.

Instantiations. We instantiate the above framework based on the DDH, QR, and DCR assumptions by extending the instantiations of $\text {KDM}^{(1)}\text {-}\text {CPA}$ secure PKE by Wee [19]. Therefore, the DDH based construction is also an extension of that proposed by Boneh et al. [4], and the QR and DCR based constructions are also extensions of those proposed by Brakerski and Goldwasser [5]. In all constructions, we can make a trapdoor for checking the membership of $\mathcal {V}$. We briefly review the DDH based instantiation.

The DDH based instantiation. In the DDH based instantiation, we set

$$\begin{aligned} \mathcal {C}=\mathbb {G}^\ell \,\text {and}\, \mathcal {V}=\left\{ \left( g_1^r,\ldots ,g_\ell ^r\right) |r\in \mathbb {Z}_{p}\right\} , \end{aligned}$$

where $\mathbb {G}$ is a cyclic group of order p, $g_1,\ldots ,g_\ell$ are random generators of $\mathbb {G}$, and $\ell$ is a parameter determined in the analysis. The uniform distribution over $\mathcal {C}$ and $\mathcal {V}$ are computationally indistinguishable based on the DDH assumption on $\mathbb {G}$. Moreover, the discrete logarithms $\alpha _i$ such that $g_i=g^{\alpha _i}$ for every $i\in [\ell ]$ can be used as a trapdoor to efficiently decide the membership of $\mathcal {V}$, where g is another generator and $[\ell ]$ denotes $\{1,\ldots ,\ell \}$.

We construct homomorphic projective hash function $\mathcal {H}$ exactly in the same way as Wee [19]. A secret key $\mathsf {sk}$ is randomly chosen $s=s_1\cdots s_\ell \in \{0,1\}^\ell$. The corresponding public key is $g_0=\prod _{i\in [\ell ]}g_i^{s_i}$. When hashing $c=(c_1,\ldots , c_\ell )\in \mathcal {C}$, we compute $\prod _{i\in [\ell ]}c_i^{s_i}$. We see that this construction satisfies the projective property and homomorphism. Moreover, we can prove the (average-case) smoothness of it based on the leftover hash lemma by taking $\ell$ appropriately.

We construct a universal projective hash function $\hat{\mathcal {H}}$ as follows. A secret key ${\hat{\mathsf {sk}}}$ is randomly chosen $(x_1,\ldots , x_\ell )\in \mathbb {Z}_{p}^\ell$. The corresponding public key is $\hat{g}_0=\prod _{i\in [\ell ]}g_i^{x_i}$. When hashing $c=(c_1,\ldots , c_\ell )\in \mathcal {C}$, we compute $\prod _{i\in [\ell ]}c_i^{x_i}$. This construction can be seen as an extension of that proposed by Cramer and Shoup [8], and we can prove its projective property and universal property.

The QR and DCR based instantiations. In the QR based construction, we use the same $\mathcal {C}$, $\mathcal {V}$, and $\mathcal {H}$ as Wee [19]. However, in the QR based construction, we slightly modify how to mask $\mathsf {csk}$ in the key generation. Roughly speaking, this is because a hash value of $\mathcal {H}$ uniformly distributes over a group of order 2, and thus we need parallelization in order to mask $\mathsf {csk}$ using the smoothness of $\mathcal {H}$. In the modified version of construction, we avoid such parallelization. However, in the construction of a universal projective hash function $\hat{\mathcal {H}}$, we still need a parallelized construction similarly to $\text {IND}\text {-}\text {CCA}$ secure PKE based on the QR assumption proposed by Cramer and Shoup [8]. When we consider CCA security, if the underlying group has a small prime factor, we need a parallelized construction.

In the DCR based construction, we also apply some modifications to the construction of $\mathcal {C}$, $\mathcal {V}$, and $\mathcal {H}$ used by Wee. In the construction of Wee, the underlying group has a small prime factor 2. Therefore, in a naive construction, we need parallelization. However, by defining hash functions so that every time we compute a hash value, we first perform a squaring, we can make the small factor useless to attack the scheme without parallelization. By this modification, the range of hash functions become a group whose order does not have a small prime factor and we can avoid parallelization.

Overhead of our constructions. The overhead of communicational complexity (that is, the size of public-keys and ciphertexts) of our $\text {KDM}^{(1)}\text {-}\text {CCA}$ secure PKE schemes from its $\text {KDM}^{(1)}\text {-}\text {CPA}$ secure counterparts [19] is very small in the DDH and DCR based constructions. A public-key and hash value of $\hat{\mathcal {H}}$ are just a single group element in the DDH and DCR based constructions. Moreover, we can use highly efficient $\text {IND}\text {-}\text {CCA}$ secure PKE schemes [13, 17] as the outer layer scheme. In this case, the overhead of communicational complexity is only few group elements.

Extension to Multi User Setting. Although the above framework based on projective hash function captures only $\text {KDM}^{(1)}\text {-}\text {CCA}$ security, we can prove the $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of concrete instantiations.

As noted before, our DDH based construction is an extension of that proposed by Boneh et al. [4], and our QR and DCR based constructions are extensions of those proposed by Brakerski and Goldwasser [5]. In both works, they first show the $\text {KDM}^{(1)}\text {-}\text {CPA}$ security of their schemes, and then prove its $\text {KDM}\text {-}\text {CPA}$ security in the multi user setting by extending the proof for $\text {KDM}^{(1)}\text {-}\text {CPA}$ security.

By using similar techniques, we can prove $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of our schemes. Especially, we prove the $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of our DDH based construction with the same parameter setting as in the single user setting. We also briefly explain how to prove the $\text {KDM}\text {-}\text {CCA}$ security in the multi user setting of our QR and DCR based constructions after proving the multi user security of the DDH based construction.

2 Preliminaries

We define some cryptographic primitives after introducing some notations and left-over hash lemma.

Notations. In this paper, $x \xleftarrow {\mathsf {r}}X$ denotes choosing an element from a finite set X uniformly at random, and $y \leftarrow \mathsf {A}(x)$ denotes assigning to y the output of an algorithm $\mathsf {A}$ on an input x. For bit strings x and y, $x \Vert y$ denotes the concatenation of x and y. For an integer $\ell$, $[\ell ]$ denotes the set of integers $\{1, \ldots , \ell \}$.

$\lambda$ denotes a security parameter. PPT stands for probabilistic polynomial time. A function $f(\lambda )$ is a negligible function if $f(\lambda )$ tends to 0 faster than $\frac{1}{\lambda ^c}$ for every constant $c>0$. We write $f(\lambda ) = \mathsf{negl}(\lambda )$ to denote $f(\lambda )$ being a negligible function.

We introduce the left-over hash lemma.

Lemma 1

(Left-over hash lemma). Let X, Y, and Z are sets. Let $\mathcal {H}:=\left\{ h:X\rightarrow Y\right\}$ be a family of 2-universal hash functions. Let $\mathsf {aux}:X\rightarrow Z$ be a function. Then, the distributions $(h, h(x), \mathsf {aux}(x))$ and $(h, y, \mathsf {aux}(x))$ are $\sqrt{\frac{\left| Y\right| \left| Z\right| }{4\cdot \left| X\right| }}$-close, where $h\xleftarrow {\mathsf {r}}\mathcal {H}$, $x\xleftarrow {\mathsf {r}}X$, and $y\xleftarrow {\mathsf {r}}Y$.

2.1 Public Key Encryption

A public-key encryption (PKE) scheme $\mathsf {PKE}$ is a three tuple $(\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})$ of PPT algorithms. Let $\mathcal {M}$ be the message space of $\mathsf {PKE}$. The key generation algorithm $\mathsf {KG}$, given a security parameter $1^\lambda$, outputs a public key $\mathsf {pk}$ and a secret key $\mathsf {sk}$. The encryption algorithm $\mathsf {Enc}$, given a public key $\mathsf {pk}$ and message $m \in \mathcal {M}$, outputs a ciphertext $\mathsf {CT}$. The decryption algorithm $\mathsf {Dec}$, given a secret key $\mathsf {sk}$ and ciphertext $\mathsf {CT}$, outputs a message $\tilde{m} \in \{ \bot \} \cup \mathcal {M}$. As correctness, we require $\mathsf {Dec}(\mathsf {sk}, \mathsf {Enc}(\mathsf {pk}, m)) = m$ for every $m \in \mathcal {M}$ and $(\mathsf {pk}, \mathsf {sk})\leftarrow \mathsf {KG}(1^\lambda )$.

Next, we define key dependent message security against chosen ciphertext attacks (KDM-CCA security) for PKE.

Definition 1

(KDM-CCA security). Let $\mathsf {PKE}$ be a PKE scheme, $\mathcal {F}$ function family, and ${n}$ the number of keys. We define the ${\mathcal {F}}\text {-}\text {KDM}^{(n)}\text {-}\text {CCA}$ game between a challenger and an adversary $\mathcal {A}$ as follows. Let $\mathcal {SK}$ and $\mathcal {M}$ be the secret key space and message space of $\mathsf {PKE}$, respectively.

• 1. First, the challenger chooses a challenge bit $b \xleftarrow {\mathsf {r}}\{0,1\}$. Next, the challenger generates ${n}$ key pairs $\left( \mathsf {pk}_{k},\mathsf {sk}_{k}\right) \leftarrow \mathsf {KG}(1^{\lambda })\left( k\in [{n}]\right)$. The challenger sets $\mathbf {sk}:=\left( \mathsf {sk}_{1}, \ldots , \mathsf {sk}_{{n}}\right)$ and sends $\left( \mathsf {pk}_{1}, \ldots , \mathsf {pk}_{{n}}\right)$ to $\mathcal {A}$. Finally, the challenger prepares a list $L_\mathsf {kdm}$ which is initially empty.

• 2. $\mathcal {A}$ may adaptively make the following queries polynomially many times.  

  KDM queries:

  $\mathcal {A}$ sends $(j, f^0,f^1)\in [{n}]\times \mathcal {F}\times \mathcal {F}$ to the challenger. We require that $f^0$ and $f^1$ be functions such that $f:\mathcal {SK}^{n} \rightarrow \mathcal {M}$. The challenger returns $\mathsf {CT}\leftarrow \mathsf {Enc}\left( \mathsf {pk}_{j}, f^b(\mathbf {sk})\right)$ to $\mathcal {A}$. Finally, the challenger adds $(j,\mathsf {CT})$ to $L_\mathsf {kdm}$.

  Decryption queries:

  $\mathcal {A}$ sends $(j, \mathsf {CT})$ to the challenger. If $(j,\mathsf {CT})\in L_\mathsf {kdm}$, the challenger returns $\bot$ to $\mathcal {A}$. Otherwise, the challenger returns $m\leftarrow \mathsf {Dec}\left( \mathsf {sk}_{j},\mathsf {CT}\right)$ to $\mathcal {A}$.

   

• 3. $\mathcal {A}$ outputs $b' \in \{0,1\}$.

We say that $\mathsf {PKE}$ is ${\mathcal {F}}\text {-}\text {KDM}^{(n)}\text {-}\text {CCA}$ secure if for any PPT adversary $\mathcal {A}$, we have $\mathsf {Adv}_{\mathsf {PKE}, \mathcal {F}, \mathcal {A}, {n}}^{\mathsf {kdmcca}}(\lambda ) = \left| \Pr [b=b']-\frac{1}{2}\right| = \mathsf{negl}(\lambda )$.

In addition, we say that $\mathsf {PKE}$ is ${\mathcal {F}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure if it is ${\mathcal {F}}\text {-}\text {KDM}^{({n})}\text {-}\text {CCA}$ secure for any polynomial ${n}={n}(\lambda )$.

Remark 1

(Difference with the previous definitions). In the original definition of KDM security defined by Black et al. [3], an adversary is required to distinguish an encryption of $f(\mathsf {sk})$ from that of some constant message such as 0, where f is a function chosen by the adversary.

In our definition of $\text {KDM}\text {-}\text {CCA}$ security, an adversary chooses two functions $(f^0,f^1)$ and is required to distinguish an encryption of $f^0(\mathsf {sk})$ from that of $f^1(\mathsf {sk})$. Such a definition was previously used by Alperin-sheriff and Peikert [1] when they defined KDM security for identity-based encryption to simplify their security proof. We also adopt this definition to simplify our security proofs.

These two types of definitions are equivalent if the function class $\mathcal {F}$ contains a constant function. This is the case for affine functions and projection functions that we focus on.

$\text {IND}\text {-}\text {CCA}$ security is a special case of $\text {KDM}\text {-}\text {CCA}$ security. More specifically, we can define $\text {IND}\text {-}\text {CCA}$ security by restricting functions an adversary can query as KDM queries in the $\text {KDM}\text {-}\text {CCA}$ game to constant functions. Thus, we omit the definition of $\text {IND}\text {-}\text {CCA}$ security.

2.2 Projective Hash Function

We review the notion of projective hash function introduced by Cramer and Shoup [8] after introducing the notion of subset membership problem.

Definition 2

(Subset membership problem). Let $\mathcal {C}$ be a group and $\mathcal {V}$ be a subgroup of $\mathcal {C}$. We say that the subset membership problem is hard for $(\mathcal {C},\mathcal {V})$ if uniform distributions over $\mathcal {C}$ and $\mathcal {V}$ are computationally indistinguishable.

In this work, for a subset membership problem $(\mathcal {C},\mathcal {V})$, we require that there exist a trapdoor that enables us to efficiently check the membership of $\mathcal {V}$. Moreover, we require that we can efficiently sample c from $\mathcal {V}$ with a witness of $c\in \mathcal {V}$.

Definition 3

(Projective hash function). A projective hash function $\mathcal {H}$ is a tuple $(\mathcal {C}, \mathcal {V}, \mathcal {K}, \mathcal {SK}, \mathcal {PK},\varLambda , \mu )$. $\mathcal {C}$ and $\mathcal {K}$ are groups and $\mathcal {V}$ is a subgroup of $\mathcal {C}$. $\mathcal {SK}$ and $\mathcal {PK}$ are sets. The hash function $\varLambda _\mathsf {sk}$ indexed by $\mathsf {sk}\in \mathcal {SK}$, given $c \in \mathcal {C}$, outputs a hash value $\mathsf {K}\in \mathcal {K}$. The projection map $\mu$, given $\mathsf {sk}\in \mathcal {SK}$, outputs $\mathsf {pk}\in \mathcal {PK}$. We require that $\mathcal {H}$ be projective, that is, for any $\mathsf {sk}\in \mathcal {SK}$ and $c \in \mathcal {V}$, the value of $\varLambda _\mathsf {sk}(c)$ is determined only by c and $\mathsf {pk}=\mu (\mathsf {sk})$. In addition, we require that there exist a public evaluation algorithm $\mathsf {Pub}$, given $\mathsf {pk}=\mu (\mathsf {sk})$, $c \in \mathcal {V}$, and an witness w that $c \in \mathcal {V}$, outputs $\varLambda _\mathsf {sk}(c)$, where $\mathsf {sk}\in \mathcal {SK}$.

In addition, we say that $\mathcal {H}$ is homomorphic if for any $\mathsf {sk}\in \mathcal {SK}$ and $c_0, c_1 \in \mathcal {C}$, it holds that $\varLambda _\mathsf {sk}(c_0 \cdot c_1)=\varLambda _\mathsf {sk}(c_0) + \varLambda _\mathsf {sk}(c_1)$, where and denote operations in $\mathcal {C}$ and $\mathcal {K}$, respectively.

We define two security notions for projective hash function.

Definition 4

(Average-case smoothness). Let $\mathcal {H}=(\mathcal {C}, \mathcal {V}, \mathcal {K}, \mathcal {SK}, \mathcal {PK}, \varLambda , \mu )$ be a projective hash function. We say that $\mathcal {H}$ is average-case smooth if the distributions $(\mathsf {pk}, c, \varLambda _\mathsf {sk}(c))$ and $(\mathsf {pk},c,\mathsf {K})$ are statistically close, where $\mathsf {sk}\xleftarrow {\mathsf {r}}\mathcal {SK}$, $\mathsf {pk}=\mu (\mathsf {sk})$, $c\xleftarrow {\mathsf {r}}\mathcal {C}$, and $\mathsf {K}\xleftarrow {\mathsf {r}}\mathcal {K}$.

Definition 5

(Universal property). Let $\mathcal {H}=(\mathcal {C}, \mathcal {V}, \mathcal {K}, \mathcal {SK}, \mathcal {PK}, \varLambda , \mu )$ be a projective hash function. We say that $\mathcal {H}$ is universal if for any $\mathsf {pk}\in \mathcal {PK}$ , $c\in \mathcal {C}\setminus \mathcal {V}$, $\mathsf {K}\in \mathcal {K}$, we have .

3 $\mathrm{KDM}^{(1)}\mathrm{\text {-}CCA}$ Secure PKE Based on Homomorphic Projective Hash Function

In this section, we show a framework for achieving $\text {KDM}^{(1)}\text {-CCA}$ secure PKE based on homomorphic projective hash function.

Let $\mathcal {H}=(\mathcal {C}, \mathcal {V}, \mathcal {K}, \mathcal {SK}, \mathcal {PK}, \varLambda , \mu )$ be a homomorphic projective hash function with a public evaluation algorithm $\mathsf {Pub}$. We denote the group operations of $\mathcal {C}$ and $\mathcal {K}$ by “$\cdot$” and “$+$”, respectively. Let $\hat{\mathcal {H}}=\left( \mathcal {C}, \mathcal {V}, \hat{\mathcal {K}}, \hat{\mathcal {SK}}, \hat{\mathcal {PK}}, \hat{\varLambda }, \hat{\mu }\right)$ be a projective hash function with a public evaluation algorithm $\hat{\mathsf {Pub}}$. Let $\mathsf {\Pi _{cca}}=(\mathsf {KG}_\mathsf {cca},\mathsf {Enc}_\mathsf {cca},\mathsf {Dec}_\mathsf {cca})$ be a PKE scheme. We assume that the secret-key space of $\mathsf {\Pi _{cca}}$ is $\mathcal {K}$ for simplicity. Using these building blocks, we construct the following PKE scheme $\mathsf {\Pi _{kdm}}=(\mathsf {KG}_\mathsf {kdm},\mathsf {Enc}_\mathsf {kdm},\mathsf {Dec}_\mathsf {kdm})$. The message space of $\mathsf {\Pi _{kdm}}$ is $\mathcal {M}$. We use an invertible map $\phi :\mathcal {M}\rightarrow \mathcal {K}$ in the construction.

• $\mathsf {KG}_\mathsf {kdm}(1^\lambda ){:}$

  • Generate $\mathsf {sk}\xleftarrow {\mathsf {r}}\mathcal {SK}$ and compute $\mathsf {pk}\leftarrow \mu (\mathsf {sk})$.

  • Generate ${\hat{\mathsf {sk}}}\xleftarrow {\mathsf {r}}\hat{\mathcal {SK}}$ and compute ${\hat{\mathsf {pk}}}\leftarrow \hat{\mu }\left( {\hat{\mathsf {sk}}}\right)$.

  • Generate $(\mathsf {cpk},\mathsf {csk}) \leftarrow \mathsf {KG}_\mathsf {cca}(1^\lambda )$.

  • Generate ${c^*}\xleftarrow {\mathsf {r}}\mathcal {C}$ and compute ${d^*}\leftarrow \varLambda _\mathsf {sk}({c^*})+\mathsf {csk}$.

  • Return $\mathsf {PK}:= \left( \mathsf {pk},{\hat{\mathsf {pk}}},\mathsf {cpk}\right)$ and $\mathsf {SK}:= \left( \mathsf {sk},{\hat{\mathsf {sk}}},{c^*},{d^*}\right)$.

• $\mathsf {Enc}_\mathsf {kdm}(\mathsf {PK}, m){:}$

  • Parse $\left( \mathsf {pk},{\hat{\mathsf {pk}}},\mathsf {cpk}\right) \leftarrow \mathsf {PK}$.

  • Generate $c \xleftarrow {\mathsf {r}}\mathcal {V}$ with an witness w of $c\in \mathcal {V}$.

  • Compute $\mathsf {K}\leftarrow \mathsf {Pub}(\mathsf {pk},c,w)$ and $d\leftarrow \mathsf {K}+\phi (m)$.

  • Compute $\pi \leftarrow \hat{\mathsf {Pub}}\left( {\hat{\mathsf {pk}}},c,w\right)$.

  • Return $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk},\left( c,d,\pi \right) \right)$.

• $\mathsf {Dec}_\mathsf {kdm}(\mathsf {SK}, \mathsf {CT}){:}$

  • Parse $\left( \mathsf {sk},{\hat{\mathsf {sk}}},{c^*},{d^*}\right) \leftarrow \mathsf {SK}$.

  • Compute $\mathsf {csk}\leftarrow {d^*}-\varLambda _\mathsf {sk}({c^*})$.

  • Compute $\left( c,d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}(\mathsf {csk},\mathsf {CT})$. If the decryption result is not in $\mathcal {C}\times \mathcal {K}\times \hat{\mathcal {K}}$, return $\bot$. Otherwise, compute as follows.

  • If $\pi \ne \hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$, return $\bot$. Otherwise, return $m \leftarrow \phi ^{-1}\left( d-\varLambda _\mathsf {sk}(c)\right)$.

Correctness. We have $\mathsf {Pub}(\mathsf {pk},c,w)=\varLambda _\mathsf {sk}(c)$ and $\hat{\mathsf {Pub}}\left( {\hat{\mathsf {pk}}},c,w\right) =\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ for $c\in \mathcal {V}$, where w is a witness of $c\in \mathcal {V}$. Then, the correctness of $\mathsf {\Pi _{kdm}}$ follows from that of $\mathsf {\Pi _{cca}}$.

$\mathsf {\Pi _{kdm}}$ is $\text {KDM}\text {-}\text {CCA}$ secure with respect to the function family $\mathcal {F}_{\mathsf {phf}}$ consisting of functions described as

$$\begin{aligned} f_e\left( \mathsf {sk},{\hat{\mathsf {sk}}},c^*,d^*\right) =\phi ^{-1}\left( \varLambda _\mathsf {sk}(e)+\phi \left( f\left( {\hat{\mathsf {sk}}},c^*,d^*\right) \right) \right) , \end{aligned}$$

where $e\in \mathcal {C}$ and $f:\hat{\mathcal {SK}}\times \mathcal {C}\times \mathcal {K}\rightarrow \mathcal {M}$ is a function. This class corresponds to affine and projection functions in the instantiations. Formally, we prove the following theorem.

Theorem 3

Let the subset membership problem $(\mathcal {C},\mathcal {V})$ be hard. Let $\mathcal {H}$ be average-case smooth and $\hat{\mathcal {H}}$ universal. Let $\mathsf {\Pi _{cca}}$ be $\text {IND}\text {-}\text {CCA}$ secure. Then, $\mathsf {\Pi _{kdm}}$ is ${\mathcal {F}_{\mathsf {phf}}}\text {-}\text {KDM}^{(1)}\text {-}\text {CCA}$ secure.

Proof of Theorem 3. Let $\mathcal {A}$ be an adversary that attacks the ${\mathcal {F}_{\mathsf {phf}}}\text {-}\text {KDM}^{(1)}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{kdm}}$. We proceed the proof via a sequence of games. For every $t \in {\{0,\ldots ,8\}}$, let $\mathtt{SUC}_{t}$ be the event that $\mathcal {A}$ succeeds in guessing the challenge bit b in Game t.  

Game 0::

This is the original ${\mathcal {F}_{\mathsf {phf}}}\text {-}\text {KDM}^{(1)}\text {-}\text {CCA}$ game regarding $\mathsf {\Pi _{kdm}}$. We have $\mathsf {Adv}_{\mathsf {\Pi _{kdm}},\mathcal {F}_{\mathsf {phf}},\mathcal {A},1}^{\mathsf {kdmcca}}(\lambda )=\left| \Pr [\mathtt{SUC}_{0}]-\frac{1}{2}\right|$.

1.:

The challenger chooses a challenge bit $b \xleftarrow {\mathsf {r}}\{0,1\}$, and runs as follows.

(a):

Generate $\mathsf {sk}\xleftarrow {\mathsf {r}}\mathcal {SK}$ and compute $\mathsf {pk}\leftarrow \mu (\mathsf {sk})$.

(b):

Generate ${\hat{\mathsf {sk}}}\xleftarrow {\mathsf {r}}\hat{\mathcal {SK}}$ and compute ${\hat{\mathsf {pk}}}\leftarrow \hat{\mu }\left( {\hat{\mathsf {sk}}}\right)$.

(c):

Generate $(\mathsf {cpk},\mathsf {csk}) \leftarrow \mathsf {KG}_\mathsf {cca}\left( 1^\lambda \right)$.

(d):

Generate ${c^*}\xleftarrow {\mathsf {r}}\mathcal {C}$ and compute ${d^*}\leftarrow \varLambda _\mathsf {sk}({c^*})+\mathsf {csk}$.

(e):

Send $\mathsf {PK}:= \left( \mathsf {pk},{\hat{\mathsf {pk}}},\mathsf {cpk}\right)$ to $\mathcal {A}$ and prepare a list $L_\mathsf {kdm}$.

2.:

The challenger responds to queries made by $\mathcal {A}$.

For a KDM query $((e^0,f^0),(e^1,f^1))$ made by $\mathcal {A}$, the challenger responds as follows.

(a):

Generate $c \xleftarrow {\mathsf {r}}\mathcal {V}$ with a witness w of $c\in \mathcal {V}$.

(b):

Compute $\mathsf {K}\leftarrow \mathsf {Pub}(\mathsf {pk},c,w)$ and $d\leftarrow \mathsf {K}+\varLambda _\mathsf {sk}(e^b)+\phi \left( f^b\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) \right)$.

(c):

Compute $\pi \leftarrow \hat{\mathsf {Pub}}\left( {\hat{\mathsf {pk}}},c,w\right)$.

(d):

Return $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk},\left( c,d,\pi \right) \right)$ to $\mathcal {A}$ and add $\mathsf {CT}$ to $L_\mathsf {kdm}$.

For a decryption query $\mathsf {CT}$ made by $\mathcal {A}$, the challenger returns $\bot$ to $\mathcal {A}$ if $\mathsf {CT}\in L_\mathsf {kdm}$, and otherwise responds as follows.

(a):

Compute $\left( c,d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}(\mathsf {csk},\mathsf {CT})$. If the decryption result is not in $\mathcal {C}\times \mathcal {K}\times \hat{\mathcal {K}}$, return $\bot$ to $\mathcal {A}$. Otherwise, responds as follows.

(b):

Return $\bot$ if $\pi \ne \hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ and $m \leftarrow \phi ^{-1}\left( d-\varLambda _\mathsf {sk}(c)\right)$ otherwise.

3.:

$\mathcal {A}$ outputs $b' \in \{0,1\}$.

 

 

Game 1::

Same as Game 0 except that when $\mathcal {A}$ makes a KDM query, the challenger computes $\mathsf {K}\leftarrow \varLambda _\mathsf {sk}(c)$ and $\pi \leftarrow \hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ instead of $\mathsf {K}\leftarrow \mathsf {Pub}(\mathsf {pk},c,w)$ and $\pi \leftarrow \hat{\mathsf {Pub}}\left( {\hat{\mathsf {pk}}},c,w\right)$, respectively.

 

Due to the projective property of $\mathcal {H}$ and $\hat{\mathcal {H}}$, this change is only conceptual and thus we have $\left| \Pr [\mathtt{SUC}_{0}]-\Pr [\mathtt{SUC}_{1}]\right| =0$.

 

Game 2::

Same as Game 1 except that when $\mathcal {A}$ makes a KDM query, the challenger generates $c \xleftarrow {\mathsf {r}}\mathcal {C}$.

 

We have $\left| \Pr [\mathtt{SUC}_{1}]-\Pr [\mathtt{SUC}_{2}]\right| =\mathsf{negl}(\lambda )$ by the hardness of the subset membership problem $(\mathcal {C},\mathcal {V})$.

 

Game 3::

Same as Game 2 except that the challenger generates $c \xleftarrow {\mathsf {r}}\mathcal {C}$ and uses $c'=c\cdot (e^b)^{-1}$ instead of c when $\mathcal {A}$ makes a KDM query $((e^0,f^0),(e^1,f^1))$.

 

We have $\left| \Pr [\mathtt{SUC}_{2}]-\Pr [\mathtt{SUC}_{3}]\right| =~0$ since if c uniformly distributes over $\mathcal {C}$, then so does $c\cdot (e^b)^{-1}$.

By this change, the answer to a KDM query $((e^0,f^0),(e^1,f^1))$ in Game 3 is $\mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk},\left( c',d,\pi \right) \right)$, where

$$\begin{aligned} c'=c\cdot (e^b)^{-1}, d=\varLambda _\mathsf {sk}(c\cdot (e^b)^{-1})+\varLambda _\mathsf {sk}(e^b)+\phi \left( f^b\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) \right) , \pi =\hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c'\right) , \end{aligned}$$

and $c\xleftarrow {\mathsf {r}}\mathcal {C}$. Moreover, by the homomorphism of $\mathcal {H}$, $d=\varLambda _\mathsf {sk}(c)+\phi \left( f^b\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) \right)$ holds.

 

Game 4::

Same as Game 3 except that when $\mathcal {A}$ makes a KDM query, the challenger generates $c \xleftarrow {\mathsf {r}}\mathcal {V}$ with a witness w of $c\in \mathcal {V}$.

 

We have $\left| \Pr [\mathtt{SUC}_{3}]-\Pr [\mathtt{SUC}_{4}]\right| =\mathsf{negl}(\lambda )$ by the hardness of the subset membership problem $(\mathcal {C},\mathcal {V})$.

 

Game 5::

Same as Game 4 except that when $\mathcal {A}$ makes a KDM query, the challenger computes $d \leftarrow \mathsf {Pub}(\mathsf {pk},c,w)+\phi \left( f^b\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) \right)$. Note that the challenger still computes $\pi$ with $\pi \leftarrow \hat{\varLambda }_{\hat{\mathsf {sk}}}(c')$.

 

Due to the projective property of $\mathcal {H}$, this change is only conceptual and thus we have $\left| \Pr [\mathtt{SUC}_{4}]-\Pr [\mathtt{SUC}_{5}]\right| =0$.

At this point, $\mathsf {sk}$ is not needed to compute answers to KDM queries. More precisely, the answer to a KDM query $((e^0,f^0),(e^1,f^1))$ is $\mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk},\left( c',d,\pi \right) \right)$, where

$$\begin{aligned} c'=c\cdot (e^b)^{-1}, d=\mathsf {Pub}(\mathsf {pk},c,w)+\phi \left( f^b\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) \right) , \pi =\hat{\varLambda }_{\hat{\mathsf {sk}}}\left( c'\right) , \end{aligned}$$

$c\xleftarrow {\mathsf {r}}\mathcal {V}$, and w is a witness of $c\in \mathcal {V}$.

 

Game 6::

Same as Game 5 except how the challenger responds decryption queries made by $\mathcal {A}$. In this game, the challenger returns $\bot$ for a decryption query related to $c\notin \mathcal {V}$. More precisely, the challenger responds as follows.

For a decryption query $\mathsf {CT}$ made by $\mathcal {A}$, the challenger returns $\bot$ to $\mathcal {A}$ if $\mathsf {CT}\in L_\mathsf {kdm}$, and otherwise responds as follows.

1.:

Compute $\left( c,d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}(\mathsf {csk},\mathsf {CT})$. If the decryption result is not in $\mathcal {V}\times \mathcal {K}\times \hat{\mathcal {K}}$, return $\bot$ to $\mathcal {A}$. Otherwise, respond as follows.

2.:

Return $\bot$ if $\pi \ne \hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ and $m\leftarrow \phi ^{-1}\left( d-\varLambda _\mathsf {sk}(c)\right)$ otherwise.

 

We define the following event in Game t ($t=5,\cdots , 8$).

 

$\mathtt{BDQ}_{t}$::

$\mathcal {A}$ makes a decryption query $\mathsf {CT}\notin L_\mathsf {kdm}$ which satisfies $c\in \mathcal {C}\setminus \mathcal {V}$ and $\pi =\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$, where $\left( c,d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}(\mathsf {csk},\mathsf {CT})$. We call such a decryption query a “bad decryption query”.

 

Games 5 and 6 are identical games unless $\mathcal {A}$ makes a bad decryption query in each game. Therefore, we have $\left| \Pr [\mathtt{SUC}_{5}]-\Pr [\mathtt{SUC}_{6}]\right| \le \Pr [\mathtt{BDQ}_{6}]$.

Below, we let $\mathsf {td}$ be a trapdoor for efficiently deciding the membership of $\mathcal {V}$.

 

Game 7::

Same as Game 6 except that the challenger generates ${d^*}\xleftarrow {\mathsf {r}}\mathcal {K}$.

 

By the previous change, $\mathcal {A}$ cannot obtain information of $\mathsf {sk}$ other than $\mathsf {pk}$ through decryption queries in Games 6 and 7. Moreover, as noted above, KDM queries are replied without using $\mathsf {sk}$ in Games 6 and 7. Thus, the view of $\mathcal {A}$ in Games 6 and 7 can be perfectly simulated by $(\mathsf {pk},{c^*},\varLambda _\mathsf {sk}({c^*}))$ and $(\mathsf {pk},{c^*},{d^*})$, respectively, where $\mathsf {sk}\xleftarrow {\mathsf {r}}\mathcal {SK}$, $\mathsf {pk}\leftarrow \mu (\mathsf {sk})$, ${c^*}\xleftarrow {\mathsf {r}}\mathcal {C}$, and ${d^*}\xleftarrow {\mathsf {r}}\mathcal {K}$. Therefore, we have $\left| \Pr [\mathtt{SUC}_{6}]-\Pr [\mathtt{SUC}_{7}]\right| = \mathsf{negl}(\lambda )$ and $\left| \Pr [\mathtt{BDQ}_{6}]-\Pr [\mathtt{BDQ}_{7}]\right| = \mathsf{negl}(\lambda )$ from the average-case smoothness of $\mathcal {H}$.⁴

$\mathsf {csk}$ is now eliminated from the view of $\mathcal {A}$. Thus, we can use $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$.

 

Game 8::

Same as Game 7 except that when $\mathcal {A}$ makes a KDM query, the challenger computes $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk}, \left( 1_\mathcal {C},1_\mathcal {K},1_{\hat{\mathcal {K}}}\right) \right)$, where $1_\mathcal {C}$, $1_\mathcal {K}$, and $1_{\hat{\mathcal {K}}}$ are identity elements of $\mathcal {C}$, $\mathcal {K}$, and $\hat{\mathcal {K}}$, respectively.

 

From the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$, we have $\left| \Pr [\mathtt{SUC}_{7}]-\Pr [\mathtt{SUC}_{8}]\right| =\mathsf{negl}(\lambda )$.

Moreover, since reduction algorithms for $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$ can detect a bad decryption query made by $\mathcal {A}$ by utilizing decryption queries, $\mathsf {td}$, and ${\hat{\mathsf {sk}}}$, we obtain $\left| \Pr [\mathtt{BDQ}_{7}]-\Pr [\mathtt{BDQ}_{8}]\right| =\mathsf{negl}(\lambda )$ from the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$.

We see that the value of b is information theoretically hidden from the view of $\mathcal {A}$ in Game 8. Thus, we have $\left| \Pr [\mathtt{SUC}_{8}]-\frac{1}{2}\right| =0$.

We estimate $\Pr [\mathtt{BDQ}_{8}]$. In Game 8, ${\hat{\mathsf {sk}}}$ is hidden from the view of $\mathcal {A}$ except ${\hat{\mathsf {pk}}}$. Moreover, $\mathcal {A}$ cannot obtain any hash value $\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ for $c\in \mathcal {C}\setminus \mathcal {V}$ since an answer to a KDM query is computed as $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk}, \left( 1_\mathcal {C},1_\mathcal {K},1_{\hat{\mathcal {K}}}\right) \right)$ in Game 8. Therefore, from the universal property of $\hat{\mathcal {H}}$, we obtain $\Pr [\mathtt{BDQ}_{8}]=\mathsf{negl}(\lambda )$.⁵

From the above arguments, we see that $\mathsf {Adv}_{\mathsf {\Pi _{kdm}}, \mathcal {F}_{\mathsf {phf}}, \mathcal {A},1}^{\mathsf {kdmcca}}(\lambda )=\mathsf{negl}(\lambda )$. Since the choice of $\mathcal {A}$ is arbitrary, $\mathsf {\Pi _{kdm}}$ is ${\mathcal {F}_{\mathsf {phf}}}\text {-}\text {KDM}^{(1)}\text {-}\text {CCA}$ secure. $\Box$ (Theorem 3)

Remark 2

(Shrink secret keys). We do not need to require any structure and homomorphism for ${\hat{\mathsf {sk}}}$ and $\mathsf {csk}$. Then, we can shrink them into a single pseudorandom function key $K_\mathsf {prf}$ and modify the construction so that $\varLambda _\mathsf {sk}\left( {c^*}\right)$ masks $K_\mathsf {prf}$. Moreover, we can maintain ${c^*}$ and ${d^*}=\varLambda _\mathsf {sk}\left( {c^*}\right) +K_\mathsf {prf}$ as a part of the corresponding public key. If we do so, the resulting secret key is just $\mathsf {sk}$.

4 Instantiation Based on the DCR Assumption

We can instantiate our framework shown in Sect. 3 under the DDH, QR, and DCR assumptions. Due to the space constraints, we show the instantiation under the DCR assumption only. For Instantiations under the DDH and QR assumptions, See full version of this paper.

Definition 6

(DCR assumption). Let $N=PQ$ be a Blum integer for $\lambda$-bit safe primes $P,Q\equiv 3 \bmod 4$ such that $P=2p+1$ and $Q=2q+1$ for primes p and q. Let $n=pq$. We can decompose $\mathbb {Z}_{N^2}^*$ as an internal direct product $G_N\otimes \langle -1\rangle \otimes G_n \otimes G_2$, where $\langle -1\rangle$ is the subgroup of $\mathbb {Z}_{N^2}^*$ generated by $-1 \bmod N^2$, and $G_N$, $G_n$, and $G_2$ are cyclic groups of order N, n, and 2, respectively. Let $T=1+N\in \mathbb {Z}_{N^2}^*$. T has order N, and thus it generates $G_N$.

We say that the DCR assumption holds if for any PPT algorithm $\mathcal {A}$, we have $|\Pr [\mathcal {A}(N,y)=1]-\Pr [\mathcal {A}(N,y')=1]|=\mathsf{negl}(\lambda )$, where $y\xleftarrow {\mathsf {r}}G_N\otimes \langle -1\rangle \otimes G_n$ and $y'\xleftarrow {\mathsf {r}}\langle -1\rangle \otimes G_n$.

We define N, $G_N$, $G_n$, $\langle -1\rangle$, and T as in Definition 6. Let $g_1,\ldots , g_\ell$ be random generators of $G_n$, where $\ell$ is determined later. We can generate a random generator g of $G_n$ by generating $\mu \xleftarrow {\mathsf {r}}\mathbb {Z}_{N^2}^*$ and setting $g=\mu ^{2N}\bmod N^2$. Then, g is a generator of $G_n$ with high probability.

We define $\mathcal {C}$ and $\mathcal {V}$ as

$$\begin{aligned} \mathcal {C}&=\Big \{\left( T^{d_1}\cdot (-1)^{\gamma _1}\cdot g_1^r, \ldots ,T^{d_\ell }\cdot (-1)^{\gamma _\ell }\cdot g_\ell ^r\right) \\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~|d_1,\ldots ,d_\ell \in \mathbb {Z}_{N},\gamma _1,\ldots ,\gamma _\ell \in \mathbb {Z}_{2},r\in \mathbb {Z}_{n}\Big \},\text {and}~\\ \mathcal {V}&=\left\{ \left( (-1)^{\gamma _1}\cdot g_1^r,\ldots ,(-1)^{\gamma _\ell }\cdot g_\ell ^r\right) |\gamma _1,\ldots ,\gamma _\ell \in \mathbb {Z}_{2},r\in \mathbb {Z}_{n}\right\} . \end{aligned}$$

$\mathcal {V}$ is a subgroup of $\mathcal {C}$ and subset membership problem of $(\mathcal {C},\mathcal {V})$ is hard under the DCR assumption. As shown by previous works [5, 19], two distributions $\left\{ T^{d_i}\cdot (-g_i)^r\right\} _{i\in [\ell ]}$ and $\left\{ (-g_i)^r\right\} _{i\in [\ell ]}$ are computationally indistinguishable under the DCR assumption, where $d_i\xleftarrow {\mathsf {r}}\mathbb {Z}_{N}$ for every $i\in [\ell ]$ and $r\xleftarrow {\mathsf {r}}\mathbb {Z}_{2n}$. We see that uniform distributions over $\mathcal {C}$ and $\mathcal {V}$ are also computationally indistinguishable under the DCR assumption.

Let g be another generator of $G_n$. Then, there exists $\alpha _i\in \mathbb {Z}_{n}^*$ such that $g^{\alpha _i}=g_i$ for every $i\in [\ell ]$. The trapdoor for checking the membership of $\mathcal {V}$ is P, Q, and $\left\{ \alpha _i\right\} _{i\in [\ell ]}$.

When sampling a random element $c=(c_1,\ldots ,c_\ell )$ from $\mathcal {V}$, we randomly choose $r\xleftarrow {\mathsf {r}}\mathbb {Z}_{\frac{N-1}{4}}$ and $\gamma _i\xleftarrow {\mathsf {r}}\mathbb {Z}_{2}$ for every $i\in [\ell ]$, and set $c_i\leftarrow (-1)^{\gamma _i}\cdot g_i^r$ for every $i\in [\ell ]$. The distribution of c is statistically close to the uniform distribution over $\mathcal {V}$. Moreover, r is a witness of $c\in \mathcal {V}$. We can sample a random element from $\mathcal {C}$ in a similar fashion.

For $(\mathcal {C},\mathcal {V})$ defined above, we construct two projective hash functions $\mathcal {H}=(\mathcal {C}, \mathcal {V}, \mathcal {K}, \mathcal {SK}, \mathcal {PK}, \varLambda , \mu )$ and $\hat{\mathcal {H}}=\left( \mathcal {C}, \mathcal {V}, \hat{\mathcal {K}}, \hat{\mathcal {SK}}, \hat{\mathcal {PK}}, \hat{\varLambda }, \hat{\mu }\right)$. The construction of $\mathcal {H}$ is a slightly modified version of projective hash function based on the DCR assumption proposed by Wee [19] thus is a generalization of the $\text {KDM}\text {-}\text {CPA}$ secure PKE scheme proposed by Brakerski and Goldwasser [5]. For the reason we need a modification, see Remark 3 after the constructions.

4.1 Construction of $\mathcal {H}$

We define $\mathbb {QR}_{N^s}=G_{N^{s-1}}\otimes G_n$ and $\mathbb {J}_{N^s}=G_{N^{s-1}}\otimes \langle -1\rangle \otimes G_n=\langle -1\rangle \otimes \mathbb {QR}_{N^s}$. We define $\mathcal {SK}=\{0,1\}^\ell$, $\mathcal {PK}=G_n$, and $\mathcal {K}=\mathbb {QR}_{N^s}$. For every $\mathsf {sk}=s_1\cdots s_\ell \in \{0,1\}^\ell$ and $c=\left( c_1,\ldots ,c_\ell \right) \in \mathcal {C}$, we also define $\mu$ and $\varLambda$ as

$$\begin{aligned} \mu (\mathsf {sk})=\prod _{i\in [\ell ]} g_i^{2s_i} \,\,\text {and}\,\, \varLambda _\mathsf {sk}(c)=\prod _{i\in [\ell ]} c_i^{2s_i}. \end{aligned}$$

Projective property. Let $\mathsf {sk}=s_1\cdots s_\ell \in \{0,1\}^\ell$, $\mathsf {pk}=\prod _{i\in [\ell ]} g_i^{2s_i}$, and $c=\left( (-1)^{\gamma _1}\cdot g_1^r,\ldots ,(-1)^{\gamma _\ell }\cdot g_\ell ^r\right)$, where $r\in \mathbb {Z}_{n}$ and $\gamma _i\in \mathbb {Z}_{2}$ for every $i\in [\ell ]$. We define the public evaluation algorithm $\mathsf {Pub}$ as $\mathsf {Pub}(\mathsf {pk},c,r)=\mathsf {pk}^{r}$. We see that

$$\begin{aligned} \mathsf {pk}^{r}=\left( \prod _{i\in [\ell ]} g_i^{2s_i}\right) ^{r}=\prod _{i\in [\ell ]} \left( g_i^r\right) ^{2s_i}= \prod _{i\in [\ell ]} \left( (-1)^{\gamma _i}\cdot g_i^r\right) ^{2s_i}=\varLambda _\mathsf {sk}(c) \end{aligned}$$

and thus $\mathcal {H}$ satisfies projective property.

Homomorphism. For every $\mathsf {sk}=s_1\cdots s_\ell \in \{0,1\}^\ell$, $c=\left( c_1,\ldots ,c_\ell \right) \in \mathcal {C}$, and $c'=\left( c'_1,\ldots ,c'_\ell \right) \in \mathcal {C}$, we have

$$\begin{aligned} \varLambda _\mathsf {sk}(c)\cdot \varLambda _\mathsf {sk}(c')=\prod _{i\in [\ell ]} c_i^{2s_i}\cdot \prod _{i\in [\ell ]} (c'_i)^{2s_i} =\prod _{i\in [\ell ]}(c_i\cdot c_i')^{2s_i}=\varLambda _\mathsf {sk}(c\cdot c') \end{aligned}$$

and thus $\mathcal {H}$ is homomorphic.

Average-case smoothness. Similarly to Wee [19], we prove a weaker property that is sufficient for our construction.

For an element $e=T^d \cdot g^r \in \mathbb {QR}_{N^s}$, we define $e \bmod G_n=T^d$. Let $c=(c_1,\ldots ,c_\ell )=\left( T^{d_1}\cdot (-1)^{\gamma _1}\cdot g_1^r,\ldots ,T^{d_\ell }\cdot (-1)^{\gamma _\ell }\cdot g_\ell ^r\right)$, where $d_1,\ldots ,d_\ell \in \mathbb {Z}_{N}$, $\gamma _1,\ldots ,\gamma _\ell \in \mathbb {Z}_{2}$, and $r\in \mathbb {Z}_{n}$. We have

$$\begin{aligned} \varLambda _\mathsf {sk}(c) \bmod G_n&= \prod _{i\in [\ell ]} \left( T^{d_i}\cdot g_i^r\right) ^{2s_i} \bmod G_n = T^{2\sum _{i\in [\ell ]}d_is_i \,{\bmod }\, N} . \end{aligned}$$

The leftover hash lemma implies that the following two distributions

$$\begin{aligned} \left( c, \sum _{i\in [\ell ]}d_is_i \bmod N, \prod _{i\in [\ell ]}g_i^{2s_i}\right) \,\,\text {and}\,\, \left( c, \mathsf {K}, \prod _{i\in [\ell ]}g_i^{2s_i}\right) \end{aligned}$$

are $\sqrt{\frac{N\cdot n}{4\cdot 2^\ell }}$-close, where $\mathsf {sk}=s_1\cdots s_\ell \xleftarrow {\mathsf {r}}\{0,1\}^\ell$, $c=(c_1,\ldots ,c_\ell )\xleftarrow {\mathsf {r}}\mathcal {C}$, and $\mathsf {K}\xleftarrow {\mathsf {r}}\mathbb {Z}_{N}$. Moreover, if $\mathsf {K}$ is uniformly at random over $\mathbb {Z}_{N}$, then so does $2\mathsf {K}\bmod N$. Therefore, by setting $\ell =3\log N$, the distribution of $\varLambda _\mathsf {sk}(c) \bmod G_n$ is statistically close to uniform over $G_N$.

4.2 Construction of $\hat{\mathcal {H}}$

We define $\hat{\mathcal {SK}}=\mathbb {Z}_{Nn}^{\ell }$,⁶ $\hat{\mathcal {PK}}=G_n$, and $\hat{\mathcal {K}}=\mathbb {QR}_{N^s}$. For every ${\hat{\mathsf {sk}}}=(x_1,\ldots ,x_\ell )\in \hat{\mathcal {SK}}$ and $c=\left( c_1,\ldots ,c_\ell \right) \in \mathcal {C}$, we also define $\hat{\mu }$ and $\hat{\varLambda }$ as

$$\begin{aligned} \hat{\mu }\left( {\hat{\mathsf {sk}}}\right) =\prod _{i\in [\ell ]} g_i^{2x_i} \,\,\text {and}\,\, \hat{\varLambda }_{{\hat{\mathsf {sk}}}}(c)=\prod _{i\in [\ell ]} c_i^{2x_i}. \end{aligned}$$

Projective property. For every ${\hat{\mathsf {sk}}}=(x_1,\ldots , x_\ell )\in \hat{\mathcal {SK}}$, ${\hat{\mathsf {pk}}}=\prod _{i\in [\ell ]} g_i^{2x_i}$, and $c= \left( (-1)^{\gamma _1}\cdot g_1^r,\ldots ,(-1)^{\gamma _\ell }\cdot g_\ell ^r\right)$, where $r\in \mathbb {Z}_{n}$ and $\gamma _i\in \mathbb {Z}_{2}$ for every $i\in [\ell ]$, we define the public evaluation algorithm $\hat{\mathsf {Pub}}$ as $\hat{\mathsf {Pub}}\left( {\hat{\mathsf {pk}}},c,r\right) ={\hat{\mathsf {pk}}}^r$. Similarly to $\mathcal {H}$, we see that $\hat{\mathcal {H}}$ satisfies projective property.

Universal property. We need to prove that the universal property holds not only for all $c\in \mathcal {C}\setminus \mathcal {V}$ but also all $c\in \mathbb {J}_{N^s}^\ell \setminus \mathcal {C}$. This is because we cannot efficiently check the membership of $\mathcal {C}$. Note that we can check the membership of $\mathbb {J}_{N^s}$ by computing Jacobi symbol with respect to N, and Jacobi symbol with respect to N can be computed without factorizations of N, that is P and Q [18, Sect. 12.3].

For every $c\in \mathbb {J}_{N^s}^\ell \setminus \mathcal {C}$, we define $\hat{\varLambda }_{\hat{\mathsf {sk}}}(c)$ in the same way as above. For every ${\hat{\mathsf {pk}}}\in \hat{\mathcal {PK}}$, $c=(c_1,\ldots ,c_\ell )\in \mathbb {J}_{N^s}^\ell$, and $\pi \in \hat{\mathcal {K}}$, we consider the following probability

(1)

We first consider the case where at least one element of $c=(c_1,\ldots ,c_\ell )$ is not in $\langle -1\rangle \otimes G_n$. Suppose that $c_{i^*}\in \mathbb {J}_{N^s}\setminus \langle -1\rangle \otimes G_n$ for some ${i^*}\in [\ell ]$.

For two elements $e_0,e_1\in \mathbb {QR}_{N^s}$, we write $e_0\equiv e_1\bmod G_n$ to denote that $e_0 \bmod G_n=e_1 \bmod G_n$. For two elements $e_0,e_1\in \mathbb {QR}_{N^s}$, if $e_0=e_1$ holds, then so does $e_0\equiv e_1\bmod G_n$. Thus, the probability of Eq. 1 is bounded by

For every $i\in [\ell ]$, $c_i^{2x_i}\bmod G_n$ is determined by only $x_i \bmod N$ and independent of $x_i \bmod n$ from the Chinese Remainder Theorem since $N=PQ$ and $n=pq$ are relatively prime. Therefore, the above probability is

$$\begin{aligned}&\Pr _{x_i\xleftarrow {\mathsf {r}}\mathbb {Z}_{Nn}}\left[ \prod _{i\in [\ell ]} c_i^{2x_i}\equiv \pi \bmod G_n \right] . \end{aligned}$$

Since $c_{i^*}\notin \langle -1\rangle \otimes G_n$, we can write $c_{i^*}=T^{d_{i^*}}\cdot (-1)^{\gamma _{i^*}}\cdot g^{r_{i^*}}$, where $d_{i^*}\in \mathbb {Z}_{N}$ such that $d_{i^*}\ne 0$, $\gamma _{i^*}\in \mathbb {Z}_{2}$, and $r_{i^*}\in \mathbb {Z}_{n}$. We have

$$\begin{aligned} c_{i^*}^{2x_{i^*}}=T^{2d_{i^*}(x_{i^*}\,{\bmod }\, N)}\cdot g^{2r_{i^*}(x_{i^*}\,{\bmod }\, n)}. \end{aligned}$$

Then, the above probability is the same as

$$\begin{aligned} \Pr _{x_i\xleftarrow {\mathsf {r}}\mathbb {Z}_{Nn}}\left[ T^{2d_{i^*}(x_{i^*}\,{\bmod }\, N)}\equiv \pi \cdot \left( \prod _{i\in [\ell ],i\ne {i^*}} c_i^{2x_i}\right) ^{-1} \bmod G_n \right] . \end{aligned}$$

This probability is smaller than $\frac{1}{P}$ or $\frac{1}{Q}$. Thus, in this case, the probability of Eq. 1 is negligible in $\lambda$.

We next consider the case where all elements of $c=(c_1,\ldots ,c_\ell )\notin \mathcal {V}$ are in $\langle -1\rangle \otimes G_n$. In this case, we can write $c_i=(-1)^{\gamma _i}\cdot g_i^{r_i}$, where $\gamma _i\in \mathbb {Z}_{2}$ and $r_i\in \mathbb {Z}_{n}$ for every $i\in [\ell ]$. Since $c\notin \mathcal {V}$, there exist $i_1,i_2\in [\ell ]$ such that $r_{i_1}\ne r_{i_2}$. Let g be a generator of $G_n$. Since $g_i$ is a generator of $G_n$, there exists $\alpha _i\in \mathbb {Z}_{n}^*$ such that $g_i=g^{\alpha _i}$ for every $i\in [\ell ]$. The probability of Eq. 1 is 0 if $\pi \notin G_n$, and thus we consider cases of $\pi \in G_n$. Then, the probability of Eq. 1 is the same as

Since $r_1\not \equiv r_2 \bmod n$, either $r_{i_1}\not \equiv r_{i_2} \bmod p$ or $r_{i_1}\not \equiv r_{i_2}\bmod q$ holds. Without loss of generality, we assume that $r_{i_1}\not \equiv r_{i_2} \bmod p$. Since p and q are primes, the above probability is bounded by

Since $r_{i_1}\not \equiv r_{i_2} \bmod p$, two equations

$$\begin{aligned} \sum _{i\in [\ell ]} \alpha _ir_ix_i \equiv 2^{-1}\cdot \log _g\pi \bmod p,\,\text {and}\, \sum _{i\in [\ell ]} \alpha _ix_i \equiv 2^{-1}\cdot \log _g{\hat{\mathsf {pk}}}\bmod p \end{aligned}$$

are linearly independent. Therefore, the above probability is $\frac{1}{p}$.

Thus, for every $c\in \mathbb {J}_{N^s}^\ell \setminus \mathcal {V}$, the probability of Eq. 1 is negligible in $\lambda$.

Remark 3

(Difference with previous works [5, 19]). The difference between our construction and previous works is that when we compute a hash value of c, we first square each element of c. By this operation, the ranges of $\mathcal {H}$ and $\hat{\mathcal {H}}$ are $\mathbb {QR}_{N^s}=G_N\cdot G_n$.

If we do not perform squaring, the ranges will be $\mathbb {J}_{N^s}=G_N\cdot \langle -1\rangle \cdot G_n$ and hash values of some elements can be predicted with high probability since the order of $\langle -1\rangle$ is 2. In fact, we can correctly guess the hash value of $(-1,\ldots ,-1)\in \langle -1\rangle ^\ell$ with probability at least $\frac{1}{2}$. In this case, to achieve universal property of $\hat{\mathcal {H}}$, we need parallelization similarly to the QR based construction.

One might think we have another option where $\mathcal {C}$ and $\mathcal {V}$ are defined as subgroups of $\mathbb {QR}_{N^s}$ and $G_n$, respectively. This option is not working. The reason is that we cannot efficiently check the membership of $\mathbb {QR}_{N^s}$. Therefore, if we use such $\mathcal {C}$ and $\mathcal {V}$, we still need to take elements of $\mathbb {J}_{N^s}$ into account, and thus we need squaring.

4.3 Associated Function Class

The message space of the DCR based construction is $\mathbb {Z}_{N}$. We define $\phi (m\in \mathbb {Z}_{N})=T^m$. Let $\mathcal {F}_{\mathsf {dcr}}$ be a family of functions described as

$$\begin{aligned} f_e\left( \mathsf {sk},{\hat{\mathsf {sk}}},c^*,d^*\right)&=\phi ^{-1}\left( \varLambda _\mathsf {sk}\left( T^{e_1/2},\ldots ,T^{e_\ell /2}\right) +\phi \left( f\left( {\hat{\mathsf {sk}}},c^*,d^*\right) \right) \right) \\&=\phi ^{-1}\left( T^{\sum _{i\in [\ell ]}e_is_i+f\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) }\right) \\&=\left( \sum _{i\in [\ell ]}e_is_i+f\left( {\hat{\mathsf {sk}}},{c^*},{d^*}\right) \right) \bmod N , \end{aligned}$$

where $\frac{1}{2}$ denotes the inverse of 2 modulo N, $e_i\in \mathbb {Z}_{N}$ for every $i\in [\ell ]$, and f is a function whose range is $\mathbb {Z}_{N}$. The DCR based construction is ${\mathcal {F}_{\mathsf {dcr}}}\text {-}\text {KDM}^{(1)}\text {-}\text {CCA}$ secure. In the construction, we can maintain ${\hat{\mathsf {sk}}}$, ${c^*}$, and ${d^*}$ as bit strings. In this case, the above function class includes affine functions and projection functions.

5 $\text {KDM}\text {-}\text {CCA}$ Secure PKE from the DDH Assumption

Although our framework shown in Sect. 3 captures only $\text {KDM}^{(1)}\text {-}\text {CCA}$ security, we can prove the $\text {KDM}\text {-}\text {CCA}$ security of concrete instantiations. In this section, we prove that our concrete instantiation based on the DDH assumption is $\text {KDM}\text {-}\text {CCA}$ secure. We also briefly explain how to prove the multi user security of our QR and DCR based schemes in Remark 5 at the end of this section. We first introduce the DDH assumption, and then provide the construction.

Definition 7

(DDH assumption). Let $\mathbb {G}$ be a cyclic group of order p and g a random generator of $\mathbb {G}$. We say that the DDH assumption holds if for any PPT algorithm $\mathcal {A}$, $\left| \Pr [\mathcal {A}(p,g,g^x,g^y,g^{xy})=1]-\Pr [\mathcal {A}(p,g,g^x,g^y,g^z)=1]=\mathsf{negl}(\lambda )\right|$ holds, where $x,y,z\xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$.

Let $\mathbb {G}$ be a cyclic group of prime order p and g a random generator of $\mathbb {G}$. Let $\mathsf {\Pi _{cca}}=(\mathsf {KG}_\mathsf {cca},\mathsf {Enc}_\mathsf {cca},\mathsf {Dec}_\mathsf {cca})$ be a PKE scheme. We assume that the secret-key space of $\mathsf {\Pi _{cca}}$ is $\mathbb {G}$ for simplicity. We construct the following PKE scheme $\mathsf {\Pi _{ddh}}=(\mathsf {KG}_\mathsf {ddh},\mathsf {Enc}_\mathsf {ddh},\mathsf {Dec}_\mathsf {ddh})$. The message space of $\mathsf {\Pi _{ddh}}$ is $\{0,1\}$.

• $\mathsf {KG}_\mathsf {ddh}(1^\lambda ){:}$

  • Generate $g_1,\ldots ,g_\ell \xleftarrow {\mathsf {r}}\mathbb {G}$.

  • Generate $s=s_1\cdots s_\ell \xleftarrow {\mathsf {r}}\{0,1\}^\ell$ and $x_1,\ldots ,x_\ell \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$.

  • Compute $g_0 \leftarrow \prod _{i\in [\ell ]}g_i^{s_i}$ and $\hat{g}_0 \leftarrow \prod _{i\in [\ell ]}g_i^{x_i}$.

  • Generate $(\mathsf {cpk},\mathsf {csk}) \leftarrow \mathsf {KG}_\mathsf {cca}(1^\lambda )$.

  • Generate $w_i \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ and set $e_i \leftarrow g_i^{w_i}$ for every $i\in [\ell ]$.

  • Compute $e_0\leftarrow \prod _{i\in [\ell ]}e_i^{s_i}$ and $u \leftarrow e_0\cdot \mathsf {csk}$.

  • Set $v := \left\{ x_i\right\} _{i\in [\ell ]}\Vert \left\{ e_i\right\} _{i\in [\ell ]}\Vert u$.

  • Return $\mathsf {PK}:= \left( \left\{ g_i\right\} _{i\in [\ell ]}, g_0, \hat{g}_0,\mathsf {cpk}\right)$ and $\mathsf {SK}:= \left( s,v\right)$.

• $\mathsf {Enc}_\mathsf {ddh}(\mathsf {PK}, m){:}$

  • Parse $\left( \left\{ g_i\right\} _{i\in [\ell ]}, g_0, \hat{g}_0,\mathsf {cpk}\right) \leftarrow \mathsf {PK}$.

  • Generate $r \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ and compute $c_i \leftarrow g_i^r$ for every $i\in [\ell ]$.

  • Compute $d\leftarrow g^m\cdot g_0^r$ and $\pi \leftarrow \hat{g}_0^r$.

  • Return $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk},\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \right)$.

• $\mathsf {Dec}_\mathsf {ddh}(\mathsf {SK}, \mathsf {CT}){:}$

  • Parse $\left( s,\left\{ x_i\right\} _{i\in [\ell ]}\Vert \left\{ e_i\right\} _{i\in [\ell ]}\Vert u\right) \leftarrow \mathsf {SK}$.

  • Compute $\mathsf {csk}\leftarrow u\cdot \left( \prod _{i\in [\ell ]}e_i^{s_i}\right) ^{-1}$.

  • Compute $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}(\mathsf {csk},\mathsf {CT})$. If the decryption result is not in $\mathbb {G}^{\ell +2}$, returns $\bot$. Otherwise, compute as follows.

  • Return $\bot$ if $\pi \ne \prod _{i\in [\ell ]}c_i^{x_i}$ and $m \leftarrow \log _g\left( d\cdot \left( \prod _{i\in [\ell ]}c_i^{s_i}\right) ^{-1}\right)$ otherwise.

Correctness. In the decryption algorithm, we need to compute discrete logarithm on $\mathbb {G}$. We can efficiently perform this operation since we restrict the message space to $\{0,1\}$. The decryption algorithm returns $\bot$ if $d\cdot \left( \prod _{i\in [\ell ]}c_i^{s_i}\right) ^{-1}\notin \{1,g\}$. Then, the correctness of $\mathsf {\Pi _{ddh}}$ follows from that of $\mathsf {\Pi _{cca}}$.

Let n be the number of key pairs in the security game. We define $\mathcal {F}_{\mathsf {ddh}}$ as a function family consisting of functions described as

$$\begin{aligned} f'\left( \left\{ s_{k},v_{k}\right\} _{k\in [n]}\right) =\sum _{k\in [n]}\left\langle a_{k},s_{k}\right\rangle +f\left( \left\{ v_{k}\right\} _{k\in [n]}\right) , \end{aligned}$$

where $\left\langle \cdot ,\cdot \right\rangle$ denotes inner product over $\mathbb {Z}_{}$, $a_{k}\in \{0,1\}^\ell$, and f is a function such that $\sum _{k\in [n]}\left\langle a_{k},s_{k}\right\rangle +f\left( \left\{ v_{k}\right\} _{k\in [n]}\right) \in \{0,1\}$ for every $\left\{ s_{k}\right\} _{k\in [n]}$ and $\left\{ v_{k}\right\} _{k\in [n]}$. By maintaining $\left\{ v_{k}\right\} _{k\in [n]}$ as bit strings, $\mathcal {F}_{\mathsf {ddh}}$ includes projection functions of single-bit output. $\mathsf {\Pi _{kdm}}$ is $\text {KDM}\text {-}\text {CCA}$ secure with respect to $\mathcal {F}_{\mathsf {ddh}}$. Formally, we prove the following theorem.

Theorem 4

Let $\mathsf {\Pi _{cca}}$ be $\text {IND}\text {-}\text {CCA}$ secure. Assuming the DDH problem is hard on $\mathbb {G}$, $\mathsf {\Pi _{ddh}}$ is ${\mathcal {F}_{\mathsf {ddh}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure.

Remark 4

(Extension to affine functions). We can construct a DDH based PKE scheme that is $\text {KDM}\text {-}\text {CCA}$ secure with respect to affine functions by applying the following modifications to the above construction. We set the message space as $\mathbb {G}$. Let $\mathsf {SK}\in \{0,1\}^L$ be a bit string that is a concatenation of s and bit representation of v. We maintain a secret-key $\mathsf {SK}=s_1\cdots s_L$ as $\left( g^{s_1},\ldots ,g^{s_L}\right)$. Then, the construction is ${\mathcal {F}_{\mathsf {aff}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure, where $\mathcal {F}_{\mathsf {aff}}$ is a function class consisting of functions described as

$$\begin{aligned} f\left( \mathsf {SK}_{1},\ldots ,\mathsf {SK}_{n}\right) =\left( \prod _{i\in [L]}\left( g^{s_{ki}}\right) ^{a_{ki}}\right) \cdot a_0, \end{aligned}$$

where $\mathsf {SK}_{k}=s_{k1}\cdots s_{kL}$ for every $k\in [n]$, $a_0\in \mathbb {G}$ and $a_{ki}\in \mathbb {Z}_{p}$ for every $i\in [\ell ]$ and $k\in [n]$. This is exactly the affine functions defined by Boneh et al. [4].

Proof of Theorem 4. Let n be the number of keys. Let $\mathcal {A}$ be an adversary that attacks the ${\mathcal {F}_{\mathsf {ddh}}}\text {-}\text {KDM}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{ddh}}$. We proceed the proof via a sequence of games. For every $t \in {\{0,\ldots ,11\}}$, let $\mathtt{SUC}_{t}$ be the event that $\mathcal {A}$ succeeds in guessing the challenge bit b in Game t.

 

Game 0::

This is the original ${\mathcal {F}_{\mathsf {ddh}}}\text {-}\text {KDM}^{(n)}\text {-}\text {CCA}$ game regarding $\mathsf {\Pi _{ddh}}$. We have $\mathsf {Adv}_{\mathsf {\Pi _{ddh}},\mathcal {F}_{\mathsf {ddh}},\mathcal {A},n}^{\mathsf {kdmcca}}(\lambda )=\left| \Pr [\mathtt{SUC}_{0}]-\frac{1}{2}\right|$.

1.:

The challenger chooses $b \xleftarrow {\mathsf {r}}\{0,1\}$ and generates $\left( \mathsf {PK}_{k},\mathsf {SK}_{k}\right)$ for every $k\in [n]$ as follows.

(a):

Generate $g_{k1},\ldots ,g_{k\ell } \xleftarrow {\mathsf {r}}\mathbb {G}$.

(b):

Generate $s_{k}=s_{k1}\cdots s_{k\ell } \xleftarrow {\mathsf {r}}\{0,1\}^\ell$ and $x_{k1},\ldots ,x_{k\ell } \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$.

(c):

Compute $g_{k0} \leftarrow \prod _{i\in [\ell ]}\left( g_{ki}\right) ^{s_{ki}}$ and $\hat{g}_{k0} \leftarrow \prod _{i\in [\ell ]}\left( g_{ki}\right) ^{x_{ki}}$.

(d):

Generate $\left( \mathsf {cpk}_{k},\mathsf {csk}_{k}\right) \leftarrow \mathsf {KG}_\mathsf {cca}(1^\lambda )$.

(e):

Generate $w_{ki} \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ and set $e_{ki} \leftarrow \left( g_{ki}\right) ^{w_{ki}}$ for every $i\in [\ell ]$.

(f):

Compute $e_{k0} \leftarrow \prod _{i\in [\ell ]}\left( e_{ki}\right) ^{s_{ki}}$ and $u_{k}\leftarrow e_{k0}\cdot \mathsf {csk}_{k}$.

(g):

Set $v_{k} := \left\{ x_{ki}\right\} _{i\in [\ell ]}\Vert \left\{ e_{ki}\right\} _{i\in [\ell ]}\Vert u_{k}$.

(h):

Set $\mathsf {PK}_{k} := \left( \mathsf {cpk}_{k}, \left\{ g_{ki}\right\} _{i\in [\ell ]}, g_{k0}, \hat{g}_{k0}\right)$ and $\mathsf {SK}_{k} := \left( s_{k},v_{k}\right)$.

The challenger sends $\left\{ \mathsf {PK}_{k}\right\} _{k\in [n]}$ to $\mathcal {A}$ and prepares a list $L_\mathsf {kdm}$.

2.:

The challenger responds to queries made by $\mathcal {A}$.

For a KDM query $\left( j,\left( \left\{ a_{k}^0\right\} _{k\in [n]},f^0\right) ,\left( \left\{ a_{k}^1\right\} _{k\in [n]},f^1\right) \right)$ made by $\mathcal {A}$, the challenger responds as follows.

(a):

Set $m := \sum _{k\in [n]}\left\langle a_{k}^b,s_{k}\right\rangle +f^b\left( \left\{ v_{k}\right\} _{k\in [n]}\right)$.

(b):

Generate $r \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ and compute $c_i \leftarrow \left( g_{ji}\right) ^r$ for every $i\in [\ell ]$.

(c):

Compute $d\leftarrow g^m\cdot \left( g_{j0}\right) ^r$ and $\pi \leftarrow \left( \hat{g}_{j0}\right) ^r$.

(d):

Return $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk}_{j},\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \right)$ and add $(j,\mathsf {CT})$ to $L_\mathsf {kdm}$.

For a decryption query $(j,\mathsf {CT})$ made by $\mathcal {A}$, the challenger returns $\bot$ to $\mathcal {A}$ if $(j,\mathsf {CT})\in L_\mathsf {kdm}$, and otherwise responds as follows.

(a):

Compute $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}(\mathsf {csk}_{j},\mathsf {CT})$. If the decryption result is not in $\mathbb {G}^{\ell +2}$, return $\bot$ and otherwise respond as follows.

(b):

Return $\bot$ if $\pi \ne \prod _{i\in [\ell ]}c_i^{x_{ji}}$ and $m \leftarrow \log _g\left( d\cdot \left( \prod _{i\in [\ell ]}c_i^{s_{ji}}\right) ^{-1}\right)$ otherwise.

3.:

$\mathcal {A}$ outputs $b' \in \{0,1\}$.

 

 

Game 1::

Same as Game 0 except how the challenger computes $\left\{ e_{ki}\right\} _{i\in [\ell ],k\in [n]}$. The challenger generates $w_i \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ for every $i\in [\ell ]$ and computes $e_{ki} \leftarrow \left( g_{ki}\right) ^{w_i}$ for every $i\in [\ell ]$ and $k\in [n]$.

 

We have $\left| \Pr [\mathtt{SUC}_{0}]-\Pr [\mathtt{SUC}_{1}]\right| =\mathsf{negl}(\lambda )$ since $\left( (g_{1i})^{w_{1i}},\ldots ,(g_{ni})^{w_{ni}}\right)$ and $\left( (g_{1i})^{w_i},\ldots ,(g_{ni})^{w_i}\right)$ are computationally indistinguishable by the DDH assumption for every $i\in [\ell ]$.

 

Game 2::

Same as Game 1 except how the challenger generates $\left\{ s_{k}\right\} _{k\in [n]}$ and $\left\{ g_{ki}\right\} _{i\in [\ell ],k\in [n]}$. The challenger first generates $s=s_1\cdots s_\ell \xleftarrow {\mathsf {r}}\{0,1\}^\ell$ and $g_1,\ldots g_\ell \xleftarrow {\mathsf {r}}\mathbb {G}$. Then, for every $k\in [n]$, the challenger generates $\varDelta _{k} \xleftarrow {\mathsf {r}}\{0,1\}^\ell$ and computes $s_{k}\leftarrow s \oplus \varDelta _{k}$. In addition, for every $i\in [\ell ]$ and $k\in [n]$, the challenger generates $\gamma _{ki}\xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ and computes $g_{ki} \leftarrow g_i^{\gamma _{ki}}$.

 

$\left| \Pr [\mathtt{SUC}_{1}]-\Pr [\mathtt{SUC}_{2}]\right| =0$ holds since the difference between Game 1 and 2 is only conceptual.

From Game 3 to 7, we change the game so that we do not need s to respond to KDM queries made by $\mathcal {A}$.

In Game 2, we have $g_{k0} =\prod _{i\in [\ell ]}\left( g_{ki}\right) ^{s_{ki}}=\prod _{i\in [\ell ]}\left( g_i^{\gamma _{ki}}\right) ^{s_i\oplus \varDelta _{ki}}$, where $\varDelta _{ki}$ is the i-th bit of $\varDelta _{k}$ for every $i\in [\ell ]$. For every $i\in [\ell ]$ and $k\in [n]$, we have

$$\begin{aligned} s_i\oplus \varDelta _{ki}={\left\{ \begin{array}{ll} s_i &{} \left( \varDelta _{ki}=0\right) \\ 1-s_i &{} \left( \varDelta _{ki}=1\right) \end{array}\right. }. \end{aligned}$$

Thus, by defining

$$\begin{aligned} \delta _{ki}={\left\{ \begin{array}{ll} 1 &{} \left( \varDelta _{ki}=0\right) \\ -1 &{} \left( \varDelta _{ki}=1\right) \end{array}\right. } , \end{aligned}$$

(2)

for every $i\in [\ell ]$ and $k\in [n]$, we have

$$\begin{aligned} g_{k0} =\prod _{i\in \varDelta _{k}}g_i^{\gamma _{ki}}\cdot \prod _{i\in [\ell ]}g_i^{\delta _{ki}\gamma _{ki}s_i} =\prod _{i\in \varDelta _{k}}g_{ki}\cdot \prod _{i\in [\ell ]}g_i^{\delta _{ki}\gamma _{ki}s_i} \end{aligned}$$

for every $k\in [n]$, where $\prod _{i\in \varDelta _{k}}X_i$ denotes $\prod _{i\in [\ell ]}X_i^{\varDelta _{ki}}$.⁷

 

Game 3::

Same as Game 2 except that the challenger uses $\delta _{ki}\gamma _{ki}$ instead of $\gamma _{ki}$ for every $i\in [\ell ]$ and $k\in [n]$. More precisely, the challenger computes $g_{ki} \leftarrow g_i^{\delta _{ki}\gamma _{ki}}$ for every $i\in [\ell ]$ and $k\in [n]$, and $g_{k0} \leftarrow \prod _{i\in \varDelta _{k}}g_{ki} \cdot \prod _{i\in [\ell ]}g_i^{\gamma _{ki}s_i}$ for every $k\in [n]$. Note that $\delta _{ki}\cdot \delta _{ki}=1$ for every $i\in [\ell ]$ and $k\in [n]$.

 

If $\gamma _{ki}$ distributes uniformly at random, then so does $\delta _{ki}\gamma _{ki}$ for every $i\in [\ell ]$ and $k\in [n]$. Therefore, we have $\left| \Pr [\mathtt{SUC}_{2}]-\Pr [\mathtt{SUC}_{3}]\right| =0$.

 

Game 4::

Same as Game 3 except how the challenger computes $g_{k0},g_{k1},\ldots ,g_{k\ell }$ for every $k\in [n]$. The challenger generates $\gamma _{k}$ for every $k\in [n]$ and computes $g_{ki} \leftarrow g_i^{\gamma _{k}\delta _{ki}}$ for every $i\in [\ell ]$ and $k\in [n]$. Moreover, the challenger computes $g_{k0} \leftarrow \prod _{i\in \varDelta _{k}}g_{ki}\cdot \prod _{i\in [\ell ]}g_i^{\gamma _{k}s_i}$ for every $k\in [n]$.

 

$\left| \Pr [\mathtt{SUC}_{3}]-\Pr [\mathtt{SUC}_{4}]\right| =\mathsf{negl}(\lambda )$ holds since $\left( g_1^{\gamma _{k1}},\ldots ,g_\ell ^{\gamma _{k\ell }}\right)$ and $\left( g_1^{\gamma _{k}},\ldots ,g_\ell ^{\gamma _{k}}\right)$ are computationally indistinguishable by the DDH assumption for every $k\in [n]$.

Below, we let $g_0=\prod _{i\in [\ell ]}g_i^{s_i}$. In Game 4, for every $k\in [n]$, we have

$$\begin{aligned} g_{ki}&= g_i^{\gamma _{k}\delta _{ki}}~(i\in [\ell ]) ,\,\text {and}\\ g_{k0}&= \prod _{i\in \varDelta _{k}}g_{ki}\cdot \prod _{i\in [\ell ]}g_i^{\gamma _{k}s_i} =\left( \prod _{i\in \varDelta _{k}}g_{ki}\right) \cdot g_0^{\gamma _{k}}. \end{aligned}$$

Then, the answer to a KDM query $\left( j,\left( \left\{ a_{k}^0\right\} _{k\in [n]},f^0\right) ,\left( \left\{ a_{k}^1\right\} _{k\in [n]},f^1\right) \right)$ in Game 4 is $\mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk}_{j},\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \right)$, where

$$\begin{aligned} c_i&=(g_{ji})^r=\left( g_i^r\right) ^{\gamma _{j}\delta _{ji}}~(i\in [\ell ]) ,~ d = g^{\sum _{k\in [k]}\left\langle a_{k}^b,s_{k}\right\rangle +f^b\left( \left\{ v_{k}\right\} _{k\in [n]}\right) }\cdot (g_{j0})^r ,\\ \pi&=\left( \hat{g}_{j0}\right) ^r =\prod _{i\in [\ell ]}c_i^{x_{ji}} ,\,\text {and}\, r \xleftarrow {\mathsf {r}}\mathbb {Z}_{p}. \end{aligned}$$

We also have

$$\begin{aligned} \sum _{k\in [n]}\left\langle a_{k}^b,s_{k}\right\rangle =\sum _{k\in [n]}\left\langle a_{k}^b,s\oplus \varDelta _{k}\right\rangle =\sum _{k\in [n]}\sum _{i\in \varDelta _{k}}a^b_{ki}+\sum _{k\in [n]}\sum _{i\in [\ell ]}a^b_{ki}\delta _{ki}s_i , \end{aligned}$$

where summation is done over $\mathbb {Z}_{}$ and $a^b_{ki}$ is the i-th bit of $a_{k}^b$ for every $i\in [\ell ]$. Thus, by defining

$$\begin{aligned} Y^b =\sum _{k\in [n]}\sum _{i\in \varDelta _{k}}a^b_{ki}+f^b\left( \left\{ v_{k}\right\} _{k\in [n]}\right) \,\text {and}\, \mu _i^b =\sum _{k\in [n]}a^b_{ki}\delta _{ki}~(i\in [\ell ]) , \end{aligned}$$

(3)

we have

$$\begin{aligned} d&=g^{Y^b+\sum _{i\in [\ell ]}\mu _i^bs_i}\cdot \left( \prod _{i\in \varDelta _{j}} g_{ji}\right) ^r \cdot \left( \prod _{i\in [\ell ]} g_i^{s_i}\right) ^{\gamma _{j}r}\\&=g^{Y^b}\cdot \prod _{i\in \varDelta _{j}}c_i\cdot \prod _{i\in [\ell ]}\left( g^{\mu _i^b}\cdot \left( g_i^r\right) ^{\gamma _{j}}\right) ^{s_i}. \end{aligned}$$

Note that $Y^b$ and $\left\{ \mu _i^b\right\} _{i\in [\ell ]}$ are computed from $\left( \left\{ a_{k}^b\right\} _{k\in [n]},f^b\right)$ and $\left\{ \delta _{ki}\right\} _{i\in [\ell ],k\in [n]}$.

Hereafter, we show the difference from the previous game by colored parts.

 

Game 5::

Same as Game 4 except how the challenger responds to KDM queries.

For a KDM query $\left( j,\left( \left\{ a_{k}^0\right\} _{k\in [n]},f^0\right) ,\left( \left\{ a_{k}^1\right\} _{k\in [n]},f^1\right) \right)$ made by $\mathcal {A}$, the challenger responds as follows.

 

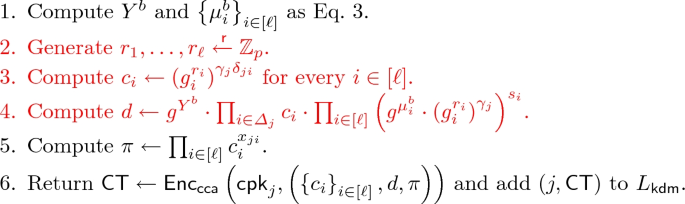
By the DDH assumption, $\left( g_1^{r},\ldots ,g_\ell ^{r}\right)$ and $\left( g_1^{r_1},\ldots ,g_\ell ^{r_\ell }\right)$ are computationally indistinguishable. Thus, we have $\left| \Pr [\mathtt{SUC}_{4}]-\Pr [\mathtt{SUC}_{5}]\right| =\mathsf{negl}(\lambda )$.

 

Game 6::

Same as Game 5 except how the challenger responds to KDM queries.

For a KDM query $\left( j,\left( \left\{ a_{k}^0\right\} _{k\in [n]},f^0\right) ,\left( \left\{ a_{k}^1\right\} _{k\in [n]},f^1\right) \right)$ made by $\mathcal {A}$, the challenger responds as follows.

 

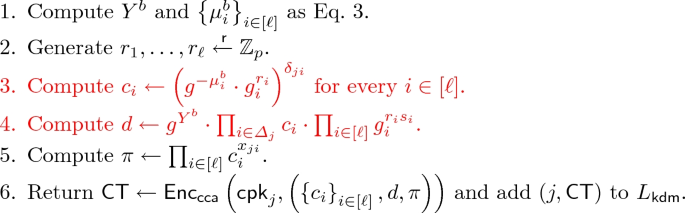
We can make this change in two steps. We first replace $g_i^{r_i\gamma _{j}}$ with $g_i^{r_i}$. We then replace $g_i^{r_i}$ with $g^{-\mu _i^b}\cdot g_i^{r_i}$. Since $r_i$ is uniformly at random for every $i\in [\ell ]$, the answer to a KDM query made by $\mathcal {A}$ identically distributes between Game 5 and 6. Thus, we have $\left| \Pr [\mathtt{SUC}_{5}]-\Pr [\mathtt{SUC}_{6}]\right| =0$.

 

Game 7::

Same as Game 6 except how the challenger responds to KDM queries.

For a KDM query $\left( j,\left( \left\{ a_{k}^0\right\} _{k\in [n]},f^0\right) ,\left( \left\{ a_{k}^1\right\} _{k\in [n]},f^1\right) \right)$ made by $\mathcal {A}$, the challenger responds as follows.

 

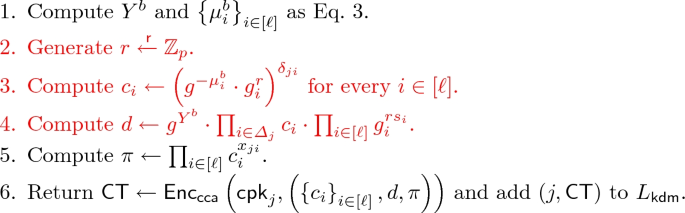
By the DDH assumption, $\left( g_1^{r},\ldots ,g_\ell ^{r}\right)$ and $\left( g_1^{r_1},\ldots ,g_\ell ^{r_\ell }\right)$ are computationally indistinguishable. Thus, $\left| \Pr [\mathtt{SUC}_{6}]-\Pr [\mathtt{SUC}_{7}]\right| =\mathsf{negl}(\lambda )$ holds.

In Game 7, d generated to respond to a KDM query is of the form

$$\begin{aligned} d= g^{Y^b}\cdot \prod _{i\in \varDelta _{j}}c_i\cdot \prod _{i\in [\ell ]}g_i^{rs_i}=g^{Y^b}\cdot \left( \prod _{i\in \varDelta _{j}}c_i\right) \cdot g_0^r. \end{aligned}$$

Thus, we can reply to a KDM query made by $\mathcal {A}$ using $g_0$ instead of s in Game 7.

Next, we eliminate secret keys of $\mathsf {\Pi _{cca}}$ from the view of $\mathcal {A}$. For this aim, we make $e_{k0}$ that is used to mask $\mathsf {csk}_{k}$ uniformly at random for every $k\in [n]$. We first change how the challenger responds to decryption queries made by $\mathcal {A}$.

 

Game 8::

Same as Game 7 except how the challenger responds to decryption queries.

For a decryption query $(j,\mathsf {CT})$ made by $\mathcal {A}$, the challenger returns $\bot$ to $\mathcal {A}$ if $(j,\mathsf {CT})\in L_\mathsf {kdm}$, and otherwise responds as follows.

1.:

Compute $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}\left( \mathsf {csk}_{j},\mathsf {CT}\right)$. If the decryption result is not in $\mathbb {G}^{\ell +2}$, return $\bot$. Otherwise, compute as follows.

2.:

⁸

3.:

Return $\bot$ if $\pi \ne \prod _{i\in [\ell ]}c_i^{x_{ji}}$ and otherwise $m \leftarrow \log _g\left( d\cdot \left( \prod _{i\in [\ell ]}c_i^{s_{ji}}\right) ^{-1}\right)$.

 

We define the following event in Game i ($i=7,\ldots , 11$).

 

$\mathtt{BDQ}_{i}$::

$\mathcal {A}$ makes a decryption query $(j,\mathsf {CT}) \notin L_\mathsf {kdm}$ which satisfies the following conditions, where $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}\left( \mathsf {csk}_{j},\mathsf {CT}\right)$.

 

• $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \in \mathbb {G}^{\ell +2}$. Then, let $c_i=g_{ji}^{r_i}$, where $r_i\in \mathbb {Z}_{p}$ for every $i\in [\ell ]$.

• There exists $i'\in \{2,\ldots ,\ell \}$ such that $r_1\ne r_{i'}$.

• $\pi =\prod _{i\in [\ell ]}c_i^{x_{ji}}$.

We call such a decryption query a “bad decryption query”.

Games 7 and 8 are identical games unless $\mathcal {A}$ make a bad decryption query in each game. Therefore, we have $\left| \Pr [\mathtt{SUC}_{7}]-\Pr [\mathtt{SUC}_{8}]\right| \le \Pr [\mathtt{BDQ}_{8}]$.

For every $k\in [n]$, we have

$$\begin{aligned} e_{ki}&=(g_{ki})^{w_i}=\left( g_i^{w_i}\right) ^{\gamma _{k}\delta _{ki}}~(i\in [\ell ])\\ e_{k0}&=\prod _{i\in [\ell ]}(e_{ki})^{s_{ki}} =\left( \prod _{i\in \varDelta _{k}}e_{ki}\right) \prod _{i\in [\ell ]}\left( e_{ki}\right) ^{\delta _{ki}s_i} =\left( \prod _{i\in \varDelta _{k}}e_{ki}\right) \left( \prod _{i\in [\ell ]}g_i^{w_is_i}\right) ^{\gamma _{k}} . \end{aligned}$$

Note that $\delta _{ki}\cdot \delta _{ki}=1$ for every $i\in [\ell ]$ and $k\in [n]$.

 

Game 9::

Same as Game 8 except that $e_0 \xleftarrow {\mathsf {r}}\mathbb {G}$ is used instead of $\prod _{i\in [\ell ]}g_i^{w_is_i}$.

  The view of $\mathcal {A}$ in Games 8 and 9 can be perfectly simulated by

$$\begin{aligned} \left( g_1,\ldots ,g_\ell ,g_1^{w_1},\ldots ,g_\ell ^{w_\ell },\prod _{i\in [\ell ]}g_i^{w_is_i},g_0\right) \,\text {and}\, \left( g_1,\ldots ,g_\ell ,g_1^{w_1},\ldots ,g_\ell ^{w_\ell },e_0,g_0\right) , \end{aligned}$$

respectively, where $g_i\xleftarrow {\mathsf {r}}\mathbb {G}$ and $w_i\xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$ for every $i\in [\ell ]$, $s=s_1\cdots s_\ell \xleftarrow {\mathsf {r}}\{0,1\}^\ell$, $e_0\xleftarrow {\mathsf {r}}\mathbb {G}$, and $g_0=\prod _{i\in [\ell ]}g_i^{s_i}$. By the leftover hash lemma, the view of $\mathcal {A}$ in Game 8 is $2^{-\frac{\ell -2\lambda }{2}}$-close to that in Game 9. Thus, by setting $\ell =3\lambda$, $\left| \Pr [\mathtt{SUC}_{8}]-\Pr [\mathtt{SUC}_{9}]\right| =\mathsf{negl}(\lambda )$ and $\left| \Pr [\mathtt{BDQ}_{8}]-\Pr [\mathtt{BDQ}_{9}]\right| = \mathsf{negl}(\lambda )$ hold.

There exists $\alpha _i\in \mathbb {Z}_{p}$ such that $g^{\alpha _i}=g_i$ for every $i\in [\ell ]$. Then, for every $k\in [n]$, we have

$$\begin{aligned} g_{ki}&= g^{\alpha _i\gamma _{k}\delta _{ki}}=\left( g^{\gamma _{k}}\right) ^{\alpha _i\delta _{ki}}~(i\in [\ell ])~,~ g_{k0} =\prod _{i\in [\ell ]}(g_{ki})^{s_{ki}}\\ e_{ki}&=(g_{ki})^{w_i}~(i\in [\ell ])~,~\text {and}~ e_{k0}=\left( \prod _{i\in \varDelta _{k}}e_{ki}\right) e_0^{\gamma _{k}} . \end{aligned}$$

 

Game 10::

Same as Game 9 except that for every $k\in [n]$, the challenger generates $e_{k0}\leftarrow \left( \prod _{i\in \varDelta _{k}}e_{ki}\right) e_0^{z_{k}}$, where $z_{k}\xleftarrow {\mathsf {r}}\mathbb {Z}_{p}$.

 

$\left| \Pr [\mathtt{SUC}_{9}]-\Pr [\mathtt{SUC}_{10}]\right| = \mathsf{negl}(\lambda )$ holds since $\left( g,e_0,g^{\gamma _{k}},e_0^{\gamma _{k}}\right)$ and $\left( g,e_0,g^{\gamma _{k}},\right. \left. e_0^{z_{k}}\right)$ are computationally indistinguishable by the DDH assumption for every $k\in [n]$.

Moreover, we can efficiently check whether $\mathcal {A}$ makes a bad decryption query or not by using $\left\{ \mathsf {csk}_{k}\right\} _{k\in [n]}$, $\left\{ \alpha _i\right\} _{i\in [\ell ]}$, and $\left\{ x_{ki}\right\} _{i\in [\ell ],k\in [n]}$. Therefore, we also have $\left| \Pr [\mathtt{BDQ}_{9}]-\Pr [\mathtt{BDQ}_{10}]\right| = \mathsf{negl}(\lambda )$ by the DDH assumption.

In Game 10, $e_{k0}$ distributes uniformly at random for every $k\in [n]$. Therefore, $\mathcal {A}$ cannot obtain any information of $\mathsf {csk}_{k}$ from $u_{k}=e_{k0}\cdot \mathsf {csk}_{k}$ for every $k\in [n]$, and thus we can use $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$.

 

Game 11::

Same as Game 10 except that the challenger responds to KDM queries made by $\mathcal {A}$ with $\mathsf {CT}\leftarrow \mathsf {Enc}_\mathsf {cca}\left( \mathsf {cpk}_{j},0^{(\ell +2)\cdot \left| g\right| }\right)$.

 

By the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$, we obtain $\left| \Pr [\mathtt{SUC}_{10}]-\Pr [\mathtt{SUC}_{11}]\right| = \mathsf{negl}(\lambda )$.

Moreover, we can efficiently check whether $\mathcal {A}$ makes a bad decryption query or not by using decryption queries for $\mathsf {\Pi _{cca}}$, $\left\{ \alpha _i\right\} _{i\in [\ell ]}$, and $\left\{ x_{ki}\right\} _{i\in [\ell ],k\in [n]}$. Thus, $\left| \Pr [\mathtt{BDQ}_{10}]-\Pr [\mathtt{BDQ}_{11}]\right| = \mathsf{negl}(\lambda )$ also holds by the $\text {IND}\text {-}\text {CCA}$ security of $\mathsf {\Pi _{cca}}$.

The value of b is information theoretically hidden from the view of $\mathcal {A}$ in Game 11. Thus, we have $\left| \Pr [\mathtt{SUC}_{11}]-\frac{1}{2}\right| =0$.

In Game 11, $x_{k1},\ldots ,x_{k\ell }$ are hidden from the view of $\mathcal {A}$ except $\hat{g}_{k0}=\prod _{i\in [\ell ]}\left( g_{ki}\right) ^{x_{ki}}$ for every $k\in [n]$. Note that $\mathcal {A}$ cannot obtain information of $x_{k1},\ldots ,x_{k\ell }$ other than $\hat{g}_{k0}$ through decryption queries for every $k\in [n]$. The reason is as follows. If a decryption query $(j, \mathsf {CT})$ made by $\mathcal {A}$ is not a bad decryption query, there exists $r_1\in \mathbb {Z}_{p}$ such that $c_i=(g_{ji})^{r_1}$ for every $i\in [\ell ]$, where $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}\left( \mathsf {csk}_{j},\mathsf {CT}\right)$. Then, we have

$$\begin{aligned} \prod _{i\in [\ell ]}c_i^{x_{ji}}&=\prod _{i\in [\ell ]}\left( g_{ji}\right) ^{r_1x_{ji}} =\left( \prod _{i\in [\ell ]}\left( g_{ji}\right) ^{x_{ji}}\right) ^{r_1} =\left( \hat{g}_{j0}\right) ^{r_1}. \end{aligned}$$

In addition, bad decryption queries made by $\mathcal {A}$ are replied with $\bot$ in Game 11. This means that for every $k\in [n]$, $\mathcal {A}$ cannot obtain information of $x_{k1},\ldots ,x_{k\ell }$ other than $\hat{g}_{k0}$ through decryption queries.

We estimate $\Pr [\mathtt{BDQ}_{11}]$. Let $(j,\mathsf {CT})$ be a decryption query made by $\mathcal {A}$ and let $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \leftarrow \mathsf {Dec}_\mathsf {cca}\left( \mathsf {csk}_{j},\mathsf {CT}\right)$. Suppose that $\left( \left\{ c_i\right\} _{i\in [\ell ]},d,\pi \right) \in \mathbb {G}^{\ell +2}$, $c_i=\left( g_{ji}\right) ^{r_i}$ for every $i\in [\ell ]$, and there exists $i'\in \{2,\ldots ,\ell \}$ such that $r_1\ne r_{i'}$. The probability that this query is a bad decryption query is

(4)

This probability is the same as

$\alpha _i\ne 0$ and $\gamma _{j}\ne 0$ holds for every $i\in [\ell ]$ and $j\in [n]$ with high probability and thus we assume so. Then, two equations

$$\begin{aligned} \sum _{i\in [\ell ]}\alpha _i\gamma _{j}\delta _{ji}r_ix_{ji}=\log _g\pi \bmod p \,\text {and}\, \sum _{i\in [\ell ]}\alpha _i\gamma _{j}\delta _{ji}x_{ji}=\log _g\hat{g}_{j0} \bmod p \end{aligned}$$

are linearly independent, and thus the probability shown in Eq. 4 is $\frac{1}{p}$. Therefore, we obtain $\Pr [\mathtt{BDQ}_{11}]=\mathsf{negl}(\lambda )$.

From the above arguments, we have $\mathsf {Adv}_{\mathsf {\Pi _{ddh}}, \mathcal {F}_{\mathsf {ddh}}, \mathcal {A},n}^{\mathsf {kdmcca}}(\lambda )=\mathsf{negl}(\lambda )$. Since the choice of $\mathcal {A}$ and n is arbitrary, $\mathsf {\Pi _{ddh}}$ is ${\mathcal {F}_{\mathsf {ddh}}}\text {-}\text {KDM}\text {-}\text {CCA}$ secure. $\Box$ (Theorem 4)

Remark 5

(The multi user security of the QR and DCR based schemes). Our QR and DCR based constructions are based on those proposed by Brakerski and Goldwasser [5]. If we allow the length of secret keys to depend on the number of users n, we can prove that our QR and DCR based constructions are $\text {KDM}^{(n)}\text {-}\text {CCA}$ secure using a technique similar to Brakerski and Goldwasser.

To prove $\text {KDM}^{(n)}\text {-}\text {CCA}$ security, we need to eliminate encrypted n secret keys of the outer $\text {IND}\text {-}\text {CCA}$ secure PKE scheme contained in secret keys of the $\text {KDM}\text {-}\text {CCA}$ secure scheme. In the above proof of DDH based scheme, by using the self reducibility of the DDH problem, we complete such a task by making a single group element $\prod _{i\in [\ell ]}g_i^{w_is_i}$ random using the leftover hash lemma.

However, when proving the $\text {KDM}^{(n)}\text {-}\text {CCA}$ security of the QR and DCR based constructions, to complete such a task, we need to make n group elements random using the leftover hash lemma. Therefore, in that case, we need to set the length of secret keys depending on n similarly to the proof of $\text {KDM}^{(n)}\text {-}\text {CPA}$ security by Brakerski and Goldwasser.