Robust Multi-view Subspace Learning Through Structured Low-Rank Matrix Recovery

Abstract

Multi-view data exists widely in our daily life. A popular approach to deal with multi-view data is the multi-view subspace learning (MvSL), which projects multi-view data into a common latent subspace to learn more powerful representation. Low-rank representation (LRR) in recent years has been adopted to design MvSL methods. Despite promising results obtained on real applications, existing methods are incapable of handling the scenario when large view divergence exists among multi-view data. To tackle this problem, we propose a novel framework based on structured low-rank matrix recovery. Specifically, we get rid of the framework of graph embedding and introduce class-label matrix to flexibly design a supervised low-rank model, which successfully learns a discriminative common subspace and discovers the invariant features shared by multi-view data. Experiments conducted on CMU PIE show that the proposed method achieves the state-of-the-art performance. Performance comparison under different random noise disturbance is also given to illustrate the robustness of our model.

1 Introduction

In our daily life, people or objects can be captured at different viewpoints or by different sensors. Consequently, one object has multiple representations, this is also known as multi-view data. Multi-view data is generally heterogeneous [4, 13] (i.e., intra-class samples from another views may have lower similarity than inter-class samples from the same view), which brings a large challenge to recognition or classification tasks. For this reason, numerous work focusing on multi-view subspace learning (MvSL) appears.

Early work on MvSL aims to learn multiple mapping functions, one for each view, to respectively project multi-view data into a common latent subspace, in which the view divergence can be decreased and the similarity of heterogeneous samples can be measured. Among these approaches, the most well-known unsupervised method is Canonical Correlation Analysis (CCA) [8]. However, CCA can only be applied to two-view scenarios. Multi-view Canonical Correlation Analysis (MCCA) [20] was later proposed to generalize CCA to multi-view situations. Moreover, some state-of-the-art methods (e.g., Generalized Multiview Analysis (GMA) [21], Multi-view discriminant analysis (MvDA) [10] and Multi-view Hybrid Embedding (MvHE) [26]) also have been proposed. Different from MCCA, these methods take into consideration discriminant information, thus improving the representation power of subspace. Despite significant results obtained by them, they fail to work during the testing phase, when the view-related information of test samples is not provided [5].

Low-rank multi-view subspace learning (LRMSL) circumvents this drawback by learning a common mapping function for all views, with the help of low-rank representation (LRR). Compared with aforementioned methods, this type of approaches do not need view-related information in testing process. Based on how the prior knowledge (i.e., view-related information and class-label information) is involved in the training phase, LRMSL approaches can be divided into three categories: unsupervised methods, weakly-supervised methods and supervised methods. Unsupervised methods (e.g., Latent Low-rank Representation (LatLRR) [17]) make no use of these two kinds of information, weakly-supervised methods (e.g., Low-rank Common Subspace (LRCS) [4]) only take into consideration view-related information, whereas supervised methods take full advantage of class-label information (e.g., Supervised Regularization based Robust Subspace (SRRS) [12] and Robust Multi-view Subspace Learning (RMSL) [5]).

LRMSL approaches did make a great progress for multi-view data, but there still exist some problems. The success of low-rank representation bases on the assumption that samples from a same class have higher similarity, but the assumption is invalid for multi-view data. Hence, unsupervised and weakly-supervised methods are incapable of effectively discovering the invariant features shared by multi-view data. Although supervised methods provide a feasible solution, existing methods (e.g., SRRS and RMSL) do not achieve significant improvement. One possible reason is that some graph embedding (e.g., Locally Linear Embedding (LLE) [19] and Locality Preserving Projections (LPP) [7]) can not be applied to multi-view data. This is because these methods require manifolds are locally linear. Unfortunately, this condition is also not met for multi-view data [22, 25].

To overcome the problems discussed above, we get rid of the framework of graph embedding and introduce class-label matrix to flexibly design a supervised low-rank model. In the process, a discriminative subspace and the shared information of multi-view data are discovered. Experimental results on face recognition demonstrate the superiority of our method.

The remainder of this paper is organized as follows. Section 2 introduces related work and Sect. 3 presents the proposed method. Optimization is given in Sect. 4. Experimental results are provided in Sect. 5. Finally, Sect. 6 concludes this paper.

2 Related Work

In this section, related work is presented to make interested readers more familiar with the low-rank multi-view subspace learning (LRMSL).

Low-rank Representation (LRR) is a popular approach that has been widely applied in many computer vision and machine learning tasks. In [3], Robust Principle Component Analysis (Robust PCA) was proposed to recover a low-rank component and a sparse component from given data, which assumes that data is homogeneous. To handle data sampled from multiple spaces, Liu et al. [15, 16] proposed LRR methods which learn a lowest-rank representation at a given dictionary. Besides discovering the global class structure, it also eliminates the influence of noises. Similar to dictionary learning approaches [1, 18], the dictionary used in LRR is also expected to be overcomplete. However, this condition is not always easily met. Thus, LatLRR [17] was proposed to construct the dictionary with both observed data and hidden data. In the area of LRR, methods all aim to find an optimal (i.e. structured) representation matrix $\varvec{Z}$ with respect to data $\varvec{X}$ [15, 16]. Specifically, assume that we have a dataset $\varvec{X}=[\varvec{X}_1,\varvec{X}_2,\cdots ,\varvec{X}_c]$ and a dictionary $\varvec{A}$, then the optimal representation $\varvec{Z}$ is expected to be block-diagonal as follows:

$$\begin{aligned} \varvec{Z}^* = \begin{pmatrix} \varvec{Z}_{1}^*&{}\varvec{0}&{}\varvec{0}&{}\varvec{0}\\ \varvec{0}&{}\varvec{Z}_{2}^*&{}\varvec{0}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\ddots &{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\varvec{0}&{}\varvec{Z}_c^*\\ \end{pmatrix}, \end{aligned}$$

(1)

where c is number of classes.

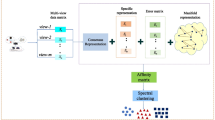
Low-rank Multi-view Subspace Learning (LRMSL) uses low-rank representation technology to learn a robust subspace, in which the intrinsic structure of data is preserved. In [4], LRCS was proposed to capture the shared structure from multiple views. SRRS [12] used fisher criterion to learn a discriminant subspace. Considering there are two kinds of structure embedded in multi-view data (i.e. class structure and view structure), Ding et al. [5] proposed RMSL to learn two kinds of low-rank structure simultaneously.

3 Robust Low-Rank Multi-view Subspace Learning

3.1 Problem Formulation

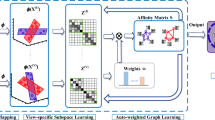
Suppose we have a multi-view dataset $\varvec{X}\!=\!\left[ \varvec{X}_1,\varvec{X}_2,\cdots ,\varvec{X}_n\right]$, where n is the number of views. $\varvec{X}_k\!=\!\left[ \varvec{X}_{k_1},\varvec{X}_{k_2},\cdots ,\varvec{X}_{k_c}\right]$ denotes the k-th view data, where c is the number of classes and $\varvec{X}_{k_i}$ represent all samples of the i-th class under the k-th view. Low-rank multi-view subspace learning (LRMSL) aims to find a component mapping function $\varvec{P}\in \mathbb {R}^{d\times {p}}$ to project multi-view data from d-dimensional space into a p-dimensional subspace ($p\le d$), in which projected samples $\varvec{P}^\mathrm {T}\varvec{X}$ can be represented as a linear combination of the bases of dictionary $\varvec{A}$, and the representation matrix exhibits low-rank characteristic. Its objective can be formulated as:

(2)

where $\varvec{E}$ in Eq. (2) is introduced to remove random noise, the orthogonal constraint on $\varvec{P}$ is used to obtain an orthogonal subspace and $\lambda _{1}\!>\!0$ can be determined by cross validation.

Equation (2) is a basic framework of LRMSL algorithms. To learn a discriminant subspace, we develop a novel supervised model below.

Fig. 1.

Illustration of structured low-rank matrix recovery for multi-view data.

3.2 Structured Low-Rank Matrix Recovery

Suppose $\varvec{A}\!=\!\left[ \varvec{A}_1,\varvec{A}_2,\cdots ,\varvec{A}_c\right]$ denotes the dictionary, where $\varvec{A}_i$ are the bases of the i-th class. According to the discussion in Sect. 2, structured low-rank matrix $\varvec{Z}$ of multi-view projected samples $\varvec{P}^\mathrm {T}\varvec{X}$ can be defined as follows:

$$\begin{aligned} \varvec{Z}^* \triangleq \left( \varvec{Z}_1^*, \varvec{Z}_2^*,\cdots ,\varvec{Z}_n^*\right) , \end{aligned}$$

(3)

where $\varvec{Z}_k^*$ is the structured representation matrix of $\varvec{P}^\mathrm {T}\varvec{X}_k$, which can be represented as

$$\begin{aligned} \varvec{Z}_k^* = \begin{pmatrix} \varvec{Z}_{k_1}^*&{}\varvec{0}&{}\varvec{0}&{}\varvec{0}\\ \varvec{0}&{}\varvec{Z}_{k_2}^*&{}\varvec{0}&{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\ddots &{}\varvec{0}\\ \varvec{0}&{}\varvec{0}&{}\varvec{0}&{}\varvec{Z}_{k_c}^*\\ \end{pmatrix}. \end{aligned}$$

(4)

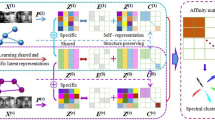
Obviously, low-rank matrix $\varvec{Z}$ is a structured matrix when each sample from the i-th class can be represented as a linear combination of the dictionary bases from the i-th class. The illustration of the structured low-rank matrix recovery for multi-view data is shown in Fig. 1. As can be seen, intra-class representations are united and inter-class representations are deviated from each other.

To this end, we use class-label matrix $\varvec{Y}\!=\![\varvec{y}_1,\varvec{y}_2,\cdots ,\varvec{y}_m]$ to design a supervised model, where m is the number of samples. Assume that $\varvec{y}_k\in \mathbb {R}^{c\times 1}$ is from the j-th class, it can be defined as

$$\begin{aligned} \varvec{y}_k=\left[ \overbrace{0,...,0}^{j-1},1,\overbrace{0,...,0}^{C-j}\right] ^\mathrm {T}. \end{aligned}$$

(5)

The objective of the proposed supervised algorithm can be formulated as

(6)

where $\varvec{Y}\!\in \!\mathbb {R}^{c\times {m_1}}$ and $\varvec{Y}_s\!\in \!\mathbb {R}^{c\times {m_2}}$ are the class-label matrices of the dictionary $\varvec{A}$ and the dataset $\varvec{X}$ respectively, and $\varvec{e}$ is a column vector with all elements equal to one. $\varvec{e}^\mathrm {T}\varvec{Z}\!=\!\varvec{e}^\mathrm {T}$ in Eq. (6) is used to normalize the representation coefficients (i.e., the sum of each column in $\varvec{Z}$ is equal to one), $\varvec{Z}\!\ge \!0$ is used to guarantee that each element in Z is non-negative. Based on the normalization and non-negative constraints, $\varvec{Y}\varvec{Z}\!=\!\varvec{Y}_s$ can guarantee that the $\varvec{Z}$ we learned is a structured matrix.

The dictionary $\varvec{A}$ is generally represented by training samples in previous algorithms, thus we replace $\varvec{A}$ with $\varvec{P}^\mathrm {T}\varvec{X}$ and we have $\varvec{Y}\!=\!\varvec{Y}_s$. Moreover, to improve the generalization performance, we introduce an error term $\varvec{E}_L$. Then, the objective function (6) can be reformulated as:

(7)

where $\lambda _{2}$ controls the contribution of $\varvec{E}_L$.

4 Optimization

Through introducing relax variable $\varvec{J}$, problem (7) can be translated into

(8)

where the augmented Lagrangian function is formulated as

(9)

where $\varvec{Y}_1$, $\varvec{Y}_2$, $\varvec{Y}_3$ and $\varvec{Y}_4$ are Lagrange multipliers and $\mu$ is a positive penalty parameter. There are five parameters in problem (9) to be optimized, and it is difficult to optimize them simultaneously. For this reason, we employ the alternating direction method of multipliers (ADMMs) [6] to alternately optimize $\varvec{J}$, $\varvec{Z}$, $\varvec{E}$, $\varvec{E}_L$ and $\varvec{P}$ one by one through fixing the other variables. For example, during the $t\!+\!1$ iteration of optimization, when we optimize $\varvec{J}$, variables $\varvec{Z}$, $\varvec{E}$, $\varvec{E}_L$ and $\varvec{P}$ are regarded as constants, i.e. inherit results of the tth iteration. In detail, we define $\varvec{J}_t$, $\varvec{Z}_t$, $\varvec{E}_t$, $\varvec{E}_{L,t}$, $\varvec{P}_t$, $\varvec{Y}_{1,t}$, $\varvec{Y}_{2,t}$, $\varvec{Y}_{3,t}$ and $\varvec{Y}_{4,t}$ as variables in the tth iteration, and then we optimize variables in the $t\ +\ 1$ iteration as follows.

Updating $\varvec{J}$ :

(10)

Updating $\varvec{E}$ :

(11)

The two problems above can be optimized by the iterative thresholding approach [14].

Updating $\varvec{E}_L$ :

$$\begin{aligned} \varvec{E}_{L,t+1} \!=\! (2\lambda _2\!+\!\mu _t)^{-1}\left( \varvec{Y}_{3,t}\!+\!\mu _{t}\varvec{Y}_s\varvec{Z}_t\!-\!\mu _t\varvec{Y}_s\right) . \end{aligned}$$

(12)

Updating $\varvec{P}$ :

$$\begin{aligned} \varvec{P}_{t+1} = \left( \left( \varvec{X}\!-\!\varvec{X}\varvec{Z}_t\right) \left( \varvec{X}\!-\!\varvec{X}\varvec{Z}_t\right) ^\mathrm {T}\right) ^{-1}\left( \left( \varvec{X}\!-\!\varvec{X}\varvec{Z}_t\right) \left( \varvec{E}_t^\mathrm {T}\!-\!\varvec{Y}_{1,t}^\mathrm {T}/\mu _{t}\right) \right) . \end{aligned}$$

(13)

Updating $\varvec{Z}$ :

$$\begin{aligned} \varvec{Z} \!=\! \varvec{Z}_1^{-1}\varvec{Z}_2, \end{aligned}$$

(14)

where $\varvec{Z}_1$ and $\varvec{Z}_2$ are represented as follows:

$$\begin{aligned}&\varvec{Z}_1 \!=\! \varvec{X}^\mathrm {T}\varvec{P}_{t}\varvec{P}_t^\mathrm {T}\varvec{X}\!+\!\varvec{I}+\varvec{Y}_s^\mathrm {T}\varvec{Y}_s\!+\!\varvec{e}\varvec{e}^\mathrm {T},\nonumber \\&\varvec{Z}_2\!=\!\varvec{X}^\mathrm {T}\varvec{P}_{t}\left( \varvec{P}_t^\mathrm {T}\varvec{X}\!-\!\varvec{E}_t\right) \!+\!\varvec{J}_t\!+\!\varvec{Y}_s^\mathrm {T}\left( \varvec{Y}_s\!+\!\varvec{E}_{L,t}\right) \!+\!\varvec{e}\varvec{e}^\mathrm {T}\nonumber \\&\quad \quad \quad \!+\!\left( \varvec{X}^\mathrm {T}\varvec{P}_t\varvec{Y}_{1,t}\!-\!\varvec{Y}_{2,t}\!-\!\varvec{Y}_s^\mathrm {T}\varvec{Y}_{3,t}\!-\!\varvec{e}\varvec{Y}_{4,t}\right) /\mu _{t}. \end{aligned}$$

Afterwards, we update multipliers $\varvec{Y}_1$, $\varvec{Y}_2$, $\varvec{Y}_3$ and $\varvec{Y}_4$ in the following way

$$\begin{aligned}&\varvec{Y}_{1,t+1} \!=\! {\varvec{Y}_1,t}\!+\!\mu _t\left( \varvec{P}_{t+1}^\mathrm {T}\varvec{X}\!-\!\varvec{P}_{t+1}^\mathrm {T}\varvec{X}\varvec{Z}_{t+1}\!-\!\varvec{E}_{t+1}\right) ,\nonumber \\&\varvec{Y}_{2,t+1} \!=\! {\varvec{Y}_2,t}\!+\!\mu _t\left( \varvec{Z}_{t+1}\!-\!\varvec{J}_{t+1}\right) ,\nonumber \\&\varvec{Y}_{3,t+1} \!=\! {\varvec{Y}_3,t}\!+\!\mu _t\left( \varvec{Y}_s\varvec{Z}_{t+1}\!-\!\varvec{Y}_s\!-\!\varvec{E}_{L,t+1}\right) ,\nonumber \\&\varvec{Y}_{4,t+1} \!=\! {\varvec{Y}_4,t}\!+\!\mu _t\left( \varvec{e}^\mathrm {T}\varvec{Z}_{t+1}-\varvec{e}^\mathrm {T}\right) ,\nonumber \\&\mu _{t+1}\!=\!\min \left( \rho \mu _t,\mu _{max}\right) , \end{aligned}$$

(15)

where $\rho > 1$ and $\mu _{max}$ is a constant. We iteratively update variables and the penalty parameter until the algorithm satisfies the convergence conditions or reaches the maximum iterations. The detailed iteration process is summarized in Algorithm 1.

5 Experiments

In this section, we first specify the evaluation protocol of MvSL algorithms. Following this, one public dataset is introduced and experimental setting is presented. In order to evaluate the performance of the proposed method, three baselines (i.e., PCA [24], LDA [2], LPP [7]) and three state-of-the-art low-rank multi-view subspace learning (LRMSL) algorithms (i.e., LRCS [4], SRRS [12] and RMSL [5]) are selected for comparison.

5.1 Evaluation Protocol

Evaluation protocol of single-view subspace learning (SvSL) methods can not precisely evaluate the performance of multi-view learning algorithms. To this end, similar to [11], we adopt a more convincing evaluation protocol as follows:

$$\begin{aligned} acc_{v_1}^{v_2} \!=\! \frac{\sum \!\left( \!x: x\in X_{probe}^{v_2}\wedge \bar{y}\!=\!y\!\right) }{\sum \!\left( \!x:x\in X_{probe}^{v_2}\!\right) },\quad \quad mACC \!=\! \left( {\sum \limits _{v_1\!=\!1}^{n}\!\sum \limits _{v_2\!=\!1}^{n}\!acc_{v_1}^{v_2}}\right) /{n^2}, \end{aligned}$$

(16)

where n is the number of views, $acc_{v_1}^{v_2}$ denotes the accuracy when gallery and probe sets are from view $v_1$ and view $v_2$ respectively. y and $\bar{y}$ are the true label and the predicted label of data x respectively. In experiments, we average results of all pairwise views as the mean accuracy (mACC).

Fig. 2.

Exemplar subjects from the CMU PIE dataset. C11, C29, C27, C05 and C37 poses are selected to construct multi-view data. The top row shows clean images and the bottom row shows images with $10\%$ random noise.

5.2 Dataset and Experimental Setting

The CMU Pose, Illumination, and Expression (PIE) Database. (CMU PIE) [23] contains 41,368 images of 68 people with 13 different poses, 43 diverse illumination conditions and 4 various expressions. Five poses (i.e., $\mathrm {C}11$, $\mathrm {C}29$, $\mathrm {C}27$, $\mathrm {C}05$ and $\mathrm {C}37$) are selected to construct multi-view data (see Fig. 2 for exemplar subjects). In experiments, each person at a given pose has 4 images, and images are cropped and resized to $64\times 64$. To make results more convincing, experiments on CMU PIE are repeated ten times by randomly dividing data into training set, validation set and test set, and we report average result as the final accuracy. Hyper-parameters of all approaches are determined by validation set.

Table 1. The average recognition accuracy $(\%)$ in 5 cases of CMU PIE in terms of mean accuracy (mACC). Bold denotes the best performance.

5.3 The Superiority of the Proposed Method

The CMU PIE is used to evaluate face recognition across poses. Similar to [4, 5], experiments are conducted in 5 cases, namely case 1: $\{\mathrm{{C}}27,~\mathrm {C}29\}$, case 2: $\{\mathrm{{C}}27,~\mathrm{{C}}11\}$, case 3: $\{\mathrm{{C}}05,~\mathrm {C}27,~\mathrm {C}29\}$, case 4: $\{\mathrm{{C}}37,~\mathrm {C}27,~\mathrm {C}11\}$ and case 5: $\{\mathrm{{C}}37,~\mathrm {C}05,~\mathrm {C}27,~\mathrm {C}29,~\mathrm {C}11\}$. In our experiments, 40 people are used as training set, 14 people serve as validation set and the rest comprise the test set.

In the first experiment, we evaluate our performance with three baselines and three state-of-the-art methods. The experimental results are summarized in Table 1. As can be seen, SvSL based methods rank the lowest due to the neglect of the view divergence. Benefited from the consideration of discriminant information, SRRS and RMSL perform better than LRCS. As expected, our method achieves a remarkable improvement compared with RMSL, which we argue can be attributed to the more effectively exploiting discriminant information.

Fig. 3.

Illustration of 2D embedding of Euclidean space, the subspace generated by LRCS, SRRS, RMSL and the proposed metho in case 5 of CMU PIE dataset. Different colors denote different classes, and different views are denoted by different markers.

Table 2. The average recognition results $(\%)$ in case 5 of CMU PIE. Bold denotes the best performance.

Table 3. The average recognition accuracy $(\%)$ in case 5 of CMU PIE with random noise in terms of mean accuracy (mACC). Bold denotes the best performance. the values in parentheses denote the relative performance loss (%) with respect to the random noise scenario. “NR” denotes noise ratio.

To better evaluate performance of the proposed method, detailed results in case 5 of CMU PIE are shown in Fig. 3 and Table 2. As can be seen in Fig. 3, all low-rank subspace learning approaches can remove the view divergence to some extent. However, LRCS, SRRS and RMSL approaches fail to distinguish the yellow class from the green one correctly, whereas these two classes are separated obviously in the subspace generated by our method. As a whole, the embeddings shown in Fig. 3 corroborate the results summarized in Table 1. Moreover, as can be seen in Table 2, one should note that our method does not achieve the best performance when the gallery and the probe data come from the same view. The reason for this phenomenon is that the constraint with respect to intra-view and intra-class samples is only based on low-rank representation. Compared with traditional graph embedded, this is a weak constraint.

At last, we evaluate the robustness of the proposed methods. we add random noise to original images by randomly replacing $5\%$, $10\%$, $15\%$ and $20\%$ pixels (see Fig. 2 for exemplar subjects) and report the results in case 5 in Table 3. As can be seen, LRCS, SRRS and RMSL are more sensitive to random noise than our method. Take the $20\%$ random noise scenario as an example, our method only suffers from a relative $5.9\%$ performance drop from its original $70.9\%$ accuracy, whereas the accuracy of RMSL decreases to $48.8\%$ with a relative performance drop nearly $21.3\%$.

6 Conclusion

In this paper, we proposed an novel framework based on structured low-rank matrix recovery to learn a discriminant subspace for multi-view data. Experiments conducted on CMU PIE show that the proposed method successfully discovers the discriminant information shared by multi-view data, thus improving the performance of subsequent recognition or classification tasks. Moreover, experimental results in the scenario of random noise disturbance indicate that our method is more robust to random noise. In the future, we are interested in develop a nonlinear version of our method to handle more challenge scenarios.