Exploring Crypto Dark Matter:

Abstract

Pseudorandom functions (PRFs) are one of the fundamental building blocks in cryptography. Traditionally, there have been two main approaches for PRF design: the “practitioner’s approach” of building concretely-efficient constructions based on known heuristics and prior experience, and the “theoretician’s approach” of proposing constructions and reducing their security to a previously-studied hardness assumption. While both approaches have their merits, the resulting PRF candidates vary greatly in terms of concrete efficiency and design complexity.

In this work, we depart from these traditional approaches by exploring a new space of plausible PRF candidates. Our guiding principle is to maximize simplicity while optimizing complexity measures that are relevant to cryptographic applications. Our primary focus is on weak PRFs computable by very simple circuits—specifically, depth-2 $\mathsf {ACC}^0$ circuits. Concretely, our main weak PRF candidate is a “piecewise-linear” function that first applies a secret mod-2 linear mapping to the input, and then a public mod-3 linear mapping to the result. We also put forward a similar depth-3 strong PRF candidate.

The advantage of our approach is twofold. On the theoretical side, the simplicity of our candidates enables us to draw many natural connections between their hardness and questions in complexity theory or learning theory (e.g., learnability of $\mathsf {ACC}^0$ and width-3 branching programs, interpolation and property testing for sparse polynomials, and new natural proof barriers for showing super-linear circuit lower bounds). On the applied side, the piecewise-linear structure of our candidates lends itself nicely to applications in secure multiparty computation (MPC). Using our PRF candidates, we construct protocols for distributed PRF evaluation that achieve better round complexity and/or communication complexity (often both) compared to protocols obtained by combining standard MPC protocols with PRFs like AES, LowMC, or Rasta (the latter two are specialized MPC-friendly PRFs).

Finally, we introduce a new primitive we call an encoded-input PRF, which can be viewed as an interpolation between weak PRFs and standard (strong) PRFs. As we demonstrate, an encoded-input PRF can often be used as a drop-in replacement for a strong PRF, combining the efficiency benefits of weak PRFs and the security benefits of strong PRFs. We conclude by showing that our main weak PRF candidate can plausibly be boosted to an encoded-input PRF by leveraging standard error-correcting codes.

Y. Ishai—Work done in part at UCLA.

1 Introduction

Today, there are two primary paradigms for designing cryptographic primitives. The “theory-oriented” or “provable security” approach is to develop constructions whose security can be provably reduced to the hardness of well-studied computational problems (e.g., factoring, discrete log, or learning with errors). The second and “practice-oriented” approach aims at obtaining efficient constructions for specific functionalities (e.g., block ciphers or hash functions). Here, designers typically try to maximize concrete efficiency at the expense of relying on heuristic arguments and prior experience to argue security. But ultimately, confidence in the underlying security assumptions or cryptographic designs only grows if they withstand the test of time.

There are several limitations to these approaches. On the one hand, both the efficiency and the structure of provably-secure constructions are inherently limited by the underlying computational problems. This leads to constructions that are far less efficient than those obtained from the practice-oriented approach. On the other hand, despite the efficiency of practical constructions, their designs are often complex, thereby complicating their analysis. Consequently, it is difficult to argue whether the lack of cryptanalysis against practical constructions is due to their actual security or due to the complexity of their design. The structure of both types of constructions often makes them poorly suited as building blocks for cryptographic applications that are different from the ones envisioned by their designers (e.g., secure multiparty computation).

In this work, we depart from these traditional approaches and consider a surprisingly unexplored space of cryptographic constructions. Our approach is driven by simplicity, and aims at circumventing some of the limitations of the existing approaches. Our hope is to obtain constructions that are (1) relatively easy to describe and analyze, (2) concretely efficient, and (3) well-suited for different applications. In particular, we aim at relying on assumptions that are simple to state, and yet at the same time, breaking them would likely require new techniques that may themselves have other applications. In a sense, the assumptions we introduce have a win-win flavor and can be of independent interest beyond the cryptographic community (e.g., to complexity theorists, learning theorists, or mathematicians). A notable example for prior work in this direction is Goldreich’s proposal of a simple one-way function candidate [29], which had an unexpected impact in different areas of cryptography and beyond (see [4] for a survey).

What Do We Mean by Simplicity? The concrete direction we take is exploring whether the simple operation of changing moduli can be a source of hardness in the context of secret-key cryptographic primitives. Our starting observation is that computing the sum of m binary-valued variables modulo 3 is actually a high-degree polynomial over $\mathbb {Z}_2$. More precisely, the mapping function $\mathsf {map}:\{0,1\}^n \rightarrow \mathbb {Z}_3$ where $\mathsf {map}(x) := \sum _{i \in [m]} x_i \pmod 3$ is a polynomial of high-degree over the binary field $\mathbb {Z}_2$ (but a simple linear function over $\mathbb {Z}_3$). Surprisingly, this simple idea of mixing different moduli enables new constructions of “piecewise-linear” symmetric primitives that are conceptually simple to describe, can plausibly achieve strong security guarantees, and are well-suited for many cryptographic applications.

Our Focus: Pseudorandom Functions. In this work, we focus specifically on pseudorandom functions (PRFs) [31]—one of the most fundamental building blocks of modern cryptography. Our primary focus is on weak pseudorandom functions, namely, functions whose behavior looks indistinguishable from that of a random function to any adversary who only observes the input-output behavior of the function on random domain elements. Since weak PRFs cannot replace standard (or strong) PRFs in all cryptographic applications, we then show how our construction can be adapted to yield a new primitive we call an encoded-input PRF. An encoded-input PRF is defined similarly to a standard (strong) PRF, except that its input domain is restricted to an efficiently recognizable set. Encoded-input PRFs can be viewed as an intermediate primitive between strong PRFs and weak PRFs that combines the security advantages of the former and efficiency advantages of the latter. Indeed, we show that in many cases they can be used as a replacement for a strong PRF. At the same time, we exhibit simple candidates of encoded-input PRFs in complexity classes where strong PRFs are not known to exist. Finally, a unique feature of our new PRF candidates is that they are very “MPC-friendly.” As we show in Sect. 5, our PRFs can be computed more efficiently in a distributed fashion compared to standard block ciphers like AES and even custom-built MPC-friendly block ciphers like LowMC [2] or Rasta [23].

Previous Work on Simple PRFs. Before describing our contributions, it is useful to survey some closely relevant previous works on low-depth PRFs (see Sects. 1.2 and 3.2 for a broader survey). We denote by $\mathsf {AC}^0$ the class of polynomial-size, constant-depth circuits with unbounded fan-in $\mathsf {AND}$, $\mathsf {OR}$, and $\mathsf {NOT}$ gates and by $\mathsf {ACC}^0[m]$ the class of such circuits that can additionally have unbounded fan-in $\mathsf {MOD}_m$ gates, which return 0 or 1 depending on whether the sum of their inputs is divisible by m. We denote by $\mathsf {ACC}^0$ the union over all m of $\mathsf {ACC}^0[m]$.

With the goal of minimizing the depth complexity of weak PRFs, Akavia et al. proposed in [1] the first candidate that can be computed by $\mathsf {ACC}^0[2]$ circuits. More precisely, their candidate construction can be computed by depth-3 circuits where the first layer consists of $\mathsf {MOD}_2$ gates computing a matrix-vector product $\mathbf {A}x$, where $\mathbf {A}\in \mathbb {Z}_2^{n \times n}$ is the secret key and $x \in \mathbb {Z}_2^n$ is the input. The second and third layer define a public DNF formula. While the Akavia et al. candidate could plausibly provide exponential security,¹ Bogdanov and Rosen [17] recently showed that this candidate (on n-bit inputs) can be approximated by a rational function of degree $O(\log n)$, which in turn gives rise to a quasi-polynomial-time attack. Applebaum and Raykov [6] show that low-complexity PRFs can be based on one-wayness assumptions. In particular, under a variant of Goldreich’s one-wayness assumption [29], they present a weak PRF with quasi-polynomial security that can be implemented (on any fixed key) by depth-3 $\mathsf {AC}^0$ circuits.

These recent results leave several open questions regarding the complexity of low-depth (weak) PRFs. First, even if one settles for quasi-polynomial time security, there is no proposed PRF candidate of any kind that can be realized by depth-2 circuits over any standard basis. When restricting attention to (weak) PRFs that offer a better level of security, the situation is even worse. While it is known that weak PRFs with better than quasi-polynomial security do not exist in $\mathsf {AC}^0$,² and that strong PRFs with similar security do not exist in $\mathsf {ACC}^0[p]$ for any prime p,³ it is plausible that weak PRFs with exponential security could still exist in $\mathsf {ACC}^0[2]$. But to the best of our knowledge, there are currently no weak PRF candidates in $\mathsf {ACC}^0$ with exponential (or even sub-exponential) security. Note that if we settle for quasi-polynomial security, then the result of Kharitonov [36, Theorem 9] (resp., Viola [51, Theorem 11]) gives a weak PRF in $\mathsf {AC}^0$ (resp., strong PRF in $\mathsf {ACC}^0[p]$ for any p) based on the hardness of factoring. This raises the question of whether it is possible to construct (weak or strong) PRFs with exponential (or even sub-exponential) security in $\mathsf {ACC}^0$. In this work, we propose a new candidate weak PRF that can be computed by depth-2 $\mathsf {ACC}^0$ circuits. Our candidate is conceptually simple and can plausibly satisfy exponential security, thus addressing both of the above challenges simultaneously. We also propose other variants of this candidate, including a candidate for an exponentially secure strong PRF that can be computed by depth-3 $\mathsf {ACC}^0$ circuits.

1.1 Our Contributions

In this section, we give a more detailed overview of the main results of this paper.

New Weak PRF Candidates. We put forward several new (weak) PRF candidates that mix linear functions over different moduli. We start by describing our most useful candidate, and will discuss other variants later. Our primary weak PRF candidate follows a very similar design philosophy as that taken by Akavia et al.  [1]. Recall first that in the Akavia et al. construction, the secret key is a matrix $\mathbf {A}\in \mathbb {Z}_2^{m\times n}$ and the input is a vector $x \in \mathbb {Z}_2^n$. The output of the PRF is defined as $\mathsf {F}_\mathbf {A}(x) := g(\mathbf {A}x)$, where the function g is a non-linear mapping (in the case of the Akavia et al. construction, the function g is a “tribes” function and can be expressed as a DNF formula). In our setting, we adopt the same high-level structure, but substitute a different and conceptually simpler non-linear function g. In our candidate, we define the non-linear function to be the function that interprets the binary outputs of $\mathbf {A}x$ as 0/1 values over $\mathbb {Z}_3$, and the output of the function is simply the sum of the input values over $\mathbb {Z}_3$. Specifically, we define the mapping function $\mathsf {map}:\{0,1\}^m\rightarrow \mathbb {Z}_3$ that maps $y \in \{0,1\}^m\mapsto \sum _{i \in [m]} y_i \pmod 3$. Our weak PRF candidate (with key $\mathbf {A}$) is then defined as

$$\begin{aligned} \mathsf {F}_\mathbf {A}(x) := \mathsf {map}(\mathbf {A}x) \text { where } \mathsf {map}(y) = \sum _{i \in [m]} y_i \pmod 3. \end{aligned}$$

(1)

We formally introduce our candidate (and discuss several generalizations⁴) in Sect. 3. We state our formal conjectures regarding the hardness of our candidate in Sect. 3.1. There are several properties of our weak PRF candidate that we want to highlight:

• Conceptual simplicity. Our candidate is conceptually very simple to describe. It reduces to computing a matrix-vector product over $\mathbb {Z}_2$, reinterpreting the output vector as a 0/1 vector mod-3 and then computing their sum. The simplicity of our construction is fairly apparent compared to block cipher candidates likes AES or number-theoretic constructions of PRFs. In spite of its simplicity, to the best of our knowledge, such a candidate has not previously been proposed, let alone studied.

• Low complexity. Our candidate can be computed by depth-2 $\mathsf {ACC}^0[2,3]$ circuits. More precisely, the first layer consists entirely of $\mathsf {MOD}_2$ gates to compute the matrix-vector product $\mathbf {A}x$, and the second layer consists of two $\mathsf {MOD}_3$ gates that computes the binary representation of the output. We refer to Remark 3.9 for a more precise definition.

• MPC friendliness. The simplicity of our candidate also lends itself nicely for use in MPC protocols. In Sect. 5, we give an efficient protocol that enables distributed evaluation of our PRF in a setting where both the key and the input are secret-shared. We discuss this further in the sequel. As we show in Table 1, the round complexity and communication complexity of our distributed evaluation protocol outperform existing MPC protocols for distributed evaluation of not only AES, but even those for MPC-friendly block ciphers like LowMC [2] and Rasta [23].

Cryptanalysis. In Sect. 4, we consider several classic cryptanalytic techniques on our weak PRF candidate. While our analysis is by no means exhaustive, we are able to rule out several classes of attacks, thereby providing some confidence into the security of our new candidate. Following the work of Akavia et al.  [1], we focus on two primary classes of attacks:

• Lack of correlation with fixed function families. First, we rule out the learning-type attacks of Linial et al.  [38] by showing that there are no fixed function families of exponential size that are noticeably correlated with our PRF candidate. (Previously, Linial et al. showed that for all $\mathsf {AC}^0$ functions, there exists a quasi-polynomial-size function family such that any $\mathsf {AC}^0$ function is noticeably correlated with a function in that class; this implies a quasi-polynomial time learning algorithm for $\mathsf {AC}^0$.)

• Inapproximability by low-degree polynomials. Next, we show that there does not exist a low-degree polynomial approximation to our PRF candidate. Our argument here follows from the well known Razborov-Smolensky lower bounds [46, 48] for $\mathsf {ACC}^0$ circuits, which say that for distinct primes p, q, the $\mathsf {MOD}_p$ function is not computable by a polynomial-size circuit in $\mathsf {ACC}^0[q]$. We conjecture that the Razborov-Smolensky lower bounds also generalize to rule out low-degree rational approximations: namely, for distinct primes p, q, there does not exist a low-degree rational function that approximates $\mathsf {MOD}_p$ gates over $\mathrm {GF}(q^\ell )$ for any $\ell$ (Conjecture 4.3). We believe that this question is of independent interest from a complexity-theoretic perspective, and leave it as an interesting challenge.

Given the above, we conjecture that our main weak PRF candidate is exponentially secure. We hope that our exploratory analysis will encourage further study and refinement of our conjectures.

Theoretical Implications. We next turn to studying the implications and applications of our new PRF candidates. We first describe several theoretical implications related to complexity theory and learning theory that are implied by our conjectures:

• Hardness of learning for depth-2 $\mathsf {ACC}^0$ and width-3 branching programs. As mentioned earlier, one of the key structural properties of our weak PRF candidate is that it can be computed by a depth-2 $\mathsf {ACC}^0$ circuit. Another low-complexity feature, which crucially depends on the choice of the moduli 2 and 3, is that it can be computed by (polynomial-length) width-3 permutation branching programs [11]. The existence of a weak PRF in any complexity class rules out learning algorithms for that class even with uniformly random examples. This means that, assuming the exponential security of our weak PRF candidate in Eq. (1), the classes of depth-2 $\mathsf {ACC}^0$ circuits and width-3 permutation branching programs are not learnable (in the standard sense of PAC-learnability [49] without membership queries), even under the uniform distribution and even when allowing sub-exponential time learning algorithms. We explore these connections in greater detail in the full version. We note that efficient learning algorithms for the above classes would imply an efficient learning algorithm for DNF formulas [25]. While there are quasi-polynomial time learning algorithms for DNF formulas (in fact, even for $\mathsf {AC}^0$ circuits) under the uniform distribution [38, 50], no such learning algorithm (even a sub-exponential one) is known for depth-2 $\mathsf {ACC}^0$ or width-3 branching programs.

• Hardness of interpolating and property-testing sparse polynomials. In the full version, we give an alternative characterization of Eq. (1) as essentially implementing a sparse multilinear polynomial over $\mathbb {Z}_3$, where the monomials are determined by the key $\mathbf {A}$. We then show that the conjectured hardness of our weak PRF candidate implies that sparse polynomials over $\mathbb {Z}_3$ (with sufficient degree and sparsity) are hard to interpolate given random evaluations drawn from a subset of the domain, namely from $\{1,2\}^n$. Similar to the previous connections to hardness of learning, if it is easy to interpolate the polynomial corresponding to the operation of the PRF (on random inputs), then the interpolation algorithm gives a trivial distinguisher for the scheme. While the problem of sparse polynomial interpolation has been the subject of extensive study [8, 13, 27, 35, 52, 56, 57], much less is known when the interpolation algorithm only sees random evaluations from a subset of the domain. Our conjectures imply hardness results for this variant of the sparse interpolation problem. In fact, as we show in the full version, our conjectures even rule out property-testing algorithms [3, 22, 34, 44] for sparse polynomials.

• Natural proofs barrier for super-linear circuit lower bounds. Our work also has relevance to minimizing the sequential time complexity or circuit size of strong PRFs. We consider the problem of constructing “asymptotically optimal” strong PRFs, namely ones that have exponential security in the input length and can be computed by linear-size circuits. This problem is motivated by the goal of ruling out natural proofs of super-linear circuit lower bounds, in the sense of Razborov and Rudich [47]. While previous works constructed PRFs that can be evaluated by linear-size circuits [33] or in linear time on a RAM machine [6], these PRFs fail to achieve full exponential security. The work of Miles and Viola [39] presented a simplified abstraction of existing block cipher designs and proved their security under a class of natural attacks. One of their constructions can be implemented by quasi-linear size circuits and is shown to have exponential security against a wide class of attacks, thus falling a bit short of the asymptotic optimality goal. In Sect. 6.3, we present a depth-3 variant of our main weak PRF candidate that can plausibly meet this goal (Remark 6.7). Thus, we give the first candidate construction for an asymptotically optimal strong PRF, which in turn rules out natural proofs of super-linear circuit lower bounds.

Applications to MPC and Distributed PRF Evaluation. A particularly appealing property of our weak PRF candidate is that it is very MPC-friendly. Protocols for PRF evaluation in a distributed setting (where the secret key and input are distributed or secret-shared between two or more parties) have received a significant amount of attention recently, and new block ciphers have been proposed specifically to be MPC-friendly [2, 23]. The structure of our weak PRF lends itself nicely to an efficient MPC protocol (with semi-honest security) for evaluating the PRF with a secret-shared key and a secret-shared input. Consider a scenario where the PRF key and input are secret-shared across multiple servers. Our protocol proceeds roughly as follows:

• If we use a linear secret-sharing scheme to share the keys and the inputs over $\mathbb {Z}_2$ (alternatively, a field or characteristic 2), then the matrix-vector product $\mathbf {A}x$ can be computed non-interactively: each party simply operates locally on their shares (of the key and input).⁵

• Next, the servers engage in a simple interactive protocol to convert their secret-shared values (over $\mathbb {Z}_2$) to a linear secret-sharing of the same value over $\mathbb {Z}_3$ (effectively implementing the non-linear step in our PRF). Working in the 3-server setting (in a semi-honest model tolerating at most one corruption), we can implement this protocol very efficiently using the protocol of Araki et al.  [7]. Here, the “share conversion” procedure essentially requires 13 bits of communication for each bit of $\mathbf {A}x$.

• Once the parties have a linear secret-sharing of $\mathbf {A}x$ over $\mathbb {Z}_3$, computing the output can again be done non-interactively. Note that to extend our weak PRF candidate to output multiple bits, we replace the summation over $\mathbb {Z}_3$ with a matrix-vector product. Namely if $y \leftarrow \mathbf {A}x \in \{0,1\}^m$, then we define the PRF output to be $\mathbf {G}y \pmod 3$, where $\mathbf {G}$ here is a fixed public matrix in $\mathbb {Z}_3^{t \times m}$ (Remark 3.3). Even with this extension, computing the output (given a $\mathbb {Z}_3$ secret-sharing of the values $\mathbf {A}x$) still corresponds to computing a linear function over $\mathbb {Z}_3$. Again, this is possible non-interactively.

The takeaway is that even though our weak PRF candidate is highly nonlinear (due to the mixing of mod-2 and mod-3 operations), the piecewise-linear structure means that it can be securely computed by a constant-round information-theoretic MPC protocol with O(|x|) bits of communication. In Table 1, we provide some concrete comparisons of our protocol for distributed evaluation of our PRF candidate to some of the existing candidates. As the baseline for our comparisons, we use the protocol of Araki et al.  [7] as the representative for 3-party secret-sharing-based MPC protocols, and optimized garbled circuit constructions [37, 55] for 2-party protocols. We compare against both the AES block cipher as well as several settings of LowMC [2] and Rasta [23], two custom-designed block ciphers tailored for MPC applications. We describe our precise methodology for deriving these estimates in Sect. 5.2.

Table 1. Comparison of semi-honest oblivious PRF evaluation protocols. In all cases, we assume that the keys and inputs have been secret-shared between the (2 or 3) servers. We estimate the round complexity and the total communication complexity (in bits) needed to evaluate the PRF on the shared key and input. All of our comparisons assume semi-honest servers with up to one corruption and assuming a concrete security parameter of $\lambda = 128$. When comparing to the LowMC block cipher [2] and the Rasta block cipher [23], we compare against two variants: a depth-optimized variant (min-depth) that minimizes the multiplicative depth of the circuit implementing the block cipher, and a gates-optimized variant (min-gates) that minimizes the number of $\mathsf {AND}$ gates. We refer to Sect. 5.2 for the parameter settings we use for our estimates. For our protocol, we set the dimensions m, n according to our concrete parameter estimates from Table 2 (in particular we let $m=n$), and set the output dimension to be $t = 128$ (for output space $\mathbb {Z}_3^{128}$).

From Table 1, we see that using an optimistic setting of parameters for our candidate, the communication and round complexity of our 3-server protocol for distributed (weak) PRF evaluation is better than the generic MPC protocols applied to existing (strong) PRF candidates in terms of both round complexity and communication complexity in almost all cases. The only case where another protocol has smaller communication complexity is the case of evaluating the $\mathsf {AND}$-gate-optimized variant of LowMC (using the Araki et al. protocol); however, evaluating this variant of LowMC requires over 250 rounds of communication compared to the 2 rounds needed for our protocol.

Compared to the communication-intensive protocols based on garbled circuits, the communication complexity of our protocol is roughly two orders of magnitude smaller than garbled circuit evaluation of LowMC and Rasta, and three orders of magnitude smaller than garbled circuit evaluation of AES. The secret-sharing-based protocols are much more competitive in terms of communication, but these protocols generally have much larger round complexities, which can be problematic in high-latency networks. To summarize, our new PRFs have the advantage that they are very friendly to compute in a distributed MPC setting when both the key and the input are secret-shared. We note that even weak PRFs are still useful in a variety of application scenarios. In the full version we describe a concrete application of MPC-friendly weak PRFs for implementing distributed flavors of secure keyword search and searchable symmetric encryption. Moreover, for applications that require strong PRFs, one can apply the encoded-input variant of our weak PRF with a modest loss of efficiency.

Alternative Weak PRF Candidate with Better Garbling Efficiency. The structure of our main weak PRF candidate makes it well-suited for three-party distributed evaluation. In a two-party setting, it is natural to rely on a “garbling scheme” such as that of Yao [53] or its optimized variants. However, the cost of this approach will be high because of the super-linear number of multiplications needed for computing the matrix-vector product. In Sect. 5.3, we introduce a variant of our weak PRF candidate (Construction 5.3) that is more suitable for two-party distributed evaluation. The core ingredient in our two-party evaluation protocol is a lightweight information-theoretic garbling scheme using arithmetic randomized encoding techniques (cf. [5]). The full two-party distributed evaluation protocol additionally relies on a single (parallel) invocation of a 1-out-of-6 oblivious transfer (OT) protocol; the overall two-party distributed evaluation protocol for this alternative candidate is thus 4 rounds (rather than the usual 2 rounds with Yao’s protocol). The output size of this garbling scheme (as well as the total communication complexity of the distributed evaluation protocol) is linear in the input size times the output size of the PRF. Thus, this candidate is particularly attractive when the PRF output is short. As we show in the full version, the garbling size of our alternative candidate (which constitutes the bulk of the protocol’s communication complexity) with 40 bits of output is smaller than that of an optimized Yao-style garbling applied to LowMC, Rasta, and AES. Thus, for applications that only require such a short PRF output (e.g., using a PRF to compute tags for a set of keywords), the better garbling complexity of our alternative candidate implies a secure two-party protocol for PRF evaluation that is better than that of protocols for evaluating AES, LowMC, or Rasta.⁶ While this alternative candidate seems better suited for distributed two-party evaluation than our main weak PRF candidate given in Eq. (1), it also has several limitations; most notably, it can at best provide (slightly) sub-exponential security. In contrast, our main candidate can plausibly provide exponential security. We give a more thorough discussion of the alternative candidate and its security in Sect. 5.3.

Towards Strong Pseudorandomness. Turning now to strong pseudorandomness, we show in the full version that our candidate is not a strong PRF, and in fact, can be learned in polynomial time given adaptive queries. Specifically, we can recast our PRF as an automaton with multiplicity, and then apply known learning results for these function families [14]. However, this attack is unlikely to extend to the setting of weak pseudorandomness. Here, we show that if the learning attack in [14] can be generalized to the weak pseudorandomness setting (where the learning algorithm is only provided function evaluations on a random subset of the domain), then the same algorithm implies a polynomial-time attack on the learning with rounding (LWR) [10] assumption with any polynomial moduli p and q.

Encoded-Input PRFs and Strong PRFs. Motivated by the fact that many applications of PRFs (e.g., message authentication codes (MACs)) do not naturally follow from weak pseudorandomness, we introduce an intermediate notion between weak PRFs and strong PRFs we refer to as encoded-input PRFs. Our new notion suffices for instantiating most applications of strong PRFs, and at the same time, still admits simple constructions (and circumvents known lower bounds on the existence of strong PRFs in various complexity classes). At a high-level, an encoded-input PRF is a function that behaves like a PRF on some (possibly sparse) subset of its domain. Moreover, this subset is specific to the PRF family, and in particular, independent of the key. For instance, a suitable subset might be the set of valid codewords in a linear error-correcting code. In Sect. 6, we formally define this notion, and then show that many standard applications of PRFs (e.g., MACs, CCA-secure encryption) can be instantiated from encoded-input PRFs by incorporating an additional validity check for the encoded input. The validity check can be made more efficient by using an additional proof provided by the evaluator. We then propose an efficient candidate construction of encoded-input PRFs by combining our weak PRFs with error-correcting codes. The resulting construction resists the adaptive attacks we describe in the full version and can remain MPC-friendly. Using our candidate encoded-input PRFs, we are able to construct MACs with low-complexity verification and CCA-secure encryption with low-complexity decryption (that is, both operations can be computed by a depth-3 $\mathsf {ACC}^0$ circuit). In fact, for a suitable instantiation of our encoding function (e.g., using a linear error-correcting code), we obtain a candidate strong PRF that can be computed by a depth-3 $\mathsf {ACC}^0$ circuit (Remark 6.6). Concretely, our depth-3 strong PRF candidate is obtained from our main weak PRF candidate by first applying a mod-3 linear encoding to the input. We also propose a variant of this candidate that can be implemented by linear-size circuits. This variant is used for the new natural proofs barrier discussed above.

1.2 Related Work

There is a large body of work on minimizing different complexity measures of (weak or strong) PRFs. Most relevant to the present work are works proposing PRF constructions that can be evaluated by different classes of low-depth circuits such as $\mathsf {AC}^0$, $\mathsf {ACC}^0$, $\mathsf {TC}^0$ [1, 6, 9, 10, 15, 18, 41,42,43, 51, 54]. Of these candidates, those in $\mathsf {AC}^0$ [6] and in $\mathsf {ACC}^0$ [1, 51] are either vulnerable to quasi-polynomial time attacks [1, 6] or can only be shown to have quasi-polynomial time security [51]. In more detail, the result of Viola [51, Theorem 11] says that assuming hardness of factoring against $2^{n^\varepsilon }$-time adversaries (for some constant $\varepsilon$), there is a strong PRF in $\mathsf {ACC}^0$ with security against quasi-polynomial time adversaries. We discuss these candidates and their cryptanalysis in greater detail in Sect. 3.2.

2 Preliminaries

We begin by defining some basic notation that we will use throughout this work. For a positive integer n, we write [n] to denote the set of integers $\{1, \ldots , n\}$. We use bold uppercase letters (e.g., $\mathbf {A}$, $\mathbf {B}$) to denote matrices.

For a finite set S, we write $x \xleftarrow {\textsc {r}}S$ to denote that x is drawn uniformly at random from S. For a distribution $\mathcal {D}$, we write $x \leftarrow \mathcal {D}$ to denote a draw from a distribution $\mathcal {D}$. Unless otherwise noted, we write $\lambda$ to denote the security parameter. We say that a function $f(\lambda )$ is negligible in $\lambda$ if $f(\lambda ) = o(1/\lambda ^c)$ for all $c \in \mathbb {N}$. We write $f(\lambda ) = \mathrm {poly}(\lambda )$ to denote that f is bounded by some (fixed) polynomial in $\lambda$. We say that an algorithm is efficient if it runs in probabilistic polynomial time in the length of its input.

For two sets $\mathcal {X}$ and $\mathcal {Y}$, we write $\mathsf {Funs}[\mathcal {X}, \mathcal {Y}]$ to denote the set of all functions from $\mathcal {X}$ to $\mathcal {Y}$. For two functions f and g on a common domain $\mathcal {X}$, we say that f is $\varepsilon$-close to g if $\mathrm {Pr}_{x}\left[ f(x) \ne g(x)\right] \le \varepsilon$ and that it is $\varepsilon$-far from g if $\mathrm {Pr}_{x}\left[ f(x) \ne g(x)\right] > \varepsilon$. Next, we review the definition of a pseudorandom function (PRF) [30].

Definition 2.1

(Pseudorandom Function). Denote by $\mathcal {K}= \{\mathcal {K}_{\lambda }\}_{\lambda \in \mathbb {N}}$, $\mathcal {X}= \{\mathcal {X}_{\lambda }\}_{\lambda \in \mathbb {N}}$, and $\mathcal {Y}= \{\mathcal {Y}_{\lambda }\}_{\lambda \in \mathbb {N}}$ three ensembles of finite sets indexed by a security parameter $\lambda$. Let $\{\mathsf {F}_\lambda \}_{\lambda \in \mathbb {N}}$ be an efficiently-computable collection of functions $\mathsf {F}_\lambda :\mathcal {K}_\lambda \times \mathcal {X}_\lambda \rightarrow \mathcal {Y}_\lambda$. Then, we say that the function family $\{\mathsf {F}_\lambda \}_{\lambda \in \mathbb {N}}$ is a $(t, \varepsilon )$-strong pseudorandom function if for all adversaries $\mathcal {A}$ running in time $t(\lambda )$, and taking $k \xleftarrow {\textsc {r}}\mathcal {K}_\lambda$ and $f_\lambda \xleftarrow {\textsc {r}}\mathsf {Funs}[\mathcal {X}_\lambda , \mathcal {Y}_\lambda ]$, we have that

$$ \left| \mathrm {Pr}[ \mathcal {A}^{\mathsf {F}_\lambda (k, \cdot )}(1^\lambda ) = 1 ] - \mathrm {Pr}[ \mathcal {A}^{f_\lambda (\cdot )}(1^\lambda ) = 1] \right| \le \varepsilon (\lambda ). $$

We say that the function family $\{\mathsf {F}_\lambda \}_{\lambda \in \mathbb {N}}$ is an $(\ell ,t,\varepsilon )$-weak pseudorandom function if for all adversaries $\mathcal {A}$ running in time $t(\lambda )$ and taking $k \xleftarrow {\textsc {r}}\mathcal {K}_\lambda$, $f_\lambda \xleftarrow {\textsc {r}}\mathsf {Funs}[\mathcal {X}_\lambda , \mathcal {Y}_\lambda ]$, $x_1, \ldots , x_\ell \xleftarrow {\textsc {r}}\mathcal {X}_\lambda$, we have that

$$ \left| \mathrm {Pr}\left[ \mathcal {A}\left( 1^\lambda , \{(x_i, \mathsf {F}_\lambda (k, x_i))\}_{i \in [\ell ]} \right) \right] - \mathrm {Pr}\left[ \mathcal {A}\left( 1^\lambda , \{(x_i, f_\lambda (x_i))\}_{i \in [\ell ]} \right) \right] \right| \le \varepsilon (\lambda ). $$

To simplify the notation, we will often drop the index $\lambda$ on $\mathsf {F}$. We will also write $\mathsf {F}_k$ to denote $\mathsf {F}(k,\cdot )$.

Domains and Their Representations. The key-space, domain, and range of all of the PRF candidates we consider in this work consist of vector spaces over finite fields (i.e., $\mathbb {Z}_p^k$ for some p and k). For notational convenience, we write everything using vector space notation. However, when measuring the complexity of evaluating the PRF, we measure everything in terms of Boolean operations (as opposed to arithmetic or finite field operations). Specifically, we view the keys, inputs, and outputs of our PRF candidates as vectors of bit-strings, where each bit-string encodes the binary representation of its respective field element. For example, a vector $v \in \mathbb {Z}_p^k$ would be represented by a binary string of length $k \cdot \left\lceil \log p \right\rceil$, where each block of $\left\lceil \log p \right\rceil$ bits represents a single component of v. This way, we can discuss the Boolean circuit complexity of evaluating a PRF over a key-space $\mathbb {Z}_p^{m\times n}$, domain $\mathbb {Z}_p^n$, and range $\mathbb {Z}_q^t$.

Circuit Classes. We also recall the definition of several basic complexity classes. First, the circuit class $\mathsf {AC}^0$ consists of all circuits with constant depth, polynomial size, and unbounded fan-in (containing only $\mathsf {AND}, \mathsf {OR}$, and $\mathsf {NOT}$ gates). The circuit class $\mathsf {TC}^0$ (resp., $\mathsf {TC}^1$) consists of all circuits with constant (resp., logarithmic) depth, polynomial size, unbounded fan-in and threshold gates.

Definition 2.2

(Modular Gates). For any integer m, the $\mathsf {MOD}_m$ gate outputs 1 if m divides the sum of its inputs, and 0 otherwise.

Definition 2.3

(Circuit Class $\mathsf {ACC}^0$). For integers $m_1, \ldots , m_k > 1$, we say that a language $\mathcal {L}$ is in $\mathsf {ACC}^0[m_1, \ldots , m_k]$ if there exists a circuit family $\{C_n\}_{n \in \mathbb {N}}$ with constant depth, polynomial size, and consisting of unbounded fan-in $\mathsf {AND}$, $\mathsf {OR}$, $\mathsf {NOT}$, and $\mathsf {MOD}_{m_1}, \ldots , \mathsf {MOD}_{m_k}$ gates that decides $\mathcal {L}$. We write $\mathsf {ACC}^0$ to denote the class of all languages that is in $\mathsf {ACC}^0[m_1, \ldots , m_k]$ for some $k \ge 0$ and integers $m_1, \ldots , m_k > 0$.

3 Candidate Weak Pseudorandom Functions

In this section, we introduce our candidate weak pseudorandom function families. We begin with a basic candidate below (Construction 3.1), and then describe several generalizations and extensions. When describing our applications in the subsequent sections, we will focus primarily on our basic construction.

Construction 3.1

(Mod-2/Mod-3 Weak PRF Candidate). Let $\lambda$ be a security parameter, and define parameters $m = m(\lambda )$ and $n = n(\lambda )$. The weak PRF candidate is a function $\mathsf {F}_\lambda : \mathbb {Z}_2^{m\times n} \times \mathbb {Z}_2^n\rightarrow \mathbb {Z}_3$ with key-space $\mathcal {K}_\lambda = \mathbb {Z}_2^{m\times n}$, domain $\mathcal {X}_\lambda = \mathbb {Z}_2^n$ and output space $\mathcal {Y}_\lambda = \mathbb {Z}_3$. For a key $\mathbf {A}\in \mathbb {Z}_2^{m\times n}$, we write $\mathsf {F}_{\mathbf {A}}(x)$ to denote the function $\mathsf {F}_\lambda (\mathbf {A}, x)$. We define $\mathsf {F}_{\mathbf {A}}$ as follows:

• On input $x \in \mathbb {Z}_2^n$, compute $y' = \mathbf {A}x \in \mathbb {Z}_2^m$.

• The output is defined by applying a non-linear mapping to $y'$. In this case, we take our non-linear mapping to be the function $\mathsf {map}: \{0,1\}^m\rightarrow \mathbb {Z}_3$ that outputs the sum of the inputs values modulo 3. Specifically, for $y' \in \{0,1\}^m$, we write $\mathsf {map}(y') := \sum _{i \in [m]} y_i' \pmod 3$.

We define $\mathsf {F}_{\mathbf {A}}(x) := \mathsf {map}(\mathbf {A}x)$. Note that we compute the matrix-vector product $\mathbf {A}x$ over $\mathbb {Z}_2$, and then re-interpret the values as their integer values 0 and 1.

Remark 3.2

(Weak PRF Candidate for Arbitrary p and q). The weak PRF candidate in Construction 3.1 can be generalized to work over two arbitrary fields $\mathbb {Z}_p$ and $\mathbb {Z}_q$ where $p \ne q$. In particular, we define the key-space to be $\mathcal {K}_\lambda = \mathbb {Z}_p^{m\times n}$, the domain to be $\mathcal {X}_\lambda = \mathbb {Z}_p^n$, and the range to be $\mathcal {Y}_\lambda = \mathbb {Z}_q$. We define the non-linear mapping $\mathsf {map}_{p, q} :\{0,1,\ldots ,p-1\}^m\rightarrow \mathbb {Z}_q$ that computes the sum of input values modulo q:

$$ \mathsf {map}_{p, q}(y') := \sum _{i \in [m]} y_i' \pmod q. $$

Putting all the pieces together, the PRF is defined to be $\mathsf {F}_{\mathbf {A}}(x) := \mathsf {map}_{p, q}(\mathbf {A}x)$. In this case, Construction 3.1 corresponds to the special case where $p = 2$ and $q = 3$. Note that for certain choices of p, q, the output of this mapping might not be balanced (this is not the case for $p = 2$ and $q = 3$), and pseudorandomness is then defined with respect to the corresponding distribution. We now describe several variations on our general candidate:

• We can consider a binary input space $\mathcal {X}_\lambda = \mathbb {Z}_2^{n'}$ rather than a mod-p input. In this case, we require that the key $\mathbf {A}$ to be compressing so that the product $\mathbf {A}x$ for a random $x \in \mathbb {Z}_2^{n'}$ is statistically close to the uniform distribution over $\mathbb {Z}_p^m$. For instance, this holds by the leftover hash lemma [32] if we take $n'(\lambda ) = \varOmega (m \log p)$.

• We can consider more complex input spaces and non-linear mappings. As a concrete example, we can define a PRF where the input domain is an elliptic curve group $E(\mathbb {Z}_q)$ of prime order p. That is, we take the domain to be $\mathcal {X}_\lambda = {E(\mathbb {Z}_q)}^n$; the key-space and range are unchanged: $\mathcal {K}_\lambda = \mathbb {Z}_p^{m \times n}$ and $\mathcal {Y}_\lambda = \mathbb {Z}_q$. In this case, the linear mapping $\mathbf {A}x$ corresponds to computing a linear combination of elliptic curve points. We can define the non-linear mapping $\mathsf {map}_{p, q}$ from $E(\mathbb {Z}_q)$ into $\mathbb {Z}_q$ to be the mapping that returns the x-coordinate of the curve point (recall that each element in $E(\mathbb {Z}_q)$ can be represented by a pair of (x, y)-coordinates in $\mathbb {Z}_q$).

Remark 3.3

(Multiple Output Bits). The output of our weak PRF candidate from Construction 3.1 consists of a single element in $\mathbb {Z}_3$. In many scenarios (such as the ones we describe in Sect. 5), we require a PRF with longer output. One way to extend Construction 3.1 to provide longer outputs is to take the vector $\mathbf {A}x \in \mathbb {Z}_2^m$, reinterpret it as a 0/1 vector $y' \in \mathbb {Z}_3^m$, and output $\mathbf {G}y' \in \mathbb {Z}_3^t$, where $\mathbf {G}\in \mathbb {Z}_3^{t\times m}$ is a fixed public matrix. Formally, we define the mapping $\mathsf {map}_\mathbf {G}:\{0,1\}^m\rightarrow \mathbb {Z}_3^t$ that maps $y' \mapsto \mathbf {G}y'$, and define the PRF candidate $\mathsf {F}:\mathbb {Z}_2^{m\times n} \times \mathbb {Z}_2^n\rightarrow \mathbb {Z}_3^t$ to be $\mathsf {F}_\mathbf {A}(x) := \mathsf {map}_\mathbf {G}(\mathbf {A}x)$. Construction 3.1 then corresponds to the special case where $\mathbf {G}= \mathbf {1}^{1 \times m}$, where $\mathbf {1}^{1 \times m}$ denotes the all-ones matrix of dimension 1-by-$m$. In our constructions, we propose taking $\mathbf {G}$ to be the generator matrix of a linear error-correcting code over $\mathbb {Z}_3$. This choice is motivated by the fact that the generator matrix of a linear code with sufficient distance implements a good extractor for a bit-fixing source [20]. As a concrete candidate for our constructions, we propose taking $\mathbf {G}$ to be the generator matrix of a BCH code over $\mathbb {Z}_3$. Note that we require $t < m$. Otherwise, if $t \ge m$, then we can use linear algebra (over $\mathbb {Z}_3$) to recover $y' = \mathbf {A}x$ from the output $\mathbf {G}y'$ (since $\mathbf {G}$ is public). Given multiple pairs $(x, y')$, we can recover the secret key $\mathbf {A}$ (over $\mathbb {Z}_2$). In particular, in our concrete parameter settings, we require $m - t \ge \lambda$.

Remark 3.4

(Using Structured Matrices as the PRF Key). We can improve the asymptotic (and concrete) efficiency of our weak PRF candidate (Construction 3.1) by taking the key to be a structured matrix rather than a random matrix. For example, we can take $\mathbf {A}$ to be a uniformly random Toeplitz matrix rather than a uniformly random matrix. In particular, if $\mathbf {A}\in \mathbb {Z}_2^{m\times n}$ is Toeplitz, then computing the matrix-vector product $\mathbf {A}x$ can be done in time that is quasi-linear rather than quadratic in the input dimension. A similar optimization of using a random Toeplitz matrix in place of a random matrix was previously proposed to improve the concrete efficiency of authentication schemes based on the learning parity with noise (LPN) problem [28, 45].

3.1 Conjectures on the Security of Weak PRF Candidates

We now state three conjectures on our new family of weak PRF candidates, sorted in order from the weakest to the strongest:

Conjecture 3.5

(General Mod-p/Mod-q Weak PRF Candidate). Let $\lambda$ be a security parameter. Then, there exist fixed primes p and q and $m, n = \mathrm {poly}(\lambda )$ such that for all $\ell , t = \mathrm {poly}(\lambda )$, there exists a function $\varepsilon = \mathrm {negl}(\lambda )$ such that the family $\{\mathsf {F}_\lambda \}_{\lambda \in \mathbb {N}}$ from Remark 3.2 is an $(\ell , t, \varepsilon )$-weak PRF.

Conjecture 3.6

(Mod-2/Mod-3 Weak PRF Candidate). Let $\lambda$ be a security parameter. Then, there exist $m, n = \mathrm {poly}(\lambda )$ such that for all $\ell , t = \mathrm {poly}(\lambda )$, there exists $\varepsilon = \mathrm {negl}(\lambda )$ such that the function family $\{\mathsf {F}_\lambda \}_{\lambda \in \mathbb {N}}$ from Construction 3.1 is an $(\ell , t, \varepsilon )$-weak PRF.

Conjecture 3.7

(Exponential Hardness of Mod-2/Mod-3 Weak PRF Candidate). Let $\lambda$ be a security parameter. Then, there exist $m, n = O(\lambda )$ such that for all $\ell = \mathrm {poly}(\lambda )$ and $t = 2^\lambda$, there exists $\varepsilon = 2^{-\varOmega (\lambda )}$ such that the function family $\{\mathsf {F}_\lambda \}_{\lambda \in \mathbb {N}}$ from Construction 3.1 is an $(\ell , t, \varepsilon )$-weak PRF.

Remark 3.8

(Further Generalizations). As stated, Conjectures 3.6 and 3.7 are specific to the security of our mod-2/mod-3 weak PRF candidate from Construction 3.1. But more generally, we can consider an analogous pair of conjectures for any fixed mod-p/mod-q candidate (where p and q are distinct primes). Going further, we can even conjecture that the analogous claims hold for all choices of p and q. In this work however, we focus on the security of the mod-2/mod-3 candidate, since that candidate is most well-suited for our MPC applications.

Remark 3.9

(Weak PRF in $\mathsf {ACC}^0$). An appealing property of the mod-2/mod-3 PRF candidate from Construction 3.1 is that the PRF can be computed by a depth-2 $\mathsf {ACC}^0$ circuit (in fact, a depth-2 $\mathsf {ACC}^0[2, 3]$ circuit suffices). Specifically, if $\mathbf {A}\in \mathbb {Z}_2^{m\times n}$ is the secret key to the PRF, then the function $\mathsf {F}_\mathbf {A}$ can be computed by a depth-2 circuit where the first layer consists of $m$ $\mathsf {MOD}_2$ gates, one associated with each row of $\mathbf {A}$ (concretely, each $\mathsf {MOD}_2$ gate takes as input the subset of input bits on which the corresponding row of $\mathbf {A}$ depends). All of the $\mathsf {MOD}_2$ gates feed into two $\mathsf {MOD}_3$ gates, each computing one bit of the binary encoding of the output value (more precisely, the $\mathsf {MOD}_3$ gate computing the most significant bit of the output outputs 1 if the sum of the inputs is $2 \bmod 3$ and the $\mathsf {MOD}_3$ gate computing the least significant bit of the outputs outputs 1 if the sum of its input bits is $1 \bmod 3$). Note that we can also implement the PRF in depth-2 $\mathsf {ACC}^0[6]$, that is, $\mathsf {ACC}^0$ with $\mathsf {MOD}_6$ gates only (using essentially the same construction). In either case, we conclude that under Conjecture 3.6, there exists a weak-PRF candidate in depth-2 $\mathsf {ACC}^0$. Intuitively, this means that under Conjecture 3.6, the complexity class $\mathsf {ACC}^0$ should be hard to learn. We formalize this intuition in the full version.

3.2 Comparison with Other Weak PRF Candidates

In the full version, we compare our weak PRF candidate (Construction 3.1) to previous candidate low-complexity PRFs, and in particular to the Akavia et al. construction [1], candidates based on hard learning problems or on expander graphs by Blum et al.  [15] and by Applebaum and Raykov [6], and to number-theoretic [41,42,43, 51] and lattice-based candidates [9, 10, 18]. Here, we also discuss several advantages of our construction.

Advantages of Our Construction. We now describe two appealing properties of our new weak PRF candidate compared to the existing ones:

• Low complexity: Our weak PRF candidate is the first that can be computed by an $\mathsf {ACC}^0$ circuit and plausibly satisfy exponential security (Conjecture 3.7). Previous PRF candidates in $\mathsf {ACC}^0$ (or $\mathsf {AC}^0$) only provided quasi-polynomial [1, 6] or sub-exponential security [51]. In fact, our candidates are computable by a depth-2 $\mathsf {ACC}^0$ circuit, which is the minimal depth possible for any PRF candidate. To our knowledge, there are no other candidates that can be computed by a depth-2 $\mathsf {AC}^0$ or $\mathsf {ACC}^0$ circuit (even if we just require polynomial hardness).

• MPC-friendliness: Another advantage of our construction is that our PRF is very MPC-friendly. Specifically, we consider scenarios where multiple parties hold shares of the PRF key as well as the PRF input, and the goal is for the parties to compute the PRF output on their joint inputs. The structure of our PRF is very amenable for use in MPC protocols. Notably, much of the computation is linear (over $\mathbb {Z}_2$ and $\mathbb {Z}_3$). Using (standard) MPC protocols based on linear secret-sharing, computing linear functions on secret-shared values can be done non-interactively. Communication is only needed to handle the non-linear transformation from values over $\mathbb {Z}_2$ to values over $\mathbb {Z}_3$. In Sect. 5, we show that this step can be done very efficiently using the recent protocol of Araki et al.  [7]. In contrast, evaluating the tribes function (in the case of Akavia et al.  [1]) or the majority function (in the case of Blum et al.  [15]) over secret-shared values will either incur additional overhead in either round complexity or communication complexity (or both).

4 Rationales for Security

In this section, we provide a brief overview of several rationales to support the conjectured security of our candidate. The detailed analysis (including proofs and further discussions) is available in the full version. First, we follow the security analysis of the weak-PRF candidate proposed by Akavia et al.  [1] and show that (1) standard learning algorithms cannot break the security of our construction, and (2) our candidate cannot be approximated by low-degree polynomials over finite fields. In addition, we conjecture that it is difficult to approximate our construction with low-degree rational functions. Finally, we suggest concrete parameters for our candidate weak PRF.

4.1 Lack of Correlation with Fixed Function Families

The most natural way to rule out the existence of pseudorandom functions in a complexity class is to provide a learning algorithm for the class. In the the full version, we show that a randomly chosen function in our PRF family does not have a noticeable correlation with any sufficiently small (but still exponential-size) collection of functions $\mathcal {H}= \{h :\{0,1\}^n \rightarrow \{0,\pm 1\}\}$. Our analysis relies on techniques similar to those used by Akavia et al.  [1, Proposition 16]. This rules out distinguishers based on learning algorithms of the form of the one by Linial et al.  [38]. Specifically, in the the full version, we show the following lemma.

Lemma 4.1

(No Correlation with Fixed Function Families). Let $\mathcal {H}= \{h:\{0,1\}^n \rightarrow \{0,\pm 1\}\}$ be a collection of functions of size s. Then,

$$ \mathrm {Pr}_{\mathbf {A}}\left[ \exists h \in \mathcal {H}~|~ \mathrm {Pr}_{x}\left[ \mathsf {map}(\mathbf {A}x) = h(x)\right] > \frac{1}{3} + \frac{1}{2^{n-1}} + \varepsilon \right] \le \frac{5s}{2^{n} \cdot \varepsilon ^2}, $$

where $\mathbf {A}\xleftarrow {\textsc {r}}\{0,1\}^{n \times n}$.

4.2 Inapproximability by Low-Degree Polynomials and Rational Functions

Another necessary condition for a PRF family is that the family should be hard to approximate by low-degree polynomials (resp. rational functions). Specifically, assume there exists a degree-d multivariate polynomial f (resp. f, g) over $\mathrm {GF}(2)$ such that $\mathsf {F}_k(x) = f(x)$ (resp. $\mathsf {F}_k(x) \cdot g(x) = f(x)$) for all $x \in \{0,1\}^n$. Then, given (sufficiently many) PRF evaluations $(x_i, \mathsf {F}_k(x_i))$ on uniformly random values $x_i$, an adversary can set up a linear system where the unknowns corresponds to the coefficients of f (resp. f, g). Since f (resp. f, g) has degree d, the resulting system has $N = \sum _{k = 0}^d \left( {\begin{array}{c}n\\ k\end{array}}\right)$ (resp. 2N) variables. Thus, given $O(2^d \cdot N)$ random samples, the adversary can solve the linear system and recover the coefficients of f (resp. f, g) (and therefore, a complete description of $\mathsf {F}_k$). We note that this attack still applies even if $\mathsf {F}_k$ is $1/O(2^d \cdot N)$-close to a degree-d polynomial (resp. rational function). In this case, the solution to the system will be $1/O(2^d \cdot N)$-close to $\mathsf {F}_k$ with constant probability (which still suffices to break pseudorandomness). Thus, for a candidate PRF family to be secure, the family should not admit a low-degree polynomial (resp. rational function) approximation.

In our setting, we are able to rule out low-degree polynomial approximations by appealing to the classic lower bounds for $\mathsf {ACC}^0$ by Razborov and Smolensky [46, 48], which essentially says that for distinct primes p and q, $\mathsf {MOD}_p$ gates cannot be computed in $\mathsf {ACC}^0[q^\ell ]$ for any $\ell > 1$. We show the following lemma in the full version.

Lemma 4.2

(Inapproximability by Low-Degree Polynomials). For $n \,{>}\, 0$ and $d < n/2$, let $B(n,d) = \frac{1}{2^n} \cdot \sum _{i = 0}^{n/2-d-1}{\left( {\begin{array}{c}n\\ i\end{array}}\right) }$. Then, for all primes $p \ne q$, the function $\mathsf {map}_{p} :\{0,1\}^n \rightarrow \mathbb {Z}_q$ on n-bit inputs that maps $x \mapsto \sum _{i\in [n]} x_i \pmod p$ is B(n, d)-far from all degree-d polynomials over $\mathrm {GF}(q^\ell )$ for all $\ell \ge 1$.

The low-degree polynomial approximation attack described above directly generalizes to the setting where the PRF $\mathsf {F}_k$ can be approximated by a low-degree rational function. For instance, suppose there exist multivariate polynomials f, g over $\mathrm {GF}(2)$ of degree at most d such that $f(x) = \mathsf {F}_k(x) \cdot g(x)$ for all $x \in \{0,1\}^n$. Then, a similar attack can be mounted, as any random input-output pair corresponds to an equation in the 2N variables (with $N = \sum _{k = 0}^d \left( {\begin{array}{c}n\\ k\end{array}}\right)$) defining polynomials f and g. Thus, if our PRF candidate is $1/O(2^d \cdot N)$-close to a degree-d rational function, then there is an $O(2^d \cdot N)$-time attack given $O(2^d \cdot N)$ evaluations of the PRF.

While the Akavia et al. weak PRF candidate [1] cannot be approximated by a low-degree polynomial, Bogdanov and Rosen [17] showed that the function can be approximated by a degree $O(\log (n))$ rational function, where n is the length of the key. This gives a quasi-polynomial distinguisher against the Akavia et al. candidate.

In our case, we conjecture that the $\mathsf {map}_p$ function (respectively, the $\mathsf {map}_{p,q}$ function for our more general candidates from Remark 3.2) cannot by approximated by a low-degree rational function over $\mathrm {GF}(q^\ell )$, for any $q \ne p$ and $\ell \ge 1$. While the Razborov-Smolensky argument used to argue hardness of approximation of $\mathsf {map}_p$ by low-degree polynomials over $\mathrm {GF}(q^\ell )$ does not generalize to rational functions, we still believe that this is a very plausible conjecture.

Conjecture 4.3

(Inapproximability by Rational Functions). For any primes $p \ne q$, any integer $\ell \ge 1$, and any $d = o(n)$, there exists a constant $\alpha < 1$ such that the function $\mathsf {map}_p :\{0,1\}^n \rightarrow \mathbb {Z}_p$ that maps $x \mapsto \sum _{i \in [n]} x_i \pmod p$ is $1/(2^d \cdot N)^\alpha$-far from all degree-d rational functions over $\mathrm {GF}(q^\ell )$.

We believe that studying this conjecture is a natural and well-motivated complexity problem. Proving or disproving this conjecture would lead to a better understanding of $\mathsf {ACC}^0$.

4.3 Resilience to Standard Cryptanalysis Techniques

In this section, we survey several other relevant cryptanalytic techniques and their impact on the conjectured security of our weak PRF candidate.

Pairwise Independence. First, we note that our candidate is pairwise independent. This is immediate as for any pair of distinct inputs, the value of $\mathbf {A}x$ will be uniformly random and independent over $\mathbb {Z}_2^m$. Pairwise-independence is sufficient to argue that basic versions of differential and linear cryptanalysis (in the sense of the definitions proposed in [39]) do not apply to our candidate. We note that these linear and differential cryptanalysis are particularly relevant when evaluating the security of our encoded-input PRF (Sect. 6.3), since there, the adversary can make adaptive queries (over a restricted subset of the domain).

Blum-Kalai-Wasserman Attacks. Due to the structural similarities between our candidate and the learning parity with noise (LPN) assumption, the Blum-Kalai-Wasserman (BKW) attack [16] seems particularly relevant.

We do not see a way to adapt such attacks to our candidate as it does not seem possible to create “fresh” samples given a collection of samples. In particular, the mixing of the mod-2 and the mod-3 operations in our basic candidate destroys the linear structure exploited by BKW.

Other Classical Techniques. Several other classical techniques used in cryptanalysis, such as algebraic or correlation attacks, are closely related to the degree of approximation by polynomials or by rational functions. Thus, we can appeal to our previous analysis and conjectures (Sects. 4.1 to 4.2) to argue that our weak PRF candidate plausibly resists those attacks.

Further Cryptanalysis. To conclude, we emphasize that the analysis we have done is not intended to be exhaustive, and we invite the community to further evaluate the security of our candidate. We believe though that the initial exploratory study we have conducted provides evidence to support the security of our candidate.

4.4 Concrete Parameters

We now propose some concrete parameters for our candidate. Our proposals (summarized in Table 2) are based on our exploration of possible attacks as well as concrete parameters for LPN with constant noise rate. Specifically, we use the parameters suggested by [26, Table 4] based on the estimated runtime on a machine with $2^{60}$ bits of memory and assuming a constant noise rate $\tau = 1/4$.⁷ We propose optimistic and conservative parameters. Our optimistic choice of parameters ($n = m = 2\lambda$, where $\lambda$ is the security parameter) suggests better parameters than those for LPN, which is in part justified by the fact that the most efficient attacks against LPN (e.g., BKW) do not seem to apply to our candidate. Our conservative parameters are the same as those suggested for LPN. We further conjecture that choosing a structured key (e.g., a Toeplitz matrix) does not significantly affect the parameters. Based on our exploratory analysis, we see no need to use larger parameters to instantiate our candidate. We encourage further cryptanalysis to support or disprove the validity of our proposals.

Table 2. Proposed parameters (for Construction 3.1, we set $m= n$) and comparison with parameters for LPN.

5 Applications to Multiparty Computation

An attractive feature of our candidate is that it supports efficient evaluation in a fully distributed setting, where both the PRF key and the PRF input are secret-shared between multiple parties. We highlight one such application of this primitive to distributed searchable symmetric encryption (SSE) in the full version.

5.1 Fully-Distributed Weak PRF Evaluation

In this section, we describe a 3-party protocol with security against one passive corruption for secure evaluation of our weak PRF candidate (Construction 3.1).⁸ At the beginning of the protocol, we assume that the servers hold a secret-sharing of both the input x and the PRF key k. At the end of the protocol execution, each server should hold a fresh secret-sharing of the output.

We assume the parties use an additive secret sharing scheme (over a ring), so additions on secret-shared values are free. For multiplications, we use the multiplication protocol from [7] that allows 3 servers to take shares of ring elements a and b and compute a share of the product ab where each server only needs to broadcast a single ring element. In particular, if we work over the binary field $\mathbb {Z}_2$, computing $\mathsf {XOR}$ is free while computing an $\mathsf {AND}$ requires 1-bit of communication. The protocol relies on pseudorandom secret sharing (PRSS) [21] and requires a one-time setup of replicated PRF keys. We note that we can achieve information-theoretic security without the need for the (trusted) setup at twice the cost of the basic protocol.

We now describe our protocol $\pi _{\mathsf {fde}}$ for distributed evaluation of our mod-2/mod-3 candidate (Construction 3.1). We assume a structured key (e.g., a Toeplitz matrix), so the key can be compactly represented by a single vector $k \in \mathbb {Z}_2^n$. This assumption is only needed to simplify the protocol description. Our protocol naturally generalizes to the setting with an unstructured (i.e., fully random) key with no overhead (in either communication or round complexity). To recall, to evaluate our PRF, we first evaluate the matrix-vector product between the key and the input: $k, x \mapsto h \in \mathbb {Z}_2^m$. We then reinterpret h as an m-dimensional vector over $\mathbb {Z}_3$. The output $\mathsf {map}_\mathbf {G}(h) \in \mathbb {Z}_3^t$ can then be computed as a linear function $\mathsf {map}_\mathbf {G}$ on h. We begin by defining the fully-distribution evaluation functionality that we seek to instantiate.

Definition 5.1

(Fully-Distributed Evaluation Functionality). The ideal fully-distributed PRF evaluation functionality is defined as follows:

• Inputs: The servers hold replicated additive shares of the input and the key over $\mathbb {Z}_2$. Concretely, let $k_1,k_2,k_3$ be vectors in $\mathbb {Z}_2^{n}$ such that $k_1\oplus k_2 \oplus k_3=k$ and similarly $x_1,x_2,x_3$ vectors in $\mathbb {Z}_2^n$ such that $x_1\oplus x_2 \oplus x_3=x$. Server i holds $k_j,x_j$ with $j\ne i$.

• Outputs: The first two servers hold random $y_1,y_2 \in \mathbb {Z}_3^t$ such that $y_1+y_2=\mathsf {F}_k(x)$.

We write $[h]_p$ to denote an additive sharing of h over $\mathbb {Z}_p$—that is, a tuple of values whose sum is $h \bmod p$. Depending on the context, this will sometimes be a triple of shares held by the 3 servers and sometimes a pair of shares held by the first 2 servers. Our protocol uses a sub-protocol $\pi _{2,3}$ that transforms an additive sharing $[h]_2$ (i.e., a mod-2 secret-sharing of h) held by the 3 servers into an additive sharing $[h]_3$ (i.e., a mod-3 secret-sharing of h) held by the first two servers. We define this functionality $f_{23}$ below.

Definition 5.2

(Share Conversion Functionality). The share-conversion functionality $f_{23}$ converts a 3-party mod-2 secret sharing of a value $h \in \{0,1\}$ into a 2-party mod-3 secret sharing of the same value h. Specifically, the functionality’s input/output behavior is as follows:

• Inputs: Every server $i \in [3]$ has an input $b_i \in \{0,1\}$. Server 1 has an additional input $c \in \mathbb {Z}_3$.

• Outputs: Servers 1 and 3 receive no output. Server 2 receives an output $d \in \mathbb {Z}_3$ such that $c + d = b_1 \oplus b_2 \oplus b_3 \pmod 3$.

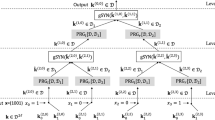
It is straightforward to design a Boolean circuit that implements the ideal share-conversion functionality from Definition 5.2. We give the circuit in Fig. 1 below. The circuit consists of 3 $\mathsf {AND}$ gates and 10 $\mathsf {XOR}$ gates. To obtain our final share-conversion protocol, we use the PRSS-based protocol by Araki et al.  [7] to evaluate the circuit in Fig. 1.

Fig. 1.

A simple circuit that implements the share-conversion functionality $f_{23}$ (Definition 5.2).

The Protocol $\pi _{\mathsf {fde}}$. We now describe our protocol $\pi _{\mathsf {fde}}$ for fully-distributed evaluation of our mod-2/mod-3 weak PRF candidate. Recall that at the beginning of the protocol, we assume that the three servers have a replicated additive secret-sharing of the input and the key. The protocol $\pi _{\mathsf {fde}}$ then consists of three phases:

• During the first phase, each server $S_i$ computes an additive share $h_i \in \mathbb {Z}_2^m$ of the linear mapping $(k,x) \mapsto h$ defined by the key. This can be done locally using the replicated additive shares of the input and the key. This follows from the fact that for any two secret-shared values a, b split into 3 shares (i.e., $a = a_1 + a_2 + a_3$ and $b = b_1 + b_2 + b_3$), we have that $ab = (a_1 + a_2 + a_3)(b_1 + b_2 + b_3) = \sum _{1 \le i,j \le 3} a_i b_j$. In a replicated secret-sharing scheme, server $S_i$ knows $a_j, b_j$ for $j \ne i$. This means that every term $a_i b_j$ in the sum can be computed by at least 1 of the servers.

• In the second step of the protocol, the three servers evaluate the share-conversion protocol $\pi _{2,3}$ to their secret-shared values. For each component of their additive share, the servers runs the interactive protocol $\pi _{2,3}$ to transform additive shares (held by the 3 servers) modulo 2 into additive shares (held by the first 2 servers) modulo 3. At the end of this phase, servers $S_1$ and $S_2$ hold a share $[h]_3$ of the linear mapping.

• In the final step of the protocol, the two parties evaluate $\mathsf {map}_\mathbf {G}$ on their share. Since the matrix $\mathbf {G}$ is public, this is a linear operation, and can be done non-interactively. The output is the output of the protocol.

Observe that by construction, only the second step of the protocol is interactive. Moreover, the protocol requires just two rounds of interaction. We give the full protocol in the full version.

5.2 Concrete Efficiency of Distributed PRF Evaluation

In this section, we compare the concrete efficiency of secure evaluation of our PRF to alternative constructions. Here, we assume that both the input x and the key k to the PRF are secret-shared across multiple servers. We measure the concrete cost in terms of the round complexity and the communication complexity needed for joint evaluation of the PRF. For all of our estimates, we use a concrete security parameter of $\lambda = 128$.

In Table 1, we provide a concrete comparison of the communication complexity and round complexity for oblivious evaluation of our PRF candidate. We compare them to the corresponding costs of using the Araki et al. protocol or an optimized garbled-circuit protocol to evaluate standard block ciphers like AES and MPC-optimized block ciphers like LowMC and Rasta. We describe the methodology we used to derive these estimates in the full version.

5.3 An Alternative Candidate with Better Garbling Complexity

While our weak PRF candidate in Construction 3.1 can be computed efficiently when the input and key are secret shared across 3 servers, the large number of multiplications makes it less amenable for garbled circuit evaluation. In this section, we introduce a variant of our weak PRF candidate that is well-suited for garbling (even compared to MPC-friendly block ciphers like LowMC and Rasta), and yet, is still plausibly secure. We give the candidate below, but defer the description of the efficient information-theoretic garbling of the candidate (based on [5]) to the full version.

Construction 5.3

(Alternative Mod-2/Mod-3 Weak PRF Candidate). Let $\lambda$ be a security parameter, and let $n = n(\lambda )$ be the key length (and input length). The weak PRF candidate is a function $\mathsf {F}_\lambda : \{0,1\}^{n} \times \{0,1\}^n\rightarrow \mathbb {Z}_3$ with key-space $\mathcal {K}_\lambda = \{0,1\}^{n}$, domain $\mathcal {X}_\lambda = \{0,1\}^n$ and output space $\mathcal {Y}_\lambda = \mathbb {Z}_3$. For a key $\mathbf {k}\in \mathbb {Z}_2^{n}$, we write $\mathsf {F}_{\mathbf {k}}(x)$ to denote the function $\mathsf {F}_\lambda (\mathbf {k}, x)$. We define $\mathsf {F}_{\mathbf {k}}$ as follows:

• On input $x \in \{0,1\}^n$,

  $$ \mathsf {F}_{\mathbf {k}}(x) = \sum _{i \in [n]} \mathbf {k}_i x_i \bmod 2 + \sum _{i \in [n]} \mathbf {k}_i x_i \bmod 3 \pmod 2. $$

• In other words, the PRF evaluation consists of computing the inner product between the key $\mathbf {k}$ and the input x modulo 2 and modulo 3, and then combining the results modulo 2, Alternatively, it can be viewed as a variant of LPN with noise rate 1 / 3 where the noise is derived deterministically from the input and key (with the noise being 1 if and only if $\langle \mathbf{k},x\rangle = 1 \pmod 3$).

Security of Construction 5.3. In the full version, we provide additional discussion on the security of our construction. In particular, while many of the rationales we discussed in Sect. 4 for security of our main candidate (e.g., lack of correlation with fixed function families and inapproximability by low-degree rational functions) also apply to the alternative candidate, there are two key limitations of this new candidate compared to Construction 3.1: (1) the BKW attack now applies to this candidate due to its structural similarity with the LWE or LPN problems, and (2) there exist non-adaptive attacks on this candidate.

6 Encoded-Input Pseudorandom Functions

In this section, we examine the security of our weak PRF candidate against adaptive attacks. In fact, we show in the full version that strong PRFs do not exist in a large class of depth-2 circuits (including our weak PRF candidate (Construction 3.1), thus ruling out adaptive security of our candidate). Our lower bound relies on a learning algorithm for automata with multiplicity by Bergadano and Varricchio [14].

There are many scenarios where a weak PRF does not suffice for security. For instance, if we consider the distributed SSE application described in the full version and impose the additional requirements of security against malicious clients, then a weak PRF no longer suffices. To address this limitation, we introduce a new notion we call an encoded-input pseudorandom function that can often be used as a drop-in replacement for strong PRFs. At a high-level, an encoded-input PRF is a function that behaves like a PRF on some (possibly sparse) subset of the domain. As a concrete example, a suitable subset might be the set of codewords under a linear error-correcting code.

In this section, we describe several natural applications of encoded-input PRFs, and then describe a candidate encoded-input PRF whose efficiency is comparable to that of our weak PRF candidate. This candidate remains MPC-friendly, and can thus be useful for MPC applications that require a strong PRF.

6.1 Definitions of (P)EI-PRFs

We define two versions of our notion: encoded-input pseudorandom function (EI-PRF) and protected encoded-input pseudorandom function (PEI-PRF).

Definition 6.1

(Encoded-Input PRF). Let $\mathcal {K}= {\{\mathcal {K}_{\lambda }\}}_{\lambda \in \mathbb {N}}$, $\mathcal {X}= {\{\mathcal {X}_{\lambda }\}}_{\lambda \in \mathbb {N}}$, $\mathcal {X}' = {\{\mathcal {X}'_{\lambda }\}}_{\lambda \in \mathbb {N}}$, and $\mathcal {Y}= {\{\mathcal {Y}_{\lambda }\}}_{\lambda \in \mathbb {N}}$ be ensembles of finite sets indexed by a security parameter $\lambda$. Let ${\{\mathsf {F}'_\lambda \}}_{\lambda \in \mathbb {N}} = {\{(\mathsf {E}_\lambda ,\mathsf {F}_\lambda )\}}_{\lambda \in \mathbb {N}}$ be an efficiently-computable collection of functions where $\mathsf {E}_\lambda :\mathcal {X}_\lambda ' \rightarrow \mathcal {X}_\lambda$ is an encoding function and $\mathsf {F}_\lambda :\mathcal {K}_\lambda \times \mathcal {X}_\lambda \rightarrow \mathcal {Y}_\lambda$ is a keyed evaluation function. Then, we say that ${\{\mathsf {F}'_\lambda \}}_{\lambda \in \mathbb {N}}$ is a $(t,\varepsilon )$-encoded-input PRF (EI-PRF) if the function $\mathcal {K}_\lambda \times \mathcal {X}_\lambda ' \rightarrow \mathcal {Y}_\lambda$ defined via $(k,x') \mapsto \mathsf {F}_\lambda (k,\mathsf {E}_\lambda (x'))$ is a $(t,\varepsilon )$-strong pseudorandom function. Moreover, we say that $\mathsf {F}'_\lambda$ is computable in $\mathcal {C}$ if $\mathsf {F}_\lambda$ is computable in $\mathcal {C}$.

While the definition of an encoded-input PRF may seem equivalent to that of a standard PRF, the important point is that the encoding function is a keyless procedure. This means that an honest user can evaluate for itself the encoding algorithm on an input to obtain a valid encoded input, and then ask for the PRF value on the encoded input. The holder of the PRF secret key only needs to evaluate $\mathsf {F}$. This is the reason we define the complexity of an EI-PRF to be the complexity of its evaluation function (rather than the composition of its evaluation and encoding functions). Furthermore, we note that even though the overall function $\mathsf {F}(\cdot ,\mathsf {E}(\cdot ))$ is a strong PRF, the function $\mathsf {F}$ itself may live in a complexity class where strong PRFs do not exist.

One of the main reasons we are interested in EI-PRFs is that we can potentially use them as a drop-in replacement for strong PRFs in concrete applications. In many of these scenarios, however, it does not make sense to assume that the evaluator behaves honestly and will only evaluate the $\mathsf {F}$ on properly-encoded inputs. This motivates our stronger notion of a protected encoded-input PRF (PEI-PRF), which augments an EI-PRF with an additional verification algorithm. The inputs to a PEI-PRF consists of a point x as well as a proof w that x is a proper encoding (with respect to the encoding function of the underlying EI-PRF). The guarantee is that the output of the PEI-PRF are pseudorandom on all properly-encoded inputs, and $\bot$ on improperly-encoded inputs.

Definition 6.2

(Protected EI-PRF). Let ${\{\mathsf {F}'_\lambda \}}_{\lambda \in \mathbb {N}} = {\{(\mathsf {E}_\lambda ,\mathsf {V}_\lambda ,\mathsf {F}_\lambda )\}}_{\lambda \in \mathbb {N}}$ be an efficiently-computable collection of functions where $\mathsf {E}_\lambda :\mathcal {X}_\lambda ' \rightarrow \mathcal {X}_\lambda \times \mathcal {W}_\lambda$ is a protected encoding function whose range is polynomial-time checkable by $\mathsf {V}_\lambda :\mathcal {X}_\lambda \times \mathcal {W}_\lambda \rightarrow \{0,1\}$. That is, $\mathsf {V}_\lambda (x,w) = 1$ if and only if (x, w) is a valid encoding. Finally, $\mathsf {F}_\lambda :\mathcal {K}_\lambda \times \mathcal {X}_\lambda \times \mathcal {W}_\lambda \rightarrow \mathcal {Y}_\lambda$ is a keyed evaluation function. Denote by $\perp$ a special element of $\mathcal {Y}_\lambda$. For a function $f \in \mathsf {Funs}[\mathcal {X}_\lambda , \mathcal {Y}_\lambda ]$, define $\mathsf {Eval}^{f}_\lambda :\mathcal {X}_\lambda \times \mathcal {W}_\lambda \rightarrow \mathcal {Y}_\lambda$ as:

$$ \mathsf {Eval}^{f}_\lambda (x,w) = {\left\{ \begin{array}{ll} f(x)~\,\text { if}~\mathsf {V}_\lambda (x,w) = 1 \\ \perp ~~~\;~\text { otherwise}. \end{array}\right. } $$

Then, we say that ${\{\mathsf {F}'_\lambda \}}_{\lambda \in \mathbb {N}}$ is a $(t,\varepsilon )$-PEI-PRF if for all adversaries $\mathcal {A}$ running in time $t(\lambda )$, and taking $k \xleftarrow {\textsc {r}}\mathcal {K}_\lambda$ and $f \xleftarrow {\textsc {r}}\mathsf {Funs}[\mathcal {X}_\lambda , \mathcal {Y}_\lambda ]$, we have that

$$ \left| \mathrm {Pr}[ \mathcal {A}^{\mathsf {F}_\lambda (k, \cdot ,\cdot )}(1^\lambda ) = 1 ] - \mathrm {Pr}[ \mathcal {A}^{\mathsf {Eval}_\lambda ^{f}(\cdot , \cdot )}(1^\lambda ) = 1] \right| \le \varepsilon (\lambda ). $$

We say that $\mathsf {F}'_\lambda$ is computable in a circuit class $\mathcal {C}$ if the mapping $(k,x,w) \mapsto \mathsf {F}_\lambda (k,x,w)$ is computable in $\mathcal {C}$. Finally, we say that a PEI-PRF is systematic if the witness w has the form $x'\Vert w'$ such that $\mathsf {V}_\lambda (x,(x'\Vert w')) = 1$ if and only if $(x,w)=\mathsf {E}_\lambda (x')$.

Remark 6.3

(Relation between EI-PRFs and PEI-PRFs). PEI-PRFs are more powerful objects than EI-PRFs: If $(\mathsf {E},\mathsf {V},\mathsf {F})$ is a PEI-PRF, then $(\mathsf {E},\mathsf {F})$ is an EI-PRF.

We first show that that PEI-PRFs can be generically constructed from EI-PRFs.

Lemma 6.4

(PEI-PRFs from EI-PRFs). Let ${\{(\mathsf {E}^*_\lambda ,\mathsf {F}^*_\lambda )\}}_\lambda$ be an EI-PRF. Then, assuming $\mathsf {F}_\lambda$ and CNF formulas can be computed by depth-d circuits in a class $\mathcal {C}$, there exists a systematic PEI-PRF ${\{(\mathsf {E}_\lambda ,\mathsf {V}_\lambda ,\mathsf {F}_\lambda )\}}_\lambda$ computable by a depth-$(d+1)$ circuit.

Proof

The lemma follows from the fact that we can check the correctness of any Boolean circuit computation using a CNF formula. In particular, we define a variable associated with each wire in the circuit, and construct a constant-size CNF associated with each gate in the circuit (checking that the gate is implemented correctly). The conjunction of all of these gate-by-gate CNFs gives a CNF for the overall circuit. For notational convenience, we drop the $\lambda$ subscripts in the description below. We now define a systematic PEI-PRF $(\mathsf {E}_\lambda ,\mathsf {V}_\lambda ,\mathsf {F}_\lambda )$ as follows:

• $\mathsf {E}(x') \rightarrow (x, w)$: On input a point $x' \in \mathcal {X}'$, output $(\mathsf {E}^*(x'), w)$, where w is the set of all of the wire values for the Boolean circuit computing $\mathsf {E}^*(x')$. Specifically, we can write $w = x' \Vert w'$, where $x'$ is the input to $\mathsf {E}^*$ and $w'$ contain the internal (and output) wire values of $\mathsf {E}^*(x')$.

• $\mathsf {V}(x, w) \rightarrow \{0,1\}$: On input an encoded input $x \in \mathcal {X}$ and a witness $w \in \mathcal {W}$, the verification algorithm interprets $w = x' \Vert w'$. Then, it invokes the CNF verification procedure (for checking correct computation of $\mathsf {E}^*$) to check that $\mathsf {E}^*(x') = (x, w)$.

• $\mathsf {F}(k, x,w) \rightarrow y$: On input the key $k \in \mathcal {K}$, an encoded input $x \in \mathcal {X}$, and a witness $w \in \mathcal {W}$, the evaluation algorithm outputs $y \leftarrow \mathsf {F}^*(k,x)$ if $V(x,w) = 1$, and $\bot$ otherwise. This can be implemented by computing an $\mathsf {AND}$ between the output of $\mathsf {V}(x,w)$ and $\mathsf {F}^*(k, x)$.

Since the verification algorithm $\mathsf {V}$ can be expressed as a CNF formula, and moreover, both $\mathsf {F}^*$ and CNFs can be computed by a circuit of depth $d > 2$, the evaluation algorithm $\mathsf {F}$ can be implemented by a circuit of depth $d + 1$.

6.2 Applications of (P)EI-PRFs

Certainly, we can instantiate any application of strong PRFs using an EI-PRF, since EI-PRFs are PRFs if we consider the combination of the encoding and the evaluation functions. However, we note here that our notions of EI-PRFs and PEI-PRFs allow us to obtain interesting alternative instantiations of many of the classic applications of PRFs. We provide details on the constructions and proofs in the full version.

Theorem 6.5

(Symmetric Low-Depth Primitives). Let $\mathcal {C}$ be a class of circuits. Then, if there exists an EI-PRF computable in $\mathcal {C}$, there exists a symmetric encryption scheme with decryption in $\mathcal {C}$ (assuming $\mathcal {C}$ is closed under composition with 2-bit $\mathsf {XOR}$). Similarly, if there exists a systematic PEI-PRF computable in $\mathcal {C}$, there exists a MAC with verification in $\mathcal {C}$ (assuming $\mathcal {C}$ is closed under composition with equality testing). Together, this yields a CCA-secure symmetric encryption scheme (in fact, an authenticated encryption scheme [12]) with decryption in $\mathcal {C}$.

6.3 Candidate Constructions of (P)EI-PRFs

In the full version, we give a heuristic construction of PEI-PRFs from weak-PRFs in the random oracle model. This construction is primarily of conceptual interest and follows from some basic observations on the connection between weak PRFs and strong PRFs [40]. We also propose a candidate PEI-PRF based on our mod-2/mod-3 weak PRF candidate (Construction 3.1) that remains MPC-friendly. We briefly describe our candidate below.

(P)EI-PRF from our candidate. At a high level, the adaptive attack on our weak PRF candidate (based on [14], see the full version) relies on querying inputs that are close (in terms of Hamming distance) and on the fact that each component of the input of the second mapping (i.e. the components of $\mathbf {A}x$) can be computed by a read-once computation (by some automaton to be precise). This suggests that using a code with large minimal distance to encode the input x should prevent this attack. For MPC-friendliness, we would like to use a linear code, as verifying that an input is a valid codeword can be done efficiently (by multiplying by the parity-check matrix for the code).

A natural candidate is to use a linear code $(\mathbf {G},\mathbf {H})$ over $\mathbb {Z}_2$: the encoding of an input $x'$ is the codeword $\mathbf {G}\cdot x'$. Unfortunately, the same attack still applies since we can always view the PRF evaluation as $\mathbf {A}\cdot (\mathbf {G}\cdot x') = (\mathbf {A}\cdot \mathbf {G}) \cdot x'$ and interpret $(\mathbf {A}\cdot \mathbf {G})$ as the key. To defend against this, we instead use a linear code over $\mathbb {Z}_3$ and define the encoded bitstring x to be the binary representation of the codeword obtained by applying the code to $x'$ (where we interpret $x' \in \{0,1\}^{n'}$ as a vector over $\mathbb {Z}_3$). By mixing mod-2 and mod-3 operations, the encoding procedure becomes non-linear, but verification can still be expressed as a linear function. At the same time, the use of the linear code ensures that (1) encoded inputs are far from each other, (2) verification is MPC-friendly as the code is linear, and (3) the input of the second mapping cannot be expressed as a read-once computation. We give the full description in the the full version.

Remark 6.6

(Candidate Strong PRF in Depth-3 $\mathsf {ACC}^0[2,3]$). Our candidate EI-PRF gives a strong PRF candidate if we consider the composition of the encoding function $\mathsf {E}$ with the evaluation function $\mathsf {F}$. In fact, since the encoding function $\mathsf {E}$ computes a linear function over $\mathbb {Z}_3$, it can be computed by a depth-1 $\mathsf {ACC}^0[3]$ circuit. As noted in Remark 3.9, the PRF evaluation function $\mathsf {F}$ can be computed by a depth-2 $\mathsf {ACC}^0[2,3]$ circuit. Thus, the composition of $\mathsf {E}$ and $\mathsf {F}$ can be computed by a depth-3 $\mathsf {ACC}^0$ circuit (note that the binary decomposition in the encoding function is easily handled via fan-in and does not increase the depth of the circuit). Thus, our construction gives a candidate strong PRF in depth-3 $\mathsf {ACC}^0[2,3]$.

Remark 6.7

(Asymptotically-Optimal PRFs and Natural Proof Barriers). As we note in Remark 6.6, our candidate EI-PRF gives a strong PRF candidate if we consider the composition of the encoding function $\mathsf {E}$ with the evaluation function $\mathsf {F}$. If both $\mathsf {E}$ and $\mathsf {F}$ can be computed by a circuit of linear size (in the length of the key and input), then we obtain a candidate strong PRF with exponential security that can be computed by linear-size circuits. This gives an “asymptotically optimal” PRF that rules out natural proofs of super-linear circuit lower bounds in the sense of Razborov and Rudich [47]. We now describe a variant of our EI-PRF that gives the first candidate instantiation of an asymptotically-optimal PRF, and correspondingly, the first natural proof barrier for proving super-linear circuit lower bounds.

Evaluating our EI-PRF candidate consists of three main steps: encoding the input over $\mathbb {Z}_3$, computing the binary decomposition of the encoded vector, and then multiplying the encoded input with the secret key $\mathbf {A}$ over $\mathbb {Z}_2$. If we instantiate the $\mathbb {Z}_3$-encoding with a linear-time encodable code over $\mathbb {Z}_3$ and then replace the key $\mathbf {A}$ with the generator matrix of a linear-time encodable code over $\mathbb {Z}_2$, then the resulting construction can be computed by a linear-size circuit. For instance, we can instantiate the code with the linear-time encodable code family proposed by Druk and Ishai [24] (building on the hash function from [33]). This family gives a randomized construction of a linear-time encodable code that has many of the combinatorial properties of a random linear code. Thus, we conjecture that sampling the key to be the generator matrix of a Druk-Ishai code does not compromise the security of our candidate. Putting these pieces together, we obtain a plausible candidate of a strong PRF with exponential security and which can be computed by a linear-size circuit. As far as we know, this is the first candidate instantiation of such an asymptotically-optimal strong PRF. Assuming it is indeed exponentially secure, natural proof techniques cannot prove super-linear circuit lower bounds.

Conclusions. We believe that the conjectures we have made in this section are strong and a healthy dose of skepticism is warranted. We hope that the applications and implications we point out will motivate further study and constructions of (P)EI-PRFs, as well as additional cryptanalysis of our concrete candidates. We also leave open the question of setting concrete parameters for our new PEI-PRF and strong PRF candidates (Remark 6.6).