Keywords

1 Introduction

Recovering 3D scenes from monocular RGB-only images is a significantly challenging problem in Computer Vision. Under the rigidity assumption, Structure-from-Motion (SfM) methods provide the theoretical basis for the solution in static environments. Nonetheless, this assumption renders invalid for deforming scenes as most medical imaging scenarios. In the case of the non-rigid scenes the theoretical foundations are not yet well defined.

We can distinguish two types of algorithms that manage non rigid 3D reconstruction: Non-Rigid Structure-from-Motion (NRSfM), which are mostly batch processes, and Shape-from-Template (SfT), which work frame-to-frame. The main difference between these methods is that NRSfM learns the deformation model from the observations while SfT assumes a previously defined deformation model to estimate the deformation for each image.

Rigid methods like Visual SLAM (Simultaneous Localisation and Mapping) have made headway to work sequentially with scenes bigger than the camera field of view [7, 8, 13, 16]. Meanwhile, non-rigid methods are mostly focused on reconstructing structures which are entirely imaged and tracked, for example, surfaces, [6, 17, 24], faces [2, 4, 20, 25], or articulated objects [15, 23].

We conceive the first real-time tracking thread integrated in a SLAM system that can locate the camera and estimate the deformation of the surface based on top of a SfT algorithm following [3, 17, 21, 24]. Our method includes automatic data association and PnP + RANSAC relocalisation algorithm. We code the deformable map as a template which consists of a mesh with a deformation model. Our template is represented as a 3D surface triangular mesh with spatial and temporal regularisers that are rotation and translation invariant. We have selected it because it is suitable for implementing physical models and with barycentric coordinates we can relate the observations with the template.

We evaluate our algorithm with experimental validation over real data both for camera location and scene deformation. This is the first work that focuses on recovering the deformable 3D just from partial images. Thus, we have created a new dataset to experiment with partially-imaged template for sake of future comparison.

2 Problem Formulation

2.1 Template Definition

We code the deformable structure of the scene as a known template \(\mathcal {T} \subset \mathbb {R}^{3}\). The template is modelled as a surface mesh composed of planar triangular facets \(\mathcal {F}\) that connect a set of nodes \(\mathcal {V}\). The facet f is defined in the frame i by its three nodes \(V_{f_j}^{i} = \{V_{f,h}^{i}\}\;\; h=1\ldots 3\). The mesh is measured through observable points \(\mathcal {X}\) which lie inside the facets. To code a point \(X_j \in \mathcal {X}\) in frame i wrt. its facet \(f_j\) nodes, we use a piecewise linear interpolation through the barycentric coordinates \(\mathbf {b}_{j}=\left[ b_{j,1}, b_{j,2} ,b_{j,3}\right] ^\top \) by means of the function \(\varphi :[\mathbb {R}^{3},\mathbb {R}^{3x3}] \rightarrow \mathbb {R}^{3}\):

$$\begin{aligned} \mathbf {X}_{j}^{i} = \varphi ({\mathbf {b}}_{j},\mathbf {V}_{f_j}^{i}) = \sum _{h=1}^3 b_{j,h} \mathbf {V}_{f_j,h}^{i} \end{aligned}$$
(1)

The camera is assumed projective, the observable point \(\mathbf {X}_{j}^{i} \in \mathcal {T}\) defined in \(\mathbb {R}^{3}\) is viewed in the frame i with the camera located in the pose \(\mathbf {T}_i\) through the projective function \(\pi :[\text{ Sim }\left( 3\right) ,\mathbb {R}^3] \rightarrow \mathbb {R}^{2}\).

$$\begin{aligned} \pi \left( \mathbf {T}_{i},\mathbf {X}_{j}^{i}\right)= & {} \left[ \begin{array}{c}f_{u}\frac{x_{j}^{i}}{z_{j}^{i}}+c_{u}\\ f_{v}\frac{y_{j}^{i}}{z_{j}^{i}}+c_{v}\end{array}\right] \end{aligned}$$
(2)
$$\begin{aligned} \left[ \begin{array}{ccc} x_{j}^{i}&y_{j}^{i}&z_{j}^{i}\end{array}\right] ^T= & {} \mathbf {R}^i \mathbf {X}_{j}^{i} + \mathbf {t}^i \end{aligned}$$
(3)

Where \(\mathbf {R}^{i} \in SO(3)\) and \(\mathbf {t}^i \in \mathbb {R}^3\) are respectively the rotation and the translation of the transformation \(\mathbf {T}_i\) and \(\left\{ f_{u},f_{v},c_{u},c_{v}\right\} \) are the focal lengths and the principal point that define the projective calibration for the camera. The algorithm works under the assumption of previously knowing the template. This is a common assumption of template methods. We effectively compute it by means of a rigid VSLAM algorithm [16]. We initialise the template from a 3D reconstruction of the shape surface at rest. We use Poisson surface reconstruction as it is proposed in [12] to construct the template triangular mesh from the sparse point cloud. Once the template is generated, only cloud points which lie close to a facet are retained and then projected into the mesh facets where their barycentric coordinates are computed.

3 Optimisation

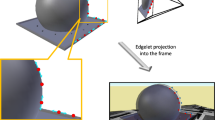
We recover the camera pose and the deformation only in the template region detected by the camera. We define the observation region, \(\mathcal {O}_i\), as the template nodes belonging to a facet with one or more matched observations in the current image i. We dilate the \(\mathcal {O}_i\) region with a layer that we call thickening layer, \(\mathcal {K}_i\) whose thickness is \(d_\mathcal {K}\). We call the template region estimated in the local step local map, \(\mathcal {L}_i\). It is defined as \(\mathcal {L}_i =\mathcal {O}_i\cup \mathcal {K}_i\) (Fig. 1).

Fig. 1.
figure 1

Left: Two step region definition for the case of three observations inside two unconnected facets. \(d_\mathcal {K}=1\) for the thickening \(\mathcal {K}_i\). Right: Ring of neighbours \(\mathcal {N}_k\) of the node K.

Full size image

We propose the next optimisation to recover both the camera pose \(T_{i}\) and the position of the local map nodes \(V_{k}^{i} \in \mathcal {L}_i\), in frame i:

$$\begin{aligned} \underset{T_{i},V_{k}^{i} \in \mathcal {L}_i}{\arg \min }&\frac{1}{N_\bullet }\sum _{j} \rho \left( \left\| \pi _i\left( T_{i}, \varphi ({\mathbf {b}}_{j},V_{f_j}^{i})\right) - x_{j}^{i}\right\| ^2 \right) \nonumber \\&+ \frac{\lambda _d}{N_\bullet } \sum _k \sum _{l \in \mathcal {N}_k}\left( \frac{\left\| V_{k}^{i}-V_{l}^{i}\right\| -\left\| V_{k}^{0}-V_{l}^{0}\right\| }{\left\| V_{k}^{0}-V_{l}^{0}\right\| }\right) ^2 \nonumber \\&+ \frac{\lambda _L}{N_\bullet } \sum _k \left( \Vert \delta _{k}^{i}\Vert -\Vert \delta _{k}^{0}\Vert \right) ^2\sum _{l \in \mathcal {N}_k}\frac{1}{\left\| V_{k}-V_{l}\right\| ^2} \\&+ \frac{\lambda _T}{SN_\bullet } \sum _k \left\| V_{k}^{i} -V_{k}^{i-1}\right\| \nonumber \end{aligned}$$
(4)

The weights of the regularisers \(\lambda _L,\lambda _d, \lambda _t\) are defined with respect to a unit weight for the data term. Additionally, we consider different normalisation factors to correct the final weight assigned to each term. We consider a correction depending on the number of addends, denoted as \(N_\bullet \), in the summation of the corresponding regularising term and a scale correction for the temporal term.

The nodes not included in the optimisation, whose position is fixed, \(V_k^i \in \left\{ \mathcal {T}\setminus \mathcal {L}_i\right\} \), are linked with those optimised, hence they are acting as boundary conditions. As a consequence most of the rigid motion between the camera and the template is included in the camera motion estimate \(\mathbf {T}_i\).

The regularisers code our deformation model, they are inspired in continuum mechanics where bodies deform generating internal energies due to normal strain and shear strain. The first term is the Cauchy or engineering strain:

$$\begin{aligned} \sum _k \sum _{l \in \mathcal {N}_k}\left( \frac{\left\| V_{k}^{i}-V_{l}^{i}\right\| -\left\| V_{k}^{0}-V_{l}^{0}\right\| }{\left\| V_{k}^{0}-V_{l}^{0}\right\| }\right) ^2 \end{aligned}$$
(5)

It penalises the normal strain energy. Per each node \(V_k^i\) we consider a summation over the ring of its neighbours \(N_k\). Per each neighbour the deformation energy is computed as proportional to the squared ratio between the distance increment and the distance at rest. Unlike other isometry or inextensibility regularisers, [10, 17], it is a dimensionless magnitude, invariant with respect to the facet size. Per each node \(V_k^i\) we consider its ring of neighbours \(\mathcal {N}_k\) in the computation.

The second regulariser is the bending energy:

$$\begin{aligned} \sum _k \left( \Vert \delta _{k}^{i}\Vert -\Vert \delta _{k}^{0}\Vert \right) ^2\sum _{l \in \mathcal {N}_k} \frac{1}{\left\| V_{k}-V_{l}\right\| ^2} \end{aligned}$$
(6)

It penalises the shear strain energy. It is coded as the squared ratio between the deflection change and the mean edge length in its ring of neighbours \(\mathcal {N}_k\). We use the ratio in order to get dimensionless magnitude invariant to the facet size. The deflection \(\delta _{k}^{i}\) also represents the mean curvature, it is computed by means of the discrete Laplace-Beltrami operator:

$$\begin{aligned} \delta _{k}^{i} = V_{k}^{i} - \frac{1}{\sum _{l \in \mathcal {N}_j} \omega _l}\sum _{l \in \mathcal {N}_j} \omega _l V_{l}^{i} \end{aligned}$$
(7)

in order to cope with irregular and obtuse meshes, \(\omega _l\) is defined by the so-called mean-value coordinates [9]:

$$\begin{aligned} \omega _l = \frac{\tan (\varOmega _{k,l}^{1}/2)+\tan (\varOmega _{k,l}^{2}/2)}{\left\| V_{k}^{0}-V_{l}^{0}\right\| } \end{aligned}$$
(8)

The \(\varOmega _{k,l}^{1}\) and \(\varOmega _{k,l}^{2}\) angles are defined in Fig. 1.

The last term codes a temporal smoothing between the nodes in \(\mathcal {L}_i\). This term is dimensionless with the term S. This term is the average length of the arcs in the mesh. We optimise with the Levenberg–Marquardt algorithm implemented in the library g2o [14].

4 SLAM Pipeline

To compose the entire tracking thread, we integrate the optimisation in a pipeline with automatic data association working with ORB points, and a DBoW keyframe database [11] that allows relocalisation in case of losing the tracking.

Our optimisation method uses as input the observations of the template points in the current frame. Specifically, multiscale FAST corner to detect the observations, and the ORB descriptor [22] to identify the matches. We apply the classical in VSLAM active matching, that sequentially process the image stream. First, the ORB points are detected in the current image. Next, with a camera motion model, it is predicted the camera pose as a function of the past camera poses. Then the last template estimate and the barycentric coordinates, are used to predict where the template points would be imaged. Around the template point prediction it is defined a search region. Among the ORB points inside the search region, the one with the closest ORB descriptor is selected as the observation. We apply a threshold on the ORB similarity to definitively accept a match. The ORB descriptor of the template point is taken from the template initialisation. The similarity is estimated as the Hamming distance between the ORB descriptors. To reduce the number of false negatives, we cluster the matches according to their geometrical innovation, difference between the predicted template point in the image and the detected one. Only the three main clusters of matches are retained.

As an approach of relocalisation algorithm, we use a relaxed rigid PnP + RANSAC algorithm. We test the original rigid PnP in five thousand images that contain deformation and we got a recall of 26% successful relocalisation, with the relaxed method up to a 49%. The precision in the relocalisation is close to the 100%.

5 Experiments

Comparison with State of the Art SfT. We benchmark our proposal with the standard Kinect paper dataset, to compare the performance of our deformation model with respect to state-of-the-art template-based algorithms. Kinect paper dataset is composed of 193 frames, each frame contains around 1300 observations coming form SIFT points. The matches for the observations are also provided. The ground truth for the matched points are computed from a Kinect RGB-D sensor. The benchmark considers a template that can be fit within the camera field of view. To make an homogeneous comparison we fixed the camera and leave the boundaries of the mesh free. In Table 1 we show the mean RMS error along the sequence compared with respect to some popular methods [3, 6, 18, 19, 24], results are taken from [19]. Ours gets 4.86 mm at 13 ms per frame, what is comparable with the similar state-of-the-art algorithms [18, 24].

Table 1. RMSE averaged over all the frames in the sequence.
Full size table

Experimental Validation. To analyse the performance of our system, we have created the mandala dataset. In this dataset, a mandala blanket is hanged and deformed manually from its back surface, meanwhile a hand-held RGB-D camera closely observes the mandala surface mimicking a scanning movement in circles. Due to the limited field of view of the camera and its proximity to the cloth, the whole mandala is never completely imaged. We run the experiments in a Intel Core i7-7700K CPU @ 4.20 GHz 8 with a 32 GB of RAM memory.

The sequence is composed of ten thousand frames, there is a first part for initialisation where the cloth remains rigid. After that, the level of hardness of the deformation is progressively increased. The video captures from big displacements in different points of the mandala to wrinkled moments and occlusions.

We evaluate the influence of the thickening layer size, \(d_\mathcal {K}\). As result of the experiment, we get a system that can run in real-time and have an RMS error of 2.30%, 2.22%, and 2.32% for \(d_{\mathcal {K}} = 0, 1\) and 2 respectively. When it comes to runtime, the optimisation algorithm is taking 17, 19 and 20 ms, and the total times per frame are 39, 40 and 41 ms. With \(d_{\mathcal {K}} = 1\) we get to reduce the error without increasing excessively the time (Fig. 2).

Fig. 2.
figure 2

From left to right: frames #1347, #2089, #9454, #10739, corresponding to the shape at rest and different deformations. Top: 2D image Bottom: 3D reconstruction

Full size image

6 Discussion

We present a new tracking method able to work in deformable environment incorporating SfT techniques to a SLAM pipeline. We have developed a full-fledged SLAM tracking thread that can robustly operate with an average time budged of 39 ms per frame in very general scenarios with an error under 3% in a real scene and with a relocalisation algorithm with a recall of a 46% in deformable environments with a precision close to the 100%.