Abstract
In recent years, there has been a proliferation of algebraically structured Learning With Errors (LWE) variants, including Ring-LWE, Module-LWE, Polynomial-LWE, Order-LWE, and Middle-Product LWE, and a web of reductions to support their hardness, both among these problems themselves and from related worst-case problems on structured lattices. However, these reductions are often difficult to interpret and use, due to the complexity of their parameters and analysis, and most especially their (frequently large) blowup and distortion of the error distributions.
In this paper we unify and simplify this line of work. First, we give a general framework that encompasses all proposed LWE variants (over commutative base rings), and in particular unifies all prior “algebraic” LWE variants defined over number fields. We then use this framework to give much simpler, more general, and tighter reductions from Ring-LWE to other algebraic LWE variants, including Module-LWE, Order-LWE, and Middle-Product LWE. In particular, all of our reductions have easy-to-analyze and frequently small error expansion; in some cases they even leave the error unchanged. A main message of our work is that it is straightforward to use the hardness of the original Ring-LWE problem as a foundation for the hardness of all other algebraic LWE problems defined over number fields, via simple and rather tight reductions.
This material is based upon work supported by the National Science Foundation under Award CNS-1606362. The views expressed are those of the authors and do not necessarily reflect the official policy or position of the National Science Foundation.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
1.1 Background
Regev’s Learning With Errors (LWE) problem [15] is a cornerstone of lattice-based cryptography, serving as the basis for countless cryptographic constructions (see, for example, the surveys [12, 16]). One primary attraction of LWE is that it can be supported by worst-case to average-case reductions from conjectured hard problems on general lattices [4, 11, 14, 15]. But while constructions based on LWE can have reasonably good asymptotic efficiency, they are often not as practically efficient as one might like, especially in terms of key and ciphertext sizes.
Inspired by the early NTRU cryptosystem [6] and Micciancio’s initial worst-case to average-case reductions for “algebraically structured” lattices over polynomial rings [10], Lyubashevsky, Peikert, and Regev [9] introduced Ring-LWE to improve the asymptotic and practical efficiency of LWE (see also [19]). Ring-LWE is parameterized by the ring of integers in a number field, and [9] supported the hardness of Ring-LWE by a reduction from conjectured worst-case-hard problems on lattices corresponding to ideals in the ring (see also [14]). Since then, several works have introduced and studied a host of other algebraically structured LWE variants—including Module-LWE [1, 3, 7], Polynomial-LWE [18, 19], Order-LWE [2], and Middle-Product LWE [17]—relating them to each other and to various worst-case problems on structured lattices. Of particular interest is the work on Middle-Product LWE (MP-LWE) [17, 18], which, building on ideas from [8], gave a reduction from Ring- or Poly-LWE over a huge class of rings to a single MP-LWE problem. This means that breaking the MP-LWE problem in question is at least as hard as breaking all of huge number of Ring-/Poly-LWE problems defined over unrelated rings.
Thanks to the above-described works, we now have a wide assortment of algebraic LWE problems to draw upon, and a thick web of reductions to support their respective hardness. However, these reductions are often difficult to interpret and use due to the complexity of their parameters, and most especially their effect on the error distributions of the problems. In particular, some reductions incur a rather large blowup and distortion in the error, which is often quite complicated to analyze and bounded loosely by large or even unspecified polynomials. Some desirable reductions, like the one from Ring-LWE to MP-LWE, even require composing multiple hard-to-analyze steps. Finally, some of the reductions require non-uniform advice in the form of special short ring elements that in general do not seem easy to compute.
All this makes it rather challenging to navigate the state of the art, and especially to draw conclusions about precisely which problems and parameters are supported by reductions and proofs. The importance of having a clear, precise view of the landscape is underscored by the fact that certain seemingly reasonable parameters of algebraic LWE problems have turned out to be insecure (ultimately for prosaic reasons); see, e.g., [5, 13] for an overview. This work aims to provide such a view.
1.2 Contributions and Technical Overview
Here we give an overview of our contributions and how they compare to prior works. At a high level, we provide a general framework that encompasses all the previously mentioned LWE variants, and in particular unifies all prior “algebraic” LWE variants defined over number fields. We then use this framework to give much simpler, more general, and tighter reductions from Ring-LWE to other algebraic LWE variants, including Module-LWE, Order-LWE, and Middle-Product LWE. A main message of our work is that it is possible to use the hardness of Ring-LWE as a foundation for the hardness of all prior algebraic LWE problems (and some new ones), via simple and easy-to-analyze reductions.
Generalized (Algebraic) LWE. In Sect. 3 we define new forms of LWE that unify and strictly generalize all previously mentioned ones.
Generalized LWE. First, in Sect. 3.1 we describe a single general framework that encompasses all the previously mentioned forms of LWE, including plain, Ring-, Module-, Poly-, Order-, and Middle-Product LWE (in both “dual” and “primal” forms, where applicable), as well as the unified algebraic LWE we describe below. The key observation is that in all such problems, the secret s, public multipliers a, and their (noiseless) products \(s \cdot a\) respectively belong to some free modules \(M_{s}, M_{a}, M_{b}\) over some commutative ring \({\mathcal {R}}\). Moreover, the products are determined by a fixed \({\mathcal {R}}\)-bilinear map \(T :M_{s} \times M_{a} \rightarrow M_{b}\). An LWE problem involves some fixed choices of these parameters, along with an error distribution. By fixing some \({\mathcal {R}}\)-bases of the modules, the map T can be represented as an order-three tensor (i.e., a three-dimensional array) where \(T_{ijk}\) is the kth coordinate of the product of the ith and jth basis elements of \(M_{s}\) and \(M_{a}\), respectively.
For example, plain LWE uses the \(\mathbb {Z}_q\)-modules \(M_{s}=M_{a}=\mathbb {Z}_q^{n}\) and \(M_{b}=\mathbb {Z}_q\), with the ordinary inner product as the bilinear map, which corresponds to the \(n \times n \times 1\) “identity matrix” tensor. Ring-LWE uses the rank-1 \(R_{q}\)-modules \(M_{s} = M_{b} = R_{q}^{\vee }\) and \(M_{a} = R_{q}\) where \(R={\mathcal {O}}_{K}\) is the ring of integers in a number field K, with field multiplication as the bilinear map, which corresponds to the scalar unity tensor.
We also show how Middle-Product LWE straightforwardly fits into this framework. Interestingly, by a judicious choice of bases, the matrix “slices” \(T_{i\cdot \cdot }\) of the middle-product tensor are seen to form the standard basis for the space of all Hankel matrices. (In a Hankel matrix, the (j, k)th entry is determined by \(j+k\).) This formulation is central to our improved reduction from Ring-LWE over a wide class of number fields to Middle-Product LWE, described in Sect. 1.2 below.
LWE over Number Field Lattices. Next, in Sect. 3.2 we define a unified class of problems that strictly generalizes prior “algebraic” LWE variants defined over number fields, including Ring-, Module-, Poly-, and Order-LWE. A member \(\mathcal {L}\)-\(\mathsf {LWE} \) of our class is parameterized by any (full-rank) lattice (i.e., discrete additive subgroup) \(\mathcal {L}\) of a number field K. Define

to be the set of field elements by which \(\mathcal {L}\) is closed under multiplication; this set is known as the coefficient ring of \(\mathcal {L}\). Letting  denote the dual lattice of \(\mathcal {L}\), it turns out that
denote the dual lattice of \(\mathcal {L}\), it turns out that  , and it is an order of K, i.e., a subring with unity that is also a lattice. Note that if \(\mathcal {L}\) itself is an order \({\mathcal {O}}\) of K or its dual \({\mathcal {O}}^{\vee }\), then \({\mathcal {O}}^{\mathcal {L}} = {\mathcal {O}}\), but in general \(\mathcal {L}\) can be any lattice, and \({\mathcal {O}}^\mathcal {L}\) is just the largest order of K by which \(\mathcal {L}\) is closed under multiplication.Footnote 1
, and it is an order of K, i.e., a subring with unity that is also a lattice. Note that if \(\mathcal {L}\) itself is an order \({\mathcal {O}}\) of K or its dual \({\mathcal {O}}^{\vee }\), then \({\mathcal {O}}^{\mathcal {L}} = {\mathcal {O}}\), but in general \(\mathcal {L}\) can be any lattice, and \({\mathcal {O}}^\mathcal {L}\) is just the largest order of K by which \(\mathcal {L}\) is closed under multiplication.Footnote 1
In all that follows, let \(\mathcal {L}_{q}\) denote the quotient group \(\mathcal {L}/q\mathcal {L}\) for any lattice \(\mathcal {L}\) of K and positive integer q. In \(\mathcal {L}\)-\(\mathsf {LWE} \), there is a secret \(s \in \mathcal {L}^{\vee }_{q}\), and we are given noisy random products
where a is uniformly random, and e is an error term that is drawn from a specified distribution (see below for discussion). Observe that the reduction modulo \(q\mathcal {L}^{\vee }\) is well defined because the (noiseless) product \(s \cdot a \in \mathcal {L}^{\vee }_{q}\), since \(\mathcal {L}^{\vee } \cdot {\mathcal {O}}^{\mathcal {L}} \subseteq \mathcal {L}^{\vee }\) due to \({{\,\mathrm{Tr}\,}}(\mathcal {L}^{\vee } \cdot {\mathcal {O}}^{\mathcal {L}} \cdot \mathcal {L}) \subseteq {{\,\mathrm{Tr}\,}}(\mathcal {L}^{\vee } \cdot \mathcal {L}) \subseteq \mathbb {Z}\).
We now explain how \(\mathcal {L}\)-\(\mathsf {LWE} \) strictly generalizes Ring-, Poly-, and Order-LWE. As already noted, when \(\mathcal {L}={\mathcal {O}}\) or \(\mathcal {L}={\mathcal {O}}^{\vee }\) for an order \({\mathcal {O}}\) of K, we have \({\mathcal {O}}^{\mathcal {L}} = {\mathcal {O}}\), so \(\mathcal {L}\)-\(\mathsf {LWE} \) specializes to:
-
1.
Ring-LWE [9] when \(\mathcal {L}={\mathcal {O}}_{K}\) is the full ring of integers of K;
-
2.
Poly-LWE [18] when \(\mathcal {L}=\mathbb {Z}[\alpha ]^{\vee }\) for some \(\alpha \in {\mathcal {O}}_{K}\); and
-
3.
Order-LWE [2] when \(\mathcal {L}={\mathcal {O}}^{\vee }\) for some arbitrary order \({\mathcal {O}}\) of K.
Notice that in the latter two cases, \(\mathcal {L}\) is the dual of some order, so the secret s and product \(s \cdot a\) belong to the order itself (modulo q). But as we shall see, for reductions it turns out to be more natural and advantageous to let \(\mathcal {L}\) itself be an order, not its dual. Furthermore, \(\mathcal {L}\)-\(\mathsf {LWE} \) also captures other cases that are not covered by the ones above, namely, those for which \(\mathcal {L}\) is not an order or its dual. For \(\mathcal {L}\)-\(\mathsf {LWE} \), we just need the \({\mathcal {O}}^{\mathcal {L}}\)-module structure of \(\mathcal {L}^{\vee }\), not any ring structure.
As mentioned above, \(\mathcal {L}\)-\(\mathsf {LWE} \) is also parameterized by an error distribution. For consistency across problems and with prior work, and without loss of generality, we always view the error distribution in terms of the canonical embedding of K. For concreteness, and following worst-case hardness theorems for Ring-LWE [9, 14], the reader can keep in mind a spherical Gaussian distribution of sufficiently large width \(r = \omega (\sqrt{\log \deg (K)})\) over the canonical embedding. While this differs syntactically from the kind of distribution often considered for Poly-\(\mathsf {LWE} \)—namely, a spherical Gaussian over the coefficient vector of the error polynomial—the two views are interchangeable via some fixed linear transformation. For Gaussians, this transformation just changes the covariance, and if desired we can also add some independent compensating error to recover a spherical Gaussian. However, our results demonstrate some advantages of working exclusively with the canonical embedding, even for Poly-LWE.
Error-Preserving Reduction for \(\varvec{\mathcal {L}}\)-\({\mathbf {\mathsf{{LWE.}}}}\) In Sect. 4 we give a simple reduction from \(\mathcal {L}\)-\(\mathsf {LWE} \) to \(\mathcal {L}'\)-\(\mathsf {LWE} \) for any lattices \(\mathcal {L}' \subseteq \mathcal {L}\) of K for which \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^{\mathcal {L}}\) and the index  is coprime with the modulus q. Essentially, the reduction transforms samples of the former problem (for an unknown secret s) to samples of the latter problem (for a related secret \(s'\)). Importantly, and unlike prior reductions of a similar flavor, our reduction is error preserving: the error distribution over the number field is exactly the same for the two problems. In addition, the reduction is sample preserving: it produces as many samples as it consumes.
is coprime with the modulus q. Essentially, the reduction transforms samples of the former problem (for an unknown secret s) to samples of the latter problem (for a related secret \(s'\)). Importantly, and unlike prior reductions of a similar flavor, our reduction is error preserving: the error distribution over the number field is exactly the same for the two problems. In addition, the reduction is sample preserving: it produces as many samples as it consumes.
The only loss associated with the reduction, which seems inherently necessary, is that when \(\mathcal {L}\ne \mathcal {L}'\), the lattice  by which the resulting noisy products \(b' \approx s' \cdot a'\) are reduced is “denser” than the lattice
by which the resulting noisy products \(b' \approx s' \cdot a'\) are reduced is “denser” than the lattice  by which the original noisy products \(b \approx s \cdot a\) are reduced. One can alternatively see this as the (unchanging) error distribution being “larger” relative to the target lattice than to the original one. This can have consequences for applications, where we typically need the accumulated error from some combined samples to be decodable modulo
by which the original noisy products \(b \approx s \cdot a\) are reduced. One can alternatively see this as the (unchanging) error distribution being “larger” relative to the target lattice than to the original one. This can have consequences for applications, where we typically need the accumulated error from some combined samples to be decodable modulo  . That is, we need to be able to efficiently recover \(e'\) (or at least a large portion of it) from the coset
. That is, we need to be able to efficiently recover \(e'\) (or at least a large portion of it) from the coset  ; standard decoding algorithms require sufficiently short elements of \(q^{-1} \mathcal {L}'\) to do this. So in general, the “sparser” we take \(\mathcal {L}' \subseteq \mathcal {L}\) to be, the denser
; standard decoding algorithms require sufficiently short elements of \(q^{-1} \mathcal {L}'\) to do this. So in general, the “sparser” we take \(\mathcal {L}' \subseteq \mathcal {L}\) to be, the denser  is, and the larger we need q to be to compensate. This weakens both the theoretical guarantees and concrete hardness of the original \(\mathcal {L}\)-\(\mathsf {LWE} \) problem, and is reason to prefer denser \(\mathcal {L}'\).
is, and the larger we need q to be to compensate. This weakens both the theoretical guarantees and concrete hardness of the original \(\mathcal {L}\)-\(\mathsf {LWE} \) problem, and is reason to prefer denser \(\mathcal {L}'\).
Implications and Comparison to Prior Work. Here we describe some of the immediate implications of our reduction, and compare to prior related reductions. Take \(\mathcal {L}={\mathcal {O}}_{K}\) to be the full ring of integers of K, which corresponds to the “master” problem of Ring-LWE, for which we have worst-case hardness theorems [9, 14]. Then these same hardness guarantees are immediately inherited by Order-LWE (and in particular, Poly-LWE) in its “dual” form, by taking \(\mathcal {L}'\) to be an arbitrary order \({\mathcal {O}}\) of K, as long as  is coprime with q. These guarantees are qualitatively similar to the ones established in [2, 18], but are obtained in a much simpler and more straightforward way; in particular, we do not need to replicate all the technical machinery of the worst-case to average-case reductions from [9, 14] for arbitrary orders \({\mathcal {O}}\), as was done in [2].
is coprime with q. These guarantees are qualitatively similar to the ones established in [2, 18], but are obtained in a much simpler and more straightforward way; in particular, we do not need to replicate all the technical machinery of the worst-case to average-case reductions from [9, 14] for arbitrary orders \({\mathcal {O}}\), as was done in [2].
Our reduction can also yield hardness for the “primal” form of Poly-LWE and Order-LWE via a different choice of \(\mathcal {L}'\) (see the next paragraph); however, it is instructive to see why it is preferable to reduce to the “dual” form of these problems. The main reason is that the dual form admits quite natural reductions, both from Ring-LWE and to Middle-Product LWE and Module-LWE, whose effects on the error distribution are easy to understand and bound entirely in terms of certain known short elements of \({\mathcal {O}}\). (See Sect. 1.2 below for further details.)
By contrast, the reduction and analysis for “primal” Order-LWE over order \({\mathcal {O}}\)—including Poly-LWE for \({\mathcal {O}}=\mathbb {Z}[\alpha ]\), as in [18]—is much more complex and cumbersome. Because \({\mathcal {O}}^{\vee } \not \subseteq {\mathcal {O}}_{K}\) (except in the trivial case \(K=\mathbb {Q}\)), we cannot simply take \(\mathcal {L}' = {\mathcal {O}}^{\vee }\). Instead, we need to apply a suitable “tweak” factor \(t \in K\), so that \(\mathcal {L}' = t {\mathcal {O}}^{\vee } \subseteq {\mathcal {O}}_{K}\) and hence  . Reducing to \(\mathcal {L}'\)-\(\mathsf {LWE} \) preserves the error distribution, but to finally convert the samples to primal Order-LWE samples we need to multiply by t, which distorts the error distribution. It can be shown that t must lie in the product of the different ideal of \({\mathcal {O}}_{K}\) and the conductor ideal of \({\mathcal {O}}\) (among other constraints), so the reduction requires non-uniform advice in the form of such a “short” t that does not distort the error too much. The existence proof for such a t from [18] is quite involved, requiring several pages of rather deep number theory. Finally, the decodability of the (distorted) error modulo \(q{\mathcal {O}}\) is mainly determined by the known short vectors in \({\mathcal {O}}^{\vee }\), which also must be analyzed. (All these issues arise under slightly different guises in [18]; in fact, there the error is distorted by \(t^{2}\), yielding an even lossier reduction.)
. Reducing to \(\mathcal {L}'\)-\(\mathsf {LWE} \) preserves the error distribution, but to finally convert the samples to primal Order-LWE samples we need to multiply by t, which distorts the error distribution. It can be shown that t must lie in the product of the different ideal of \({\mathcal {O}}_{K}\) and the conductor ideal of \({\mathcal {O}}\) (among other constraints), so the reduction requires non-uniform advice in the form of such a “short” t that does not distort the error too much. The existence proof for such a t from [18] is quite involved, requiring several pages of rather deep number theory. Finally, the decodability of the (distorted) error modulo \(q{\mathcal {O}}\) is mainly determined by the known short vectors in \({\mathcal {O}}^{\vee }\), which also must be analyzed. (All these issues arise under slightly different guises in [18]; in fact, there the error is distorted by \(t^{2}\), yielding an even lossier reduction.)
Reduction from \(\varvec{{\mathcal {O}}}\)-\({\mathbf {\mathsf{{LWE}}}}\) to \({\mathbf {\mathsf{{MP}}}}\)-\({\mathbf {\mathsf{{LWE.}}}}\) In Sect. 5 we give a simple reduction from \({\mathcal {O}}\)-\(\mathsf {LWE} \), for a wide class of number fields K and orders \({\mathcal {O}}\) including polynomial rings of the form \({\mathcal {O}}=\mathbb {Z}[\alpha ] \cong \mathbb {Z}[x]/f(x)\), to a single Middle-Product LWE problem. Together with the error-preserving reduction described above, this yields a Ring/MP-LWE connection similar to the one obtained in [17, 18], which implies that breaking the MP-LWE problem in question is at least as hard as breaking all of a wide class of Ring-LWE problems over unrelated number fields. However, our result subsumes the prior one by being simpler, more general, and tighter: it drops certain technical conditions on the order, and the overall distortion in the error distribution (starting from Ring-LWE) is given entirely by the spectral norm  of a certain known basis \(\vec {p}\) of \({\mathcal {O}}\). In particular, spherical Gaussian error over the canonical embedding of \({\mathcal {O}}\) translates to spherical Gaussian MP-LWE error (over the reals) that is just a
of a certain known basis \(\vec {p}\) of \({\mathcal {O}}\). In particular, spherical Gaussian error over the canonical embedding of \({\mathcal {O}}\) translates to spherical Gaussian MP-LWE error (over the reals) that is just a  factor wider. These advantages arise from the error-preserving nature of our \(\mathcal {L}\)-\(\mathsf {LWE} \) reduction (described above), and the judicious use of dual lattices in the definition of \({\mathcal {O}}\)-\(\mathsf {LWE} \).
factor wider. These advantages arise from the error-preserving nature of our \(\mathcal {L}\)-\(\mathsf {LWE} \) reduction (described above), and the judicious use of dual lattices in the definition of \({\mathcal {O}}\)-\(\mathsf {LWE} \).
At heart, what makes our reduction work is the hypothesis that the order \({\mathcal {O}}\) has a “tweaked” power basis \(\vec {p} = t \cdot (x^{i})\) for some \(t,x \in {\mathcal {O}}\); clearly any monogenic order \({\mathcal {O}}=\mathbb {Z}[\alpha ]\) has such a basis (with tweak factor \(t=1\)), but it seems plausible that some non-monogenic orders may have such bases as well.Footnote 2 Using our generalized LWE framework from Sect. 3.1 (described above in Sect. 1.2), we show that when using a tweaked power basis \(\vec {p}\) and its dual \(\vec {p}^{\vee }\) for \({\mathcal {O}}\) and \({\mathcal {O}}^{\vee }\) respectively, all the “slices” \(T_{i \cdot \cdot }\) of the tensor T representing multiplication \({\mathcal {O}}^{\vee } \times {\mathcal {O}} \rightarrow {\mathcal {O}}^{\vee }\) are Hankel matrices. So, using the fact that the slices \(M_{i\cdot \cdot }\) of the middle-product tensor M form the standard basis for the space of all Hankel matrices, we can transform \({\mathcal {O}}\)-\(\mathsf {LWE} \) samples to \({\mathsf {MP\text {-}LWE}}\) samples. The resulting MP-LWE error distribution is simply the original error distribution represented in the \(\vec {p}^{{\vee }}\) basis, which is easily characterized using the geometry of \(\vec {p}\).
The above perspective is helpful for finding other reductions from wide classes of LWE problems to a single LWE problem. Essentially, it suffices that all the slices \(T_{i \cdot \cdot }\) of all the source-problem tensors T over a ring \({\mathcal {R}}\) lie in the \({\mathcal {R}}\)-span of the slices of the target-problem tensor. We use this observation in our final reduction, described next.
Reduction from \(\varvec{{\mathcal {O}}'}\)-\({\mathbf {\mathsf{{LWE}}}}\) to \(\varvec{{\mathcal {O}}}\)-\(\mathbf {Module}\)-\({\mathbf {\mathsf{{LWE}}}}\). Finally, in Sect. 6 we give a reduction establishing the hardness of Module-LWE over an order \({\mathcal {O}}\) of a number field K, based on the hardness of Ring-LWE over any one of a wide class of orders \({\mathcal {O}}'\) of a number field extension \(K'/K\). This is qualitatively analogous to what is known for Middle-Product LWE, but is potentially more beneficial because Module-LWE is easier to use in applications, and is indeed much more widely used in theory and in practice.
A bit more precisely, we give a simple reduction from \({\mathcal {O}}'\)-\(\mathsf {LWE} \), for a wide class of orders \({\mathcal {O}}'\), to a single \({\mathcal {O}}\)-\(\mathsf {LWE} ^{k}\) problem, i.e., rank-k Module-\(\mathsf {LWE} \) over an order \({\mathcal {O}}\). (In \({\mathcal {O}}\)-\(\mathsf {LWE} ^{k}\), the secret \(\vec {s}\) and public multipliers \(\vec {a}\) are simply k-dimensional vectors over their respective domains from \({\mathcal {O}}\)-\(\mathsf {LWE} \), and we are given their noisy inner products.) The only technical condition we require is that \({\mathcal {O}}'\) should be a rank-k free \({\mathcal {O}}\)-module. For example, this is easily achieved by defining \({\mathcal {O}}={\mathcal {O}}[\alpha ] \cong {\mathcal {O}}[x]/f(x)\) for some root \(\alpha \) of an arbitrary degree-k monic irreducible polynomial \(f(x) \in {\mathcal {O}}[x]\). Once again, due to the use of duality in the definition of the problems, the reduction’s effect on the error distribution is very easy to characterize: the output error is simply the trace (from \(K'\) to K) of the input error. In particular, the typical example of spherical Gaussian error in the canonical embedding of \(K'\) maps to spherical Gaussian error in the canonical embedding of K, because the trace just sums over a certain partition of the coordinates.
We point out that our result is reminiscent of, but formally incomparable to, the kind of worst-case hardness theorem given in [7]: there the worst-case problem involves arbitrary rank-k module lattices over \({\mathcal {O}}\), whereas here our source problem is an average-case Order-LWE problem for an order that is a rank-k module over \({\mathcal {O}}\).
2 Preliminaries
In this work, by “ring” we always mean a commutative ring with identity.
2.1 Algebraic Number Theory
Number Fields. An (algebraic) number field K is a finite-dimensional field extension of the rationals \(\mathbb {Q}\). More concretely, it can be written as \(K = \mathbb {Q}( \zeta )\), by adjoining to \(\mathbb {Q}\) some element \(\zeta \) that satisfies the relation \(f ( \zeta ) = 0\) for some irreducible polynomial \(f ( x ) \in \mathbb {Q}[ x ]\). The polynomial f is called the minimal polynomial of \(\zeta \), and the degree of f is called the degree of K, which is denoted by n in what follows.
Trace and Norm. The (field) trace \({{\,\mathrm{Tr}\,}}= {{\,\mathrm{Tr}\,}}_{K / \mathbb {Q}} :K \rightarrow \mathbb {Q}\) and (field) norm \(N = N_{K / \mathbb {Q}} :K \rightarrow \mathbb {Q}\) of \(x \in K\) are the trace and determinant, respectively, of the \(\mathbb {Q}\)-linear transformation on K (viewed as a vector space over \(\mathbb {Q}\)) representing multiplication by x. More concretely, fixing any \(\mathbb {Q}\)-basis of K lets us uniquely represent every element of K as a vector in \(\mathbb {Q}^{n}\), and multiplication by any \(x \in K\) corresponds to multiplication by a matrix \(M_{x} \in \mathbb {Q}^{n \times n}\); the trace and norm of x are respectively the trace and determinant of this matrix.
Lattices and Duality. For the purposes of this work, a lattice \(\mathcal {L}\) in K is a discrete additive subgroup of K for which \({{\,\mathrm{span}\,}}_{\mathbb {Q}}(\mathcal {L})=K\). A lattice is generated as the integer linear combinations of n basis elements \(\vec {b} = (b_{1}, \ldots , b_{n}) \in K^{n}\), as  ; in other words, \(\mathcal {L}\) is a free \(\mathbb {Z}\)-module of rank n. For convenience, we let \(\mathcal {L}_{q}\) denote the quotient group \(\mathcal {L}/q\mathcal {L}\) for any positive integer q.
; in other words, \(\mathcal {L}\) is a free \(\mathbb {Z}\)-module of rank n. For convenience, we let \(\mathcal {L}_{q}\) denote the quotient group \(\mathcal {L}/q\mathcal {L}\) for any positive integer q.
For any two lattices \(\mathcal {L}, \mathcal {L}' \subset K\), their product \(\mathcal {L}\cdot \mathcal {L}'\) is the set of all integer linear combinations of terms \(x \cdot x'\) for \(x \in \mathcal {L}, x' \in \mathcal {L}'\). This set is itself a lattice, and given bases for \(\mathcal {L}, \mathcal {L}'\) we can efficiently compute a basis for \(\mathcal {L}\cdot \mathcal {L}'\) via the Hermite normal form.
For a lattice \(\mathcal {L}\), its dual lattice \(\mathcal {L}^{\vee }\) (which is indeed a lattice) is defined as

It is easy to see that if \(\mathcal {L}\subseteq \mathcal {L}'\) are lattices in K, then  , and if \(\vec {b}\) is a basis of \(\mathcal {L}\), then its dual basis \(\vec {b}^{\vee } = (b_{1}^{\vee }, \ldots , b_{n}^{\vee })\) is a basis of \(\mathcal {L}^{\vee }\), where \(\vec {b}^{\vee }\) is defined so that \({{\,\mathrm{Tr}\,}}(b_{i} \cdot b_{j}^{\vee })\) is 1 when \(i=j\), and is 0 otherwise. Observe that by definition, \(x = \vec {b}^{t} \cdot {{\,\mathrm{Tr}\,}}(\vec {b}^{\vee } \cdot x)\) for every \(x \in K\).
, and if \(\vec {b}\) is a basis of \(\mathcal {L}\), then its dual basis \(\vec {b}^{\vee } = (b_{1}^{\vee }, \ldots , b_{n}^{\vee })\) is a basis of \(\mathcal {L}^{\vee }\), where \(\vec {b}^{\vee }\) is defined so that \({{\,\mathrm{Tr}\,}}(b_{i} \cdot b_{j}^{\vee })\) is 1 when \(i=j\), and is 0 otherwise. Observe that by definition, \(x = \vec {b}^{t} \cdot {{\,\mathrm{Tr}\,}}(\vec {b}^{\vee } \cdot x)\) for every \(x \in K\).
Orders. An order \({\mathcal {O}}\) of K is a lattice that is also a subring with unity, i.e., \(1 \in {\mathcal {O}}\) and \({\mathcal {O}}\) is closed under multiplication. An element \(\alpha \in K\) is an algebraic integer if there exists a monic integer polynomial f such that \(f(\alpha )=0\). The set of algebraic integers in K, denoted \({\mathcal {O}}_{K}\), is called the ring of integers of K, and is its maximal order: every order \({\mathcal {O}} \subseteq {\mathcal {O}}_{K}\). For any order \({\mathcal {O}}\) of K, we have \({\mathcal {O}} \cdot {\mathcal {O}}^{\vee } = {\mathcal {O}}^{\vee }\) because \({\mathcal {O}}^{\vee } = 1 \cdot {\mathcal {O}}^{\vee } \subseteq {\mathcal {O}} \cdot {\mathcal {O}}^{\vee }\) and \({{\,\mathrm{Tr}\,}}(({\mathcal {O}} \cdot {\mathcal {O}}^{\vee }) \cdot {\mathcal {O}}) = {{\,\mathrm{Tr}\,}}({\mathcal {O}}^{\vee } \cdot {\mathcal {O}}) \subseteq \mathbb {Z}\), since \({\mathcal {O}} \cdot {\mathcal {O}} = {\mathcal {O}}\).
The Space \(K_{\mathbb {R}}\). In order to formally define Gaussian distributions (see Sect. 2.2 below) we define the field tensor product \(K_{\mathbb {R}} = K \otimes _{\mathbb {Q}} \mathbb {R}\), which is essentially the “real analogue” of \(K/\mathbb {Q}\), obtained by generalizing rational scalars to real ones. In general this is not a field, but it is a ring; in fact, it is isomorphic to the ring product \(\mathbb {R}^{s_{1}} \times \mathbb {C}^{s_{2}}\), where K has \(s_{1}\) real embeddings and \(s_{2}\) conjugate pairs of complex ring embeddings, and \(n=s_{1} + 2s_{2}\). Therefore, there is a “complex conjugation” involution \(\tau :K_{\mathbb {R}} \rightarrow K_{\mathbb {R}}\), which corresponds to the identity map on each \(\mathbb {R}\) component, and complex conjugation on each \(\mathbb {C}\) component.
We extend the trace to \(K_{\mathbb {R}}\) in the natural way, writing \({{\,\mathrm{Tr}\,}}_{K_{\mathbb {R}}/\mathbb {R}}\) for the resulting \(\mathbb {R}\)-linear transform. It turns out that under the ring isomorphism with \(\mathbb {R}^{s_{1}} \times \mathbb {C}^{s_{2}}\), this trace corresponds to the sum of the real components plus twice the sum of the real parts of the complex components. From this it can be verified that \(K_{\mathbb {R}}\) is an n-dimensional real inner-product space, with inner product  . In particular, \(K_{\mathbb {R}}\) has some (non-unique) orthonormal basis \(\vec {b}\), and hence \(\vec {b}^{\vee } = \tau (\vec {b})\).
. In particular, \(K_{\mathbb {R}}\) has some (non-unique) orthonormal basis \(\vec {b}\), and hence \(\vec {b}^{\vee } = \tau (\vec {b})\).
Extension Fields. For the material in Sect. 6 we need to generalize some of our definitions to number field extensions \(K'/K\), where possibly \(K \ne \mathbb {Q}\). The (field) trace \({{\,\mathrm{Tr}\,}}= {{\,\mathrm{Tr}\,}}_{K'/K} :K' \rightarrow K\) and (field) norm \(N = N_{K'/K} :K' \rightarrow K\) of \(x \in K'\) are the trace and determinant, respectively, of the K-linear transformation on \(K'\) (viewed as a vector space over K) representing multiplication by x. We extend the trace to the real inner-product spaces \(K'_{\mathbb {R}}\) and \(K_{\mathbb {R}}\) in the natural way, writing \({{\,\mathrm{Tr}\,}}_{K'_{\mathbb {R}}/K_{\mathbb {R}}}\) for the resulting \(\mathbb {R}\)-linear transform.
Let  be a K-basis of \(K'\). Its dual basis
be a K-basis of \(K'\). Its dual basis  is defined so that
is defined so that  is 1 when \(i=j\), and is 0 otherwise.
is 1 when \(i=j\), and is 0 otherwise.
Lemma 1
Let \(K'/K\) be a number field extension with K-basis \(\vec {b}\), and let  for some \(\vec {x},\vec {y}\) over K. Then
for some \(\vec {x},\vec {y}\) over K. Then  .
.
Proof
Letting \({{\,\mathrm{Tr}\,}}= {{\,\mathrm{Tr}\,}}_{K'/K}\), by K-linearity of \({{\,\mathrm{Tr}\,}}\) we have

We also will need the following standard fact, whose proof is straightforward.
Lemma 2
Let \(K'/K\) be a number field extension, \({\mathcal {O}}\) be an order of K, and \({\mathcal {O}}'\) be an order of \(K'\) that is a free \({\mathcal {O}}\)-module with basis \(\vec {b}\). Then \(\vec {b}^\vee \) is an \({\mathcal {O}}^\vee \)-basis of  .
.
2.2 Gaussians
Here let H be an n-dimensional real inner-product space (e.g., \(H=\mathbb {R}^{n}\) or \(H=K_{\mathbb {R}}\)) and fix an orthonormal basis, so that any element \(x \in H\) may be uniquely represented as a real vector \(\mathbf {x}\in \mathbb {R}^{n}\) relative to that basis.
Definition 1
For a positive definite \(\varSigma \in \mathbb {R}^{n \times n}\), called the covariance matrix, the Gaussian function \(\rho _{\sqrt{\varSigma }} :H \rightarrow \left( 0, 1 \right] \) is defined as  , and the Gaussian distribution \(D_{\sqrt{\varSigma }}\) on H is the one having the normalized probability density function \(\det (\varSigma )^{-1} \cdot \rho _{\sqrt{\varSigma }}\).Footnote 3
, and the Gaussian distribution \(D_{\sqrt{\varSigma }}\) on H is the one having the normalized probability density function \(\det (\varSigma )^{-1} \cdot \rho _{\sqrt{\varSigma }}\).Footnote 3
When \(\varSigma = r^2 \cdot \mathbf {I}\) for some \(r > 0\), we often write \(\rho _r\) and \(D_r\) instead, and refer to these as spherical Gaussians with parameter r. In this case, the choice of orthonormal basis for H is immaterial, i.e., any orthonormal basis yields the same \(\varSigma = r^{2} \cdot \mathbf {I}\).
It is well known that the sum of two independent Gaussians having covariances \(\varSigma _{1}, \varSigma _{2}\) (respectively) is distributed as a Gaussian with covariance \(\varSigma _{1} + \varSigma _{2}\). Therefore, a Gaussian of covariance \(\varSigma \) can be transformed into one of any desired covariance \(\varSigma ' \succ \varSigma \), i.e., one for which \(\varSigma ' - \varSigma \) is positive definite, simply by adding an independent compensating Gaussian of covariance \(\varSigma ' - \varSigma \).
3 Generalized (Algebraic) Learning with Errors
In this section we define new forms of LWE that unify and strictly generalize previous ones. First, in Sect. 3.1 we give an overarching framework that encompasses all LWE variants (over commutative rings) that we are aware of. We employ this framework only in our reductions to MP-LWE and Module-LWE, but expect that it may be useful for other purposes in the future. Then, in Sect. 3.2 we generalize and unify algebraic forms of LWE like Ring-, Order-, and Poly-LWE into a single problem that is merely parameterized by a lattice in a number field.
3.1 Generalized LWE
Here we describe a general framework that captures all variants of Learning With Errors (over commutative rings) that we are aware of, and will be helpful in linking some of them together. Our starting point is the observation that in all such problems, the secret s, public multipliers a, and their “products” \(s \cdot a\) (without noise) all belong to some respective free modules over a particular finite commutative ring \({\mathcal {R}}\). Moreover, the products are determined by a fixed \({\mathcal {R}}\)-bilinear map from (the direct product of) the former two modules to the latter one. As a few examples:
-
Ordinary LWE uses the inner-product map
 , where \(\mathbb {Z}_q^{n}\) and \(\mathbb {Z}_q\) are \(\mathbb {Z}_q\)-modules of ranks n and 1, respectively.
, where \(\mathbb {Z}_q^{n}\) and \(\mathbb {Z}_q\) are \(\mathbb {Z}_q\)-modules of ranks n and 1, respectively. -
Ring-LWE uses the multiplication map \(R^{\vee }_{q} \times R_{q} \rightarrow R^{\vee }_{q}\) where \(R={\mathcal {O}}_{K}\) is a number ring; here \(R^{\vee }_{q}\) and \(R_{q}\) can be seen as \(R_{q}\)-modules of rank one, or as \(\mathbb {Z}_q\)-modules of rank \(n=\deg (R/\mathbb {Z})\).
-
Module-LWE interpolates between the above two cases, using the inner-product map
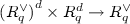 , where here the input modules are of rank d over \(R_{q}\), or rank dn over \(\mathbb {Z}_q\).
, where here the input modules are of rank d over \(R_{q}\), or rank dn over \(\mathbb {Z}_q\).
In general, an LWE variant involves: (1) a finite commutative ring \({\mathcal {R}}\), (2) some finite-rank free \({\mathcal {R}}\)-modules \(M_{s}, M_{a}, M_{b}\), and (3) an \({\mathcal {R}}\)-bilinear map \(T :M_{s} \times M_{a} \rightarrow M_{b}\). The associated LWE problem is concerned with “noisy products” \((a \leftarrow M_{a}, b \approx T(s, a))\) for some fixed \(s \in M_{s}\). Clearly, each bilinear map T (and choice of error distribution) potentially yields a different distribution of noisy products.
By fixing bases for the modules, the map T can be represented via a third-order tensor \(T_{ijk}\) over \({\mathcal {R}}\). Specifically, if we fix bases \(\vec {s}, \vec {a}, \vec {b}\) for \(M_{s}, M_{a}, M_{b}\) (respectively), then \(T_{ijk}\) is the coefficient of \(b_{k}\) in \(T(s_{i}, a_{j}) \in M_{b}\). By bilinearity, the coefficient vector of T(a, s) is the product of the tensor T with the coefficient vectors of a, s along the appropriate dimensions. This naturally generalizes to fixed generating sets in place of bases for \(M_{s}\) and \(M_{a}\) (and even \(M_{b}\), if we do not need a unique representation of the output).
Due to the generality of \({\mathcal {R}}\) and (often desirable) possibility of error distributions over supersets of \(M_{b} \cong {\mathcal {R}}^{l}\) (for some l), we do not give a fully general formal definition of LWE problems in this framework. However, we remark that frequently \({\mathcal {R}} = {\mathcal {O}}_{q}\) for an order \({\mathcal {O}}\) of some number field K, in which case one would usually consider an error distribution over \(K_{\mathbb {R}}^{l}\).
Middle-Product LWE. The Middle-Product LWE (\(\mathsf {MP\text {-}LWE}\)) problem from [17] can be seen as an instance of the above framework, as follows. The middle-product operation \(\odot _{d}\) takes two polynomials of fixed degree bounds, multiplies them together, and outputs only the “middle” d coefficients of the product. More specifically, the product of two polynomials respectively having degrees \(< n+d-1\) and \(< n\) has degree \(< 2n+d-2\); the middle-product discards the lowest and highest \(n-1\) coefficients, and outputs the remaining d coefficients. Middle-Product LWE is concerned with random noisy middle products of a secret polynomial over \(\mathbb {Z}_q\).
To see this in the above framework, define \(M_{s} = \mathbb {Z}_q^{n+d-1}\) and \(M_{a} = \mathbb {Z}_q^{n}\), which we respectively identify with the \(\mathbb {Z}_q\)-modules \(\mathbb {Z}_q^{< n+d-1}[x]\) and \(\mathbb {Z}_q^{< n}[x]\) of polynomials of degrees \(< n+d-1\) and \(< n\), via the bases \(\vec {s}=(1,x,\ldots , x^{n+d-2})\) and \(\vec {a}=(x^{n-1}, x^{n-2},\ldots , 1)\), respectively. (Basis \(\vec {a}\) is in decreasing order by degree for reasons that will become clear shortly.) Define \(M_{b} = \mathbb {Z}_q^{d}\), which we identify with the \(\mathbb {Z}_q\)-module \(x^{n-1} \cdot \mathbb {Z}_q^{< d}[x]\) via the basis \(\vec {b}=(x^{n-1}, x^{n}, \ldots , x^{n+d-2})\).
The middle-product bilinear form \(M_{s} \times M_{a} \rightarrow M_{b}\) is then represented by the third-order tensor M (which is indexed from zero in all dimensions) defined by
This is because \(s_i \cdot a_j = x^{i} \cdot x^{n-1-j} = x^{(n-1) + (i-j)}\), which equals \(b_{i-j}\) if \(0 \le i-j < d\), and vanishes under the middle product otherwise. Therefore, the “slice” matrix \(M_{i \cdot \cdot }\), obtained by fixing the i coordinate arbitrarily, is the \(n \times d\) rectangular Hankel matrix defined by the standard basis vector \(\mathbf {e}_{i} \in \mathbb {Z}^{n+d-1}\), which is 1 in the ith coordinate and zero elsewhere (again indexing from zero).Footnote 4 Importantly, these \(M_{i \cdot \cdot }\) slices form the standard basis of all \(n \times d\) Hankel matrices.
For the following definitions, let M be the third-order tensor defined above in Eq. (1).
Definition 2
(\(\mathsf {MP\text {-}LWE} \) distribution). Let n, d, q be positive integers and \(\psi \) be a distribution over \(\mathbb {R}^d\). For \(\mathbf {s}\in \mathbb {Z}_q^{n+d-1}\), a sample from the \(\mathsf {MP\text {-}LWE} \) distribution \(C_{n,d,q,\psi } ( \mathbf {s})\) over \(\mathbb {Z}_q^n \times (\mathbb {R}/q\mathbb {Z})^d\) is generated by choosing \(\mathbf {a}\leftarrow \mathbb {Z}_q^n\) uniformly at random, choosing \(\mathbf {e}\leftarrow \psi \), and outputting \(( \mathbf {a}, \mathbf {b}= M(\mathbf {s}, \mathbf {a}) + \mathbf {e}\bmod q\mathbb {Z})\).
Definition 3
(\(\mathsf {MP\text {-}LWE} \) problem, decision). The decision \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ,\ell }\) problem is to distinguish between \(\ell \) samples from \(C_{n,d,q,\psi } ( \mathbf {s})\) for \(\mathbf {s}\leftarrow U (\mathbb {Z}_q^{n+d-1})\), and \(\ell \) samples from  .
.
Definition 4
(\(\mathsf {MP\text {-}LWE} \) problem, search). The search \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ,\ell }\) problem is, given \(\ell \) samples from  for some arbitrary \(\mathbf {s}\in \mathbb {Z}_q^{n+d-1}\), find s.
for some arbitrary \(\mathbf {s}\in \mathbb {Z}_q^{n+d-1}\), find s.
We remark that MP-LWE becomes no harder as d decreases (and the corresponding final coordinate(s) of the error distribution are dropped), because the degree-\((n+d-2)\) monomial of the secret can affect only the monomial of the same degree in the middle product. Therefore, dropping the latter just has the effect of dropping the former. In the tensor M, this corresponds to removing the “slices” \(M_{(n+d-2)\cdot \cdot }\) and \(M_{\cdot \cdot (d-1)}\), which yields the tensor for parameters n and \(d-1\).
3.2 LWE over Number Field Lattices
We now define an algebraic form of LWE that strictly generalizes prior ones including Ring-, Module-, Order-, and Poly-LWE. The key observation is that all these problems arise simply from parameterizing by a suitable lattice in a given number field, and taking the public multipliers to be over the lattice’s coefficient ring (modulo q), which we now define.
Coefficient Ring. For any lattice \(\mathcal {L}\) in a number field K, an \(x \in K\) for which \(x\mathcal {L}\subseteq \mathcal {L}\) is called a coefficient of \(\mathcal {L}\). It turns out that the set of coefficients of \(\mathcal {L}\) is an order of K, and equals  . For elucidation we recall the (easy) proofs of these facts.
. For elucidation we recall the (easy) proofs of these facts.
Definition 5
(Coefficient ring). For a lattice \(\mathcal {L}\) in a number field K, its coefficient ring is defined as

Lemma 3
We have \({\mathcal {O}}^{\mathcal {L}} = {( \mathcal {L}\cdot \mathcal {L}^\vee )}^\vee \). In particular, \(\mathcal {L}\) and \(\mathcal {L}^{\vee }\) have the same coefficient ring \({\mathcal {O}}^{\mathcal {L}} = {\mathcal {O}}^{\mathcal {L}^{\vee }}\), and if \(\mathcal {L}\) is an order \({\mathcal {O}}\) of K or its dual \({\mathcal {O}}^{\vee }\), then \({\mathcal {O}}^{\mathcal {L}} = {\mathcal {O}}\).
Proof
For any \(x \in K\), we have

The final claim follows by recalling that \({\mathcal {O}} \cdot {\mathcal {O}}^{\vee } = {\mathcal {O}}^{\vee }\).
Lemma 4
The coefficient ring \({\mathcal {O}}^{\mathcal {L}}\) is an order of K.
Proof
It is clear that  is a lattice in K (because \(\mathcal {L}\cdot \mathcal {L}^{\vee }\) is), thus we only need to show that it is a subring of K with unity. By definition of \({\mathcal {O}}^{\mathcal {L}}\), we clearly have \(1 \in {\mathcal {O}}^{\mathcal {L}}\). Moreover, for any \(x, y \in {\mathcal {O}}^{\mathcal {L}}\), we have \((x y) \mathcal {L}= x (y\mathcal {L}) \subseteq x\mathcal {L}\subseteq \mathcal {L}\), so \(xy \in {\mathcal {O}}^{\mathcal {L}}\), as desired.
is a lattice in K (because \(\mathcal {L}\cdot \mathcal {L}^{\vee }\) is), thus we only need to show that it is a subring of K with unity. By definition of \({\mathcal {O}}^{\mathcal {L}}\), we clearly have \(1 \in {\mathcal {O}}^{\mathcal {L}}\). Moreover, for any \(x, y \in {\mathcal {O}}^{\mathcal {L}}\), we have \((x y) \mathcal {L}= x (y\mathcal {L}) \subseteq x\mathcal {L}\subseteq \mathcal {L}\), so \(xy \in {\mathcal {O}}^{\mathcal {L}}\), as desired.
An immediate corollary is that \({\mathcal {O}}^{\mathcal {L}} \subseteq {\mathcal {O}}_{K}\), the ring of integers (i.e., maximal order) of K.Footnote 5
\(\varvec{\mathcal {L}}\)-\(\mathsf {LWE} \) Problem. Using the coefficient ring, we now define a general algebraic LWE problem that is parameterized by an arbitrary number-field lattice \(\mathcal {L}\).
Definition 6
(\(\mathcal {L}\)-\(\mathsf {LWE} \) distribution). Let \(\mathcal {L}\) be a lattice in a number field K, \({\mathcal {O}}^{\mathcal {L}}\) be the coefficient ring of \(\mathcal {L}\), \(\psi \) be a distribution over \(K_\mathbb {R}\), and q, k be positive integers. For  , a sample from the \(\mathcal {L}\)-\(\mathsf {LWE} \) distribution \(A_{q,\psi }^{\mathcal {L},k} ( \vec {s} )\) over
, a sample from the \(\mathcal {L}\)-\(\mathsf {LWE} \) distribution \(A_{q,\psi }^{\mathcal {L},k} ( \vec {s} )\) over  is generated by choosing
is generated by choosing  uniformly at random, choosing \(e \leftarrow \psi \), and outputting
uniformly at random, choosing \(e \leftarrow \psi \), and outputting  .
.
Definition 7
(\(\mathcal {L}\)-\(\mathsf {LWE} \) problem, decision). The decision \(\mathcal {L}\)-\(\mathsf {LWE} _{q,\psi ,\ell }^k\) problem is to distinguish between \(\ell \) samples from \(A_{q,\psi }^{\mathcal {L},k} ( \vec {s} )\) where  , and \(\ell \) samples from
, and \(\ell \) samples from  .
.
Definition 8
(\(\mathcal {L}\)-\(\mathsf {LWE} \) problem, search). The search \(\mathcal {L}\)-\(\mathsf {LWE} _{q,\psi ,\ell }^k\) problem is given \(\ell \) samples from \(A_{q,\psi }^{\mathcal {L},k} ( \vec {s} )\) for some arbitrary  , find \(\vec {s}\)
, find \(\vec {s}\)
For both of the above definitions, we often omit k when \(k=1\). Notice that in this case, we have \(s \in \mathcal {L}^\vee _q\), \(a \in {\mathcal {O}}^\mathcal {L}_q\), and a sample from the distribution  has the form
has the form  .
.
The above definitions strictly generalize all prior algebraic LWE variants defined over number fields or polynomial rings. For simplicity, take \(k=1\) (taking \(k>1\) simply yields “Module” analogues of what follows). Recall that if \(\mathcal {L}\) is an order \({\mathcal {O}}\) of K or its dual \({\mathcal {O}}^{\vee }\), then \({\mathcal {O}}^{\mathcal {L}} = {\mathcal {O}}\). Therefore, by taking \(\mathcal {L}= {\mathcal {O}}_{K}\) to be the full ring of integers, we get the Ring-LWE problem as originally defined in [9]. Alternatively, by taking \(\mathcal {L}= {\mathcal {O}}^{\vee }\) we get the “primal” form of Order-LWE over \({\mathcal {O}}\) [2], which corresponds to the Poly-LWE problem [18] when \({\mathcal {O}} = \mathbb {Z}[\alpha ]\) for some \(\alpha \in {\mathcal {O}}_{K}\). By instead taking \(\mathcal {L}= {\mathcal {O}}\), we get a natural “dual” variant of Order-LWE, where the secret s and products \(s \cdot a\) are in \({\mathcal {O}}^{\vee }/q{\mathcal {O}}^{\vee }\); this formulation has advantages in terms of simplicity and tightness of reductions. Finally, by taking \(\mathcal {L}\) to be neither an order nor the dual of an order, we get other problems that are not covered by any of the prior ones.
4 Error-Preserving Reduction from \(\mathcal {L}\)-\(\mathsf {LWE} \) to \(\mathcal {L}'\)-\(\mathsf {LWE} \)
In this section, we present an efficient, deterministic reduction from \(\mathcal {L}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to \(\mathcal {L}'\)-\(\mathsf {LWE} _{q,\psi ,\ell }\), where \(\mathcal {L}' \subseteq \mathcal {L}\) are lattices in a number field K such that \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^{\mathcal {L}}\) and the index  is coprime with q. We stress that the reduction preserves the error distribution \(\psi \) and the number of samples \(\ell \) exactly.
is coprime with q. We stress that the reduction preserves the error distribution \(\psi \) and the number of samples \(\ell \) exactly.
4.1 Helpful Lemmas
Before presenting the main theorem in Sect. 4.2 below, we introduce a couple of helpful lemmas. For any lattices \(\mathcal {L}' \subseteq \mathcal {L}\) in K, the natural inclusion map \(\mathcal {L}'_{q} \rightarrow \mathcal {L}_{q}\) sends \(x + q\mathcal {L}'\) to \(x + q\mathcal {L}\). (This can be seen as the composition of a natural homomorphism and an inclusion map.) The following lemmas give conditions under which maps of this kind are bijections.
Lemma 5
Let \(\mathcal {L}' \subseteq \mathcal {L}\) be lattices in a number field K and let q be a positive integer. Then the natural inclusion map \(h :\mathcal {L}'_q \rightarrow \mathcal {L}_q\) is a bijection if and only if q is coprime with the index  ; in this case, h is efficiently computable and invertible given an arbitrary basis of \(\mathcal {L}'\) relative to a basis of \(\mathcal {L}\).
; in this case, h is efficiently computable and invertible given an arbitrary basis of \(\mathcal {L}'\) relative to a basis of \(\mathcal {L}\).
Because  , the same conclusions hold for the natural inclusion map
, the same conclusions hold for the natural inclusion map  .
.
Proof
Let \(\vec {b}, \vec {b}'\) respectively be some \(\mathbb {Z}\)-bases of \(\mathcal {L}, \mathcal {L}'\) (and hence \(\mathbb {Z}_q\)-bases of \(\mathcal {L}_{q}, \mathcal {L}'_{q}\)). Then \(\vec {b}' = \mathbf {T}\cdot \vec {b}\) for some given square matrix \(\mathbf {T}\). This \(\mathbf {T}\) is integral because \(\mathcal {L}' \subseteq \mathcal {L}\), and we have  . Letting \(\mathbf {x}'\) be the coefficient vector (over \(\mathbb {Z}_q\)) of some arbitrary
. Letting \(\mathbf {x}'\) be the coefficient vector (over \(\mathbb {Z}_q\)) of some arbitrary  , we have
, we have  , so \(\mathbf {x}= \mathbf {T}^{t} \cdot \mathbf {x}'\) is the coefficient vector (over \(\mathbb {Z}_q\)) of \(h(x') \in \mathcal {L}_{q}\) relative to \(\vec {b}\). Moreover, \(\mathbf {x}\) and \(\mathbf {x}'\) are in bijective correspondence if and only if \(\mathbf {T}\) is invertible modulo q, i.e., if
, so \(\mathbf {x}= \mathbf {T}^{t} \cdot \mathbf {x}'\) is the coefficient vector (over \(\mathbb {Z}_q\)) of \(h(x') \in \mathcal {L}_{q}\) relative to \(\vec {b}\). Moreover, \(\mathbf {x}\) and \(\mathbf {x}'\) are in bijective correspondence if and only if \(\mathbf {T}\) is invertible modulo q, i.e., if  is coprime with q, and we can efficiently evaluate and invert this bijection given \(\mathbf {T}\).
is coprime with q, and we can efficiently evaluate and invert this bijection given \(\mathbf {T}\).
Lemma 6
Let \(\mathcal {L}' \subseteq \mathcal {L}\) be lattices in a number field K, and let q be a positive integer that is coprime with the index  . If \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^\mathcal {L}\), then the natural inclusion map \(g :{\mathcal {O}}^{\mathcal {L}'}_q \rightarrow {\mathcal {O}}^\mathcal {L}_q\) is a bijection.
. If \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^\mathcal {L}\), then the natural inclusion map \(g :{\mathcal {O}}^{\mathcal {L}'}_q \rightarrow {\mathcal {O}}^\mathcal {L}_q\) is a bijection.
Proof
Let \(h :\mathcal {L}'_{q} \rightarrow \mathcal {L}_{q}\) be the natural inclusion map, which by Lemma 5 is a bijection. First, notice that for any \(a \in {\mathcal {O}}^{\mathcal {L}'}_q\) and \(x \in \mathcal {L}'_q\), we have \(h(a \cdot x) = g(a) \cdot h(x)\). This is because

Now, let \(a,b \in {\mathcal {O}}^{\mathcal {L}'}_q\) satisfy \(g(a) = g(b)\). Then for all \(x \in \mathcal {L}'\), we have

Since h is a bijection, it follows that \(a \cdot x = b \cdot x \pmod {q \mathcal {L}'}\) for all \(x \in \mathcal {L}'\). Therefore,

Thus, g is injective. Since the sets \({\mathcal {O}}^{\mathcal {L}'}_q\) and \({\mathcal {O}}^\mathcal {L}_q\) have the same cardinality \(q^{\deg (K/\mathbb {Q})}\), g must bijective.
4.2 Reduction
Theorem 1
Let \(\mathcal {L}' \subseteq \mathcal {L}\) be lattices in a number field K, \(\psi \) be a distribution over \(K_\mathbb {R}\), and q be a positive integer. If \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^\mathcal {L}\) and the natural inclusion map \(g :{\mathcal {O}}^{\mathcal {L}'}_q \rightarrow {\mathcal {O}}^\mathcal {L}_q\) is an efficiently invertible bijection, then there is an efficient deterministic transform which:
-
1.
maps distribution
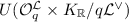 to distribution
to distribution 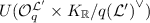 , and
, and -
2.
maps distribution
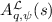 to distribution
to distribution  , where
, where  .
.
Proof
The claimed transform is as follows: for each given sample  , output
, output

It is clear that this transform sends uniformly random a to uniformly random \(a'\), because g is a bijection. Also, since \(\mathcal {L}' \subseteq \mathcal {L}\), we know that  . Therefore, the transform sends uniformly random b to uniformly random \(b'\).
. Therefore, the transform sends uniformly random b to uniformly random \(b'\).
It remains to show that if \(b = a \cdot s + e \bmod {q\mathcal {L}^\vee }\), then  . To see this, observe that \(a = a' \pmod {q {\mathcal {O}}^\mathcal {L}}\), because g is the natural inclusion map. Therefore,
. To see this, observe that \(a = a' \pmod {q {\mathcal {O}}^\mathcal {L}}\), because g is the natural inclusion map. Therefore,

where in the first and third containments we have used \({\mathcal {O}}^{\mathcal {L}} \cdot \mathcal {L}^{\vee } \subseteq \mathcal {L}^{\vee }\) and  , respectively. The claim follows by adding e to both sides.
, respectively. The claim follows by adding e to both sides.
Corollary 1
Adopt the notation from Theorem 1, and assume that  is coprime with q, that \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^{\mathcal {L}}\), and that bases of \(\mathcal {L}', {\mathcal {O}}^{\mathcal {L}'}\) relative to bases of \(\mathcal {L}, {\mathcal {O}}^{\mathcal {L}}\) (respectively) are known. Then there is an efficient deterministic reduction from \(\mathcal {L}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to \(\mathcal {L}'\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) for both the search and decision versions.
is coprime with q, that \({\mathcal {O}}^{\mathcal {L}'} \subseteq {\mathcal {O}}^{\mathcal {L}}\), and that bases of \(\mathcal {L}', {\mathcal {O}}^{\mathcal {L}'}\) relative to bases of \(\mathcal {L}, {\mathcal {O}}^{\mathcal {L}}\) (respectively) are known. Then there is an efficient deterministic reduction from \(\mathcal {L}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to \(\mathcal {L}'\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) for both the search and decision versions.
A main case of interest is when \(\mathcal {L}= {\mathcal {O}}^{\mathcal {L}}\) and \(\mathcal {L}' = {\mathcal {O}}^{\mathcal {L}'}\) are themselves orders, in which case the above coprimality hypothesis is implied by the conductor of \(\mathcal {L}'\) in \(\mathcal {L}\) being coprime with \(q \mathcal {L}\), as ideals of \(\mathcal {L}\). The latter hypothesis is used in [18], so our hypothesis is no stronger.
Proof
We first note that by Lemmas 5 and 6, the natural inclusion maps \(h :\mathcal {L}'_{q} \rightarrow \mathcal {L}_{q}\) and \(g :{\mathcal {O}}^{\mathcal {L}'}_{q} \rightarrow {\mathcal {O}}^{\mathcal {L}}_{q}\) are efficiently computable and invertible bijections. For the decision problems, use the deterministic transform from Theorem 1 to transform the input samples of the \(\mathcal {L}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) problem. This will produce the same number of samples for the \(\mathcal {L}'\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) problem, where uniform samples map to uniform ones, and samples from \(A^{\mathcal {L}}_{q,\psi }(s)\) map to samples from \(A^{\mathcal {L}'}_{q,\psi }(s')\) for  . Also, because h is a bijection, the uniformly random secret \(s \in \mathcal {L}^{\vee }_{q}\) maps to a uniformly random secret
. Also, because h is a bijection, the uniformly random secret \(s \in \mathcal {L}^{\vee }_{q}\) maps to a uniformly random secret  , as needed. For the search problems, it suffices to also note that we can recover the original secret s from \(s'\) by computing \(h^{-1}(s')\).
, as needed. For the search problems, it suffices to also note that we can recover the original secret s from \(s'\) by computing \(h^{-1}(s')\).
5 Reduction from \({\mathcal {O}}\)-\(\mathsf {LWE} \) to \(\mathsf {MP\text {-}LWE} \)
Rosca et al. [17] introduced the Middle-Product LWE (\(\mathsf {MP\text {-}LWE} \)) problem and gave a hardness theorem for it, by showing a reduction from a wide class of Poly-LWE instantiations—and by extension, Ring-LWE instantiations [18]—over various polynomial rings of the form \(\mathbb {Z}[\alpha ] \cong \mathbb {Z}[x]/f(x)\) for f(x) satisfying mild conditions. Here we give a reduction that, when combined with our error-preserving reduction from Sect. 4, subsumes the prior Ring/MP-LWE connection in the simplicity of its descriptions and analysis, and the tightness of its error distortion (or expansion). These advantages arise from our use of \({\mathcal {O}}\)-\(\mathsf {LWE} \) as an intermediate problem, and in particular its use of dual lattices (in contrast to the entirely “primal” nature of Poly-LWE).
5.1 Reduction
We start with a slight generalization of the notion of a power basis, by allowing a “tweak” factor.
Definition 9
For an order \({\mathcal {O}}\) of a number field, a tweaked power basis of \(\mathcal {L}\) is a \(\mathbb {Z}\)-basis \(\vec {p}\) of \({\mathcal {O}}\) of the form \(t \cdot (1, x, x^2, \ldots , x^{d-1})\) for some \(t,x \in {\mathcal {O}}\).
For simplicity, in the rest of this section the reader may wish to focus initially on the case \(d=n\).
Theorem 2
Let \(d \le n\) be positive integers, \({\mathcal {O}}\) be an order of a degree-d number field K with a tweaked power basis \(\vec {p}\), \(\psi \) be a distribution over \(K_\mathbb {R}\), and q be a positive integer. There is an efficient randomized transform which:
-
1.
maps distribution
 to distribution
to distribution 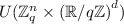 , and
, and -
2.
maps the \({\mathcal {O}}\)-\(\mathsf {LWE} \) distribution \(A_{q,\psi }^{{\mathcal {O}}} ( s )\) to the \(\mathsf {MP\text {-}LWE} \) distribution \(C_{n,d,q,\psi '} ( \mathbf {s}' )\), where \(\mathbf {s}'\) is some fixed linear function (depending only on \(\vec {p}\)) of s, and \(\psi ' = {{\,\mathrm{Tr}\,}}_{K_{\mathbb {R}}/\mathbb {R}}(\psi \cdot \vec {p})\).
In particular, there is an efficient randomized reduction from (search or decision) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to (search or decision, respectively) \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ',\ell }\).
Proof
First, we extend the tweaked power basis \(\vec {p} = t \cdot (x^{i})_{i=0,\ldots ,d-1}\) of \({\mathcal {O}}\) into a tweaked power generating set \(\vec {p}' = t \cdot (x^{i})_{i=0,\ldots ,n-1}\) in the natural way, by including more powers of x (if necessary).
The transform, given a sample \((a, b) \in {\mathcal {O}}_{q} \times K_{\mathbb {R}}/q{\mathcal {O}}^{\vee }\), computes and outputs the (coefficient) vectors

where \(\mathbf {a}\) is a uniformly random solution to  . This can be generated by adding to any particular solution (e.g., the unique one using just the elements of \(\vec {p}\)) a uniformly random element of the subgroup
. This can be generated by adding to any particular solution (e.g., the unique one using just the elements of \(\vec {p}\)) a uniformly random element of the subgroup  (for which we can find a \(\mathbb {Z}_q\)-basis using standard methods). This transform sends uniformly random a to uniformly random \(\mathbf {a}\), since a corresponds to a uniformly random coset of G. In addition, the transform sends uniformly random b to uniformly random \(\mathbf {b}\), because \({{\,\mathrm{Tr}\,}}_{K_{\mathbb {R}}/\mathbb {R}}(b \cdot \vec {p})\) is the coefficient vector of b with respect to \(\vec {p}^{\vee }\), which is a \(\mathbb {Z}\)-basis of \({\mathcal {O}}^{\vee }\), and thus an \(\mathbb {R}\)-basis of \(K_{\mathbb {R}}\).
(for which we can find a \(\mathbb {Z}_q\)-basis using standard methods). This transform sends uniformly random a to uniformly random \(\mathbf {a}\), since a corresponds to a uniformly random coset of G. In addition, the transform sends uniformly random b to uniformly random \(\mathbf {b}\), because \({{\,\mathrm{Tr}\,}}_{K_{\mathbb {R}}/\mathbb {R}}(b \cdot \vec {p})\) is the coefficient vector of b with respect to \(\vec {p}^{\vee }\), which is a \(\mathbb {Z}\)-basis of \({\mathcal {O}}^{\vee }\), and thus an \(\mathbb {R}\)-basis of \(K_{\mathbb {R}}\).
It remains to show that if \(b = s \cdot a + e \bmod {q {\mathcal {O}}^{\vee }}\) for some \(s \in {\mathcal {O}}^{\vee }_q\) and \(e \leftarrow \psi \), then \((\mathbf {a}, \mathbf {b})\) is a properly distributed \(\mathsf {MP\text {-}LWE} \) sample for secret \(\mathbf {s}'\). To do this we use definition of \(\mathsf {MP\text {-}LWE} \) in the generalized LWE framework from Sect. 3.1. Specifically, consider the \(\mathbb {Z}_q\)-bilinear multiplication map \(T :{\mathcal {O}}^{\vee }_{q} \times {\mathcal {O}}_{q} \rightarrow {\mathcal {O}}^{\vee }_{q}\), and consider the generating sets \(\vec {p}^{\vee }, \vec {p}'\) for the \(\mathbb {Z}_q\)-modules \({\mathcal {O}}^{\vee }_{q}, {\mathcal {O}}_{q}\), respectively. Then letting \({{\,\mathrm{Tr}\,}}= {{\,\mathrm{Tr}\,}}_{K/\mathbb {Q}}\), the third-order tensor representing T relative to \(\vec {p}^{\vee }, \vec {p}'\) is given by
where \(g_{j+k} = p'_{j} \cdot p_{k} = t^2 \cdot x^{j+k}\) depends only on \(j+k\).
In particular, each “slice” \(T_{i \cdot \cdot }\) for fixed i is a Hankel matrix, so it can be written as a \(\mathbb {Z}_q\)-linear combination of the slices \(M_{i \cdot \cdot }\) of the tensor for the middle-product bilinear form \(M :\mathbb {Z}_q^{n+d-1} \times \mathbb {Z}_q^{n} \rightarrow \mathbb {Z}_q^{d}\), because these slices form the standard basis for the set of \(n \times d\) Hankel matrices over \(\mathbb {Z}_q\). In other words, there exists a matrix \(\mathbf {P}\in \mathbb {Z}_q^{(n+d-1) \times d}\) such that \(T_{i \cdot \cdot } = \sum _{i'} M_{i' \cdot \cdot } \mathbf {P}_{i' i}\) for all i; specifically, the ith column of \(\mathbf {P}\) is simply the vector defining the Hankel matrix \(T_{i \cdot \cdot }\). Therefore,
where \(\mathbf {s}= {{\,\mathrm{Tr}\,}}(s \cdot \vec {p}) \in \mathbb {Z}_q^{d}\) is the coefficient vector of s with respect to \(\vec {p}^{\vee }\).
Finally, we address the error term. By linearity and the above, we have \(\mathbf {b}= M(\mathbf {P}\mathbf {s}, \mathbf {a}) + \mathbf {e}\bmod q\mathbb {Z}^{d}\) where \(\mathbf {e}= {{\,\mathrm{Tr}\,}}(e \cdot \vec {p})\), which has distribution \(\psi '\) because e has distribution \(\psi \) over \(K_{\mathbb {R}}\).
Notice that for the search and decision reductions, we cannot simply apply the claimed transformation to each input sample, because the resulting distribution on \(\mathbf {s}'\) is not uniform. However, this is easily addressed by the standard technique of re-randomizing the secret, choosing a uniformly random \(\mathbf {r}\in \mathbb {Z}_q^{n+d-1}\) and transforming each given sample \((\mathbf {a}, \mathbf {b})\) to \((\mathbf {a}, \mathbf {b}+ M(\mathbf {r},\mathbf {a}))\). This preserves the uniform distribution in the random case, and maps secret \(\mathbf {s}\) to a uniformly random secret \(\mathbf {s}'+\mathbf {r}\) in the LWE case.
To obtain the claimed search reduction, first apply the above transforms to each input sample of the \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) problem. This produces the same number of samples for the \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ',\ell }\) problem. We can then compute the original secret s from the transformed secret \(\mathbf {s}'+\mathbf {r}\) via \(\mathbf {s}= \mathbf {P}_{L}^{-1} \cdot \mathbf {s}'\), and  where \(\mathbf {P}_{L}^{-1}\) is a left inverse of \(\mathbf {P}\). For the claimed decision reduction, it suffices that the transform also maps uniform samples to uniform samples.
where \(\mathbf {P}_{L}^{-1}\) is a left inverse of \(\mathbf {P}\). For the claimed decision reduction, it suffices that the transform also maps uniform samples to uniform samples.
Corollary 2
Adopt the notation from Theorem 2, and let \({\mathcal {O}}' \subseteq {\mathcal {O}}\) be a suborder which has a known tweaked power basis \(\vec {p}\) and for which  is coprime with q. There is a randomized sample-preserving reduction from \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ',\ell }\), where
is coprime with q. There is a randomized sample-preserving reduction from \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ',\ell }\), where  .
.
Proof
We can reduce \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) to \({\mathcal {O}}'\)-\(\mathsf {LWE} _{q,\psi ,\ell }\) by Corollary 1, and then to \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ',\ell }\) by Theorem 2.
5.2 Managing the Error Distribution
The reduction described in Theorem 2 reduces \({\mathcal {O}}\)-\(\mathsf {LWE} \) with error distribution \(\psi \) to \(\mathsf {MP\text {-}LWE} \) with error distribution  where \(\vec {p}\) is some tweaked power basis of \({\mathcal {O}}\). However, we ultimately want a reduction from many \({\mathcal {O}}\)-\(\mathsf {LWE} \) problems to a single \(\mathsf {MP\text {-}LWE} \) problem, so we need to further control the resulting error distribution. To this end, we consider the usual case where \(\psi \) is a Gaussian distribution over \(K_{\mathbb {R}}\), in which case it turns out that \(\psi '\) is a Gaussian over \(\mathbb {R}^{n}\) whose covariance is related to the Gram matrix of \(\vec {p}\). Moreover, by a standard technique we can add some independent Gaussian error having a compensating covariance to arrive at any desired target covariance that is sufficiently large.
where \(\vec {p}\) is some tweaked power basis of \({\mathcal {O}}\). However, we ultimately want a reduction from many \({\mathcal {O}}\)-\(\mathsf {LWE} \) problems to a single \(\mathsf {MP\text {-}LWE} \) problem, so we need to further control the resulting error distribution. To this end, we consider the usual case where \(\psi \) is a Gaussian distribution over \(K_{\mathbb {R}}\), in which case it turns out that \(\psi '\) is a Gaussian over \(\mathbb {R}^{n}\) whose covariance is related to the Gram matrix of \(\vec {p}\). Moreover, by a standard technique we can add some independent Gaussian error having a compensating covariance to arrive at any desired target covariance that is sufficiently large.
Throughout this section, we use the following notation. Let \({{\,\mathrm{Tr}\,}}= {{\,\mathrm{Tr}\,}}_{K_{\mathbb {R}}/\mathbb {R}}\), and given a tweaked basis \(\vec {p}\) of \({\mathcal {O}}\), let  denote the (positive definite) Gram matrix of \(\vec {p}\), whose (i, j)th entry is
denote the (positive definite) Gram matrix of \(\vec {p}\), whose (i, j)th entry is  . Fix some orthonormal \(\mathbb {R}\)-basis \(\vec {b} = \tau (\vec {b}^{\vee })\) of \(K_\mathbb {R}\), and let
. Fix some orthonormal \(\mathbb {R}\)-basis \(\vec {b} = \tau (\vec {b}^{\vee })\) of \(K_\mathbb {R}\), and let  . Then by \(\mathbb {R}\)-linearity of \(\tau \) and trace, we have
. Then by \(\mathbb {R}\)-linearity of \(\tau \) and trace, we have

For a real matrix \(\mathbf {A}\), let

denote the spectral (or operator) norm of \(\mathbf {A}\); observe that by the above, we have  .
.
Corollary 3
Let \(d \le n\) be positive integers, \({\mathcal {O}}\) be an order of a degree-d number field K with a tweaked power basis \(\vec {p}\), \(\varSigma \in \mathbb {R}^{d \times d}\) be a positive definite matrix, and q be a positive integer. For any \(\varSigma ' \succ \mathbf {P}_b^{t} \cdot \varSigma \cdot \mathbf {P}_b\), there is an efficient randomized reduction from (search or decision) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,D_{\sqrt{\varSigma }},\ell }\) to (search or decision, respectively) \(\mathsf {MP\text {-}LWE} _{n,d,q,D_{\sqrt{\varSigma '}},\ell }\).
In particular, for any  , there is an efficient randomized reduction from (search or decision) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,D_{r},\ell }\) to (search or decision, respectively) \(\mathsf {MP\text {-}LWE} _{n,d,q,D_{r'},\ell }\).
, there is an efficient randomized reduction from (search or decision) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,D_{r},\ell }\) to (search or decision, respectively) \(\mathsf {MP\text {-}LWE} _{n,d,q,D_{r'},\ell }\).
Proof
By applying Theorem 2 we obtain an efficient randomized reduction from \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,D_{\sqrt{\varSigma }},\ell }\) to \(\mathsf {MP\text {-}LWE} _{n,d,q,\psi ',\ell }\), where \(\psi '\) is a distribution over \(\mathbb {R}^{d}\) and is analyzed as follows. Let \(D=D_{\sqrt{\varSigma }}\) be the original error distribution over \(K_{\mathbb {R}}\), which (because \(\vec {b}\) is an orthonormal basis of \(K_{\mathbb {R}}\)) has the form \(D=\vec {b}^{t} \cdot C\) where the coefficient distribution \(C=D_{\sqrt{\varSigma }}\) is a Gaussian over \(\mathbb {R}^{n}\). Then by \(\mathbb {R}\)-linearity of the trace,

where \(\varSigma _1 = \mathbf {P}_b^{t} \cdot \varSigma \cdot \mathbf {P}_b\).
Since \(\varSigma ' \succ \varSigma _1\) by assumption, we may transform the error distribution \(D_{\sqrt{\varSigma _1}}\) to \(D_{\sqrt{\varSigma '}}\) by adding (to the \(\mathbf {b}\)-part of each \(\mathsf {MP\text {-}LWE} \) sample) a fresh error term from the compensating Gaussian distribution of covariance \(\varSigma ' - \varSigma _{1}\). This yields the desired error distribution and completes the proof of the first claim.
For the second claim, notice that if \(\varSigma = r^2 \cdot \mathbf {I}\), then  , because
, because  is positive definite, since
is positive definite, since  for any \(\mathbf {x}\).
for any \(\mathbf {x}\).
5.3 Example Instantiations
Corollary 3 bounds the expansion of the error distribution by the square root of the spectral norm of the Gram matrix \(\mathbf {P}\) of a tweaked power basis \(\vec {p}\) of \({\mathcal {O}}\). Here we show that there are large families of orders with well-behaved power bases (with tweak factor \(t=1\)).
Let \(\alpha \) be an algebraic integer with minimal polynomial \(f(x) \in \mathbb {Z}[x]\) of degree d, and consider the order \({\mathcal {O}} = \mathbb {Z}[\alpha ] \subset K = \mathbb {Q}(\alpha )\), which has power basis  . Consider the Vandermonde matrix
. Consider the Vandermonde matrix
where the \(\alpha _i\) are the d distinct roots of f, i.e., the conjugates of \(\alpha \). This \(\mathbf {V}\) represents the linear transform \(\sigma \) that maps coefficient vectors with respect to \(\vec {p}\) to the canonical (or Minkowski) embedding.
It is easy to see that the Gram matrix of \(\vec {p}\) is \(\mathbf {P}= \mathbf {V}^{*} \mathbf {V}\), where \(\mathbf {V}^{*}\) denotes the conjugate transpose of \(\mathbf {V}\), so  . Therefore, we immediately have the bound
. Therefore, we immediately have the bound  , where the maximum is taken over
, where the maximum is taken over  . That is, the Frobenius and Euclidean norms of the power-basis elements (in the canonical embedding) yield bounds on the error expansion. The following lemma gives an alternative bound directly in terms of the minimal polynomial f(x).
. That is, the Frobenius and Euclidean norms of the power-basis elements (in the canonical embedding) yield bounds on the error expansion. The following lemma gives an alternative bound directly in terms of the minimal polynomial f(x).
Lemma 7
Adopt the above notation, and assume that the minimal polynomial \(f(x) = x^{d} - g(x) \in \mathbb {Z}[x]\), where \(g(x) = a_{k} x^{k} + \cdots + a_{1} x + a_{0}\) has degree at most \(k < d\). Then  where
where  . In particular, if \(k = (1-c) d\) for some \(c \in (0,1)\), then
. In particular, if \(k = (1-c) d\) for some \(c \in (0,1)\), then  .
.
For example, if all the  and \(c < 1\) is any positive constant, then
and \(c < 1\) is any positive constant, then  . This enlarges the set of moduli f(x) yielding polynomial error expansion from those considered in [17].
. This enlarges the set of moduli f(x) yielding polynomial error expansion from those considered in [17].
Proof
We bound  as follows. Let
as follows. Let  be the maximum magnitude of any root of f. Then
be the maximum magnitude of any root of f. Then  . Now, because the \(\alpha _{i}\) satisfy \(\alpha _{i}^{d} = g(\alpha _{i})\), by the triangle inequality we have \(\alpha _{*}^{d} \le \alpha _{*}^{k} \cdot A\) and hence \(\alpha _{*}^{d-k} \le A\). The claim follows by raising to the \(d/(d-k)\) power.
. Now, because the \(\alpha _{i}\) satisfy \(\alpha _{i}^{d} = g(\alpha _{i})\), by the triangle inequality we have \(\alpha _{*}^{d} \le \alpha _{*}^{k} \cdot A\) and hence \(\alpha _{*}^{d-k} \le A\). The claim follows by raising to the \(d/(d-k)\) power.
6 Reduction from \({\mathcal {O}}'\)-\(\mathsf {LWE} \) to \({\mathcal {O}}\)-\(\mathsf {LWE} ^{k}\)
In this section we give a simple reduction from \({\mathcal {O}}'\)-\(\mathsf {LWE} \), for a wide class of orders \({\mathcal {O}}'\), to a single rank-k Module-\(\mathsf {LWE} \) problem over an order \({\mathcal {O}}\).
6.1 Reduction
Theorem 3
Let \(K'/K\) be a number field extension; \({\mathcal {O}}\) be an order of K; \({\mathcal {O}}'\) be an order of \(K'\) that is a rank-k free \({\mathcal {O}}\)-module with known basis \(\vec {b}\); \(\psi '\) be a distribution over \(K'_\mathbb {R}\); and q be a positive integer. Then there is an efficient, deterministic transform which:
-
1.
maps distribution
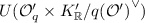 to
to  , and
, and -
2.
maps distribution
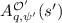 to
to 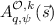 , for
, for 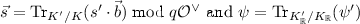 .
.
It immediately follows that there is an efficient, deterministic reduction from (search or decision) \({\mathcal {O}}'\)-\(\mathsf {LWE} _{q,\psi ',\ell }^{1}\) to (search or decision, respectively) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }^{k}\).
Proof
Let \({{\,\mathrm{Tr}\,}}= {{\,\mathrm{Tr}\,}}_{K'_{\mathbb {R}}/K_{\mathbb {R}}}\), which coincides with \({{\,\mathrm{Tr}\,}}_{K'/K}\) on \(K'\). The claimed transform is as follows. Given a sample  , output
, output

Clearly, this transform sends uniformly random \(a' \in {\mathcal {O}}'_q\) to uniformly random \(\vec {a} \in {\mathcal {O}}_q^k\), because \(\vec {b}\) is an \({\mathcal {O}}_q\)-basis of \({\mathcal {O}}'_q\), and  is the coefficient vector of a with respect to this basis. Also, the transform sends uniformly random
is the coefficient vector of a with respect to this basis. Also, the transform sends uniformly random  to uniformly random \(b \in K_\mathbb {R}/ q {\mathcal {O}}^\vee \), because \({{\,\mathrm{Tr}\,}}:K'_\mathbb {R}\rightarrow K_\mathbb {R}\) is a surjective \(K_{\mathbb {R}}\)-linear map and
to uniformly random \(b \in K_\mathbb {R}/ q {\mathcal {O}}^\vee \), because \({{\,\mathrm{Tr}\,}}:K'_\mathbb {R}\rightarrow K_\mathbb {R}\) is a surjective \(K_{\mathbb {R}}\)-linear map and  , since
, since  .
.
What remains to show is that if \(b' = s' \cdot a' + e'\) then  for
for  and \(e={{\,\mathrm{Tr}\,}}(e')\). Observe that
and \(e={{\,\mathrm{Tr}\,}}(e')\). Observe that  and
and  . Therefore, by Lemma 1, we know that
. Therefore, by Lemma 1, we know that  . The claim then follows by linearity of \({{\,\mathrm{Tr}\,}}\).
. The claim then follows by linearity of \({{\,\mathrm{Tr}\,}}\).
To obtain the claimed search reduction, simply apply the above transform to the input samples for the \({\mathcal {O}}'\)-\(\mathsf {LWE} _{q,\psi ',\ell }^1\) problem. This produces the same number of samples for the \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }^k\) problem. It is clear that this maps the uniformly random secret  to uniformly random
to uniformly random  , because \(\vec {b}^\vee \) is an \({\mathcal {O}}^\vee _q\)-basis of
, because \(\vec {b}^\vee \) is an \({\mathcal {O}}^\vee _q\)-basis of  by Lemma 2, and
by Lemma 2, and  is the coefficient vector of s with respect to this basis. Furthermore, we can compute the original secret s from the transformed secret \(\vec {s}\), as
is the coefficient vector of s with respect to this basis. Furthermore, we can compute the original secret s from the transformed secret \(\vec {s}\), as  . For the claimed decision reduction, it is suffices that the transform also maps uniform samples to uniform ones.
. For the claimed decision reduction, it is suffices that the transform also maps uniform samples to uniform ones.
6.2 Managing the Error Distribution
Similarly to our reduction from \({\mathcal {O}}\)-\(\mathsf {LWE} \) to \(\mathsf {MP\text {-}LWE} \) in Sect. 5, we want a reduction from many \({\mathcal {O}}'\)-\(\mathsf {LWE} \) problems to a single \({\mathcal {O}}\)-\(\mathsf {LWE} ^k\) problem. To control the resulting error distribution, we consider the usual case where the original error distribution \(\psi '\) is a Gaussian, in which case it turns out that the resulting error distribution \(\psi \) is also a Gaussian. As in Sect. 5.2, we can add some independent Gaussian error with a compensating covariance to obtain any large enough desired target covariance. Alternatively, when \(\psi '\) is a spherical Gaussian, then \(\psi \) is one as well, with a covariance that is a k factor larger, so no compensating error is needed. (Also note that  can be much denser than \({\mathcal {O}}^{\vee }\)—or seen another way, \({\mathcal {O}}\) can have shorter vectors than \({\mathcal {O}}'\)—so the increase in covariance does not necessarily represent a real loss.)
can be much denser than \({\mathcal {O}}^{\vee }\)—or seen another way, \({\mathcal {O}}\) can have shorter vectors than \({\mathcal {O}}'\)—so the increase in covariance does not necessarily represent a real loss.)
In what follows, let \(K'/K\) be a number field extension, fix some orthonormal \(\mathbb {R}\)-bases  and
and  of \(K'_{\mathbb {R}}\) and \(K_{\mathbb {R}}\) (respectively) for defining Gaussian distributions, and let
of \(K'_{\mathbb {R}}\) and \(K_{\mathbb {R}}\) (respectively) for defining Gaussian distributions, and let  be the real matrix whose (i, j)th entry is
be the real matrix whose (i, j)th entry is  . The proof below shows that \(\mathbf {A}^{t} \cdot \mathbf {A}= k \mathbf {I}\) where \(k = \deg (K'/K)\); by choosing the bases appropriately we can obtain, e.g., \(\mathbf {A}= \mathbf {1}_{k} \otimes \mathbf {I}\) where \(\mathbf {1}_{k} \in \mathbb {Z}^{k}\) is the all-ones vector.
. The proof below shows that \(\mathbf {A}^{t} \cdot \mathbf {A}= k \mathbf {I}\) where \(k = \deg (K'/K)\); by choosing the bases appropriately we can obtain, e.g., \(\mathbf {A}= \mathbf {1}_{k} \otimes \mathbf {I}\) where \(\mathbf {1}_{k} \in \mathbb {Z}^{k}\) is the all-ones vector.
Corollary 4
Adopt the notation and hypotheses of Theorem 3, with \(\psi ' = D_{\sqrt{\varSigma '}}\) over \(K'_{\mathbb {R}}\) for some positive definite matrix \(\varSigma '\). For any \(\varSigma \succ \mathbf {A}^t \cdot \varSigma ' \cdot \mathbf {A}\), there is an efficient, randomized reduction from (search or decision) \({\mathcal {O}}'\)-\(\mathsf {LWE} _{q,D_{\sqrt{\varSigma '}},\ell }^{1}\) to (search or decision, respectively) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,D_{\sqrt{\varSigma }},\ell }^{k}\).
Moreover, for \(r = r' \sqrt{k}\), there is an efficient deterministic reduction from (search or decision) \({\mathcal {O}}'\)-\(\mathsf {LWE} _{q,D_{r'},\ell }^{1}\) to (search or decision, respectively) \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,D_{r},\ell }^{k}\).
Proof
By Theorem 3, there exists an efficient, deterministic reduction from \({\mathcal {O}}'\)-\(\mathsf {LWE} _{q,D_{\sqrt{\varSigma '}},\ell }^{1}\) to \({\mathcal {O}}\)-\(\mathsf {LWE} _{q,\psi ,\ell }^{k}\) where \(\psi \) is a distribution over \(K_\mathbb {R}\) and is analyzed as follows. Let \(D' = D_{\sqrt{\varSigma '}}\) be the original error distribution over \(K'_\mathbb {R}\), which has the form \(D' = \vec {c}'^t \cdot C'\) where the coefficient distribution \(C' = D_{\sqrt{\varSigma '}}\) is a Gaussian over \(\mathbb {R}^{kn}\). Further, let \(\varSigma _1 = \mathbf {A}^t \cdot \varSigma ' \cdot \mathbf {A}\) and let \(D = D_{\sqrt{\varSigma _1}}\) be a Gaussian over \(K_\mathbb {R}\), which has the form \(D = \vec {c}^t \cdot C\) where the coefficient distribution \(C = D_{\sqrt{\varSigma _1}}\) is a Gaussian over \(\mathbb {R}^n\). Then by linearity,

Since \(\varSigma \succ \varSigma _1\) by assumption, we can transform the error distribution \(D_{\sqrt{\varSigma _1}}\) to \(D_{\sqrt{\varSigma '}}\) by adding (to the b-part of each Module-\(\mathsf {LWE}\) sample) a fresh error term from the compensating Gaussian distribution of covariance \(\varSigma ' - \varSigma _{1}\). This yields the desired error distribution and completes the proof of the first claim.
For the second claim, observe that because \(\vec {c}'\) and \(\vec {c}\) are orthonormal,

Therefore, if  and \(\varSigma = r^{2} \cdot \mathbf {I}\), then
and \(\varSigma = r^{2} \cdot \mathbf {I}\), then  , so no compensating error is needed, yielding a deterministic reduction.
, so no compensating error is needed, yielding a deterministic reduction.
6.3 Instantiations
It is straightforward to instantiate Theorem 3 and Corollary 4 to get reductions from a huge class of Order-LWE problems to a single Module-LWE problem. Let \({\mathcal {O}}\) be an arbitrary order of a number field K, and let \(\alpha \) denote some root of an arbitrary monic irreducible degree-k polynomial \(f(X) \in {\mathcal {O}}[X]\). Then we can satisfy the hypotheses of Theorem 3 by letting \(K'=K(\alpha )\) and \({\mathcal {O}}' = {\mathcal {O}}[\alpha ]\), so that  is an \({\mathcal {O}}\)-basis of \({\mathcal {O}}'\). (We emphasize that there are no restrictions on the choice of the algebraic integer \(\alpha \), other than its degree over \({\mathcal {O}}\).) Letting, e.g., \(\psi ' = D_{r}\) be a spherical Gaussian over \(K'_{\mathbb {R}}\) and \(\psi = D_{r\sqrt{k}}\) be the corresponding spherical Gaussian over \(K_{\mathbb {R}}\), we have an efficient, deterministic reduction from \({\mathcal {O}}'\)-\(\mathsf {LWE} ^{1}_{q,\psi ',\ell }\) to \({\mathcal {O}}\)-\(\mathsf {LWE} ^{k}_{q,\psi ,\ell }\).
is an \({\mathcal {O}}\)-basis of \({\mathcal {O}}'\). (We emphasize that there are no restrictions on the choice of the algebraic integer \(\alpha \), other than its degree over \({\mathcal {O}}\).) Letting, e.g., \(\psi ' = D_{r}\) be a spherical Gaussian over \(K'_{\mathbb {R}}\) and \(\psi = D_{r\sqrt{k}}\) be the corresponding spherical Gaussian over \(K_{\mathbb {R}}\), we have an efficient, deterministic reduction from \({\mathcal {O}}'\)-\(\mathsf {LWE} ^{1}_{q,\psi ',\ell }\) to \({\mathcal {O}}\)-\(\mathsf {LWE} ^{k}_{q,\psi ,\ell }\).
Notes
- 1.
We caution that \({\mathcal {O}}^\mathcal {L}\) is not “monotonic” in \(\mathcal {L}\) under set inclusion, i.e., \(\mathcal {L}' \subseteq \mathcal {L}\) does not imply any inclusion relationship between \({\mathcal {O}}^{\mathcal {L}'}\) and \({\mathcal {O}}^{\mathcal {L}}\), in either direction. In particular, \(\mathcal {L}\) and \(c\mathcal {L}\) have the same coefficient ring for any integer \(c > 1\), but there can exist \(\mathcal {L}'\) with \(c\mathcal {L}\subsetneq \mathcal {L}' \subsetneq \mathcal {L}\) that has a different coefficient ring.
- 2.
For example, consider the ring of integers \({\mathcal {O}}_K\) where \(K = \mathbb {Q}(\alpha )\) for \(\alpha ^3-\alpha ^2-2\alpha -8=0\). In a classical result, Dedekind showed that this order is non-monogenic, but it has \(\vec {p} = (t, tx, tx^{2})\) as a basis, where \(x=(\alpha ^{2}-\alpha -2)/4\) and \(t=1-2x\). We caution that \(x \not \in {\mathcal {O}}_{K}\), so this is actually not a tweaked power basis according to our definition, but it still suffices for a special case of our reduction that does not extend \(\vec {p}\) by more powers of x.
- 3.
Note that the covariance of \(D_{\sqrt{\varSigma }}\) is actually \(\varSigma /(2\pi )\), due to the normalization factor in the definition of \(\rho _{\sqrt{\varSigma }}\).
- 4.
Recall that a matrix H is Hankel if each entry \(H_{jk}\) is determined by \(j+k\) (equivalently, it is an “upside down” Toeplitz matrix). So, an \(n \times d\) Hankel matrix is defined by an \((n+d-1)\)-dimensional vector whose ith entry defines the entries \(H_{jk}\) for \(i=j+k\).
- 5.
This can also be seen by using one of the characterizations of algebraic integers, that x is an algebraic integer if and only if \(x\mathcal {L}\subseteq \mathcal {L}\) for some nonzero finitely generated \(\mathbb {Z}\)-module \(\mathcal {L}\subseteq \mathbb {C}\).
References
Albrecht, M.R., Deo, A.: Large modulus ring-LWE \(\ge \) module-LWE. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 267–296. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_10
Bolboceanu, M., Brakerski, Z., Perlman, R., Sharma, D.: Order-LWE and the hardness of Ring-LWE with entropic secrets. Cryptology ePrint Archive, Report 2018/494 (2018). https://eprint.iacr.org/2018/494
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (Leveled) fully homomorphic encryption without bootstrapping. TOCT 6(3), 13 (2014). Preliminary version in ITCS 2012
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: STOC, pp. 575–584 (2013)
Castryck, W., Iliashenko, I., Vercauteren, F.: Provably weak instances of ring-LWE revisited. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 147–167. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_6
Hoffstein, J., Pipher, J., Silverman, J.H.: NTRU: a ring-based public key cryptosystem. In: Buhler, J.P. (ed.) ANTS 1998. LNCS, vol. 1423, pp. 267–288. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054868
Langlois, A., Stehlé, D.: Worst-case to average-case reductions for module lattices. Des. Codes Crypt. 75(3), 565–599 (2015)
Lyubashevsky, V.: Digital signatures based on the hardness of ideal lattice problems in all rings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 196–214. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_7
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. J. ACM 60(6), 43:1–43:35 (2013). Preliminary version in Eurocrypt 2010
Micciancio, D.: Generalized compact knapsacks, cyclic lattices, and efficient one-way functions. Comput. Complex. 16(4), 365–411 (2007). Preliminary version in FOCS 2002
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem. In: STOC, pp. 333–342 (2009)
Peikert, C.: A decade of lattice cryptography. Found. Trends Theor. Comput. Sci. 10(4), 283–424 (2016)
Peikert, C.: How (not) to instantiate ring-LWE. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 411–430. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_22
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of Ring-LWE for any ring and modulus. In: STOC, pp. 461–473 (2017)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 1–40 (2009). Preliminary version in STOC 2005
Regev, O.: The learning with errors problem (invited survey). In: IEEE Conference on Computational Complexity, pp. 191–204 (2010)
Roşca, M., Sakzad, A., Stehlé, D., Steinfeld, R.: Middle-product learning with errors. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 283–297. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_10
Rosca, M., Stehlé, D., Wallet, A.: On the ring-LWE and polynomial-LWE problems. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 146–173. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_6
Stehlé, D., Steinfeld, R., Tanaka, K., Xagawa, K.: Efficient public key encryption based on ideal lattices. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 617–635. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_36
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Peikert, C., Pepin, Z. (2019). Algebraically Structured LWE, Revisited. In: Hofheinz, D., Rosen, A. (eds) Theory of Cryptography. TCC 2019. Lecture Notes in Computer Science(), vol 11891. Springer, Cham. https://doi.org/10.1007/978-3-030-36030-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-36030-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-36029-0
Online ISBN: 978-3-030-36030-6
eBook Packages: Computer ScienceComputer Science (R0)





 , where
, where 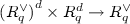 , where here the input modules are of rank d over
, where here the input modules are of rank d over 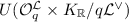 to distribution
to distribution 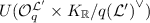 , and
, and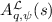 to distribution
to distribution  , where
, where  .
. to distribution
to distribution 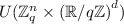 , and
, and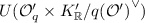 to
to  , and
, and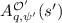 to
to 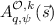 , for
, for 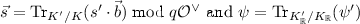 .
.