Integrating Agent-Based Modelling with Copula Theory: Preliminary Insights and Open Problems

Abstract

The paper sketches and elaborates on a framework integrating agent-based modelling with advanced quantitative probabilistic methods based on copula theory. The motivation for such a framework is illustrated on a artificial market functioning with canonical asset pricing models, showing that dependencies specified by copulas can enrich agent-based models to capture both micro-macro effects (e.g. herding behaviour) and macro-level dependencies (e.g. asset price dependencies). In doing that, the paper highlights the theoretical challenges and extensions that would complete and improve the proposal as a tool for risk analysis.

1 Introduction

Complex systems like markets are known to exhibit properties and phenomenal patterns at different levels (e.g. trader decision-making at micro-level and average asset price at macro-level, individual defaults and contagion of defaults, etc.). In general, such stratifications are irreducible: descriptions at the micro-level cannot fully reproduce phenomena observed at macro-level, plausibly because additional variables are failed to be captured or cannot be so. Yet, anomalies of behaviour at macro-level are typically originated by the accumulation and/or structuration of divergences of behaviour occurring at micro-level, (see e.g. [1] for trade elasticities). Therefore, at least in principle, it should be possible to use micro-divergences as a means to evaluate and possibly calibrate the macro-level model. One of the crucial aspects for such an exercise would be to map which features of the micro-level models impact (and do not impact) the macro-level model. From a conceptual (better explainability) and a computational (better tractability) point of view, such mapping would enable a practical decomposition of the elements at stake, thus facilitating parameter calibration and estimation from data. Moreover, supposing these parameters to be adequately extracted, one could put the system in stress conditions and see what kind of systematic response would be entailed by the identified dependence structure. The overall approach could provide an additional analytical tool for systematic risk.

With the purpose of studying and potentially providing a possible solution to these requirements, we are currently working on establishing a theoretical framework integrating agent-based modelling (ABM) with advanced quantitative probabilistic methods based on copula theory. The intuition behind this choice is the possibility to connect the causal, agentive dependencies captured by agent-based models with the structural dependencies statistically captured by copulas, in order to facilitate the micro-macro mappings, as well as the extraction of dependencies observable at macro-level.

To the best of our knowledge, even if many research efforts targeting hybrid qualitative-quantitative methods exist in the computational science and artificial intelligence literature, the methodological connection of ABM with copula theory is still an underexplored topic. A large-scale agent-based model of trader agents incorporating serial dependence analysis, copula theory and co-evolutionary artificial market, allowing traders to change their behaviour during crisis periods, has been developed in [2]; the authors rely on copula to capture cross-market linkages on macro-level. A similar approach is taken in [4]. Examples of risk analysis in network-based setting can be found for instance in [5, 6], in which the mechanisms of defaults and default contagion are separated from other dependencies observed in the market. In [3], copula is used to model low-level dependencies of natural hazards with agent-based models, in order to study their impact at macro-level. In the present paper, we will use copula to model dependencies among agents at micro-level, and we will propose a method to combine aggregated micro-correlations at market scale.

The paper is structured as follows. Section 2 provides some background: it elaborates on the combined need of agent-based modeling and of quantitative methods, illustrating the challenges on a running example based on canonical trader models for asset pricing, and gives a short presentation on copula theory. Section 3 reports on the simulation of one specific hand-crafted instanciation of copula producing a relevant result from the running example, and will elaborate on extensions and theoretical challenges that remain to be solved for the proposal to be operable. A note on future developments ends the paper.

2 Agent-Based Modeling and Copula Theory

In financial modelling, when statistical models are constructed from time series data, it is common practice to separately estimate serial dependencies and cross-sectional dependencies. The standard approach to capture serial dependence (also referred to as autocorrelation) is to use autoregressive models [10]. If the time series exhibit volatility clustering–i.e. large changes tend to be followed by large changes, of either sign, small changes tend to be followed by small changes—then it is typical to use the generalized autoregressive conditional heteroskedasticity model (GARCH) [11], or one of its variants [12]. Once the GARCH model is estimated, the cross-sectional dependence analysis can be performed on the residuals. Unfortunately, autoregressive models provide only little information useful for interpretation; this is no surprise since these models are purely quantitative, and suffer problems similar to all data-driven methods. As low interpretability goes along with limited possibility of performing counterfactual or what-if reasoning (see e.g. the discussion in [9]), such models are weakly justifiable in policy-making contexts, as for instance in establishing sound risk balancing measures to be held by economic actors.

2.1 Agent-Based Modelling

An alternative approach is given by agent-based modelling (ABM), through which several interacting heterogeneous agents can be used to replicate patterns in data (see e.g. [2]). Typically, agent models are manually specified from known or plausible templates of behaviour. To a certain extent, their parameters can be set or refined by means of some statistical methods. Model validation is then performed by comparing the model execution results against some expected theoretical outcome or observational data. These models can be also used to discover potential states of the system not yet observed [23], thus becoming a powerful tool for policy-making. Independently from their construction, agent models specify, at least qualitatively, both serial dependencies (for the functional dependence between actions) and cross-sectional dependencies (for the topological relationships between components), and are explainable in nature. However, they do not complete the full picture of the social system, as the focus of the designers of agent-based models is typically on the construction of its micro-level components. Nevertheless, to elaborate on the connection between micro-level and macro-level components of a social system we still need to start from capturing behavioural variables associated to micro-level system components, assuming them to have the strongest effect at micro-level (otherwise the micro-level would be mostly determined by the macro-level).

Running Example: Asset Market. We will then consider a paradigmatic scenario for ABM: an asset market, in which traders concurrently sell, buy or hold their assets. Our running example is based on canonical asset pricing models, proceeding along [17].

Fundamental Value. The target asset has a publicly available fundamental value given by a random walk process:

$$\begin{aligned} {} F_{t} = F_{t-1} + \eta \end{aligned}$$

(1)

where $\eta$ is a normally distributed random variable with mean zero and standard deviation $\sigma _{\eta }$.

Market-Maker Agent. At the end of each trading day, a market-maker agent sets the price at which a trader agent can buy or sell the asset according to a simple rule:

$$\begin{aligned} {} p_{t+1} = p_t + \varDelta p_t \end{aligned}$$

(2)

where:

$$ \varDelta p_t = a(1 + D(t) - S(t)) + \delta $$

The variable D(t) denotes the number of buy orders at time t, S(t) denotes number of sell orders at time t and $\delta$ is a normally distributed random variable with zero mean and constant standard deviation $\sigma _{\delta }$. The positive coefficient a can be interpreted as the speed of price adjustment.

Fundamental Traders. Fundamental traders operate with the assumption that the price of an asset eventually returns to its fundamental value. Therefore, for them it is rational to sell if the value of an asset is above its fundamental value and buy if the value of an asset is below its fundamental value. Their price expectation can be written as:

$$\begin{aligned} {} E^{\textit{fund}}_t[p_{t+1}] = p_t + x_{\textit{fund}} (F_t - p_t) + \alpha \end{aligned}$$

(3)

where $\alpha$ is a normally distributed random variable with mean zero and standard deviation $\sigma _{\alpha }$. $x_{\textit{fund}}$ can be interpreted as the strength of a mean-reverting belief (i.e. the belief that the average price will return to the fundamental value).

Technical Traders. In contrast, technical traders, also referred to as chartists, decide on the basis of past trend in data. They will buy if the value of an asset is on the rise, because they expect this rise to continue and sell if the value is on decline. Their expectation can be written as:

$$\begin{aligned} {} E^{tech}_t[p_{t+1}] = p_t + x_{tech} (p_t - p_{t-1}) + \beta \end{aligned}$$

(4)

where $\beta$ is a normally distributed random variable with mean zero and standard deviation $\sigma _{\beta }$. $x_{tech}$ can be interpreted as a strength of reaction to the trend.

Relevant Scenario: Herding Behaviour. Because they are intrinsic characteristics of each agent, $x_{\textit{fund}}$ and $x_{tech}$ can be seen as capturing the behavioural variables we intended to focus on at the beginning of this section.

Now, if for all traders $x_{\textit{fund}}$ or $x_{tech}$ happen to be realized with unexpectedly large values at the same time, the effect of $\alpha$ and $\beta$ will be diminished, and this will result in higher (lower) expected value of the asset price and then in the consequent decision of traders to buy (sell). Purchases (sales) in turn will lead the market-maker agent to set the price higher (lower) at the next time step, thus reinforcing the previous pattern and triggering herding behaviour. Such chain of events are known to occur in markets, resulting in periods of rapid increase of asset prices followed by periods of dramatic falls. Note however that this scenario is not directly described by the agent-based models, but is entailed as a possible consequence of specific classes of instantiations.

2.2 Combining Agent-Based Models with Probability

Herding behaviour is recognized to be a destabilizing factor in markets, although extreme time-varying volatility is usually both a cause and an effect of its occurrence. In the general case, factors contributing to herding behaviour are: the situation on the global market, the situation in specific market sectors, policies implemented by policy makers, etc. All these factors are somehow processed by each human trader. However, because such mental reasoning is only partially similar amongst the agents, and often includes non-deterministic components (including the uncertainty related to the observational input), it is unlikely that it can be specified by predefined, deterministic rules. For these reasons, probabilistic models are a suitable candidate tool to recover the impossibility to go beyond a certain level of model depth, in particular to capture the mechanisms behind behavioural variables as $x_{\textit{fund}}$ and $x_{tech}$. In the following, we will therefore consider two normally distributed random variables $X_{\textit{fund}}$ and $X_{tech}$ realizing them.¹ This means that the traders will perceive the price difference in parenthesis of Eqs. (3) and (4) differently, attributing to it different importance at each time step.

Looking at Eqs. (3) and (4) we can see that the essence of an agent’s decision making lies in balancing his decision rule (e.g. for the fundamental trader $x_{\textit{fund}}(F_t - p_t)$) with the uncertainty about the asset price (e.g. $\alpha$). If for instance the strength of the mean-reversing belief $x_{\textit{fund}}$ happens to be low (in probabilistic terms, it would be a value from the lower tail), then the uncertainty $\alpha$ will dominate the trader’s decision. In contrast, if $x_{\textit{fund}}$ happens to be very high (i.e. from the upper tail), then the trader will be less uncertain and trader’s decision to buy or sell will be determined by $(F_t - p_t)$. Similar considerations apply to technical traders.

Assuming that behavioural random variables are normally distributed, obtaining values from the upper tail is rather unlikely and, even if some agent’s behavioural variable is high, it will not influence the asset price very much since the asset price is influenced collectively. However, if all traders have strong beliefs about the rise or fall of the price of the asset, then the price will change dramatically. The dependence of the price on a collective increase in certainty cannot be directly modeled by the standard toolkit of probability, and motivates the use of copulas.

2.3 Copulas

Copula theory is a sub-field of probability theory dealing with describing dependencies holding between random variables. Application-wise, copulas are well established tools for quantitative analysis in many domains, as e.g. economic time series [15] and hydrological data [16].

Consider a random variable $\mathbf {U} = (U_1,...,U_d)$ described as a d-dimensional vector. If all components of $\mathbf {U}$ are independent, we can compute its joint probability distribution function as $F_{\mathbf {U}}(u_1,..,u_d)=F_{U_1}(u_1) \cdot ... \cdot F_{U_d}(u_d)$, i.e. the product of marginal distributions. In case of dependence among components we need some function that specifies this dependence. The concept of copula is essentially presented as a specific class of such functions, specifically defined on uniform marginals [13]:

Definition 1

$C: [0,1]^d \rightarrow [0,1]$ is a d-dimensional copula if C is a joint cumulative distribution function of a d-dimensional random vector on the unit cube $[0,1]^d$ with uniform marginals.

To obtain a uniform marginal distribution from any random variable we can perform a probability integral transformation $u_i = F_i(x_i)$, where $F_i$ is the marginal distribution function of the random variable $X_i$. In practice, when we estimate the copula from data we estimate the marginals and copula components separately. We can then introduce the most important theorem of copula theory:

Theorem 1

Let F be a distribution function with marginal distribution functions $F_1,...,F_d$. There exists a copula C such that for all $(x_1,...,x_d) \in [-\infty ,\infty ]^d$,

$$\begin{aligned} {} F(x_1,...,x_d)=C(F_1(x_1),...,F_d(x_d)) \end{aligned}$$

(5)

If $F_1,...,F_d$ are continuous this copula is unique.

If we consider the partial derivatives of Eq. (5) we obtain the density function in the form:

$$\begin{aligned} f(x_1,...,x_d)=c(F_1(x_1),...,F_d(x_d)) \prod _{i=1}^{d}f_i(x_i). \end{aligned}$$

(6)

where c is density of the copula and $f_i$ is marginal density of random variable $X_i$. The reason why copulas gained popularity is that the cumulative distribution function $F_i$ contains all the information about the marginal, while the copula contains the information about the structure of dependence, enabling a principled decomposition for estimations.

Fig. 1.

(picture taken from http://pilot.52north.org/shinyApps/copulatheque/copulas/)

Density and scatter plot of a bivariate Joe copula, with parameter set to 8.

Correspondingly to the high variety of dependence structures observed in the real world, there exists many parametric families of copulas, specializing for specific types of dependence. The most interesting type for economic applications is tail dependence. For example, if there is nothing unusual happening on the market and time series revolve around its mean value, then the time series might seem only weakly correlated. However, co-movements far away from mean value tend to be correlated much more strongly. In probabilistic terms, the copula describing such dependence between random variables has strong tail dependence. Tail dependence does not have to be always symmetrical. Certain types of copulas have strong upper tail dependence and weaker lower tail dependence. In simple terms this means that there is higher probability of observing random variables together realized in the upper quantile of their distribution than in the lower quantile. One of the parametric copulas having such properties is the Joe copula [13], illustrated in Fig. 1.

3 Tracking Dependencies

This section aims to show how copulas can be effectively used to enrich stochastic agent-based models with additional dependencies, relative to micro- and macro- levels. In particular, we will focus on the phenomenon of dependence of the asset price to a collective increase in strength of belief associated to herding behaviour scenarios, observed in Sect. 2.2. To model the balance between certainty and uncertainty of each trader with respect to current price of the asset, we need to set the marginal distribution functions of $X_{\textit{fund}}$ and $X_{tech}$ to have a mean value and standard deviation such that if herding behaviour occurs then the uncertainty parameters $\alpha$ and $\beta$ will play essentially no role, but if herding behaviour is not occurring, then $\alpha$ and $\beta$ will stop traders from massive buying or selling. Therefore the parameters for $X_{\textit{fund}}$, $X_{tech}$ and $\alpha$, $\beta$ are not entirely arbitrary.

Table 1. Table of parameters used for the simulations

3.1 Market Simulation

To illustrate the influence of dependence structures of behavioural random variables we will compare simulations of the market with independent behavioural random variables to simulations of the market whose random variables have a dependence structure defined by Joe copula. It is important to make clear that this exercise does not have any empirical claim: it is meant just to show that copula can be used for a probabilistic characterization of the social behaviour of the system.

Consider a group of $N_{total} = 1000$ trader agents consisting of $N_{\textit{fund}}=300$ fundamental traders and $N_{tech}=700$ technical traders (this ration roughly reflects the situation of a real market). Let us denote with $\mathbf {X}$ the vector collecting all behavioural random variables of the traders. Table 1 reports all parameters we have used for our simulation. The sequence of fundamental values $\{ F_t \}_{t=1}^{T}$ is generated by Eq. (1) at the beginning and remains the same for all simulations.

Fig. 2.

100 simulations when behavioural variables are independent.

Independence Scenario. At first, we will assume that the (normally distributed) behavioural random variable assigned to each trader is independent of other normally distributed behavioural variables. This means that the probability density function capturing all behavioural variables of market can be written as a simple product of marginal density functions:

$$\begin{aligned} {} f_{\mathbf {X}}(\mathbf {x}) = \prod _{i=1}^{N_{\textit{fund}}} f_{X_{\textit{fund}}}(x_{\textit{fund}}) \prod _{i=1}^{N_{\textit{tech}}} f_{X_{\textit{tech}}}(x_{\textit{tech}}) \end{aligned}$$

(7)

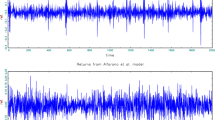
We have considered $T=502$ time steps with initialization $p_1 = 10$ and $p_2 = 10.02574$. Figure 2 illustrates the output of 100 simulations of the market with a probability density function given by the Eq. (7). The simulations on average follow the fundamental price of an asset. The marginal distribution of the increments $\varDelta p_t$ taking realizations of the generated time series (Fig. 2) clearly follows a normal distribution (left of Fig. 4).

Fig. 3.

100 simulations when behavioural random variables have a dependence structure of defined by Joe copula.

Fig. 4.

Histogram of increments for an independence structure (left) and dependence structure defined by Joe copula (right).

Dependence Scenario. Let us keep same number of agents and exactly the same parameters, but this time consider a dependence structure between the behavioural variables described by a Joe copula with parameter equal to 8. As shown in Fig. 1, this copula has strong right upper tail dependence. The Joe copula is an Archimedean copula, which means it attributes an univariate generator, hence drawing samples from this copula is not time consuming, even for large dimensions. In our case, each sample will be a $N_{total}$ dimensional vector $\mathbf {U}$ with components $u_i$ from the unit interval. For each agent, a quantile transformation will be made $x_{A,i} = Q_{X_{A,i}} (u_i)$ by the quantile function $Q_{X_{A,i}}$ of i-the agent $A= \{\textit{fund}, \textit{tech} \}$ to obtain the realization from the agent’s density function. Here the i-th agent A’s behavioural random variable is again distributed following what specified in Table 1.

Fig. 5.

Normal QQ-plots comparing distribution functions of increments $\varDelta p_t$ to normal distribution of behavioural variables with an independence structure (left) and with a dependence structure defined by Joe copula (right).

Running 100 market simulations, the time-series we obtain this time are much more unstable (Fig. 3). This is due to the structural change in the marginal distribution function of $\varDelta p_t$, which has now much fatter tails. The fatter tails can be seen on the right histogram on Fig. 4, and on the comparison of both histograms by normal QQ-plots in Fig. 5. We see that for independence the increments follow a normal distribution very closely, but for dependence defined by Joe copula the tails of marginal distribution deviate greatly and approximates a normal distribution only around the mean.

3.2 Directions for Model Aggregation

For applications in finance it would be desirable to extend this model to consider broader contexts: e.g. a market with many assets, whose prices in general may exhibit mutual dependencies. A way to obtain this extension is to introduce adequate aggregators, following for instance what was suggested in [14, 3.11.3]. In order to apply this method, however, we need to make explicit a few assumptions.

Step-Wise Computation Assumption. The increase or the decrease of the price of the asset $\varDelta p_t$ is obtained via the simulation of the agent-based market model. As it can be seen in formulas (3) and (4), the increment $\varDelta p_t$ at time t depends on the realization of random variables $\mathbf {X}$ at time t with agents observing previous market values $p_{t-1}$ and $p_{t-2}$. This means that $\varDelta p_t$ is also a continuous random variable and its probability density function should be written as $f_{ \varDelta p_t | p_{t-1}, p_{t-2}, \mathbf {X}}$. Note that this function can be entirely different at each time t depending on what values of $p_{t-1}, p_{t-2}$ the agents observe. Since the time steps are discrete, then the density functions forms a sequence $\{ f_{ \varDelta p_t | p_{t-1}, p_{t-2}, \mathbf {X}} \}_{t=t_0}^{t=T}$. In this paper, for simplicity, we will not describe the full dynamics of this sequence; we will focus only on one density function in one time step, assuming therefore that the computation can be performed step-wise. By fixing time, $p_{t-1}, p_{t-2}$ are also fixed (they have already occurred), so we can omit them and write just $f_{ \varDelta p_t | \mathbf {X}}$.

Generalizing to Multiple Assets. Consider m non-overlapping groups of absolutely continuous random variables $\mathbf {X}_1,...,\mathbf {X}_m$, where each group consists of behavioural random variables, or, to make our interpretation more general, predictor variables that determine the value of an asset. Each group $\mathbf {X}_g$ forms a random vector and has a scalar aggregation random variable $V_g = h_g (\mathbf {X}_g)$. This means that each value of an asset is determined by a mechanism specified by the function $h_g$, which might be an agent-based model similar to the one explored in the previous section, but this time each group of predictor random variables will have its own distribution function. We can write then:

$$\begin{aligned} {} f_{\mathbf {X}_1,...,\mathbf {X}_m}(\mathbf {x}_1,...,\mathbf {x}_m) = \frac{f_{\mathbf {V}}(v_1,...,v_m)}{\prod _{i=1}^{m} f_{V_{i}}(v_i)} \prod _{i=1}^{m} f_{\mathbf {X}_i}(\mathbf {x}_i) \end{aligned}$$

(8)

where f denotes the marginal (joint) probability density function of the corresponding variable (variables) written as a subscript. The validity of (8) relies on two assumptions: (a) conditional independence of the groups given aggregation variables $V_1,..,V_m$ and (b) conditional distribution function of the group $\mathbf {X}_g$ conditioned on $V_1,...,V_m$ is the same as the conditional distribution of $\mathbf {X}_g$ conditioned on $V_g$ (for a 2-dimensional proof see [14]). These assumptions are in principle not problematic in our application because we are assuming that all interactions on micro-level of the agents are sufficiently well captured by the distribution of aggregation variables. Hence formula (8) should be viewed as a crucial means for simplification, because it enables a principled decomposition.

Expressing the density function of $\mathbf {V}$ in (8) using formula (6) as copula, we obtain:

$$\begin{aligned} {} f_{\mathbf {X}_1,...,\mathbf {X}_m}(\mathbf {x}_1,...,\mathbf {x}_m) = c_{\mathbf {V}}(F_{V_1}(v_1),...,F_{V_m}(v_m)) \prod _{i=1}^{m} f_{\mathbf {X}_i}(\mathbf {x}_i) \end{aligned}$$

(9)

This formula provides us a way to integrate in the same model mechanisms associated to the different assets in the market by means of a copula at aggregate level. In other words, by this formula, it is possible to calculate the probability of rare events, and therefore estimate systematic risk, based on the dependencies of aggregation variables and on the knowledge of micro-behaviour specified by group density functions of the agent-based models. The marginal distribution functions $F_{V_i}(v_i)$ can be estimated either from real world data (e.g. asset price time series), or from simulations. Note that whether we estimate from real world data or an agent-based market model should not matter in principle, since, if well constructed, the agent-based model should generate the same distribution of $\varDelta p$ as the distribution estimated from real world data. The density function $f_{\mathbf {X}_g}(\mathbf {x}_g)$ of an individual random vector $\mathbf {X}_g$ can be defined as we did in our simulation study. However, to bring this approach into practice, three problems remain be investigated:

• estimation of copula. We need to consider possible structural time dependencies and serial dependencies in the individual aggregation variables. Additionally, the agents might change their behavioural script (e.g. traders might pass from technical to fundamental at certain thresholds conditions).

• high dimensionality of Eqs. (8) and (9). If we consider N predictor variables for each group $g=1,...,m$ we will end up with a $N \cdot m$-dimensional density function.

• interpolation of function $h_g$. Calculating high-dimensional integrals that occur for instance in formula (8), with function $h_g$ being implicitly computed by the simulation of an agent-based market model, is clearly intractable.

For the first problem, we observe that time dependence with respect to copulas is still an active area of research. Most estimation methods do not allow for serial dependence of random variables. One approach to solve this is to filter the serial dependence by an autoregressive model as described at the beginning of Sect. 2. Another approach is to consider a dynamic copula, similarly as in [14, 20, 21]. A very interesting related work is presented in [22], where ARMA-GARCH and ARMA-EGARCH are used to filter serial dependence, but the regime switching copula is considered on the basis of two-states Markov models. Using an agent-based model instead of (or integrated with) a Markov model would be a very interesting research direction, because the change of regime would also have a qualitative interpretation.

For the second problem, although in our example we have used 1000 agents, in general this might be not necessary, considering that ABMs might be not as heterogeneous, and aggregators might work with intermediate layers between micro and macro-levels.

For the third problem, a better approach would be to interpolate the ABM simulation by some function with closed form. In future works, we are going to evaluate the use of neural networks (NNs), which means creating a model of our agent-based model, that is, a meta-model. The general concept of meta-models is a well-established design pattern [18] and the usage of NNs for such purposes dates back to [19]. In our example the basic idea would be to obtain samples from the distribution $f_{\mathbf {X}_g}(\mathbf {x}_g)$ as input, the results of an ABM simulation $v_g$ as output, and then feed both input and output to train a dedicated NN, to be used at runtime. This would be done for each group g. The biggest advantage of this approach, if applicable in our case, is that we will have both a quick way to evaluate a function approximating $h_g$, but we will also have the interpretative power of the agent-based market model, resulting in an overall powerful modelling architecture.

4 Conclusions and Future Developments

Agent-based models are a natural means to integrate expert (typically qualitative) knowledge, and directly support the interpretability of computational analysis. However, both the calibration on real-data and the model exploration phases cannot be conducted by symbolic means only. The paper sketched a framework integrating agent-based models with advanced quantitative probabilistic methods based on copula theory, which comes with a series of data-driven tools for dealing with dependencies. The framework has been illustrated with canonical asset pricing models, exploring dependencies at micro- and macro- levels, showing that it is indeed possible to capture quantitatively social characteristic of the systems. This also provided us with a novel view on market destabilization, usually explained in terms of strategy switching [24, 25]. Second, the paper formally sketched a principled model decomposition, based on theoretical contributions presented in the literature.

The ultimate goal of integrating agent-based models, advanced statistical methods (and possibly neural networks) is to obtain an unified model for risk evaluation, crucially centered around Eq. (9). Clearly, additional theoretical challenges for such a result remains to be investigated, amongst which: (a) probabilistic models other than copulas to be related to the agent’s decision mechanism, (b) structural changes of dependence structures, (c) potential causal mechanisms on the aggregation variables and related concepts as time dependencies (memory effects, hysteresis, etc.) and latency of responses. These directions, together with the development of a prototype testing the applicability of the approach, set our future research agenda.