Computational Complexity of Hierarchically Adapted Meshes

Abstract

We show that for meshes hierarchically adapted towards singularities there exists an order of variable elimination for direct solvers that will result in time complexity not worse than $\mathcal {O}(\max (N, N^{3\frac{q-1}{q}}))$, where N is the number of nodes and q is the dimensionality of the singularity. In particular, we show that this formula does not change depending on the spatial dimensionality of the mesh. We also show the relationship between the time complexity and the Kolmogorov dimension of the singularity.

1 Introduction

Computational complexity, especially time complexity, is one of the most fundamental concepts of theoretical computer science, first defined in 1965 by Hartmanis and Stearns [1]. The time complexity of direct solvers [2, 3] for certain classes of meshes, especially regular meshes, is well known. The problem of finding the optimal order of elimination of unknowns for the direct solver, in general, is indeed NP-complete [7], however there are several heuristical algorithms analyzing the sparsity pattern of the resulting matrix [8,9,10,11,12].

In particular, for three-dimensional uniformly refined grids, the computational cost is of the order of $\mathcal{O}(N^2)$ [4, 5]. For three-dimensional grids adapted towards a point, edge, and face, the time complexities are $\mathcal{O}(N), \mathcal{O}(N)$, and $\mathcal{O}(N^{1.5})$, respectively [6]. These estimates assume a prescribed order of elimination of variables [13, 14].

Similarly, for two dimensions, the time complexity for uniform grids is known to be $\mathcal{O}(N^{1.5})$, and for the grids refined towards a point or edge it is $\mathcal{O}(N)$ [15]. These estimates assume a prescribed order of elimination of variables [16]. The orderings resulting in such linear or quasi-linear computational costs can also be used as preconditioners for iterative solvers [17].

For all others, there is no known general formula or method of calculation of the computational complexity. It is neither hard to imagine that such a formula or method might not be discovered any time soon, nor that such formula or method would be simple enough to be applicable in real-world problems. Thus in this paper, we focus on a specific class of problems: hierarchically adapted meshes refined towards singularities. This paper generalizes results discussed in [6] into an arbitrary spatial dimension and arbitrary type of singularity. We, however, do not take into the account the polynomial order of approximation p, and we assume that this is a constant in our formula.

Singularities in the simulated mesh can lead, depending on the stop condition, to an unlimited number of refinements. Thus, usually the refinement algorithm will be capped by a certain refinement level that is common to the whole mesh. In this paper, we analyze how the computational cost grows when the refinement level is increased. The analysis is done only for a very specific class of meshes, however the conclusions extend to a much wider spectrum of problems.

This publication is structured as follows. First, in Sect. 2 we define the problem approached by this paper. Secondly, in Sect. 3 we show a method to calculate an upper bound for the computational cost of direct solvers for sparse matrices. Then, in Sect. 4 we calculate time complexity for meshes meeting a certain set of criteria. Section 5 contains the analysis of properties of typical h-adaptive meshes and the final Sect. 6 concludes the proof by showing how those properties fit in with the earlier calculations.

2 Problem Definition

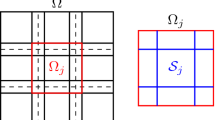
In this paper we analyze finite element method meshes that are hierarchically adapted towards some singularity – by singularity we mean a subset of the space over which the finite element method never converges. The existence of a singularity might cause the mesh to grow infinitely large, so a limit of refinement rounds is necessary – we will call it the refinement level of the mesh. As the refinement level of the mesh grows, the number of variables will grow as well and so will the computational cost. For instance, if the singularity is defined over a two-dimensional h-adaptive grid as shown in Fig. 1, each refinement of an element will increase the number of elements by three and (assuming that $p=2$ over the whole grid).

Fig. 1.

Example of hierarchical adaptation towards a singularity (in green). Here, apart from the refinement of elements overlapping the singularity, the 1-irregularity rule is applied (see Sect. 5 for definition). (Color figure online)

When referring to a mesh hierarchically refined towards a singularity S up to a refinement level R we will have in mind a mesh that has been through R refinement rounds from its initial state. During each refinement round, all elements that have an overlap with the singularity S of at least one point will undergo a division into smaller elements, then, if required by given type of the finite element method, some extra elements might also get divided to keep some mesh constraints. We generally assume that the hierarchical refinements are done uniformly for all dimensions of the grid, however the findings from this paper should also extend to other types of refinements.

In this paper we analyze the relationship between the computational cost of the solver as a direct function of the number of variables and state it using big $\mathcal {O}$ notation. By definition of the big $\mathcal {O}$ notation, when we denote that the time complexity of the problem is $T(N) = \mathcal {O}(f(N))$, it means that for some large enough $N_0$ there exists a positive constant C such as the computational cost is no larger than $C \cdot f(N)$ for all $N \ge N_0$. In this paper, we are considering how the computational cost increases as the number of variables N grows. As N is a function of the refinement level R, we can alternatively state the definition of time complexity as follows:

$$\begin{aligned} T(N) = \mathcal {O}(f(N)) \Longleftrightarrow \exists R_0 \ge 0, C > 0 : \forall R \ge R_0 : |T(N(R))| \le C \cdot f(N(R)) \end{aligned}$$

(1)

As the polynomial order p is constant in the analyzed meshes, the number of variables grows linearly proportional with the growth of the number of all elements of the mesh. Thus, in almost all formulas for time complexity, we can use the number of elements and the number of variables interchangeably.

3 Time Complexity of Sparse Matrix Direct Solvers

In the general case, the time complexity of solving a system of equations for a finite element method application in exact numbers (that is using a direct solver) will be the complexity of general case of Gaussian elimination – that is a pessimistic $\mathcal {O}(N^3)$, where N is the number of variables. However, on sparse matrices the complexity of the factorization can be lowered if a proper row elimination order is used – in some cases even a linear time complexity can be achieved. The matrices corresponding to hierarchically adapted meshes are not only sparse but will also have a highly regular structure that corresponds to the geometrical structure of the mesh.

In the matrices constructed for finite element method, we assign exactly one row and column (with the same indexes) to each variable. A non-zero value on an intersection of a row and column is only allowed if the basis functions corresponding to the variables assigned to that row and column have overlapping supports.

If a proper implementation of the elimination algorithm is used, when eliminating a row we will only need to do a number of subtractions over the matrix that is equal to the number of non-zero elements in that row multiplied by the number of non-zero values in the column of the leading coefficient in the remaining rows. This way, as long as we are able to keep the sparsity of the matrix high during the run of the algorithm, the total computation cost will be lower. To achieve that we can reorder the matrix rows and columns.

In this paper we will analyze the speed improvements gained from the ordering created through recursive section of the mesh and traversal of generated elimination tree. The tree will be built according to the following algorithm, starting with the whole mesh with all the variables as the input:

• 1. If there is only one variable, create an elimination tree node with it and return it.

• 2. Else:

  • (a) Divide the elements in the mesh into two or more continuous submeshes using some division strategy. The division strategy should be a function that assigns each element to one and exactly one resulting submesh.

  • (b) For each submesh, assign to it all the variables, which have their support contained in the elements of that submesh.

  • (c) Create an elimination tree node with all the variables that have not been assigned in the previous step. Those variables correspond to basis functions with support spread over two or more of the submeshes.

  • (d) For each submesh that has been assigned at least one variable, recursively run the same algorithm, using that submesh and the assigned variables as the new input. Any submeshes without any variables assigned can be skipped.

  • (e) Create and return the tree created by taking the elimination tree node created in step 2c as its root and connecting the roots of the subtrees returned from the recursive calls in step 2d as its children.

An example of such process has been shown on Fig. 2.

From the generated tree we will create an elimination order by listing all variables in nodes visited in post-order direction. An example of an elimination tree with the order of elimination can be seen on Fig. 3.

Fig. 2.

Example of the generation of an elimination tree for h-adaptive mesh of $p = 2$. Large green nodes are assigned to the new node created during each recursive call. In the first recursion, a vertical cut through the vertices 3 and 17 is made. Vertex basis functions 3 and 17 and edge basis function 8 have supports spreading over both sides of the cut. The remaining sets of variables are then divided into the two submeshes created and the process is repeated until all variables are assigned. The cuts shown on the example are not necessarily optimal. (Color figure online)

The created tree has an important property that if two variables have non-zero values on the intersection of their columns and rows, then one of them will either be listed in the elimination tree node that is an ancestor of elimination tree node containing the other variable, or they can be both listed in the same node.

The computational cost of elimination can be analyzed as a sum of costs of elimination of rows for each tree node. Let us make the following set of observations:

• 1. A non-zero element in the initial matrix happens when the two basis functions corresponding to that row and column have overlapping supports (see the example in the left side of Fig. 4). Let us denote the graph generated from the initial matrix (if we consider it to be an adjacency matrix) as an overlap graph. Two variables cannot be neighbors in overlap graph unless the supports of their basis functions overlap.

• 2. When a row is eliminated, the new non-zero elements will be created on the intersection of columns and rows that had non-zero values in the eliminated row or the column of the lead coefficient (see the right side of Fig. 4). If we analyze the matrix as a graph, then elimination of the row corresponding to a graph node will potentially produce edges between all nodes that were neighbors of the node being removed.

• 3. If at any given time during the forward elimination step a non-zero element exists on the intersection of a row and column corresponding to two grid nodes, then either those two nodes are neighbors in the overlap graph, or that there exists a path between those two nodes in the overlap graph that traverses only graph nodes corresponding to rows eliminated already.

• 4. All variables corresponding to the neighboring nodes of the graph node of the variable x in the overlap graph will be either:

  • (a) listed in one of the elimination tree nodes that are descendants of the elimination tree node listing the variable x – and those variables are eliminated already by the time this variable is eliminated, or

  • (b) listed in the same elimination tree node as the variable x, or

  • (c) having support of the corresponding basis function intersected by the boundary of the submesh of the elimination tree node containing the variable x – those graph nodes will be listed in one of the ancestors of the elimination tree node listing the variable x.

  Thus, in the overlap graph there are no edges between nodes that belong to two different elimination tree nodes that are not in an ancestor-descendant relationship. At the same time, any path that connects a pair of non-neighboring nodes in the overlap graph will have to go through at least one graph node corresponding to a variable that is listed in a common ancestor of the elimination tree nodes containing the variables from that pair of nodes.

We can infer from Observations 3 and 4 that by the time a row (or analogously column) is eliminated, the non-zero values can exist only on intersections with other variables eliminated together in the same tree node and variables corresponding to basis functions intersected by the boundary of the subspace of the tree node. During traversal of one tree node we eliminate a variables from b variables with rows or columns potentially modified, where $b-a$ is the number of variables on the boundary of that tree node. Thus, the cost of elimination of variables of a single tree node is equal to the cost of eliminating a variables from a matrix of size b – let us denote that by $C_r(a,b) = \mathcal {O}(ab^2)$.

Fig. 3.

Elimination tree generated in the process shown on Fig. 2. Induced ordering is: 1, 2, 6, 7, then 15, 16, then 4, 5, 9, 11, then 13, 14, 18, 19, then 10, 12, then 3, 8, 17.

4 Quasi-optimal Elimination Trees for Dimensionality q

A method of elimination tree generation will generate quasi-optimal elimination trees for dimensionality q, if each elimination tree generated:

• (a) is a K-nary tree, where $K \ge 2$ is shared by all trees generated (a tree is K-nary if each node has up to K children; a binary tree has $K = 2$.);

• (b) has height not larger than some $H = \lceil {\log _K{N}}\rceil +H_0$, where $H_0$ is a constant for the method (for brevity, let us define the height of the tree H as the longest path from a leaf to the root plus 1; a tree of single root node will have height $H = 1$). This also means that $\mathcal {O}(N)=\mathcal {O}(K^H)$;

• (c) its nodes will not have more than $J \cdot \max (h,K^{\frac{q-1}{q}h})$ variables assigned to each of them; J is some constant shared by each tree generated and h is the height of the whole tree minus the distance of that node from the root (i.e. $h=H$ for the root node, $h=H-1$ for its children, etc. For brevity, later in this paper we will call such defined h as the height of tree node, slightly modifying the usual definition of the height of a node). This limit is equivalent to $J\cdot h$ for $q\le 1$ and $J \cdot K^{\frac{q-1}{q}h}$ for $q>1$);

• (d) for each node, the supports of the variables assigned to that tree node will overlap with no more than $J \cdot \max (h,K^{h\frac{q-1}{q}})$ supports of the variables assigned to tree nodes that are the ancestors of that tree node.

Fig. 4.

On the left, the matrix generated for the mesh from Fig. 2 – potentially non-zero elements are marked in grey. On the right, the first elimination of a row (variable 1) is shown; all the elements changed during that elimination are marked: blue elements are modified with a potentially non-zero value, yellow elements are zeroed. (Color figure online)

For a quasi-optimal elimination tree, the cost of eliminating of all the variables belonging to a tree node $S_h$ with height h will be no more than:

$$\begin{aligned} T = {\left\{ \begin{array}{ll} C_r(J\cdot h , 2 J\cdot h) =O(4J^3h^3) &{} \text {if } q \le 1 \\ C_r(J\cdot (K^{h\frac{q-1}{q}}), 2 J\cdot (K^{h\frac{q-1}{q}})) = \mathcal {O}(4J^3 \cdot (K^{3h\frac{q-1}{q}}) ) &{} \text {if } q>1 \end{array}\right. } \end{aligned}$$

(2)

This means that for $q \le 1$, the computational cost of a solver will be no more than:

$$\begin{aligned} T(N)&= \sum _{h=1}^H \mathcal {O}(K^{H-h}) \cdot \mathcal {O}(4(J^3h^3)) \nonumber \\&\qquad \qquad \qquad \quad \,\, \text {// } There\,\,are\,\,no\,\,more\,\,than\,\,K^{H-h} nodes\,\,of\,\,height\,\,h. \nonumber \\&= \mathcal {O}(4J^3 K^{H}\sum _{h=1}^H(K^{-h}h^3)) \nonumber \\&= \mathcal {O}(4 J^3 K^{H}(\frac{1^3}{K^1} + \frac{2^3}{K^2} + \frac{3^3}{K^3} + \dots + \frac{(H-1)^3}{K^{H-1}}+ \frac{H^3}{K^H})) \nonumber \\&\qquad \quad \! \text {// } This\,\,summation\,\,converges\,\,to\,some\,C \le 26\, (C=26\, for\, K=2). \nonumber \\&= \mathcal {O}(4 J^3 K^H C) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, \text {// } Eliminating\,\, the\,\,constants. \nonumber \\&= \mathcal {O}(K^H) = \mathcal {O}(K^{\log _K(N)}K^{H_0}) = \mathcal {O}(N \cdot K^{H_0}) = \mathcal {O}(N) \end{aligned}$$

(3)

For $q > 1$, the computational cost of the solver will be no more than:

$$\begin{aligned} T(N)&= \sum _{h=1}^H \mathcal {O}(K^{H-h}) \cdot \mathcal {O}(4J^3(K^{3h\frac{q-1}{q}})) = \mathcal {O}(4J^3 \sum _{h=1}^H K^{H - h + 3h\frac{q-1}{q}}) \nonumber \\&= \mathcal {O}(4J^3 K^{H}\sum _{h=1}^H K^{(2 -\frac{3}{q})h}) = \mathcal {O}(4J^3 K^{H}\sum _{h=1}^H (K^{2-\frac{3}{q}})^h) \nonumber \\ \end{aligned}$$

(4)

Then, depending on the value of q, this will become:

$$\begin{aligned} \text {If }1< q < \frac{3}{2}\text { : } \qquad \qquad T(N)&= \mathcal {O}(4J^3K^HK^2\frac{1-K^{H(2-\frac{3}{q})}}{K^{\frac{3}{q}} - K^2}) \nonumber \\&= \mathcal {O}(4J^3K^{H+2}) = \mathcal {O}(K^H) = \mathcal {O}(N) \end{aligned}$$

(5)

$$\begin{aligned} \text {If }q = \frac{3}{2}\text { : }\qquad \qquad T(N)&= \mathcal {O}(4J^3K^H H) = \mathcal {O}(K^H H) \nonumber \\&= \mathcal {O}(K^{\log _K{N}}\log _K{N}) = \mathcal {O}(N\log {N}) \end{aligned}$$

(6)

$$\begin{aligned} \text {If }q > \frac{3}{2}\text { : } \qquad \qquad T(N)&= \mathcal {O}(4J^3K^HK^2\frac{K^{H(2-\frac{3}{q})}-1}{K^2 - K^{\frac{3}{q}}}) \nonumber \\&= \mathcal {O}(4J^3 K^HK^2K^{H(2-\frac{3}{q})}) \nonumber \\&= \mathcal {O}(K^{H+H(2-\frac{3}{q})}) = \mathcal {O}((K^{H})^{3-\frac{3}{q}}) \nonumber \\&= \mathcal {O}(N^{3-\frac{3}{q}}) = \mathcal {O}(N^{3\frac{q-1}{q})}) \end{aligned}$$

(7)

Let us denote a singularity of a shape with Kolmogorov dimension q as q-dimensional singularity. For example, point singularity is 0-dimensional, linear singularity (that is, a singularity in a shape of a curve or line segment) is 1-dimensional, surface singulararity (in shape of a finite surface) is 2-dimensional, etc. A union of finite number of non-fractal singularities will have the Kolmogorov dimension equal to the highest of dimensions of the components, so, for example, a singularity consisting of a finite number of points will also be 0-dimensional.

With the calculation above, if we can show that for a sequence of meshes of consecutive refinement levels over a q-dimensional singularity there exists a method that constructs quasi-optimal elimination trees for dimensionality q, we will prove that there exists a solver algorithm with time complexity defined by the following formula:

$$\begin{aligned} T(N) = {\left\{ \begin{array}{ll} \mathcal {O}(N) &{} \text {if }q < \frac{3}{2} \\[1pt] \mathcal {O}(N\log {N}) &{} \text {if }q = \frac{3}{2} \\[1pt] \mathcal {O}(N^{3\frac{q-1}{q}}) &{} \text {if }q>\frac{3}{2} \end{array}\right. } \end{aligned}$$

(8)

5 h-adaptive Meshes

In this section we will show how the proof framework from the preceding Sect. 4 applies to real meshes by focusing on h-adaptive meshes. Those meshes have basis functions defined over geometrical features of its elements: vertices and segments in 1D, vertices, edges and interiors in 2D, vertices, edges, faces and interiors in 3D, vertices, edges, faces, hyperfaces and interiors in 4D, etc. Basis functions in 2D with their supports have been shown on Fig. 5. For illustrative purposes the h-adaptation analyzed here has only uniform refinements into $2^D$ elements with length of the edge 2 times smaller, where D is the dimensionality of the mesh – the observations will also hold for refinements into any $K^D$ elements for any small natural K.

Fig. 5.

Basis functions of 2-dimensional h-adaptive mesh with $p=2$ and their support – based on vertex, edge and interior respectively.

It is worth noting that, during the mesh adaptation, if the basis functions are created naively, one basis function of lower refinement level can possibly have a support that completely contains the support of another basis function of the same type but higher level. In such instance, the function of lower refinement level will be modified by subtracting the other function multiplied by such factor that it cancels out part of the support of the lower level function, as illustrated in Fig. 6 – let us refer to this procedure as indentation of a basis function. This modification doesn’t change the mathematical properties of the basis, but will significantly reduce the number of non-zero elements in the generated matrix.

Fig. 6.

Basis function indentation.

In addition to the above, a 1-irregularity rule will be enforced: two elements sharing any point cannot differ in refinement level by more than 1 (a variant of 1-irregularity rule constraining elements sharing an edge instead of a vertex is also sometimes used, but the vertex version is easier to analyze). When splitting an element in the refinement process, any larger elements sharing a vertex should be split as well. This procedure will reduce the number of different shapes of basis functions created during the indentation, which will make the implementation easier. At the same time, if not for this rule, a single basis function could have overlap with an arbitrarily large number of other functions what would disrupt the sparsity of the generated matrix, as illustrated in Fig. 7.

Fig. 7.

If 1-irregularity rule is not met, one basis function can overlap any number of others.

It is important to note that during a refinement round an element will be split only if it overlaps a part of singularity or one of its neighbors overlaps a part of singularity, the distance between an element and the closest point of singularity cannot be larger than the length of the size of the element multiplied by a small constant. This has several important implications:

• (a) The number of new elements created with each refinement level is $\mathcal {O}(2^{Rq})$ as refinement level $R \rightarrow \infty$, where q is the Kolmogorov dimension (also known as Minkowski dimension or box-counting dimension) of the singularity (or $\mathcal {O}(K^{Rq})$ if the refinements are into $K^D$ elements). This also means that as $R \rightarrow \infty$, the total number of elements is $\mathcal {O}(R)$ if $q = 0$ or $\mathcal {O}(2^{Rq})$ if $q > 0$. The same will hold for the number of variables, as it is linearly proportional to the number of elements (as long as p is constant).

• (b) If we consider a cut (i.e. a surface, volume, hypervolume, etc. dividing the mesh into two parts) of a mesh with a singularity with a simple topology (i.e. not fractal), then, as $R \rightarrow \infty$, the number of elements intersecting with the cut (assuming that elements are open sets, i.e. don’t contain their boundaries) will grow as $\mathcal {O}(2^{Rs})$ (or $\mathcal {O}(R)$ for $s=0$), where s is the Kolmogorov dimension of the intersection of that cut and the singularity. Intuitively, this observation should also extend to singularities that are well-behaved fractals.

6 Time Complexity of Hierarchical Meshes Based on Singularities

It is easy to see that for topologically simple sets (i.e. non-fractals) of integer Kolmogorov dimension q it is possible to divide them by a cut such that the Kolmogorov dimension of the intersection will be no more than $q-1$. For example, if we consider a singularity in a shape of line segment embedded in 3-dimensional space, any plane that is not parallel to the segment will have intersection of at most a single point. By recursively selecting such a cut that divides elements into two roughly equal parts (that is, as $R \rightarrow \infty$, the proportion of the number of elements in the two parts will approach 1:1), we can generate an elimination tree with cuts having no more than $\mathcal {O}(\max {(R,(2^{Rq})^\frac{q-1}{q})})$ elements (finding the exact method of how such cuts should be generated is out of scope of this paper). The resulting elimination tree will have the following properties:

• 1. Each elimination tree node will have up to two children ($K = 2$).

• 2. As each subtree of a tree node will have at most half of the variables, the height of the tree H will not exceed $\lceil {log_2{N}}\rceil$.

• 3. Depending on the value of q:

  • (a) If $q > 1$, as the R grows by 1, the height of the given subtree grows by about q, but the number of variables that will be cut through grows by about $2^{q-1}$. Thus the number of variables in a root of a subtree of height h will be no more than $J\cdot 2^{\frac{q-1}{q}h }$.

  • (b) If $q \le 1$, each tree node will have at most $J\cdot h$ variables – the number of elements of each refinement level that are being cut through such cut is limited by a constant.

• 4. Variables from a tree node can only overlap with the variables on the boundary of the subspace corresponding to that tree node. The amount of variables of the boundary should not exceed then $J\cdot 2^{\frac{q-1}{q}h }$ if $q>1$ or $J\cdot h$ if $q\le 1$.

Thus, h-adaptive meshes with q-dimensional singularity are quasi-optimal as defined in Sect. 4. To generalize, the same will hold true for any hierarchical meshes that fulfill the following constraints:

• (a) each basis function can be assigned to an element (let us call it an origin of the function) such that its support will not extend further than some constant radius from that element, measured in the number of elements to be traversed (for example, in case of h-adaptation, supports do not extend further than 2 elements from its origin).

• (b) the elements will not have more than B basis functions with supports overlapping them, where B is some small constant specific for the type of mesh; in particular, one element can be the origin of at most B basis functions. For example, h-adaptive mesh in 2D with $p=2$ will have $B=9$, as each element can have at most 4 vertex basis functions, 4 edge basis functions and 1 interior basis function.

• (c) and no basis functions will overlap more than C elements, where C is another some small constant specific for the type of mesh. For example, $C=8$ in h-adaptive mesh in 2D with $p=2$ as long as the 1-irregularity rule is observed, as a basis function defined over a vertex and indented twice can overlap 8 elements.

Those constraints are also met by meshes with T-splines or with meshes in which elements have shapes of triangles, which means that well formed hierarchically adapted meshes can be solved by direct solvers with time complexity of $\mathcal {O}(\max (N, N^{3\frac{q-1}{q}}))$, where N is the number of nodes and q is the dimensionality of the singularity.This means that for point, edge and face singularities, the time complexity will be $\mathcal {O}(N)$, $\mathcal {O}(N)$ and $\mathcal {O}(N^{1.5})$ respectively, which corresponds to the current results in the literature for both two and three dimensional meshes [6, 15]. For higher dimensional singularities, the resulting time complexity is $\mathcal {O}(N^2)$, $\mathcal {O}(N^{2.25})$, $\mathcal {O}(N^2.4)$ and $\mathcal {O}(N^2.5)$ for singularities of dimensionality 3, 4, 5 and 6 respectively.

An important observation here is that the time complexity does not change when the dimensionality of the mesh changes, as long as the dimensionality of the singularity stays the same.

7 Conclusions and Future Work

In this paper we have shown that for meshes hierarchically adapted towards singularities there exists an order of variable elimination that results in computational complexity of direct solvers not worse than $\mathcal {O}(\max (N, N^{3\frac{D-1}{D}}))$, where N is the number of nodes and q is the dimensionality of the singularity. This formula does not depend on the spatial dimensionality of the mesh. We have also shown the relationship between the time complexity and the Kolmogorov dimension of the singularity.

Additionally, we claim the following conjecture:

Conjecture 1

For any set of points S with Kolmogorov dimension $q \ge 1$ defined in Euclidean space with dimension D and any point in that space p there exists a cut of the space that divides the set S into two parts of equal size, for which the intersection of that cut and the set S has Kolmogorov dimension of $q-1$ or less. Parts of equal size for $q < D$ are to be meant intuivitely: as the size of covering boxes (as defined in the definition of Kolmogorov dimension) decreases to 0, the difference between the number of boxes in both parts should decrease to 0.

It remains to be verified if the Conjecture 1 is true for well-behaved fractals and what kinds of fractals can be thought of as well behaved. If so, then meshes of the kinds that fulfill the constraints set in previous Sect. 6 built on a signularities in the shape of well-behaved fractals of non-integer Kolmogorov dimension q can be also solved with time complexity stated in Eq. 8. The proof of the conjecture is left for future work.

We can however illustrate the principle by the example of Sierpinski’s triangle – a fractal of Kolmogorov dimension of $\frac{\log {3}}{\log {2}} = 1.58496250072116\dots$. To build an elimination tree, we will divide the space into three roughly equal parts as shown in Fig. 8. The Kolmogorov dimension of the boundary of such division is 0, which is less than $\frac{\log {3}}{\log {2}}-1$.

Fig. 8.

Division of the space for Sierpinski triangle.

As the refinement level R grows, the number of elements grows as $\mathcal {O}(2^{\frac{\log {3}}{\log {2}}R})=\mathcal {O}(3^R)$ and as the elimination tree s ternary, the partition tree will have height of $\log _3{3^R} + H_0 = \log _K{N} + H_0$. In addition, as the Kolmogorov dimension of the boundary of each elimination tree node is 0, there are at most $\mathcal {O}(\log {h})$ variables in each elimination tree node and on the overlap with nodes of ancestors is also limited by the same number. As this number is less than $\mathcal {O}(3^{h\frac{q-1}{q}})$, both conditions of quasi-optimal mesh with q-dimensional singularity are met, which means that it is possible to solve system build on a singularity of the shape of Sierpinski triangle in time not worse than $\mathcal {O}(N^ {3\frac{\log {3}/\log {2}-1}{\log {3}/\log {2}}}) = \mathcal {O}(N^{1.10721\dots })$.