Abstract
We present a framework for formal refutational completeness proofs of abstract provers that implement saturation calculi, such as ordered resolution or superposition. The framework relies on modular extensions of lifted redundancy criteria. It allows us to extend redundancy criteria so that they cover subsumption, and also to model entire prover architectures in such a way that the static refutational completeness of a calculus immediately implies the dynamic refutational completeness of a prover implementing the calculus, for instance within an Otter or
 loop. Our framework is mechanized in Isabelle/
loop. Our framework is mechanized in Isabelle/
 .
.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In their Handbook chapter [5, Sect. 4], Bachmair and Ganzinger remark that “unfortunately, comparatively little effort has been devoted to a formal analysis of redundancy and other fundamental concepts of theorem proving strategies, while more emphasis has been placed on investigating the refutational completeness of a variety of modifications of inference rules, such as resolution.” As a remedy, they present an abstract framework for saturation up to redundancy. Briefly, theorem proving derivations take the form \(N_0 \rhd N_1 \rhd \cdots \), where \(N_0\) is the initial clause set and each step either adds inferred clauses or deletes redundant clauses. Given a suitable notion of fairness, the limit \(N_*\) of a fair derivation is saturated up to redundancy. If the calculus is refutationally complete and \(N_*\) does not contain the false clause \(\bot \), then \(N_0\) has a model.
Bachmair and Ganzinger also define a concrete prover, \(\mathsf {RP}\), based on a first-order ordered resolution calculus and the given clause procedure. However, like all realistic resolution provers, \(\mathsf {RP}\) implements subsumption deletion. This operation is not covered by the standard definition of redundancy, according to which a clause C is redundant w.r.t. a clause set N if all its ground instances \(C\theta \) are entailed by strictly smaller ground instances of clauses belonging to N. As a result, \(\mathsf {RP}\)-derivations are not \(\rhd \)-derivations, and the framework is not applicable.
There are two ways to address this problem. In the Handbook, Bachmair and Ganzinger start from scratch and prove the dynamic refutational completeness of \(\mathsf {RP}\) by relating nonground derivations to ground derivations. This proof, though, turns out to be rather nonmodular—it refers simultaneously to properties of the calculus, to properties of the prover, and to the fairness of the derivations. Extending it to other calculi or prover architectures would be costly. As a result, most authors stop after proving static refutational completeness of their calculi.
An alternative approach is to extend the redundancy criterion so that subsumed clauses become redundant. As demonstrated by Bachmair and Ganzinger in 1990 [3], this is possible by redefining redundancy in terms of closures \((C,\theta )\) instead of ground instances \(C\theta \). We show that this approach can be generalized and modularized: First, any redundancy criterion that is obtained by lifting a ground criterion can be extended to a redundancy criterion that supports subsumption without affecting static refutational completeness (Sect. 3). Second, by applying this property to labeled formulas, it becomes possible to give generic completeness proofs for prover architectures in a straightforward way.
Most saturation provers implement a variant of the given clause procedure. We present an abstract version of the procedure (Sect. 4) that can be refined to obtain an Otter [18] or
 [1] loop and prove it refutationally complete. We also present a generalization that decouples scheduling and computation of inferences, to support orphan deletion [16, 25] and dovetailing [9].
[1] loop and prove it refutationally complete. We also present a generalization that decouples scheduling and computation of inferences, to support orphan deletion [16, 25] and dovetailing [9].
When these prover architectures are instantiated with a concrete saturation calculus, the dynamic refutational completeness of the combination follows in a modular way from the properties of the prover architecture and the static refutational completeness proof for the calculus. Thus, the framework is applicable to a wide range of calculi, including ordered resolution [5], unfailing completion [2], standard superposition [4], constraint superposition [19], theory superposition [28], hierarchic superposition [7], and clausal \(\lambda \)-superposition [9].
Detailed proofs are included in a technical report [29], together with more explanations, examples, and discussions. When Schlichtkrull, Blanchette, Traytel, and Waldmann [24] mechanized Bachmair and Ganzinger’s chapter using the Isabelle/
 proof assistant [21], they found quite a few mistakes, including one that compromised \(\mathsf {RP}\)’s dynamic refutational completeness. This motivated us to mechanize our framework as well (Sect. 5).
proof assistant [21], they found quite a few mistakes, including one that compromised \(\mathsf {RP}\)’s dynamic refutational completeness. This motivated us to mechanize our framework as well (Sect. 5).
2 Preliminaries
Inferences and Redundancy. Let A be a set. An A-sequence is a finite sequence \((a_i)_{i=0}^k = a_0,a_1,\ldots ,a_k\) or an infinite sequence \((a_i)_{i=0}^\infty = a_0,a_1,\ldots \) with \(a_i \in A\) for all i. We write \((a_i)_{i\ge 0}\) or \((a_i)_i\) for both finite and infinite sequences. Nonempty sequences can be split into a head \(a_0\) and a tail \((a_i)_{i\ge 1}\). Given \({\rhd } \subseteq A \times A\), a \(\rhd \)-derivation is a nonempty A-sequence such that \(a_i \rhd a_{i+1}\) for all i.
A set \({\mathbf {F}}\) of formulas is a set with a nonempty subset \({\mathbf {F}}_\bot \subseteq {\mathbf {F}}\). Elements of \({\mathbf {F}}_\bot \) represent false. Typically, \({\mathbf {F}}_\bot := \{\bot \}\). In Sect. 4, different elements of \({\mathbf {F}}_\bot \) will represent different situations in which a contradiction has been derived.
A consequence relation  over \({\mathbf {F}}\) is a relation
over \({\mathbf {F}}\) is a relation  with the following properties for all \(N_1, N_2, N_3 \subseteq {\mathbf {F}}\):
with the following properties for all \(N_1, N_2, N_3 \subseteq {\mathbf {F}}\):
-
(C1)
 for every \(\bot \in {\mathbf {F}}_\bot \);
for every \(\bot \in {\mathbf {F}}_\bot \); -
(C2)
\(N_2 \subseteq N_1\) implies
 ;
; -
(C3)
if
 for every \(C \in N_2\), then
for every \(C \in N_2\), then  ;
; -
(C4)
if
 and
and  , then
, then  .
.
Consequence relations are used to discuss soundness (and the addition of formulas) and to discuss refutational completeness (and the deletion of formulas). An example that requires this distinction is constraint superposition [19], where one uses entailment w.r.t. the set of all ground instances,  , for soundness, but entailment w.r.t. a subset of those instances,
, for soundness, but entailment w.r.t. a subset of those instances,  , for refutational completeness. Some calculus-dependent argument is then necessary to show that refutational completeness w.r.t.
, for refutational completeness. Some calculus-dependent argument is then necessary to show that refutational completeness w.r.t.  implies refutational completeness w.r.t.
implies refutational completeness w.r.t.  .
.
An \({\mathbf {F}}\)-inference \(\iota \) is a tuple \((C_n,\ldots ,C_0) \in {\mathbf {F}}^{n+1}\), \(n \ge 0\). The formulas \(C_n,\ldots , C_1\) are called premises of \(\iota \); \(C_0\) is called the conclusion of \(\iota \), denoted by \( concl (\iota )\). An \({\mathbf {F}}\)-inference system \( Inf \) is a set of \({\mathbf {F}}\)-inferences. If \(N \subseteq {\mathbf {F}}\), we write \( Inf (N)\) for the set of all inferences in \( Inf \) whose premises are contained in N, and \( Inf (N, M) := Inf (N \cup M) \setminus Inf (N \setminus M)\) for the set of all inferences in \( Inf \) such that one premise is in M and the other premises are contained in \(N \cup M\).
A redundancy criterion for an inference system \( Inf \) and a consequence relation  is a pair \( Red = ( Red _{\mathrm {I}}, Red _{\mathrm {F}})\), where \( Red _{\mathrm {I}}: \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}( Inf )\) and \( Red _{\mathrm {F}}: \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}({\mathbf {F}})\) are mappings that satisfy the following conditions for all \(N, N'\):
is a pair \( Red = ( Red _{\mathrm {I}}, Red _{\mathrm {F}})\), where \( Red _{\mathrm {I}}: \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}( Inf )\) and \( Red _{\mathrm {F}}: \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}({\mathbf {F}})\) are mappings that satisfy the following conditions for all \(N, N'\):
-
(R1)
if
 for some \(\bot \in {\mathbf {F}}_\bot \), then
for some \(\bot \in {\mathbf {F}}_\bot \), then  ;
; -
(R2)
if \(N \subseteq N'\), then \( Red _{\mathrm {F}}(N) \subseteq Red _{\mathrm {F}}(N')\) and \( Red _{\mathrm {I}}(N) \subseteq Red _{\mathrm {I}}(N')\);
-
(R3)
if \(N' \subseteq Red _{\mathrm {F}}(N)\), then \( Red _{\mathrm {F}}(N) \subseteq Red _{\mathrm {F}}(N \setminus N')\) and \( Red _{\mathrm {I}}(N) \subseteq Red _{\mathrm {I}}(N \setminus N')\);
-
(R4)
if \(\iota \in Inf \) and \( concl (\iota ) \in N\), then \(\iota \in Red _{\mathrm {I}}(N)\).
Inferences in \( Red _{\mathrm {I}}(N)\) and formulas in \( Red _{\mathrm {F}}(N)\) are called redundant w.r.t. N.Footnote 1 Intuitively, (R1) states that deleting redundant formulas preserves inconsistency. (R2) and (R3) state that formulas or inferences that are redundant w.r.t. a set N remain redundant if arbitrary formulas are added to N or redundant formulas are deleted from N. (R4) ensures that computing an inference makes it redundant.
We define the relation
 such that
such that
 if and only if
if and only if
 .
.
Refutational Completeness. Let  be a consequence relation, let \( Inf \) be an inference system, and let \( Red \) be a redundancy criterion for
be a consequence relation, let \( Inf \) be an inference system, and let \( Red \) be a redundancy criterion for  and \( Inf \).
and \( Inf \).
A set \(N \subseteq {\mathbf {F}}\) is called saturated w.r.t. \( Inf \) and \( Red \) if \( Inf (N) \subseteq Red _{\mathrm {I}}(N)\). The pair \(( Inf , Red )\) is called statically refutationally complete w.r.t.  if for every saturated set \(N \subseteq {\mathbf {F}}\) such that
if for every saturated set \(N \subseteq {\mathbf {F}}\) such that  for some \(\bot \in {\mathbf {F}}_\bot \), there exists a \(\bot ' \in {\mathbf {F}}_\bot \) such that \(\bot ' \in N\).
for some \(\bot \in {\mathbf {F}}_\bot \), there exists a \(\bot ' \in {\mathbf {F}}_\bot \) such that \(\bot ' \in N\).
Let \((N_i)_i\) be a \(\mathcal {P}({\mathbf {F}})\)-sequence. Its limit is the set  . Its union is the set
. Its union is the set  . A sequence is called fair if
. A sequence is called fair if  . The pair \(( Inf , Red )\) is called dynamically refutationally complete w.r.t.
. The pair \(( Inf , Red )\) is called dynamically refutationally complete w.r.t.  if for every fair
if for every fair
 derivation \((N_i)_i\) such that
derivation \((N_i)_i\) such that  for some \(\bot \in {\mathbf {F}}_\bot \), we have \(\bot ' \in N_i\) for some i and some \(\bot ' \in {\mathbf {F}}_\bot \). Properties (R1)–(R3) allow the passage from a static set of formulas to a dynamic prover:
for some \(\bot \in {\mathbf {F}}_\bot \), we have \(\bot ' \in N_i\) for some i and some \(\bot ' \in {\mathbf {F}}_\bot \). Properties (R1)–(R3) allow the passage from a static set of formulas to a dynamic prover:
Lemma 1
\(( Inf , Red )\) is dynamically refutationally complete w.r.t.  if and only if it is statically refutationally complete w.r.t.
if and only if it is statically refutationally complete w.r.t.  .
.
Intersections of Redundancy Criteria. In the sequel, it will be useful to define consequence relations and redundancy criteria as intersections of previously defined consequence relations or redundancy criteria.
Let Q be an arbitrary set, and let  be a Q-indexed family of consequence relations over \({\mathbf {F}}\). Then
be a Q-indexed family of consequence relations over \({\mathbf {F}}\). Then  qualifies as a consequence relation. Moreover, let \( Inf \) be an inference system, and let \(( Red ^q)_{q \in Q}\) be a Q-indexed family of redundancy criteria, where each \( Red ^q = ( Red _{\mathrm {I}}^q, Red _{\mathrm {F}}^q)\) is a redundancy criterion for \( Inf \) and
qualifies as a consequence relation. Moreover, let \( Inf \) be an inference system, and let \(( Red ^q)_{q \in Q}\) be a Q-indexed family of redundancy criteria, where each \( Red ^q = ( Red _{\mathrm {I}}^q, Red _{\mathrm {F}}^q)\) is a redundancy criterion for \( Inf \) and  . Let
. Let  and
and  . Then \( Red ^\cap := ( Red _{\mathrm {I}}^\cap , Red _{\mathrm {F}}^\cap )\) qualifies as a redundancy criterion for
. Then \( Red ^\cap := ( Red _{\mathrm {I}}^\cap , Red _{\mathrm {F}}^\cap )\) qualifies as a redundancy criterion for  and \( Inf \).
and \( Inf \).
Lemma 2
A set \(N \subseteq {\mathbf {F}}\) is saturated w.r.t. \( Inf \) and \( Red ^\cap \) if and only if it is saturated w.r.t. \( Inf \) and \( Red ^q\) for every \(q \in Q\).
Often, the consequence relations  agree for all \(q \in Q\). For calculi where they disagree, such as constraint superposition [19], one can typically demonstrate the static refutational completeness of \(( Inf , Red ^\cap )\) in the following form:
agree for all \(q \in Q\). For calculi where they disagree, such as constraint superposition [19], one can typically demonstrate the static refutational completeness of \(( Inf , Red ^\cap )\) in the following form:
Lemma 3
If for every set \(N \subseteq {\mathbf {F}}\) that is saturated w.r.t. \( Inf \) and \( Red ^\cap \) and does not contain any \(\bot ' \in {\mathbf {F}}_\bot \) there exists some \(q \in Q\) such that  for some \(\bot \in {\mathbf {F}}_\bot \), then \(( Inf , Red ^\cap )\) is statically refutationally complete w.r.t.
for some \(\bot \in {\mathbf {F}}_\bot \), then \(( Inf , Red ^\cap )\) is statically refutationally complete w.r.t.  .
.
3 Lifting
A standard approach for establishing the refutational completeness of a calculus is to first concentrate on the ground case and then lift the results to the nonground case. In this section, we show how to perform this lifting abstractly, given a suitable grounding function \({\mathcal {G}}\). The function maps every formula \(C \in {\mathbf {F}}\) to a set \({\mathcal {G}}(C)\) of formulas from a set of formulas \({\mathbf {G}}\). Depending on the logic and the calculus, \({\mathcal {G}}(C)\) may be, for example, the set of all ground instances of C or a subset thereof. Similarly, \({\mathcal {G}}\) maps \( FInf \)-inferences to sets of \( GInf \)-inferences.
There are calculi where some \( FInf \)-inferences \(\iota \) do not have a counterpart in \( GInf \), such as the PosExt inferences of higher-order superposition calculi [9]. In these cases, we set \({\mathcal {G}}(\iota ) = undef \).
Standard Lifting. Given two sets of formulas \({\mathbf {F}}\) and \({\mathbf {G}}\), an \({\mathbf {F}}\)-inference system \( FInf \), a \({\mathbf {G}}\)-inference system \( GInf \), and a redundancy criterion \( Red \) for \( GInf \), let \({\mathcal {G}}\) be a function that maps every formula in \({\mathbf {F}}\) to a subset of \({\mathbf {G}}\) and every \({\mathbf {F}}\)-inference in \( FInf \) to \( undef \) or to a subset of \( GInf \). \({\mathcal {G}}\) is called a grounding function if
-
(G1)
for every \(\bot \in {\mathbf {F}}_\bot \), \(\emptyset \not = {\mathcal {G}}(\bot ) \subseteq {\mathbf {G}}_\bot \);
-
(G2)
for every \(C \in {\mathbf {F}}\), if \(\bot \in {\mathcal {G}}(C)\) and \(\bot \in {\mathbf {G}}_\bot \) then \(C \in {\mathbf {F}}_\bot \);
-
(G3)
for every \(\iota \in FInf \), if \({\mathcal {G}}(\iota ) \not = undef \), then \({\mathcal {G}}(\iota ) \subseteq Red _{\mathrm {I}}({\mathcal {G}}( concl (\iota )))\).
\({\mathcal {G}}\) is extended to sets \(N \subseteq {\mathbf {F}}\) by defining  . Analogously, for a set \(I \subseteq FInf \),
. Analogously, for a set \(I \subseteq FInf \),  .
.
Example 4
In standard superposition, \({\mathbf {F}}\) is the set of all universally quantified first-order clauses over some signature \(\Sigma \), \({\mathbf {G}}\) is the set of all ground first-order clauses over \(\Sigma \), and \({\mathcal {G}}\) maps every clause C to the set of its ground instances \(C\theta \) and every superposition inference \(\iota \) to the set of its ground instances \(\iota \theta \).
Let \({\mathcal {G}}\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf \), and let \({\models }\) be a consequence relation over \({\mathbf {G}}\). We define the relation \({\models _{\mathcal {G}}} \subseteq \mathcal {P}({\mathbf {F}}) \times \mathcal {P}({\mathbf {F}})\) such that \(N_1 \models _{\mathcal {G}}N_2\) if and only if \({\mathcal {G}}(N_1) \models {\mathcal {G}}(N_2)\). We call \({\models _{\mathcal {G}}}\) the \({\mathcal {G}}\)-lifting of \({\models }\). It qualifies as a consequence relation over \({\mathbf {F}}\) and corresponds to Herbrand entailment. If Tarski entailment (i.e.,  if and only if any model of \(N_1\) is also a model of \(N_2\)) is desired, the mismatch can be repaired by showing that the two notions of entailment are equivalent as far as refutations are concerned.
if and only if any model of \(N_1\) is also a model of \(N_2\)) is desired, the mismatch can be repaired by showing that the two notions of entailment are equivalent as far as refutations are concerned.
Let \( Red = ( Red _{\mathrm {I}}, Red _{\mathrm {F}})\) be a redundancy criterion for \(\models \) and \( GInf \). We define functions \( Red _{\mathrm {I}}^{\mathcal {G}}: \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}( FInf )\) and \( Red _{\mathrm {F}}^{\mathcal {G}}: \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}({\mathbf {F}})\) by

We call \( Red ^{\mathcal {G}}:= ( Red _{\mathrm {I}}^{\mathcal {G}}, Red _{\mathrm {F}}^{\mathcal {G}})\) the \({\mathcal {G}}\)-lifting of \( Red \). It qualifies as a redundancy criterion for \(\models _{\mathcal {G}}\) and \( FInf \). We get the following folklore theorem:
Theorem 5
If \(( GInf , Red )\) is statically refutationally complete w.r.t. \(\models \), and if we have \( GInf ({\mathcal {G}}(N)) \subseteq {\mathcal {G}}( FInf (N)) \cup Red _{\mathrm {I}}({\mathcal {G}}(N))\) for every \(N \subseteq {\mathbf {F}}\) that is saturated w.r.t. \( FInf \) and \( Red ^{\mathcal {G}}\), then \(( FInf , Red ^{\mathcal {G}})\) is statically refutationally complete w.r.t. \(\models _{\mathcal {G}}\).
Adding Tiebreaker Orderings. We now strengthen the \({\mathcal {G}}\)-lifting of redundancy criteria to also support subsumption deletion. Let \(\sqsupset \) be a well-founded strict partial ordering on \({\mathbf {F}}\). We define \( Red _{\mathrm {F}}^{{\mathcal {G}},\sqsupset } : \mathcal {P}({\mathbf {F}}) \rightarrow \mathcal {P}({\mathbf {F}})\) as follows:

Notice how  is used to break ties between C and \(C'\), possibly making C redundant. We call \( Red ^{{\mathcal {G}},\sqsupset } := ( Red _{\mathrm {I}}^{\mathcal {G}}, Red _{\mathrm {F}}^{{\mathcal {G}},\sqsupset })\) the \(({\mathcal {G}},\sqsupset )\)-lifting of \( Red \). We get the previously defined \( Red ^{\mathcal {G}}\) as a special case of \( Red ^{{\mathcal {G}},\sqsupset }\) by setting
is used to break ties between C and \(C'\), possibly making C redundant. We call \( Red ^{{\mathcal {G}},\sqsupset } := ( Red _{\mathrm {I}}^{\mathcal {G}}, Red _{\mathrm {F}}^{{\mathcal {G}},\sqsupset })\) the \(({\mathcal {G}},\sqsupset )\)-lifting of \( Red \). We get the previously defined \( Red ^{\mathcal {G}}\) as a special case of \( Red ^{{\mathcal {G}},\sqsupset }\) by setting  .
.
We obtain our first main result:
Theorem 6
Let \( Red \) be a redundancy criterion for \(\models \) and \( GInf \), let \({\mathcal {G}}\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf \), and let \(\sqsupset \) be a well-founded strict partial ordering on \({\mathbf {F}}\). Then the \(({\mathcal {G}},\sqsupset )\)-lifting \( Red ^{{\mathcal {G}},\sqsupset }\) of \( Red \) is a redundancy criterion for \(\models _{\mathcal {G}}\) and \( FInf \).
Observe that \(\sqsupset \) appears only in the second component of \( Red ^{{\mathcal {G}},\sqsupset } = ( Red _{\mathrm {I}}^{\mathcal {G}}, Red _{\mathrm {F}}^{{\mathcal {G}},\sqsupset })\) and that the definitions of a saturated set and of static refutational completeness do not depend on the second component of a redundancy criterion. The following lemmas are immediate consequences of these observations:
Lemma 7
A set \(N \subseteq {\mathbf {F}}\) is saturated w.r.t. \( FInf \) and \( Red ^{{\mathcal {G}},\sqsupset }\) if and only if it is saturated w.r.t. \( FInf \) and \( Red ^{{\mathcal {G}},\emptyset }\).
Lemma 8
\(( FInf , Red ^{{\mathcal {G}},\sqsupset })\) is statically refutationally complete w.r.t. \(\models _{\mathcal {G}}\) if and only if \(( FInf , Red ^{{\mathcal {G}},\emptyset })\) is statically refutationally complete w.r.t. \(\models _{\mathcal {G}}\).
Combining Lemmas 1 and 8, we obtain our second main result:
Theorem 9
Let \( Red \) be a redundancy criterion for \(\models \) and \( GInf \), let \({\mathcal {G}}\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf \), and let \(\sqsupset \) be a well-founded strict partial ordering on \({\mathbf {F}}\). If \(( FInf , Red ^{{\mathcal {G}},\emptyset })\) is statically refutationally complete w.r.t. \(\models _{\mathcal {G}}\), then \(( FInf , Red ^{{\mathcal {G}},\sqsupset })\) is dynamically refutationally complete w.r.t. \(\models _{\mathcal {G}}\).
Example 10
For resolution or superposition in standard first-order logic, we can define the subsumption quasi-ordering  on clauses by
on clauses by  if and only if \(C = C'\sigma \) for some substitution \(\sigma \). The subsumption ordering
if and only if \(C = C'\sigma \) for some substitution \(\sigma \). The subsumption ordering  is well founded. By choosing
is well founded. By choosing  , we obtain a criterion \( Red ^{{\mathcal {G}},\sqsupset }\) that includes standard redundancy and also supports subsumption deletion. Similarly, for proof calculi modulo associativity and commutativity, we can let
, we obtain a criterion \( Red ^{{\mathcal {G}},\sqsupset }\) that includes standard redundancy and also supports subsumption deletion. Similarly, for proof calculi modulo associativity and commutativity, we can let  be true if there exists a substitution \(\sigma \) such that C equals \(C'\sigma \) up to the equational theory.
be true if there exists a substitution \(\sigma \) such that C equals \(C'\sigma \) up to the equational theory.
Example 11
Constraint superposition with ordering constraints [19] is an example of a calculus where the subsumption ordering  is not well founded: A ground instance of a constrained clause \(C\,[\![K]\!]\) is a ground clause \(C\theta \) for which \(K\theta \) evaluates to true. Define
is not well founded: A ground instance of a constrained clause \(C\,[\![K]\!]\) is a ground clause \(C\theta \) for which \(K\theta \) evaluates to true. Define  by stating that
by stating that  if and only if every ground instance of \(C\,[\![K]\!]\) is a ground instance of \(C'\,[\![K']\!]\), and define
if and only if every ground instance of \(C\,[\![K]\!]\) is a ground instance of \(C'\,[\![K']\!]\), and define  . If \(\succ \) is a simplification ordering, then
. If \(\succ \) is a simplification ordering, then  is an infinite chain.
is an infinite chain.
Example 12
For higher-order calculi such as higher-order resolution [17] and clausal \(\lambda \)-superposition [9], subsumption is also not well founded, as witnessed by the chain 
Even if the subsumption ordering for some logic is not well founded, as in the two examples above, we can always define \(\sqsupset \) as the intersection of the subsumption ordering and an appropriate ordering based on formula sizes or weights.
Conversely, the \(\sqsupset \) relation can be more general than subsumption. In Sect. 4, we will use it to justify the movement of formulas between sets in the given clause procedure.
Example 13
For some superposition-based decision procedures [6], one would like to define \(\sqsupset \) as the reverse subsumption ordering  on first-order clauses. Even though
on first-order clauses. Even though  is not well founded in general, it is well founded on \(\{C \in {\mathbf {F}} \mid D \in {\mathcal {G}}(C) \}\) for every \(D \in {\mathbf {G}}\). As shown in the technical report [29], our framework can be extended to support this case by defining \( Red _{\mathrm {F}}^{{\mathcal {G}},\sqsupset }\) using a \({\mathbf {G}}\)-indexed family \((\sqsupset _D)_{D \in {\mathbf {G}}}\) of well-founded strict partial orderings instead of a single \(\sqsupset \).
is not well founded in general, it is well founded on \(\{C \in {\mathbf {F}} \mid D \in {\mathcal {G}}(C) \}\) for every \(D \in {\mathbf {G}}\). As shown in the technical report [29], our framework can be extended to support this case by defining \( Red _{\mathrm {F}}^{{\mathcal {G}},\sqsupset }\) using a \({\mathbf {G}}\)-indexed family \((\sqsupset _D)_{D \in {\mathbf {G}}}\) of well-founded strict partial orderings instead of a single \(\sqsupset \).
Intersections of Liftings. The above results can be extended in a straightforward way to intersections of lifted redundancy criteria. As before, let \({\mathbf {F}}\) and \({\mathbf {G}}\) be two sets of formulas, and let \( FInf \) be an \({\mathbf {F}}\)-inference system. In addition, let Q be a set. For every \(q \in Q\), let  be a consequence relation over \({\mathbf {G}}\), let \( GInf ^q\) be a \({\mathbf {G}}\)-inference system, let \( Red ^q\) be a redundancy criterion for
be a consequence relation over \({\mathbf {G}}\), let \( GInf ^q\) be a \({\mathbf {G}}\)-inference system, let \( Red ^q\) be a redundancy criterion for  and \( GInf ^q\), and let \({\mathcal {G}}^q\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf ^q\). Let \(\sqsupset \) be a well-founded strict partial ordering on \({\mathbf {F}}\).
and \( GInf ^q\), and let \({\mathcal {G}}^q\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf ^q\). Let \(\sqsupset \) be a well-founded strict partial ordering on \({\mathbf {F}}\).
For each \(q \in Q\), we know by Theorem 6 that the \({({\mathcal {G}}^q,\emptyset )}\)-lifting \( Red ^{q,{\mathcal {G}}^q,\emptyset } = ( Red _{\mathrm {I}}^{q,{\mathcal {G}}^q}, Red _{\mathrm {F}}^{q,{\mathcal {G}}^q,\emptyset })\) and the \({({\mathcal {G}}^q,\sqsupset )}\)-lifting \( Red ^{q,{\mathcal {G}}^q,\sqsupset } = ( Red _{\mathrm {I}}^{q,{\mathcal {G}}^q}, Red _{\mathrm {F}}^{q,{\mathcal {G}}^q,\sqsupset })\) of \( Red ^q\) are redundancy criteria for \(\models ^{q}_{{\mathcal {G}}^q}\) and \( FInf \). Consequently, the intersections

are redundancy criteria for  and \( FInf \).
and \( FInf \).
Theorem 14
If \(( GInf ^q, Red ^q)\) is statically refutationally complete w.r.t. \(\models ^q\) for every \(q \in Q\), and if for every \(N \subseteq {\mathbf {F}}\) that is saturated w.r.t. \( FInf \) and \( Red ^{\cap {\mathcal {G}}}\) there exists a q such that \( GInf ^q({\mathcal {G}}^q(N)) \subseteq {\mathcal {G}}^q( FInf (N)) \cup Red _{\mathrm {I}}^q({\mathcal {G}}^q(N))\), then \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.  .
.
Lemma 15
A set \(N \subseteq {\mathbf {F}}\) is saturated w.r.t. \( FInf \) and \( Red ^{\cap {\mathcal {G}},\sqsupset }\) if and only if it is saturated w.r.t. \( FInf \) and \( Red ^{\cap {\mathcal {G}}}\).
Lemma 16
\(( FInf , Red ^{\cap {\mathcal {G}},\sqsupset })\) is statically refutationally complete w.r.t.  if and only if \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.
if and only if \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.  .
.
Theorem 17
If \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.  , then \(( FInf , Red ^{\cap {\mathcal {G}},\sqsupset })\) is dynamically refutationally complete w.r.t.
, then \(( FInf , Red ^{\cap {\mathcal {G}},\sqsupset })\) is dynamically refutationally complete w.r.t.  .
.
Example 18
Intersections of liftings are needed to support selection functions in superposition [4]. The calculus \( FInf \) is parameterized by a function \( fsel \) on the set \({\mathbf {F}}\) of first-order clauses that selects a subset of the negative literals in each \(C \in {\mathbf {F}}\). There are several ways to extend \( fsel \) to a selection function \( gsel \) on the set \({\mathbf {G}}\) of ground clauses such that for every \(D \in {\mathbf {G}}\) there exists some \(C \in {\mathbf {F}}\) such that \(D = C\theta \) and D and C have corresponding selected literals. For every such \( gsel \),  is first-order entailment, \( GInf ^{ gsel }\) is the set of ground inferences satisfying \({ gsel }\), and \( Red ^{ gsel }\) is the redundancy criterion for \( GInf ^{ gsel }\). The grounding function \({\mathcal {G}}^{ gsel }\) maps \(C \in {\mathbf {F}}\) to \(\{C\theta \in {\mathbf {G}} \mid \theta \text { is a substitution} \}\) and \(\iota \in FInf \) to the set of ground instances of \(\iota \) in \( GInf ^{ gsel }\) with corresponding literals selected in the premises. In the static refutational completeness proof, only one \( gsel \) is needed, but this \( gsel \) is not known during a derivation, so fairness must be guaranteed w.r.t. \( Red _{\mathrm {I}}^{{ gsel },{\mathcal {G}}^{ gsel }}\) for every possible extension \( gsel \) of \( fsel \). Thus, checking \( Red _{\mathrm {I}}^{\cap {\mathcal {G}}}\) amounts to a worst-case analysis, where we must assume that every ground instance \({C\theta }\) of a premise \(C \in {\mathbf {F}}\) inherits the selection of C.
is first-order entailment, \( GInf ^{ gsel }\) is the set of ground inferences satisfying \({ gsel }\), and \( Red ^{ gsel }\) is the redundancy criterion for \( GInf ^{ gsel }\). The grounding function \({\mathcal {G}}^{ gsel }\) maps \(C \in {\mathbf {F}}\) to \(\{C\theta \in {\mathbf {G}} \mid \theta \text { is a substitution} \}\) and \(\iota \in FInf \) to the set of ground instances of \(\iota \) in \( GInf ^{ gsel }\) with corresponding literals selected in the premises. In the static refutational completeness proof, only one \( gsel \) is needed, but this \( gsel \) is not known during a derivation, so fairness must be guaranteed w.r.t. \( Red _{\mathrm {I}}^{{ gsel },{\mathcal {G}}^{ gsel }}\) for every possible extension \( gsel \) of \( fsel \). Thus, checking \( Red _{\mathrm {I}}^{\cap {\mathcal {G}}}\) amounts to a worst-case analysis, where we must assume that every ground instance \({C\theta }\) of a premise \(C \in {\mathbf {F}}\) inherits the selection of C.
Example 19
Intersections of liftings are also necessary for constraint superposition calculi [19]. Here the calculus \( FInf \) operates on the set \({\mathbf {F}}\) of first-order clauses with constraints. For a convergent rewrite system R,  is first-order entailment up to R on the set \({\mathbf {G}}\) of unconstrained ground clauses, \( GInf ^R\) is the set of ground superposition inferences, and \( Red ^R\) is redundancy up to R. The grounding function \({\mathcal {G}}^R\) maps \(C\,[\![K]\!] \in {\mathbf {F}}\) to \(\{D \in {\mathbf {G}} \mid D = C\theta ,\ K\theta = \mathrm {true},\ x\theta \text { is R-irreducible for all } x \}\)Footnote 2 and \(\iota \in FInf \) to the set of ground instances of \(\iota \) where the premises and conclusion of \({\mathcal {G}}^R(\iota )\) are the \({\mathcal {G}}^R\)-ground instances of the premises and conclusion of \(\iota \). In the static refutational completeness proof, only one particular R is needed, but this R is not known during a derivation, so fairness must be guaranteed w.r.t. \( Red _{\mathrm {I}}^{R,{\mathcal {G}}^R}\) for every convergent rewrite system R.
is first-order entailment up to R on the set \({\mathbf {G}}\) of unconstrained ground clauses, \( GInf ^R\) is the set of ground superposition inferences, and \( Red ^R\) is redundancy up to R. The grounding function \({\mathcal {G}}^R\) maps \(C\,[\![K]\!] \in {\mathbf {F}}\) to \(\{D \in {\mathbf {G}} \mid D = C\theta ,\ K\theta = \mathrm {true},\ x\theta \text { is R-irreducible for all } x \}\)Footnote 2 and \(\iota \in FInf \) to the set of ground instances of \(\iota \) where the premises and conclusion of \({\mathcal {G}}^R(\iota )\) are the \({\mathcal {G}}^R\)-ground instances of the premises and conclusion of \(\iota \). In the static refutational completeness proof, only one particular R is needed, but this R is not known during a derivation, so fairness must be guaranteed w.r.t. \( Red _{\mathrm {I}}^{R,{\mathcal {G}}^R}\) for every convergent rewrite system R.
Almost every redundancy criterion for a nonground inference system \( FInf \) that can be found in the literature can be written as \( Red ^{{\mathcal {G}},\emptyset }\) for some grounding function \({\mathcal {G}}\) from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf \), and some redundancy criterion \( Red \) for \( GInf \), or as an intersection \( Red ^{\cap {\mathcal {G}}}\) of such criteria. By Theorem 17, every static refutational completeness result for \( FInf \) and \( Red ^{\cap {\mathcal {G}}}\)—which does not permit the deletion of subsumed formulas during a run—yields immediately a dynamic refutational completeness result for \( FInf \) and \( Red ^{\cap {\mathcal {G}},\sqsupset }\)—which permits the deletion of subsumed formulas during a run, provided that they are larger w.r.t. \(\sqsupset \).
Adding Labels. In practice, the ordering  used in \(({\mathcal {G}},\sqsupset )\)-lifting often depends on meta-information about a formula, such as its age or the way in which it has been processed so far during a derivation. To capture this meta-information, we extend formulas and inference systems in a rather trivial way with labels. As before, let \({\mathbf {F}}\) and \({\mathbf {G}}\) be two sets of formulas, let \( FInf \) be an \({\mathbf {F}}\)-inference system, let \( GInf \) be a \({\mathbf {G}}\)-inference system, let \({\models } \subseteq \mathcal {P}({\mathbf {G}}) \times \mathcal {P}({\mathbf {G}})\) be a consequence relation over \({\mathbf {G}}\), let \( Red \) be a redundancy criterion for \(\models \) and \( GInf \), and let \({\mathcal {G}}\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf \).
used in \(({\mathcal {G}},\sqsupset )\)-lifting often depends on meta-information about a formula, such as its age or the way in which it has been processed so far during a derivation. To capture this meta-information, we extend formulas and inference systems in a rather trivial way with labels. As before, let \({\mathbf {F}}\) and \({\mathbf {G}}\) be two sets of formulas, let \( FInf \) be an \({\mathbf {F}}\)-inference system, let \( GInf \) be a \({\mathbf {G}}\)-inference system, let \({\models } \subseteq \mathcal {P}({\mathbf {G}}) \times \mathcal {P}({\mathbf {G}})\) be a consequence relation over \({\mathbf {G}}\), let \( Red \) be a redundancy criterion for \(\models \) and \( GInf \), and let \({\mathcal {G}}\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf \).
Let \({\mathbf {L}}\) be a nonempty set of labels. Define \({\mathbf {FL}}:= {\mathbf {F}}\times {\mathbf {L}}\) and \({\mathbf {FL}}_\bot := {\mathbf {F}}_\bot \times {\mathbf {L}}\).
Notice that there are at least as many false values in \({\mathbf {FL}}\) as there are labels in \({\mathbf {L}}\). We use \(\mathcal {M}, \mathcal {N}\) to denote labeled formula sets. Given a set \(\mathcal {N}\subseteq {\mathbf {FL}}\), let \(\lfloor \mathcal {N}\rfloor := \{C \mid (C,l) \in \mathcal {N} \}\) denote the set of formulas without their labels. We call an \({\mathbf {FL}}\)-inference system \( FLInf \) a labeled version of \( FInf \) if it has the following properties:
-
(L1)
for every inference \((C_n,\dots ,C_0) \in FInf \) and every tuple \((l_1,\dots ,l_n) \in {\mathbf {L}}^n\), there exists an \(l_0 \in {\mathbf {L}}\) and an inference \(((C_n,l_n),\dots ,(C_0,l_0)) \in FLInf \);
-
(L2)
if \(\iota = ((C_n,l_n),\dots ,(C_0,l_0))\) is an inference in \( FLInf \), then \((C_n,\dots ,C_0)\) is an inference in \( FInf \), denoted by \(\lfloor \iota \rfloor \).
Let \( FLInf \) be a labeled version of \( FInf \). Define \({\mathcal {G}}_{\mathbf {L}}\) by \({\mathcal {G}}_{\mathbf {L}}((C,l)) := {\mathcal {G}}(C)\) for every \((C,l) \in {\mathbf {FL}}\) and by \({\mathcal {G}}_{\mathbf {L}}(\iota ) := {\mathcal {G}}(\lfloor \iota \rfloor )\) for every \(\iota \in FLInf \). It qualifies as a grounding function from \({\mathbf {FL}}\) and \( FLInf \) to \({\mathbf {G}}\) and \( GInf \). Let \(\models _{{\mathcal {G}}_{\mathbf {L}}}\) be the \({\mathcal {G}}_{\mathbf {L}}\)-lifting of \(\models \). Let \( Red ^{{{\mathcal {G}}_{\mathbf {L}}},\emptyset }\) be the \(({\mathcal {G}}_{\mathbf {L}},\emptyset )\)-lifting of \( Red \). The following lemmas are obvious:
Lemma 20
If a set \(\mathcal {N}\subseteq {\mathbf {FL}}\) is saturated w.r.t. \( FLInf \) and \( Red ^{{{\mathcal {G}}_{\mathbf {L}}},\emptyset }\), then \(\lfloor \mathcal {N}\rfloor \subseteq {\mathbf {F}}\) is saturated w.r.t. \( FInf \) and \( Red ^{{\mathcal {G}},\emptyset }\).
Lemma 21
If \(( FInf , Red ^{{\mathcal {G}},\emptyset })\) is statically refutationally complete w.r.t. \(\models _{\mathcal {G}}\), then \(( FLInf , Red ^{{{\mathcal {G}}_{\mathbf {L}}},\emptyset })\) is statically refutationally complete w.r.t. \(\models _{{\mathcal {G}}_{\mathbf {L}}}\).
The extension to intersections of redundancy criteria is also straightforward. Let \({\mathbf {F}}\) and \({\mathbf {G}}\) be two sets of formulas, and let \( FInf \) be an \({\mathbf {F}}\)-inference system. Let Q be a set. For every \(q \in Q\), let  be a consequence relation over \({\mathbf {G}}\), let \( GInf ^q\) be a \({\mathbf {G}}\)-inference system, let \( Red ^q\) be a redundancy criterion for
be a consequence relation over \({\mathbf {G}}\), let \( GInf ^q\) be a \({\mathbf {G}}\)-inference system, let \( Red ^q\) be a redundancy criterion for  and \( GInf ^q\), and let \({\mathcal {G}}^q\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf ^q\). Then for every \(q \in Q\), the \({({\mathcal {G}}^q,\emptyset )}\)-lifting \( Red ^{q,{\mathcal {G}}^q,\emptyset }\) is a redundancy criterion for the \({\mathcal {G}}^q\)-lifting \(\models ^{q}_{{\mathcal {G}}^q}\), and so \( Red ^{\cap {\mathcal {G}}}\) is a redundancy criterion for
and \( GInf ^q\), and let \({\mathcal {G}}^q\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf ^q\). Then for every \(q \in Q\), the \({({\mathcal {G}}^q,\emptyset )}\)-lifting \( Red ^{q,{\mathcal {G}}^q,\emptyset }\) is a redundancy criterion for the \({\mathcal {G}}^q\)-lifting \(\models ^{q}_{{\mathcal {G}}^q}\), and so \( Red ^{\cap {\mathcal {G}}}\) is a redundancy criterion for  and \( FInf \).
and \( FInf \).
Now let \({\mathbf {L}}\) be a nonempty set of labels, and define \({\mathbf {FL}}\), \({\mathbf {FL}}_\bot \), and \( FLInf \) as above. For every \(q \in Q\), define the function \({\mathcal {G}}_{\mathbf {L}}^q\) by \({\mathcal {G}}_{\mathbf {L}}^q((C,l)) := {\mathcal {G}}^q(C)\) for every \((C,l) \in {\mathbf {FL}}\) and by \({\mathcal {G}}_{\mathbf {L}}^q(\iota ) := {\mathcal {G}}^q(\lfloor \iota \rfloor )\) for every \(\iota \in FLInf \). Then for every \(q \in Q\), the \({({\mathcal {G}}_{\mathbf {L}}^q,\emptyset )}\)-lifting \( Red ^{q,{\mathcal {G}}_{\mathbf {L}}^q} = ( Red _{\mathrm {I}}^{q,{\mathcal {G}}_{\mathbf {L}}^q}, Red _{\mathrm {F}}^{q,{\mathcal {G}}_{\mathbf {L}}^q,\emptyset })\) of \( Red ^q\) is a redundancy criterion for the \({\mathcal {G}}_{\mathbf {L}}^q\)-lifting \(\models _{{\mathcal {G}}_{\mathbf {L}}^q}^q\) of \(\models ^q\) and \( FLInf \), and so

is a redundancy criterion for  and \( FLInf \).
and \( FLInf \).
Lemma 22
If a set \(\mathcal {N}\subseteq {\mathbf {FL}}\) is saturated w.r.t. \( FLInf \) and \( Red ^{\cap {\mathcal {G}}_{\mathbf {L}}}\), then \(\lfloor \mathcal {N}\rfloor \subseteq {\mathbf {F}}\) is saturated w.r.t. \( FInf \) and \( Red ^{\cap {\mathcal {G}}}\).
Theorem 23
If \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.  , then \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}}})\) is statically refutationally complete w.r.t.
, then \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}}})\) is statically refutationally complete w.r.t.  .
.
4 Prover Architectures
We now use the above results to prove the refutational completeness of a popular prover architecture: the given clause procedure [18]. The architecture is parameterized by an inference system and a redundancy criterion. A generalization of the architecture decouples scheduling and computation of inferences.
Given Clause Procedure. Let \({\mathbf {F}}\) and \({\mathbf {G}}\) be two sets of formulas, and let \( FInf \) be an \({\mathbf {F}}\)-inference system without premise-free inferences. Let Q be a set. For every \(q \in Q\), let  be a consequence relation over \({\mathbf {G}}\), let \( GInf ^q\) be a \({\mathbf {G}}\)-inference system, let \( Red ^q\) be a redundancy criterion for
be a consequence relation over \({\mathbf {G}}\), let \( GInf ^q\) be a \({\mathbf {G}}\)-inference system, let \( Red ^q\) be a redundancy criterion for  and \( GInf ^q\), and let \({\mathcal {G}}^q\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf ^q\). Assume \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.
and \( GInf ^q\), and let \({\mathcal {G}}^q\) be a grounding function from \({\mathbf {F}}\) and \( FInf \) to \({\mathbf {G}}\) and \( GInf ^q\). Assume \(( FInf , Red ^{\cap {\mathcal {G}}})\) is statically refutationally complete w.r.t.  . Furthermore, let \({\mathbf {L}}\) be a nonempty set of labels, let \({\mathbf {FL}}:= {\mathbf {F}}\times {\mathbf {L}}\), and let the \({\mathbf {FL}}\)-inference system \( FLInf \) be a labeled version of \( FInf \). By Theorem 23, \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}}})\) is statically refutationally complete w.r.t.
. Furthermore, let \({\mathbf {L}}\) be a nonempty set of labels, let \({\mathbf {FL}}:= {\mathbf {F}}\times {\mathbf {L}}\), and let the \({\mathbf {FL}}\)-inference system \( FLInf \) be a labeled version of \( FInf \). By Theorem 23, \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}}})\) is statically refutationally complete w.r.t.  .
.
Let  be an equivalence relation on \({\mathbf {F}}\), let
be an equivalence relation on \({\mathbf {F}}\), let  be a well-founded strict partial ordering on \({\mathbf {F}}\) such that
be a well-founded strict partial ordering on \({\mathbf {F}}\) such that  is compatible with
is compatible with  (i.e.,
(i.e.,  ,
,  ,
,  implies
implies  ), such that
), such that  implies \({\mathcal {G}}^q(C) = {\mathcal {G}}^q(D)\) for all \(q \in Q\), and such that
implies \({\mathcal {G}}^q(C) = {\mathcal {G}}^q(D)\) for all \(q \in Q\), and such that  implies \({\mathcal {G}}^q(C) \subseteq {\mathcal {G}}^q(D)\) for all \(q \in Q\). We define
implies \({\mathcal {G}}^q(C) \subseteq {\mathcal {G}}^q(D)\) for all \(q \in Q\). We define  . In practice,
. In practice,  is typically \(\alpha \)-renaming,
is typically \(\alpha \)-renaming,  is either the subsumption ordering
is either the subsumption ordering  (provided it is well founded) or some well-founded ordering included in
(provided it is well founded) or some well-founded ordering included in  , and for every \(q \in Q\), \({\mathcal {G}}^q\) maps every formula \(C \in {\mathbf {F}}\) to the set of ground instances of C, possibly modulo some theory.
, and for every \(q \in Q\), \({\mathcal {G}}^q\) maps every formula \(C \in {\mathbf {F}}\) to the set of ground instances of C, possibly modulo some theory.
Let  be a well-founded strict partial ordering on \({\mathbf {L}}\). We define the ordering \(\sqsupset \) on \({\mathbf {FL}}\) by \((C,l) \sqsupset (C',l')\) if either
be a well-founded strict partial ordering on \({\mathbf {L}}\). We define the ordering \(\sqsupset \) on \({\mathbf {FL}}\) by \((C,l) \sqsupset (C',l')\) if either  or else
or else  and
and  . By Lemma 16, the static refutational completeness of \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}}})\) w.r.t.
. By Lemma 16, the static refutational completeness of \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}}})\) w.r.t.  implies the static refutational completeness of \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset })\), which by Lemma 1 implies the dynamic refutational completeness of \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset })\).
implies the static refutational completeness of \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset })\), which by Lemma 1 implies the dynamic refutational completeness of \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset })\).
This result may look intimidating, so let us unroll it. The \({\mathbf {FL}}\)-inference system \( FLInf \) is a labeled version of \( FInf \), which means that we get an \( FLInf \)-inference by first omitting the labels of the premises \((C_n,l_n),\dots ,(C_1,l_1)\), then performing an \( FInf \)-inference \((C_n,\dots ,C_0)\), and finally attaching an arbitrary label \(l_0\) to the conclusion \(C_0\). Since \({\mathcal {G}}_{\mathbf {L}}^q\) differs from \({\mathcal {G}}^q\) only by the omission of the labels and the first components of \( Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }\) and \( Red ^{\cap {\mathcal {G}}_{\mathbf {L}}}\) agree, we get this result:
Lemma 24
An \( FLInf \)-inference \(\iota \) is redundant w.r.t. \( Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }\) and \(\mathcal {N}\) if and only if the underlying \( FInf \)-inference \(\lfloor \iota \rfloor \) is redundant w.r.t. \( Red ^{\cap {\mathcal {G}}}\) and \(\lfloor \mathcal {N}\rfloor \).
Lemma 25
Let \(\mathcal {N}\subseteq {\mathbf {FL}}\), and let (C, l) be a labeled formula. Then \((C,l) \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }(\mathcal {N})\) if (i) \(C \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\lfloor \mathcal {N}\rfloor )\), or (ii)  for some \(C' \in \lfloor \mathcal {N}\rfloor \), or (iii)
for some \(C' \in \lfloor \mathcal {N}\rfloor \), or (iii)  for some \((C',l') \in \mathcal {N}\) with
for some \((C',l') \in \mathcal {N}\) with  .
.
The given clause procedure that lies at the heart of saturation provers can be presented and studied abstractly. We assume that the set of labels \({\mathbf {L}}\) contains at least two values, including a distinguished  -smallest value denoted by active, and that the labeled version \( FLInf \) of \( FInf \) never assigns active to a conclusion.
-smallest value denoted by active, and that the labeled version \( FLInf \) of \( FInf \) never assigns active to a conclusion.
The state of a prover is a set of labeled formulas. The label identifies to which formula set each formula belongs. The active label identifies the active formula set from the familiar given clause procedure. The other, unspecified formula sets are considered passive. Given a set \(\mathcal {N}\) and a label l, we define the projection \(\mathcal {N}{\downarrow }_l\) as consisting only of the formulas labeled by l.
The given clause prover \(\mathsf {GC}\) is defined as the following transition system:
-
Process \(\mathcal {N}\uplus \mathcal {M}\,\Longrightarrow _\mathsf {GC}\, \mathcal {N}\cup \mathcal {M}'\)
where \(\mathcal {M}\subseteq Red _{\mathrm {F}}^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }(\mathcal {N}\cup \mathcal {M}')\) and \(\mathcal {M}'{\downarrow }_\textsf {active} = \emptyset \)
-
Infer \(\mathcal {N}\uplus \{(C, l)\} \,\Longrightarrow _\mathsf {GC}\, \mathcal {N}\cup \{(C, \textsf {active})\} \cup \mathcal {M}\)
where \(l \not = \textsf {active}\), \(\mathcal {M}{\downarrow }_\textsf {active} = \emptyset \), and
\( FInf (\lfloor \mathcal {N}{\downarrow }_\textsf {active}\rfloor , \{C\}) \subseteq Red _{\mathrm {I}}^{\cap {\mathcal {G}}}(\lfloor \mathcal {N}\rfloor \cup \{C\} \cup \lfloor \mathcal {M}\rfloor )\)
The Process rule covers most operations performed in a theorem prover. By Lemma 25, this includes deleting \( Red _{\mathrm {F}}^{\cap {\mathcal {G}}}\)-redundant formulas with arbitrary labels and adding formulas that make other formulas \( Red _{\mathrm {F}}^{\cap {\mathcal {G}}}\)-redundant (i.e., simplifying w.r.t. \( Red _{\mathrm {F}}^{\cap {\mathcal {G}}}\)), by (i); deleting formulas that are  -subsumed by other formulas with arbitrary labels, by (ii); deleting formulas that are
-subsumed by other formulas with arbitrary labels, by (ii); deleting formulas that are  -subsumed by other formulas with smaller labels, by (iii); and replacing the label of a formula by a smaller label different from active, also by (iii).
-subsumed by other formulas with smaller labels, by (iii); and replacing the label of a formula by a smaller label different from active, also by (iii).
Infer is the only rule that puts a formula in the active set. It relabels a passive formula C to active and ensures that all inferences between C and the active formulas, including C itself, become redundant. Recall that by Lemma 24, \( FLInf (\mathcal {N}{\downarrow }_\textsf {active}, \{(C,\textsf {active})\}) \subseteq Red _{\mathrm {I}}^{\cap {\mathcal {G}}_{\mathbf {L}}}(\mathcal {N}\cup \{(C, \textsf {active})\} \cup \mathcal {M})\) if and only if \( FInf (\lfloor \mathcal {N}{\downarrow }_\textsf {active}\rfloor , \{C\}) \subseteq Red _{\mathrm {I}}^{\cap {\mathcal {G}}}(\lfloor \mathcal {N}\rfloor \cup \{C\} \cup \lfloor \mathcal {M}\rfloor )\). By property (R4), every inference is redundant if its conclusion is contained in the set of formulas, and typically, inferences are in fact made redundant by adding their conclusions to any of the passive sets. Then, \(\lfloor \mathcal {M}\rfloor \) equals \( concl ( FInf (\lfloor \mathcal {N}{\downarrow }_\textsf {active}\rfloor , \{C\}))\).
Since every \(\Longrightarrow _\mathsf {GC}\)-derivation is also a \(\rhd _{ Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }}\)-derivation and \(( FLInf , Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset })\) is dynamically refutationally complete, it now suffices to show fairness to prove the refutational completeness of \(\mathsf {GC}\).
Lemma 26
Let \((\mathcal {N}_i)_i\) be a \(\Longrightarrow _\mathsf {GC}\)-derivation. If \(\mathcal {N}_0{\downarrow }_\mathsf{active} = \emptyset \) and \(\mathcal {N}_*{\downarrow }_l = \emptyset \) for all \(l \not = \mathsf{active}\), then \((\mathcal {N}_i)_i\) is a fair \(\rhd _{ Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }}\)-derivation.
Theorem 27
Let \((\mathcal {N}_i)_i\) be a \(\Longrightarrow _\mathsf {GC}\)-derivation, where \(\mathcal {N}_0{\downarrow }\) \(_\mathsf{active}\) \(= \emptyset \) and \(\mathcal {N}_*{\downarrow }_l = \emptyset \) for all \(l \not = \mathsf{active}\). If  for some \(\bot \in {\mathbf {F}}_\bot \), then some \(\mathcal {N}_i\) contains \((\bot ',l)\) for some \(\bot ' \in {\mathbf {F}}_\bot \) and \(l \in {\mathbf {L}}\).
for some \(\bot \in {\mathbf {F}}_\bot \), then some \(\mathcal {N}_i\) contains \((\bot ',l)\) for some \(\bot ' \in {\mathbf {F}}_\bot \) and \(l \in {\mathbf {L}}\).
Example 28
The following Otter loop [18, Sect. 2.3.1] prover \(\mathsf {OL}\) is an instance of the given clause prover \(\mathsf {GC}\). This loop design is inspired by Weidenbach’s prover without splitting from his Handbook chapter [30, Tables 4–6]. The prover’s state is a five-tuple \(N \mid X \mid P \mid Y \mid A\) of formula sets. The N, P, and A sets store the new, passive, and active formulas. The X and Y sets are subsingletons (i.e., sets of at most one element) that can store a chosen new or passive formula. Initial states are of the form \(N \mid \emptyset \mid \emptyset \mid \emptyset \mid \emptyset \).
-
ChooseN \(N \uplus \{C\} \mid \emptyset \mid P \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, N \mid \{C\} \mid P \mid \emptyset \mid A\)
-
DeleteFwd \(N \mid \{C\} \mid P \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, N \mid \emptyset \mid P \mid \emptyset \mid A\)
if \(C \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(P \cup A)\) or
 for some \(C' \in P \cup A\)
for some \(C' \in P \cup A\) -
SimplifyFwd \(N \mid \{C\} \mid P \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, N \mid \{C'\} \mid P \mid \emptyset \mid A\)
if \(C \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(P \cup A \cup \{C'\})\)
-
DeleteBwdP \(N \mid \{C\} \mid P \uplus \{C'\} \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, N \mid \{C\} \mid P \mid \emptyset \mid A\)
if \(C' \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\{C\})\) or

-
SimplifyBwdP \(N \mid \{C\} \mid P \uplus \{C'\} \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, N \cup \{C''\} \mid \{C\} \mid P \mid \emptyset \mid A\)
if \(C' \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\{C,C''\})\)
-
DeleteBwdA \(N \mid \{C\} \mid P \mid \emptyset \mid A \uplus \{C'\} \,\Longrightarrow _\mathsf {OL}\, N \mid \{C\} \mid P \mid \emptyset \mid A\)
if \(C' \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\{C\})\) or

-
SimplifyBwdA \(N \mid \{C\} \mid P \mid \emptyset \mid A \uplus \{C'\} \,\Longrightarrow _\mathsf {OL}\, N \cup \{C''\} \mid \{C\} \mid P \mid \emptyset \mid A\)
if \(C' \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\{C,C''\})\)
-
Transfer \(N \mid \{C\} \mid P \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, N \mid \emptyset \mid P \cup \{C\} \mid \emptyset \mid A\)
-
ChooseP \(\emptyset \mid \emptyset \mid P \uplus \{C\} \mid \emptyset \mid A \,\Longrightarrow _\mathsf {OL}\, \emptyset \mid \emptyset \mid P \mid \{C\} \mid A\)
-
Infer \(\emptyset \mid \emptyset \mid P \mid \{C\} \mid A \,\Longrightarrow _\mathsf {OL}\, M \mid \emptyset \mid P \mid \emptyset \mid A \cup \{C\}\)
if \( FInf (A, \{C\}) \subseteq Red _{\mathrm {I}}^{\cap {\mathcal {G}}}(A \cup \{C\} \cup M)\)
A reasonable strategy for applying the \(\mathsf {OL}\) rules is presented below. It relies on a well-founded ordering \(\succ \) on formulas to ensure that the backward simplification rules actually “simplify” their target, preventing nontermination of the inner loop. It also assumes that \( FInf (N, \{C\})\) is finite if N is finite. Briefly, the strategy corresponds to the regular expression \(\bigl (\bigl (\textsc {ChooseN}{;}\; \textsc {SimplifyFwd}^*{;} (\textsc {DeleteFwd} \mid (\textsc {DeleteBwdP}^*{;}\; \textsc {DeleteBwd}\) \(\textsc {A}^*{;}\; \textsc {SimplifyBwdP}^*{;}\; \textsc {Simpli}\) \(\textsc {fyBwdA}^*{;}\; \textsc {Transfer}))\bigr )^* {;}\; (\textsc {ChooseP}{;}\; \textsc {Infer})^?\bigr )^*\), where ; denotes concatenation and \(*\) and ? are given an eager semantics. Simplifications are applicable only if the result is \(\succ \)-smaller than the original formula. Moreover, ChooseC always chooses the oldest formula in N, and the choice of C in ChooseP must be fair.
The instantiation of \(\mathsf {GC}\) relies on five labels  representing N, X, P, Y, A. Let
representing N, X, P, Y, A. Let  be a derivation following the strategy, where \(N_0\) is finite and
be a derivation following the strategy, where \(N_0\) is finite and  . We can show that
. We can show that  . Therefore, by Theorem 27, \(\mathsf {OL}\) is dynamically refutationally complete.
. Therefore, by Theorem 27, \(\mathsf {OL}\) is dynamically refutationally complete.
In most calculi, \( Red \) is defined in terms of some total and well-founded ordering \(\succ _{\mathbf {G}}\) on \({\mathbf {G}}\). We can then define \(\succ \) so that \(C \succ C'\) if the smallest element of \({\mathcal {G}}^q(C)\) is greater than the smallest element of \({\mathcal {G}}^q(C')\) w.r.t. \(\succ _{\mathbf {G}}\), for some arbitrary fixed \(q \in Q\). This allows a wide range of simplifications typically implemented in superposition provers. To ensure fairness when applying ChooseP, one approach is to use an \(\mathbb {N}\)-valued weight function that is strictly antimonotone in the age of the formula [22, Sect. 4]. Another option is to alternate between heuristically choosing n formulas and taking the oldest formula [18, Sect. 2.3.1]. To guarantee soundness, we can require that the formulas added by simplification and Infer are  -entailed by the formulas in the state before the transition. This can be relaxed to consistency-preservation, e.g., for calculi that perform skolemization.
-entailed by the formulas in the state before the transition. This can be relaxed to consistency-preservation, e.g., for calculi that perform skolemization.
Example 29
Bachmair and Ganzinger’s resolution prover \(\mathsf {RP}\) [5, Sect. 4.3] is another instance of \(\mathsf {GC}\). It embodies both a concrete prover architecture and a concrete inference system: ordered resolution with selection (\(\mathsf {O}^\succ _S\)). States are triples \(N \mid P \mid O\) of finite clause sets. The instantiation relies on three labels  . Subsumption can be supported as described in Example 10.
. Subsumption can be supported as described in Example 10.
Delayed Inferences. An orphan is a passive formula that was generated by an inference for which at least one premise is no longer active. The given clause prover \(\mathsf {GC}\) presented above is sufficient to describe a prover based on an Otter loop as well as a basic
 loop prover, but to describe a
loop prover, but to describe a
 loop prover with orphan deletion, we need to decouple the scheduling of inferences and their computation. The same scheme can be used for inference systems that contain premise-free inferences or that may generate infinitely many conclusions from finitely many premises. Yet another use of the scheme is to save memory: A delayed inference can be stored more compactly than a new formula, as a tuple of premises together with instructions on how to compute the conclusion.
loop prover with orphan deletion, we need to decouple the scheduling of inferences and their computation. The same scheme can be used for inference systems that contain premise-free inferences or that may generate infinitely many conclusions from finitely many premises. Yet another use of the scheme is to save memory: A delayed inference can be stored more compactly than a new formula, as a tuple of premises together with instructions on how to compute the conclusion.
The lazy given clause prover \(\mathsf {LGC}\) generalizes \(\mathsf {GC}\). It is defined as the following transition system on pairs \((T,\mathcal {N})\), where T (“to do”) is a set of inferences and \(\mathcal {N}\) is a set of labeled formulas. We use the same assumptions as for \(\mathsf {GC}\) except that we now permit premise-free inferences in \( FInf \). Initially, T consists of all premise-free inferences of \( FInf \).
-
Process \((T,\mathcal {N}\uplus \mathcal {M}) \,\Longrightarrow _\mathsf {LGC}\, (T,\mathcal {N}\cup \mathcal {M}')\)
where \(\mathcal {M}\subseteq Red _{\mathrm {F}}^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }(\mathcal {N}\cup \mathcal {M}')\) and \(\mathcal {M}'{\downarrow }_\textsf {active} = \emptyset \)
-
ScheduleInfer \((T,\mathcal {N}\uplus \{(C, l)\}) \,\Longrightarrow _\mathsf {LGC}\, (T \cup T', \mathcal {N}\cup \{(C, \textsf {active})\})\)
where \(l \not = \textsf {active}\) and \(T' = FInf (\lfloor \mathcal {N}{\downarrow }_\textsf {active}\rfloor , \{C\})\)
-
ComputeInfer \((T \uplus \{\iota \}, \mathcal {N}) \,\Longrightarrow _\mathsf {LGC}\, (T,\mathcal {N}\cup \mathcal {M})\)
where \(\mathcal {M}{\downarrow }_\textsf {active} = \emptyset \) and \(\iota \in Red _{\mathrm {I}}^{\cap {\mathcal {G}}}(\lfloor \mathcal {N}\cup \mathcal {M}\rfloor )\)
-
DeleteOrphans \((T \uplus T', \mathcal {N}) \,\Longrightarrow _\mathsf {LGC}\, (T,\mathcal {N})\)
where \(T' \cap FInf (\lfloor \mathcal {N}{\downarrow }_\textsf {active}\rfloor ) = \emptyset \)
ScheduleInfer relabels a passive formula C to active and puts all inferences between C and the active formulas, including C itself, into the set T. ComputeInfer removes an inference from T and makes it redundant by adding appropriate labeled formulas to \(\mathcal {N}\) (typically the conclusion of the inference). DeleteOrphans can delete scheduled inferences from T if some of their premises have been deleted from \(\mathcal {N}{\downarrow }_\textsf {active}\) in the meantime. Note that the rule cannot delete premise-free inferences, since the side condition is then vacuously false.
Abstractly, the T component of the state is a set of inferences \((C_n,\ldots ,C_0)\). In an actual implementation, it can be represented in different ways: as a set of compactly encoded recipes for computing the conclusion \(C_0\) from the premises \((C_n,\ldots ,C_1)\) as in Waldmeister [16], or as a set of explicit formulas \(C_0\) with information about their parents \((C_n,\ldots ,C_1)\) as in E [25]. In the latter case, some presimplifications may be performed on \(C_0\); this could be modeled more faithfully by defining T as a set of pairs \((\iota , simp (C_0))\).
Lemma 30
If \((T_i,\mathcal {N}_i)_i\) is a \(\Longrightarrow _\mathsf {LGC}\)-derivation, then \((\mathcal {N}_i)_i\) is a \(\rhd _{ Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }}\)- derivation.
Lemma 31
Let \((T_i,\mathcal {N}_i)_i\) be a \(\Longrightarrow _\mathsf {LGC}\)-derivation. If \(\mathcal {N}_0{\downarrow }_\mathsf{active} = \emptyset \), \(\mathcal {N}_*{\downarrow }_l = \emptyset \) for all \(l \not = \mathsf{active}\), \(T_0\) is the set of all premise-free inferences of \( FInf \), and \(T_* = \emptyset \), then \((\mathcal {N}_i)_i\) is a fair \(\rhd _{ Red ^{\cap {\mathcal {G}}_{\mathbf {L}},\sqsupset }}\)-derivation.
Theorem 32
Let \((T_i,\mathcal {N}_i)_i\) be a \(\Longrightarrow _\mathsf {LGC}\)-derivation, where \(\mathcal {N}_0{\downarrow }_\mathsf{active} = \emptyset \), \(\mathcal {N}_*{\downarrow }_l = \emptyset \) for all \(l \not = \mathsf{active}\), \(T_0\) is the set of all premise-free inferences of \( FInf \), and \(T_* = \emptyset \). If  for some \(\bot \in {\mathbf {F}}_\bot \), then some \(\mathcal {N}_i\) contains \((\bot ',l)\) for some \(\bot ' \in {\mathbf {F}}_\bot \) and \(l \in {\mathbf {L}}\).
for some \(\bot \in {\mathbf {F}}_\bot \), then some \(\mathcal {N}_i\) contains \((\bot ',l)\) for some \(\bot ' \in {\mathbf {F}}_\bot \) and \(l \in {\mathbf {L}}\).
Example 33
The following
 loop [1] prover \(\mathsf {DL}\) is an instance of the lazy given clause prover \(\mathsf {LGC}\). This loop design is inspired by the description of E [25]. The prover’s state is a four-tuple \(T \mid P \mid Y \mid A\), where T is a set of inferences and P, Y, A are sets of formulas. The T, P, and A sets correspond to the scheduled inferences, the passive formulas, and the active formulas. The Y set is a subsingleton that can store a chosen passive formula. Initial states have the form \(T \mid P \mid \emptyset \mid \emptyset \), where T is the set of all premise-free inferences of \( FInf \).
loop [1] prover \(\mathsf {DL}\) is an instance of the lazy given clause prover \(\mathsf {LGC}\). This loop design is inspired by the description of E [25]. The prover’s state is a four-tuple \(T \mid P \mid Y \mid A\), where T is a set of inferences and P, Y, A are sets of formulas. The T, P, and A sets correspond to the scheduled inferences, the passive formulas, and the active formulas. The Y set is a subsingleton that can store a chosen passive formula. Initial states have the form \(T \mid P \mid \emptyset \mid \emptyset \), where T is the set of all premise-free inferences of \( FInf \).
-
ComputeInfer \(T \uplus \{\iota \} \mid P \mid \emptyset \mid A \,\Longrightarrow _\mathsf {DL}\, T \mid P \mid \{C\} \mid A\)
if \(\iota \in Red _{\mathrm {I}}^{\cap {\mathcal {G}}}(A \cup \{C\})\)
-
ChooseP \(T \mid P \uplus \{C\} \mid \emptyset \mid A \,\Longrightarrow _\mathsf {DL}\, T \mid P \mid \{C\} \mid A\)
-
DeleteFwd \(T \mid P \mid \{C\} \mid A \,\Longrightarrow _\mathsf {DL}\, T \mid P \mid \emptyset \mid A\)
if \(C \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(A)\) or
 for some \(C' \in A\)
for some \(C' \in A\) -
SimplifyFwd \(T \mid P \mid \{C\} \mid A \,\Longrightarrow _\mathsf {DL}\, T \mid P \mid \{C'\} \mid A\)
if \(C \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(A \cup \{C'\})\)
-
DeleteBwd \(T \mid P \mid \{C\} \mid A \uplus \{C'\} \,\Longrightarrow _\mathsf {DL}\, T \mid P \mid \{C\} \mid A\)
if \(C' \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\{C\})\) or

-
SimplifyBwd \(T \mid P \mid \{C\} \mid A \uplus \{C'\} \,\Longrightarrow _\mathsf {DL}\, T \mid P \cup \{C''\} \mid \{C\} \mid A\)
if \(C' \in Red _{\mathrm {F}}^{\cap {\mathcal {G}}}(\{C,C''\})\)
-
ScheduleInfer \(T \mid P \mid \{C\} \mid A \,\Longrightarrow _\mathsf {DL}\, T \cup T' \mid P \mid \emptyset \mid A \cup \{C\}\)
if \(T' = FInf (A, \{C\})\)
-
DeleteOrphans \(T \uplus T' \mid P \mid Y \mid A \,\Longrightarrow _\mathsf {DL}\, T \mid P \mid Y \mid A\)
if \(T' \cap FInf (A) = \emptyset \)
A reasonable strategy for applying the \(\mathsf {DL}\) rules along the lines of that for \(\mathsf {OL}\) and with the same assumptions follows: \(\bigl ((\textsc {ComputeInfer} \mid \textsc {ChooseP}){;} \textsc {SimplifyFwd}^*{;}\; (\textsc {DeleteFwd} \mid (\textsc {DeleteBwd}^*{;}\; \textsc {SimplifyBwd}^*{;}\; \textsc {Delete}\) \(\textsc {Orphans}{;}\; \textsc {ScheduleInfer}))\bigr )^*\). In ComputeInfer, the first formula from \(T \cup P\), organized as a single queue, is chosen. The instantiation of \(\mathsf {LGC}\) relies on three labels  corresponding to the sets P, Y, A.
corresponding to the sets P, Y, A.
Example 34
Higher-order unification can give rise to infinitely many incomparable unifiers. As a result, in clausal \(\lambda \)-superposition [9], performing all inferences between two clauses can lead to infinitely many conclusions, which need to be enumerated fairly. The Zipperposition prover [9] performs this enumeration in an extended
 loop. Another instance of infinitary inferences is the n-ary Acycl and Uniq rules of superposition with (co)datatypes [14].
loop. Another instance of infinitary inferences is the n-ary Acycl and Uniq rules of superposition with (co)datatypes [14].
Abstractly, a Zipperposition loop prover \(\mathsf {ZL}\) operates on states \(T \mid P \mid Y \mid A\), where T is organized as a finite set of possibly infinite sequences \((\iota _i)_i\) of inferences, and P, Y, A are as in \(\mathsf {DL}\). The ChooseP, DeleteFwd, SimplifyFwd, DeleteBwd, and SimplifyBwd rules are as in \(\mathsf {DL}\). The other rules follow:
-
ComputeInfer \(T \uplus \{(\iota _i)_i\} \mid P \mid \emptyset \mid A \,\Longrightarrow _\mathsf {ZL}\, T \cup \{(\iota _i)_{i\ge 1}\} \mid P \cup \{C\} \mid \emptyset \mid A\)
if \(\iota _0 \in Red _{\mathrm {I}}^{\cap {\mathcal {G}}}(A \cup \{C\})\)
-
ScheduleInfer \(T \mid P \mid \{C\} \mid A \,\Longrightarrow _\mathsf {ZL}\, T \cup T' \mid P \mid \emptyset \mid A \cup \{C\}\)
if \(T'\) is a finite set of sequences \((\iota _i^j)_i\) of inferences such that the set of all \(\iota _i^j\) equals \( FInf (A, \{C\})\)
-
DeleteOrphan \(T \uplus \{(\iota _i)_i\} \mid P \mid Y \mid A \,\Longrightarrow _\mathsf {ZL}\, T \mid P \mid Y \mid A\) if \(\iota _i \notin FInf (A)\) for all i
ComputeInfer works on the first element of sequences. ScheduleInfer adds new sequences to T. Typically, these sequences store \( FInf (A, \{C\})\), which may be countably infinite, in such a way that all inferences in one sequence have identical premises and can be removed together by DeleteOrphan. To produce fair derivations, a prover needs to choose the sequence in ComputeInfer fairly and to choose the formula in ChooseP fairly, thereby achieving dovetailing.
Example 35
The prover architectures described above can be instantiated with saturation calculi that use a redundancy criterion obtained as an intersection of lifted redundancy criteria. Most calculi are defined in such a way that this requirement is obviously satisfied. The outlier is unfailing completion [2].
Although unfailing completion predates the introduction of Bachmair–Ganzinger-style redundancy, it can be incorporated into that framework by defining that formulas (i.e., rewrite rules and equations) and inferences (i.e., orientation and critical pair computation) are redundant if for every rewrite proof using that rewrite rule, equation, or critical peak, there exists a smaller rewrite proof. The requirement that the redundancy criterion must be obtained by lifting (which is necessary to introduce the labeling) can then be trivially fulfilled by “self-lifting”—i.e., by defining \({\mathbf {G}}:= {\mathbf {F}}\) and  and by taking \({\mathcal {G}}\) as the function that maps every formula or inference to the set of its \(\alpha \)-renamings.
and by taking \({\mathcal {G}}\) as the function that maps every formula or inference to the set of its \(\alpha \)-renamings.
5 Isabelle Development
The framework described in the previous sections has been formalized in Isabelle/
 [20, 21], including all the theorems and lemmas and the prover architectures \(\mathsf {GC}\) and \(\mathsf {LGC}\) but excluding the examples. The Isabelle theory files are available in the Archive of Formal Proofs [26]. The development is also part of the IsaFoL (Isabelle Formalization of Logic) [12] effort, which aims at developing a reusable computer-checked library of results about automated reasoning.
[20, 21], including all the theorems and lemmas and the prover architectures \(\mathsf {GC}\) and \(\mathsf {LGC}\) but excluding the examples. The Isabelle theory files are available in the Archive of Formal Proofs [26]. The development is also part of the IsaFoL (Isabelle Formalization of Logic) [12] effort, which aims at developing a reusable computer-checked library of results about automated reasoning.
The development relies heavily on Isabelle’s locales [8]. These are contexts that fix variables and make assumptions about these. With locales, the definitions and lemmas look similar to how they are stated on paper, but the proofs often become more complicated: Layers of locales may hide definitions, and often these need to be manually unfolded before the desired lemma can be proved.
We chose to represent basic nonempty sets such as \({\mathbf {F}}\) and \({\mathbf {L}}\) by types. It relieved us from having to thread through nonemptiness conditions. Moreover, objects are automatically typed, meaning that lemmas could be stated without explicit hypotheses that given objects are formulas, labels, or indices. On the other hand, for sets such as \({\mathbf {F}}_\bot \) and \( FInf \) that are subsets of other sets, it was natural to use simply typed sets. Derivations, which are used to describe the dynamic behavior of a calculus, are represented by the same lazy list codatatype [13] and auxiliary definitions that were used in the mechanization of the ordered resolution prover \(\mathsf {RP}\) (Example 29) by Schlichtkrull et al. [23, 24].
The framework’s design and its mechanization were carried out largely in parallel. This resulted in more work on the mechanization side, but it also helped shape the theory itself. In particular, an attempt at verifying \(\mathsf {RP}\) in Isabelle using an earlier version of the framework made it clear that the theory was not general enough yet to support selection functions (Example 18). In ongoing work, we are completing the \(\mathsf {RP}\) proof and are developing a verified superposition prover.
6 Conclusion
We presented a formal framework for saturation theorem proving inspired by Bachmair and Ganzinger’s Handbook chapter [5]. Users can conveniently derive a dynamic refutational completeness result for a concrete prover based on a statically refutationally complete calculus. The key was to strengthen the standard redundancy criterion so that all prover operations, including subsumption deletion, can be justified by inference or redundancy. The framework is mechanized in Isabelle/
 , where it can be instantiated to verify concrete provers.
, where it can be instantiated to verify concrete provers.
To employ the framework, the starting point is a statically complete saturation calculus that can be expressed as the lifting \(( FInf , Red ^{\mathcal {G}})\) or \(( FInf , Red ^{\cap {\mathcal {G}}})\) of a ground calculus \(( GInf , Red )\), where \( Red \) qualifies as a redundancy criterion and \({\mathcal {G}}\) qualifies as a grounding function or grounding function family. The framework can be used to derive two main results:
-
1.
After defining a well-founded ordering \(\sqsupset \) that captures subsumption, invoke Theorem 17 to show \(( FInf , Red ^{\cap {\mathcal {G}},\sqsupset })\) dynamically complete.
-
2.
Based on the previous step, invoke Theorem 27 or 32 to derive the dynamic completeness of a prover architecture building on the given clause procedure, such as the Otter loop, the
 loop, or the Zipperposition loop.
loop, or the Zipperposition loop.
The framework can also help establish the static completeness of the nonground calculus. For many calculi (with the notable exceptions of constraint superposition and hierarchic superposition), Theorem 5 or 14 can be used to lift the static completeness of \(( GInf , Red )\) to \(( FInf , Red ^{\mathcal {G}})\) or \(( FInf , Red ^{\cap {\mathcal {G}}})\).
The main missing piece of the framework is a generic treatment of clause splitting. The only formal treatment of splitting we are aware of, by Fietzke and Weidenbach [15], hard-codes both the underlying calculus and the splitting strategy. Voronkov’s
 architecture [27] is more flexible and yields impressive empirical results, but it offers no dynamic completeness guarantees.
architecture [27] is more flexible and yields impressive empirical results, but it offers no dynamic completeness guarantees.
Notes
- 1.
One can find several slightly differing definitions for redundancy criteria, fairness, and saturation in the literature [5, 7, 28]. However, as shown in the technical report [29], the differences are typically insignificant as far as static or dynamic refutational completeness is concerned. Here we mostly follow Waldmann [28].
- 2.
For a variable x that occurs only in positive literals \(x \approx t\), the condition is slightly more complicated.
References
Avenhaus, J., Denzinger, J., Fuchs, M.: DISCOUNT: a system for distributed equational deduction. In: Hsiang, J. (ed.) RTA 1995. LNCS, vol. 914, pp. 397–402. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-59200-8_72
Bachmair, L., Dershowitz, N., Plaisted, D.A.: Completion without failure. In: Aït-Kaci, H., Nivat, M. (eds.) Rewriting Techniques—Resolution of Equations in Algebraic Structures, vol. 2, pp. 1–30. Academic Press (1989)
Bachmair, L., Ganzinger, H.: On restrictions of ordered paramodulation with simplification. In: Stickel, M.E. (ed.) CADE 1990. LNCS, vol. 449, pp. 427–441. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-52885-7_105
Bachmair, L., Ganzinger, H.: Rewrite-based equational theorem proving with selection and simplification. J. Log. Comput. 4(3), 217–247 (1994)
Bachmair, L., Ganzinger, H.: Resolution theorem proving. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. I, pp. 19–99. Elsevier and MIT Press (2001)
Bachmair, L., Ganzinger, H., Waldmann, U.: Superposition with simplification as a decision procedure for the monadic class with equality. In: Gottlob, G., Leitsch, A., Mundici, D. (eds.) KGC 1993. LNCS, vol. 713, pp. 83–96. Springer, Heidelberg (1993). https://doi.org/10.1007/BFb0022557
Bachmair, L., Ganzinger, H., Waldmann, U.: Refutational theorem proving for hierarchic first-order theories. Appl. Algebra Eng. Commun. Comput. 5, 193–212 (1994)
Ballarin, C.: Locales: a module system for mathematical theories. J. Autom. Reason. 52(2), 123–153 (2014)
Bentkamp, A., Blanchette, J., Tourret, S., Vukmirović, P., Waldmann, U.: Superposition with lambdas. In: Fontaine, P. (ed.) CADE 2019. LNCS (LNAI), vol. 11716, pp. 55–73. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-29436-6_4
Bentkamp, A., Blanchette, J.C., Cruanes, S., Waldmann, U.: Superposition for lambda-free higher-order logic. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 28–46. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_3
Bhayat, A., Reger, G.: A combinator-based superposition calculus for higher-order logic. In: Peltier, N., Sofronie-Stokkermans, V. (eds.) IJCAR 2020. LNCS (LNAI). Springer, Heidelberg (2020)
Blanchette, J.C.: Formalizing the metatheory of logical calculi and automatic provers in Isabelle/HOL (invited talk). In: Mahboubi, A., Myreen, M.O. (eds.) CPP 2019, pp. 1–13. ACM (2019)
Blanchette, J.C., Hölzl, J., Lochbihler, A., Panny, L., Popescu, A., Traytel, D.: Truly modular (Co)datatypes for Isabelle/HOL. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 93–110. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08970-6_7
Blanchette, J.C., Peltier, N., Robillard, S.: Superposition with datatypes and codatatypes. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 370–387. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_25
Fietzke, A., Weidenbach, C.: Labelled splitting. Ann. Math. Artif. Intell. 55(1–2), 3–34 (2009)
Hillenbrand, T., Löchner, B.: The next Waldmeister loop. In: Voronkov, A. (ed.) CADE 2002. LNCS (LNAI), vol. 2392, pp. 486–500. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45620-1_38
Huet, G.P.: A mechanization of type theory. In: Nilsson, N.J. (ed.) IJCAI 1973, pp. 139–146. William Kaufmann (1973)
McCune, W., Wos, L.: Otter—the CADE-13 competition incarnations. J. Autom. Reason. 18(2), 211–220 (1997)
Nieuwenhuis, R., Rubio, A.: Theorem proving with ordering and equality constrained clauses. J. Symb. Comput. 19(4), 321–351 (1995)
Nipkow, T., Klein, G.: Concrete Semantics: With Isabelle/HOL. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-319-10542-0
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A proof assistant for higher-order logic. LNCS, vol. 2283. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45949-9
Schlichtkrull, A., Blanchette, J.C., Traytel, D.: A verified prover based on ordered resolution. In: Mahboubi, A., Myreen, M.O. (eds.) CPP 2019, pp. 152–165. ACM (2019)
Schlichtkrull, A., Blanchette, J.C., Traytel, D., Waldmann, U.: Formalization of Bachmair and Ganzinger’s ordered resolution prover. Archive of Formal Proofs 2018 (2018). https://www.isa-afp.org/entries/Ordered_Resolution_Prover.html
Schlichtkrull, A., Blanchette, J.C., Traytel, D., Waldmann, U.: Formalizing Bachmair and Ganzinger’s ordered resolution prover. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS, vol. 10900, pp. 89–107. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-319-94205-6_7
Schulz, S.: E—a brainiac theorem prover. AI Commun. 15(2–3), 111–126 (2002)
Tourret, S.: A comprehensive framework for saturation theorem proving. Arch. Formal Proofs 2020 (2020). https://www.isa-afp.org/entries/Saturation_Framework.shtml
Voronkov, A.: AVATAR: the architecture for first-order theorem provers. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 696–710. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_46
Waldmann, U.: Cancellative abelian monoids and related structures in refutational theorem proving (part I). J. Symb. Comput. 33(6), 777–829 (2002)
Waldmann, U., Tourret, S., Robillard, S., Blanchette, J.: A comprehensive framework for saturation theorem proving (technical report). Technical report (2020). http://matryoshka.gforge.inria.fr/pubs/saturate_report.pdf
Weidenbach, C.: Combining superposition, sorts and splitting. In: Robinson, A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. II, pp. 1965–2013. Elsevier and MIT Press (2001)
Acknowledgment
We thank Alexander Bentkamp for discussions about prover architectures for higher-order logic and for feedback from instantiating the framework, Mathias Fleury and Christian Sternagel for their help with the Isabelle development, and Robert Lewis, Visa Nummelin, Dmitriy Traytel, and the anonymous reviewers for their comments and suggestions. Blanchette’s research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 713999, Matryoshka). He also benefited from the Netherlands Organization for Scientific Research (NWO) Incidental Financial Support scheme and he has received funding from the NWO under the Vidi program (project No. 016.Vidi.189.037, Lean Forward).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Waldmann, U., Tourret, S., Robillard, S., Blanchette, J. (2020). A Comprehensive Framework for Saturation Theorem Proving. In: Peltier, N., Sofronie-Stokkermans, V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science(), vol 12166. Springer, Cham. https://doi.org/10.1007/978-3-030-51074-9_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-51074-9_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51073-2
Online ISBN: 978-3-030-51074-9
eBook Packages: Computer ScienceComputer Science (R0)


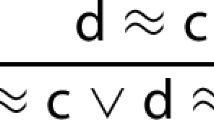


 for every
for every  ;
; for every
for every  ;
; and
and  , then
, then  .
. for some
for some  ;
; for some
for some 

 for some
for some 
 loop, or the Zipperposition loop.
loop, or the Zipperposition loop.