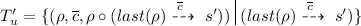Synthesis for Multi-weighted Games with Branching-Time Winning Conditions

Abstract

We investigate the synthesis problem in a quantitative game-theoretic setting with branching-time objectives. The objectives are given in a recursive modal logic with semantics defined over a multi-weighted extension of a Kripke structure where each transition is annotated with multiple nonnegative weights representing quantitative resources such as discrete time, energy and cost. The objectives may express bounds on the accumulation of each resource both in a global scope and in a local scope (on subformulae) utilizing a reset operator. We show that both the model checking problem as well as the synthesis problem are decidable and that the model checking problem is EXPTIME-complete, while the synthesis problem is in 2-EXPTIME and is NEXPTIME-hard. Furthermore, we encode both problems to the calculation of maximal fixed points on dependency graphs, thus achieving on-the-fly algorithms with the possibility of early termination.

1 Introduction

Formal verification is used to ensure that a system model M conforms to a given specification $\varphi$, denoted by . It relies on having/creating a model of the system and formalising the system’s specification in some (temporal) logic. We can distinguish the following verification problems. Satisfiability: given a specification $\varphi$, does there exist a model M s.t. ? Model checking: given a specification $\varphi$ and a model M, is it the case that ? Synthesis: given a specification $\varphi$ and a partial design D, can we construct a controller strategy $\sigma$ s.t. for the restricted design ?

We consider the synthesis problem where we are given a specification and some initial (unfinished) design [26]. The goal is then to finish the design s.t. the resulting system satisfies the given specification. The design can model both the behaviour we can control as well as the uncontrollable behaviour that results from the influence of some external environment. In some sense, the synthesis problem can be seen as a generalization of both model checking and satisfiability, as the initial design can express a high degree of freedom for the controller (allowing us to check for satisfiability) or none at all (model checking).

We study the synthesis problem in a multi-weighted setting with nonnegative weights. This allows to reason about resources such as discrete time, energy and cost. In contrast to other works, we investigate the problem for specifications expressed in a branching-time recursive modal logic where the accumulated cost of an execution in the system can be bounded both globally and locally. The branching nature of the logic allows us to express both possibility (the existential case), certainty (the universal case) or a mixture of both.

Fig. 1.

Task scheduling in a heat sensitive environment and the result of applying a strategy to the choices of using fast/slow processor

To argue for the relevance of the problem, we present a simple motivating example. Consider a processor working on a set of tasks. Depending on a set of outside factors such as the state of the hardware, the duration of the sessions etc. it will vary how long a task takes to finish and how much excess heat it produces. We model a simple version of this scenario in a game graph illustrated in Fig. 1a. In the initial state (i) the processor is idle and does not produce any heat nor complete any tasks. From this state there are two possible actions modelled as transitions annotated with nonnegative weights, representing the number of completed tasks, the time units spent and the amount of excess heat produced. Both of these are controllable (illustrated as solid arrows) and represent a choice we have in either using the regular slow setting (s) or to utilize over-clocking to get a faster result (f). From each of these states there are two arrows leading back to the idle state. These represent the influence of the environment (and are therefore illustrated as dashed arrows) and differ in the produced excess heat.

We see that as a side result of over-clocking, the processor produces more heat than the regular setting (relative to the spent time units). However, we also see that the number of tasks completed in a single time unit is doubled.

We can now use this model to consider optimistic objectives such as “can we possibly (if the environment cooperates i.e. the arriving tasks are computationally easy) complete 4 tasks within 2 time units?”. We can also ensure certain worst case invariant properties like “can we ensure that there is never produced more than 15 units of excess heat within 2 time units?”. This specific property keeps us from overheating. We are able to express the conjunction of these properties as the branching time specification allows us to reason about both a single branch (possibility) and all branches (certainty).

For these types of specifications, where we are concerned with the use of resources, the correct choice for the controller in any given state of the game will depend on the values of these resources and the possible future involvement of the environment. In our example it is necessary to at least alternate between over-clocking and regular settings to ensure that we never overheat. However this in itself does not give us a productive enough schedule in the best case. To have the possibility of completing 4 tasks within 2 time units, we must begin with over-clocking the processor as the regular settings will use the entire time span on 2 tasks. In the event that the environment picks the transition $f \xrightarrow {(2,1,5)} i$ we can safely pick the fast option again as our strategy. Otherwise, we must choose the slow option not to risk overheating. If we unfold the game according to this informally presented strategy we get a structure like the multi-weighted Kripke structure illustrated in Fig. 1b on which we can verify our objectives.

Our Contributions. We present a recursive modal logic with semantics defined over a nonnegative multi-weighted extension of Kripke structures. We consider this formalism in a game theoretic setting and investigate both the model checking problem (essentially a single player with no choice) and the synthesis problem (two players representing a controller and an uncontrollable environment). For model checking we show that the problem is EXPTIME-complete.

Synthesis in a branching-time setting is challenged by the fact that it is not compositional in the structure of the formula. Consider the game presented in Fig. 1a with a winning condition stating that we are able to reach s before completing the first task (i.e. the first component is equal to 0) and at the same time we are able to reach f before completing the first task. Separately, each subformula has a winning strategy as we can reach either s or f before completing the first task. However, when these two formula are considered in conjunction, there is no winning strategy. As a result, all subformulae in a conjunction must be kept together as we require a uniform control strategy choice for all of them. To deal with this complication, we provide a translation to a suitable weight-annotated normal form and show that the synthesis problem can then be solved in 2-EXPTIME by reducing it to the calculation of the maximal fixed-point assignment on a dependency graph [23]. Last, we provide an NEXPTIME lower-bound for the synthesis problem.

Related Work. One reason to use quantities is to argue about the performance of a system [1, 3, 4] while another reason is to model and optimize quantitative aspects of a system such as the use of resources. In this paper we consider the latter approach and study a quantitative version of branching-time logic for specifying winning conditions in a weighted game. An obvious choice for such a logic is some variant of weighted CTL. Indeed this type of logic has previously been considered for model checking  [2, 5, 13, 15, 23] where (some subset) of CTL is extended to express bounds on the accumulated cost of the resources. We have taken inspiration in these logics but have chosen to look at a more general type of logic, namely a modal logic with recursive definitions. Our syntax is inspired by the weighted version of the alternation-free modal $\mu$-calculus presented in [22] which was studied in the context of satisfiability checking.

In regards to synthesis, the problem was for expressive logics like $\mu -$calculus and its sub-logics such as CTL, LTL and CTL* [9, 18,19,20, 24, 25, 28]. However, the synthesis problem is still open for many quantitative extensions of these logics, and to our knowledge there is no work on quantitative branching-time logics in this area. Synthesis has been studied in a weighted setting in the form of energy, mean-payoff and weighted parity games [6, 10, 11, 17, 17]. Objectives that allow one to reason (in conjunction) about several complex quantitative requirements on a system has only recently received attention [27].

The main novelty of our work is that we consider a branching-time logic for expressing the specifications, allowing us to capture, at the same time, the quantitative goals for both the optimistic and pessimistic scenarios as demonstrated in our introductory example. Similar objectives are pursued in [8].

2 Preliminaries

An n-Weighted Kripke Structure (n-WKS) is a tuple $K = (S, s_0, \mathcal {AP}, L, T)$ where S is a set of states, $s_0 \in S$ is the initial state, $\mathcal {AP}$ is a set of atomic propositions, $L: S \rightarrow \mathcal {P}(\mathcal {AP})$ is a labelling function and $T \subseteq S \times \mathbb {N}^n \times S$ is a transition relation, with a weight vector of n dimensions, where for all $s \in S$ there is some outgoing transition $(s, \overline{{c}} , s') \in T$. When $(s, \overline{{c}} , s') \in T$, where $s,s' \in S$ and $\overline{{c}} \in \mathbb {N}^n$, we write $s \xrightarrow {\overline{{c}}} s'$. We define the set of outgoing transitions from a state $s \in S$ as $out(s) = \{ s \xrightarrow {\overline{{c}}} s' \in T \}$. For the remainder of the section we fix an n-WKS $K = (S, s_0, \mathcal {AP}, L, T)$ where K is finite i.e. S is a finite set of states and T is a finite transition relation and $\mathcal {AP}$ is a finite set of atomic propositions.

Let $\overline{{w}}\in \mathbb {N}^n$ be a vector of dimension n. We denote the ith component of $\overline{{w}}$ by $\overline{{w}}{}[i]$, where $1 \le i \le n$. To set the ith component of $\overline{{w}}{}$ to a specific value $k \in \mathbb {N}$ we write $\overline{{w}}{} [i \rightarrow k]$ and to set multiple components to a specific value $k \in \mathbb {N}$ we write $\overline{{w}}{} [I \rightarrow k]$ where $I \subseteq \{1, \dots ,n\}$. Given $\overline{{w}}, \overline{{w}}' \in \mathbb {N}^n$, we write $\overline{{w}}\le \overline{{w}}'$ iff $\overline{w}[i] \le \overline{w}'[i]$ for all $1 \le i \le n$.

A run in K is a sequence of states and transitions $\rho = s_0 \xrightarrow {\overline{{c}}_0} s_1 \xrightarrow {\overline{{c}}_1} s_2 \xrightarrow {\overline{{c}}_2} \dots$ where $s_{i} \xrightarrow {\overline{{c}}_i} s_{i+1} \in T$ for all $i \ge 0$. Given a position $i \in \mathbb {N}$ along $\rho$, let $\rho (i) = s_i$, and $last(\rho )$ be the state at the last position along $\rho$, if $\rho$ is finite. We also define the concatenation operator $\circ$, s.t. if $(\rho = s_0 \xrightarrow {\overline{{c}}_0} s_1 \xrightarrow {\overline{{c}}_1} \dots \xrightarrow {\overline{{c}}_{m-1}}s_m)$ then $\rho \circ (s_m \xrightarrow {\overline{{c}}_m} s_{m+1}) = (s_0 \xrightarrow {\overline{{c}}_0} s_1 \xrightarrow {\overline{{c}}_1} s_2 \dots s_m \xrightarrow {\overline{{c}}_m} s_{m+1})$. We denote the set of all runs $\rho$ in K of the form $(\rho = s_0 \xrightarrow {\overline{{c}}_0} s_1 \xrightarrow {\overline{{c}}_1} \dots )$ as $\varPi _{K}$. Furthermore, we denote the set of all finite runs $\rho$ in K of the form $(\rho = s_0 \xrightarrow {\overline{{c}}_0} \dots \xrightarrow {\overline{{c}}_{m-1}} s_m)$ as $\varPi _{K}^{fin}$.

Given a run $(\rho = s_0 \xrightarrow {\overline{{c}}_0} s_1 \xrightarrow {\overline{{c}}_1} \dots ) \in \varPi _{K}$, the cost of $\rho$ at position $i \in \mathbb {N}$ is then defined as: $cost_{\rho }(i) = 0^n$ if $i = 0$ and $cost_{\rho }(i) = \sum \limits _{j=0}^{i-1}\overline{{c}}_j$ otherwise. If $\rho$ is finite, we denote $cost_{}(\rho )$ as the cost of the last position along $\rho$. Lastly, we define a state and cost pair $(s,\overline{{w}}) \in S \times \mathbb {N}^n$ as a configuration. The set of all configurations in K is denoted $\mathcal {C}_K$.

3 RML and the Model Checking Problem

We can now define our logic.

Definition 1

(RML equation system). Let $\mathcal {AP}$ be a set of atomic propositions and $\mathcal {V}ar= \{X_0, \dots , X_m \}$ be a finite set of variables. A Recursive Modal Logic (RML) equations system is a function $\mathcal {E} : \mathcal {V}ar \rightarrow \mathcal {F}_{\mathcal {V}ar}$, denoted by $\mathcal {E} = [X_0 = \varphi _{0}, \ldots , X_m = \varphi _{m}]$, where $\mathcal {F}_{\mathcal {V}ar}$ is the set of all RML formulae given by:

$$\begin{aligned}&\varphi \ :=\ \ \varphi _1 \wedge \varphi _2 \mid \varphi _1 \vee \varphi _2 \mid \beta \\&\beta \ := \ \ \textsc {true}\mid \textsc {false}\mid a \mid \lnot a \mid e \bowtie c \mid reset \; R \; in \; EX (X) \mid reset \; R \; in \; AX (X) \\&e \ :=\ \ \#i \mid c \mid e_1 \oplus e_2 \end{aligned}$$

where $a \in \mathcal {AP}$, $\bowtie \; \in \{ >, \ge , =, \le ,< \}$, $1 \le i \le n$ is the index of a vector component, $R \subseteq \{1, \dots , n\}$ is a set of indexes of vector components, $c \in \mathbb {N}$, $\oplus \in \{ + , \cdot \}$ and $X \in \mathcal {V}ar$ is a variable.

Given a formula $reset \; R \; in \; EX (X)$ (or $reset \; R \; in \; AX (X)$) where $R = \emptyset$ we relieve the notation slightly and simply write $EX (X)$ (or $AX (X)$) instead. We denote the set of all subformulae in a formula $\varphi$ as $Sub(\varphi )$. Furthermore, we refer to a formula given by the syntactical category $\beta$ as a basic formula and a formula given by e as an expression.

Remark 1

We limit ourselves to bounds of the form $(e \bowtie c)$ as more expressive bounds of the form $(e_1 \bowtie e_2)$ allows us to simulate a two-counter Minsky machine and thus make the model checking problem undecidable [14].

Given n-WKS K, a variable $X \in \mathcal {V}ar$ is evaluated in an environment $\epsilon : \mathcal {V}ar \rightarrow 2^{\mathcal {C}_K}$ assigning a set of configurations $(s,\overline{{w}}) \in \mathcal {C}_K$ to a variable X. We denote the set of all environments as Env and assume the ordering s.t. for $\epsilon ,\epsilon ' \in Env$ we have $\epsilon \subseteq \epsilon '$ if $\epsilon (X) \subseteq \epsilon '(X)$ for all $X \in \mathcal {V}ar$. Formally the semantics of an RML formula is a function $\mathcal {F}_{\mathcal {V}ar} \times Env \rightarrow 2^{\mathcal {C}_K}$ mapping a RML formula and an environment to a set of configurations. The semantics for a formula $\varphi$ is thus defined based on an environment $\epsilon$ as follows:

$$\begin{aligned}&\llbracket \varphi _1 \vee \varphi _2 \rrbracket _\epsilon = \llbracket \varphi _1 \rrbracket _\epsilon \cup \llbracket \varphi _2 \rrbracket _\epsilon&\llbracket \varphi _1 \wedge \varphi _2 \rrbracket _\epsilon = \llbracket \varphi _1 \rrbracket _\epsilon \cap \llbracket \varphi _2 \rrbracket _\epsilon \end{aligned}$$

and the semantics for a basic formula $\beta$ is defined as follows:

where $eval_{\overline{{w}}}(c) = c$, $eval_{\overline{{w}}}(\#i) = \overline{w}[i]$ and $eval_{\overline{{w}}}(e_1 \oplus e_2) = eval_{\overline{{w}}}(e_1) \oplus eval_{\overline{{w}}}(e_2)$.

The semantics of an RML equation system is defined by the function $\mathcal {F} : Env \rightarrow Env$ where for all $\mathcal {E}(X) = \varphi$ we have $\mathcal {F}(\epsilon )(X) = \llbracket \varphi \rrbracket _\epsilon$. By the semantics, we have that $\mathcal {F}$ is monotonic, given the complete lattice formed by $(2^{\mathcal {C}_K},\subseteq )$. Hence by Knaster-Tarski’s theorem we have that there exists a unique maximal fixed point defined as

$$\begin{aligned} \nu \mathcal {E}&= \bigcup \{ \epsilon \in Env {\mid } \epsilon \subseteq \mathcal {F} (\epsilon ) \}. \end{aligned}$$

Let K be an n-WKS and $\mathcal {E}$ be an RML equation system. If $(s,\overline{{w}}) \in \llbracket \varphi \rrbracket _{\nu \mathcal {E}}$ we write . When the n-WKS K is obvious from context, we omit it and simply write .

Definition 2

(Model checking problem). The model checking problem asks, given an n-WKS $K = (S, s_0, \mathcal {AP}, L, T)$, a configuration $(s,\overline{{w}}) \in \mathcal {C}_K$, an RML equation system $\mathcal {E}$ and an RML formula $\varphi$ in $\mathcal {E}$ as input, whether .

In the remainder of the paper, we assume, unless otherwise indicated, that the model checking problem for an n-WKS K and an RML equation system $\mathcal {E}$ is the question of whether where $X_0$ is the first variable in $\mathcal {E}$.

Remark 2

In our logic, we can encode some instances of reachability, specifically cost-bounded reachability, in an n-WKS where cost in divergent i.e. there are no infinite runs where the cost-component does not increase. Consider a formula that specifies that we can fulfil in all paths some property $\varphi$ before the first cost-component reaches 10. In a weighted CTL-style syntax, this will be written as $AF_{\#1\le 10} \ \varphi$. This is a cost-bounded reachability property and we can encode it as the following equation system $\mathcal {E} = [ X = ((AX(X) \vee \varphi ) \wedge (\#1 \le 10)) ]$. As the environment $\nu \mathcal {E}$ is a maximum fixed point, the satisfaction of this formula may be in general witnessed also by an infinite run satisfying $(\#1 \le 10)$ but never satisfying $\varphi$. However, as all cycles are strictly increasing in the first component, this is not possible and the only way to satisfy the specification is to eventually reach $\varphi$ within the bound $(\#1 \le 10)$.

Consider now the following properties used in our motivating example.

• 1. It is always the case that the produced excess heat never exceeds 15 units within 2 time units.

• 2. There is a possibility of completing 4 tasks within 2 time units.

We now formalise the conjunction of these objectives as an RML equation system $\mathcal {E}$. Recall that the first component counts the number of completed tasks while the second component measures the time units and the third measures the produced excess heat. First, we express the bound on the excess heat in the formula $p_H=( \#2 > 2 \vee \#3 \le 15 )$ which states that if less than 2 units of time have gone by then the amount of excess heat is not allowed to be larger than 15 units. The first equation enforces $p_H$ in the current state and it ensures that it is always satisfied in the future.

$$\mathcal {E}(X_H) = p_H \wedge AX (X_H) \wedge reset \; \{2,3\} \; in \; AX (X_H) $$

We add the last conjunction $reset \; \{2,3\} \; in \; AX (X_H)$ so that we do not stop checking the property the first time component two exceeded 2 units. By resetting the components every time we take a step, we ensure that this invariant is checked with “fresh values” no matter the cost of any previous steps. Next, we express the possibility of completing 4 tasks within 2 time units by $p_{T} = (\#1 \ge 4 \wedge \#2 \le 2)$. We define the second equation

$$\mathcal {E}(X_T) = p_T \vee ( EX (X_T) \wedge \#2 \le 2)$$

where the condition $\#2 \le 2$ in the second part of the equation ensures that only finite runs which satisfy $p_T$ at some point are considered (see Remark 2). The final property is now formulated as the conjunction of $X_H$ and $X_T$.

3.1 Finite Representation

Given a finite n-WKS and an RML equation system over the finite set of variables $\mathcal {V}ar = \{X_0, \dots , X_m \}$, we only need to consider a finite number of configurations when evaluating a variable X in $\mathcal {E}$.

First, we fix a finite n-WKS $K = (S, s_0, \mathcal {AP}, L, T)$ and an RML equation system $\mathcal {E}$. We define the set of all subformulae in the equation system $\mathcal {E}$ as

$$Sub(\mathcal {E})= \bigcup _{i \in \{0, \dots , m \}} Sub(\mathcal {E}(X_i)).$$

Second, let $gb = \max \{ c {\mid } (e \bowtie c) \in Sub(\mathcal {E}) \}$ be the largest bound of $\mathcal {E}$. (Note that if there are no expressions of the type $e \bowtie c$ then the weights can be simply ignored.) This gives an upper-bound to the value of the cost vectors we need to consider. We say that the constant gb is derived from $\mathcal {E}$ and based on it we define a function Cut used to limit the number of vectors we need to represent.

Definition 3

(Cut). Let gb be the constant derived from $\mathcal {E}$. The function ${Cut} : \mathbb {N}^n \rightarrow \mathbb {N}^n$ is then defined for all $1\le i \le n$:

$$ Cut(\overline{{w}})[i] = {\left\{ \begin{array}{ll} \overline{{w}}[i] &{} \text {if } \overline{{w}}[i] \le gb\\ gb + 1 &{} \text {otherwise}. \end{array}\right. } $$

Based on the finite set of configurations $\mathcal {C}_K^{cut} = \{ (s,Cut(\overline{{w}})) {\mid } (s,\overline{{w}}) \in \mathcal {C}_K \}$ we can define a new cut environment. The new semantics is a straightforward extension. The main changes are made to the rules concerning the bounds and the next operators:

The semantics for an RML equation system is then defined as the regular semantics but with cut environments:

$$\begin{aligned} \nu \mathcal {E}_{cut}&= \bigcup \{ \epsilon _{cut} \in Env_{cut} {\mid } \epsilon _{cut} \subseteq \mathcal {F}(\epsilon _{cut}) \}. \end{aligned}$$

If $(s,\overline{{w}}) \in \llbracket \varphi \rrbracket ^{cut}_{\nu \mathcal {E}_{cut}}$ then we write .

Lemma 1 (Equivalence of the cut semantics)

Let K be an n-WKS and $\mathcal {E}$ be an RML equation system. Given a configuration $(s,\overline{{w}}) \in \mathcal {C}_K$ we have iff .

Proof (Sketch)

We show by structural induction on the formula $\varphi$ that $(s,\overline{{w}}) \in \llbracket \varphi \rrbracket _\epsilon$ iff $(s,\overline{{w}}) \in \llbracket \varphi \rrbracket ^{cut}_{\epsilon _{cut}}$ whenever we cut with a constant gb derived from $\mathcal {E}$. This means that in any environment $\epsilon$ we have $\epsilon \subseteq \mathcal {F}(\epsilon )$ iff $\epsilon _{cut} \subseteq \mathcal {F}( \epsilon _{cut})$.    $\square$

Lemma 2 (Hardness of Model Checking)

The model checking problem is EXPTIME-hard, already for an n-WKS K with a single weight.

Proof

We show that the problem is EXPTIME-hard by reduction from countdown games that are EXPTIME-complete [16]. A countdown game (Q, R) consists of a finite set of states Q and a finite transition relation $R \subseteq Q \times \mathbb {N}\times Q$. We write transitions as $(q,k,q') \in R$ and say that the duration of the transition is k. A configuration in the game is a pair (q, c) where $q\in Q$ and $c \in \mathbb {N}$. Given the configuration (q, c) the rules of the game are defined as follows:

• $\circ$ if $c = 0$ then player 1 wins, else

• $\circ$ if for all transitions $(q,k,q') \in R$ we have $k > c$ and $c > 0$ player 2 wins,

• $\circ$ otherwise there exists some transition $(q,k,q') \in R$ s.t. $k \le c$. Player 1 must choose such a duration k while player 2 chooses a target state $q'$ s.t. $(q,k,q') \in R$. The new configuration is $(q',c-k)$. We repeat this until a winner is found.

We now reduce the problem of deciding which player is the winner of the countdown game (Q, R) given the configuration (q, c) to deciding the model checking problem for an n-WKS and an RML equation system. We create the 1-WKS $K = (S, s_0, \mathcal {AP}, L, T)$ from the countdown game (Q, R) as follows: $S = Q \cup \{s^k_q {\mid } \exists (q,k,q') \in R \}$ with the initial state $s_0 = q_0$, $\mathcal {AP} = \emptyset$ and the set of transitions are defined as $T = \{ (q,k,s^k_q) {\mid } \exists (q,k,q') \in R \text { and } \exists s^k_q \in S \} \cup \{ (s^k_q,0,q') {\mid } \exists s^k_q \in S \text { and } \exists (q,k,q') \in R \}$. To enforce the rules, we create the following RML equation system:

Now we can observe that iff player 1 has a winning strategy in the corresponding countdown game given the initial configuration $(q_0,c)$.    $\square$

Theorem 1

(Model Checking Complexity). Given an n-WKS and an RML equation system, the model checking problem is EXPTIME-complete.

Proof

The upper-bound follows from Lemma 1 and noticing that the fixed-point computation (based on the cut semantics) runs in exponential time; there are at most exponentially many cut configurations and it takes at most an exponential number of rounds to reach the fixed point. The lower-bound is by Lemma 2.    $\square$

4 Game Theoretic Framework

In this section we introduce multi-weighted two-player games, where one player acts as the controller and one player act as the uncontrollable environment. We end the section by expressing the synthesis problem as the problem of finding a winning strategy for the controller in such a game.

Definition 4

(n-Weighted Game Graph). An n-Weighted Game Graph (n-WGG) is a tuple $\mathcal {G}= (S, s_0, \mathcal {AP}, L, T_c, T_u)$ where $T_c$ and $T_u$ are disjoint sets and $K_\mathcal {G}= (S, s_0, \mathcal {AP}, L, T_c \cup T_u)$ is the underlying n-WKS.

We fix an n-WGG $\mathcal {G}= (S, s_0, \mathcal {AP}, L, T_c, T_u)$ for the remainder of the section. The set of transitions $T_c$ are owned by the controller while the set $T_u$ is owned by the uncontrollable environment. When $(s, \overline{{c}} , s') \in T_c$, we write $s \xrightarrow {\overline{{c}}} s'$ and when $(s,\overline{{c}},s') \in T_u$ we write . When s has some outgoing controllable transition we write $s \xrightarrow {}$ (or for uncontrollable transitions). Similarly, if there are no outgoing transitions we write (or for uncontrollable transitions).

Definition 5

(Game). An n-Weighted Game (n-WG) is a tuple $(\mathcal {G},\mathcal {E})$ where $\mathcal {G}$ is an n-WGG and the winning condition is an RML equation system $\mathcal {E}$.

In an n-WG the controller’s actions are based on a strategy that specifies which transition to take at a given position. Formally a strategy $\sigma$ is a function that, given the history of the game (the current branch), outputs the controller’s next move. Recall that $K_\mathcal {G}$ is the underlying n-WKS of an n-WGG $\mathcal {G}$ and $\varPi _{K_\mathcal {G}}^{fin}$ is the set of all finite runs in $K_\mathcal {G}$.

Definition 6

(Strategy). A strategy for the controller is a function $\sigma :\varPi _{K_\mathcal {G}}^{fin} \rightarrow T_c \cup \{\textsc {nil}\}$ mapping a finite run $\rho$ to a transition s.t.

$$ \sigma (\rho ) = {\left\{ \begin{array}{ll} last(\rho ) \xrightarrow {\overline{{c}}} s' &{} \text {if } last(\rho ) \rightarrow \\ \textsc {nil}&{} \text {otherwise } \end{array}\right. } $$

where $\textsc {nil}$ is the choice to do nothing which is only allowed if there is no controllable transition to choose.

For the uncontrollable actions, we are forced to consider all possible options as the winning condition allows us to reason about branching properties. Based on the strategy’s choices and all choices available to the environment, we unfold the game into an n-WKS on which we can verify the objective.

Definition 7

(Strategy restricted n-WKS). Given a game graph $\mathcal {G}$ and a strategy $\sigma$, we define ${\mathcal {G}{\upharpoonright }\sigma }= (S', s_0, \mathcal {AP}, L', T_c{\upharpoonright }\sigma \cup T_u')$ as the n-WKS resulting from restricting the game graph under the strategy $\sigma$ s.t:

• $\circ$ $S' = \varPi _{K_G}^{fin}$

• $\circ$ $L'(\rho ) = L(last(\rho ))$

• $\circ$

• $\circ$

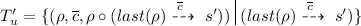
A strategy $\sigma$ is winning for the game $(\mathcal {G},\mathcal {E})$ iff .

Definition 8

(Synthesis Problem). Given the n-WG $(\mathcal {G}, \mathcal {E})$, the synthesis problem is to decide if there is a strategy $\sigma$ s.t. .

We return to the motivating example of a processor completing a set of tasks introduced earlier. Let $\mathcal {G}$ be the n-WGG presented in Fig. 1a and $\mathcal {E}$ be the formalised winning condition presented in Sect. 3. As stated in the introduction, one winning strategy is to initially choose the fastest option $i \xrightarrow {(0,0,0)} f$ and repeat this choice whenever the preceding uncontrollable move did not generate more than 5 units of excess heat. In all other situations we choose the safe slow option. However, we notice that there is a simpler alternative which still satisfies the winning condition.

After the first two turns, we no longer need to consider the optimistic objective which aims to finish 4 units of work in 2 time units, as 2 time units have already passed. We can therefore focus solely on keeping the excess heat down and can simply always choose the slow option after that. We formally define this simpler strategy $\sigma$ below:

The result of applying $\sigma$ to the game graph $\mathcal {G}$ is the strategy restricted game graph ${\mathcal {G}{\upharpoonright }\sigma }$ illustrated in Fig. 2. As the second property only expresses a possibility it is enough that our first move might lead to completing the tasks and this defined strategy is indeed winning.If we are to formally define the strategy $\sigma _{alt}$, which is the first option discussed, we need to know some of the history of the play in order to choose alternating transitions from the state i. In fact, we need to look at the last four transitions to ensure a safe pick. In the remainder of this paper, we carefully consider the memory requirements of winning strategies for RML winning conditions (we encode the memory needed as the remainder of the winning condition which is still to be satisfied).

Fig. 2.

Strategy restricted game graph ${\mathcal {G}{\upharpoonright }\sigma }$ for $\mathcal {G}$ from Fig. 1a

5 Dependency Graphs

To solve the synthesis problem we shall propose a reduction to the problem of calculating the maximal fixed-point assignment of a dependency graph. A dependency graph [23] is a pair $D=(V,H)$ where V is a finite set of nodes and $H: V \times \mathcal {P}(V)$ is a finite set of hyper-edges. Given a hyper-edge $h = (v,T) \in H$ we say that $v \in V$ is the source node and $T \subseteq V$ is the set of target nodes.

An assignment of a dependency graph D is a function $A:V\rightarrow \{0,1\}$ that assigns value 0 (false) or 1 (true) to each node in the graph. We also assume a component-wise ordering $\sqsubseteq$ of assignments s.t. $A_1 \sqsubseteq A_2$ whenever $A_1(v) \le A_2(v)$ for all $v \in V$. The set of all assignments is denoted by $\mathcal {A}$ and clearly $(\mathcal {A},\sqsubseteq )$ is a complete lattice. A (post) fixed-point assignment of D is an assignment A s.t. for any $v \in V$ if for all $(v,T) \in H$ there exists an $u \in T$ s.t. $A(u) = 0$ then we have that $A(v) = 0$. This is formalized by the monotonic function $f: \mathcal {A} \rightarrow \mathcal {A}$ defined as

$$f(A)(v) = \bigvee _{(v,T)\in H}\bigwedge _{(u\in T)}A(u)$$

where, by convention, conjunction over the empty set is true while disjunction over the empty set is false. By Knaster-Tarski’s theorem we know that there exists a unique maximum fixed-point assignment of D, denoted $A^{max}_D$. When the dependency graph D is clear from context, we simply denote the fixed-point assignment as $A^{max}$. To compute the maximum fixed-point assignment, we apply f repeatedly on the assignment, starting with $f(A^1)$ where $A^1$ is the initial assignment defined s.t. $A^{1}(v) = 1$ for all $v \in V$, as shown in Fig. 3.

Fig. 3.

Dependency graph D and the fixed point assignment $A^{max}$

Theorem 2

([23]). There is a linear time (on-the-fly) algorithm to compute the maximal fixed point of a dependency graph.

6 On-the-Fly Synthesis Algorithm for n-WG

We shall now present our encoding of the synthesis problem to the problem of calculating the maximal fixed-point assignment of a dependency graph. The initial idea is that given a game $(\mathcal {G},\mathcal {E})$, we construct a dependency graph $D_{(\mathcal {G},\mathcal {E})}$ with nodes of the form $\langle \varphi , (s,\overline{{w}}) \rangle$ such that $A^{max}(\langle \varphi , (s,\overline{{w}}) \rangle ) = 1$ iff there exists a strategy $\sigma$ where . We are referring to this as an on-the-fly algorithm as we do not necessarily need to calculate the maximal fixed-point assignment of the entire dependency graph to terminate.

The first challenge in the encoding is to keep track of which parts of the winning condition must be considered together (i.e. cannot be looked at compositionally). We can analyse disjunction compositionally by decomposing it to the individual disjuncts. However, for conjunction, we must consider the whole formula together as the controller’s choice must be done in agreement with all subformulae. As a consequence of keeping all conjuncts together, the reset operator may force us to evaluate the same subformula for (possibly several) different cost vectors at any given point.

This technical challenge is solved by annotating the basic formulae with weight vectors under which they must be evaluated. Then we transform the weight annotated formulae into a disjunctive normal form such that we can separate the disjuncts (as they can be solved independently) and then for a given disjunct select one controllable transition. To create such an annotated normal form, we now propose a more succinct notation for evaluating a formula with respect to multiple different cost vectors.

Definition 9

(Weighted basic formula). We define the function $\varphi [\overline{{w}}]$ as the operation of pushing the cost vector $\overline{{w}}$ through an RML formula $\varphi$ s.t. each basic formula is prefixed with the cost vector:

The result is a positive Boolean combination of weighted basic formulae for which we write whenever .

Notice that for propositions of the form a, $\lnot a$, $\textsc {true}$ and $\textsc {false}$ the cost vector $\overline{{w}}$ does not impact the satisfiability and can be ignored such that instead of we simply consider . For $(e \bowtie c)$ this corresponds to $eval_{\overline{{w}}}(e) \bowtie c$ which evaluates to either $\textsc {true}$ or $\textsc {false}$ and can be replaced by its truth value.

We use the function $dnf$ to transforms the conjunction $\bigwedge _{m \in M}\varphi _m[\overline{{w}}_m]$ into an equivalent formula in disjunctive normal form $dnf (\bigwedge _{m \in M}(\varphi _m[\overline{{w}}_m])) = \bigvee _{i \in I} \psi _i$ where each $\psi _i$ is of the form:

$$\begin{aligned} \bigwedge _{\ell \in L} p_{\ell } \wedge \bigwedge _{j \in J} \overline{{w}}_{j} :reset \; R_{j} \; in \; EX ({X_{j}}) \wedge \bigwedge _{k \in K} \overline{{w}}_{k} : reset \; R_{k} \; in \; AX (X_{k}) \ \end{aligned}$$

(1)

where $p := a {\mid } \lnot a {\mid } \textsc {true}{\mid } \textsc {false}$.

For the remainder of the section, we fix a conjunction of weighted basic formulae $\psi$ such that L, J or K refer to the indices used in Eq. (1). Additionally, we fix an n-WGG $\mathcal {G}= (S, s_0, \mathcal {AP}, L, T_c, T_u)$. Based on a strategy choice $s \xrightarrow {\overline{{c}}}s' \in T_c$ we define the set of final transitions as $finalOut(s \xrightarrow {\overline{{c}}}s') = \{ (s\xrightarrow {\overline{{c}}_u}s_u) \in T_u\} \cup \{ (s \xrightarrow {\overline{{c}}} s') \}$.

6.1 Determining a Winning Move

Given a conjunction of weighted basic formulae $\psi$, a strategy choice $s \xrightarrow {\overline{{c}}} s'$ is winning if all propositions and bounds are fulfilled i.e. and (i) every $(\overline{{w}}_j : reset \; R_j \; in \; EX ({X_j}) )$ subformula is satisfied by some final outgoing transition, and (ii) all $(\overline{{w}}_k : reset \; R_k \; in \; AX (X_k))$ subformulae are satisfied by all final outgoing transitions.

The second challenge in the encoding is thus to determine how the formula should envolve in the different branches of the resulting computation tree i.e. which existential subformula should be satisfied by a given final transition. We frame this choice as a mapping from existential subformulae to final transitions $\alpha : J \rightarrow finalOut(s \xrightarrow {\overline{{c}}} s')$. Given such a mapping we can formally define the remaining winning condition for each final transition $(s,\overline{{c}}',s'') \in finalOut(s \xrightarrow {\overline{{c}}} s')$ in the move function where $move({\psi },\alpha ,(s,\overline{{c}}',s'')) = \textsc {false}$ if $\exists \ell \in L$ s.t. and otherwise $move({\psi },\alpha ,(s,\overline{{c}}',s'')) =$

$$\begin{aligned} \bigwedge _{ j \in J \text { s.t. }\atop \alpha (j) = (s,\overline{{c}}',s'') } \mathcal {E}(X_{j})[(Cut(\overline{{w}}_j[R_{j} \rightarrow 0] + \overline{{c}}' )] \wedge \bigwedge _{ k \in K } \mathcal {E}(X_{k})[(Cut(\overline{{w}}_k[R_k \rightarrow 0] + \overline{{c}}')] \ . \end{aligned}$$

In Fig. 4 we show an illustration of the final outgoing transitions as well as the remaining formula based on the move function.

Fig. 4.

Successor states assigned their remaining formula

6.2 Dependency Graph Encoding

We are now ready to present the encoding of the synthesis problem to the computation of the maximal fixed-point assignment on a dependency graph. The encoding consists of two types of nodes. Either $\langle \psi ,s \rangle$ which represent the synthesis problem from the state s and winning condition $\psi$, or intermediate nodes with additional information used to explore possible strategies and mappings.

Given the game $(\mathcal {G},\mathcal {E})$ and the initial state $s_0$, we construct the dependency graph $D_{(\mathcal {G},\mathcal {E})}$ with the root node $\langle \mathcal {E}(X_0)[0^n ],s_0\rangle$. The outgoing hyper-edges are defined in Fig. 5. Notice that the nodes representing synthesis problems are illustrated as square boxes, while intermediate nodes are illustrated as ellipses. Below a brief description of the encoding is given:

• 1. Given a conjunction $\bigwedge _{m \in M}(\mathcal {E}(X_m)[\overline{{w}}_m])$, we first put it into disjunctive normal form (Fig. 5a),

• 2. and then the resulting formula $\bigvee _{i \in I}\psi _i$ is split into conjunctions of weighted basic formulae (Fig. 5b).

• 3. The propositions $\textsc {true}$ (Fig. 5c) and $\textsc {false}$ (Fig. 5d) are handled in the obvious way (note that $\textsc {false}$ has no outgoing edges and evaluates to 0).

• 4. For a conjunction of weighted basic formulae $\psi$, we create hyper-edges to intermediate nodes which explore each possible strategy (Fig. 5e).

• 5. From the intermediate node, we create a hyper-edge with a target node for each outgoing transition. Each target node records the last state and updates the remaining formula based on the move function (Fig. 5f). Goto step 1.

• 6. If there are no outgoing controllable transitions, we combine steps 4 and 5 and explore all mappings and advance the formula by one step (Fig. 5g).

Fig. 5.

Encoding of the synthesis problem

Given a dependency graph $D_{(\mathcal {G},\mathcal {E})}$ with the maximal fixed-point assignment $A^{max}$, we have that if $A^{max}(\langle \mathcal {E}(X_0)[0^n],s_0\rangle ) = 1$ we can extract a winning strategy from the initial state $s_0$ by evaluating how the node got that assignment. Essentially for a node $\langle s, \psi \rangle$ we follow the assignment through either Fig. 5e and Fig. 5f, or Fig. 5g and extract the strategy from the intermediate node (if there is one). We generate the runs used for the next strategy choices based on the final transitions. If there is no remaining winning condition to satisfy (or no way of satisfying it in the future) we go to Fig. 5c or 5d.

Lemma 3 (Correctness of the encoding)

Let $(\mathcal {G}, \mathcal {E})$ be an n-WG. There is a strategy $\sigma$ such that iff $A^{max}_{D_{(\mathcal {G},\mathcal {E})}}(\langle \mathcal {E}(X_0)[0^n], s_0\rangle )=1$.

Theorem 3

The synthesis problem for n-WGs is in 2-EXPTIME.

Proof

To show that the problem is in 2-EXPTIME, we first notice that given a game $(\mathcal {G},\mathcal {E})$, the number of nodes in the dependency graph $D_{(\mathcal {G},\mathcal {E})}$ is doubly exponential in the size of $K_\mathcal {G}$. This is because there is an exponential number of weighted basic formulae and the nodes can contain an arbitrary conjunction (subset of) weighted basic formulae. As finding the maximal fixed point of a dependency graph can be then done in linear time in the size of the dependency graph (Theorem 2), this gives us a doubly exponential algorithm.    $\square$

6.3 Hardness of the Synthesis Problem

We shall now argue that the synthesis problem is NEXPTIME-hard. This is proved by a reduction from Succinct Hamiltonian path problem.

Definition 10

(Succinct Hamiltonian). Let $n, r \in \mathbb {N}$ be natural numbers and let $\varphi (x_1,x_2,\dots ,x_{2n+r})$ be a Boolean formula over the variables $x_1, \ldots , x_{2n+r}$. This input defines a directed graph $G = (V,E)$ where $V=\{0,1\}^n$ and $(v,v') \in E$ iff there exists $y\in \{0,1\}^r$ such that $\varphi (v,v',y) = \textsc {true}$. The Succinct Hamiltonian problem is to decide if there is a Hamiltonian path in G (containing each vertex exactly once).

Lemma 4

The Succinct Hamiltonian problem is NEXPTIME-complete.

Proof

In [12] the succinct Hamiltonian path problem is proved NEXPTIME-complete where the edge relation is defined by a Boolean circuit. The Boolean formula representation is obtained by employing the Tseytin transformation.    $\square$

Theorem 4

The synthesis problem for n-WGs is NEXPTIME-hard.

Proof

By polynomial time reduction from Succinct Hamiltonian problem. Let $n, r \in \mathbb {N}$ and $\varphi (x_1,x_2,\dots ,x_{2n+r})$ be an instance of the problem. We construct an $(3n+r+1)$-WG $\mathcal {G}$ and a formula such that the answer to the synthesis problem is positive iff there is a Hamiltonian path. The cost-vectors that we use are of the form

$$\begin{aligned} \overline{{w}}&= [ \underbrace{1,\dots ,n}_{u_1}, \underbrace{n+1,\dots ,2n}_{u_2}, \underbrace{2n+1,\dots ,3n}_{u_3}, \underbrace{3n+1,\dots ,3n+r}_{y}, \underbrace{3n+r+1}_\text {counter}] \end{aligned}$$

where $(u_1,u_2)$ or $(u_2,u_1)$ represents the current edge that we are exploring (the direction of the edge depends on the phase of the edge generation process), $u_3$ stores the encoding of a node that must appear in the path, y represents the internal variables for the evaluation of $\varphi$ and the last weight coordinate is a counter where we store the number of processed edges. Whenever we write $u_1$ we refer to the first n components of the cost-vector, for $u_2$ we refer to the next n components etc. The constructed game graph $\mathcal {G}$ together with the winning condition is given in Fig. 6 such that the notation $\#i{\mathbf {++}}$ represents a vector where at position i the weight value is 1 and at all other positions the value is 0. Notice that all transitions in the game graph are controllable. Let us now argue about the correctness of the reduction.

Fig. 6.

Game graph and winning condition

First, let us assume that there is a Hamiltonian path in G, i.e. a sequence $v_1,v_2, \dots ,v_{2^n} \in V$ where every node from V is part of the sequence and for all i, $1 \le i < 2^n$, there is $y \in \{0,1\}^r$ such that $\varphi (v_i,v_{i+1},y) = \textsc {true}$. We shall define a winning strategy $\sigma$ for the constructed game graph with a winning condition defined by the variable $X_0$. The strategy $\sigma$ moves from the initial state to $s_u$ that satisfies the proposition $unf$ and then loops n times in $s_u$. Afterwards, it proceeds to $s_{c_1}$ as this is the only way to satisfy the equations for variables $X_0$ to $X_n$. From this point, we define a strategy based on the Hamiltonian path $v_1,v_2, \dots ,v_{2^n}$. First, we move from $s_{c_1}$ to $s_{c_2}$ and bit by bit select the appropriate edges so that the encoding of node $v_1$ is stored in the first n bits of the weight vector. Then we select the encoding for the y part of the weight vector and increase the counter value to 1. We repeat the process in the symmetric lower part of the loop and store the encoding of the node $v_2$ in the second part of the weight vector, making sure that the y part is selected so that $\varphi (v_1,v_2,y)=\textsc {true}$. Then the control strategy is defined so that the node $v_3$ is stored instead of the node $v_1$ and an appropriate vector y is generated so that $\varphi (v_2,v_3,y)=\textsc {true}$. Next, the node $v_4$ is generated instead of the node $v_2$ with the corresponding vector y and so on until the whole Hamiltonian path is traversed in this way, until we move to the state $s_f$. It remains to show that the strategy $\sigma$ satisfies the variable $X_0$.

To argue that this is a winning strategy we consider both the invariant $X_{Edge}$ and $X_{Find}$, activated by $X_{Path}$ in the state $s_{c_1}$. The use of $reset$ in the equations from $X_0$ to $X_n$ created $2^n$ active versions of the remaining winning condition $X_{Path}$ by creating a new cost-prefix for every Boolean combination of the components in $u_3$. Hence every node in the graph has an active version of $X_{Find}$ trying to satisfy the subformula $\varphi _{eq}$ that proves that the vector in the third weight component ($u_3$) appears within less than $2^n$ steps at least once in the generated sequence of nodes. As the generated path is Hamiltonian, this is indeed the case and $X_{Find}$ is hence satisfied. Next we argue for the satisfiability of the invariant $X_{Edge}$. The satisfiability of this variable is never affected by $u_3$ and so we can ignore the multiple active versions. In the strategy $\sigma$ we are generating nodes according to the Hamiltonian path and every time we are in $s_{c_1}$ that satisfies the proposition check1 we must guarantee we have a valid edge between $u_1$ and $u_2$ (required by $\varphi _1$) and similarly we must satisfy $\varphi _2$ whenever we are in $s_{c_2}$. Again, as the generated sequence is a path in the graph, this is the case.

Let us now assume that there is a winning strategy $\sigma$ for $(\mathcal {G},\mathcal {E})$. We shall argue that the sequence of nodes generated in $u_1$ and $u_2$ defines a Hamiltonian path. As $\sigma$ is winning it must include a move to $s_u$, n loops on $s_u$ and finally a move to $s_{c1}$. This is needed to satisfy the equations from $X_0$ to $X_n$. Given this sequence of moves, we have that from $s_{c1}$ the strategy must enforce $2^n$ active versions of $X_{Edge}$ and $X_{Find}$. To satisfy all active versions of $X_{Find}$ all nodes must be represented in either $u_1$ or $u_2$ before the counter reaches $2^n$. As there are exactly $2^n$ nodes, this implies that there cannot be a repetition of any node in the first $2^n$ nodes generated by $\sigma$. To satisfy $X_{Edge}$ the only choices are to either continuously satisfy the second or third clause or move to $s_f$ where the last clause trivially holds. If the strategy choice is the move to $s_f$ before all nodes in V have been represented in either $u_1$ or $u_2$, not all active versions of $X_{Find}$ will be satisfied. Hence this would not be a winning strategy. The only alternative is that $\sigma$ satisfies the second or third clause $2^n$ times before moving to $s_f$. By definition of $X_{Edge}$ this implies that $\sigma$ generates $2^n$ nodes which form a valid sequence of edges (to satisfy the checks performed by $\varphi _1$ and $\varphi _2$). Hence the existence of a winning strategy implies the existence of a Hamiltonian path.    $\square$

7 Conclusion

We presented a recursive modal logic with semantics defined over a nonnegative multi-weighted extension of Kripke structures. We proved that the model checking problem is EXPTIME-complete and EXPTIME-hard even for a single weight. We then introduced the synthesis problem given multi-weighted two-player games (with a controller and an environment as players) with objectives formulated in the recursive modal logic and with the game-arena given by a multi-weighted Kripke structure. We proved that the synthesis problem is in 2-EXPTIME and is NEXPTIME-hard. The containment result is achieved by a (doubly exponential) reduction to dependency graph that allows for on-the-fly algorithms for finding the maximum fixed-point value of a given node. It required a nontrivial treatment of conjunctive subformulae, as in the branching-time setting we have to guarantee that uniform choices of controllable transitions are made across all formulae in a conjunction.