Abstract
In this work, we say that a computation is reversible if one can find a procedure to undo the steps of a standard (or forward) computation in a deterministic way. While logic programs are often invertible (e.g., one can use the same predicate for adding and for subtracting natural numbers), computations are not reversible in the above sense. In this paper, we present a so-called Landauer embedding for SLD resolution, the operational principle of logic programs, so that it becomes reversible. A proof-of-concept implementation of a reversible debugger for Prolog that follows the ideas in this paper has been developed and is publicly available.
This work is partially supported by the EU (FEDER) and the Spanish MCI/AEI under grants TIN2016-76843-C4-1-R/PID2019-104735RB-C41, by the Generalitat Valenciana under grant Prometeo/2019/098 (DeepTrust), and by the COST Action IC1405 on Reversible Computation - extending horizons of computing.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In this work, we say that a semantics is reversible if there exists a deterministic procedure to undo the steps of any computation (often called backward determinism). The ability to explore the steps of a computation back and forth is particularly useful in the context of program debugging, as witnessed by several previous tools like Undo [8], rr [6] or CauDEr [4], to name a few.
In this paper, we present a reversible version of SLD resolution [5], the operational semantics of logic programs, that may constitute the basis of a reversible debugger for Prolog. As is well known, logic programming is already invertible, i.e., one can exchange the input and output arguments of a predicate so that, e.g., the same predicate is used both for addition and for subtraction of natural numbers. However, SLD resolution is in principle irreversible according to the definition above. Nevertheless, given an irreversible semantics, one can always define an instrumented version which is reversible (this process is often called reversibilization) by defining an appropriate Landauer embedding [3], i.e., by adding a “history” to each state with enough information to undo the steps of a computation. However, defining a non-trivial Landauer embedding for SLD resolution is particularly challenging due to non-determinism and unification.
Let us first briefly recall some basic notions from logic programming (see, e.g., [1, 5] for more details). A query is a finite conjunction of atoms which is denoted by a sequence of the form \(A_1,\ldots , A_n\), where the empty query is denoted by true. A clause has the form \(H\leftarrow B_1,\ldots , B_n\), where H (the head) and \(B_1,\ldots ,B_n\) (the body) are atoms, \(n\ge 0\) (thus we only consider definite logic programs, i.e., logic programs without negated atoms in the body of the clauses). Clauses with an empty body, \(H\leftarrow true\), are called facts, and are typically denoted by H.
In the following, atoms are ranged over by \(A,B,C,H,\ldots \) while queries (possibly empty sequences of atoms) are ranged over by  Substitutions and their operations are defined as usual; they are ranged over by \(\sigma ,\theta ,\ldots \) In particular, the application of a substitution \(\theta \) to a syntactic object o is denoted by juxtaposition, i.e., we write \(o\theta \) rather than \(\theta (o)\). We denote by \(\sigma \circ \theta \) the composition of substitutions \(\sigma \) and \(\theta \). Moreover, \({ id }\) denotes the identity substitution A variable renaming is a substitution that is a bijection on the domain of variables. A substitution \(\theta \) is a unifier of two atoms A and B iff \(A\theta = B\theta \); furthermore, \(\theta \) is the most general unifier of A and B, denoted by \(\mathsf {mgu}(A,B)\) if, for every other unifier \(\sigma \) of A and B, we have that \(\theta \) is more general than \(\sigma \).
Substitutions and their operations are defined as usual; they are ranged over by \(\sigma ,\theta ,\ldots \) In particular, the application of a substitution \(\theta \) to a syntactic object o is denoted by juxtaposition, i.e., we write \(o\theta \) rather than \(\theta (o)\). We denote by \(\sigma \circ \theta \) the composition of substitutions \(\sigma \) and \(\theta \). Moreover, \({ id }\) denotes the identity substitution A variable renaming is a substitution that is a bijection on the domain of variables. A substitution \(\theta \) is a unifier of two atoms A and B iff \(A\theta = B\theta \); furthermore, \(\theta \) is the most general unifier of A and B, denoted by \(\mathsf {mgu}(A,B)\) if, for every other unifier \(\sigma \) of A and B, we have that \(\theta \) is more general than \(\sigma \).
A logic program is a finite sequence of clauses. Given a program P, we say that  is an SLD resolution stepFootnote 1 if
is an SLD resolution stepFootnote 1 if  is a renamed apart clause (i.e., with fresh variables) of program P, in symbols,
is a renamed apart clause (i.e., with fresh variables) of program P, in symbols,  , and \(\sigma = \mathsf {mgu}(A,H)\). The subscript P will often be omitted when the program is clear from the context. An SLD derivation is a (finite or infinite) sequence of SLD resolution steps. A terminating SLD derivation can be either successful, if it ends with the query true, or failed, if it ends in a query where the leftmost atom does not unify with the head of any clause. SLD derivations are represented by a (possibly infinite) finitely branching tree, which is called SLD tree, where choice points (queries with more than one child) correspond to queries where the leftmost atom unifies with the head of more than one program clause.
, and \(\sigma = \mathsf {mgu}(A,H)\). The subscript P will often be omitted when the program is clear from the context. An SLD derivation is a (finite or infinite) sequence of SLD resolution steps. A terminating SLD derivation can be either successful, if it ends with the query true, or failed, if it ends in a query where the leftmost atom does not unify with the head of any clause. SLD derivations are represented by a (possibly infinite) finitely branching tree, which is called SLD tree, where choice points (queries with more than one child) correspond to queries where the leftmost atom unifies with the head of more than one program clause.
Consider, for instance, the following simple logic program:
Given the query p(X, b, b), r(b, X), we have the following SLD derivation:

with \(\theta =\{X/b,Y/b\}\). In order to undo, e.g., the first step in this derivation, we face several problems:
-
First, one needs to know the applied rule, since there exist several possibilities; for instance, one can always consider undoing the application of a fact by adding a call to this predicate to the left of the current query. E.g., one could go backwards from q(b), r(b, b), r(b, b) to q(b), q(b), r(b, b), r(b, b), which is not the desired backward step.
-
Second, we need to “unapply” the computed substitution in this step (which is applied to all the atoms of the query). Unfortunately, there is no deterministic way to do that. E.g., given the last atom r(b, b) in the second query, we can undo the application of \(\theta \) and get r(b, X) but also r(X, b) or r(X, X).
-
Finally, we have no deterministic way to obtain the selected call in the previous goal, even if we know the applied rule and the computed unifier (this is also related to the previous point and the fact that there is no deterministic way to undo the application of a substitution).
Of course, one could define a trivial Landauer embedding where all queries in a derivation are stored, e.g.,

but the overhead would be very high since we would need to store the entire derivation. In the next section, we present a more efficient approach.
2 A Reversible Semantics for Logic Programs
In this section, we present a reversible version of SLD resolution. In principle, in order to avoid the nondeterminism when undoing the application of a substitution, one could consider some non-standard queries where computed substitutions (\(\mathsf {mgu}\)’s) are not applied to the atoms of the query but stored in a list. For instance, one could redefine SLD resolution as follows:

if  and \(\mathsf {mgu}(A\theta _1\ldots \theta _n,H) = \theta _{n+1}\). An initial query
and \(\mathsf {mgu}(A\theta _1\ldots \theta _n,H) = \theta _{n+1}\). An initial query  would now have the form
would now have the form  . Of course, this definition introduces some additional (possibly unavoidable) overhead since the computed substitutions must be composed and applied at each resolution step.
. Of course, this definition introduces some additional (possibly unavoidable) overhead since the computed substitutions must be composed and applied at each resolution step.
However, this is not enough to make SLD resolution reversible. Additionally, one would also need to store the selected call of the previous query, since it cannot be obtained even if we know the applied rule and keep the computed substitutions in a list. Furthermore, we need to know how many (leftmost) atoms should be discarded when performing a backward step (i.e., we need to store the number of atoms in the body of the applied clause).
In summary, we define our (forward) reversible SLD resolution semantics (denoted by \(\rightharpoonup \)) as shown in Fig. 1, where the auxiliary function \(\mathsf {subst}\) is used to compute the (partial) answer computed so far from the current history (this notion is formalized below). In this semantics, reversible queries have the form  , where
, where  is a standard query (a sequence of atoms) and
is a standard query (a sequence of atoms) and  , the history, is a list of elements of the form
, the history, is a list of elements of the form  or \(\mathsf {unf}(A,H,m)\). The first one,
or \(\mathsf {unf}(A,H,m)\). The first one,  , is used to denote that
, is used to denote that  is the last query of a failing derivation (i.e., the leftmost atom in
is the last query of a failing derivation (i.e., the leftmost atom in  unifies with the head of no clause). The second one, \(\mathsf {unf}(A,H,m)\), is used for unfolding steps, where A is the selected call of the query (the leftmost atom), H is the head of the applied clause, and m is the number of atoms in the body of this clause. This is enough to make SLD resolution reversible.
unifies with the head of no clause). The second one, \(\mathsf {unf}(A,H,m)\), is used for unfolding steps, where A is the selected call of the query (the leftmost atom), H is the head of the applied clause, and m is the number of atoms in the body of this clause. This is enough to make SLD resolution reversible.
It is worthwhile to note that we have chosen to store elements of the form \(\mathsf {unf}(A,H,m)\) instead of \(\mathsf {unf}(A,\theta ,m)\) as observed above. This decision might introduce some additional overhead since we should not only compose and apply the computed substitutions at each step, but we must also recompute the \(\mathsf {mgu}\)’s of all considered pairs of atoms (A, H) once per forward step. Nevertheless, storing pairs (A, H) instead of the corresponding \(\mathsf {mgu}\)’s is rather convenient since we do not need to implement (expensive) operations like substitution composition and application, but rely on Prolog’s native unification and propagation of variable bindings. There are, however, several possible optimizations that can be applied to improve performance, like storing \(\mathsf {mgu}\)’s as lists of pairs \( Variable = value \) (as suggested by one of the reviewers of this paper). This is left as future work.
In the following, we use Haskell’s notation for lists so that  denotes a history where E is the first element and
denotes a history where E is the first element and  contains the remaining elements of the list; the empty history is denoted by an empty list \([\,]\). Moreover, we also use Haskell’s list concatenation operator,
contains the remaining elements of the list; the empty history is denoted by an empty list \([\,]\). Moreover, we also use Haskell’s list concatenation operator,  , so that
, so that  denotes a history that begins with the elements of list
denotes a history that begins with the elements of list  and ends with element E.
and ends with element E.
Let us briefly explain the rules of the reversible forward semantics in Fig. 1:
-
Rule success is used to denote the end of a successful derivation. Here, \(\sigma \) denotes the computed answer substitution of the derivation (typically restricted to the variables of the initial goal), where the auxiliary function \(\mathsf {subst}\) is defined as follows:
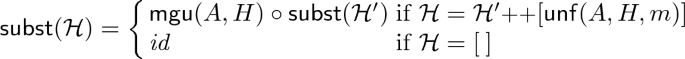
Intuitively speaking,
 computes the substitution encoded by the elements in
computes the substitution encoded by the elements in  . In this rule, we add nothing to the current history since the step is trivially reversible.
. In this rule, we add nothing to the current history since the step is trivially reversible. -
Rule failure is used to denote the end of a failing derivation. Essentially, a query fails when the (instantiated) leftmost atom, \(A\sigma \), does not unify with the head of any program clause, where \(\sigma \) is the substitution encoded by the current history. In this case, we store an element
 since the current goal is needed to undo the step.
since the current goal is needed to undo the step. -
Finally, rule unfold performs an unfolding step. In this case, we add an element \(\mathsf {unf}(A,H,m)\) to the history, where A is the selected atom (the leftmost atom of the query), H is the head of the considered (renamed apart) clause, and m is the number of atoms in the body of this clause.
Consider again the program from Sect. 1 and the initial query p(X, b, b), r(b, X). An (incomplete) reversible SLD derivation is then as follows:

Now, we have enough information in each query in order to deterministically undo a step. The corresponding backward semantics (denoted by \(\leftharpoondown \)) is shown in Fig. 2, where each forward rule (e.g., \(\text{ unfold }\)) has a counterpart in the backward semantics (e.g., \(\overline{\text{ unfold }}\)). The rules are self-explanatory. Note that H is not needed in rule \(\mathsf {\overline{unfold}}\); it was only stored in order to be able to compute the \(\mathsf {mgu}\)’s of the derivation for the next steps of the forward computation.
We note that extending our developments to SLD resolution with an arbitrary computation rule (i.e., different from Prolog’s rule, which always selects the leftmost atom) is not difficult. Basically, one only needs to extend the \(\mathsf {unf}\) elements as follows: \(\mathsf {unf}(A,H,i,m)\), where i is the position of the selected atom, and m is the number of atoms in the body of the applied clause (as before).
The following result states the correctness of our reversible semantics (it can be proved by a simple induction on the length of the considered derivation):
Theorem 1
Let P be a logic program and  a query. Given a forward derivation
a query. Given a forward derivation  , there exists a unique (deterministic) backward derivation of the form
, there exists a unique (deterministic) backward derivation of the form  . Moreover, both derivations perform exactly the same number of steps.
. Moreover, both derivations perform exactly the same number of steps.
For instance, given the previous (incomplete) forward derivation, we can produce the following backward derivation:

3 Discussion
To the best of our knowledge, no other reversible debugger for Prolog has been defined. Typical Prolog debuggers are based on the so called “box model”, where every predicate call or atom, A, has four associated events: call, the initial call to A; exit, when unification of A with the head of a program clause succeeds; redo, when A is tried again after backtracking; and fail, when A does not unify with any other head clause. Typically, debuggers can only proceed forward in the computation or redo the current goal. The closer approach we are aware of is that of Opium [2], which introduces a trace query language for inspecting and analyzing trace histories. In this tool, the trace history of the considered execution is stored in a database, which is then used for trace querying. Several analysis can then be defined in Prolog itself by using a set of given primitives to explore the trace elements.
A proof-of-concept implementation of a Prolog reversible debugger that follows the ideas in this paper has been developed. It is publicly available from https://github.com/mistupv/Prolog-reversible-debugger. The main features of our debugger are the following:
-
It implements both the (nondeterministic) forward semantics and the (deterministic) backward semantics presented in the previous section. Some additional extensions include dealing with built-in’s, using colors and other visual improvements, etc. Essentially, the debugger shows a trace including every call and whether it succeeds (exit) or fails. Calls that unify with the head of more than one clause (choice points) are distinguished in bold. In contrast to traditional Prolog debuggers, we show the entire goal and underline the selected atom, rather than showing only the selected atom.
-
The SLD tree of a query can be explored step by step using the cursor arrows: down (next step), up (previous step), left/right (considering alternative clauses for choice points). When a derivation ends with failure, pressing the down arrow will jump to the next pending choice (backtracking). In particular, we follow Prolog’s search strategy, where clauses are considered in their textual order (from top to bottom) and the SLD tree is explored using a depth-first strategy with backtracking (despite the fact that this strategy is incomplete [1]). However, the debugger cannot undo a backtracking step. If we press the up arrow after a backtracking step jumps to the next alternative of a choice point, the debugger will show the previous goal in this derivation (the parent of this node) rather than the failing leaf that caused backtracking. This was a design decision to ease the exploration of a given computation (following the ideas in this paper). Finally, if a derivation ends with an empty query (a successful derivation), the computed answer is shown. Alternative derivations (if any) can be explored by typing “;” (as in Prolog).
-
We have also implemented a “continuous” mode (pressing “s”, a shorthand for “skip”), where the entire trace up to a leaf of the SLD tree (either a failure or a success) is shown.
Consider, for instance, the following example:

where the built-in \(\mathtt{is/2}\) evaluates the expression in the second argument and unifies it with the first argument. A typical session looks as follows:

so our first derivation is a failing one. Now, if we press the up arrow once, we get back to

and we can consider the next choice (pressing the right arrow), ending up with the following successful derivation:

Our reversible debugger can be a useful tool both for program understanding and for locating the source of a misbehaviour.
The development of a reversible debugger is an ongoing work, so several extensions are planned. In particular, we would like to consider more Prolog features (e.g., deal with exceptions, so that one can explore a computation backwards from a runtime error) as well as introducing a technique for record and replay. Often, one is not interested in exploring all the SLD tree but just a single root-to-leaf derivation (the one that led to the misbehaviour). Here, being able to produce a log of the considered computation and use this log to replay only this particular derivation in our reversible debugger might be useful.
As for the overhead, we consider several possibilities: first, we can consider a more efficient representation by storing pairs \( Variable = value \) instead of atoms, as discussed in Sect. 2; moreover, we could simplify the stored unification problems (the pairs A, H) when they cannot affect the current query (e.g., when they are ground or the bindings do not affect to other atoms); also, one might consider the introduction of “spy points” (as in the standard debugger for Prolog) so that the reversible mode is restricted to some computations rather than the entire SLD tree. Finally, we also plan to explore the definition of a reversible linear semantics for Prolog, analogous to that of [7]. This approach might be useful to undo backtracking steps.
Notes
- 1.
In this paper, we only consider Prolog’s computation rule, so that the selected atom in a query is always the leftmost one.
References
Apt, K.: From Logic Programming to Prolog. Prentice Hall, Upper Saddle River (1997)
Ducassé, M.: Opium: an extendable trace analyzer for prolog. J. Log. Program. 39(1–3), 177–223 (1999). https://doi.org/10.1016/S0743-1066(98)10036-5
Landauer, R.: Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 5, 183–191 (1961)
Lanese, I., Palacios, A., Vidal, G.: Causal-consistent replay debugging for message passing programs. In: Pérez, J.A., Yoshida, N. (eds.) FORTE 2019. LNCS, vol. 11535, pp. 167–184. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-21759-4_10
Lloyd, J.: Foundations of Logic Programming, 2nd edn. Springer, Berlin (1987). https://doi.org/10.1007/978-3-642-83189-8
O’Callahan, R., Jones, C., Froyd, N., Huey, K., Noll, A., Partush, N.: Engineering record and replay for deployability: Extended technical report (2017). CoRR abs/1705.05937, http://arxiv.org/abs/1705.05937
Ströder, T., Emmes, F., Schneider-Kamp, P., Giesl, J., Fuhs, C.: A linear operational semantics for termination and complexity analysis of ISO prolog. In: Vidal, G. (ed.) LOPSTR 2011. LNCS, vol. 7225, pp. 237–252. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32211-2_16
Undo Software: Increasing software development productivity with reversible debugging (2014). https://undo.io/media/uploads/files/Undo_ReversibleDebugging_Whitepaper.pdf
Acknowledgements
The author gratefully acknowledges the anonymous referees for their useful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Vidal, G. (2020). Reversible Computations in Logic Programming. In: Lanese, I., Rawski, M. (eds) Reversible Computation. RC 2020. Lecture Notes in Computer Science(), vol 12227. Springer, Cham. https://doi.org/10.1007/978-3-030-52482-1_15
Download citation
DOI: https://doi.org/10.1007/978-3-030-52482-1_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-52481-4
Online ISBN: 978-3-030-52482-1
eBook Packages: Computer ScienceComputer Science (R0)






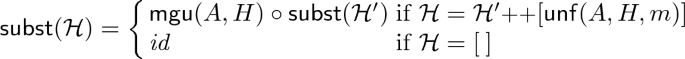
 computes the substitution encoded by the elements in
computes the substitution encoded by the elements in  . In this rule, we add nothing to the current history since the step is trivially reversible.
. In this rule, we add nothing to the current history since the step is trivially reversible. since the current goal is needed to undo the step.
since the current goal is needed to undo the step.