Abstract
Secure messaging (SM) protocols allow users to communicate securely over untrusted infrastructure. In contrast to most other secure communication protocols (such as TLS, SSH, or Wireguard), SM sessions may be long-lived (e.g., years) and highly asynchronous. In order to deal with likely state compromises of users during the lifetime of a session, SM protocols do not only protect authenticity and privacy, but they also guarantee forward secrecy (FS) and post-compromise security (PCS). The former ensures that messages sent and received before a state compromise remain secure, while the latter ensures that users can recover from state compromise as a consequence of normal protocol usage.
SM has received considerable attention in the two-party case, where prior work has studied the well-known double-ratchet paradigm, in particular, and SM as a cryptographic primitive, in general. Unfortunately, this paradigm does not scale well to the problem of secure group messaging (SGM). In order to address the lack of satisfactory SGM protocols, the IETF has launched the message-layer security (MLS) working group, which aims to standardize an eponymous SGM protocol. In this work we analyze the TreeKEM protocol, which is at the core of the SGM protocol proposed by the MLS working group.
On a positive note, we show that TreeKEM achieves PCS in isolation (and slightly more). However, we observe that the current version of TreeKEM does not provide an adequate form of FS. More precisely, our work proceeds by formally capturing the exact security of TreeKEM as a so-called continuous group key agreement (CGKA) protocol, which we believe to be a primitive of independent interest. To address the insecurity of TreeKEM, we propose a simple modification to TreeKEM inspired by recent work of Jost et al. (EUROCRYPT ’19) and an idea due to Kohbrok (MLS Mailing List). We then show that the modified version of TreeKEM comes with almost no efficiency degradation but achieves optimal (according to MLS specification) CGKA security, including FS and PCS. Our work also lays out how a CGKA protocol can be used to design a full SGM protocol.
S. Coretti—Work partially done at NYU and supported by NSF grants 1314568 and 1319051.
Y. Dodis—Partially supported by gifts from VMware Labs, Facebook and Google, and NSF grants 1314568, 1619158, 1815546.
Y. Tselekounis—Work done at NYU and supported by NSF grants 1314568 and 1319051.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Secure messaging. End-to-end Secure Messaging (SM) allows people to exchange messages without compromising their authenticity nor privacy. To further their applicability the protocols in this work are designed for the, so called, asynchronous setting. In the context of (secure) messaging “asynchronous” means that no assumptions are made about the online/offline behavior of participants. E.g. at times no participant at all may be online. Some participants may be offline for long periods while others are online only irregularly. It may even be that for the duration of a session no more than a single participant is online simultaneously nor should they rely on any particular user being online to perform operations.Footnote 1 Thus, protocols for the asynchronous setting must eschew interactive communication (which greatly increases the difficulty of achieving strong security properties). In other words all protocol operations (e.g. creating a new session, adding/removing participants to an existing session and sending a messages in a session) must always be performed by sending out a single packet to enact the desired operation. In fact, (due to desired constraints on bandwidth) all protocols in this work actually send out the same packet to all participants as a single broadcast.
In contrast to common secure communication protocols such as TLS, IPSEC and SSH, SM protocols are designed for settings where sessions may exist for long periods of time. SM protocols are therefore expected to satisfy so-called forward secrecy (FS) and post-compromise security (PCS) (a.k.a. backward secrecy). The former means that even when a participant’s key material is compromised, past messages (delivered before the compromise) remain secure. Conversely, PCS means that once the compromise ends, the participants will eventually recover full security as a side effect of continued normal protocol usage.
The rigorous design and analysis of two-party asynchronous SM protocols has received considerable attention in recent years. This is in no small part due to advent of the double ratchet paradigm, introduced by Marlinspike and Perrin [27]. Forming the cryptographic core of a slew of popular messaging applications (e.g., Signal, who first introduced it, as well as WhatsApp, Facebook Messenger, Skype, Google Allo, Wire, and more), double ratchet protocols are now regularly used by over a billion people worldwide.
However, double ratchet protocols are inherently designed for the case where only two users communicate with each other. In order to employ them for groups with more than two users, there is thus little or no alternative to running double ratchets between all pairs of users (at least to distribute and update key material). Unfortunately, that means the double ratchet paradigm does not scale well in settings with a large number of users. In particular, the communication complexity to update key material (an operation crucial to providing PCS) grows linearly in the group size. In fact, this poor performance holds for all, currently deployed, SM protocols enjoying some form of FS and PCS (i.e., including non-double ratchet based ones [20]).
This begs the natural question of how to build secure asynchronous group messaging protocols (SGM) that enjoy similar security properties to the two-party ones but whose efficiency scales (say) logarithmically in the group size.
Message layer security and TreeKEM. In order to address the lack of satisfactory SGM protocols, the IETF has launched the message-layer security (MLS) working group, which aims to standardize an eponymous SGM protocol [5, 29]. Following in the footsteps of the double ratchet, the MLS protocol promises to be widely deployed and heavily used. Indeed, the working group already includes various messaging companies (Cisco, Facebook, Google, Wickr, Wire, Twitter, etc.) whose combined messaging user base includes everything from government agencies, political organizations, and NGOs, to companies both large and small—not to mention a major part of the world’s consumer population.
The heart of the MLS standard is the so-called TreeKEM protocol. TreeKEM continuously generates fresh, shared, and secret randomness used by the participating parties to evolve the group key material. Each new group key is used to initiate a fresh symmetric hash ratchet that defines a stream of nonce/key pairs used to symmetrically encrypt/decrypt higher-level application messages (such as texts in a chat) using an AEAD (authenticated encryption with associated data). A stream is used until the next evolution of the group key at which point a new stream is initiated.
So not only is TreeKEM the most novel and intricate part of the MLS draft, but understanding it is also central to understanding the security and efficiency properties of full MLS protocol itself. In particular, TreeKEM is crucially involved in achieving PCS and FS.
1.1 Contributions
Continuous group key agreement. This paper makes progress in the formal study of secure group-messaging protocols (SGMs) by studying the security of the latest version of the TreeKEM protocol. First, our work defines the notion of continuous group key agreement (CGKA) and casts TreeKEM as a CGKA protocol. CGKA protocols provide methods for adding as well as removing group members and, most crucially, for performing updates. Each update operation is initiated by an arbitrary user and results in a new so-called update secret. Update secrets are high-entropy random values that the parties use to refresh their group key material in the higher-level protocols (e.g., in the SGM). In an update operation, the initiator also suitably encrypts information about the update secret for other group members.
Our security definition for CGKA protocols requires that (i) users obtain the same update secrets (correctness), (ii) update secrets look random to an attacker observing the protocol messages, (iii) past update secrets remain random even if the state of a party is compromised by the attacker (FS), and (iv) parties can recover from state compromise (PCS). All of these properties are captured by a single, fairly intuitive security game.
We argue that the formal security properties of CGKA are phrased in such a way that it is a suitable building block for full SGM protocols. In particular, CGKA is inspired by the modularization of Alwen et al. [2], who constructed a secure two-party messaging protocol (based on the double-ratchet paradigm) by combining three primitives: continuous key agreement (CKA), forward secure authenticated encryption with associated data (FS-AEAD), and a so-called PRF-PRNG, which is a two-input hash function that is a pseudorandom function (resp. generator) with respect to its first (resp. second) input. CGKA is therefore to be seen as the multi-user analogue of CKA and is tailored to be used in conjunction with a PRF-PRNG and the multi-user version of FS-AEAD. Specifically, the update secret is run through the PRF-PRNG in order to obtain new keys for the multi-user FS-AEAD. Due to the already quite high complexity of CGKA itself, this work focuses exclusively on CGKA and sketches how it can be used in a higher-level protocol to obtain a full SGM protocol.
TreeKEM has poor forward secrecy. Having defined the notion of CGKA, we analyze the latest version of TreeKEM w.r.t. the new definition. By doing so, we observe that there are serious issues with TreeKEM’s forward secrecy, stemming from the fact that its users do not erase old keys sufficiently fast. Specifically, note that in order to efficiently perform updates (with packet sizes logarithmic in the number of users), TreeKEM arranges all group members at the leaves of a binary tree and uses public-key encryption (PKE) to encrypt information about update secrets, denoted by \(I\), to specific subsets of members (determined by their position in the tree). After processing the update, however, parties do not erase or modify the PKE secret keys used to decrypt the update information, since they might need them to process future updates. Hence, corrupting any party other than the update initiator will completely reveal \(I\) to an attacker, thereby violating FS. In fact, we show that in a group with n members, in order for \(I\) to remain secret upon state compromise of an arbitrary user, even in the best case at least \(\Omega (n/\log (n))\) many additional updates are required before the compromise in the best case. This can rise to \(\Omega (n)\) many updates in the worst case (depending on the order of updates). Even worse, unless the sibling (in the tree) of \(I\)’s initiator performs an update, \(I\) is never forward secret regardless of who else updates.
Our work formally captures the exact type of FS achieved by TreeKEM by providing an appropriate weakening of the CGKA security definition and proving that TreeKEM satisfies it. On a positive note, even the weakened definition provides PCS, i.e., TreeKEM’s update secrets are at least backward secure.
Fixing TreeKEM. In order to remedy TreeKEM’s issues with FS, we devise a new type of public-key encryption (PKE) (based on work by Jost et al. [24] and a suggestion by Konrad Kohbrok on the MLS mailing list [26]) and show that using it in lieu of the (standard) PKE within TreeKEM results in a protocol with optimal FS. Specifically, with the new flavor of PKE, public and secret keys suitably change with every encryption and decryption, respectively. This kind of key evolution ensures that after decryption, the (evolved) secret key leaks no information about the original message, thereby thwarting the above attack. We also provide a very efficient instantiation of the new PKE notion, thereby ending up with a practical fix and going from very loose to optimal security at negligible cost, albeit under the following assumption about the order in which messages are delivered to all participants.
Global ordering of messages. Our main CGKA security definitions encode the assumption that the delivery server (which caches protocol messages until users come online again) delivers CGKA messages in the same order to all users in a session. Having said that, the delivery server (which we modeled formally as the adversary) may still drop or delay messages at will, as well as decide on the delivery order between users arbitrarily (as long as each user eventually gets the same order of protocol messages). We remark that this assumptions is made explicitly in the MLS design spec. (cf. Section 11 of version 8 [5]) albeit only in terms of conditions required to guarantee functionality, not security. Moreover, the TreeKEM protocol was designed with that in mind. (It is worth noting that the assumption could also be practically realized in the public bulletin board model, e.g., using a block-chain protocol.)
Of course, an alternative approach would have been to remove the assumption from our security definitions. The correctness and security implications of doing this are somewhat subtle; for example, it is inevitable that the current group can easily be split into disjoint sub-groups, who might not even be aware of each other, simply thinking that people in other subgroups are offline rather than “split”. We discuss these issues in Sect. 7, pointing out that the “right” security level desired in this case is not yet settled and agreed upon in the MLS community (for good reasons rather than lack of effort, as we explain in Sect. 7). We also note that it is relatively trivial for a higher level protocol building on the CGKA (such as MLS) to ensure users only accept CGKA messages in the same order as intended by their sender. E.g. MLS ensures this by having sender and receivers of CGKA packets necessarily agree on the hash of the preceding transcript in order to authenticate and decrypt new CGKA packets.
Given this state of affairs, we feel that we are justified to follow the current MLS guidelines, by building the global ordering of messages assumption into our model, so that we can: (1) achieve the strongest possible security (including FS, PCS and guaranteed agreement), as well as (2) analyze TreeKEM in the security model it was designed for. However, in Sect. 7 we discuss what happens in TreeKEM (and our improved version) when the order delivery assumption does not hold, including the following two security guarantees: (1) Compromising user \(\mathsf {ID}\), who was removed from the perspective of sub-group A, should not compromise the security of A, even if \(\mathsf {ID}\) “split” to a different subgroup B prior to removal from A; (2) Compromising user \(\mathsf {ID}\), who updated its state after “splitting” from A, should not compromise the security of A.
Adaptive security. The security of both TreeKEM and the improved version mentioned above is proved w.r.t. a non-adaptive attacker, i.e., an attacker that is required to announce all corruptions at the beginning (as opposed to being able to corrupt on-the-fly depending on values and messages produced by the protocol).
The difficulty in handling adaptive security is inherent for any cryptographic protocol where keys can encrypt others keys, and the attacker might ask to selectively corrupt some subset of keys. Prominent examples include multicast and generalized selective decryption [16, 30], constraint PRFs [17], and Yao’s garbled circuits [23], among many others. In each of these setting, going from non-adaptive to adaptive security naively would result in exponential security loss in some natural parameter n for the corresponding setting.
A major breakthrough in improving the state of provable security security against adaptive attackers in such settings came from a series of works, starting with Panjwani [30], and culminating with a very clever and general reduction technique of Jafargholi et al. [22]. These highly non-trivial works which showed that in certain cases, one can get adaptive security at the multiplicative reduction factor of “only” \(n^{\log n}\ll 2^n\). While these provable, yet “super-polynomial”, reductions are still far from being usable in the real world, they are substantially better than the trivial exponential security loss mentioned above, and serve as further evidence that the corresponding protocols are likely secure “in the real world” — a view commonly shared by the majority of practitioners.
Fortunately, we managed to adapt the same non-trivial reduction technique to the setting of TreeKEM, showing the slightly super-polynomial security even in the adaptive setting. As mentioned above, this is the best we can do using the current state-of-the-art in adaptive security in all the “selective decryption” applications we know.
In the full version of the paper [3] we discuss several research directions related to SM.
1.2 Related Work
The double ratchet paradigm was introduced by Marlinspike and Perrin [27], based on the OTR (off-the-record) protocol [7], and an early analysis was performed by Cohn-Gordon et al. [10]. An important line of work [6, 13, 21, 24, 31] formally studied two-party secure messaging. In particular, Jost et al. [24] introduced the notion of updatable PKE which is related to the one used in this paper. However, in our setting a simpler definition suffices, although we use the same efficient construction as [24]. Alwen et al. [2] provided a modular design for double-ratchet algorithms and formal definition of secure messaging in the two-party setting. In the group setting, Cremers et al. [11] note TreeKEM’s disadvantages w.r.t. PCS for multiple groups, and Weider [36] suggests Causal TreeKEM, a variant that requires less ordering of protocol messages. TreeKEM was suggested in [4, 32]. The most influential precursor to TreeKEM, the asynchronous ratchet tree (ART) protocol, was introduced by Cohn-Gordon et al. [9], focusing on adaptive security (informally sketched) for static groups. ART uses an older technique called “Tree-based DH groups” [33, 35, 38] which is also used by [25] to build key agreement. However, TreeKEM and ART differ significantly from [25], as we discuss in the full version [3]. Besides MLS, several other end-to-end secure group messaging protocols have been proposed and even deployed [14, 18,19,20, 34, 37]. Also, TreeKEM is related to schemes for (symmetric-key) broadcast encryption [12, 15] and multicast encryption [8, 28, 38]. A more detailed comparison between protocols and notions can be found in the full version [3]. Finally, the recent follow-up work of [1] also analyzes TreeKEM’s security and introduces a new CGKA construction improving on TreeKEM. However, beyond this high-level similarity the results are relatively orthogonal, using different security models, and focusing on complementary aspects of TreeKEM, such as efficiency and adaptive reduction tightness.
2 Preliminaries
This section introduces some general notation and basic concepts around binary trees. Definitions of PRGs and CPA-secure public-key encryption can be found in the full version [3].
Notation. For a positive integer a, [a] denotes the set \(\{1, 2, \ldots , a\}\). For an integer n, \({\mathsf {mp2}} (n)\) is the maximum power of 2 smaller than n, dividing n. Security games in this work involve dictionaries. The value stored with key x in a dictionary D is denoted by D[x]. The statement \(D[\cdot ] \leftarrow y\) (for any type of y) initializes a dictionary D in which the default initial value for each key is y. This work considers rooted binary trees, in which all nodes have between 0 and 2 unique children. The height of \(\tau \) is the length of the longest path from the root to any leaf.Footnote 2 A node with no children is called a leaf; all other nodes are called internal. A tree \(\tau \) is full if it has height h and \(2^h\) leaves. For an integer \(h\ge 0\), denote by \({\mathsf {FT}} _h\) the full binary tree of height h. For two leaf nodes \(\ell \) and \(\ell '\) in some tree, let \(\mathsf {LCA}(\ell ,\ell ')\) be the least common ancestor of \(\ell \) and \(\ell '\), i.e., the node where the paths from these leaves to the root meet.
3 Continuous Group Key Agreement
The purpose of continuous group key-agreement (CGKA) is to continuously provide members of a messaging group with fresh secret random values, which they use to refresh their key material (in a higher-level protocol). This section formally defines the syntax of CGKA schemes and presents a security notion that simultaneously captures correctness, key indistinguishability, forward secrecy, as well as post-compromise security.
3.1 CGKA Syntax
A CGKA scheme provides algorithms to create a group, add as well as remove users, perform updates, and process protocol messages.
Definition 1
A continuous group key-agreement (CGKA) scheme \({\mathsf {CGKA}} = ({\mathsf {init}},{\mathsf {create}},{\mathsf {add}},{\mathsf {rem}},{\mathsf {upd}},\mathsf {proc})\) consists of the following algorithms:
-
Initialization: \({\mathsf {init}} \) takes an ID \(\mathsf {ID}\) and outputs an initial state \(\gamma \).
-
Group creation: \({\mathsf {create}} \) takes a state \(\gamma \), a list of IDs \(\mathsf {G}= (\mathsf {ID}_1,\ldots ,\mathsf {ID}_n)\), and outputs a new state \(\gamma '\) and a control message \(W\).
-
Add: \({\mathsf {add}} \) takes a state \(\gamma \) an ID \(\mathsf {ID}'\), and outputs a new state \(\gamma \) as well as control messages \(W\) and \(T\).
-
Remove: \({\mathsf {rem}} \) takes a state \(\gamma \) and an ID \(\mathsf {ID}'\) and outputs a new state \(\gamma '\) and a control message \(T\).
-
Update: \({\mathsf {upd}} \) takes a state \(\gamma \) and outputs a new state \(\gamma '\) and a control message \(T\).
-
Process: \(\mathsf {proc}\) takes a state \(\gamma \) and a control message \(T\) and outputs a new state \(\gamma '\) and an update secret \(I\).
The basic usage of a CGKA scheme is as follows: Generally, once a group is established using \({\mathsf {create}} \), any group member, referred to as the sender, may call any of the algorithms to add or remove members or to perform updates. Each time, such a call results in a new so-called epoch. It is implicitly the task of a server connecting the parties to then relay the resulting control messages to all current group members (including the sender). Observe that there are two types of control messages: welcome messages \(W\), which are sent to parties joining a group, and normal control messages \(T\), which are intended for parties already in the group. Whenever the server delivers a control message to a group member, they process it using \(\mathsf {proc}\). Algorithm \(\mathsf {proc}\) also outputs an update secret \(I\), where the intention is that \(I\ne \bot \) if and only if the control message corresponds to an update.
3.2 CGKA Security
Informally, the basic properties that any CGKA scheme must satisfy are the following: Correctness: All group members output the same update secret \(I\) in update epochs. Privacy: The update secrets look random given the transcript of control messages. Forward secrecy (FS): If the state of any group member is leaked at some point, all previous update secrets remain hidden from the attacker. Post-compromise security (PCS): After every group member whose state was leaked performs an update (that is processed by the group) update secrets become secret again.
These properties are captured by the security game presented in this section (cf. Fig. 1). In the game the attacker is given access to various oracles to drive the execution of a CGKA protocol. It is important to note that the capabilities of the attacker and restrictions on the order in which the attacker may call the oracles is motivated by how a CGKA protocol would be used in a higher-level protocol. Most importantly, the attacker will not be allowed to modify or inject any control messages. The corresponding design choices are justified in Sect. 3.3.
Epochs. The main oracles to drive the execution are the oracles to create groups, add users, remove users, and to deliver control messages, i.e.,
 , and
, and
 . The first four oracles allow the adversary to instruct parties to initiate new epochs, whereas the deliver oracle makes parties actually proceed to the next epoch. The server connecting the parties is trusted to provide parties with a consistent view of which operation takes place in each epoch. That is, while multiple parties may initiate a new epoch, the attacker is forced to pick a single operation that defines the new epoch; the corresponding sender is referred to as the leader of the epoch. Observe that the parties may advance at various speeds and therefore be in epochs arbitrarily far apart.
. The first four oracles allow the adversary to instruct parties to initiate new epochs, whereas the deliver oracle makes parties actually proceed to the next epoch. The server connecting the parties is trusted to provide parties with a consistent view of which operation takes place in each epoch. That is, while multiple parties may initiate a new epoch, the attacker is forced to pick a single operation that defines the new epoch; the corresponding sender is referred to as the leader of the epoch. Observe that the parties may advance at various speeds and therefore be in epochs arbitrarily far apart.
The game forces the attacker to initially, i.e., in epoch 1, create a group. Thereafter, any group member may add new parties, remove current group members, or perform an update. The attacker may also corrupt any party at any point (thereby learning that party’s secret state) and challenge the update secret in any epoch where the leader performed an update operation. Furthermore, the adversary can instruct parties to stop deleting old secrets. There will be restrictions checked at the end of the execution of the game to ensure that the attacker’s challenge/corruption/no-deletion behavior does not lead to trivial attacks.
Initialization. The \(\mathbf {init}\) oracle sets up the game and all the variables needed to keep track of the execution. The random bit b is used for real-or-random challenges, and the dictionary \(\gamma \) keeps track of all the users’ states. For every epoch, the dictionaries \(\mathsf {lead}\), \(\mathbf{I}\), and \(\mathbf{G}\) record the leader, the update secret, and the group members, respectively, and \(\mathsf {ep}\) records which epoch each user is currently in. The array \(\mathsf {ctr}\) counts all new operations initiated by a user in their current epoch. Moreover, \(D\) keeps track of which parties delete their old values and which do not. Dictionary \(\mathsf {chall}\) is used to ensure that the adversary can issue at most a single challenge per (update) epoch. Finally, \(M\) records all control messages produced by parties; the adversary has read access to \(M\) (as indicated by the keyword
 ).
).
Initiating operations and choosing epoch leaders. As mentioned above, the attacker must choose a leader in every epoch, i.e., a sender whose control message is ultimately processed by all group members. More precisely, for each user \(\mathsf {ID}\) currently in some epoch \(t\), \(\mathsf {ctr}[\mathsf {ID}]\) can be thought of as a (local) “version number” that counts the various operations initiated by \(\mathsf {ID}\) in epoch \(t\). The counter is incremented each time \(\mathsf {ID}\) initiates a new operation. The resulting control messages for users \(\mathsf {ID}_i\) are stored in \(M\) with key \((t+1,\mathsf {ID},\mathsf {ID}_i,\mathsf {ctr}[\mathsf {ID}])\), representing the number of the next epoch, the sender, the recipient, and the (local) version number of the operation. Similarly, dictionary \(\mathbf{G}\) stores the new group that would result from the operation with key \((t+1,\mathsf {ID},\mathsf {ctr}[\mathsf {ID}])\).
For every epoch \(t\), the first control message \(M[t,\mathsf {ID},\mathsf {ID}',c]\) delivered via
 , for some users \(\mathsf {ID}\) and \(\mathsf {ID}'\) and version number c, determines that \(\mathsf {ID}\) is the leader and c the version that was chosen by the server. Correspondingly, the game records \(\mathsf {lead}[t] \leftarrow (\mathsf {ID},c)\) and sets the group membership to \(\mathbf{G}[t] \leftarrow \mathbf{G}[t,\mathsf {ID},c]\).
, for some users \(\mathsf {ID}\) and \(\mathsf {ID}'\) and version number c, determines that \(\mathsf {ID}\) is the leader and c the version that was chosen by the server. Correspondingly, the game records \(\mathsf {lead}[t] \leftarrow (\mathsf {ID},c)\) and sets the group membership to \(\mathbf{G}[t] \leftarrow \mathbf{G}[t,\mathsf {ID},c]\).
In general, whenever a party \(\mathsf {ID}'\) processes any control message, the counter \(\mathsf {ctr}[\mathsf {ID}']\) is reset to 0 as all operations initiated by \(\mathsf {ID}'\) in its current epoch are now obsolete (either processed by \(\mathsf {ID}\) or rejected by the server in favor of some other operation). Note that the sender of an operation also sends a control message addressed to themselves to the server. The server confirms an operation by returning that message back to the sender.
Group creation. The oracle
 causes \(\mathsf {ID}_0\) to create a group with members \({\{\mathsf {ID}_0,\ldots ,\mathsf {ID}_n\}}\). This is only allowed if \(\mathsf {ID}_0\) is currently in epoch 0, which is enforced by the
causes \(\mathsf {ID}_0\) to create a group with members \({\{\mathsf {ID}_0,\ldots ,\mathsf {ID}_n\}}\). This is only allowed if \(\mathsf {ID}_0\) is currently in epoch 0, which is enforced by the
 statement. Thereafter, \(\mathsf {ID}_0\) calls the group creation algorithm and sends the resulting welcome messages to all users involved (including itself).
statement. Thereafter, \(\mathsf {ID}_0\) calls the group creation algorithm and sends the resulting welcome messages to all users involved (including itself).
Adding and removing users and performing updates. For all three oracles
 and
and
 , the
, the
 statement checks that the call makes sense (e.g., checking that a party added to the group is not currently a group member). Subsequently, the oracles call the corresponding CGKA algorithms (\({\mathsf {add}} \), \({\mathsf {rem}} \), and \({\mathsf {upd}} \), respectively) and store the resulting control messages in \(M\).
statement checks that the call makes sense (e.g., checking that a party added to the group is not currently a group member). Subsequently, the oracles call the corresponding CGKA algorithms (\({\mathsf {add}} \), \({\mathsf {rem}} \), and \({\mathsf {upd}} \), respectively) and store the resulting control messages in \(M\).
Delivering control messages. The oracle
 is called with the same four arguments \((t,\mathsf {ID},\mathsf {ID}',c)\) that are used as keys for the \(M\) array. The
is called with the same four arguments \((t,\mathsf {ID},\mathsf {ID}',c)\) that are used as keys for the \(M\) array. The
 statement at the beginning checks that (1) either there is no leader for epoch \(t\) yet or version c of \(\mathsf {ID}\) is the leader already and (2) the recipient \(\mathsf {ID}'\) is currently either in epoch \(t-1\) or a newly added group member, which is checked by predicate \(\mathsf {added}\) defined by \(\mathsf {added}(t,\mathsf {ID},\mathsf {ID}',c)\ := \mathsf {ID}' \notin \mathbf{G}[t-1] \wedge \mathsf {ID}' \in \mathbf{G}[t,\mathsf {ID},c]\). If the checks are passed, the appropriate control message is retrieved from \(M\) and run through \({\mathsf {proc}} \) on the state of \(\mathsf {ID}'\). If there is no leader for epoch \(t\) yet, the game sets the leader as explained above and also records the update secret \(\mathbf{I}[t]\) output by \({\mathsf {proc}} \). In all future calls to
statement at the beginning checks that (1) either there is no leader for epoch \(t\) yet or version c of \(\mathsf {ID}\) is the leader already and (2) the recipient \(\mathsf {ID}'\) is currently either in epoch \(t-1\) or a newly added group member, which is checked by predicate \(\mathsf {added}\) defined by \(\mathsf {added}(t,\mathsf {ID},\mathsf {ID}',c)\ := \mathsf {ID}' \notin \mathbf{G}[t-1] \wedge \mathsf {ID}' \in \mathbf{G}[t,\mathsf {ID},c]\). If the checks are passed, the appropriate control message is retrieved from \(M\) and run through \({\mathsf {proc}} \) on the state of \(\mathsf {ID}'\). If there is no leader for epoch \(t\) yet, the game sets the leader as explained above and also records the update secret \(\mathbf{I}[t]\) output by \({\mathsf {proc}} \). In all future calls to
 , the values \(I\) output by process will be checked against \(\mathbf{I}[t]\), and, in case of a mismatch, the instruction
, the values \(I\) output by process will be checked against \(\mathbf{I}[t]\), and, in case of a mismatch, the instruction
 reveals the secret bit b to the attacker; this ensures correctness. Finally, the epoch counter for \(\mathsf {ID}'\) is incremented—or set to \(-1\) if the operation just processed removes \(\mathsf {ID}'\) from the group. This involves a check via predicate \(\mathsf {removed}\) defined by \(\mathsf {removed}(t,\mathsf {ID}') \ := \mathsf {ID}' \in \mathbf{G}[t-1] \wedge \mathsf {ID}' \notin \mathbf{G}[t] \).
reveals the secret bit b to the attacker; this ensures correctness. Finally, the epoch counter for \(\mathsf {ID}'\) is incremented—or set to \(-1\) if the operation just processed removes \(\mathsf {ID}'\) from the group. This involves a check via predicate \(\mathsf {removed}\) defined by \(\mathsf {removed}(t,\mathsf {ID}') \ := \mathsf {ID}' \in \mathbf{G}[t-1] \wedge \mathsf {ID}' \notin \mathbf{G}[t] \).
Challenges, corruptions, and deletions. In order to capture that update secrets must look random, the attacker is allowed to issue a challenge for any epoch corresponding to an update operation. When calling  for some t, the oracle first checks that t indeed corresponds to an update epoch and that a leader already exists. Similarly, using
for some t, the oracle first checks that t indeed corresponds to an update epoch and that a leader already exists. Similarly, using
 , the attacker can simply learn the update secret of an epoch. It is also ensured that for each epoch, the attacker can make at most one call to either
, the attacker can simply learn the update secret of an epoch. It is also ensured that for each epoch, the attacker can make at most one call to either
 or
or
 .
.
To formally model forward secrecy and PCS, the attacker is also allowed to learn the current state of any party by calling the oracle
 . Finally, the attacker can instruct a party \(\mathsf {ID}\) to stop deleting old values by calling
. Finally, the attacker can instruct a party \(\mathsf {ID}\) to stop deleting old values by calling  . Subsequently, the game will implicitly store all old states of \(\mathsf {ID}\) (instead of overriding them) and leak it to the attacker when he calls
. Subsequently, the game will implicitly store all old states of \(\mathsf {ID}\) (instead of overriding them) and leak it to the attacker when he calls
 .Footnote 3 The game also sets the corresponding flag.
.Footnote 3 The game also sets the corresponding flag.
Avoiding trivial attacks. In order to ensure that the attacker may not win the CGKA security game with trivial attacks (such as, e.g., challenging an epoch \(t\)’s update secret and leaking some party’s state in epoch \(t\)), at the end of the game, the predicate
 is run on the queries \(\mathbf {q}_1,\ldots ,\mathbf {q}_q\) in order to determine whether the execution was devoid of such attacks. The predicate tests whether the attacker can trivially compute the update secret in a challenge epoch \(t^*\) using the state of a party \(\mathsf {ID}\) in some epoch \(t\) and the control messages observed on the network. This is the case if either (1) \(\mathsf {ID}\) has not performed an update or been removed before epoch \(t^*\) or (2) \(\mathsf {ID}\) stopped deleting values at some point up to epoch \(t^*\) and was corrupted thereafter. The predicate is depicted in Fig. 2. The figure uses the function \(\mathsf {q2e}(\mathbf {q})\), which returns the epoch corresponding to query \(\mathbf {q}\). Specifically, for
is run on the queries \(\mathbf {q}_1,\ldots ,\mathbf {q}_q\) in order to determine whether the execution was devoid of such attacks. The predicate tests whether the attacker can trivially compute the update secret in a challenge epoch \(t^*\) using the state of a party \(\mathsf {ID}\) in some epoch \(t\) and the control messages observed on the network. This is the case if either (1) \(\mathsf {ID}\) has not performed an update or been removed before epoch \(t^*\) or (2) \(\mathsf {ID}\) stopped deleting values at some point up to epoch \(t^*\) and was corrupted thereafter. The predicate is depicted in Fig. 2. The figure uses the function \(\mathsf {q2e}(\mathbf {q})\), which returns the epoch corresponding to query \(\mathbf {q}\). Specifically, for  , if \(\mathsf {ID}\) is member of the group when \(\mathbf {q}\) is made, \(\mathsf {q2e}(\mathbf {q})\) is the value of \(\mathsf {ep}[\mathsf {ID}]\) (when the query is made), otherwise, \(\mathsf {q2e}(\mathbf {q})\) returns \(\bot \). For
, if \(\mathsf {ID}\) is member of the group when \(\mathbf {q}\) is made, \(\mathsf {q2e}(\mathbf {q})\) is the value of \(\mathsf {ep}[\mathsf {ID}]\) (when the query is made), otherwise, \(\mathsf {q2e}(\mathbf {q})\) returns \(\bot \). For  , \(\mathsf {q2e}(\mathbf {q})\), is the epoch for which \(\mathsf {ID}\) initiates the operation. If \(\mathbf {q}\) is not processed by any user we set \(\mathsf {q2e}(\mathbf {q})=\bot \).Footnote 4
, \(\mathsf {q2e}(\mathbf {q})\), is the epoch for which \(\mathsf {ID}\) initiates the operation. If \(\mathbf {q}\) is not processed by any user we set \(\mathsf {q2e}(\mathbf {q})=\bot \).Footnote 4
Observe that the predicate  can in general be replaced by any other predicate \(\mathsf {P}\), potentially weakening the resulting security notion.
can in general be replaced by any other predicate \(\mathsf {P}\), potentially weakening the resulting security notion.
Advantage. In the following, a \((t,c,n)\)-attacker is an attacker \(\mathcal {A}\) that runs in time at most \(t\), makes at most \(c\) challenge queries, and never produces a group with more than \(n\) members. For any adversary \(\mathcal {A}\) for which the safety predicate evaluates to \(\mathsf {true}\) on the queries made by it, \(\mathcal {A}\) wins the CGKA security game if he correctly guesses the random bit b in the end. The advantage of \(\mathcal {A}\) with safety predicate \(\mathsf {P}\) against a CGKA scheme \({\mathsf {CGKA}} \) is defined by \(\mathsf {Adv^{CGKA,\mathsf {P}}_{\mathrm {cgka\text {-}{}na}}}(\mathcal {A}) \ := \left| {\mathsf {Pr}[\mathcal {A}\text { wins}]} - \frac{1}{2} \right| \).
Definition 2 (Non-adaptive CGKA security)
A continuous group key-agreement protocol \({\mathsf {CGKA}} \) is non-adaptively \((t,c,n,\mathsf {P},\varepsilon )\)-secure if for all \((t,c,n)\)-attackers, \(\mathsf {Adv^{CGKA,\mathsf {P}}_{\mathrm {cgka\text {-}{}na}}}(\mathcal {A}) \ \le \ \varepsilon \).
3.3 Explanation of Assumptions in Definition
CGKA in higher-level protocol. Syntax and security of CGKA protocols are defined in such a way that they can be used by a higher-level protocol—in particular a full secure group-messaging (SGM) scheme (e.g., the entire MLS protocol)—in a modular fashion. As explained below, this modularity allows to assume that the parties are connected by authenticated channels and messages are delivered in order in the CGKA security definition.
Authenticated channels. Any sensible SGM security definition allows the attacker to inject, i.e., forge and/or replay, protocol messages at will. However, this behavior is easy to defend against by having group members sign all messages they send. In particular, CGKA control messages can be authenticated this way. Therefore, the CGKA security game may assume that channels are authenticated since any injections of control messages can be taken care of by the corresponding security reduction.
The only time this is problematic is when the attacker learns some user’s singing keys via state leakage. However, authenticity can be recovered in a generic way by using ephemeral signature keys as part of the higher-level protocol. That is, users periodically sample fresh signature keys and publish the public key as well as a signature on it using their previous secret key. Of course this requires that the attacker remain passive, i.e., that he not inject, during the time window between compromise and key update. While this is arguably not the strongest adversarial model one might consider, observe that not making such an assumptionFootnote 5 would essentially require security against insider attacks (attacks in which group members deviate from the protocol arbitrarily). This is an interesting and important issue, but it is outside the scope of this paper (not to mention much if not all of the academic literature on SGM). Nor is defending against any such attack part of MLS’s goals.Footnote 6 In fact, it is not clear whether completely defending against insider attacks can result in a practical protocol at all. We believe the study of SGM secure against insider attacks to be one of the main open problems in the area.
Message ordering. Any SGM protocol using CGKA as a component (and authenticating CGKA control messages as described above) may additionally ensure that CGKA messages are delivered in order by, e.g., transcript hashing: Group members keep a running hash value h, which is updated as \(h_{\mathsf {new}}\leftarrow H(h_{\mathsf {old}}|| T)\) each time a CGKA control message T is sent. In addition, \(h_{\mathsf {old}}\) is sent along with T, and T is only processed by a party if \(h_{\mathsf {old}}\) matches the local running hash. Therefore, while the full SGM security definition allows the attacker to reorder messages, CGKA security need not consider out-of-order messages (as this can be handled by the security reduction).
In Sect. 7 we discuss security in the presence of group splitting attacks.
4 TreeKEM
4.1 Overview
The TreeKEM CGKA protocol is based on so-called (binary) ratchet trees (RTs). In a TreeKEM RT, group members are arranged at the leaves, and all nodes have an associated public-key encryption (PKE) key pair, except for the root. The tree invariant is that each user knows all secret keys on their direct path, i.e., on the path from their leaf node to the root. In order to perform an update—the most crucial operation of a CGKA—and produce a new update secret \(I\), a party first generates fresh key pairs on every node of their direct path. Then, for every node \(v'\) on its co-path—the sequence of siblings of nodes on the direct path—it encrypts specific information under the public key of \(v'\) that allows each party in the subtree of \(v'\) to learn all new secret keys from v’s parent up to the root (cf. Fig. 3 and Sect. 4.4).
An update operation initiated by the party at leaf \(v_0\). First, a random “seed value” \(s_0\) is chosen. Thereafter, a PRG is applied iteratively at every level i of \(v_0\)’s direct path in order to derive (i) a PKE secret key \(\mathsf {sk}_i\) for that level (from which a public key can be computed using the key generation algorithm) and (ii) a seed \(s_{i+1}\) for the next level. Every seed \(s_i\) is encrypted using the public key of the corresponding co-path node \(v_{i-1}'\). Sometimes, such a node can be blank, in which case \(s_i\) must be encrypted using the public keys of each node in the resolution, which is the smallest set of nodes covering all leaves in the subtree of \(v_{i-1}'\). This ensures that all these nodes are able to compute the keys from \(v_i\) upward. The update secret \(I\) produced by such an update is the seed value \(s_d\) at the root.
Before presenting the formal description of TreeKEM in Sect. 4.4, basic concepts around ratchet trees are explored in Sect. 4.3. Moreover, Sect. 4.2 quickly discusses the simple PKI model used in this work.
4.2 PKI
The TreeKEM protocol requires a public-key infrastructure (PKI) where parties can register ephemeral keys. The MLS documents [5, 29] lay out explicitly how users are to generate, authenticate, distribute, and verify each others initialization keys. For simplicity and in order not to detract from the essential components of TreeKEM, this work models the PKI by providing protocol algorithms and attackers with access to the following PKI functionality: (1) Any user \(\mathsf {ID}\) may request a fresh (encryption) public key pertaining to some other user \(\mathsf {ID}'\). That is, when \(\mathsf {ID}\) calls \(\mathsf {get\text {-}{}pk}(\mathsf {ID}')\), the PKI functionality generates a fresh key pair \((\mathsf {pk},\mathsf {sk})\) and returns \(\mathsf {pk}\) to \(\mathsf {ID}\). The PKI also records the triple \((\mathsf {pk},\mathsf {sk},\mathsf {ID}')\) and passes the information \((\mathsf {pk},\mathsf {ID}')\) to the attacker. (2) Any user \(\mathsf {ID}'\) may request secret keys corresponding to public keys associated with them. Specifically, when \(\mathsf {ID}'\) calls \(\mathsf {get\text {-}{}sk}(\mathsf {pk})\), if a triple \((\mathsf {pk},\mathsf {sk},\mathsf {ID}')\) is recorded, the PKI functionality returns \(\mathsf {sk}\) to \(\mathsf {ID}'\). Note in particular that the PKI ensures that every public key is only used once. Of course, in practice such a PKI functionality would actually be implemented by having users generate key pairs themselves and registering them with the PKI. However, the above formalization simplifies the description of the protocols.
4.3 Ratchet Trees
Basics. The following are some basic concepts around TreeKEMs ratchet trees.
LBBTs. An RT in TreeKEM is a so-called left-balanced binary tree (LBBT). In a nutshell, an LBBT on n nodes (is defined recursively and) has a maximal full binary tree as its left child and an LBBT on the remaining nodes as its right child:
Definition 3 (Left-Balanced Binary Tree)
For \(n\in \mathbb {N}\) the left-balanced binary tree (LBBT) on n nodes \({\mathsf {LBBT}} _n\) is the binary tree constructed as follows: The tree \({\mathsf {LBBT}} _1\) is a single node. Let \(x = {\mathsf {mp2}} (n)\).Footnote 7 Then, the root of \({\mathsf {LBBT}} _n\) has the full subtree \({\mathsf {FT}} _x\) as the left subtree and \({\mathsf {LBBT}} _{n-x}\) as the right subtree.
Observe that \({\mathsf {LBBT}} _n\) has exactly n leaves and that every internal node has two children. In an RT, nodes are labeled as follows: Root: The root is labeled by an update secret \(I\). Internal nodes: Internal nodes are labeled by a key pair \((\mathsf {pk},\mathsf {sk})\) for the PKE scheme \(\Pi \). Leaf nodes: Leaf nodes are labeled like internal nodes, except that they additionally have an owner \(\mathsf {ID}\).
Labels are referred to using dot-notation (e.g., \(v.\mathsf {pk}\) is v’s public key). As a shorthand, \(\tau .\mathsf {ID}\) is the leaf node with label \(\mathsf {ID}\). Any subset of a node’s labels may be undefined, which is indicated by the special symbol \(\bot \). Furthermore, a node v may be blank. A blank node has all of its labels set to \(\bot \). As explained below, all internal nodes in a freshly initialized RT are blank, and, moreover, blanks can result from adding and removing users to and from a group, respectively.
Paths and blanking. As hinted at the beginning of this section, it will be useful to consider the following types of paths: the direct path \(\mathsf {dPath}(\tau ,\mathsf {ID})\), which is the path from the leaf node labeled by \(\mathsf {ID}\) to the root; the co-path \(\mathsf {coPath}(\tau ,\mathsf {ID})\), which is the sequence of siblings of nodes on the direct path \(\mathsf {dPath}(\tau ,\mathsf {ID})\). Furthermore, given an ID \(\mathsf {ID}\) and an RT \(\tau \), the function \(\tau ' \leftarrow {\textsc {Blank}} (\tau ,\mathsf {ID})\) blanks all nodes on \(\mathsf {dPath}(\tau ,\mathsf {ID})\).
Resolutions and representatives. A crucial notion in TreeKEM is that of a resolution. Intuitively, the resolution of a node v is the smallest set of non-blank nodes that covers all leaves in v’s subtree.
Definition 4 (Resolution)
Let \(\tau \) be a tree with node set V. The resolution \({\mathsf {Res}} (v) \subseteq V\) of a node \(v\in V\) is defined recursively as follows: If v is not blank, then \({\mathsf {Res}} (v) = \{v\}\), else if v is a blank leaf, then \({\mathsf {Res}} (v) = \emptyset \), otherwise, \({\mathsf {Res}} (v) := \cup _{v' \in C(v)} {\mathsf {Res}} (v')\), where \(C(v)\) are the children of v.
Each leaf \(\ell '\) in the subtree \(\tau '\) of some node \(v'\) has a representative in \(\tau '\):
Definition 5 (Representative)
Consider a tree \(\tau \) and two leaf nodes \(\ell \) and \(\ell '\).
-
1.
Assume \(\ell '\) is non-blank and in the subtree rooted at \(v'\). The representative \({\mathsf {Rep}} (v',\ell ')\) of \(\ell '\) in the subtree of \(v'\) is the first filled node on the path from \(v'\) (down) to \(\ell \).
-
2.
Consider the least common ancestor \(w = \mathsf {LCA}(\ell ,\ell ')\) of \(\ell \) and \(\ell '\). Let v be the child of w on the direct path of \(\ell \), and \(v'\) that on the direct path of \(\ell '\). The representative \({\mathsf {Rep}} (\ell ,\ell ')\) of \(\ell '\) w.r.t. \(\ell \) is defined to be the representative \({\mathsf {Rep}} (v',\ell ')\) of \(\ell '\) in the subtree of \(v'\).
It is easily seen that \({\mathsf {Rep}} (v',\ell ') \in {\mathsf {Res}} (v')\).
Simple RT operations. The following paragraphs describe how RTs are initialized as well as how they grow and shrink. The proofs of Lemmas 1 and 2 below can be found in the full version [3].
RT initialization. Given lists of users \(G=(\mathsf {ID}_0,\mathsf {ID}_1,\ldots ,\mathsf {ID}_n)\) and public keys \(\mathbf {pk}= (\mathsf {pk}_0,\mathsf {pk}_1,\ldots ,\mathsf {pk}_n)\) as well as an integer j and a secret key \(\mathsf {sk}_j\), a new RT is initialized as the left-balanced binary tree \({\mathsf {LBBT}} _{n+1}\) where all the internal nodes as well as the root are blanked, the label of every leaf i is set to \((\mathsf {ID}_i,\mathsf {pk}_i,\bot )\), and the secret key at leaf j is additionally set to \(\mathsf {sk}_j\). In the following, the above operation is denoted by \({\textsc {Init}} (G, \mathbf {pk},j,\mathsf {sk}_j)\).
Adding IDs to the RT. Given an RT \(\tau \), the procedure \(\tau ' \leftarrow {\textsc {AddID}} (\tau ,\mathsf {ID},\mathsf {pk})\), sets the labels of the first blank leaf of \(\tau \) to \((\mathsf {ID},\mathsf {pk},\bot )\), and outputs the resulting tree, \(\tau '\). If there is no blank leaf in the tree \(\tau ={\mathsf {LBBT}} _n\), method \({\textsc {AddLeaf}} (\tau )\) is called, which adds a leaf z to it, resulting in a new tree \(\tau ' = {\textsc {AddLeaf}} (\tau )\): If n is a power of 2, create a new node \(r'\) for \(\tau '\). Attach the root of \(\tau \) as its left child and z as its right child. Otherwise, let r be the root of \(\tau \), and let \(\tau _{\mathsf L}\) and \(\tau _{\mathsf R}\) be r’s left and right subtrees, respectively. Recursively insert z into \(\tau _{\mathsf R}\) to obtain a new tree \(\tau _{\mathsf R}'\), and let \(\tau '\) be the tree with r as a root, \(\tau _{\mathsf L}\) as its left subtree and \(\tau _{\mathsf R}'\) as its right subtree.
Lemma 1
If \(\tau = {\mathsf {LBBT}} _n\), then \(\tau ' = {\mathsf {LBBT}} _{n+1}\).
Removing an ID. The procedure \(\tau ' \leftarrow {\textsc {RemID}} (\tau ,\mathsf {ID})\) blanks the leaf labeled with \(\mathsf {ID}\) and truncates the tree such that the rightmost non-blank leaf is the last node of the tree. Specifically, the following recursive procedure \({\textsc {Trunc}} (v)\) is called on the rightmost leaf \(v\) of \(\tau \), resulting in a new tree \(\tau ' \leftarrow {\textsc {Trunc}} (\tau )\):Footnote 8 If \(v\) is blank and not the root, remove \(v\) as well as its parent and place its sibling \(v'\) where the parent was. Then, execute \({\textsc {Trunc}} (v')\). If \(v\) is non-blank and the root, execute \({\textsc {Trunc}} (v'')\) on the rightmost leaf node in the tree. Otherwise, do nothing.
Lemma 2
If \(\tau = {\mathsf {LBBT}} _n\), then \(\tau ' = {\mathsf {LBBT}} _y\) for some \(0 < y \le n\). Furthermore, unless \(y = 1\), the rightmost leaf of \(\tau '\) is non-blank.
Public copy of an RT. Given an RT \(\tau \), \(\tau ' \leftarrow {\textsc {Pub}} (\tau )\) creates a public copy, \(\tau '\), of the RT by setting all secret-key labels to \(\bot \).
4.4 TreeKEM Protocol
This section now explains the TreeKEM protocol in detail by describing all the algorithms involved in the scheme, which is depicted in Fig. 4. For simplicity, the state \(\gamma \) is not made explicit; it consists of the variables initialized by \({\mathsf {init}} \). TreeKEM makes (black-box) use of the following cryptographic primitives: a pseudo random generator \({\mathsf {prg}} \), and a CPA-secure public-key encryption scheme \(\Pi = (\mathsf {PKEG}, \mathsf {Enc}, \mathsf {Dec})\). TreeKEM as described here is slightly different from TreeKEM as described in the current MLS draft [5]. These differences are elaborated on in the full version [3]. Essentially, they are small efficiency improvements that do not affect security.
Initialization. The initialization procedure \({\text{ TK-init }} \) expects as input an ID \(\mathsf {ID}\) and initializes several state variables: Variable \(\mathsf {ME}\) remembers the ID of the party running the scheme and \(\tau \) will keep track of the RT used. The other variables are used to keep track of all the operations (creates, adds, removes, and updates) initiated by \(\mathsf {ME}\) but not confirmed yet by the server. Specifically, each time a party performs a new operation, it increases \(\mathsf {ctr}\) and stores the potential next state in \(\tau '[\mathsf {ctr}]\). Moreover, \(\mathsf {conf}[\mathsf {ctr}]\) will store the control message the party expects from the server as confirmation that the operation was accepted. These variables are reset each time \({\mathsf {proc}} \) processes a control message (which can either be one of the messages in \(\mathsf {conf}\) or a message sent by another party).
Group creation. Given lists of users \(G=(\mathsf {ID}_1,\ldots ,\mathsf {ID}_n)\), \({\text{ TK-create }} \) initializes a new ratchet tree by first creating a new PKE key pair \((\mathsf {pk}_0,\mathsf {sk}_0)\), fetching public keys \(\mathbf {pk}= (\mathsf {pk}_1,\ldots ,\mathsf {pk}_n)\) corresponding to the IDs in \(G\) from the PKI, and then calling \({\textsc {Init}} \) withFootnote 9 \(G' = (\mathsf {ID}_0,G)\) and \(\mathbf {pk}' = (\mathsf {pk}_0,\mathbf {pk})\) as well as 0 and \(\mathsf {sk}_0\). The welcome message simply consists of \(G'\) and \(\mathbf {pk}'\).
Adding a group member. To add new group member \(\mathsf {ID}'\), \({\mathsf {add}} \) first obtains a corresponding public key \(\mathsf {pk}'\) from the PKI and then updates the RT by calling \({\textsc {AddID}} \) (described above) followed by \({\textsc {Blank}} \), which removes all keys from the new party’s leaf up to the root. This ensures that the new user does not know any secret keys used by the other group members before he joined. The welcome message for the new user simply consists of a public copy of the current RT (specifically, \({\textsc {Pub}} \) sets the sender’s secret-key label to \(\bot \)), and the control message for the remaining group members of the IDs of the sender and the new user as well as the latter’s public key.
Removing a group member.
A group member \(\mathsf {ID}'\) is removed by first blanking all the keys from the leaf node of \(\mathsf {ID}'\) to the root. This prevents parties from using keys known to \(\mathsf {ID}'\) in the future. User \(\mathsf {ID}'\) is subsequently removed from the tree by calling \({\textsc {RemID}} \). The control message for the remaining group members consists of the IDs of the sender and the removed user.
Performing an update.
A user \(\mathsf {ME}\) performs an update by choosing new key pairs on their direct path as follows:
-
Compute path secrets: Let \(v_0 = v,v_1,\ldots ,v_d\), be the nodes on the direct path of the \(\mathsf {ME}\)’s leaf node v. First, \(\mathsf {ME}\) chooses a uniformly random \(s_0\). Then, they compute \(\mathsf {sk}_i \Vert s_{i+1} \leftarrow {\mathsf {prg}} (s_i),\, \ \text {for}\, i = 0,\ldots ,d-1.\)
-
Update RT labels: For \(i=0,\ldots ,d-1\), \(\mathsf {ME}\) computes \(\mathsf {pk}_i \leftarrow \mathsf {PKEG}(\mathsf {sk}_i)\) and updates the PKE label of \(v_i\) to \((\mathsf {pk}_i,\mathsf {sk}_i)\).
-
Root node: For the root node, \(\mathsf {ME}\) sets \(I:= s_d\).
The above operation is denoted by \(\tau ' \leftarrow {\textsc {PropUp}} (\tau ,v,s_0)\). Having computed the new keys on its direct path, \(\mathsf {ME}\) proceeds as follows:
-
Encrypt path secrets: Let \(v_0',\ldots ,v_{d-1}'\) be the nodes on the co-path of v (i.e., \(v_{i}'\) is the sibling of \(v_{i}\)). For every value \(s_i\) and every node \(v_j \in {\mathsf {Res}} (v_{i-1}')\), \(\mathsf {ME}\) computes \(c_{ij} \leftarrow \mathsf {Enc}(v_j.\mathsf {pk},s_i)\).
-
Output: All ciphertexts \(c_{ij}\) are concatenated to an overall ciphertext \(\mathbf {c}\) (in some canonical orderFootnote 10). Let \(U\leftarrow (\mathsf {PK},\mathbf {c})\), where \(\mathsf {PK}:= (\mathsf {pk}_0,\ldots ,\mathsf {pk}_{d-1})\) be the update information for the remaining group members.
The entire update process described above is denoted by \((\tau ',U) \leftarrow {\textsc {UpGen}} (\tau ,\mathsf {ID})\). The control message for this operation simply consists of \(\mathsf {ME}\)’s ID and \(U\).
Notation. It will also be convenient to refer to the set of secret keys \( \mathsf {RecKeys}(s_i)\,:=\,\{\mathsf {sk}_i,\ldots ,\mathsf {sk}_{d-1},s_d\}\) that can be recovered from path secret \(s_i\). Moreover, let \(\mathsf {PKeys}(s_i) \ := \{ \mathsf {sk}\ |\, s_i\) is encrypted under PK corresponding to \(\mathsf {sk}\}\) be the set of secret keys such that \(s_i\) is encrypted under the corresponding public keys.
Processing control messages.
When processing a control message \(T\), a user first checks whether \(T\) corresponds to an operation they initiated. If so, they simply adopt the corresponding RT in \(\tau '[\cdot ]\).
Whenever \(T\) was sent from another user, depending on the type of the control message, \({\mathsf {proc}} \) operates as follows:
-
\(T= ({\mathtt {create}},G,\mathbf {pk})\): In this case, simply determine the position j of \(\mathsf {ME}\) in the \(G\) list, retrieve the appropriate secret key \(\mathsf {sk}_j\) from the PKI, and initialize the RT via \(\tau \leftarrow {\textsc {Init}} (G,\mathbf {pk},j,\mathsf {sk}_j)\).
-
\(W= ({\mathtt {wel}},\tilde{\tau })\): Simply adopt \(\tilde{\tau }\) as the current RT \(\tau \) and set the secret key at \(\mathsf {ME}\)’s node to the key \(\mathsf {get\text {-}{}sk}(\tau .\mathsf {ME}.\mathsf {pk})\) retrieved from the PKI.
-
\(T= ({\mathtt {add}},\mathsf {ID},\mathsf {ID}',\mathsf {pk}')\): Add the new user \(\mathsf {ID}'\) to the RT and blank all nodes in the direct path of the new user.
-
\(T= ({\mathtt {rem}},\mathsf {ID},\mathsf {ID}')\): Blank all nodes on the direct path of user \(\mathsf {ID}'\) and remove \(\mathsf {ID}'\) from the RT.
-
\(T= ({\mathtt {up}},\mathsf {ID},U)\): A user \(\mathsf {ID}'\) at some leaf \(\ell '\) receiving \(U= (\mathsf {PK},\mathbf {c})\), issued by the user with id \(\mathsf {ID}\) at leaf v, recovers the update information as follows: Let \(w := {\mathsf {Rep}} (v,\ell ')\). The user with \(\mathsf {ID}'\), uses \(w.\mathsf {sk}\) to decrypt \(c_{ij}\) (for the appropriate j) and obtain \(s_i\). Finally, update the ratchet tree by overriding the public-key labels on the v-root-path by the keys in \(\mathsf {PK}\), and by then producing a new tree \(\tau ' \leftarrow {\textsc {PropUp}} (\tau ,\mathsf {LCA}(v,\ell '),s_i)\). The entire process just described is denoted by \(\tau ' \ \leftarrow {\textsc {UpPro}} (\tau ,\mathsf {ID},\mathsf {ID}',U)\).
Irrespective of whether \(T\) was created by \(\mathsf {ME}\) or another user, after processing it, \({\text{ TK-proc }} \) resets the variables pertaining to keeping track of \(\mathsf {ME}\)’s unconfirmed operations.
5 Security of TreeKEM
A ratchet tree showing only the epoch numbers of secret keys; empty nodes are blank. This tree was created by (say) the following sequence of 11 operations: initialization with eight parties \(\mathsf {ID}_1,\ldots ,\mathsf {ID}_8\); updates by \(\mathsf {ID}_5\), \(\mathsf {ID}_2\), \(\mathsf {ID}_5\), \(\mathsf {ID}_3\), and \(\mathsf {ID}_7\); removal of \(\mathsf {ID}_8\); update by \(\mathsf {ID}_2\); removal of \(\mathsf {ID}_2\); updates by \(\mathsf {ID}_4\) and \(\mathsf {ID}_6\). The boxed nodes contain keys from which the attacker can compute the update secret of epoch 11.
Ideally, a CGKA scheme satisfies Definition 2 w.r.t. the safety predicate
 . However, this is not the case for TreeKEM. Specifically, while TreeKEM achieves post-compromise security (PCS), it only provides a very weak notion of forward secrecy. We first illustrate this with a simple example in Sect. 5.1 and then proceed to characterize the exact security of the TreeKEM protocol in Sect. 5.2, using a predicate \({\mathbf {tkm}}\). While precise (cf. Sect. 4.4), predicate \({\mathbf {tkm}}\) is quite unintuitive and cumbersome. To that end, we show that a scheme secure w.r.t. \({\mathbf {tkm}}\) is also secure w.r.t. to the slightly weaker but more intuitive predicates \({\mathbf {fsu}}\) and \({\mathbf {pcs}}\); the former captures a notion of forward security while the latter captures PCS without guaranteeing forward secrecy.
. However, this is not the case for TreeKEM. Specifically, while TreeKEM achieves post-compromise security (PCS), it only provides a very weak notion of forward secrecy. We first illustrate this with a simple example in Sect. 5.1 and then proceed to characterize the exact security of the TreeKEM protocol in Sect. 5.2, using a predicate \({\mathbf {tkm}}\). While precise (cf. Sect. 4.4), predicate \({\mathbf {tkm}}\) is quite unintuitive and cumbersome. To that end, we show that a scheme secure w.r.t. \({\mathbf {tkm}}\) is also secure w.r.t. to the slightly weaker but more intuitive predicates \({\mathbf {fsu}}\) and \({\mathbf {pcs}}\); the former captures a notion of forward security while the latter captures PCS without guaranteeing forward secrecy.
5.1 TreeKEM Is Not Forward Secret
On an intuitive level, the reason the TreeKEM protocol fails to be forward secret is that after processing the messages generated by an update operation, parties must keep the secret keys used to decrypt the update information since they might be needed for processing future updates. Therefore, corrupting any party other than the update initiator completely reveals the update secret of the previous epoch, and potentially keys of older epochs as well, violating forward secrecy.
In order to better understand this issue, imagine that for every secret key that appears in the ratchet tree, the epoch number in which it was created is recorded; for keys retrieved from the PKI, epoch 0 is assigned. At any point during the game, the annotated ratchet tree will be of the following type: each node is either blank or has a secret key whose epoch number equals the maximum of the epoch numbers of its children (where, for simplicity, the epoch number is \(-\infty \) for blank nodes). An example of a ratchet tree annotated with these epoch numbers is given in Fig. 5.
Consider the security of the update secret \(I\) produced in epoch 11 against future corruptions. As per TreeKEMs definition, information about \(I\) is encrypted under the public keys of all nodes on the co-path of \(\mathsf {ID}_6\). The nodes on said co-path are the epoch-4 key at \(\mathsf {ID}_5\)’s leaf, the epoch-6 key at \(\mathsf {ID}_7\)’s leaf, and highest epoch-10 key in the tree. The latter key, however, can also be recovered from the initial key of \(\mathsf {ID}_1\) or the epoch-5 key at \(\mathsf {ID}_3\)’s leaf (since those keys are on the co-path of \(\mathsf {ID}_4\), who performed the update in epoch 10). These “dangerous” keys are highlighted by boxes in Fig. 5.
Observe now that if the attacker corrupts any party \(\mathsf {ID}\) after epoch 11 but before a boxed key known to \(\mathsf {ID}\) is overridden by an update, he can compute \(I\). In particular, each of the parties in \({\{\mathsf {ID}_1,\mathsf {ID}_3,\mathsf {ID}_5,\mathsf {ID}_7\}}\) must execute an update before they are corrupted in order for \(I\) to remain secure (as these parties are the only ones that can override the corresponding boxed leaf keys).
5.2 Capturing TreeKEM’s Security
In order to capture the security level achieved by the TreeKEM protocol exactly, this section defines a safety predicate \({\mathbf {tkm}}\) based on the notion of a key graph. The key graph records the relationships among secret keys in an execution of the protocol. That is, it keeps track of which keys can be computed given which other keys (learned via state compromise). Specifically, given a sequence of oracle queries  the key graph \((\mathcal {V}_t,\mathcal {E}_t) \leftarrow \mathsf {KG}(Q)\) is defined as follows:
the key graph \((\mathcal {V}_t,\mathcal {E}_t) \leftarrow \mathsf {KG}(Q)\) is defined as follows:
-
 : The
: The  operation defines \((\mathcal {V}_0,\mathcal {E}_0)\) as follows: (1) \(\mathcal {V}_0 \leftarrow \{\mathsf {sk}_{\mathsf {ID}_1},\ldots ,\mathsf {sk}_{\mathsf {ID}_n}\}\), i.e., \(\mathcal {V}_0\) consists of the secret keys of all users in the initial group. (2) \(\mathcal {E}_0\leftarrow \emptyset \).
operation defines \((\mathcal {V}_0,\mathcal {E}_0)\) as follows: (1) \(\mathcal {V}_0 \leftarrow \{\mathsf {sk}_{\mathsf {ID}_1},\ldots ,\mathsf {sk}_{\mathsf {ID}_n}\}\), i.e., \(\mathcal {V}_0\) consists of the secret keys of all users in the initial group. (2) \(\mathcal {E}_0\leftarrow \emptyset \). -
 : Let \(\mathsf {sk}_0,\ldots ,\mathsf {sk}_{d-1}\) and \(s_0,\ldots ,s_d\) be the secret keys and path secrets generated by the update operation. ComputeFootnote 11 (i) \(\mathcal {V}_i \leftarrow \mathcal {V}_{i-1} \cup \{\mathsf {sk}_0,\ldots ,\mathsf {sk}_{d-1},s_d\}\), (ii) For \(j=1,\ldots ,d\), \(K_j \leftarrow \{ (\mathsf {sk}, \mathsf {sk}') \ | \ \mathsf {sk}\in \mathsf {PKeys}(s_j), \mathsf {sk}' \in \mathsf {RecKeys}(s_j) \}\), (iii) Set \(\mathcal {E}_i \leftarrow \mathcal {E}_{i-1} \cup \left( \bigcup _{j \in [d]} K_j\right) \).
: Let \(\mathsf {sk}_0,\ldots ,\mathsf {sk}_{d-1}\) and \(s_0,\ldots ,s_d\) be the secret keys and path secrets generated by the update operation. ComputeFootnote 11 (i) \(\mathcal {V}_i \leftarrow \mathcal {V}_{i-1} \cup \{\mathsf {sk}_0,\ldots ,\mathsf {sk}_{d-1},s_d\}\), (ii) For \(j=1,\ldots ,d\), \(K_j \leftarrow \{ (\mathsf {sk}, \mathsf {sk}') \ | \ \mathsf {sk}\in \mathsf {PKeys}(s_j), \mathsf {sk}' \in \mathsf {RecKeys}(s_j) \}\), (iii) Set \(\mathcal {E}_i \leftarrow \mathcal {E}_{i-1} \cup \left( \bigcup _{j \in [d]} K_j\right) \). -
 : Set \(\mathcal {V}_i \leftarrow \mathcal {V}_{i-1} \cup \{\mathsf {sk}_{\mathsf {ID}'}\}\).
: Set \(\mathcal {V}_i \leftarrow \mathcal {V}_{i-1} \cup \{\mathsf {sk}_{\mathsf {ID}'}\}\).
The queries  ,
,  , do not make any modifications to the key graph, but they indirectly affect the way it evolves.
, do not make any modifications to the key graph, but they indirectly affect the way it evolves.
Let \((\mathcal {V},\mathcal {E})\) be the key graph defined by executing a sequence of operations of the TreeKEM protocol. For a user with ID \(\mathsf {ID}\) and an epoch t, \(\mathcal {K}_{\mathsf {ID}}^t\) consists of the following elements: (1) The private keys in the state of \(\mathsf {ID}\) in epoch t. (2) The private keys in \(\mathcal {V}\) that are are reachable from the above keys in the key graph \((\mathcal {V},\mathcal {E})\).
Having defined TreeKEM’s key graph, admissible adversaries are now captured via the predicate \({\mathbf {tkm}}\) in Fig. 6. The predicate essentially makes sure that the attacker does not learn any keys from which a challenged update secret is reachable (Fig. 7).
More intuitive predicates. Since predicate \({\mathbf {tkm}}\) is very specific to TreeKEM, the security level achieved by TreeKEM is perhaps understood more easily by considering the following two predicates: (1) The PCS predicate, denoted \({\mathbf {pcs}}\), captures PCS only, i.e., without any kind of forward secrecy. This is achieved by excluding corruptions after any challenge (on top of the normal safety predicate). (2) The notion of limited forward secrecy (FS) captured here is FS with updates (FSU). Specifically, when the state of a party \(\mathsf {ID}\) is leaked, then all keys before the most recent update by \(\mathsf {ID}\) remain secret.
In the following lemma, we establish relations between the these predicates and \({\mathbf {tkm}}\). The proof of the lemma can be found in the full version [3].
Lemma 3
For any sequence of queries \(Q\), if \({\mathbf {pcs}}(Q)=1\) or \({\mathbf {fsu}}(Q)=1\), then \({\mathbf {tkm}}(Q)=1\).
In the full version [3], we also show that the formalization introduced above is necessary for evaluating and proving security for the TreeKEM protocol.
5.3 Proof of Security of TreeKEM
This section presents the following security result for the TreeKEM protocol and provides high-level intuition for the security proof. The details of the proof can be found in the full version [3].
Theorem 1 (Non-adaptive security of TreeKEM)
Assume that \({\mathsf {prg}} \) is a \((t_{\mathsf {prg}},\varepsilon _{\mathsf {prg}})\)-secure pseudo-random generator, \(\Pi \) is a \((t_{\mathsf {cpa}},\varepsilon _{\mathsf {cpa}})\)-CPA-secure public-key encryption scheme. Then, TreeKEM is a \((t,c,n,\mathsf {P},\varepsilon )\)-secure CGKA protocol, for \(\mathsf {P}\in \{{\mathbf {tkm}},{\mathbf {pcs}},{\mathbf {fsu}}\}\), \(\varepsilon = 2 cn(\varepsilon _{\mathsf {prg}}+ \varepsilon _{\mathsf {cpa}})\), and \(t\approx t_{\mathsf {prg}}\approx t_{\mathsf {cpa}}\).
Proof intuition. Consider an execution of the (single-challenge) CGKA game with the TreeKEM scheme. Recall that an update operation by a node at depth d produces, for a uniformly random \(s_0\), the values \( s_0 {\mathop {\longrightarrow }\limits ^{{\mathsf {prg}}}}(\mathsf {sk}_0,s_1) {\mathop {\longrightarrow }\limits ^{{\mathsf {prg}}}}(\mathsf {sk}_1,s_2) {\mathop {\longrightarrow }\limits ^{{\mathsf {prg}}}}\ldots {\mathop {\longrightarrow }\limits ^{{\mathsf {prg}}}}(\mathsf {sk}_{d-1},s_d) \) where \(I= s_d\) is the update secret. In the example tree in Fig. 5, assume that the update secret \(I= s_3\) created in epoch 11 is challenged. Observe that the last update (by \(\mathsf {ID}_6\)) encrypts information about \(I\) under the keys at the nodes on \(\mathsf {ID}_6\)’s co-path. These keys stem from epochs 4, 6, and 10, respectively. To use the CPA security of said keys to argue that no information about \(I\) is obtained by the attacker, one has to recursively check under which other keys information about them has been encrypted. For example, in epoch 10, information was encrypted using a key from epoch 5 and the initial key of \(\mathsf {ID}_1\) (who has never performed an update).
Therefore, the proof proceeds in a series of hybrids that fake ciphertexts and replace PRG outputs by random values in a bottom-up fashion, i.e., beginning with the nodes at the greatest depths. In the example of Fig. 5, the hybrids would be the following (highlighting the differences in each step):
-
\(H^{\mathsf {c}}_{d}\): Is identical to the original CGKA experiment.
-
\(H^{\mathsf {p}}_{d}\): When the updates in epochs 4, 5, 10, and 11 are computed, the output of the first application of the PRG is replaced by a uniformly random value, i.e., instead of computing \((\mathsf {sk}_0,s_1) \leftarrow {\mathsf {prg}} (s_0)\), \(\mathsf {sk}_0\) and \(s_1\) are simply chosen randomly. The rest of the update is computed normally. The security of this step follows from that of the PRG.
-
\(H^{\mathsf {c}}_{d-1}\): When the updates in epochs 10 and 11 are computed, instead of encrypting \(s_1\) under the corresponding key on the co-path, the all-zero string is encrypted. This step is safe by the CPA security of the PKE in use and the fact that the secret keys at depth d produced by the updates in epochs 4, 5, 10, and 11 are chosen randomly.
-
\(H^{\mathsf {p}}_{d-1}\): When the updates in epochs 6, 10, and 11 are computed, all PRG computations at depth \(d-1\) are replaced by choosing uniformly random values. That is, instead of applying the PRG, the values \((\mathsf {sk}_0,s_1)\) (in the case of epoch 6) and \((\mathsf {sk}_1,s_2)\) (in the case of epoch 10 and 11) are chosen randomly. The security of this step follows from that of the PRG and by observing that encryptions of \(s_1\) have been replaced by dummy encryptions in the previous hybrid.
-
\(H^{\mathsf {c}}_{d-1}\): When the updates in epochs 10 and 11 are computed, instead of encrypting \(s_2\) under the corresponding keys on the resolution of the co-path nodes, the all-zero string is encrypted. This step is safe by the CPA security of the PKE in use and the fact that the secret key at depth \(d-1\) produced by the update in epoch 6 and the initial key of \(\mathsf {ID}_1\) are chosen randomly.
-
\(H^{\mathsf {p}}_{d-2}\): Similarly to \(H^{\mathsf {p}}_{d-1}\), values \((\mathsf {sk}_2,s_3)\) are chosen randomly when computing updates in epochs 10 and 11.
-
\(H^{\mathsf {c}}_{d-3}\): In epoch 11, the encryption of \(s_3\) is replaced by a dummy encryption. Observe that in \(H^{\mathsf {c}}_{d-3}\), the adversary is now not provided with any information about \(s_3 = I\) in update 11. Hence, its advantage in the final hybrid is 0.
Adaptive security for TreeKEM. Due to space limitations, adaptive security is discussed in the full version [3], where we derive that TreeKEM is adaptively secure with security loss factor of \(O(n^{\log n})\).
A ratchet tree showing only the epoch and version numbers of secret keys; empty nodes are blank. This tree was created by (say) the following sequence of 11 operations: initialization with eight parties \(\mathsf {ID}_1,\ldots ,\mathsf {ID}_8\); updates by \(\mathsf {ID}_5\), \(\mathsf {ID}_2\), \(\mathsf {ID}_5\), \(\mathsf {ID}_3\), and \(\mathsf {ID}_7\); removal of \(\mathsf {ID}_8\); update by \(\mathsf {ID}_2\); removal of \(\mathsf {ID}_2\); updates by \(\mathsf {ID}_4\) and \(\mathsf {ID}_6\). The boxed nodes contain keys under whose earlier versions information leading to update secret of epoch 11 was encrypted.
6 Optimal Forward Secrecy
The level of security satisfied by the TreeKEM protocol is limited, as shown in Sect. 5. In order to achieve better security, this section presents a modified version of TreeKEM that is secure even w.r.t. to predicate
 . The new version of the protocol is based on a suggestion by Kohbrok
[26] on the MLS mailing list and uses so-called updatable public-key encryption (UPKE) (cf. Jost et al.
[24]). In this work we use a variant of UPKE, which we formally present in Sect. 6.2; a construction of a slightly stronger variant can be found in the full version
[3].
. The new version of the protocol is based on a suggestion by Kohbrok
[26] on the MLS mailing list and uses so-called updatable public-key encryption (UPKE) (cf. Jost et al.
[24]). In this work we use a variant of UPKE, which we formally present in Sect. 6.2; a construction of a slightly stronger variant can be found in the full version
[3].
6.1 Fixing TreeKEM
In a nutshell, the new TreeKEM protocol uses UPKE instead of normal PKE. On an intuitive level, the encryption algorithm of a UPKE scheme outputs a new public key (to be used for future encryptions) along with the ciphertext. Similarly, the decryption algorithm outputs a corresponding new secret key. This is done in such a fashion that even given the new version of the secret key, no information about the plaintexts encrypted under older versions is revealed.
In order to better understand how this solves the issue with TreeKEM’s subpar forward secrecy (FS), consider the example execution of the TreeKEM protocol depicted in Fig. 8 (which was already used in Sect. 5). Once more, imagine that for every secret key that appears in the ratchet tree, the epoch number in which it was created is recorded, where keys retrieved from the PKI and used when the group is created, are assigned epoch 0. Imagine further that, in addition to the epoch number, the version number of each key is recorded. More precisely, a UPKE key generated by an update operation has version 0, and with every plaintext encrypted under it, the version number is incremented by 1. For example, in Fig. 8, the initial key of \(\mathsf {ID}_1\) has been used by four different update operations.
It is now easy to see how UPKE solves the FS issue: While in the plain version, the boxed keys could be used to recover the update secret \(I\) of epoch 11, in the new TreeKEM, the information that would allow recovery of \(I\) was encrypted under the second most recent version of the boxed keys. However, UPKE now guarantees that the most recent version of any boxed key obtained upon corruption of a corresponding user after epoch 11 reveals no information about \(I\). For example, information about epoch 11’s update secret was encrypted under version 0 of the highest epoch-10 key. In turn, information about the latter key was encrypted under version 3 of the key at \(\mathsf {ID}_1\)’s leaf. As a result of these encryptions the two keys are now at versions 1 and 4, respectively. Thus, even if, say, \(\mathsf {ID}_1\) is compromised after epoch 11, the new key versions reveal no useful information about epoch 11’s update secret.
6.2 Updatable Public-Key Encryption
Below we define a variant of UPKE in which the public (resp. private) key update functionality is implemented by the encryption (resp. decryption) operation. This is how our UPKE notion deviaties from that of [24], in which the key update operations are implemented by independent functionalities.
Definition 6
An updatable public-key encryption (UPKE) scheme is a triple of algorithms \(\mathsf {UPKE}= (\mathsf {PKEG}, \mathsf {Enc}, \mathsf {Dec})\) with the following syntax:
-
Key generation: \(\mathsf {PKEG}\) receives a uniformly random key \(\mathsf {sk}_0\) and outputs a fresh initial public key \(\mathsf {pk}_0 \leftarrow \mathsf {PKEG}(\mathsf {sk}_0)\).
-
Encryption: \(\mathsf {Enc}\) receives a public key \(\mathsf {pk}\) and a message \(m\) and produces a ciphertext \(c\) and a new public key \(\mathsf {pk}'\).
-
Decryption: \(\mathsf {Dec}\) receives a secret key \(\mathsf {sk}\) and a ciphertext \(c\) and outputs a message \(m\) and a new secret key \(\mathsf {sk}'\).
Correctness. A UPKE scheme must satisfy the following correctness property. For any sequence of randomness and message pairs \(\{r_i,m_i\}_{i=1}^q\),
The notion of CPA security that we define below is along the lines of CPA-secure PKE, with the only difference being that for honestly generated ciphertexts the adversary receives access to the randomness that produced them. In this way we capture protocol executions in which prior to the challenge epoch, the adversary receives access to the ciphertexts generated by users (by observing the network), as well as to the randomness used by corrupted users to encrypt path secrets prior to the challenge epoch.
IND-CPA security for UPKE. For any adversary \({\mathcal {A}} \) with running time \(t\) we consider the IND-CPA security game:
-
Sample \(\mathsf {sk}_0 \leftarrow \mathcal {SK}\), \(\mathsf {pk}_0 \leftarrow \mathsf {PKEG}(\mathsf {sk}_0)\), \(b \leftarrow \{0,1\}\).
-
\({\mathcal {A}} \) receives \(\mathsf {pk}_0\) and for \(i=1,\ldots ,q\), \(\mathcal {A}\) outputs \(m_i\) and receives \((c_i,\mathsf {pk}_i,r_i)\) such that \((c_i, \mathsf {pk}_i) \leftarrow \mathsf {Enc}(\mathsf {pk}_{i-1},m_i;r_i)\), for uniformly random \(r_i\)
-
\(\mathcal {A}\) outputs \((m_0^*,m_1^*)\)
-
For \(i=1,\ldots ,q\), compute \((m_i,\mathsf {sk}_i) \leftarrow \mathsf {Dec}(\mathsf {sk}_{i-1}, c_i)\)
-
Compute \((c^*,\mathsf {pk}^*) \leftarrow \mathsf {Enc}(\mathsf {pk}_q,m_b^*)\), \((\cdot ,\mathsf {sk}^*) \leftarrow \mathsf {Dec}(\mathsf {sk}_q,c^*)\)
-
\(b' \leftarrow {\mathcal {A}} (\mathsf {pk}^*,\mathsf {sk}^*,c^*)\)
\({\mathcal {A}} \) wins the game if \(b=b'\). The advantage of \({\mathcal {A}} \) in winning the above game is denoted by \(\mathsf {Adv^{\mathsf {UPKE}}_{\mathrm {cpa}}}({\mathcal {A}})\).
Definition 7
An updatable public-key encryption scheme \(\mathsf {UPKE}\) is \((t,\varepsilon )\)-CPA-secure if for all \(t\)-attackers \(\mathcal {A}\), \(\mathsf {Adv^{\mathsf {UPKE}}_{\mathrm {cpa}}} (\mathcal {A}) \ \le \ \varepsilon \).
6.3 An Optimally Secure Protocol
The new TreeKEM protocol presented in the this section uses UPKE CPA-secure encryption in place of standard CPA-secure encryption. Using UPKE when a user issues an update operation not only updates the PKE keys in its direct path but also the PKE keys of all nodes in the resolution of the co-path nodes. The new TreeKEM protocol is presented by highlighting the differences to TreeKEM.
The initialization, group creation, user addition/removal operations of the protocol are identical to those of TreeKEM. The only difference is the use of UPKE. The update and process operations work as shown next.
Performing an update.
A user performs an update as follows:
-
Compute path secrets: Let \(v_0 = v,v_1,\ldots ,v_d\), be the nodes along the direct path of the node v who issues an update. For uniformly random \(s_0\) compute \(\mathsf {sk}_i \Vert s_{i+1} \leftarrow {\mathsf {prg}} (s_i), \text {for}\, i = 0,\ldots ,d-1\).
-
Update the RT labels along the direct path: For \(i=0,\ldots ,d-1\), compute \(\mathsf {pk}_i \leftarrow \mathsf {PKEG}(\mathsf {sk}_i)\) and the PKE label of \(v_i\) is updated to \((\mathsf {pk}_i,\mathsf {sk}_i)\).
-
Root node: For the root, set \(I:= s_d\).
Up to now, the computation is identical to the one in the TreeKEM protocol.
-
Encrypt path secrets and update public keys: Let \(v_0',\ldots ,v_{d-1}'\), be the nodes on the co-path of v (i.e., \(v_{i}'\) is the sibling of \(v_{i}\)). For every value \(s_i\) and every node \(v_j \in {\mathsf {Res}} (v_{i-1}')\), compute \((c_{ij},\mathsf {pk}_{ij}) \leftarrow \mathsf {Enc}(v_j.\mathsf {pk},s_i)\) and set the public key of \(v_j\) to \(\mathsf {pk}_{ij}\).
-
Output: All ciphertexts \(c_{ij}\) are concatenated to an overall ciphertext \(\mathbf {c}\) and all keys \(\mathsf {pk}_{ij}\) are stored in \(\bar{\mathsf {PK}}\). Return \(U\leftarrow (\mathsf {PK},\bar{\mathsf {PK}},\mathbf {c})\), where \(\mathsf {PK}:= (\mathsf {pk}_0,\ldots ,\mathsf {pk}_{d-1})\). This extended update process is denoted by
Processing control messages. Processing control messages is similar to the TreeKEM protocol. The main difference is in the way the users process the output of the public key encryption scheme. In particular, for any node of the ratchet tree, v, when processing the output of the encryption operation under the public key of v, \((c,\mathsf {pk}_v') \leftarrow \mathsf {Enc}(\mathsf {pk}_v,s)\), users compute \((s,\mathsf {sk}_v') \leftarrow \mathsf {Dec}(v.\mathsf {sk},c)\), process the path secret s as in TreeKEM, but in addition they set the public and secret key of v to \(\mathsf {pk}_v'\) and \(\mathsf {sk}_v'\), respectively.
6.4 Security of the New TreeKEM
The modified version of the TreeKEM protocol satisfies optimal security, i.e., security w.r.t. the predicate
 . The proof of Theorem 2 can be found in the full version
[3].
. The proof of Theorem 2 can be found in the full version
[3].
Theorem 2 (Non-adaptive security of Modified TreeKEM)
Assume that \({\mathsf {prg}} \) is a \((t_{\mathsf {prg}},\varepsilon _{\mathsf {prg}})\)-secure pseudo-random generator, \(\Pi \) is a \((t_{\mathsf {cpa}},\varepsilon _{\mathsf {cpa}})\)-CPA-secure updatable public-key encryption scheme. Then, the protocol of Sect. 6.3 is a  -secure CGKA protocol, for \(\varepsilon = 2 cn(\varepsilon _{\mathsf {prg}}\,+\,\varepsilon _{\mathsf {cpa}})\) and \(t\approx t_{\mathsf {prg}}\approx t_{\mathsf {cpa}}\).
-secure CGKA protocol, for \(\varepsilon = 2 cn(\varepsilon _{\mathsf {prg}}\,+\,\varepsilon _{\mathsf {cpa}})\) and \(t\approx t_{\mathsf {prg}}\approx t_{\mathsf {cpa}}\).
Adaptive security for Modified TreeKEM. Due to space limitations, adaptive security is discussed in the full version [3], where we argue that Modified TreeKEM is adaptively secure with security loss factor of \(O(n^{\log n})\).
7 Group Splitting
Group splitting occurs when the attacker, who (in any reasonable SGM definition) has full control over message delivery, does not properly resolve race conditions for control messages. For example, if two group members A and B having processed the same set of protocol messages, both produce an update, the attacker may choose to deliver A’s update to a subset \(\mathcal {A}\) of parties and B’s update to the set \(\mathcal {B}\) of remaining parties. The two sets of parties are now potentially in incompatible (yet not independent) states and any state compromise of users in \(\mathcal {A}\) can potentially compromise the secrets generated by users in \(\mathcal {B}\). This can only be avoided if each CGKA protocol operation updates all the key material in the users’ states, so that, after processing the updates, the users in \(\mathcal {A}\) (resp. \(\mathcal {B}\)) do not share common private keys with users in \(\mathcal {B}\) (resp. \(\mathcal {A}\)), and therefore, they cannot process protocols messages generated by users in that group. Clearly, if we aim for practical efficiency, this is not a tenable solution as it requires complexity linear in the size of the group. Thus, we believe it is essential to make a compromise between efficiency and security against splitting attacks.
The security properties that suggested below constitute a reasonable trade-off between security and efficiency, since they only require “touching” a \(O(\log n)\) keys in the users’ states.
-
1.
Group re-merging: Either by accident or by design, groups could potentially end up in compatible states again if they process a suitable set of protocol messages. This is not necessarily a problem, but it is in general undesirable as it contradicts detection of group-splitting attacks that could potentially affect the higher level protocol. Re-merging can easily be avoided by using the transcript-hashing technique outlined above.
-
2.
Security in split groups: Should compromising users in \(\mathcal {B}\) help break security of users in \(\mathcal {A}\)? Such a requirement seems quite strong considering the fact that all group members will still believe that the group has not split and consists of all parties in \(\mathcal {A}\cup \mathcal {B}\). However, the security of users in \(\mathcal {A}\) should be maintained in either one in the following two cases:
-
(a)
Security for \(\mathcal {A}\) is guaranteed once all compromised users from \(\mathcal {B}\) have been removed in \(\mathcal {A}\)’s view of the group. (Not providing this guarantee would imply that former group members might still be able to learn group keys after they have left the group.)
-
(b)
Security for \(\mathcal {A}\) is guaranteed if all users compromised in \(\mathcal {B}\) performed an update sometime prior to compromise but after they split from \(\mathcal {A}\). (Not providing this guarantee would mean that under the right circumstances even when all compromised user have updated PCS might still not be achieved.)
It is not hard to see that TreeKEM and modified TreeKEM satisfy 2.(a) and 2.(b). For TreeKEM, after users in \(\mathcal {A}\) remove a user that, according to their view, belongs to \(\mathcal {A}\) (but he is actually a member of \(\mathcal {B}\) due to split), all future protocol operations are independent of the secret keys that that the removed user knows. Therefore, he cannot process those messages. A similar argument holds for 2.(b): if users compromised in \(\mathcal {B}\) have issued an update sometime prior to compromise, then all their secret keys have been updated, and control messages generated by users in \(\mathcal {A}\) require the erased keys in order to be processed. Similar arguments hold for the modified TreeKEM.
Notes
- 1.
Classic insecure examples of such messaging applications are SMS and eMail.
- 2.
In particular, the tree of height 0 consists of a single node, the root.
- 3.
Modeling no-deletions explicitly would clutter Fig. 1 quite a bit.
- 4.
Any boolean expression containing \(\bot \) is false.
- 5.
Note that this assumption is universal in the 2-party SM literature.
- 6.
In particular, its well understood that an insider in an MLS session can, at the very least, perform denial of service attacks on group members by sending out malformed packets.
- 7.
Recall that \({\mathsf {mp2}} (n)\) is the maximum power of two dividing n.
- 8.
Overloading function \({\textsc {Trunc}} \) for convenience here.
- 9.
Here we slightly abuse vector notation.
- 10.
For the sake of concreteness, consider the order obtained by first sorting the \(c_{ij}\) by i and then by j, using the natural ordering for resolutions obtained by first considering the left child and then the right child (cf. Definition 4).
- 11.
See Sect. 4.4, for a definition of the sets \(\mathsf {PKeys}\) and \(\mathsf {RecKeys}\).
References
Alwen, J., et al.: Keep the dirt: tainted treekem, an efficient and provably secure continuous group key agreement protocol. Cryptology ePrint Archive, Report 2019/1489 (2019). https://eprint.iacr.org/2019/1489
Alwen, J., Coretti, S., Dodis, Y.: The double ratchet: security notions, proofs, and modularization for the signal protocol. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 129–158. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_5
Alwen, J., Coretti, S., Dodis, Y., Tselekounis, Y.: Security analysis and improvements for the IETF MLS standard for group messaging. Cryptology ePrint Archive, Report 2019/1189 (2019). https://eprint.iacr.org/2019/1189
Barnes, R.: Subject: [MLS] remove without double-join (in TreeKEM). MLS Mailing List. Mon, 06 August 2018 13:01 UTC (2018). https://mailarchive.ietf.org/arch/msg/mls/Zzw2tqZC1FCbVZA9LKERsMIQXik
Barnes, R., Beurdouche, B., Millican, J., Omara, E., Cohn-Gordon, K., Robert, R.: The Messaging Layer Security (MLS) Protocol. Internet-Draft draft-ietf-mls-protocol-08, Internet Engineering Task Force, November 2019. Work in Progress
Bellare, M., Singh, A.C., Jaeger, J., Nyayapati, M., Stepanovs, I.: Ratcheted encryption and key exchange: the security of messaging. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part III. LNCS, vol. 10403, pp. 619–650. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_21
Borisov, N., Goldberg, I., Brewer, E.A.: Off-the-record communication, or, why not to use PGP. In: Proceedings of the 2004 ACM Workshop on Privacy in the Electronic Society, WPES 2004, 28 October 2004, pp. 77–84 (2004)
Canetti, R., Garay, J.A., Itkis, G., Micciancio, D., Naor, M., Pinkas, B.: Multicast security: a taxonomy and some efficient constructions. In: IEEE INFOCOM 1999, New York, NY, USA, 21–25 March 1999, pp. 708–716 (1999)
Cohn-Gordon, K., Cremers, C., Garratt, L., Millican, J., Milner, K.: On ends-to-ends encryption: asynchronous group messaging with strong security guarantees. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) ACM CCS 2018, pp. 1802–1819. ACM Press, October 2018
Cohn-Gordon, K., Cremers, C., Dowling, B., Garratt, L., Stebila, D.: A formal security analysis of the signal messaging protocol. In: 2017 IEEE European Symposium on Security and Privacy, EuroS&P 2017, pp. 451–466 (2017)
Cremers, C., Hale, B., Kohbrok, K.: Revisiting post-compromise security guarantees in group messaging. Cryptology ePrint Archive, Report 2019/477 (2019). https://eprint.iacr.org/2019/477
Dodis, Y., Fazio, N.: Public key broadcast encryption for stateless receivers. In: Feigenbaum, J. (ed.) DRM 2002. LNCS, vol. 2696, pp. 61–80. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-44993-5_5
Durak, F.B., Vaudenay, S.: Bidirectional asynchronous ratcheted key agreement with linear complexity. In: Attrapadung, N., Yagi, T. (eds.) IWSEC 2019. LNCS, vol. 11689, pp. 343–362. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26834-3_20
eQualit.ie. (n + 1)sec (2016). https://learn.equalit.ie/wiki/Np1sec
Fiat, A., Naor, M.: Broadcast encryption. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 480–491. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_40
Fuchsbauer, G., Jafargholi, Z., Pietrzak, K.: A quasipolynomial reduction for generalized selective decryption on trees. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 601–620. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_29
Fuchsbauer, G., Konstantinov, M., Pietrzak, K., Rao, V.: Adaptive security of constrained PRFs. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 82–101. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_5
Goldberg, I., Ustaoglu, B., Van Gundy, M., Chen, H.: Multi-party off-the-record messaging. In: Al-Shaer, E., Jha, S., Keromytis, A.D. (eds.) Proceedings of the 2009 ACM Conference on Computer and Communications Security, CCS 2009, Chicago, Illinois, USA, 9–13 November 2009, pp. 358–368. ACM (2009)
NCC Group: Olm cryptographic review - 1 November 2016 version 2 (2016). https://www.nccgroup.trust/globalassets/our-research/us/public-reports/2016/november/ncc_group_olm_cryptogrpahic_review_2016_11_01.pdf
Howell, C., Leavy, T., Alwen, J.: Wickr messaging protocol: technical paper (2018). https://wickr.com/wickrs-messaging-protocol/
Jaeger, J., Stepanovs, I.: Optimal channel security against fine-grained state compromise: the safety of messaging. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part I. LNCS, vol. 10991, pp. 33–62. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_2
Jafargholi, Z., Kamath, C., Klein, K., Komargodski, I., Pietrzak, K., Wichs, D.: Be adaptive, avoid overcommitting. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 133–163. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_5
Jafargholi, Z., Wichs, D.: Adaptive security of Yao’s garbled circuits. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part I. LNCS, vol. 9985, pp. 433–458. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_17
Jost, D., Maurer, U., Mularczyk, M.: Efficient ratcheting: almost-optimal guarantees for secure messaging. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 159–188. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_6
Kim, Y., Perrig, A., Tsudik, G.: Group key agreement efficient in communication. IEEE Trans. Comput. 53(7), 905–921 (2004)
Kohbrok, K.: Subject: [MLS] improve FS granularity at a cost. MLS Mailing List. Thu, 24 January 2019 09:51 UTC (2019). https://mailarchive.ietf.org/arch/msg/mls/WRdXVr8iUwibaQu0tH6sDnqU1no
Marlinspike, M., Perrin, T.: The double ratchet algorithm, November 2016. https://whispersystems.org/docs/specifications/doubleratchet/doubleratchet.pdf
Mittra, S.: Iolus: a framework for scalable secure multicasting. In: Proceedings of ACM SIGCOMM, Cannes, France, 14–18 September 1997, pp. 277–288 (1997)
Omara, E., Beurdouche, B., Rescorla, E., Inguva, S., Kwon, A., Duric, A.: The Messaging Layer Security (MLS) Architecture. Internet-Draft draft-ietf-mls-architecture-03, Internet Engineering Task Force, September 2019. Work in Progress
Panjwani, S.: Tackling adaptive corruptions in multicast encryption protocols. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 21–40. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_2
Poettering, B., Rösler, P.: Towards bidirectional ratcheted key exchange. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part I. LNCS, vol. 10991, pp. 3–32. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_1
Rescorla, E.: Subject: [MLS] TreeKEM: an alternative to ART. MLS Mailing List. Thu, 03 May 2018 14:27 UTC (2018). https://mailarchive.ietf.org/arch/msg/mls/WRdXVr8iUwibaQu0tH6sDnqU1no
Steer, D.G., Strawczynski, L., Diffie, W., Wiener, M.: A secure audio teleconference system. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 520–528. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_37
Open Whisper Systems: The signal application (2020). https://github.com/signalapp
Wallner, D., Hardner, E., Agee, R.: Key management for multicast: issues and architectures. IETF RFC2676 (1999). https://tools.ietf.org/html/rfc2627
Weidner, M.: Group messaging for secure asynchronous collaboration. M.Phil. dissertation (2019). https://mattweidner.com/acs-dissertation.pdf. Advisors: Beresford, A., Kleppmann, M
Whatsapp: Encryption overview 2017, 19 December 2017. https://www.whatsapp.com/security/WhatsApp-Security-Whitepaper.pdf
Wong, C.K., Gouda, M., Lam, S.S.: Secure group communications using key graphs. IEEE/ACM Trans. Netw. 8(1), 16–30 (2000)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Alwen, J., Coretti, S., Dodis, Y., Tselekounis, Y. (2020). Security Analysis and Improvements for the IETF MLS Standard for Group Messaging. In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12170. Springer, Cham. https://doi.org/10.1007/978-3-030-56784-2_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-56784-2_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56783-5
Online ISBN: 978-3-030-56784-2
eBook Packages: Computer ScienceComputer Science (R0)



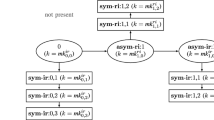







 : The
: The  operation defines
operation defines  : Let
: Let  : Set
: Set 

