Abstract
We study the concrete security of high-performance implementations of half-gates garbling, which all rely on (hardware-accelerated) AES. We find that current instantiations using k-bit wire labels can be completely broken—in the sense that the circuit evaluator learns all the inputs of the circuit garbler—in time \(O(2^k/C)\), where C is the total number of (non-free) gates that are garbled, possibly across multiple independent executions. The attack can be applied to existing circuit-garbling libraries using \(k=80\) when \(C \approx 10^9\), and would require \(267\) machine-months and cost about $\(3500\) to implement on the Google Cloud Platform. Since the attack can be fully parallelized, it could be carried out in about a month using \({\approx }250\) machines.
With this as our motivation, we seek a way to instantiate the hash function in the half-gates scheme so as to achieve better concrete security. We present a construction based on AES that achieves optimal security in the single-instance setting (when only a single circuit is garbled). We also show how to modify the half-gates scheme so that its concrete security does not degrade in the multi-instance setting. Our modified scheme is as efficient as prior work in networks with up to 2 Gbps bandwidth.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Roughly 35 years ago, Yao proposed the idea of garbled circuits for constant-round (semi-honest) secure two-party computation [44]. Over the past 15 years, spurred by initial implementations demonstrating its practicality [20, 33, 37], circuit garbling has received a considerable amount of attention and Yao’s initial scheme has been significantly improved. Notable examples of such improvements include the point-and-permute technique [1], garbled row reduction [35], free-XOR [26], fleXOR [25], and half-gates garbling [46], as well as optimizations involving AES when modeled as a pseudorandom function [17] or when used with a fixed key and modeled as a random permutation [5]. Overall, these improvements have not only decreased the computational requirements of garbling, but have also—perhaps more importantly—reduced the communication complexity of garbled circuits. (Indeed, in current implementations of semi-honest secure two-party computation the overall running time is dominated by the communication time, and network bandwidth is the primary bottleneck.)
As these improvements to circuit garbling have been developed, however, there has been—perhaps somewhat surprisingly—a relative lack of attention on the concrete security [4] of these proposals.Footnote 1 Understanding concrete security here is important for at least two reasons. First, as is well understood in the context of both public-key (e.g., [7, 12]) and symmetric-key (e.g., [4]) cryptography, when comparing the efficiency of different schemes it is important to take into account the concrete-security bound they each achieve; otherwise, the comparison may be inaccurate or misleading. Moreover, concrete security is critical for constructions based on symmetric-key primitives (such as AES), where there is no “security parameter” that can be arbitrarily adjusted as in the public-key world. (In particular, for AES the block size is fixed at 128 bits, and the maximum available key length is 256 bits.) There is thus the risk that a scheme that is only proven asymptotically secure—but has a poor concrete-security bound—may be insecure in practice for the available range of parameters.
When evaluating the concrete security of garbling, one can consider the “standard,” single-instance setting where a single circuit is garbled, but it is also natural to consider a multi-instance setting where multiple circuits, for possibly different functions, are (independently) garbled—whether by the same user or distinct users—and, informally, the attacker succeeds if it is able to violate the security of any of those garbled circuits. Concrete security in the multi-instance setting has received a lot of attention in the context of both public-key [3, 24] and symmetric-key [2, 8, 9, 19, 40] cryptography, but to the best of our knowledge it has not been previously considered in the setting of secure computation.Footnote 2
1.1 Our Contributions
We study the concrete security of garbling. We begin by examining the concrete security of existing, state-of-the-art implementations of the half-gates scheme (which is the most efficient garbling scheme currently known), and showing that it is worse than perhaps previously thought. We then propose a new way to instantiate the half-gates scheme that achieves better concrete-security bounds. Our results are described in further detail in what follows.
Concrete Security of Current Half-Gates Garbling. The half-gates scheme is a technique for circuit garbling that is compatible with free-XOR (so uses no communication and negligible computation for XOR gates) and requires only 2k bits of communication for non-XOR gates, where k denotes the length of the wire labels. The half-gates scheme is based, abstractly, on a hash function H. Zahur et al. [46], motivated by JustGarble [5], propose to instantiate H using fixed-key AES in a particular way. Their suggestion was adopted by many existing implementations [13, 15, 38, 41,42,43, 45] since it is much more efficient than instantiating H with a cryptographic hash function such as SHA-256 or SHA-3.
Let C be the number of (non-free) gates garbled. We show an attack on the half-gates scheme that results in a complete break (that is, the circuit evaluator learns all the inputs of the circuit garbler) in time \(O(2^k/C)\). The attack works in the claimed time even when C denotes the total number of gates garbled across multiple, independent circuits. (In this case the attack completely violates privacy for at least one of the garbled circuits.)
We experimentally verify the feasibility of our attack against existing implementations of garbling that use “short” wire labels. In particular, we show that garbling 1 billion gatesFootnote 3 (i.e., \(C=10^9\)) with existing implementations of half-gates garbling that use wire labels of length \(k=80\) is vulnerable to an attack that can be carried out in \(267\) machine-months at a cost of $\(3500\). Since the attack can be fully parallelized, it can be carried out in about a month using \({\approx }250\) machines. Due to our attack, we urge users of the half-gates scheme to no longer use 80-bit wire labels (unless the scheme is modified as discussed below).
Better Concrete Security for Half-Gates Garbling. Looking more closely at our attack, we observe that it does not arise due to any weakness in the half-gates scheme itself, but instead is possible because of the way H is instantiated. In particular, we show that the half-gates scheme has a tight security reduction (namely, requires time \(\varTheta (2^k)\) to attack) if the hash function H being used is modeled as a random oracle. (See Appendix B.) As noted earlier, however, in existing implementations H is instantiated using (fixed-key) AES for better performance; this instantiation is not indifferentiable from a random oracle and our attack can be viewed as exploiting that gap.
The fact that the proposed instantiation of H is not indifferentiable from a random oracle was also observed by Guo et al. [18]. They define a property called tweakable circular correlation robustness (TCCR) for hash functions, show that using a TCCR hash function suffices for security of the half-gates scheme, and give a provably secure construction of a TCCR hash function based on fixed-key AES. They did not focus on obtaining better concrete security, and indeed, in Appendix C we show that using their hash function in the half-gates scheme would admit an attack with complexity similar to the one described above.
We thus turn to constructing a TCCR hash function with tight concrete security. In this context, the hash function H is evaluated on both a tweak and an input and, with our eventual application to garbling in mind, we use a fine-grained notion of concrete security that separately bounds the total number of calls the adversary makes to H as well as the maximum number of times \(\mu \) the adversary repeats any particular tweak. As our main result, we show a construction of a TCCR hash function based on AES (modeled as an ideal cipher) that has tight concrete security when \(\mu \) is small.
Importantly, \(\mu =1\) when a single circuit is garbled using the half-gates scheme, and so when our new hash function is used to instantiate the half-gates approach we immediately obtain a garbling scheme with tight security in the single-instance setting. In the multi-instance setting, however, \(\mu \) can potentially be as large the number of circuits being garbled; thus, absent any changes, we would obtain a poor concrete-security bound, even when using our hash function, when many circuits are independently garbled. To address this, we show a simple way to randomize the tweaks used in the half-gates scheme in order to avoid significant degradation in the concrete security.
In contrast to the prior work of Guo et al. [18], the hash function we propose involves re-keying AES (and modeling AES as an ideal cipher) rather than relying on fixed-key AES (and modeling the result as a random permutation). Nevertheless, we show in Sect. 6 that by incorporating state-of-the-art optimizations for AES key scheduling [17], our hash function is almost as efficient as the one proposed by Guo et al. when used for circuit garbling.
1.2 Practical Implications
We show that existing implementations of half-gates garbling are much less secure than previously thought, and puts forth an improved way to instantiate half-gates garbling with better concrete security. Our work has already had an impact on existing libraries for secure computation. For example, OblivC [45] changed the length of their labels from 80 bits to 128 bits due to our work, and our new method for instantiating the half-gates scheme is being used in the latest implementations (e.g., [11]). We are also aware of industry implementations (that we are unable to disclose) that have changed because of our work.
1.3 Overview of the Paper
In Sect. 2 we establish notation and review relevant definitions for garbling schemes, including concrete security definitions for garbling in a multi-instance setting. We also describe the half-gates garbling scheme based on an abstract hash function H. In Sect. 3 we describe the instantiation of H based on fixed-key AES that was proposed by Zahur et al. and that is used in existing implementations; we then show an attack with running time \(O(2^k/C)\) that completely violates the privacy of that instantiation. We define the notion of multi-instance tweakable circular correlation robustness (miTCCR) for hash functions in Sect. 4.1, and show that the concrete security of the half-gates scheme when instantiated with a hash function H can be reduced to the concrete security of H in the sense of miTCCR. As our main positive result, we then show in Sect. 4.2 how to construct a hash function from an ideal cipher with tight security in that sense. In Sect. 5 we show how to slightly modify the half-gates scheme so as to also achieve good concrete security in the multi-instance setting. We discuss the performance of the resulting garbling scheme in Sect. 6.
2 Circuit Garbling
We adapt the definitions of garbling by Bellare et al.
[6] to our setting. We consider boolean circuits containing AND and XOR gates with fan-in 2. (NOT gates can be handled by XORing with 1.) We represent any such circuit by a tuple \(f=(n, m, {\ell }, \mathsf{Gates})\), where \(n\ge 2\) denotes the number of input wires, \(m\ge 1\) is the number of output wires, and \({\ell }\) is the number of gates. Such a circuit has exactly \(n+{\ell }\) wires that we number starting from 1; we let \(\mathsf{Inputs}= \{1,\ldots , n\}\) and \(\mathsf{Outputs}= \{n+{\ell }-m+1,\ldots , n+{\ell }\}\). The set \(\mathsf{Gates}=\{(a, b, c, T)\}\), containing \({\ell }\) tuples, specifies the wiring of the circuit; a tuple \((a, b, c, T) \in \mathsf{Gates}\) with \(a, b, c \in \{1, \ldots , n+{\ell }\}\) represents a gate of type \(T \in \{\mathsf{XOR}, \mathsf{AND}\}\) with input wires a, b and output wire c. For a circuit f we let \(|f|=C\) denote the number of AND gates in f. With slight abuse of notation, we let f also denote the function  computed by the circuit.
computed by the circuit.
We consider a restricted class of garbling schemes in which garbling involves assigning two k-bit labels to each wire of the circuit, and evaluation involves computing one label for each output wire. (Our definition is thus similar to the one considered by Katz and Ostrovsky [23].) While this is less general than the class of garbling schemes considered by Bellare et al., this formulation suffices for analyzing the half-gates construction that is the focus of this paper.
Definition 1
A circuit-garbling scheme  is a tuple of algorithms where:
is a tuple of algorithms where:
-
 takes as input a circuit f, and returns \((\mathsf{GC}, \{ W_i^0, W_i^1\}_{i \in \mathsf{Inputs}}, d)\), where \(\mathsf{GC}\) denotes a garbled circuit,
takes as input a circuit f, and returns \((\mathsf{GC}, \{ W_i^0, W_i^1\}_{i \in \mathsf{Inputs}}, d)\), where \(\mathsf{GC}\) denotes a garbled circuit, 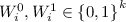 are the labels for the ith input wire, and d represents decoding information.
are the labels for the ith input wire, and d represents decoding information. -
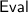 takes as input a garbled circuit \(\mathsf{GC}\) and input-wire labels \(\{W_i\}_{i \in \mathsf{Inputs}}\). It returns output-wire labels \(\{W_i\}_{i \in \mathsf{Outputs}}\).
takes as input a garbled circuit \(\mathsf{GC}\) and input-wire labels \(\{W_i\}_{i \in \mathsf{Inputs}}\). It returns output-wire labels \(\{W_i\}_{i \in \mathsf{Outputs}}\). -
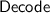 takes as input output-wire labels \(\{W_i\}_{i \in \mathsf{Outputs}}\) and decoding information d, and returns either \(\bot \) or a string
takes as input output-wire labels \(\{W_i\}_{i \in \mathsf{Outputs}}\) and decoding information d, and returns either \(\bot \) or a string 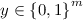 .
.
Correctness requires that for any circuit f and any  , if we compute
, if we compute

and  , then
, then  .
.
When we work in the ideal-cipher model (ICM), all algorithms (including any adversary) are given access to a random keyed permutation  as well as its inverse \(E ^{-1}\); i.e., for every
as well as its inverse \(E ^{-1}\); i.e., for every  and input
and input  it holds that \(E ^{-1}(\mathsf{key}, E (\mathsf{key}, x))=x\). We require correctness to hold for all such E. We sometimes also consider the random-permutation model (RPM) in which all parties have access to a random permutation \(\pi \) and its inverse. The RPM can be obtained from the ICM by setting \(\pi (x) = E(0^L, x)\).
it holds that \(E ^{-1}(\mathsf{key}, E (\mathsf{key}, x))=x\). We require correctness to hold for all such E. We sometimes also consider the random-permutation model (RPM) in which all parties have access to a random permutation \(\pi \) and its inverse. The RPM can be obtained from the ICM by setting \(\pi (x) = E(0^L, x)\).
Security notions for garbling are considered in the following section.
2.1 (Multi-instance) Security of Garbling
The canonical security definition for garbling schemes, which suffices for semi-honest secure computation, is privacy. As Bellare et al. [6] note, however, some other applications of garbling require alternate definitions. For completeness, we thus also consider the notions of obliviousness and authenticity in Appendix A. In contrast to prior work, here we provide concrete-security definitions in a multi-instance setting in which an attacker may be given values produced by the (independent) garbling of \(u \ge 1\) circuits.
Roughly speaking, privacy requires that the information needed to evaluate a garbled circuit (namely, \(\mathsf{GC}\), \(\{W_i^{x_i}\}\), and d) reveals nothing other than \(y=f(x)\). This is formalized by requiring the existence of a simulator  that takes the circuit f and a value y as input, and outputs values that are indistinguishable from \(\mathsf{GC}\), \(\{W_i^{x_i}\}\), d. In the multi-instance setting, we compare the output of
that takes the circuit f and a value y as input, and outputs values that are indistinguishable from \(\mathsf{GC}\), \(\{W_i^{x_i}\}\), d. In the multi-instance setting, we compare the output of  to the outputs obtained from independently garbling u circuits. The following definition is specialized to the ICM for concreteness and since our main construction is in that model; it can be naturally adapted to the RPM.
to the outputs obtained from independently garbling u circuits. The following definition is specialized to the ICM for concreteness and since our main construction is in that model; it can be naturally adapted to the RPM.
Definition 2
Garbling scheme  is \((p, u, C, \varepsilon )\) -private if there is a simulator
is \((p, u, C, \varepsilon )\) -private if there is a simulator  so that for any distinguisher D making p queries to \(E \) and any \(\{(f^i,x^i)\}_{i\in [u]}\) with \(\sum _i|f^i|=C\), we have
so that for any distinguisher D making p queries to \(E \) and any \(\{(f^i,x^i)\}_{i\in [u]}\) with \(\sum _i|f^i|=C\), we have

where both probabilities are also over choice of E.
In the definition above, D may be unbounded so long as the number of queries it makes to E is bounded. The definition does not explicitly consider the running time of the simulator  , but one can verify that the running time of the simulator for our construction is O(C). We remark further that while the distinguisher is given the circuits/inputs used in all the instances, we require the simulator to simulate each instance independently. (That is, when simulating the ith instance the simulator is only given \(f^i, f^i(x^i)\).)
, but one can verify that the running time of the simulator for our construction is O(C). We remark further that while the distinguisher is given the circuits/inputs used in all the instances, we require the simulator to simulate each instance independently. (That is, when simulating the ith instance the simulator is only given \(f^i, f^i(x^i)\).)
2.2 The Half-Gates Garbling Scheme
The half-gates scheme \(\mathsf {HalfGates} \)
[46] is an approach for garbling that is compatible with the free-XOR technique, and only requires communicating 2k bits per AND gate. As the most efficient garbling scheme currently known, it is widely used in existing implementations of secure two-party computation in both the semi-honest and malicious settings. \(\mathsf {HalfGates} \) is based on an abstract hash function  . We describe the scheme generically here, and discuss specific instantiations of H later.
. We describe the scheme generically here, and discuss specific instantiations of H later.
We provide a high-level description, and refer to Fig. 1 for details. To garble a circuit, the half-gates scheme begins by choosing a k-bit string R that is uniform subject to its least-significant bit being 1. For the ith wire of the circuit with associated labels \(W_i^0, W_i^1\), it will always be the case that  . The garbler next chooses uniform 0-labels \(\{W_i^0\}_{i \in \mathsf{Inputs}}\) for each input wire of the circuit. (This defines the 1-labels
. The garbler next chooses uniform 0-labels \(\{W_i^0\}_{i \in \mathsf{Inputs}}\) for each input wire of the circuit. (This defines the 1-labels  for the input wires as well.) The garbled circuit is then generated gate-by-gate in topological order. For each XOR gate in the circuit, with ingoing wires a, b and outgoing wire c, the garbler simply sets
for the input wires as well.) The garbled circuit is then generated gate-by-gate in topological order. For each XOR gate in the circuit, with ingoing wires a, b and outgoing wire c, the garbler simply sets  (and nothing is included in the garbled circuit for this gate). Each AND gate in the circuit is numbered topologically with a unique gate identifier gid ranging from 1 to C. For each AND gate in the circuit, with ingoing wires a, b and outgoing wire c, the garbler uses \(W_a^0, W_b^0\), R, and the gate’s identifier \(\mathsf{gid}\) to compute the garbled table \((T_{G}, T_{E})\) as well as the 0-label \(W_c^0\). This is done using a complicated procedure GbAnd that is defined in Fig. 1. The garbled circuit consists of all the garbled AND gates. The correctness of the garbling scheme can be easily verified given that
(and nothing is included in the garbled circuit for this gate). Each AND gate in the circuit is numbered topologically with a unique gate identifier gid ranging from 1 to C. For each AND gate in the circuit, with ingoing wires a, b and outgoing wire c, the garbler uses \(W_a^0, W_b^0\), R, and the gate’s identifier \(\mathsf{gid}\) to compute the garbled table \((T_{G}, T_{E})\) as well as the 0-label \(W_c^0\). This is done using a complicated procedure GbAnd that is defined in Fig. 1. The garbled circuit consists of all the garbled AND gates. The correctness of the garbling scheme can be easily verified given that
To evaluate a garbled circuit, starting with labels \(\{W_i\}_{i \in \mathsf{Inputs}}\) (where the evaluator does not necessarily know if \(W_i=W_i^0\) or \(W_i=W_i^1\)), the evaluator proceeds as follows. For an XOR gate with ingoing wires a, b and outgoing wire c, the evaluator computes  . For an AND gate with ingoing wires a, b and outgoing wire c, the evaluator computes \(W_c\) from \(W_a, W_b\), and the gate’s identifier gid using the corresponding garbled table (see Fig. 1). The final output is obtained using the least-significant bits of the output-wire labels.
. For an AND gate with ingoing wires a, b and outgoing wire c, the evaluator computes \(W_c\) from \(W_a, W_b\), and the gate’s identifier gid using the corresponding garbled table (see Fig. 1). The final output is obtained using the least-significant bits of the output-wire labels.
3 Attacking Implementations of the Half-Gates Scheme
Inspired by earlier work of Bellare et al.
[5], Zahur et al.
[46] proposed to instantiate the hash function H in the half-gates schemes with a construction based on fixed-key AES (modeled as a random permutation \(\pi \)). Namely, they suggested to implement H as  .
.
Here, we show an attack that violates privacy when H is implemented in this way. Our attack succeeds with probability \(O(p \cdot C/2^k)\), where p denotes the number of queries the attacker makes to \(\pi \), and C denotes the number of AND gates garbled. Importantly, the attack also extends to the multi-instance setting, where C then denotes the total number of AND gates garbled. Our attack does not contradict the security proof by Zahur et al. (or the later proof of Guo et al. [18]), who only claim that an attacker’s success probability cannot exceed this bound. Here we show an attack meeting that bound.
Note that Guo et al. [18] have previously shown an attack on the above instantiation of H that violates (tweakable) correlation robustness with probability \(O(pC/2^k)\) using p queries to \(\pi \) and C queries to a keyed version of H (i.e., the oracle). However, their attack explicitly relies on the attacker’s ability to make arbitrary H-queries and to obtain the full responses to those queries. Neither condition holds in our case, where the H-oracle queries are made by the honest garbler (and so are outside the control of the attacker) and the attacker is given the resulting garbled circuit but is not directly given the output of the oracle.
3.1 Attack Details
We describe the intuition behind the attack here, and give the details in Fig. 2. The attack works by recovering the hidden global shift R used by the circuit garbler; note that once this value is obtained, the evaluator can use R along with the rest of the garbled circuit to learn, for each wire of the circuit, which labels are associated with which bits and thus, using the input labels it was sent, determine the actual input of the garbler. We focus on showing how to learn R. Observe that for each AND gate in the circuit with ingoing wires a, b and outgoing wire c, the circuit evaluator learns one of the two wire labels \(W_a \in \{W_a^0, W_a^1\}\) as well as the value

from the garbled gate. (Note that j depends on the gate identifier gid of the gate but we leave that implicit.) Recall further that  . The circuit evaluator can thus compute
. The circuit evaluator can thus compute

A key observation is that \(p_b=0\) with probability 1/2! Thus, the circuit evaluator obtains, in expectation, C/2 values of the form  with \(W_a, j\) known. (We use \(H^+_a\) to refer to an \(H_a\)-value for which \(p_b=0\).)
with \(W_a, j\) known. (We use \(H^+_a\) to refer to an \(H_a\)-value for which \(p_b=0\).)
We now rely on the specific details of how H is implemented. When  we have
we have

If the circuit evaluator chooses a uniform \(W^*_i\), it can check whether
for some a. If so, then (as we justify below in our discussion of false positives) with constant probability it will be the case that

Once the evaluator finds a \(W^*_i\) for which Eq. (2) holds, it can then easily solve for R. (Note also that it is easy to verify a candidate value R; see the \(\mathsf{Check}\) routine in Fig. 2.) The time to carry out the attack is therefore dominated by the time to find a solution to Eq. (2). Assume for simplicity we have exactly C/2 values \(\{H^+_a\}\). Then if p uniform values \(W^*_1, \ldots , W^*_p\) are chosen, the probability that Eq. (2) holds for some i, a is \(p\cdot (C/2) \cdot 2^{-k}=p\cdot C/2^{k+1}\), as claimed.
Extension to the Multi-instance Setting. The above attack readily extends to the case when multiple circuits are (independently) garbled. In this case, C is simply the total number of AND gates garbled across all the circuits, and the attack recovers the shift R used for one of them.
False Positives. We now more carefully account for the number of queries to \(\pi \) made during the course of the attack. We argued above that after p evaluations of H (which requires p evaluations of \(\pi \)) the attack finds R with probability \(pC/2^{k+1}\). This analysis, however, does not account for false positives (i.e., a \(W^*\) for which Eq. (1) holds but Eq. (2) does not); note that every false positive incurs additional \(\pi \)-queries because it causes the \(\mathsf{Check}\) routine to be executed. We now show that we expect only \(\approx 2\) false positives for every true positive.
To see this, fix some particular a and associated  , and consider a uniform \(W^*\). There are three cases in which \(H(W^*, 0) = H_a\):
, and consider a uniform \(W^*\). There are three cases in which \(H(W^*, 0) = H_a\):
-
Case 1: \(p_b=0\) and
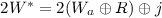 . This occurs with probability \(1/2^{k+1}\), and is a true positive.
. This occurs with probability \(1/2^{k+1}\), and is a true positive. -
Case 2: \(p_b=0\) and
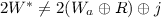 , yet \(H(W^*, 0) = H_a\). The probability of the first event is 1/2, and the probability of the second is slightly less than 1. But conditioned on these events, the third event occurs only if
, yet \(H(W^*, 0) = H_a\). The probability of the first event is 1/2, and the probability of the second is slightly less than 1. But conditioned on these events, the third event occurs only if 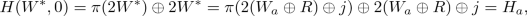
which occurs with probability roughly \(1/2^k\) since \(\pi \) is a random permutation. Overall, then, the probability of this case is also \(1/2^{k+1}\).
-
Case 3: \(p_b=1\), yet \(H(W,0)=H_a\). The probability of the first event is 1/2. But conditioned on this, the second event occurs only if
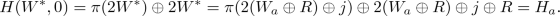
There are now two sub-cases. If
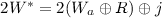 (which occurs with probability \(2^{-k}\)), then since R has min-entropy \(k-1\) the probability that the above equality holds is at most \(2^{-k+1}\). If
(which occurs with probability \(2^{-k}\)), then since R has min-entropy \(k-1\) the probability that the above equality holds is at most \(2^{-k+1}\). If 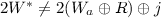 , then because \(\pi \) is a uniform permutation the probability that the above equality holds is at most \(1/(2^k-1)\). Overall, then, the probability of this case is \(1/2^{k+1} + 1/2^{2k} \approx 1/2^{k+1}\).
, then because \(\pi \) is a uniform permutation the probability that the above equality holds is at most \(1/(2^k-1)\). Overall, then, the probability of this case is \(1/2^{k+1} + 1/2^{2k} \approx 1/2^{k+1}\).
Summarizing: if the attack chooses p values \(W^*_1, \ldots , W^*_p\), we expect a true positive with probability \(pC/2^{k+1}\) and a false positive with probability \(pC/2^{k}\). Put differently, if we set p such that \(pC/2^{k+1} \approx 1\) then we expect to obtain R with probability \({\approx } 1\) while incurring only \({\approx } 2\) false positives. (Note that only O(1) queries to \(\pi \) are made during calls to \(\mathsf{Check}\), so the net result is only a small number of additional queries to \(\pi \).)
3.2 Attack Implementation
Here we describe our implementation of the attack described above.
Implementation Optimizations. Above, we focused on the complexity of the attack in terms of the number of queries to \(\pi \). In practice, though, the lookups in  also incur significant cost. For example, when \(C=2^{30}\) then
also incur significant cost. For example, when \(C=2^{30}\) then  requires roughly 24 GB to store; this impacts both the running time of the attack (due to cache misses on memory accesses) and its dollar cost (since more-powerful machines are needed). To mitigate this, we made the following optimizations:
requires roughly 24 GB to store; this impacts both the running time of the attack (due to cache misses on memory accesses) and its dollar cost (since more-powerful machines are needed). To mitigate this, we made the following optimizations:
-
1.
We first observe that it suffices to search for matches on \(H_a\)-values, and we thus store (only) those values in a hash table
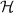 . Once a match on \(H_a\) is found, we can do a lookup in
. Once a match on \(H_a\) is found, we can do a lookup in 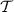 to find the corresponding \(j, W_a\) values. Moreover, we store only 64 bits of each \(H_a\) value in
to find the corresponding \(j, W_a\) values. Moreover, we store only 64 bits of each \(H_a\) value in  rather than the entire value. (This has only a small impact on the false-positive rate.) We store
rather than the entire value. (This has only a small impact on the false-positive rate.) We store  in memory, but can store
in memory, but can store  on disk since it will be accessed only O(1) times during the course of the attack.
on disk since it will be accessed only O(1) times during the course of the attack. -
2.
We implement the hash table
 using the “power of two choices” scheme
[34]. In this construction, every element is mapped to two random buckets (each capable of holding eight 64-bit strings); an element is inserted in the bucket with lower occupancy, and lookups simply access both buckets. To further reduce the cost of memory accesses, we modified the way hashing is done to make sure that elements are always mapped to buckets within 16 kB of each other in memory. In this way, both buckets for a given element will likely lie on the same page of memory, in which case both will be brought into the CPU cache when the memory access for the first bucket is made. This reduces the overall number of cache misses.
using the “power of two choices” scheme
[34]. In this construction, every element is mapped to two random buckets (each capable of holding eight 64-bit strings); an element is inserted in the bucket with lower occupancy, and lookups simply access both buckets. To further reduce the cost of memory accesses, we modified the way hashing is done to make sure that elements are always mapped to buckets within 16 kB of each other in memory. In this way, both buckets for a given element will likely lie on the same page of memory, in which case both will be brought into the CPU cache when the memory access for the first bucket is made. This reduces the overall number of cache misses.
Verifying the Attack Complexity. We implemented our attack (with the above optimizations) to verify its correctness and complexity. We ran the attack with label lengths \(k \in \{40, 48\}\) and number of gates C ranging from \(2^{20}\)–\(2^{28}\) until the true value R was found; the attack was run 100 times for each set of parameters. We found that the average number of false positives (which cause lookups in  and invocations of the \(\mathsf{Check}\) routine) was less than 5 in all cases. We plot the number of \(\pi \)-queries and the bound of \(2^{k+1}/C\) given by our analysis in Fig. 3a; our analysis is always within a factor of 2–3\(\times \) of the experimental results. We believe our use of a hash table (which can cause additional false positives) partially contributes to the additional overhead.
and invocations of the \(\mathsf{Check}\) routine) was less than 5 in all cases. We plot the number of \(\pi \)-queries and the bound of \(2^{k+1}/C\) given by our analysis in Fig. 3a; our analysis is always within a factor of 2–3\(\times \) of the experimental results. We believe our use of a hash table (which can cause additional false positives) partially contributes to the additional overhead.
Real-World Running Time and Cost. We estimate time and cost of implementing our attack when \(k=80\) and \(C=2^{30}\). For the purposes of this estimate, we assume customized preemptive instances with one Skylake CPU and 9 GB memory, each of which can be rented for $13.17/month on the Google Cloud Platform as of 2019. By extrapolating experimental results for smaller values of k (see Fig. 3b), we find that we can approximate the running time T of the attack (in milliseconds) as a function of k by the equation \(T(k) = 2^{0.989k-39.8}\). For \(k=80\), this gives \(T=2^{39.3}\) ms or \(267\) machine-months. Such an attack would cost about $\(3500\) to carry out. Since our attack can be fully parallelized, the wall-clock time can be made arbitrarily small using multiple instances, without increasing the cost. For example, using \(267\) instances the attack would finish in about a month.
4 Better Concrete Security for the Half-Gates Scheme
The attack in the previous section does not exploit any weakness in the half-gates scheme per se, but rather exploits a weakness in the way the underlying hash function is implemented. Building on the work of Guo et al. [18], we introduce here a security notion for hash functions called multi-instance tweakable circular correlation robustness (miTCCR) and show that this is an appropriate definition for analyzing the concrete security of the half-gates scheme.
4.1 Multi-instance TCCR
Our definition of miTCCR differs from the related notion formalized by Guo et al. in two respects. First, we consider an attacker who is given access to multiple (independently keyed) functions, rather than just one. Second, we explicitly allow the concrete security bound to depend on the maximum number of times \(\mu \) an attacker repeats any particular tweak.
Given a function \(H: \mathcal {W} \times \mathcal {T} \rightarrow \mathcal {W} \) (that depends on an ideal cipher E), define  . Let
. Let  denote the set of functions from
denote the set of functions from  to \(\mathcal {W} \).
to \(\mathcal {W} \).
Definition 3
Given a function \(H^E: \mathcal {W} \times \mathcal {T} \rightarrow \mathcal {W} \), a distribution  on \(\mathcal {W} \), and a distinguisher \(D \), define
on \(\mathcal {W} \), and a distinguisher \(D \), define

where both probabilities are also over choice of E and we require that
-
1.
\(D \) never queries both (w, i, 0) and (w, i, 1) to the same oracle (for any w, i).
-
2.
For all \(i\in \mathcal {T} \), the number of queries (across all oracles) of the form \((\star ,i,\star )\) is at most \(\mu \).
We say H is \((p, q, u, \mu , \rho , \varepsilon )\)-\(\text {miTCCR}\), if for all distinguishers \(D \) making at most p queries to E and at most q queries (in total) to its other oracles, and all distributions  with min-entropy at least \(\rho \), we have
with min-entropy at least \(\rho \), we have  .
.
We recover the definition from Guo et al. if we set \(u=1\) and \(\mu = |\mathcal {T} |\).
The concrete security of the half-gates scheme is directly related to the concrete security (in the sense of \(\text {miTCCR}\)) of the underlying hash function used.
Theorem 1
Let H be \((p, 2C, u, u, k-1, \varepsilon )\)-\(\text {miTCCR}\). Then the garbling scheme \(\mathsf {HalfGates} ^H\) is \((p, u, C, \varepsilon )\)-private.
A proof of the above follows along the same lines as the proof of the more general result we show later (cf. Theorem 3), so we omit it.
The challenge is thus to design a hash function with good concrete security in the sense of miTCCR. We remark that, as one might expect, a random oracle is one such candidate; see Appendix B. However, as discussed extensively by Guo et al. [18], it is not trivial to use a random oracle when implementing the half-gates scheme: there is a significant performance penalty when instantiating H using a cryptographic hash function like SHA-256 or SHA-3 (see also Table 1), and indifferentiable constructions of a random oracle from an ideal cipher E that are both efficient and have good concrete security are not known. (In particular, work of Gauravaram et al. [16] shows a construction using two calls to E with birthday-bound security; the construction we show in the next section is both more efficient and has better concrete security in the sense of \(\text {miTCCR}\).)
4.2 Designing a Hash Function with Better Concrete Security
We construct (from an ideal cipher  ) a hash function with good concrete security in the sense of miTCCR. Specifically, define
) a hash function with good concrete security in the sense of miTCCR. Specifically, define  as
as

where \(\sigma \) is a linear orthomorphism. (We say  is linear if
is linear if  for all
for all  . It is an orthomorphism if it is a permutation, and the function \(\sigma '\) given by
. It is an orthomorphism if it is a permutation, and the function \(\sigma '\) given by  is also a permutation.) As shown by Guo et al.
[18], \(\sigma \) can be efficiently instantiated as
is also a permutation.) As shown by Guo et al.
[18], \(\sigma \) can be efficiently instantiated as  where \(x_L\) and \(x_R\) are the left and right halves of the input, respectively; in assembly code, this becomes
where \(x_L\) and \(x_R\) are the left and right halves of the input, respectively; in assembly code, this becomes  where \(\mathtt{mask}=1^{64}\Vert 0^{64}\). We have:
where \(\mathtt{mask}=1^{64}\Vert 0^{64}\). We have:
Theorem 2
If \(\sigma \) is a linear orthomorphism and \(E\) is modeled as an ideal cipher, then \(\widehat{\mathsf {MMO}}^{E} \) is \((p, q, u, \mu , \rho , \varepsilon )\)-\(\text {miTCCR}\), where
Proof
Our proof uses the H-coefficient technique [10, 36], which we review in Appendix D (specialized for our proof). Fix a deterministic distinguisher \(D \) making queries to \(u+1\) oracles. The first is the ideal cipher (and its inverse); in the real world, the remaining oracles are of the form

(for u independent keys \(R_1,\ldots ,R_u\) sampled from  ), but in the ideal world they are u independent random functions from
), but in the ideal world they are u independent random functions from  to
to  . Following the notation from Appendix D, denote the transcript of D’s interaction by
. Following the notation from Appendix D, denote the transcript of D’s interaction by  We only consider attainable transcripts. For
We only consider attainable transcripts. For  define
define  . Clearly,
. Clearly,  .
.
We say a transcript  is bad if:
is bad if:
-
(B-1) There is a query
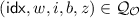 and a query of the form
and a query of the form 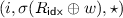 or of the form
or of the form 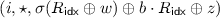 in
in 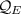 .
. -
(B-2) There are distinct queries \((\mathsf{idx}, w, i, b, z)\),
 using the same “tweak” i such that
using the same “tweak” i such that 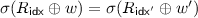 or
or 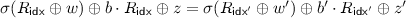 .
.
We bound the probabilities of the above events in the ideal world. Consider (B-1). Imagine that first all the oracles are chosen (which defines  ) and then the keys
) and then the keys  are chosen. Fix some
are chosen. Fix some  . It is immediate that
. It is immediate that

since the min-entropy of  is \(\rho \). Moreover,
is \(\rho \). Moreover,

by linearity of \(\sigma \). Now, note that:
-
When \(b=0\), the above probability is at most \(\big |\mathcal {Q} _E [i]\big | \cdot 2^{-\rho }\) since \(\sigma \) is a permutation and the min-entropy of
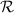 is \(\rho \).
is \(\rho \). -
When \(b=1\), the above probability is also at most \(\big |\mathcal {Q} _E [i]\big |\cdot 2^{-\rho }\) since \(\sigma \) is an orthomorphism and the min-entropy of
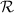 is \(\rho \).
is \(\rho \).
Therefore,

We next consider (B-2). For fixed \(i\in \{0,1\}^L\), consider a pair of distinct queries \((\mathsf{idx}, w, i, b, z)\),  . If \(\mathsf{idx} \ne \mathsf{idx} '\), we have
. If \(\mathsf{idx} \ne \mathsf{idx} '\), we have

and

as in the discussion of (B-1). If \(\mathsf{idx} =\mathsf{idx} '\), then  is not possible. Furthermore, with
is not possible. Furthermore, with  ,
,


using the fact that  are uniform and independent. Thus, for any pair of queries in
are uniform and independent. Thus, for any pair of queries in  , the probability that (B-2) holds is at most \(2/2^{\rho }\). If we let \(C_i \le \mu \) denote the number of queries in
, the probability that (B-2) holds is at most \(2/2^{\rho }\). If we let \(C_i \le \mu \) denote the number of queries in  using tweak i, then
using tweak i, then

Summarizing, the probability of a bad transcript in the ideal world is at most \(\frac{2\mu p}{2^\rho }+\frac{(\mu -1)\cdot q}{2^{\rho }}\).
Fix a good transcript  . The probability that the ideal world is consistent with this transcript is given by Eq. (7). The probability that the real world is consistent with this transcript is
. The probability that the ideal world is consistent with this transcript is given by Eq. (7). The probability that the real world is consistent with this transcript is

We can express the numerator of the above as

Note that  iff
iff  , i.e.,
, i.e.,

Since the transcript is good, there is no query of the form  in \(\mathcal {Q} _E \) (since (B-1) does not occur), nor is
in \(\mathcal {Q} _E \) (since (B-1) does not occur), nor is  determined by the fact that
determined by the fact that  (since (B-2) does not occur). Similarly, there is no query of the form
(since (B-2) does not occur). Similarly, there is no query of the form  in \(\mathcal {Q} _E \) (since (B-1) does not occur), nor is
in \(\mathcal {Q} _E \) (since (B-1) does not occur), nor is  determined by the fact that
determined by the fact that  for all \(\ell <j\) (since (B-2) does not occur). Thus, for all j we have
for all \(\ell <j\) (since (B-2) does not occur). Thus, for all j we have

It follows that

and so the probability that the real world is consistent with the transcript is at least the probability that the ideal world is consistent with the transcript. This completes the proof.
Using Shorter Wire Labels. Our construction above gives a hash function  , where L is the block length and key length of the underlying cipher E. In some applications of the half-gates scheme, one may prefer using wire labels of length \(k < L\). This is easily done by defining
, where L is the block length and key length of the underlying cipher E. In some applications of the half-gates scheme, one may prefer using wire labels of length \(k < L\). This is easily done by defining  as
as
where \([z]_k\) denotes the k least-significant bits of z. It is not hard to see that if H is \((p, q, u, \mu , \rho , \varepsilon )\)-\(\text {miTCCR}\) then so is \(H'\). (Of course, for \(H'\) it must be the case that \(\rho \le k\).)
Putting Everything Together. Say \(\widehat{\mathsf {MMO}}^{E} \) is used in the half-gates scheme with k-bit wire labels (as discussed above). Theorems 1 and 2 then imply that the resulting garbling scheme is \((p, u, C, \varepsilon )\)-private with
Taking \(u=1\) (i.e., looking at the single-instance setting), we have \(\varepsilon =p/2^{k-2}\), which is independent of the circuit size C and optimal up to a (small) constant. When \(u>1\), however, security degrades linearly in u; since u can be \(\varTheta (C)\), the security bound can be as bad as \(O((pC+C^2)/2^k)\) in the multi-instance setting. We show in the next section how to rectify this.
5 Achieving Better Multi-instance Security
As discussed at the end of the previous section, our new hash function gives an optimal concrete-security bound for the half-gates scheme in the single-instance setting. In the multi-instance setting, however, the security bound degrades as the number of instances increases.
Looking at our construction and the proof of miTCCR security (Theorem 2), we observe that the fundamental reason for the poor security bound in the multi-instance case is that \(\mu \) (namely, the number of times a given “tweak” may be re-used; cf. Definition 3) can be as large as u (the number of circuits being garbled). Tracing back to the half-gates scheme, we see that this is because the scheme always assigns sequential gate identifiers (gids) starting at 1 to the AND gates in a circuit, and so in particular each circuit that is garbled will at least use the “tweak” \(i=1\). We fix this issue by modifying the scheme so that it instead numbers the gates sequentially beginning at a random starting point determined by the garbler (and sent to the evaluator along with the garbled circuit). That is, the only changes with respect to Fig. 1 are that (1) in Garble, the initial value of gid is a uniform L-bit string, and (2) the initial value of gid is included in \(\mathsf{GC}\). We denote the modified scheme by \(\widehat{\mathsf {HalfGates}}\). To analyze the resulting construction, we start with the following lemma.
Lemma 1
Fix integers L, q, an integer \(u\le q\), and a sequence of positive integers \((q_1,\ldots ,q_u)\) with \(\sum _i q_i = q\). Consider the following experiment involving a set of \(2^L\) bins and q balls: for each \(i\in [u]\), \(q_i\) balls are placed in consecutive bins (wrapping around modulo \(2^L\)), where the initial bin is uniform. If \(\mu ^*\) is the random variable denoting the maximum number of balls in any bin, then
Proof
Consider some \(\mu \) sequences of balls, i.e., the \(i_1\)th, ..., \(i_\mu \)th, and consider the event that there is a \(k\in \{0,1\}^L\) such that every one of those sequences hits the kth bin. It can be seen that the probability is
Since \(\mu ^*\) is the maximum number of balls in any of the \(2^L\) bins, we have
Observing that
we have
Therefore,
This complete the proof. \(\square \)
With the above in place, we now prove:
Theorem 3
Let H be \((p, 2C, u, \mu , k-1, \varepsilon )\)-\(\text {miTCCR}\). Then the garbling scheme \(\widehat{\mathsf {HalfGates}}^H\) is \((p, u, C, \varepsilon ')\)-private, where
Proof
We describe a simulator  that takes as input a circuit f and an output y, and generates a simulated garbled circuit, input-wire labels, and the decoding table. See below for details.
that takes as input a circuit f and an output y, and generates a simulated garbled circuit, input-wire labels, and the decoding table. See below for details.

Fix some \(\{(f^i, x^i)\}_{i \in [u]}\). We now show indistinguishability between the two distributions in Definition 2. To do so, we consider a sequence of hybrid distributions.
Ideal. Here, we run  for \(i\in [u]\).
for \(i\in [u]\).
\(\mathbf{Hybrid}_2\). Here, we run  for \(i\in [u]\), where
for \(i\in [u]\), where  is defined below. Intuitively, the description of
is defined below. Intuitively, the description of  is from the perspective of the garbler (who knows the \(\{W^0_i\}\)), while that of
is from the perspective of the garbler (who knows the \(\{W^0_i\}\)), while that of  is from the perspective of the evaluator (who knows the \(\{W^{v_i}_i\}\) only); the distribution of the outputs remains the same.
is from the perspective of the evaluator (who knows the \(\{W^{v_i}_i\}\) only); the distribution of the outputs remains the same.

We claim that distribution \(\mathbf{Hybrid}_2\) is identical to distribution \(\mathbf{Ideal}\). This is because the values \(((\textsf {gid} ^*, \mathsf{GC}), \{W^0_i\}_{i\in \mathsf{Inputs}})\) in \(\mathbf{Hybrid}_1\) and the corresponding values \(((\textsf {gid} ^*, \mathsf{GC}), \{W^{v_i}_i\}_{i\in \mathsf{Inputs}})\) in Ideal are all uniform, and in both distributions we have

where we slightly abuse notation and let \(\mathsf{lsb} (W_1,\ldots ,W_n)=\mathsf{lsb} (W_1),\ldots ,\mathsf{lsb} (W_n)\).
\(\mathbf{Hybrid}_3\). Here, we run  for \(i\in [u]\), where
for \(i\in [u]\), where  is defined below.
is defined below.  is the same as
is the same as  except that it uses oracles
except that it uses oracles  in place of the random function \(\mathsf{Rand}\), and it computes values \(\{W^{\bar{v}}\}\) that do not affect the output.
in place of the random function \(\mathsf{Rand}\), and it computes values \(\{W^{\bar{v}}\}\) that do not affect the output.

Let \(\mu ^*\) denote the maximum frequency of any tweak used as the input to  , across all u executions of
, across all u executions of  . We claim that no distinguisher D making at most p queries to E can distinguish between \(\mathbf{Hybrid}_2\) and \(\mathbf{Hybrid}_3\) with probability better than \(\varepsilon + \Pr [\mu ^* > \mu ]\). Indeed, we can easily reduce any such distinguisher to a distinguisher against H (in the sense of miTCCR) that respects the bound \(\mu \) on the number of times a tweak may be repeated so long as \(\mu ^* \le \mu \). Note further that Lemma 1 implies \(\Pr [\mu ^* > \mu ] \le \frac{(2C)^{\mu +1}}{(\mu +1)!\times 2^{\mu L}}\).
. We claim that no distinguisher D making at most p queries to E can distinguish between \(\mathbf{Hybrid}_2\) and \(\mathbf{Hybrid}_3\) with probability better than \(\varepsilon + \Pr [\mu ^* > \mu ]\). Indeed, we can easily reduce any such distinguisher to a distinguisher against H (in the sense of miTCCR) that respects the bound \(\mu \) on the number of times a tweak may be repeated so long as \(\mu ^* \le \mu \). Note further that Lemma 1 implies \(\Pr [\mu ^* > \mu ] \le \frac{(2C)^{\mu +1}}{(\mu +1)!\times 2^{\mu L}}\).
\(\mathbf{Hybrid}_4\). Here, we run  for \(i\in [u]\), where
for \(i\in [u]\), where  is defined below.
is defined below.  is identical to
is identical to  except that \(v_i\) is always set to 0 and
except that \(v_i\) is always set to 0 and  is expanded to
is expanded to  . It is immediate that distributions \(\mathbf{Hybrid}_3\) and \(\mathbf{Hybrid}_4\) are identical.
. It is immediate that distributions \(\mathbf{Hybrid}_3\) and \(\mathbf{Hybrid}_4\) are identical.

One may observe that \(\mathbf{Hybrid}_4\) is identical to the real-world distribution that is obtained by running \(\widehat{\mathsf {HalfGates}}^H(f^i)\) and then including the input-wire labels corresponding to \(x^i\). This completes the proof. \(\square \)
6 Concrete Security and Efficiency
Using Theorems 2 and 3 we see that when we instantiate  with \(\widehat{\mathsf {MMO}}^{E}\), the overall garbling scheme is \((p, u, C, \varepsilon )\)-private, with
with \(\widehat{\mathsf {MMO}}^{E}\), the overall garbling scheme is \((p, u, C, \varepsilon )\)-private, with
Above, \(k \le L\) denotes the length of the wire labels and is chosen as part of the implementation, while \(\mu \) is a free parameter that can be set to optimize the bound. The expression above can be separated into two terms: a term \(\mu p/2^{k-2}\) that represents the computational security (as it depends on the query complexity p of the attacker) and a term \(\frac{(\mu -1)\cdot C}{2^{k-2}} + \frac{(2C)^{\mu +1}}{(\mu +1)!\times 2^{\mu L}}\) that corresponds to statistical security. To illustrate, we consider two particular options assuming \(L=128\) (to match the case where AES-128 is the cipher E):
-
1.
\(k=80\), \(C\le 2^{43.5}\). The overall security bound here is optimized when \(\mu =1\), in which case
$$\varepsilon = \frac{p}{2^{78}}+\frac{2C^2}{2^{128}} \le \frac{p}{2^{78}}+2^{-40}.$$I.e., this gives 78-bit computational security and 40-bit statistical security.
-
2.
\(k=128\), \(C\le 2^{61}\). Now the overall security bound is maximized when \(\mu =2\), in which case
$$\varepsilon \le \frac{p}{2^{125}}+\frac{8\cdot C^3}{3\times 2^{256}}\le \frac{p}{2^{125}}+2^{-64}.$$I.e., this gives 125-bit computational security and 64-bit statistical security.
Optimizations. Compared to the hash function proposed by Zahur et al. [46], which uses fixed-key AES, evaluation of our hash function involves re-keying AES each time it is called. In our implementation, we apply the optimizations introduced by Gueron et al. [17] that allow us to do key scheduling using AES-NI instructions with pipelining. In our current implementation, we batch two key-scheduling operations for each gate. In fact, since the AES key being used to garble a given gate (which depends on the gid) is entirely predictable, we can batch more than two key-scheduling operations to achieve even better efficiency. Our optimized implementation will be made publicly available in EMP [43].
Performance. In Table 1 we evaluate the performance of different hash functions in the half-gates scheme. “Zahur et al.” refers to using \(\mathsf {HalfGates} \) with their proposed hash function; the other rows refer to using \(\widehat{\mathsf {HalfGates}}\) where we instantiate the hash function either with \(\widehat{\mathsf {MMO}}^E\) (using AES-128 as the ideal cipher E), or with SHA-256 or SHA-3 (as random oracles).
 . Reported rates are in \(10^6\) AND gates per second.
. Reported rates are in \(10^6\) AND gates per second.We see that compared to the work of Zahur et al., when using wire labels of the same length \(k=128\) our scheme achieves better concrete security and is equally efficient as long as the network bandwidth is below 2 Gbps (so the network communication is the bottleneck). When the network is faster, the throughput (i.e., number of gates per second) of our scheme is lower but only by about 35%. Compared to instantiations using cryptographic hash functions, we see that garbling using SHA-256 without SHA-NI is up to \(13\times \) slower than our AES-based solution in a fast network; even with SHA-NI, garbling is up to \(6{\times }\) slower. Compared to the instantiation using SHA-3, our AES-based construction is up to \(50\times \) faster. For completeness, we also show the running time of our scheme using \(k=88\), which provides roughly the same security as the 128-bit scheme of Zahur et al.. We observe that in this case our scheme is about 1.5\(\times \) faster in a 2 Gbps network, due to the shorter labels.
Notes
- 1.
- 2.
- 3.
References
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols. In: 22nd Annual ACM Symposium on Theory of Computing (STOC), pp. 503–513. ACM Press (1990)
Bellare, M., Bernstein, D.J., Tessaro, S.: Hash-function based PRFs: AMAC and its multi-user security. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 566–595. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_22
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Desai, A., Jokipii, E., Rogaway, P.: A concrete security treatment of symmetric encryption. In: 38th Annual Symposium on Foundations of Computer Science (FOCS), pp. 394–403. IEEE (1997)
Bellare, M., Hoang, V.T., Keelveedhi, S., Rogaway, P.: Efficient garbling from a fixed-key blockcipher. In: 2013 IEEE Symposium on Security and Privacy (S&P), pp. 478–492 (2013)
Bellare, M., Hoang, V.T., Rogaway, P.: Foundations of garbled circuits. In: 2012 ACM Conference on Computer and Communications Security (CCS), pp. 784–796. ACM Press (2012)
Bellare, M., Rogaway, P.: The exact security of digital signatures-how to sign with RSA and Rabin. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 399–416. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_34
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 247–276. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_10
Bose, P., Hoang, V.T., Tessaro, S.: Revisiting AES-GCM-SIV: multi-user security, faster key derivation, and better bounds. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_18
Chen, S., Steinberger, J.P.: Tight security bounds for key-alternating ciphers. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 327–350. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_19
Chen, W., Popa, R.A.: Metal: a metadata-hiding file-sharing system. In: Network and Distributed System Security Symposium. The Internet Society (2020)
Coron, J.-S.: Optimal security proofs for PSS and other signature schemes. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 272–287. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_18
Data61: Multi-Protocol SPDZ (2016). https://github.com/data61/MP-SPDZ
Doerner, J., Evans, D., Shelat, A.: Secure stable matching at scale. In: 2016 ACM Conference on Computer and Communications Security (CCS), pp. 1602–1613. ACM Press (2016)
Engineering Cryptographic Protocols Group: ABY - A Framework for Efficient Mixed-protocol Secure Two-party Computation (2015). https://github.com/encryptogroup/ABY
Gauravaram, P., Bagheri, N., Knudsen, L.R.: Building indifferentiable compression functions from the PGV compression functions. Des. Codes Cryptogr. 78(2), 547–581 (2014). https://doi.org/10.1007/s10623-014-0020-z
Gueron, S., Lindell, Y., Nof, A., Pinkas, B.: Fast garbling of circuits under standard assumptions. J. Cryptol. 31(3), 798–844 (2017). https://doi.org/10.1007/s00145-017-9271-y
Guo, C., Katz, J., Wang, X., Yu, Y.: Efficient and secure multiparty computation from fixed-key blockciphers. In: IEEE Symposium on Security and Privacy (S&P) (2020). https://eprint.iacr.org/2019/074
Hoang, V.T., Tessaro, S.: Key-alternating ciphers and key-length extension: exact bounds and multi-user security. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 3–32. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_1
Huang, Y., Evans, D., Katz, J., Malka, L.: Faster secure two-party computation using garbled circuits. In: 2011 USENIX Security Symposium. USENIX Association (2011)
Huang, Y., Katz, J., Evans, D.: Efficient secure two-party computation using symmetric cut-and-choose. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 18–35. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_2
Huang, Y., Katz, J., Kolesnikov, V., Kumaresan, R., Malozemoff, A.J.: Amortizing garbled circuits. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 458–475. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_26
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_21
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 33–61. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_2
Kolesnikov, V., Mohassel, P., Rosulek, M.: FleXOR: flexible garbling for XOR gates that beats free-XOR. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 440–457. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_25
Kolesnikov, V., Schneider, T.: Improved garbled circuit: free XOR gates and applications. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008. LNCS, vol. 5126, pp. 486–498. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70583-3_40
Kreuter, B., Shelat, A., Shen, C.-H.: Billion-gate secure computation with malicious adversaries. In: 2012 USENIX Security Symposium, pp. 285–300. USENIX Association (2012)
Lindell, Y.: Fast cut-and-choose based protocols for malicious and covert adversaries. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_1
Lindell, Y., Pinkas, B.: An efficient protocol for secure two-party computation in the presence of malicious adversaries. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 52–78. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_4
Lindell, Y., Pinkas, B.: Secure two-party computation via cut-and-choose oblivious transfer. J. Cryptol. 25(4), 680–722 (2011). https://doi.org/10.1007/s00145-011-9107-0
Lindell, Y., Riva, B.: Cut-and-choose Yao-based secure computation in the online/offline and batch settings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 476–494. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_27
Lindell, Y., Riva, B.: Blazing fast 2PC in the offline/online setting with security for malicious adversaries. In: 2015 ACM Conference on Computer and Communications Security (CCS), pp. 579–590. ACM Press (2015)
Malkhi, D., Nisan, N., Pinkas, B., Sella, Y.: Fairplay—secure two-party computation system. In: 2004 USENIX Security Symposium, pp. 287–302. USENIX Association (2004)
Mitzenmacher, M.: The power of two choices in randomized load balancing. IEEE Trans. Parallel Distrib. Syst. 12(10), 1094–1104 (2001)
Naor, M., Pinkas, B., Sumner, R.: Privacy preserving auctions and mechanism design. In: Proceedings of the 1st ACM Conference on Electronic Commerce (EC), pp. 129–139. ACM (1999)
Patarin, J.: The “coefficients H” technique (invited talk). In: Avanzi, R.M., Keliher, L., Sica, F. (eds.) SAC 2008. LNCS, vol. 5381, pp. 328–345. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04159-4_21
Pinkas, B., Schneider, T., Smart, N.P., Williams, S.C.: Secure two-party computation is practical. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 250–267. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_15
Rindal, P.: libOTe: an efficient, portable, and easy to use oblivious transfer library. https://github.com/osu-crypto/libOTe
Shelat, A., Shen, C.-H.: Two-output secure computation with malicious adversaries. In: Paterson, K.G. (ed.) EUROCRYPT 2011, Part II. LNCS, vol. 6632, pp. 386–405. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_22
Tessaro, S.: Optimally secure block ciphers from ideal primitives. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 437–462. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_18
Unbound Tech: Protecting cryptographic signing keys and seed secrets with multi-party computation (2018). https://github.com/unbound-tech/blockchain-crypto-mpc
University of Bristol: APRICOT: advanced protocols for real-world implementation of computational oblivious transfers (2016). https://github.com/bristolcrypto/apricot
Wang, X., Malozemoff, A.J., Katz, J.: EMP-toolkit: efficient multiparty computation toolkit (2016). https://github.com/emp-toolkit
Yao, A.C.-C.: How to generate and exchange secrets. In: 27th Annual Symposium on Foundations of Computer Science (FOCS), pp. 162–167. IEEE (1986)
Zahur, S., Evans, D.: Obliv-C: a language for extensible data-oblivious computation. Cryptology ePrint Archive, Report 2015/1153 (2015). http://eprint.iacr.org/2015/1153
Zahur, S., Rosulek, M., Evans, D.: Two halves make a whole—reducing data transfer in garbled circuitsusing half gates. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 220–250. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_8
Zhu, R., Huang, Y., Katz, J., Shelat, A.: The cut-and-choose game and its application to cryptographic protocols. In: 2016 USENIX Security Symposium, pp. 1085–1100. USENIX Association (2016)
Acknowledgments
The authors thank Mike Rosulek for his helpful feedback on the paper. Work of Chun Guo was supported by the Program of Qilu Young Scholars (Grant No. 61580089963177) of Shandong University, the National Natural Science Foundation of China (Grant No. 61602276), and the Shandong Nature Science Foundation of China (Grant No. ZR2016FM22). Work of Jonathan Katz was supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), via 2019-1902070008. The views and conclusions herein are those of the authors and should not be interpreted as necessarily representing the official policies, expressed or implied, of ODNI, IARPA, or the U.S. Government. Work of Yu Yu was supported by the National Natural Science Foundation of China (Grant Nos. 61872236 and 61971192) and the National Cryptography Development Fund (Grant No. MMJJ20170209) and the National Key Research and Development Program of China (Grant No. 2018YFA0704701). Xiao Wang and Yu Yu also thank PlatON for their generous support.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Appendices
A (Multi-instance) Obliviousness and Authenticity
We recall definitions of obliviousness and authenticity for garbling schemes, adapted for the multi-instance setting. We then argue that our construction (with small modifications) achieves optimal security bounds for those notions.
1.1 A.1 Obliviousness
Obliviousness, informally, requires that \((\mathsf{GC},\{W^{x_i}_i\})\) reveal nothing about x, including f(x). This is formalized by requiring the existence of a simulator  that takes the circuit f and outputs values that are indistinguishable from \((\mathsf{GC},\{W^{x_i}_i\})\). In the multi-instance setting, we compare the output of
that takes the circuit f and outputs values that are indistinguishable from \((\mathsf{GC},\{W^{x_i}_i\})\). In the multi-instance setting, we compare the output of
 to the outputs obtained when independently garbling u circuits.
to the outputs obtained when independently garbling u circuits.
Definition 4
Garbling scheme  is \((p, u, C, \varepsilon )\) -oblivious if there is a simulator
is \((p, u, C, \varepsilon )\) -oblivious if there is a simulator  such that for any distinguisher D making p queries to \(E \) and any
such that for any distinguisher D making p queries to \(E \) and any  with \(\sum _i|f^i|=C\), we have
with \(\sum _i|f^i|=C\), we have

where both probabilities are also over choice of E.
Theorem 4
Let H be \((p, 2C, u, \mu , k-1, \varepsilon )\)-\(\text {miTCCR}\). Then the garbling scheme \(\widehat{\mathsf {HalfGates}}^H\) is \((p, u, C, \varepsilon ')\)-oblivious, where
We briefly justify the above bound. Observe that the simulator (for privacy) in the proof of Theorem 3 only uses the output y when computing the decoding information d. The simulator for obliviousness is identical except that it omits that step. The concrete security bound we obtain for obliviousness is thus (at most) the bound we prove for privacy.
1.2 A.2 Authenticity
Informally, authenticity requires that an attacker given \((\mathsf{GC},\{W^{x_i}_i\})\) should be unable to generate output-wire labels that cause the decoding algorithm to produce a valid output other than f(x). In the multi-instance generalization, the adversary succeeds if it can do this for any of u instances.
Definition 5
Garbling scheme  is \((p, u, C, m, \varepsilon )\) -authentic if for any
is \((p, u, C, m, \varepsilon )\) -authentic if for any  making p queries to \(E \) and any \(\{(f^i,x^i)\}_{i\in [u]}\) with \(\sum _i|f^i|=C\) and \(\sum _i m_i = m\), we have
making p queries to \(E \) and any \(\{(f^i,x^i)\}_{i\in [u]}\) with \(\sum _i|f^i|=C\) and \(\sum _i m_i = m\), we have

where the probability is also over choice of E.
In order to obtain authenticity, we need to modify \(\widehat{\mathsf {HalfGates}}\) slightly. Specifically, the decoding information \(d_i\) for the ith output wire will now be
Decoding of a label \(W_i\) on the ith output wire involves checking whether \(H(W_i, \textsf {gid})\) is equal to \(d_i[0]\) or \(d_i[1]\) (and returning \(\bot \) if neither holds). We refer to the resulting scheme as \(\overline{\mathsf {HalfGates}}\).
Theorem 5
Let H be \((p, 2C+m, u, \mu , k-1, \varepsilon )\)-\(\text {miTCCR}\). Then the garbling scheme \(\overline{\mathsf {HalfGates}}^H\) is \((p, u, C, m, \varepsilon ')\)-authentic, where
Our proof of the above proceeds in two steps: (1) we construct a simulator for the garbling scheme and show that the simulated garbled circuits are indistinguishable from real garbled circuits; (2) we show that the adversary cannot break authenticity for simulated garbled circuits. For (1), the simulator is almost identical to the privacy simulator we show in the proof of Theorem 3, except that it chooses uniform  and sets \(d_i=(H(W^0_i,\textsf {gid}), d_i[1])\) if \(y_i=0\), and chooses uniform
and sets \(d_i=(H(W^0_i,\textsf {gid}), d_i[1])\) if \(y_i=0\), and chooses uniform  and sets \(d_i=(d_i[0], H(W^0_i,\textsf {gid}))\) if \(y_i=1\). By an argument similar to that used in the proof of Theorem 3, any distinguisher making at most p queries to E can distinguish between simulated garbled circuits and real garbled circuits with probability at most \(\varepsilon +\frac{(2C+m)^{\mu +1}}{(\mu +1)!\times 2^{\mu L}}\). (The only difference is that we need to also count the oracle queries needed to decode.) For (2), since output labels are uniform and independent, the probability an attacker can violate authenticity is \(2^{-k}\).
and sets \(d_i=(d_i[0], H(W^0_i,\textsf {gid}))\) if \(y_i=1\). By an argument similar to that used in the proof of Theorem 3, any distinguisher making at most p queries to E can distinguish between simulated garbled circuits and real garbled circuits with probability at most \(\varepsilon +\frac{(2C+m)^{\mu +1}}{(\mu +1)!\times 2^{\mu L}}\). (The only difference is that we need to also count the oracle queries needed to decode.) For (2), since output labels are uniform and independent, the probability an attacker can violate authenticity is \(2^{-k}\).
B A Random Oracle as an \(\text {miTCCR}\) Hash Function
We show that a random oracle  (also) has good concrete security in the sense of \(\text {miTCCR}\). For completeness, we give the relevant definition (obtained by suitable modifying Definition 3). Recall that
(also) has good concrete security in the sense of \(\text {miTCCR}\). For completeness, we give the relevant definition (obtained by suitable modifying Definition 3). Recall that  .
.
Definition 6
Given a distribution  on
on  and a distinguisher \(D \), define
and a distinguisher \(D \), define

where both probabilities are also over choice of \(\mathsf {RO} \) and we require that
-
1.
\(D \) never queries both (x, i, 0) and (x, i, 1) to the same oracle (for any x, i).
-
2.
For all
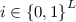 , the number of queries (across all oracles) of the form \((\star ,i,\star )\) is at most \(\mu \).
, the number of queries (across all oracles) of the form \((\star ,i,\star )\) is at most \(\mu \).
We say \(\mathsf {RO} \) is \((p, q, u, \mu , \rho , \varepsilon )\)-\(\text {miTCCR}\), if for all distinguishers \(D \) making at most p queries to \(\mathsf {RO} \) and at most q queries (in total) to its other oracles, and all distributions  with min-entropy at least \(\rho \), we have
with min-entropy at least \(\rho \), we have  .
.
Theorem 6
\(\mathsf {RO} \) is \((p, q, u, \mu , \rho , \varepsilon )\)-\(\text {miTCCR}\), where
Proof
Fix a deterministic distinguisher \(D \) making queries to \(u+1\) oracles. The first is  ; in the real world, the remaining u oracles are
; in the real world, the remaining u oracles are  , where the \(R_i\) are chosen independently from distribution \({\mathcal {R}}\), while in the ideal world they are u independent random functions with the correct domain and range. Denote the transcript of D’s interaction by
, where the \(R_i\) are chosen independently from distribution \({\mathcal {R}}\), while in the ideal world they are u independent random functions with the correct domain and range. Denote the transcript of D’s interaction by  , where \(\mathcal {Q} _\mathsf {RO} = \{(x_1,i_1, y_1), \ldots \}\) means that D queried \(\mathsf {RO} (x, i)\) and received response y.
, where \(\mathcal {Q} _\mathsf {RO} = \{(x_1,i_1, y_1), \ldots \}\) means that D queried \(\mathsf {RO} (x, i)\) and received response y.
An attainable transcript  is bad if:
is bad if:
-
(B-1) There is a query
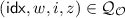 and a query of the form
and a query of the form 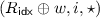 in
in  .
. -
(B-2) There exist two distinct queries \((\mathsf{idx}, w, i, z)\),
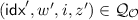 such that
such that 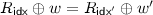 .
.
It is easy to show that

where \(\mathcal {Q} _\mathsf {RO} [i]:=\{(x, y):(x, i, y)\in \mathcal {Q} _\mathsf {RO} \}\) is defined similarly to Eq. (6). On the other hand, with \(C_i\) denoting the number of queries under i in  we have
we have
(using \(C_i\le \mu \)). Hence, the probability of a bad transcript in the ideal world is at most \(\frac{\mu p}{2^\rho }+\frac{(\mu -1)q}{2^{\rho +1}}\).
The remaining analysis resembles that of the proof of Theorem 2, giving

and so the probability that the real world is consistent with the transcript is the same as (7).
C Concrete Security of Using \(\mathsf {TMMO} ^{\pi }\) in \(\mathsf {HalfGates}\)
Here we show an attack on the half-gates scheme that runs in time \(O(2^k/C)\) when the underlying hash function is instantiated using the hash function from Guo et al. [18]. We concentrate on the single-instance setting for simplicity.
The construction \(\mathsf {TMMO}\) defined by Guo et al. is based on a single permutation \(\pi \), and is defined as

The attack is given in Figure 4. Essentially, the attack looks for a query \((H_{a}, j, W_a)\) and a permutation query \(\pi (X^*)=Y^*\) such that the evaluation of the former internally calls the latter. By construction, this means  , which justifies our checking condition in Step 3. Given a query \((H_{a}, j, W_a)\), for a uniform permutation query \(\pi (X^*)=Y^*\), the probability to have a match
, which justifies our checking condition in Step 3. Given a query \((H_{a}, j, W_a)\), for a uniform permutation query \(\pi (X^*)=Y^*\), the probability to have a match  is \(1/2^n\): the analysis is thus similar to that of Sect. 3.1.
is \(1/2^n\): the analysis is thus similar to that of Sect. 3.1.
D The H-Coefficient Technique
We provide a brief review of the H-coefficient technique, adapted from
[18]. Fix a deterministic distinguisher \(D\) that is given access to an ideal cipher  , as well as u oracles
, as well as u oracles  that can be of two types: in the real world they are functions that depend on u keys \(R_1,\ldots ,R_u\) sampled according to a distribution
that can be of two types: in the real world they are functions that depend on u keys \(R_1,\ldots ,R_u\) sampled according to a distribution  , while in the ideal world they are u functions chosen independently from
, while in the ideal world they are u functions chosen independently from  . We are interested in bounding the maximum difference between the probabilities that \(D\) outputs 1 in the real world vs. the ideal world, where the maximum is taken over all \(D \) making p queries to \(E\) and q queries to its other oracles.
. We are interested in bounding the maximum difference between the probabilities that \(D\) outputs 1 in the real world vs. the ideal world, where the maximum is taken over all \(D \) making p queries to \(E\) and q queries to its other oracles.
A transcript of D’s interaction takes the form  , where \(\mathcal {Q} _E = \{(k_1,x_1, y_1), \ldots \}\) records \(D\) ’s queries/answers to/from \(E \) or \(E ^{-1}\) (with \((k, x, y) \in \mathcal {Q} _E \) meaning \(E (k, x)=y\), regardless of whether the query was to \(E \) or \(E ^{-1}\)) and where
, where \(\mathcal {Q} _E = \{(k_1,x_1, y_1), \ldots \}\) records \(D\) ’s queries/answers to/from \(E \) or \(E ^{-1}\) (with \((k, x, y) \in \mathcal {Q} _E \) meaning \(E (k, x)=y\), regardless of whether the query was to \(E \) or \(E ^{-1}\)) and where  records \(D\) ’s queries/answers to/from the remaining oracles (where the tuple
records \(D\) ’s queries/answers to/from the remaining oracles (where the tuple  means that
means that  ). The keys \(\mathbf {R} =(R_1,\ldots ,R_u)\) are appended to the transcript as well (even though they are not part of D’s view) to facilitate the analysis: in the real world, these are the actual keys used by the oracles, whereas in the ideal world they are simply “dummy” keys sampled independently from
). The keys \(\mathbf {R} =(R_1,\ldots ,R_u)\) are appended to the transcript as well (even though they are not part of D’s view) to facilitate the analysis: in the real world, these are the actual keys used by the oracles, whereas in the ideal world they are simply “dummy” keys sampled independently from  . A transcript \(\mathcal {Q} \) is attainable for some fixed \(D\) if there exist some oracles such that the interaction of \(D\) with those oracles would lead to transcript \(\mathcal {Q} \).
. A transcript \(\mathcal {Q} \) is attainable for some fixed \(D\) if there exist some oracles such that the interaction of \(D\) with those oracles would lead to transcript \(\mathcal {Q} \).
Fix some \(D\). Let  denote the set of attainable transcripts, let
denote the set of attainable transcripts, let  and \(\Pr _\mathsf{ideal}[\cdot ]\) denote the probabilities of events in the real and ideal worlds, respectively, and let
and \(\Pr _\mathsf{ideal}[\cdot ]\) denote the probabilities of events in the real and ideal worlds, respectively, and let  denote the random variable corresponding to D’s transcript. The H-coefficient technique involves defining a partition of
denote the random variable corresponding to D’s transcript. The H-coefficient technique involves defining a partition of  into a “bad” set
into a “bad” set  and a “good” set
and a “good” set  , and then showing that
, and then showing that

and

The distinguishing advantage of \(D\) is then at most \(\varepsilon _1+\varepsilon _2\).
One of the key insights of the H-coefficient technique is that the value of \(\Pr _\mathsf{real}[\mathcal {Q} ^*=\mathcal {Q} ]/\Pr _\mathsf{ideal}[\mathcal {Q} ^*=\mathcal {Q} ]\) is equal to the ratio between the probability that the real-world oracles are consistent with \(\mathcal {Q} \) and the probability that the ideal-world oracles are consistent with \(\mathcal {Q} \). For each \(v\in \{0,1\}^L\), define \(\mathcal {Q} _E [v] \subseteq \mathcal {Q} _E \) as
The probability that an ideal cipher (with L-bit blocks and L-bit keys) is consistent with the p queries in \(\mathcal {Q} _E \) is exactly
where for integers \(1\le b\le a\), we set \((a)_b=a\cdot (a-1)\cdots (a-b+1)\), with \((a)_0=1\) by convention. For any attainable transcript  , the probability that the ideal world is consistent with \(\mathcal {Q} \) is always exactly
, the probability that the ideal world is consistent with \(\mathcal {Q} \) is always exactly
(We assume  , i.e., D always makes exactly q queries to its other oracles.) Bounding the distinguishing advantage of \(D\) thus reduces to bounding the probability that the real world is consistent with transcripts
, i.e., D always makes exactly q queries to its other oracles.) Bounding the distinguishing advantage of \(D\) thus reduces to bounding the probability that the real world is consistent with transcripts  .
.
Let \(E \vdash \mathcal {Q} _E \) denote the event that block cipher \(E \) is consistent with the queries/answers in \(\mathcal {Q} _E \), i.e., that \(E (v, x)=y\) for all \((v, x, y) \in \mathcal {Q} _E \). Since, in the real world, the behavior of the second oracle is completely determined by \(E \) and \(\mathbf {R} \), we can also write  to denote the event that cipher \(E \) and keys \(\mathbf {R} \) are consistent with the queries/answers in
to denote the event that cipher \(E \) and keys \(\mathbf {R} \) are consistent with the queries/answers in  . For a (good) transcript
. For a (good) transcript  , the probability that the real world is consistent with \(\mathcal {Q} \) is exactly
, the probability that the real world is consistent with \(\mathcal {Q} \) is exactly

(using independence of \(\mathbf {R} \) and \(E \)). We have \(\Pr [E \vdash \mathcal {Q} _E ] = 1/\prod _{v\in \{0,1\}^L}(2^L)_{|\mathcal {Q} _E [v]|}\) exactly as before. The crux of the proof thus reduces to showing a bound on  . Note that we can equivalently express this as
. Note that we can equivalently express this as  .
.
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Guo, C., Katz, J., Wang, X., Weng, C., Yu, Y. (2020). Better Concrete Security for Half-Gates Garbling (in the Multi-instance Setting). In: Micciancio, D., Ristenpart, T. (eds) Advances in Cryptology – CRYPTO 2020. CRYPTO 2020. Lecture Notes in Computer Science(), vol 12171. Springer, Cham. https://doi.org/10.1007/978-3-030-56880-1_28
Download citation
DOI: https://doi.org/10.1007/978-3-030-56880-1_28
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56879-5
Online ISBN: 978-3-030-56880-1
eBook Packages: Computer ScienceComputer Science (R0)




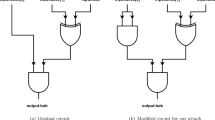
 takes as input a circuit f, and returns
takes as input a circuit f, and returns 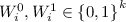 are the labels for the ith input wire, and d represents decoding information.
are the labels for the ith input wire, and d represents decoding information. takes as input a garbled circuit
takes as input a garbled circuit 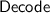 takes as input output-wire labels
takes as input output-wire labels 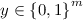 .
.

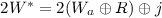 . This occurs with probability
. This occurs with probability 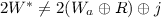 , yet
, yet 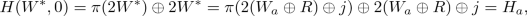
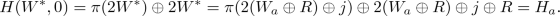
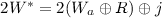 (which occurs with probability
(which occurs with probability 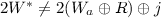 , then because
, then because 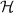 . Once a match on
. Once a match on 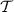 to find the corresponding
to find the corresponding  rather than the entire value. (This has only a small impact on the false-positive rate.) We store
rather than the entire value. (This has only a small impact on the false-positive rate.) We store  in memory, but can store
in memory, but can store 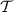 on disk since it will be accessed only O(1) times during the course of the attack.
on disk since it will be accessed only O(1) times during the course of the attack.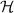 using the “power of two choices” scheme
[
using the “power of two choices” scheme
[
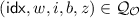 and a query of the form
and a query of the form 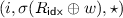 or of the form
or of the form 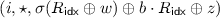 in
in 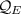 .
. using the same “tweak” i such that
using the same “tweak” i such that 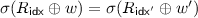 or
or 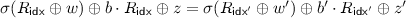 .
.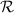 is
is  is
is 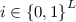 , the number of queries (across all oracles) of the form
, the number of queries (across all oracles) of the form 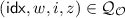 and a query of the form
and a query of the form 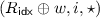 in
in  .
.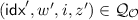 such that
such that 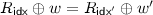 .
.
