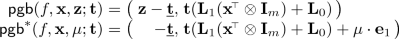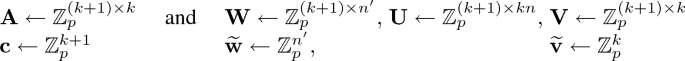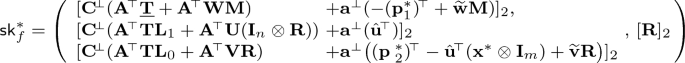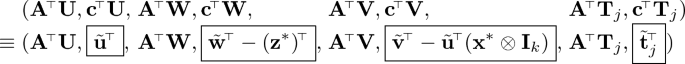Abstract
We present simple and improved constructions of public-key functional encryption (FE) schemes for quadratic functions. Our main results are:
-
an FE scheme for quadratic functions with constant-size keys as well as shorter ciphertexts than all prior schemes based on static assumptions;
-
a public-key partially-hiding FE that supports NC1 computation on public attributes and quadratic computation on the private message, with ciphertext size independent of the length of the public attribute.
Both constructions achieve selective, simulation-based security against unbounded collusions, and rely on the (bilateral) k-linear assumption in prime-order bilinear groups. At the core of these constructions is a new reduction from FE for quadratic functions to FE for linear functions.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In this work, we study functional encryption for quadratic functions. That is, we would like to encrypt a message \(\mathbf {z}\) to produce a ciphertext \( \textsf {ct}\), and generate secret keys \( \textsf {sk}_f\) for quadratic functions f, so that decrypting \( \textsf {ct}\) with \( \textsf {sk}_f\) returns \(f(\mathbf {z})\) while leaking no additional information about \(\mathbf {z}\). In addition, we want (i) short ciphertexts that grow linearly with the length of \(\mathbf {z}\), as well as (ii) simulation-based security against collusions, so that an adversary holding \( \textsf {ct}\) and secret keys for different functions \(f_1,f_2,\ldots \) learns nothing about \(\mathbf {z}\) beyond the outputs of these functions. Functional encryption for quadratic functions have a number of applications, including traitor-tracing schemes whose ciphertext size is sublinear in the total number of users [5, 6, 8, 11, 16]; obfuscation from simple assumptions [4, 13, 18, 19]; as well as privacy-preserving machine learning for neural networks with quadratic activation functions [21].
1.1 Our Results
We present new pairing-based public-key functional encryption (FE) schemes for quadratic functions, improving upon the recent constructions in [5, 12, 19, 20]. Our main results are:
-
A FE scheme for quadratic functions with constant-size keys, whose ciphertext size is shorter than those of all prior public-key schemes based on static assumptions [5, 12]; moreover, when instantiated over the BLS12-381 curve where \(|\mathbb {G}_2| = 2|\mathbb {G}_1|\), our ciphertext size basically matches that of the most efficient scheme in the generic group model [21] (see Fig. 1).
-
A partially-hiding FE that supports NC1 computation on public attributes \(\mathbf {x}\) and quadratic computation on the private message \(\mathbf {z}\); moreover, the ciphertext size grows linearly with \(\mathbf {z}\) and independent of \(\mathbf {x}\). The previous constructions in [13, 19] have ciphertext sizes that grow linearly with both \(\mathbf {z}\) and \(\mathbf {x}\).
Both constructions achieve selectiveFootnote 1, simulation-based security against unbounded collusions, and rely on the bilateral k-linear assumption in prime-order bilinear groups.
At the core of these constructions is a new reduction from public-key FE for quadratic functions to that for linear functions. The reduction relies on the (bilateral) k-Lin assumption, and blows up the input size by a factor k. Note that the trivial reduction blows up the input size by \(|\mathbf {z}|\). Our reduction is simpler and more direct than the previous reductions due to Lin [20] and Gay [12]: (i) we do not require function-hiding FE for linear functions, and (ii) our reduction works directly in the public-key setting. Thanks to (i), we can also decrease the secret key size from linear to constant.
Comparison with prior public-key functional encryption schemes for quadratic functions \(f : \mathbb {Z}_p^{n_1} \times \mathbb {Z}_p^{n_2} \rightarrow \mathbb {Z}_p\), as well as a concurrent work [14]. Note that \(| \textsf {sk}|\) ignores the contribution from the function f, which is “public”. Here, SXDH = 1-Lin, and bi-k-Lin (bilateral k-Lin) is a strengthening of k-Lin. 3-PDDH asserts that \([abc]_2\) is pseudorandom given \([a]_1,[b]_2,[c]_1,[c]_2\). In bilinear groups where \(|\mathbb {G}|_2 = 2|\mathbb {G}_1|\), we achieve \(| \textsf {ct}| = (2n_1 + 4n_2 + 2) |\mathbb {G}_1|\) under SXDH, bi 2-Lin, almost matching \(| \textsf {ct}| = (2n_1 + 4n_2 + 1) |\mathbb {G}_1|\) in RDGBP19.
1.2 Technical Overview
We proceed to provide an overview of our constructions. We rely on an asymmetric bilinear group \((\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e)\) of prime order p where \(e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\). We use \([\cdot ]_1,[\cdot ]_2,[\cdot ]_T\) to denote component-wise exponentiations in respective groups \(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T\) [10]. We use bold-face lower case to denote row vectors. The k-Lin assumption in \(\mathbb {G}_b\) asserts that
The bilateral k-Lin assumption is a strengthening of k-Lin, and asserts that
Note that bilateral 1-Lin is false, for the same reason DDH is false in symmetric bilinear groups.
FE for Quadratic Functions. Consider the class of quadratic functions over \(\mathbb {Z}_p^n \times \mathbb {Z}_p^n\) given by
where \(\mathbf {f}\in \mathbb {Z}_p^{n^2}\) is the coefficient vector. We will first mask \(\mathbf {z}_1,\mathbf {z}_2\) in the ciphertext using:
where the matrices
are specified in the master public key. Next, observe that
Following [12, 20], we will express the cross terms as a linear function evaluated on inputs of length O(kn); the key difference in this work is that the linear function can be derived from the master public key and \(\mathbf {f}\).
More precisely, we write

where the second equality uses the mixed-product property of the tensor product, which tells us that \((\mathbf {M}_1 \otimes \mathbf {M}_2) (\mathbf {M}_3 \otimes \mathbf {M}_4) = (\mathbf {M}_1 \mathbf {M}_3) \otimes (\mathbf {M}_2 \mathbf {M}_4)\), and \(\Vert \) denotes row vector concatenation. Multiplying both sides on the right by \(\mathbf {f}^{\!\scriptscriptstyle {\top }}\) and rearranging the terms yields:
where \(\mathbf {M}:= {\mathbf {A}_1 \otimes \mathbf {I}_{n} \atopwithdelims ()\mathbf {I}_{n} \otimes \mathbf {A}_2}\). As we mentioned earlier, the boxed term (= cross terms in (1))
corresponds to a linear computation where
-
the input \((\mathbf {s}_1 \otimes \mathbf {z}_2 \Vert \mathbf {y}_1 \otimes \mathbf {s}_2)\) has length O(kn);
-
the linear function \(\mathbf {M}\mathbf {f}^{\!\scriptscriptstyle {\top }}\) can be computed given \(\mathbf {f}\) and the matrices \(\mathbf {A}_1,\mathbf {A}_2\) in the public key.
The latter property pertaining to \(\mathbf {M}\mathbf {f}^{\!\scriptscriptstyle {\top }}\) is what allows us to significantly simplify the previous reductions in [12, 20], since there is nothing “secret” about the linear function \(\mathbf {M}\mathbf {f}^{\!\scriptscriptstyle {\top }}\). In the prior works, the linear function leaks information about the master secret key beyond what can be computed from the master public key.
In particular, we can use a public-key FE for linear functions (linear FE for short) [1, 3, 22] to compute (3). That is, we encrypt \([\mathbf {s}_1 \otimes \mathbf {z}_2 \Vert \mathbf {y}_1 \otimes \mathbf {s}_2]_1\), and generate a secret key for \([\mathbf {M}\mathbf {f}^{\!\scriptscriptstyle {\top }}]_2\). The linear FE schemes in [3, 22] extend readily to this setting where both the input and function are specified “in the exponent”; moreover, these schemes achieve selective, simulation-based security under the k-Lin assumption, with constant-size secret keys. The linear FE ciphertext would lie in \(\mathbb {G}_1\), whereas both \(\mathbf {M}\) and the secret key would lie in \(\mathbb {G}_2\). Note that in order to compute \([\mathbf {M}]_2\), we would also publish \([\mathbf {A}_1]_2\) in the public key. We present a self-contained description of our quadratic FE in Sect. A.
Security Overview. Security, intuitively, is fairly straight-forward:
-
First, observe that \([\mathbf {y}_1]_1,[\mathbf {y}_2]\) leaks no information about \(\mathbf {z}_1,\mathbf {z}_2\), thanks to the k-Lin assumption;
-
Next, we can simulate the ciphertext and secret key for the linear FE given \((\mathbf {s}_1 \otimes \mathbf {z}_2 \Vert \mathbf {y}_1 \otimes \mathbf {s}_2) \mathbf {M}\mathbf {f}^{\!\scriptscriptstyle {\top }}\), which we can rewrite as \((\mathbf {z}_1 \otimes \mathbf {z}_2) \mathbf {f}^{\!\scriptscriptstyle {\top }}- (\mathbf {y}_1 \otimes \mathbf {y}_2) \mathbf {f}^{\!\scriptscriptstyle {\top }}\). We can in turn compute the latter given just \(\mathbf {y}_1,\mathbf {y}_2\) and the output of the ideal functionality and therefore the linear FE ciphertext-key pair leaks no additional information about \(\mathbf {z}_1,\mathbf {z}_2\).
In the reduction, we would need to compute \([\mathbf {y}_1 \otimes \mathbf {y}_2]_2\) in order to simulate the secret key for the linear FE. This is something we can compute given either \(\mathbf {y}_1,[\mathbf {y}_2]_2\) or \([\mathbf {y}_1]_2,\mathbf {y}_2\). The latter along with publishing \([\mathbf {A}_1]_2\) in the public key is why we require the bilateral k-Lin assumption. For the most efficient concrete instantiation, we will use the bilateral 2-Lin assumption together with SXDH (i.e., 1-Lin), where we sample \(\mathbf {A}_1 \leftarrow \mathbb {Z}_p^{2 \times n}, \mathbf {A}_2 \leftarrow \mathbb {Z}_p^{1 \times n}\). We leave the question of basing quadratic FE solely on the standard k-Lin assumption as an open problem.
Extension to Partially Hiding FE. Our approach extends readily to partially hiding FE (PHFE) for the class
where f captures NC1 –more generally, any arithmetic branching program– computation on the public attribute \(\mathbf {x}\) and outputs a vector in \(\mathbb {Z}_p^{n^2}\). Note that FE for quadratic functions corresponds to the special case where f is a constant function (independent of \(\mathbf {x}\)). The idea behind the extension to PHFE is to replace \(\mathbf {f}^{\!\scriptscriptstyle {\top }}\) in (2) with \(f(\mathbf {x})\) (the decryptor can compute \(f(\mathbf {x})\) since \(\mathbf {x}\) is public), which yields:
To compute the new boxed term, we will rely on the partially-hiding linear FE scheme in [2] for the class
We can augment the construction to take into account the matrix \(\mathbf {M}\); some care is needed as the decryption algorithm only gets \([\mathbf {M}]_2\) and not \(\mathbf {M}\). In the ensuing scheme as with [2], the ciphertext size grows linearly with the message and independent of \(\mathbf {x}\), which we then inherit in our partially-hiding quadratic FE.
2 Preliminaries
Notations. We denote by \(s \leftarrow S\) the fact that s is picked uniformly at random from a finite set S. We use \(\approx _s\) to denote two distributions being statistically indistinguishable, and \(\approx _c\) to denote two distributions being computationally indistinguishable. We use lower case boldface to denote row vectors and upper case boldcase to denote matrices. We use \(\mathbf {e}_i\) to denote the i’th elementary row vector (with 1 at the i’th position and 0 elsewhere, and the total length of the vector specified by the context). For any positive integer N, we use [N] to denote \(\{1,2,\ldots ,N\}\).
The tensor product (Kronecker product) for matrices \(\mathbf {A}= (a_{i,j}) \in \mathbb {Z}^{\ell \times m}\), \(\mathbf {B}\in \mathbb {Z}^{n\times p}\) is defined as
The mixed-product property for tensor product says that
Arithmetic Branching Programs. A branching program is defined by a directed acyclic graph (V, E), two special vertices \(v_0, v_1 \in V\) and a labeling function \(\phi \). An arithmetic branching program (ABP), where p is a prime, computes a function \(f : \mathbb {Z}^n_p \rightarrow \mathbb {Z}_p\). Here, \(\phi \) assigns to each edge in E an affine function in some input variable or a constant, and f(x) is the sum over all \(v_0\)-\(v_1\) paths of the product of all the values along the path. We refer to \(|V|+|E|\) as the size of f. The definition extends in a coordinate-wise manner to functions \(f : \mathbb {Z}_p^n \rightarrow \mathbb {Z}_p^{n'}\). Henceforth, we use \(\mathcal {F}_{\mathsf {ABP},n,n'}\) to denote the class of ABP \(f : \mathbb {Z}_p^n \rightarrow \mathbb {Z}_p^{n'}\).
We note that there is a linear-time algorithm that converts any boolean formula, boolean branching program or arithmetic formula to an arithmetic branching program with a constant blow-up in the representation size. Thus, ABPs can be viewed as a stronger computational model than all of the above. Recall also that branching programs and boolean formulas correspond to the complexity classes LOGSPACE and NC1 respectively.
2.1 Prime-Order Bilinear Groups
A generator \(\mathcal {G}\) takes as input a security parameter \(1^\lambda \) and outputs a description \(\mathbb {G}:= (p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e)\), where p is a prime of \(\varTheta (\lambda )\) bits, \(\mathbb {G}_1\), \(\mathbb {G}_2\) and \(\mathbb {G}_T\) are cyclic groups of order p, and \(e : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is a non-degenerate bilinear map. We require that the group operations in \(\mathbb {G}_1\), \(\mathbb {G}_2\), \(\mathbb {G}_T\) and the bilinear map e are computable in deterministic polynomial time in \(\lambda \). Let \(g_1 \in \mathbb {G}_1\), \(g_2 \in \mathbb {G}_2\) and \(g_T = e(g_1,g_2) \in \mathbb {G}_T\) be the respective generators. We employ the implicit representation of group elements: for a matrix \(\mathbf {M}\) over \(\mathbb {Z}_p\), we define \([\mathbf {M}]_1:=g_1^{\mathbf {M}},[\mathbf {M}]_2:=g_2^{\mathbf {M}},[\mathbf {M}]_T:=g_T^{\mathbf {M}}\), where exponentiation is carried out component-wise. Also, given \([\mathbf {A}]_1,[\mathbf {B}]_2\), we let \(e([\mathbf {A}]_1,[\mathbf {B}]_2) = [\mathbf {A}\mathbf {B}]_T\). We recall the matrix Diffie-Hellman (MDDH) assumption on \(\mathbb {G}_1\) [10]:
Assumption 1
(\(\mathrm {MDDH}^{d}_{k,k'}\) Assumption). Let \(k,\ell ,d \in \mathbb {N}\). We say that the \(\mathrm {MDDH}^{d}_{k,\ell }\) assumption holds if for all PPT adversaries \(\mathcal {A}\), the following advantage function is negligible in \(\lambda \).

where \(\mathbb {G}:= (p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e) \leftarrow \mathcal {G}(1^\lambda )\), \(\mathbf {M}\leftarrow \mathbb {Z}_p^{\ell \times k}\), \(\mathbf {S}\leftarrow \mathbb {Z}_p^{k \times d}\) and \(\mathbf {U}\leftarrow \mathbb {Z}_p^{\ell \times d}\).
The MDDH assumption on \(\mathbb {G}_2\) can be defined in an analogous way. Escala et al. [10] showed that
with a tight security reduction. (In the setting where \(\ell \le k\), the \(\mathrm {MDDH}_{k,\ell }^d\) assumption holds unconditionally.)
The bilateral MDDH assumption is defined analogously with the advantage function:

2.2 Partially-Hiding Functional Encryption (PHFE)
We recall the notion of partially-hiding functional encryption [4, 7, 15, 22] for the function class
where \(h : \mathbb {Z}_p^{n'} \rightarrow \mathbb {Z}_p^{n''}\) is fixed and \(f \in \mathcal {F}_{\mathsf {ABP},n,n''}\) is specified by the secret key. We will be primarily interested in the settings \(h(\mathbf {z}) = \mathbf {z}\) and \(h(\mathbf {z}_1,\mathbf {z}_2) = \mathbf {z}_1 \otimes \mathbf {z}_2\), which generalize FE for linear functions and quadratic functions respectively.
Syntax. A partially-hiding functional encryption scheme (PHFE) consists of four algorithms:
-
\(\mathsf {Setup}(1^\lambda ,1^{n},1^{n'},h):\) The setup algorithm gets as input the security parameter \(1^\lambda \) and function parameters \(1^{n},1^{n'}\) and \(h : \mathbb {Z}_p^{n'} \rightarrow \mathbb {Z}_p^{n''}\). It outputs the master public key \( \textsf {mpk}\) and the master secret key \( \textsf {msk}\).
-
\(\mathsf {Enc}( \textsf {mpk},\mathbf {x},\mathbf {z}):\) The encryption algorithm gets as input \( \textsf {mpk}\) and message \(\mathbf {x},\mathbf {z}\in \mathbb {Z}_p^{n}\times \mathbb {Z}_p^{n'}\). It outputs a ciphertext \( \textsf {ct}_{(\mathbf {x},\mathbf {z})}\) with \(\mathbf {x}\) being public.
-
\(\mathsf {KeyGen}( \textsf {msk},f):\) The key generation algorithm gets as input \( \textsf {msk}\) and a function \(f \in \mathcal {F}_{\mathsf {ABP},n,n''}\). It outputs a secret key \( \textsf {sk}_f\) with f being public.
-
\(\mathsf {Dec}(( \textsf {sk}_f,f),( \textsf {ct}_{(\mathbf {x},\mathbf {z})},\mathbf {x}):\) The decryption algorithm gets as input \( \textsf {sk}_f\) and \( \textsf {ct}_{(\mathbf {x},\mathbf {z})}\) along with f and \(\mathbf {x}\). It outputs a value in \(\mathbb {Z}_p\).
Correctness. For all \((\mathbf {x},\mathbf {z}) \in \mathbb {Z}_p^{n}\times \mathbb {Z}_p^{n'}\) and \(f \in \mathcal {F}_{\mathsf {ABP},n,n''}\), we require
Remark 1
(Relaxation of correctness.). Our scheme only achieves a relaxation of correctness where the decryption algorithm takes an additional bound \(1^B\) (and runs in time polynomial in B) and outputs \(h(\mathbf {z}) f(\mathbf {x})^{\!\scriptscriptstyle {\top }}\) if the value is bounded by B. This limitation is also present in prior works on (IP)FE from DDH and bilinear groups [1, 3, 5, 20], due to the reliance on brute-force discrete log to recover the answer “from the exponent”. We stress that the relaxation only refers to functionality and does not affect security.
Security Definition. We consider semi-adaptive [9] (strengthening of selective), simulation-based security, which stipulates that there exists a randomized simulator \((\mathsf {Setup}^*,\mathsf {Enc}^*,\) \(\mathsf {KeyGen}^*)\) such that for every efficient stateful adversary \(\mathcal {A}\),

such that whenever \(\mathcal {A}\) makes a query f to \(\mathsf {KeyGen}\), the simulator \(\mathsf {KeyGen}^*\) gets f along with \(h(\mathbf {z}^*) f(\mathbf {x}^*)^{\!\scriptscriptstyle {\top }}\). We use \(\mathsf {Adv}^{\text {FE}}_{\mathcal {A}}(\lambda )\) to denote the advantage in distinguishing the real and ideal games.
3 Main Construction
In this section, we present our PHFE scheme for the class
The scheme is SA-SIM-secure under the bilateral k-Lin assumption and the \(k'\)-Lin assumption in \(\mathbb {G}_1,\mathbb {G}_2\) (for the most efficient concrete instantiation, we set \(k=2,k'=1\)). In our scheme, decryption actually computes \([(\mathbf {z}_1 \otimes \mathbf {z}_2) f(\mathbf {x})^{\!\scriptscriptstyle {\top }}]_T\), whereas the simulator only needs to get \([(\mathbf {z}_1 \otimes \mathbf {z}_2) f(\mathbf {x})^{\!\scriptscriptstyle {\top }}]_2\). Note that FE for quadratic functions is a special case of our PHFE (where f has the quadratic function hard-wired into it). We present a self-contained description of our quadratic FE in Sect. A.
As a building block, we rely on a SA-SIM-secure PHFE scheme \((\mathsf {Setup}_0,\mathsf {Enc}_0,\mathsf {KeyGen}_0,\mathsf {Dec}_0)\) for the class
parameterized by a matrix \([\mathbf {M}]_2 \in \mathbb {G}_1^{(k'n'_1 + k n'_2) \times n'_1 n'_2}\), where encryption gets \([\mathbf {z}]_1\) and the simulator gets \([\mathbf {z}\mathbf {M}f(\mathbf {x})^{\!\scriptscriptstyle {\top }}]_2\). We instantiate the building block in Sect. 4.
3.1 Our Scheme
-
\(\mathsf {Setup}(p,1^n,1^{n'_1},1^{n'_2})\): Run \(\mathbb {G}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e) \leftarrow \mathcal {G}(p)\). Sample
$$ \mathbf {A}_1 \leftarrow \mathbb {Z}_p^{k \times n'_1}, \mathbf {A}_2 \leftarrow \mathbb {Z}_p^{k' \times n'_2}, ( \textsf {mpk}_0, \textsf {msk}_0) \leftarrow \mathsf {Setup}_0(p,1^n,1^{k'n'_1 + k n'_2},[\mathbf {M}]_2) $$where
$$\begin{aligned} \mathbf {M}:= {\mathbf {A}_1 \otimes \mathbf {I}_{n'_2} \atopwithdelims ()\mathbf {I}_{n'_1} \otimes \mathbf {A}_2}\in \mathbb {Z}_p^{(k'n'_1 + k n'_2) \times n'_1n'_2} \end{aligned}$$and output
$$ \textsf {mpk}= \big (\,\mathbb {G},\,[\mathbf {A}_1]_1,\,[\mathbf {A}_1]_2,\,[\mathbf {A}_2]_2,\, \textsf {mpk}_0\,\big ) \quad \text{ and }\quad \textsf {msk}= \textsf {msk}_0 $$Observe that given \( \textsf {mpk}\), we can compute \([\mathbf {M}]_2\).
-
\(\mathsf {Enc}( \textsf {mpk},\mathbf {x},(\mathbf {z}_1,\mathbf {z}_2))\): Sample
$$\mathbf {s}_1 \leftarrow \mathbb {Z}_p^k, \mathbf {s}_0,\mathbf {s}_2 \leftarrow \mathbb {Z}_p^{k'}, \; \textsf {ct}_0 \leftarrow \mathsf {Enc}_0\bigl ( \textsf {mpk}_0,\mathbf {x},[\mathbf {s}_1 \otimes \mathbf {z}_2 \Vert (\underbrace{\mathbf {s}_1 \mathbf {A}_1 + \mathbf {z}_1}_{\mathbf {y}_1}) \otimes \mathbf {s}_2]_1 \bigr )$$and output
$$ \textsf {ct}= \big (\, [\underbrace{\mathbf {s}_1 \mathbf {A}_1 + \mathbf {z}_1}_{\mathbf {y}_1}]_1, \, [\underbrace{\mathbf {s}_2 \mathbf {A}_2 + \mathbf {z}_2}_{\mathbf {y}_2}]_2, \, \textsf {ct}_0\,\big ) $$ -
\(\mathsf {KeyGen}( \textsf {msk}, f)\): Output
$$ \textsf {sk}_{f} \leftarrow \mathsf {KeyGen}_0( \textsf {msk}_0,f) $$ -
\(\mathsf {Dec}( \textsf {sk}_f,f, \textsf {ct},\mathbf {x})\): Output
$$[(\mathbf {y}_1 \otimes \mathbf {y}_2) \cdot f(\mathbf {x})^{\!\scriptscriptstyle {\top }}]_T \cdot \Biggl ( \mathsf {Dec}_0( \textsf {sk}_f,(f,[\mathbf {M}]_2), \textsf {ct}_0,\mathbf {x}) \Biggr )^{-1}$$
Correctness. First, observe that we have

where the second equality uses the mixed-product property of the tensor product. Multiplying both sides of (4) by \(f(\mathbf {x})^{\!\scriptscriptstyle {\top }}\) and rearranging the terms yields:
Next, correctness of the underlying scheme tells us that
Correctness then follows readily.
3.2 Simulator
We start by describing the simulator.
-
\(\mathsf {Setup}^*(p,1^n,1^{n'_1},1^{n'_2})\): Run \(\mathbb {G}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e) \leftarrow \mathcal {G}(p)\). Sample
$$ \mathbf {A}_1 \leftarrow \mathbb {Z}_p^{k \times n'_1}, \mathbf {A}_2 \leftarrow \mathbb {Z}_p^{k' \times n'_2}, ( \textsf {mpk}^*_0, \textsf {msk}^*_0) \leftarrow \mathsf {Setup}^*_0(p,1^n,1^{k'n_1 + kn_2}) $$and output
$$ \textsf {mpk}^* = \big (\,\mathbb {G},\,[\mathbf {A}_1]_1,\,[\mathbf {A}_1]_2,\,[\mathbf {A}_2]_2,\, \textsf {mpk}^*_0\,\big ) \quad \text{ and }\quad \textsf {msk}^* = \textsf {msk}^*_0 $$ -
\(\mathsf {Enc}^*( \textsf {msk}^*_0,\mathbf {x}^*)\): Sample
$$\mathbf {y}_1 \leftarrow \mathbb {Z}_p^{n'_1}, \,\mathbf {y}_2 \leftarrow \mathbb {Z}_p^{n'_2}, \, \textsf {ct}_0^* \leftarrow \mathsf {Enc}_0^*( \textsf {msk}^*_0,\mathbf {x}^*) $$and output
$$ \textsf {ct}^* = \big (\, [\mathbf {y}_1]_1,\,[\mathbf {y}_2]_1,\, \textsf {ct}_0^*\,\big ) $$ -
\(\mathsf {KeyGen}^*( \textsf {msk}^*,\mathbf {x}^*,f,[\mu ]_2)\): Output
$$ \textsf {sk}_f \leftarrow \mathsf {KeyGen}_0^*( \textsf {msk}_0^*, \mathbf {x}^*, f, [(\mathbf {y}_1 \otimes \mathbf {y}_2) f(\mathbf {x}^*)]_T \cdot [\mu ]_2^{-1} ) $$
3.3 Proof of Security
We proceed via a series of games and we use \(\mathsf {Adv}_i\) to denote the advantage of \(\mathcal {A}\) in Game i. Let \(\mathbf {x}^*,(\mathbf {z}^*_1,\mathbf {z}^*_2)\) denote the semi-adaptive challenge.
Game 0. Real game.
Game 1. Replace \((\mathsf {Setup}_0,\mathsf {Enc}_0,\mathsf {KeyGen}_0)\) in \(\mathsf {Game}_0\) with \((\mathsf {Setup}^*_0,\mathsf {Enc}^*_0,\mathsf {KeyGen}^*_0)\) where
We have \(\mathsf {Game}_1 \approx _c \mathsf {Game}_0\), by security of the underlying PHFE scheme. The reduction samples
and upon receiving \(\mathbf {x}^*,(\mathbf {z}^*_1,\mathbf {z}^*_2)\) from \(\mathcal {A}\), sends
as the semi-adaptive challenge.
Game 2. Replace \( \textsf {sk}_f\) in Game 1 with

Here, we have \(\mathsf {Game}_2 \equiv \mathsf {Game}_1\), thanks to (5), which tells us that
Game 3. We replace \(\boxed {[\mathbf {s}_1 \mathbf {A}_1 + \mathbf {z}^*_1]_1}\) in \( \textsf {ct}^*\) in \(\mathsf {Game}_2\) with  where
where  . Then, we have \(\mathsf {Game}_3 \approx _c \mathsf {Game}_2\) via the bi-lateral k-Lin assumption. The assumption tells us that for all \(\mathbf {z}^*_1\),
. Then, we have \(\mathsf {Game}_3 \approx _c \mathsf {Game}_2\) via the bi-lateral k-Lin assumption. The assumption tells us that for all \(\mathbf {z}^*_1\),
where \(\mathbf {s}\leftarrow \mathbb {Z}_p^k, \mathbf {y}_1 \leftarrow \mathbb {Z}_p^{n'_1}\). Note that this holds even if \(\mathbf {z}^*_1\) is adaptively chosen after seeing \([\mathbf {A}_1]_1,[\mathbf {A}_1]_2\). The reduction then samples
sets \(\mathbf {y}_2 := \mathbf {s}_2 \mathbf {A}_2 + \mathbf {z}^*_2\), and uses the fact that in Games 2 and 3,
-
it can compute \( \textsf {mpk}^*, \textsf {ct}^*\) given \([\mathbf {A}_1]_1, [\mathbf {A}_1]_2, [\mathbf {y}_1]_1\) respectively;
-
it can sample \( \textsf {sk}_f\) by using \([\mathbf {y}_1]_2, \mathbf {y}_2\) to compute \([\mathbf {y}_1 \otimes \mathbf {y}_2]_2\).
Game 4. We replace \(\boxed {[\mathbf {s}_2 \mathbf {A}_2 + \mathbf {z}^*_2]_1}\) in \( \textsf {ct}^*\) in \(\mathsf {Game}_3\) with  where
where  . Then, we have \(\mathsf {Game}_4 \approx _c \mathsf {Game}_3\) via the \(k'\)-Lin assumption in \(\mathbb {G}_2\). Here, we use the fact that we can sample \( \textsf {sk}_f\) in Games 3 and 4 using \(\mathbf {y}_1, [\mathbf {y}_2]_2\) to compute \([\mathbf {y}_1 \otimes \mathbf {y}_2]_2\).
. Then, we have \(\mathsf {Game}_4 \approx _c \mathsf {Game}_3\) via the \(k'\)-Lin assumption in \(\mathbb {G}_2\). Here, we use the fact that we can sample \( \textsf {sk}_f\) in Games 3 and 4 using \(\mathbf {y}_1, [\mathbf {y}_2]_2\) to compute \([\mathbf {y}_1 \otimes \mathbf {y}_2]_2\).
Finally, note that \(\mathsf {Game}_4\) is exactly the output of the simulator.
4 Partially-Hiding FE for Linear Functions
In this section, we present our PHFE scheme for the class
parameterized by a matrix \([\mathbf {M}]_2\), where encryption gets \([\mathbf {z}]_1\), and the simulator gets \([\mathbf {z}\mathbf {M}f(\mathbf {x})^{\!\scriptscriptstyle {\top }}]_2\). In fact, we present a scheme for a more general setting where the matrix \([\mathbf {M}]_2\) is specified by the function corresponding to the secret key (that is, we allow a different \([\mathbf {M}]_2\) for each secret key, rather than the same matrix for all keys). The scheme is a somewhat straight-forward modification of that in [2]; some care is needed as the decryption algorithm only gets \([\mathbf {M}]_2\) and not \(\mathbf {M}\). This scheme achieves simulation-based semi-adaptive security under k-Lin. Most of the text in this section is copied verbatim from [2], with minor adaptations to account for \(\mathbf {M}\).
4.1 Partial Garbling Scheme
The partial garbling scheme [2, 17, 22] for \(\mathbf {z}f(\mathbf {x})^{\!\scriptscriptstyle {\top }}\) with \(f \in \mathcal {F}_{\mathsf {ABP},n,n'}\) is a randomized algorithm that on input f outputs an affine function in \(\mathbf {x},\mathbf {z}\) of the form:
where \(\mathbf {L}_0 \in \mathbb {Z}_p^{t \times mn},\mathbf {L}_1 \in \mathbb {Z}_p^{t \times m}\) depends only on f; \(\mathbf {t}\leftarrow \mathbb {Z}_p^t\) is the random coin and \(\underline{\mathbf {t}}\) consists of the last \(n'\) entries in \(\mathbf {t}\), such that given \((\mathbf {p}_{f,\mathbf {x},\mathbf {z}}, f, \mathbf {x})\), we can recover \(\mathbf {z}f(\mathbf {x})^{\!\scriptscriptstyle {\top }}\), while learning nothing else about \(\mathbf {z}\).
Lemma 1
(partial garbling [2, 17, 22]). There exists four efficient algorithms \((\mathsf {lgen},\mathsf {pgb}, \mathsf {rec},\mathsf {pgb}^*)\) with the following properties:
-
syntax: on input \(f \in \mathcal {F}_{\mathsf {ABP},n,n'}\), \(\mathsf {lgen}(f)\) outputs \(\mathbf {L}_0 \in \mathbb {Z}_p^{t \times mn},\mathbf {L}_1 \in \mathbb {Z}_p^{t \times m}\), and
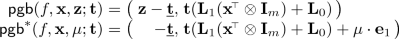
where \(\mathbf {t}\in \mathbb {Z}_p^t\) and \(\underline{\mathbf {t}}\) consists of the last \(n'\) entries in \(\mathbf {t}\) and m, t are linear in the size of f.
-
reconstruction: \(\mathsf {rec}(f,\mathbf {x})\) outputs \(\mathbf {d}^{\!\scriptscriptstyle {\top }}_{f,\mathbf {x}}\in \mathbb {Z}_p^{n'+ m}\) such that for all \(f,\mathbf {x},\mathbf {z},\mathbf {t}\), we have \( \mathbf {p}_{f,\mathbf {x},\mathbf {z}}\mathbf {d}^{\!\scriptscriptstyle {\top }}_{f,\mathbf {x}} = \mathbf {z}f(\mathbf {x})^{\!\scriptscriptstyle {\top }}\) where \(\mathbf {p}_{f,\mathbf {x},\mathbf {z}} = \mathsf {pgb}(f,\mathbf {x},\mathbf {z}; \mathbf {t})\).
-
privacy: for all \(f,\mathbf {x},\mathbf {z}\), we have \(\mathsf {pgb}(f,\mathbf {x},\mathbf {z};\mathbf {t}) \approx _s \mathsf {pgb}^*(f,\mathbf {x},\mathbf {z}f(\mathbf {x})^{\!\scriptscriptstyle {\top }};\mathbf {t})\) where the randomness is over \(\mathbf {t}\leftarrow \mathbb {Z}_p^t\).
4.2 Construction
Our scheme \(\varPi \) is similar to \(\mathrm{\Pi }_\mathsf {one}\) in [2], with the modifications marked using boxed terms. We rely on partial garbling to compute \(\mathsf {pgb}(f,\mathbf {x},\boxed {\mathbf {z}\mathbf {M}};\mathbf {t})\) instead of \(\mathsf {pgb}(f,\mathbf {x},\mathbf {z};\mathbf {t})\) “in the exponent” over \(\mathbb {G}_T\); applying the reconstruction algorithm (which requires knowing \(f,\mathbf {x}\) but not \(\mathbf {M}\)) then returns \([\boxed {\mathbf {z}\mathbf {M}} f(\mathbf {x})^{\!\scriptscriptstyle {\top }}]_T\).
-
\(\mathsf {Setup}(1^\lambda ,1^{n},1^{n'})\): Run \(\mathbb {G}= (p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e) \leftarrow \mathcal {G}(1^\lambda )\). Sample
$$ \mathbf {A}\leftarrow \mathbb {Z}_p^{k \times (k+1)} \quad \text{ and }\quad \mathbf {W}\leftarrow \mathbb {Z}_p^{(k+1)\times n'},\, \mathbf {U}\leftarrow \mathbb {Z}_p^{(k+1)\times kn},\, \mathbf {V}\leftarrow \mathbb {Z}_p^{(k+1)\times k} $$and output
$$ \textsf {mpk}= \big (\,\mathbb {G},\,[\mathbf {A}]_1,\,[\mathbf {A}\mathbf {W}]_1,\,[\mathbf {A}\mathbf {U}]_1,\,[\mathbf {A}\mathbf {V}]_1\,\big ) \quad \text{ and }\quad \textsf {msk}= \big (\,\mathbf {W},\,\mathbf {U},\,\mathbf {V}\,\big ). $$ -
\(\mathsf {Enc}( \textsf {mpk},(\mathbf {x},\mathbf {z}))\): Sample \(\mathbf {s}\leftarrow \mathbb {Z}_p^{k}\) and output
$$ \textsf {ct}_{\mathbf {x},\mathbf {z}} = \big (\, [\mathbf {s}\mathbf {A}]_1,\,[\mathbf {z}+ \mathbf {s}\mathbf {A}\mathbf {W}]_1,\, [\mathbf {s}\mathbf {A}\mathbf {U}(\mathbf {x}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_k) + \mathbf {s}\mathbf {A}\mathbf {V}]_1\,\big ) \quad \text{ and }\quad \mathbf {x}. $$Note that it is sufficient for \(\mathsf {Enc}\) to get \([\mathbf {z}]_1\).
-
\(\mathsf {KeyGen}( \textsf {msk},(f,[\mathbf {M}]_2))\): Run \((\mathbf {L}_1,\mathbf {L}_0) \leftarrow \mathsf {lgen}(f)\) where \(\mathbf {L}_1 \in \mathbb {Z}_p^{t\times mn},\mathbf {L}_0 \in \mathbb {Z}_p^{t\times m}\) (cf. Sect. 4.1). Sample \(\mathbf {T}\leftarrow \mathbb {Z}_p^{(k+1) \times t}\) and \(\mathbf {R}\leftarrow \mathbb {Z}_p^{k \times m}\) and output
$$ \textsf {sk}_{f,\mathbf {M}} = \big (\, [\underline{\mathbf {T}}+ \boxed {\mathbf {W}\mathbf {M}}]_2,\, [\mathbf {T}\mathbf {L}_1 + \mathbf {U}(\mathbf {I}_n\otimes \mathbf {R})]_2,\, [\mathbf {T}\mathbf {L}_0 + \mathbf {V}\mathbf {R}]_2,\, [\mathbf {R}]_2 \,\big ) \quad \text{ and }\quad (f,[\mathbf {M}]_2). $$where \(\underline{\mathbf {T}}\) refers to the matrix composed of the right most \(n'\) columns of \(\mathbf {T}\).
-
\(\mathsf {Dec}(( \textsf {sk}_{f,\mathbf {M}},(f,[\mathbf {M}]_2)),( \textsf {ct}_{\mathbf {x},\mathbf {z}},\mathbf {x}))\): On input key:
$$ \textsf {sk}_{f,\mathbf {M}} = \big (\, [\mathbf {K}_1]_2, [\mathbf {K}_2]_2, [\mathbf {K}_3]_2, [\mathbf {R}]_2 \,\big )\quad \text{ and }\quad (f,[\mathbf {M}]_2) $$and ciphertext:
$$ \textsf {ct}_{\mathbf {x},\mathbf {z}} = \big (\, [\mathbf {c}_0]_1,\,[\mathbf {c}_1]_1,\,[\mathbf {c}_2]_1 \,\big )\quad \text{ and }\quad \mathbf {x}$$the decryption works as follows:
-
1.
compute
$$\begin{aligned}{}[\mathbf {p}_1]_T = e([\mathbf {c}_1]_1,\boxed {[\mathbf {M}]_2}) \cdot e([\mathbf {c}_0]_1,[-\mathbf {K}_1]_2) \end{aligned}$$(6) -
2.
compute
$$\begin{aligned}{}[\mathbf {p}_2]_T = e([\mathbf {c}_0]_1,[\mathbf {K}_2 (\mathbf {x}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_m) + \mathbf {K}_3]_2) \cdot e([-\mathbf {c}_2]_1,[\mathbf {R}]_2) \end{aligned}$$(7) -
3.
run \(\mathbf {d}_{f,\mathbf {x}}\leftarrow \mathsf {rec}(f,\mathbf {x})\) (cf. Sect. 4.1), compute
$$\begin{aligned}{}[D]_T = [(\mathbf {p}_1 \Vert \mathbf {p}_2)\mathbf {d}^{\!\scriptscriptstyle {\top }}_{f,\mathbf {x}}]_T \end{aligned}$$(8)
-
1.
Correctness. For \( \textsf {ct}_{\mathbf {x},\mathbf {z}}\) and \( \textsf {sk}_{f,\mathbf {M}}\), we have
Here (11) follows from the fact that
and reconstruction of the partial garbling in (6); the remaining two equalities follow from:

in which we use the equality \((\mathbf {I}_n\otimes \mathbf {R})(\mathbf {x}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_m)=(\mathbf {x}^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_k)\mathbf {R}\). This readily proves the correctness.
Simulator. We describe the simulator. We defer the analysis to Sect. B.
-
\(\mathsf {Setup}^*(1^\lambda ,1^{n},1^{n'})\): Run \(\mathbb {G}= (p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e) \leftarrow \mathcal {G}(1^\lambda )\). Sample
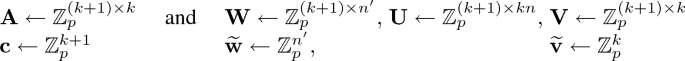
and output
$$\begin{aligned} \textsf {mpk}= & {} \big (\,\mathbb {G},\,[\mathbf {A}^{\!\scriptscriptstyle {\top }}]_1,\,[\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {W}]_1,\,[\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {U}]_1,\,[\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {V}]_1\,\big )\\ \textsf {msk}^*= & {} \big (\,\mathbf {W},\,\mathbf {U},\,\mathbf {V},\,\widetilde{\mathbf {w}},\, \widetilde{\mathbf {v}},\,\mathbf {c},\mathbf {C}^{\!\scriptscriptstyle {\perp }},\mathbf {A},\mathbf {a}^{\!\scriptscriptstyle {\perp }}\,\big ) \end{aligned}$$where \((\mathbf {A}| \mathbf {c})^{\!\scriptscriptstyle {\top }}(\mathbf {C}^{\!\scriptscriptstyle {\perp }}| \mathbf {a}^{\!\scriptscriptstyle {\perp }}) = \mathbf {I}_{k+1}\). Here we assume that \((\mathbf {A}| \mathbf {c})\) has full rank, which happens with probability \(1-1/p\).
-
\(\mathsf {Enc}^*( \textsf {msk}^*,\mathbf {x}^*)\): Output
$$ \textsf {ct}^* = \big (\, [\mathbf {c}^{\!\scriptscriptstyle {\top }}]_1,\,[\widetilde{\mathbf {w}}]_1,\, [\widetilde{\mathbf {v}}]_1\,\big ) \quad \text{ and }\quad \mathbf {x}^*. $$ -
\(\mathsf {KeyGen}^*( \textsf {msk}^*,\mathbf {x}^*,(f,[\mathbf {M}]_2),[\mu ]_2)\): Run
$$ (\mathbf {L}_1,\mathbf {L}_0) \leftarrow \mathsf {lgen}(f) \quad \text{ and }\quad ([\mathbf {p}^*_1]_2,[\mathbf {p}^*_2]_2) \leftarrow \mathsf {pgb}^*(f,\mathbf {x}^*,[\mu ]_2). $$Sample \(\mathbf {T}\leftarrow \mathbb {Z}_p^{(k+1) \times t}\), \(\hat{\mathbf {u}}\leftarrow \mathbb {Z}_p^{nm}\) and \(\mathbf {R}\leftarrow \mathbb {Z}_p^{k \times m}\) and output
$$\begin{aligned} \textsf {sk}^*_f = \big (\,\mathbf {C}^{\!\scriptscriptstyle {\perp }}\cdot \textsf {sk}^*_f[1] + \mathbf {a}^{\!\scriptscriptstyle {\perp }}\cdot \textsf {sk}^*_f[2] ,\,[\mathbf {R}]_2\,\big ) \quad \text{ and }\quad f \end{aligned}$$(12)where
$$\begin{aligned} \textsf {sk}^*_f[1]= & {} \big (\, [\mathbf {A}^{\!\scriptscriptstyle {\top }}\underline{\mathbf {T}}+ \mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {W}\mathbf {M}]_2,\, [\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {T}\mathbf {L}_1 + \mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {U}(\mathbf {I}_n\otimes \mathbf {R})]_2,\, [\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {T}\mathbf {L}_0 + \mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {V}\mathbf {R}]_2 \,\big ) \\ \textsf {sk}^*_f[2]= & {} \big (\, [-(\mathbf {p}_1^*)^{\!\scriptscriptstyle {\top }}+ \widetilde{\mathbf {w}}\mathbf {M}]_2,\, [ \hat{\mathbf {u}}^{\!\scriptscriptstyle {\top }}]_2,\, [(\mathbf {p}_2^*)^{\!\scriptscriptstyle {\top }}- \hat{\mathbf {u}}^{\!\scriptscriptstyle {\top }}(\mathbf {x}^* \otimes \mathbf {I}_m)+\widetilde{\mathbf {v}}\mathbf {R}]_2 \,\big ) \end{aligned}$$Here \(\underline{\mathbf {T}}\) refers to the matrix composed of the right most \(n'\) columns of \(\mathbf {T}\). That is,
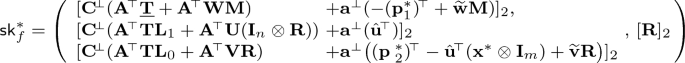
Notes
- 1.
We actually achieve semi-adaptive security [9], a slight strengthening of selective security.
References
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_33
Abdalla, M., Gong, J., Wee, H.: Functional encryption for attribute-weighted sums from k-Lin. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020. LNCS, vol. 12170, pp. 685–716. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56784-2_23
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_12
Ananth, P., Jain, A., Lin, H., Matt, C., Sahai, A.: Indistinguishability obfuscation without multilinear maps: new paradigms via low degree weak pseudorandomness and security amplification. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 284–332. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_10
Baltico, C.E.Z., Catalano, D., Fiore, D., Gay, R.: Practical functional encryption for quadratic functions with applications to predicate encryption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 67–98. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_3
Boneh, D., Sahai, A., Waters, B.: Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 573–592. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_34
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_16
Boneh, D., Waters, B.: A fully collusion resistant broadcast, trace, and revoke system. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.), ACM CCS 2006, pp. 211–220. ACM Press, October/November 2006
Chen, J., Wee, H.: Semi-adaptive attribute-based encryption and improved delegation for boolean formula. In: Abdalla, M., De Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 277–297. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10879-7_16
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Garg, S., Kumarasubramanian, A., Sahai, A., Waters, B.: Building efficient fully collusion-resilient traitor tracing and revocation schemes. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 121–130. ACM Press, October 2010
Gay, R.: A new paradigm for public-key functional encryption for degree-2 polynomials. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020. LNCS, vol. 12110, pp. 95–120. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45374-9_4
Gay, R., Jain, A., Lin, H., Sahai, A.: Indistinguishability obfuscation from simple-to-state hard problems: new assumptions, new techniques, and simplification. Cryptology ePrint Archive, Report 2020/764 (2020)
Gong, J., Qian, H.: Simple and efficient FE for quadratic functions. Cryptology ePrint Archive, Report 2020/1026 (2020)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Goyal, R., Koppula, V., Waters, B.: New approaches to traitor tracing with embedded identities. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11892, pp. 149–179. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36033-7_6
Ishai, Y., Wee, H.: Partial garbling schemes and their applications. In: Esparza, J., Fraigniaud, P., Husfeldt, T., Koutsoupias, E. (eds.) ICALP 2014. LNCS, vol. 8572, pp. 650–662. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43948-7_54
Jain, A., Lin, H., Matt, C., Sahai, A.: How to leverage hardness of constant-degree expanding polynomials overa \(\mathbb{R}\) to build \(i\cal{O}\). In: Ishai, Y., Rijmen, V. (eds.) Part I. LNCS, vol. 11476, pp. 251–281. Springer, Heidelberg (2019)
Jain, A., Lin, H., Sahai, A.: Simplifying constructions and assumptions for IO. IACR Cryptology ePrint Archive 2019:1252 (2019)
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 599–629. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_20
Ryffel, T., Pointcheval, D., Bach, F., Dufour-Sans, E., Gay, R.: Partially encrypted deep learning using functional encryption. In: Advances in Neural Information Processing Systems, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019, pp. 4519–4530 (2019)
Wee, H.: Attribute-hiding predicate encryption in bilinear groups, revisited. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 206–233. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_8
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Concrete Scheme for Quadratic Functions
We present a self-contained description of our functional encryption scheme for quadratic functions specified by \(\mathbf {f}\in \mathbb {Z}_p^{n_1 \times n_2}\) where
The scheme is SA-SIM-secure under the bilateral k-Lin assumption and the \(k'\)-Lin assumption in \(\mathbb {G}_1,\mathbb {G}_2\). For the most efficient concrete instantiation (cf. Fig. 1), we set \(k=2,k'=1\).
-
\(\mathsf {Setup}(p,1^{n_1},1^{n_2})\): Run \(\mathbb {G}= (\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e) \leftarrow \mathcal {G}(p)\). Sample
$$ \mathbf {A}_1 \leftarrow \mathbb {Z}_p^{k \times n_1}, \mathbf {A}_2 \leftarrow \mathbb {Z}_p^{k' \times n_2}, \mathbf {A}_0 \leftarrow \mathbb {Z}_p^{k' \times (k'+1)}, \mathbf {W}\leftarrow \mathbb {Z}_p^{(k'+1)\times (k'n_1 + kn_2)}, $$and output
$$ \textsf {mpk}= \big (\,\mathbb {G},\,[\mathbf {A}_0]_1,\,[\mathbf {A}_0\mathbf {W}]_1,\,[\mathbf {A}_1]_1,\,[\mathbf {A}_1]_2,\,[\mathbf {A}_2]_2\,\big ) \quad \text{ and }\quad \textsf {msk}= \mathbf {W}$$ -
\(\mathsf {Enc}( \textsf {mpk},(\mathbf {z}_1,\mathbf {z}_2))\): Sample \(\mathbf {s}_1 \leftarrow \mathbb {Z}_p^k, \mathbf {s}_0,\mathbf {s}_2 \leftarrow \mathbb {Z}_p^{k'}\) and output
$$\begin{aligned} \textsf {ct}= & {} \big (\, [\underbrace{\mathbf {s}_1 \mathbf {A}_1 + \mathbf {z}_1}_{\mathbf {y}_1}]_1, \, [\underbrace{\mathbf {s}_2 \mathbf {A}_2 + \mathbf {z}_2}_{\mathbf {y}_2}]_2, [\underbrace{\mathbf {s}_0\mathbf {A}_0}_{\mathbf {c}_0}]_1,\, [\underbrace{\mathbf {s}_0 \mathbf {A}_0 \mathbf {W}+ (\mathbf {s}_1 \otimes \mathbf {z}_2 \mid \mathbf {y}_1 \otimes \mathbf {s}_2)}_{\mathbf {y}_0}]_1\,\big ) \\&\in \mathbb {G}_1^{n_1} \times \mathbb {G}_2^{n_2} \times \mathbb {G}_1^{k'+1} \times \mathbb {G}_1^{k'n_1+kn_2} \end{aligned}$$ -
\(\mathsf {KeyGen}( \textsf {msk}, \mathbf {f})\): Output
$$ \textsf {sk}_{\mathbf {f}} = \Biggl [\mathbf {W}\cdot {(\mathbf {A}_1 \otimes \mathbf {I}_{n_2}) \mathbf {f}^{\!\scriptscriptstyle {\top }}\atopwithdelims ()(\mathbf {I}_{n_1} \otimes \mathbf {A}_2) \mathbf {f}^{\!\scriptscriptstyle {\top }}}\Biggr ]_2 \in \mathbb {G}_2^{(k'+1) \times 1} $$ -
\(\mathsf {Dec}( \textsf {sk}_\mathbf {f},\mathbf {f}, \textsf {ct})\): Parse \( \textsf {sk}_\mathbf {f}= [\mathbf {k}^{\!\scriptscriptstyle {\top }}]_2\) and output the discrete log of
$$[(\mathbf {y}_1 \otimes \mathbf {y}_2) \cdot \mathbf {f}^{\!\scriptscriptstyle {\top }}]_T \cdot e([\mathbf {c}_0]_1, [\mathbf {k}^{\!\scriptscriptstyle {\top }}]_2) \cdot e\Biggl ([\mathbf {y}_0]_1, \Biggl [{(\mathbf {A}_1 \otimes \mathbf {I}_{n_2}) \mathbf {f}^{\!\scriptscriptstyle {\top }}\atopwithdelims ()(\mathbf {I}_{n_1} \otimes \mathbf {A}_2) \mathbf {f}^{\!\scriptscriptstyle {\top }}}\Biggr ]_2 \Biggr )^{-1}$$
B Security Proof for Sect. 4
We complete the security proof for the scheme \(\varPi \) in Sect. 4.2.
Theorem 1
For all \(\mathcal {A}\), there exist \(\mathcal {B}_1\) and \(\mathcal {B}_2\) with \(\mathsf {Time}(\mathcal {B}_1),\mathsf {Time}(\mathcal {B}_2) \approx \mathsf {Time}(\mathcal {A})\) such that
where \(n\) is length of public input \(\mathbf {x}^*\) in the challenge, m is the parameter depending on size of function f and Q is the number of key queries.
Note that this yields a tight security reduction to the k-Lin assumption.
Game Sequence. We use \((\mathbf {x}^*,\mathbf {z}^*)\) to denote the semi-adaptive challenge and for notational simplicity, assume that all key queries \(f_j\) share the same parameters t and m. We prove Theorem 1 via a series of games.
-
\(\underline{\mathsf {Game}_0}\): Real game.
-
\(\underline{\mathsf {Game}_1}\): Identical to \(\mathsf {Game}_0\) except that \( \textsf {ct}^*\) for \((\mathbf {x}^*,\mathbf {z}^*)\) is given by
$$ \textsf {ct}^* = \big (\, [\boxed {\mathbf {c}^{\!\scriptscriptstyle {\top }}}]_1,\,[(\mathbf {z}^*)^{\!\scriptscriptstyle {\top }}+ \boxed {\mathbf {c}^{\!\scriptscriptstyle {\top }}}\mathbf {W}]_1,\, [\boxed {\mathbf {c}^{\!\scriptscriptstyle {\top }}}\mathbf {U}((\mathbf {x}^*)^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_k) + \boxed {\mathbf {c}^{\!\scriptscriptstyle {\top }}}\mathbf {V}]_1\,\big ) $$where \(\mathbf {c}\leftarrow \mathbb {Z}_p^{k+1}\). We claim that \(\mathsf {Game}_0 \approx _c \mathsf {Game}_1\). This follows from \(\mathrm {MDDH}^{1}_{k,k+1}\) assumption:
$$ [\mathbf {A}^{\!\scriptscriptstyle {\top }}]_1,\,[\mathbf {s}^{\!\scriptscriptstyle {\top }}\mathbf {A}^{\!\scriptscriptstyle {\top }}]_1 \approx _c [\mathbf {A}^{\!\scriptscriptstyle {\top }}]_1,\,\boxed {[\mathbf {c}^{\!\scriptscriptstyle {\top }}]_1}. $$In the reduction, we sample \(\mathbf {W},\mathbf {U},\mathbf {V}\) honestly and use them to simulate \( \textsf {mpk}\) and \(\mathsf {KeyGen}( \textsf {msk},\cdot )\) along with \([\mathbf {A}^{\!\scriptscriptstyle {\top }}]_1\); the challenge ciphertext \( \textsf {ct}^*\) is generated using the challenge term given above.
-
\(\underline{\mathsf {Game}_2}\): Identical to \(\mathsf {Game}_1\) except that the j-th query \(f_j\) to \(\mathsf {KeyGen}( \textsf {msk},\cdot )\) is answered with
$$ \textsf {sk}_{f_j} = \big (\,\mathbf {C}^{\!\scriptscriptstyle {\perp }}\cdot \textsf {sk}_{f_j}[1] + \mathbf {a}^{\!\scriptscriptstyle {\perp }}\cdot \textsf {sk}_{f_j}[2] ,\,[\mathbf {R}_j]_2\,\big ) $$with
$$\begin{aligned} \textsf {sk}_{f_j}[1]= & {} \big (\, [\mathbf {A}^{\!\scriptscriptstyle {\top }}\underline{\mathbf {T}}_j + \mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {W}\mathbf {M}_j]_2,\, [\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {T}_j\mathbf {L}_{1,j} + \mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {U}(\mathbf {I}_n\otimes \mathbf {R}_j)]_2,\, [\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {T}_j\mathbf {L}_{0,j} + \mathbf {A}^{\!\scriptscriptstyle {\top }}\widetilde{\mathbf {V}}\mathbf {R}_j]_2 \,\big ) \\ \textsf {sk}_{f_j}[2]= & {} \big (\, [\mathbf {c}^{\!\scriptscriptstyle {\top }}\underline{\mathbf {T}}_j + \mathbf {c}^{\!\scriptscriptstyle {\top }}\mathbf {W}\mathbf {M}_j]_2,\, [\mathbf {c}^{\!\scriptscriptstyle {\top }}\mathbf {T}_j\mathbf {L}_{1,j} + \mathbf {c}^{\!\scriptscriptstyle {\top }}\mathbf {U}(\mathbf {I}_n\otimes \mathbf {R}_j)]_2,\, [\mathbf {c}^{\!\scriptscriptstyle {\top }}\mathbf {T}_j\mathbf {L}_{0,j} + \mathbf {c}^{\!\scriptscriptstyle {\top }}\mathbf {V}\mathbf {R}_j]_2 \,\big ) \end{aligned}$$where \((\mathbf {L}_{1,j},\mathbf {L}_{0,j})\leftarrow \mathsf {lgen}(f_j)\), \(\mathbf {T}_j \leftarrow \mathbb {Z}_p^{(k+1)\times t}\), \( \mathbf {R}_j \leftarrow \mathbb {Z}_p^{k \times m}\), \(\mathbf {c}\) is the randomness in \( \textsf {ct}^*\) and \(\mathbf {C}^{\!\scriptscriptstyle {\perp }}\) is defined such that \((\mathbf {A}| \mathbf {c})^{\!\scriptscriptstyle {\top }}(\mathbf {C}^{\!\scriptscriptstyle {\perp }}| \mathbf {a}^{\!\scriptscriptstyle {\perp }}) = \mathbf {I}_{k+1}\) (cf. \(\mathsf {Setup}^*\) in Sect. 4.2). By basic linear algebra, we have \(\mathsf {Game}_1=\mathsf {Game}_2\).
-
\(\underline{\mathsf {Game}_3}\): Identical to \(\mathsf {Game}_2\) except that we replace \(\mathsf {Setup},\mathsf {Enc}\) with \(\mathsf {Setup}^*,\mathsf {Enc}^*\) where \( \textsf {ct}^*\) is given by
$$ \textsf {ct}^* = \big (\, [\mathbf {c}^{\!\scriptscriptstyle {\top }}]_1,\,\boxed { [\widetilde{\mathbf {w}}^{\!\scriptscriptstyle {\top }}]_1,\, [ \widetilde{\mathbf {v}}^{\!\scriptscriptstyle {\top }}]_1 }\,\big ) $$and replace \(\mathsf {KeyGen}( \textsf {msk},\cdot )\) with \(\mathsf {KeyGen}^*_3( \textsf {msk}^*,\cdot )\), which works as \(\mathsf {KeyGen}( \textsf {msk},\cdot )\) in \(\mathsf {Game}_2\) except that, for the j-th query \(f_j\), we compute
$$ \textsf {sk}_{f_j}[2] = \left( \, \begin{array}{c} {\boxed {[\underline{\tilde{\mathbf {t}}}^{\!\scriptscriptstyle {\top }}_j - (\mathbf {z}^*)^{\!\scriptscriptstyle {\top }}\mathbf {M}_j + \widetilde{\mathbf {w}}^{\!\scriptscriptstyle {\top }}\mathbf {M}_j]_2},\, [\boxed {\tilde{\mathbf {t}}_j^{\!\scriptscriptstyle {\top }}}\mathbf {L}_{1,j} + \boxed {\tilde{\mathbf {u}}^{\!\scriptscriptstyle {\top }}}(\mathbf {I}_n\otimes \mathbf {R}_j)]_2,}\\ {[\boxed {\tilde{\mathbf {t}}_j^{\!\scriptscriptstyle {\top }}}\mathbf {L}_{0,j} \boxed { - \tilde{\mathbf {u}}^{\!\scriptscriptstyle {\top }}(\mathbf {I}_n\otimes \mathbf {R}_j)((\mathbf {x}^*)^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_m) + \widetilde{\mathbf {v}}^{\!\scriptscriptstyle {\top }}\mathbf {R}_j}]_2} \end{array} \,\right) $$where \(\tilde{\mathbf {w}},\tilde{\mathbf {v}}\) are given in \( \textsf {msk}^*\) (output by \(\mathsf {Setup}^*\)) and \(\tilde{\mathbf {u}} \leftarrow \mathbb {Z}_p^{k n}, \mathbf {t}_j \leftarrow \mathbb {Z}_p^t, \mathbf {R}_j \leftarrow \mathbb {Z}_p^{k \times m}\). We claim that \(\mathsf {Game}_2 \approx _s \mathsf {Game}_3\). This follows from the following statement: for any full-rank \((\mathbf {A}|\mathbf {c})\), we have
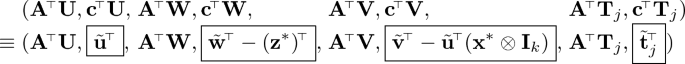
-
\(\underline{\mathsf {Game}_4}\): Identical to \(\mathsf {Game}_3\) except that we replace \(\mathsf {KeyGen}^*_3\) with \(\mathsf {KeyGen}^*_4\) which works as \(\mathsf {KeyGen}^*_3\) except that, for the j-th query \(f_j\), we compute
$$ \textsf {sk}_{f_j}[2] = \big (\, [\underline{\tilde{\mathbf {t}}}^{\!\scriptscriptstyle {\top }}_j - (\mathbf {z}^*)^{\!\scriptscriptstyle {\top }}\mathbf {M}_j + \widetilde{\mathbf {w}}^{\!\scriptscriptstyle {\top }}\mathbf {M}_j]_2,\, [\tilde{\mathbf {t}}_j^{\!\scriptscriptstyle {\top }}\mathbf {L}_{1,j} + \boxed {\hat{\mathbf {u}}_j^{\!\scriptscriptstyle {\top }}}]_2,\, [\tilde{\mathbf {t}}_j^{\!\scriptscriptstyle {\top }}\mathbf {L}_{0,j} - \boxed {\hat{\mathbf {u}}_j^{\!\scriptscriptstyle {\top }}} ((\mathbf {x}^*)^{\!\scriptscriptstyle {\top }}\otimes \mathbf {I}_m) + \widetilde{\mathbf {v}}^{\!\scriptscriptstyle {\top }}\mathbf {R}_j]_2 \,\big ) $$where \(\hat{\mathbf {u}}_j \leftarrow \mathbb {Z}_p^{nm}\) and \(\mathbf {R}_j \leftarrow \mathbb {Z}_p^{k \times m}\). We claim that \(\mathsf {Game}_3 \approx _c \mathsf {Game}_4\). This follows from \(\mathrm {MDDH}^{n}_{k,mQ}\) assumption which tells us that
$$ \big \{ \, [\widetilde{\mathbf {u}}^{\!\scriptscriptstyle {\top }}(\mathbf {I}_n\otimes \mathbf {R}_j)]_2,\,[\mathbf {R}_j]_2 \, \big \}_{j\in [Q]} \approx _c \big \{ \, \boxed {[\hat{\mathbf {u}}_j^{\!\scriptscriptstyle {\top }}]_2},\,[\mathbf {R}_j]_2 \, \big \}_{j\in [Q]} $$where Q is the number of key queries.
-
\(\underline{\mathsf {Game}_5}\): Identical to \(\mathsf {Game}_4\) except that we replace \(\mathsf {KeyGen}^*_4\) with \(\mathsf {KeyGen}^*\); this is the ideal game. We claim that \(\mathsf {Game}_4 \approx _s \mathsf {Game}_5\). This follows from the privacy of partial garbling scheme in Sect. 4.1.
We use \(\mathsf {Adv}^\textsf {xx}_\mathcal {A}(\lambda )\) to denote the advantage of adversary \(\mathcal {A}\) in \(\mathsf {Game}_\textsf {xx}\). We prove the following lemmas showing the indistinguishability of adjacent games listed above.
Lemma 2
(\(\mathsf {Game}_{0} \approx _c \mathsf {Game}_{1}\)). For all \(\mathcal {A}\), there exists \(\mathcal {B}_1\) with \(\mathsf {Time}(\mathcal {B}_1) \approx \mathsf {Time}(\mathcal {A})\) such that
Lemma 3
(\(\mathsf {Game}_{2} \approx _c \mathsf {Game}_{3}\)). For all \(\mathcal {A}\), we have \(\mathsf {Adv}^3_\mathcal {A}(\lambda ) \approx \mathsf {Adv}^2_\mathcal {A}(\lambda )\).
The proof is the same as before, except we replace  in \( \textsf {sk}_{f_j}[2]\) with
in \( \textsf {sk}_{f_j}[2]\) with 
Proof
(of Lemma 3). Recall that the difference between the two games lies in \( \textsf {ct}^*\) and \( \textsf {sk}_{f_j}[2]\): instead of computing
in \(\mathsf {Game}_2\), we compute


in \(\mathsf {Game}_3\).
This follows readily from the following statement: for all \(\mathbf {x}^*,\mathbf {z}^*\),

where \(\mathbf {U},\mathbf {W},\mathbf {V},\tilde{\mathbf {w}},\tilde{\mathbf {v}}\) are sampled as in \(\mathsf {Setup}^*\) and \(\tilde{\mathbf {u}} \leftarrow \mathbb {Z}_p^{kn},\mathbf {T}_j \leftarrow \mathbb {Z}_p^{(k+1)\times t},\mathbf {t}_j \leftarrow \mathbb {Z}_p^t\). We clarify that in the semi-adaptive security game, \((\mathbf {x}^*,\mathbf {z}^*)\) are chosen after seeing \(\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {U},\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {W},\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {V}\). Since the two distributions are identically distributed, the distinguishing advantage remains 0 even for adaptive choices of \(\mathbf {x}^*,\mathbf {z}^*\) via a random guessing argument.
Finally, note that \(\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {U},\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {W},\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {V},\mathbf {A}^{\!\scriptscriptstyle {\top }}\mathbf {T}_j\) are used to simulate \( \textsf {mpk}\), \( \textsf {sk}_{f_j}[1]\), whereas the boxed/gray terms are used to simulate \( \textsf {sk}_{f_j}[2]\). This readily proves the lemma. \(\square \)
Lemma 4
(\(\mathsf {Game}_{3} \approx _c \mathsf {Game}_{4}\)). For all \(\mathcal {A}\), there exists \(\mathcal {B}_2\) with \(\mathsf {Time}(\mathcal {B}_2) \approx \mathsf {Time}(\mathcal {A})\) such that
where \(n\) is length of public input \(\mathbf {x}\) in the challenge, m is the maximum size of function f and Q is the number of key queries.
Lemma 5
(\(\mathsf {Game}_4 \approx _s \mathsf {Game}_5\)). For all \(\mathcal {A}\), we have \(\mathsf {Adv}^5_\mathcal {A}(\lambda ) \approx \mathsf {Adv}^4_\mathcal {A}(\lambda )\).
The proof is the same as before except we replace \(\mathbf {z}^*\) in \( \textsf {sk}_{f_j}[2], \mathsf {pgb}, \mathsf {pgb}^*\) with \(\mathbf {z}^* \mathbf {M}_j\) and \(\tilde{\mathbf {w}}\) in \( \textsf {sk}_{f_j}[2]\) with \(\tilde{\mathbf {w}} \mathbf {M}_j\).
Proof
Recall that the difference between the two games lies in \( \textsf {sk}_{f_j}[2]\): instead of computing
in \(\mathsf {KeyGen}^*_4\) (i.e., \(\mathsf {Game}_4\)), we compute

in \(\mathsf {KeyGen}^*\) (i.e., \(\mathsf {Game}_5\)). By change of variable \(\hat{\mathbf {u}}_j^{\!\scriptscriptstyle {\top }}\mapsto \hat{\mathbf {u}}_j^{\!\scriptscriptstyle {\top }}- \tilde{\mathbf {t}}_j^{\!\scriptscriptstyle {\top }}\mathbf {L}_{1,j}\) for all \(j \in [Q]\) in \(\mathsf {Game}_4\), we can rewrite in the form:
where

Then the lemma immediately follows from the privacy of underlying partial garbling scheme which means \(\mathsf {pgb}(f_j,\mathbf {x}^*,\mathbf {z}^*\mathbf {M}_j) \approx _s \mathsf {pgb}^*(f_j,\mathbf {x}^*,\mathbf {z}^*\mathbf {M}_j f_j(\mathbf {x}^*)^{\!\scriptscriptstyle {\top }})\). \(\square \)
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Wee, H. (2020). Functional Encryption for Quadratic Functions from k-Lin, Revisited. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12550. Springer, Cham. https://doi.org/10.1007/978-3-030-64375-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-64375-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64374-4
Online ISBN: 978-3-030-64375-1
eBook Packages: Computer ScienceComputer Science (R0)