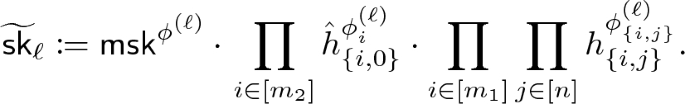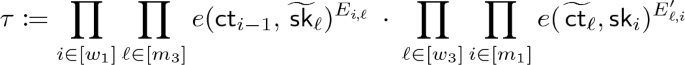Abstract
Attribute-based encryption (ABE) is a cryptographic primitive which supports fine-grained access control on encrypted data, making it an appealing building block for many applications. Pair encodings (Attrapadung, EUROCRYPT 2014) are simple primitives that can be used for constructing fully secure ABE schemes associated to a predicate relative to the encoding. We propose a generic transformation that takes any pair encoding scheme (PES) for a predicate \(P\) and produces a PES for its negated predicate \(\bar{P}\). This construction finally solves a problem that was open since 2015. Our techniques bring new insight to the expressivity and generality of PES and can be of independent interest. We also provide, to the best of our knowledge, the first pair encoding scheme for negated doubly spatial encryption (obtained with our transformation) and explore several other consequences of our results.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Attribute-based encryption (ABE) is a form of public-key encryption that generalizes the traditional single-recipient variant, providing fine-grained access control on the encrypted data. In this new paradigm, ciphertexts and keys have attributes attached and the decryption ability of a key on a ciphertext is determined by a potentially complex access control policy involving these attributes. More concretely, an ABE scheme for predicate \(P\) guarantees that the decryption of a ciphertext \(\mathsf {ct}_x\) with a secret key \(\mathsf {sk}_y\) is successful if and only if the ciphertext attribute x and the key attribute y verify the predicate, i.e., \(P(x,y) = 1\).
ABE was first conceived by Sahai and Waters [30] and later introduced by Goyal et al. [19]. Originally, ABE was designed in the flavour of key-policy ABE (KP-ABE), where value x is a Boolean vector, value y is a Boolean function and predicate \(P(x,y)\) is defined as  . On the other hand, in the analogous version, ciphertext-policy ABE (CP-ABE), the roles of values x and y are swapped. Nowadays, the notion of ABE has been generalized and, thanks to a considerable effort by the community of cryptographers, there exist efficient schemes for a rich variety of predicates. For example, identity-based encryption (IBE) [31] can be obtained as
. On the other hand, in the analogous version, ciphertext-policy ABE (CP-ABE), the roles of values x and y are swapped. Nowadays, the notion of ABE has been generalized and, thanks to a considerable effort by the community of cryptographers, there exist efficient schemes for a rich variety of predicates. For example, identity-based encryption (IBE) [31] can be obtained as  , zero-inner product encryption (ZIPE) [23] can be obtained by setting
, zero-inner product encryption (ZIPE) [23] can be obtained by setting  , where \(\varvec{x}\) and \(\varvec{y}\) belong to some vector space; other examples are span programs [22], non-monotonic access structures [28], hierarchical IBE [26], large universe ABE [29], polynomial size circuits [18], or regular languages [33]. Despite such a great progress in the field, designing better schemes in terms of size, performance, security and expressivity became an excessively hard and tedious task. Until two astonishing works appeared in 2014.
, where \(\varvec{x}\) and \(\varvec{y}\) belong to some vector space; other examples are span programs [22], non-monotonic access structures [28], hierarchical IBE [26], large universe ABE [29], polynomial size circuits [18], or regular languages [33]. Despite such a great progress in the field, designing better schemes in terms of size, performance, security and expressivity became an excessively hard and tedious task. Until two astonishing works appeared in 2014.
Modular Frameworks for ABE. In 2014, Wee [34] and Attrapadung [4] independently proposed two generic and unifying frameworks for designing attribute-based encryption schemes for different predicates. Both works define a simple primitive called encoding and follow the dual system methodology by Lewko and Waters [25, 32] to construct a compiler that, on input an encoding (for certain predicate \(P\)), produces a fully secure attribute-based encryption scheme for \(P\). Wee defines so-called predicate encodings, an information-theoretic primitive inspired by linear secret sharing, while Attrapadung introduces the notion of pair encodings, a similar primitive that admits both information-theoretic and computational security definitions. These frameworks remarkably simplify the design and study of ABE schemes: the designer can focus on the construction of the simpler encoding (for the desired predicate), which requires weaker security properties that are more easily verifiable. In fact, the potential of this new frameworks is evidenced by the invention of new constructions and performance improvements on existing primitives. Although these frameworks were designed over composite-order groups, they were both extended, in [15] and [5] respectively, to the prime-order setting (under the Matrix-DH assumption). Subsequent works propose variations and extensions of these modular frameworks [1, 2, 14], some of them even redefining the core encoding primitive [24] (defining so-called tag-based encodings). However, note that the frameworks based on pair encodings are the most general and expressiveFootnote 1 and they have led to breakthrough constructions such as constant-size ciphertext KP-ABE (with large universes) [4], fully-secure functional encryption for regular languages [4], constant-size ciphertext CP-ABE [1] or completely-unbounded KP-ABE for non-monotone span programs (NSP) over large universes [6]. Note that, even nowadays, it is still unknown how to construct any of these powerful schemes based on predicate encodings or tag-based encodings.
Generic Predicate Transformations. In order to further simplify the design of these encodings, a common practice is to develop techniques to modify or combine existing ones. For example, the DUAL transformation, that swaps the ciphertext attribute and the key attribute, or the AND transformation, that joins two predicates in conjunction, can be achieved for pair encodings [4, 10]. Among many applications, these transformations can be used to build dual-policy attribute-based encryption (DP-ABE) [7, 10]; or to enhance any encoding with direct revocation of keys by combining (in conjunction) the original encoding with, e.g., an encoding for broadcast encryption.
In the framework of [15], Ambrona et al. [3] designed new general transformations for the DUAL, OR and AND connectors and, remarkably, the NOT transformation (that negates the predicate of the encoding). This functionally complete set of Boolean transformers provides a rich combination of predicates and arguably broadens the expressivity of the framework, however, such a negation is limited to the framework based on predicate encodings. Designing a similar negation transformation that is applicable to all pair encoding schemes (PES) is a very appealing problem, since it would facilitate the design of new encodings and would immediately expand the expressivity of the PES framework by applying it to all existing ones. Note that, as we have already mentioned, pair encodings have proven themselves to be significantly more expressive than any other related framework.
However, recent works have considered the problem of designing such a general negation to be intrinsically hard [2, 6] (see our discussion in Sect. 3, we also refer to this section for more details about relevant related works). To the best of our knowledge, a general NOT transformation that is applicable to the framework of pair encodings does not exist in the literature.
1.1 Our Contribution
We pursue the study of pair encoding schemes and establish several general results that can lead to performance improvements, and new encodings that broaden their scope.
Generic Negation of Pair Encodings. We propose a generic transformation that takes any pair encoding scheme for a predicate \(P\) and produces a pair encoding scheme for its negated predicate, \(\bar{P}\). Our transformation is applicable to pair encodings that follow the most recent and refined definition given in [2]. Our construction finally solves a problem that was open since 2015, when several other transformation for pair encodings (like conjunction or duality) were proposed [10], but no generic negation was provided (nor designed in subsequent works). In fact, several works had suggested that finding such a transformation was non-obvious [2, 6], since it relates to the problem of generically finding a short “certificate” of security of the encoding. We elaborate on this idea in Sect. 3.
Algebraic Characterization of Pair Encodings. En route to designing our generic negation, we define an algebraic characterization of PES that brings new insight to their expressivity and generality and can be of independent interest. Our characterization allows us to express the security of a pair encoding scheme as the (in)existence of solutions to a system of matrix equations. This is the bridge that allows us to leverage Lemma 1, a very powerful result from linear algebra (commonly used in cryptography), in order to design and prove our generic negation.
New Encodings. Our generic negation facilitates the design of new pair encoding schemes. It will immediately provide us with a negated version of any encoding, something particularly useful for encodings for which a negated counterpart is not known. A relevant example of a PES with (previously) unknown negation is the case of doubly spatial encryption.
Doubly spatial encryption [20] is an important primitive that generalizes both spatial encryption and negated spatial encryption [8]. A negated doubly spatial encryption scheme serves as its revocation analogue and can lead to powerful generalizations in the same way that negated (standard) spatial encryption unifies existing primitives, e.g. it subsumes non-zero-mode inner-product encryption (IPE) [8]. In Sect. 6.1 we provide, to the best of our knowledge, the first pair encoding scheme for negated doubly spatial encryption, obtained with our transformation.
Other Implications of Our Results. We believe the results presented in this work improve our understanding of pair encodings and how expressive they are. In particular, we now know that the set of predicates that can be expressed with PES is closed under negation. In Sect. 6.2, we elaborate on the conclusions we could derive from this fact as well as discuss how our generic transformation can also lead to performance improvements when implementing ABE schemes. Furthermore, note that our generic negation is compatible with the very recent framework proposed by Attrapadung [6], designed to perform dynamic pair encoding compositions. We believe our new transformation complements his work, where the proposed non-monotone formulae composition was only semi-generic (but dynamic), because he had to rely on encodings for which a negated version was available.
2 Preliminaries
2.1 Notation
We write  to denote that s is uniformly sampled from a set S. For integers m, n, we define [m, n] as the range \(\{m,\dots ,n\}\) and we denote by [n] the range [1, n]. We use the same conventions for matrix-representations of linear maps on finite-dimensional spaces. For a ring R, we define vectors \(\varvec{v} \in R^n\) as column matrices, denote the transpose of a matrix A by
to denote that s is uniformly sampled from a set S. For integers m, n, we define [m, n] as the range \(\{m,\dots ,n\}\) and we denote by [n] the range [1, n]. We use the same conventions for matrix-representations of linear maps on finite-dimensional spaces. For a ring R, we define vectors \(\varvec{v} \in R^n\) as column matrices, denote the transpose of a matrix A by  and its trace by \(\mathrm{tr}(A)\). We denote by \(|\varvec{v}|\) the length or dimension of vector \(\varvec{v}\) and by \(v_i\) its i-th component, for all \(i \in \{1,\dots ,|\varvec{v}|\}\). Similarly, \(A_i\) denotes the i-th row of matrix A (we do not use this notation when the name of the matrix already contains a subindex). We denote by \(\mathrm{span}(A)\) the linear column span of matrix A. We denote the identity matrix of dimension n by \(I_{\text {{n}}}\), a zero vector of length n by \(\varvec{0}_{\text {{n}}}\) and a zero matrix of m rows and n columns by
and its trace by \(\mathrm{tr}(A)\). We denote by \(|\varvec{v}|\) the length or dimension of vector \(\varvec{v}\) and by \(v_i\) its i-th component, for all \(i \in \{1,\dots ,|\varvec{v}|\}\). Similarly, \(A_i\) denotes the i-th row of matrix A (we do not use this notation when the name of the matrix already contains a subindex). We denote by \(\mathrm{span}(A)\) the linear column span of matrix A. We denote the identity matrix of dimension n by \(I_{\text {{n}}}\), a zero vector of length n by \(\varvec{0}_{\text {{n}}}\) and a zero matrix of m rows and n columns by  . We denote by \(\varvec{e}_{\text {{i}}}^{n}\) the i-th vector of the standard basis of an n-dimensional space, for all \(i \in [n]\). We sometimes denote \(\varvec{e}_{\text {{1}}}^{n}\) by \(\varvec{1}_{\text {{n}}}\). Similarly, we denote by
. We denote by \(\varvec{e}_{\text {{i}}}^{n}\) the i-th vector of the standard basis of an n-dimensional space, for all \(i \in [n]\). We sometimes denote \(\varvec{e}_{\text {{1}}}^{n}\) by \(\varvec{1}_{\text {{n}}}\). Similarly, we denote by  the matrix
the matrix  , i.e., a null matrix of m rows and n columns whose component in the first row and first column is 1. Given two matrices A and B, we denote by \(A \otimes B\) their Kronecker product.
, i.e., a null matrix of m rows and n columns whose component in the first row and first column is 1. Given two matrices A and B, we denote by \(A \otimes B\) their Kronecker product.
We consider a bilinear group generator \(\mathcal{G}\) that takes a security parameter \(\lambda \in \mathbb {N}\) and outputs the description of a bilinear group \((p, G_{\mathsf{1}}, G_{\mathsf{2}}, G_{\mathsf{t}}, g_\mathsf{1}, g_\mathsf{2}, e)\) where \(G_{\mathsf{1}}\), \(G_{\mathsf{2}}\) and \(G_{\mathsf{t}}\) are cyclic groups of order p (for a \(\lambda \)-bits prime p), \(g_\mathsf{1}\) and \(g_\mathsf{2}\) are generators of \(G_{\mathsf{1}}\) and \(G_{\mathsf{2}}\) respectively and \(e : G_{\mathsf{1}}\times G_{\mathsf{2}}\rightarrow G_{\mathsf{t}}\) is a (non-degenerate) bilinear map, satisfying \(e(g_\mathsf{1}^a, g_\mathsf{2}^b) = e(g_\mathsf{1}, g_\mathsf{2})^{ab}\) for all \(a,b \in \mathbb {N}\). Observe that the element \(g_\mathsf{t}= e(g_\mathsf{1}, g_\mathsf{2})\) generates \(G_{\mathsf{t}}\).
2.2 Attribute-Based Encryption
Attribute-based encryption (ABE) [30] is a form of of public-key encryption that supports fine-grained access control of encrypted data.
Definition 1
(Attribute-based encryption). An ABE scheme for predicate \(P: \mathcal{X}\times \mathcal{Y}\rightarrow \{0,1\}\) consists of four probabilistic polynomial-time algorithms:
-
\(\mathsf{Setup}(1^\lambda ,\mathcal{X},\mathcal{Y}) \rightarrow (\mathsf {mpk}, \mathsf {msk})\), on input the security parameter \(\lambda \) and attribute universes \(\mathcal{X}, \mathcal{Y}\), outputs a master public key and a master secret key, defining a key space \(\mathcal{K}\).
-
\(\mathsf{Enc}(\mathsf {mpk}, x)\rightarrow (\mathsf {ct}_x, \tau )\), on input \(\mathsf {mpk}\) and a ciphertext attribute \(x \,{\in }\,\mathcal{X}\), outputs a ciphertext \(\mathsf {ct}_x\) and a symmetric encryption key \(\tau \in \mathcal{K}\).
-
\(\mathsf{KeyGen}(\mathsf {msk},y) \rightarrow \mathsf {sk}_y\), on input the master secret key and a key attribute \(y \in \mathcal{Y}\), outputs a secret key \(\mathsf {sk}_y\).
-
\(\mathsf{Dec}(\mathsf {mpk},\mathsf {sk}_y,\mathsf {ct}_x,x) \rightarrow \tau /\bot \), on input \(\mathsf {sk}_y\) and \(\mathsf {ct}_x\), outputs a symmetric key \(\tau \in \mathcal{K}\) if \(P(x,y) = 1\) or \(\bot \) otherwise.
Correctness. For all \(\lambda \in \mathbb {N}\), \(x \in \mathcal{X}\) and \(y \in \mathcal{Y}\) such that \(P(x,y) = 1\), it holds:
Security. Informally, an ABE scheme is secure if no probabilistic polynomial-time (PPT) adversary can distinguish the symmetric encryption key associated to a ciphertext \(\mathsf {ct}_{x^{\!\star }}\) (for some attribute \(x^\star \)) from a uniformly chosen one from \(\mathcal{K}\), even after requesting several secret keys for attributes y of their choice, as long as they all satisfy \(P(x^\star , y) = 0\).
In this work we focus on pair encodings (see the next section) as a building block for constructing ABE schemes and we refer to Appendix B.1 for a formal security definition of ABE, which we do not state here. Instead, we will formally state and reason about the security requirements for pair encodings.
2.3 Pair Encodings
We consider the refined definition of pair encodings introduced by Agrawal and Chase in [2].
Definition 2
(Pair encoding). A pair encoding scheme (PES) for a predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\) indexed by \(\kappa = (N,\mathsf{par})\) consists of the following deterministic and efficiently computable algorithms:
-
\(\mathsf{Param}(\mathsf{par})\): on input certain parameters outputs an integer n, specifying the number of common variables, denoted by \(\varvec{b} = (b_1,\dots ,b_n)\).
-
\(\mathsf{EncKey}(N,y)\): on input \(N \in \mathbb {N}\) and \(y \in \mathcal{Y}_{(N,\mathsf{par})}\), outputs a vector of polynomials \(\varvec{k} = (k_1,\dots ,k_{m_3})\) in the non-lone variables \(\varvec{r} = (r_1,\dots ,r_{m_1})\), the lone variables \(\hat{\varvec{r}} = (\alpha , \hat{r}_1, \dots , \hat{r}_{m_2})\) and the common variables \(\varvec{b}\).
-
\(\mathsf{EncCt}(N,x)\): on input \(N \in \mathbb {N}\) and \(x \in \mathcal{X}_{(N,\mathsf{par})}\), outputs a vector of polynomials \(\varvec{c} = (c_1,\dots ,c_{w_3})\) in the non-lone variables \(\varvec{s} = (s_0,s_1,\dots ,s_{w_1{-}1})\), the lone variables \(\hat{\varvec{s}} = (\hat{s}_1,\dots ,\hat{s}_{w_2})\) and the common variables \(\varvec{b}\).
-
\(\mathsf{Pair}(N,x,y)\): on input \(N \in \mathbb {N}\) and attributes x and y, outputs a pair of matrices \((E, E')\) with coefficients in \(\mathbb {Z}_N\) of dimensions \(w_1 \times m_3\) and \(w_3 \times m_1\) respectively.
We require that the following properties be satisfied:
-
reconstructability: For every \(\kappa = (N,\mathsf{par})\), \(x \in \mathcal{X}_{\kappa }\) and \(y \in \mathcal{Y}_{\kappa }\) such that \(P_{\kappa }(x,y) = 1\), the following equation holds symbolically:
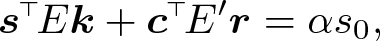
where \(\varvec{k} \leftarrow \mathsf{EncKey}(N,x)\), \(\varvec{c} \leftarrow \mathsf{EncCt}(N,y)\) and \((E,E') \leftarrow \mathsf{Pair}(N,x,y)\).
-
structural constraints: The polynomials produced by \(\mathsf{EncKey}\) only contain monomials of the form \(\alpha \), \(r_i b_j\) or \(\hat{r}_{i'}\) for some \(i \in [m_1]\), \(j \in [n]\) and \(i' \in [m_2]\).
On the other hand, the polynomials produced by \(\mathsf{EncCt}\) only contain monomials of the form \(s_{i}b_j\) or \(\hat{s}_{i'}\) for some \(i \in [0,w_1{-}1]\), \(j \in [n]\) and \(i' \in [w_2]\).
-
security (non-reconstructability): For all \(\kappa \,{\in }\,(N,\mathsf{par})\), \(x \,{\in }\,\mathcal{X}_{\kappa }\) and \(y \,{\in }\,\mathcal{Y}_{\kappa }\) such that \(P_{\kappa }(x,y) = 0\), and for every pair of matrices \(E\) and \(E'\), over \(\mathbb {Z}_N\),
 , where \(\varvec{k} \leftarrow \mathsf{EncKey}(N,x)\) and \(\varvec{c} \leftarrow \mathsf{EncCt}(N,y)\).
, where \(\varvec{k} \leftarrow \mathsf{EncKey}(N,x)\) and \(\varvec{c} \leftarrow \mathsf{EncCt}(N,y)\).
Remark 1
Observe that \(m_1\) and \(w_1\) representFootnote 2 the number of non-lone variables \(\varvec{r}\) and \(\varvec{s}\) respectively; \(m_2\) and \(w_2\) represent the number of lone variables \(\hat{\varvec{r}}\) and \(\hat{\varvec{s}}\) respectively; and \(m_3\) and \(w_3\) represent the number of polynomials produced by \(\mathsf{EncKey}\) and \(\mathsf{EncCt}\) respectively. Also note that \(m_3\) may depend on the key attribute y and \(w_3\) may depend on the ciphertext attribute x. We will use this notation throughout the paper.
Agrawal and Chase [2] showed that an encoding with the non-reconstructability property (coined non-trivially broken) satisfies the symbolic property, a concept introduced by them which is a sufficient condition to build attribute-based encryption in the standard model under the so-called q-ratio assumption.
We refer to Appendix B.2 for details about how the compiler from PES to fully secure ABE works. In this work we directly reason about PES and do not need to explicitly define such a compiler. However, for the sake of understanding, we provide an intuition of how a PES can be used to create an ABE scheme in the following section.
Example 1
(PES for identity-based encryption). The following is a pair encoding scheme for the IBE predicate  , for \(x,y \in \mathbb {Z}_N\). (With \(m_1 = 1\), \(m_2 = 0\), \(m_3 = 2\) and \(w_1 = 2\), \(w_2 = 0\), \(w_3 = 1\).)
, for \(x,y \in \mathbb {Z}_N\). (With \(m_1 = 1\), \(m_2 = 0\), \(m_3 = 2\) and \(w_1 = 2\), \(w_2 = 0\), \(w_3 = 1\).)

Furthermore, in this case \(\mathsf{Param}\) is an algorithm that simply outputs \(n = 3\) and \(\mathsf{Pair}(N,x,y)\) returns matrices \(E = I_{\text {{2}}}\) and \(E' = {-}I_{\text {{1}}}\). For reconstructability, observe that  equals \(s_0\alpha + s_1r_1(yb_2 + b_3) - s_1r_1 (xb_2 + b_3)\) which equals \(\alpha s_0\) whenever \(x = y\), as desired.
equals \(s_0\alpha + s_1r_1(yb_2 + b_3) - s_1r_1 (xb_2 + b_3)\) which equals \(\alpha s_0\) whenever \(x = y\), as desired.
Arguing security, i.e., non-reconstructability whenever \(x \ne y\), is a little trickier. One needs to show that for all matrices \(E \in \mathbb {Z}_N^{2\times 2}\), \(E' \in \mathbb {Z}_N\), the above linear combination is never equal to \(\alpha s_0\). This could be done by unfolding the list of polynomials in \(\varvec{s} \otimes \varvec{k}\), \(\varvec{c} \otimes \varvec{r}\) into a matrix A with \(w_1 m_3 + w_3 m_1\) rows (as many as polynomials) and as many columns as different monomials appear in them, where the element at row i and column j of the matrix represents the coefficient of the j-th monomial in the i-th polynomial. (Let the first column be the one associated to monomial \(\alpha s_0\).) One could then argue security by checking that the row span of A does not contain the vector \((1\,0\,\dots \,0)\) when \(P(x,y) = 0\).
However, there is a simpler way of proving non-reconstructability. Simply evaluate the polynomials produced by \(\mathsf{EncKey}\) and \(\mathsf{EncCt}\) in:
Since all the polynomials evaluate to 0, but \(\alpha s_0\) evaluates to \(1 \ne 0\), it must be impossible to symbolically reconstruct \(\alpha s_0\) with some pair of matrices \(E,E'\). Otherwise, we would have a contradiction:

The above variable substitution that vanishes all polynomials, but does not vanish polynomial \(\alpha s_0\) can be considered to be a short “certificate” of the security of the scheme (and it is well-defined as long as \(x \,{\ne }\, y\)). We elaborate on this interesting method for arguing security in Sect. 3. \(\blacksquare \)
2.4 ABE from PES
The compiler from pair encodings to attribute-based encryption is defined over bilinear groups implemented as dual system groups (DSG) [2, 16, 17]. Here, we define a simplified version of the compiler and avoid DSG for simplicity, but note that the actual scheme produced by these compilers uses vectors of group elements where we write single group elements. We provide a complete description of the compiler from [2] in Appendix B.2.
Informally, the symmetric encryption key is computed as  , where \(s_0\) is fresh randomness and \(g_\mathsf{t}^{\alpha }\) is part of the master public key. Both ciphertexts and keys are made of group elements (created based on the recipe given by the corresponding PES polynomials). It is possible to recover \(\tau \) when the predicate is satisfied. More concretely, for \(\varvec{k} \leftarrow \mathsf{EncKey}(x)\) and \(\varvec{c} \leftarrow \mathsf{EncCt}(y)\), the compiler could be summarized as follows:
, where \(s_0\) is fresh randomness and \(g_\mathsf{t}^{\alpha }\) is part of the master public key. Both ciphertexts and keys are made of group elements (created based on the recipe given by the corresponding PES polynomials). It is possible to recover \(\tau \) when the predicate is satisfied. More concretely, for \(\varvec{k} \leftarrow \mathsf{EncKey}(x)\) and \(\varvec{c} \leftarrow \mathsf{EncCt}(y)\), the compiler could be summarized as follows:

Decryption is done by pairing \(g_\mathsf{1}^{\varvec{s}}\) with \(g_\mathsf{2}^{\varvec{k}}\), \(g_\mathsf{1}^{\varvec{c}}\) with \(g_\mathsf{2}^{\varvec{r}}\), and linearly combining the resulting elements, according to the coefficients given by \(\mathsf{Pair}(x,y)\), obtaining \(\alpha s_0\) in the exponent.
2.5 Linear Algebra Tools
In order to prove the validity of our generic negation of pair encodings, we will use a very powerful result from linear algebra that has been widely used in the literature [1,2,3, 11]. It states that given a field K, a matrix \(A \in K^{m \times n}\) and a vector \(\varvec{z} \in K^m\), it holds that \(A\varvec{v} \ne \varvec{z}\) for all \(\varvec{v} \in K^{n}\) if and only if there exists a vector \(\varvec{w} \in K^{m}\) such that  and
and  . We refer to [11, Claim 2] for a formal proof.
. We refer to [11, Claim 2] for a formal proof.
Here, for the sake of presentation, we state a variant of the above result, which can be shown to be equivalent, but that facilitates its application in the proof of Lemma 2.
Lemma 1
Let V and W be vector spaces over a field K. Let \(f : V \rightarrow W\) be a linear operator and let \(\varvec{z} \in W\). We have that:
Here, \(W^{*}\!\!\) denotes the dual space of W, i.e., the set of all linear maps \(\varphi : W \rightarrow K\).
3 Overview of Our Generic Negation Transformation
Our starting point is the generic negation for the (less expressive) framework of predicate encodings from [3]. In order to achieve their transformation, Ambrona, Barthe, and Schmidt first defined an algebraic characterization of predicate encodings where the security of the encoding (previously defined as an equality between distributions) was redefined into a purely algebraic statement related to the existence of solutions to a linear system of equations. This observation allowed them to link the notions of security and non-reconstructability and define what they coined the implicit predicate of an encoding. This implies, in a nutshell, that all functions mapping attributes into matrices define a valid predicate encoding for a certain predicate, informally defined as all pairs of attributes (x, y) that map into matrices that lead to reconstructability.
Now that security has been proven to be equivalent to non-reconstructability, and given the simple structure of predicate encodings (which are essentially matrices over \(\mathbb {Z}_p\)), it is possible to find a short “witness” of non-reconstructability by simply finding a solution to a dual system of equations.Footnote 3 What we want to highlight here is that their new understanding of predicate encodings allows them to view both reconstructability and non-reconstructability as essentially the same kind of property. This suggests that one may be able to build a generic negation of predicate encodings by transposing the matrices induced by them.Footnote 4 This is in fact what the negation by Ambrona et al. does, but extra care is needed to make things really work.
Unfortunately, in the case of pair encodings things are not as simple. Their structure is significantly more convoluted, involving abstract polynomials that do not allow the kind of reasoning that was possible before (standard linear algebra). However, in 2017, Agrawal and Chase introduced a new security notion applicable to pair encodings called the symbolic property [2]. They also showed how to adapt the previous modular frameworks [1, 5] to define a compiler that takes pair encodings satisfying the symbolic property and produces fully secure predicate encryption schemes under the q-ratio assumption, a new q-type assumption proposed by them that is implied by other assumptions of this kind [27]. This symbolic property can be seen as a generalization of the “trick” that we have used in Example 1 to argue the security of the encoding. The main difference is that scalar variables in the PES may be substituted by vectors or matrices (not necessarily scalars as in our example) in such a way that, after the substitution, all the polynomials evaluate to zero, but there is an extra constraint relating the inner product of the vectors that replaced the special variables that guarantees that \(\alpha s_0\) is non-zero. As mentioned by Attrapadung [6], the above methodology generalizes the well-known Boneh-Boyen cancellation technique for identity-based encryption [12]. What is remarkable about this idea is that the substitution can be used as a “witness” or “certificate” (as coined by the authors of [2]) of the security of the scheme. Furthermore, Agrawal and Chase also showed that any pair encoding that is not trivially broken satisfies the symbolic property, a result that is closely related to the algebraic characterization of privacy on predicate encodings from [3].
It may seem that after these relevant results on pair encodings, and the similarity with those in the framework of predicate encodings, we are in a position to define a generic negation transformation for pair encodings. However, the more involved structure of pair encodings makes it difficult to find and prove a valid conversion. In fact, recent works have considered the problem of designing such a general negation to be non-trivial (see [6, Appendix L.5]), since in the framework of pair encodings it is generally hard to find the mentioned “certificates” that can be interpreted as a short proof of security. (Note that any possible NOT transformation would, at least implicitly, use such certificates as decryption credentials for the transformed encoding, whereas the decryption credentials of the original encoding would become the security certificate of the negated one.)
In order to construct a valid negation of pair encodings, we first need to treat them in a simplified manner, closer to linear algebra. To do so, we provide an algebraic characterization of pair encodings (Sect. 4), whose security can be expressed as a system of matrix equations, very similar to the statement i) from Lemma 2. Intuitively, we split the polynomials produced by the encoding into layers, each being a matrix that corresponds to one of the (common, lone or non-lone) variables. We then show how the security of the scheme can be expressed as a linear system involving these matrices. Our characterization makes an structural assumption on the form of the pair encoding (that can be made without loss of generality and has been used in the literature for other purposes [2, 6]). Namely, we assume that \(\mathsf{EncKey}\) only produces one polynomial that depends on \(\alpha \), which is of the form \(\alpha + r_1 b_1\). This assumption introduces a “symmetry” between the nature of key and ciphertext polynomials (now that the special variable \(\alpha \) is out of the way) that allows us to express the security of the PES as the symmetric algebraic statement of Definition 3. The next step is to leverage Lemma 1 in order to prove our following lemma, linking the inexistence of a solution to the system in i) with the existence of a solution to ii). This is the main tool on which we base our negation transformation. The last (but non-trivial) step is to define a new encoding (in algebraic form) such that the solution from statement ii) serves as a decryption credential for it.
Lemma 2
Let K be a field, let \(n \in \mathbb {N}\) and let \(\{A_i, B_i, C_i\}_{i \in [n]}\), \(\hat{A}, \hat{B}\) be matrices:

for certain \(\ell ,m,r,s,\hat{m},\hat{r} \in \mathbb {N}\) and every \(i \in [n]\). The following are equivalent:
-
i)
There do not exist X, Y with \(X \in K^{r \times \ell }\), \(Y \in K^{s \times m}\) such that:
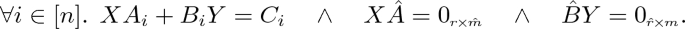
-
ii)
There exist \(Z_1,\dots ,Z_n \in K^{m \times r}\) and
 ,
,  such that
such that 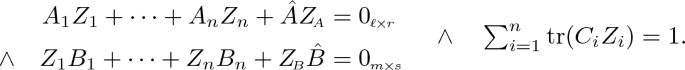
Proof
Let f be the linear map defined as
Observe that the first statement of the lemma is equivalent to saying that

which, by Lemma 1 is equivalent to the existence of \(\varphi : W \rightarrow K\), where in this case  , such that
, such that

which is equivalent to the existence of matrices \(Z_1,\dots ,Z_n \in K^{m \times r}\) and  ,
,  such that
such that


which is equivalent to the second statement of the lemma, quod erat demonstrandum. To see why, note that Eq. (2) is present in both cases and observe that if the second statement of the lemma holds, then (for any X, Y) we have

where in \(\dag \) we have used the fact that the trace is invariant under cyclic permutations. Finally, to see the converse, note that if Eq. (1) holds for any X,Y, it must hold for  , which would imply that for every \(X \in K^{r\times \ell }\),
, which would imply that for every \(X \in K^{r\times \ell }\),

but that can only happen if  is the zero matrix.
is the zero matrix.
Analogously, evaluating (1) on  , we get
, we get

for every \(Y \in K^{s \times m}\), which can only happen if  is the null matrix. \(\square \)
is the null matrix. \(\square \)
4 Characterization of Pair Encodings
In this section we propose a characterization of pair encodings that will be used to define our generic transformation for the negated predicate.
The first step towards our characterization is to assume that only one polynomial from \(\mathsf{EncKey}\) depends on \(\alpha \) and is of the form \(\alpha + r_1b_1\). This assumption is without loss of generalityFootnote 5, and has been utilized before in the literature [2, 6]. The rest of polynomials can be expressed as \(\varvec{k} = B_y \varvec{r} + C_y \hat{\varvec{r}}\), for some matrix \(B_y\) whose terms are linear polynomials in \(\mathbb {Z}_N[b_1,\dots ,b_n]\), and some matrix \(C_y\) with coefficients in \(\mathbb {Z}_N\). Given that \(\alpha + r_1b_1\) is always present, for the sake of notation, we redefine \(m_3\) to be the total number of polynomials produced by \(\mathsf{KeyGen}\) excluding \(\alpha + r_1b_1\). Similarly, the polynomials from \(\mathsf{EncCt}\) can be expressed as \(\varvec{c} = B'_x \varvec{s} + C'_x \hat{\varvec{s}}\). Such an analogy in the form of \(\varvec{k}\) and \(\varvec{c}\) (only achieved after getting rid of variable \(\alpha \)) allows us to express the encodings in an algebraic form, amenable to be combined with different results of linear algebra.
Definition 3
(Algebraic pair encoding). An algebraic pair encoding scheme for a predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\) indexed by \(\kappa = (N,\mathsf{par})\) consists of the following deterministic and efficiently computable algorithms:
-
\(\mathsf{Param}^{\mathsf{alg}}(\mathsf{par})\): on input certain parameters outputs an integer \(n \in \mathbb {N}\).
-
\(\mathsf{EncKey}^{\mathsf{alg}}(N,x)\): on input \(N \in \mathbb {N}\) and \(x \in \mathcal{X}_{(N,\mathsf{par})}\), outputs a list of \(n{+}1\) matrices with coefficients in \(\mathbb {Z}_N\), \((B_1, \dots , B_n,C)\), where \(B_j\) has dimension \(m_3 \times m_1\), for \(j \in [n]\), and \(C\) has dimension \(m_3 \times m_2\).
-
\(\mathsf{EncCt}^{\mathsf{alg}}(N,y)\): on input \(N \in \mathbb {N}\) and \(y \in \mathcal{Y}_{(N,\mathsf{par})}\), outputs a list of \(n{+}1\) matrices with coefficients in \(\mathbb {Z}_N\), \((B'_1, \dots , B'_n, C')\), where \(B'_j\) has dimension \(w_3 \times w_1\), for \(j \in [n]\), and \(C'\) has dimension \(w_3 \times w_2\).
Furthermore, for every \(\kappa = (N,\mathsf{par})\), \(x \in \mathcal{X}_{\kappa }\) and \(y \in \mathcal{Y}_{\kappa }\), \(P_{\kappa }(x,y) = 1\) if and only if there exist matrices \(E \in \mathbb {Z}_N^{w_1 \times m_3}\) and \(E' \in \mathbb {Z}_N^{w_3 \times m_1}\) such that

where \((B_1,\dots ,B_n,C) \leftarrow \mathsf{EncKey}^{\mathsf{alg}}(N,x)\) and \((B'_1,\dots ,B'_n,C') \leftarrow \mathsf{EncCt}^{\mathsf{alg}}(N,y)\).
Theorem 1
(Characterization). There exists a pair encoding for predicate family \(P_{\kappa }\) if and only if there exists an algebraic pair encoding for \(P_{\kappa }\). Furthermore, there is an efficient conversion in both directions.
The above theorem is a consequence of our following two lemmas.
Lemma 3
(From algebraic to standard). Let \((\mathsf{Param}^{\mathsf{alg}}, \mathsf{EncKey}^{\mathsf{alg}}, \mathsf{EncCt}^{\mathsf{alg}})\) be an algebraic pair encoding scheme for predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\). Then, algorithms \((\mathsf{Param}, \mathsf{EncKey}, \mathsf{EncCt}, \mathsf{Pair})\) (defined below) constitute a pair encoding scheme for \(P_{\kappa }\).
-
 run \(n \leftarrow \mathsf{Param}^{\mathsf{alg}}(\mathsf{par})\), output n and let \(\varvec{b} = (b_1,\dots ,b_n)\).
run \(n \leftarrow \mathsf{Param}^{\mathsf{alg}}(\mathsf{par})\), output n and let \(\varvec{b} = (b_1,\dots ,b_n)\). -
 run \((B_1,\dots , B_n, C) \leftarrow \mathsf{EncKey}^{\mathsf{alg}}(N,x)\), output the vector of polynomials given by \(\alpha + r_1b_1\) and \((b_1 B_1 + \dots + b_n B_n)\varvec{r} + C \hat{\varvec{r}}\), where \(\varvec{r} = (r_1,\dots ,r_{m_{\!\!\,1}})\) and \(\hat{\varvec{r}} = (\hat{r}_1,\dots ,\hat{r}_{m_{\!\!\,2}})\).
run \((B_1,\dots , B_n, C) \leftarrow \mathsf{EncKey}^{\mathsf{alg}}(N,x)\), output the vector of polynomials given by \(\alpha + r_1b_1\) and \((b_1 B_1 + \dots + b_n B_n)\varvec{r} + C \hat{\varvec{r}}\), where \(\varvec{r} = (r_1,\dots ,r_{m_{\!\!\,1}})\) and \(\hat{\varvec{r}} = (\hat{r}_1,\dots ,\hat{r}_{m_{\!\!\,2}})\). -
 run \((B'_1,\dots ,B'_n,C') \leftarrow \mathsf{EncCt}^{\mathsf{alg}}(N,y)\), output the vector of polynomials given by \((b_1 B'_1 + \dots + b_n B'_n)\varvec{s} + C' \hat{\varvec{s}}\), where \(\varvec{s} = (s_0,\dots ,s_{w_{\!\!\,1}{-}1})\) and \(\hat{\varvec{s}} = (\hat{s}_1,\dots ,\hat{s}_{w_{\!\!\,2}})\).
run \((B'_1,\dots ,B'_n,C') \leftarrow \mathsf{EncCt}^{\mathsf{alg}}(N,y)\), output the vector of polynomials given by \((b_1 B'_1 + \dots + b_n B'_n)\varvec{s} + C' \hat{\varvec{s}}\), where \(\varvec{s} = (s_0,\dots ,s_{w_{\!\!\,1}{-}1})\) and \(\hat{\varvec{s}} = (\hat{s}_1,\dots ,\hat{s}_{w_{\!\!\,2}})\). -
 find matrices \((E,E')\) satisfying Eq. (3), that exist if and only if \(P_{\kappa }(x,y) = 1\), output
find matrices \((E,E')\) satisfying Eq. (3), that exist if and only if \(P_{\kappa }(x,y) = 1\), output  .
.
Proof
Observe that the structural constraints on the polynomials of \(\mathsf{EncKey}\) and \(\mathsf{EncCt}\) are satisfied. To see reconstructability, simply note that for any \(N \in \mathbb {N}\), \(x \in \mathcal{X}_{\kappa }\) and \(y \in \mathcal{Y}_{\kappa }\) with \(P(x,y) = 1\), and for \((E,E')\) satisfying (3), it holds:

For security, note that if the new pair encoding were trivially broken, there would exist a pair \((x,y) \in \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa }\) with \(P_{\kappa }(x,y) = 0\), and matrices \(E,E'\) satisfying Eq. (3). For details about this fact, we refer to the proof Lemma 4 (the part about reconstructability). \(\square \)
Lemma 4
(From standard to algebraic). Let \((\mathsf{Param}, \mathsf{EncKey}, \mathsf{EncCt}, \mathsf{Pair})\) be a pair encoding schemeFootnote 6 for predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\). Then, algorithms \((\mathsf{Param}^{\mathsf{alg}}, \mathsf{EncKey}^{\mathsf{alg}}, \mathsf{EncCt}^{\mathsf{alg}})\) (defined below) constitute an algebraic pair encoding scheme for \(P_{\kappa }\).
-
 .
. -
 run \((\alpha + r_1b_1, \varvec{k}) \leftarrow \mathsf{EncKey}(N,x)\), and let \(m_3 = |\varvec{k}|\). For \(j \in [n]\), define matrix \(B_j\) as the matrix whose element at the \(\ell \)-th row and i-th column is the coefficient of monomial \(r_ib_j\) in polynomial \(k_{\ell }\). Define \(C\) as the matrix whose element at the \(\ell \)-th row and \(i'\)-th column is the coefficient of monomial \(\hat{r}_{i'}\) in polynomial \(k_{\ell }\), for \(i \in [m_1]\), \(i' \in [m_2]\) and \(\ell \in [m_3]\). Output \((B_1,\dots , B_n, C)\).
run \((\alpha + r_1b_1, \varvec{k}) \leftarrow \mathsf{EncKey}(N,x)\), and let \(m_3 = |\varvec{k}|\). For \(j \in [n]\), define matrix \(B_j\) as the matrix whose element at the \(\ell \)-th row and i-th column is the coefficient of monomial \(r_ib_j\) in polynomial \(k_{\ell }\). Define \(C\) as the matrix whose element at the \(\ell \)-th row and \(i'\)-th column is the coefficient of monomial \(\hat{r}_{i'}\) in polynomial \(k_{\ell }\), for \(i \in [m_1]\), \(i' \in [m_2]\) and \(\ell \in [m_3]\). Output \((B_1,\dots , B_n, C)\). -
 run \(\varvec{c} \leftarrow \mathsf{EncCt}(N,y)\). For \(j \in [n]\), define matrix \(B'_j\) as the matrix whose element at the \(\ell \)-th row and \((i{+}1)\)-th column is the coefficient of monomial \(s_ib_j\) in polynomial \(c_{\ell }\). Define \(C'\) as the matrix whose element at the \(\ell \)-th row and \(i'\)-th column is the coefficient of monomial \(\hat{s}_{i'}\) in polynomial \(c_{\ell }\), for \(i \in [0,w_{\!\!\,1}{-}1]\), \(i' \in [w_{\!\!\,2}]\) and \(\ell \in [w_3]\). Output \((B'_1,\dots , B'_n, C')\).
run \(\varvec{c} \leftarrow \mathsf{EncCt}(N,y)\). For \(j \in [n]\), define matrix \(B'_j\) as the matrix whose element at the \(\ell \)-th row and \((i{+}1)\)-th column is the coefficient of monomial \(s_ib_j\) in polynomial \(c_{\ell }\). Define \(C'\) as the matrix whose element at the \(\ell \)-th row and \(i'\)-th column is the coefficient of monomial \(\hat{s}_{i'}\) in polynomial \(c_{\ell }\), for \(i \in [0,w_{\!\!\,1}{-}1]\), \(i' \in [w_{\!\!\,2}]\) and \(\ell \in [w_3]\). Output \((B'_1,\dots , B'_n, C')\).
Proof
Note that the structural constraints on the PES enforce that for every \(N \in \mathbb {N}\), \(x \in \mathcal{X}_{\kappa }\) and \(y \in \mathcal{Y}_{\kappa }\), \((\alpha + r_1b_1, \varvec{k}) \leftarrow \mathsf{EncKey}(N,x)\), \(\varvec{c} \leftarrow \mathsf{EncCt}(N,y)\), \((B_1, \dots , B_n, C) \leftarrow \mathsf{EncKey}^{\mathsf{alg}}(N,x)\), \((B'_1, \dots , B'_n, C') \leftarrow \mathsf{EncCt}^{\mathsf{alg}}(N,y)\), it holds:
Now, note that, due to reconstructability of the original encoding, for any \(N \in \mathbb {N}\), \(x \in \mathcal{X}_{\kappa }\) and \(y \in \mathcal{Y}_{\kappa }\) such that \(P(x,y) = 1\), if we let  , it holds:
, it holds:

which is equivalent to 
 , but then:
, but then:

and because the above equality must hold symbolically, it must be the case that  and
and  for every \(j \in [2,n]\). Moreover,
for every \(j \in [2,n]\). Moreover,  and
and  . Finally, note that the non-reconstructability of the original encoding enforces that the above system does not have a solution when \(P_{\kappa }(x,y) = 0\). \(\square \)
. Finally, note that the non-reconstructability of the original encoding enforces that the above system does not have a solution when \(P_{\kappa }(x,y) = 0\). \(\square \)
5 Generic Negation of Algebraic Pair Encodings
Although the general definition of pair encodings defines polynomials with coefficients over \(\mathbb {Z}_N\) for an arbitrary integer \(N \in \mathbb {N}\). In this section we assume that N is a prime number and write p instead. The reason is that our transformation for the negated encoding leverages a result from linear algebra (our Lemma 2) which requires that the underlying structure be a field. Note that this restriction does not significantly weaken our result, since prime-order groups are preferred over composite over groups.
Theorem 2
Let \((\mathsf{Param}^{\mathsf{alg}}, \mathsf{EncKey}^{\mathsf{alg}}, \mathsf{EncCt}^{\mathsf{alg}})\) be an algebraic pair encoding for a predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\). The encoding \((\bar{\mathsf{Pair}}, \bar{\mathsf{EncKey}}, \bar{\mathsf{EncCt}})\) described in Fig. 1 is an algebraic pair encoding for the predicate family \(\bar{P}_{\kappa }\) given by \(\bar{P}(x,y) = 1 \Leftrightarrow P(x,y) = 0\) for all \(x \in \mathcal{X}_{\kappa }\), \(y \in \mathcal{Y}_{\kappa }\).
Proof
We need to show that whenever \(P(x,y) \,{=}\, 0\), there exist matrices \(\bar{E}\) and \(\bar{E}'\) of dimension \(w_{\!\!\,1}{\times }(1{+}m_{\!\!\,1}n {+} m_{\!\!\,2})\) and \((w_{\!\!\,1}{+}w_{\!\!\,1}n{+}w_{\!\!\,2}){\times } m_{\!\!\,1}\) respectively, with coefficients in \(\mathbb {Z}_p\), such that:

where \((\bar{B}_0,\dots ,\bar{B}_{n{+}1},\bar{C}) \leftarrow \bar{\mathsf{EncKey}}(p,x)\), \((\bar{B}'_0,\dots ,\bar{B}'_{n{+}1},\bar{C}') \leftarrow \bar{\mathsf{EncCt}}(p,y)\). Now, our original encoding guarantees that \(P(x,y) = 0\) if and only if there do not exist matrices \(E\), \(E'\) such that:

for \((B_1, \dots , B_n, C) \leftarrow \mathsf{EncKey}(p,x)\) and \((B'_1, \dots , B'_n, C') \leftarrow \mathsf{EncCt}(p,y)\). But that is equivalent, in virtue of Lemma 2, to the existence of \(Z_1,\dots ,Z_n \in \mathbb {Z}_p^{m_{\!\!\,1}\times w_{\!\!\,1}}\),  and
and  such that:Footnote 7
such that:Footnote 7

Now, for certain \(\varvec{v} \in \mathbb {Z}_p^{w_{\!\!\,1}}\) and \(V \in \mathbb {Z}_p^{m_{\!\!\,1}\times w_{\!\!\,1}}\) we can consider the matrices:

and observe that they satisfy all the equations in (4) if we set \(\varvec{v}\) to be the first column of  multiplied by \({-}1\) (with the exception that \(v_1 = 0\)) and we set V to be the null matrix except for its first row, that is set to
multiplied by \({-}1\) (with the exception that \(v_1 = 0\)) and we set V to be the null matrix except for its first row, that is set to  .
.
To conclude, observe that the converse is also true, i.e., if the equations in (4) admit a solution, then (5) is satisfiable. To see this, note that the left-hand side equations of (4) imply that any solution to them must be of the form of (6) for certain \(\varvec{v}\), V,  . Furthermore, the right-hand side equations of (4) guarantee that such matrices \(Z_i\), for \(i \in \{1,\dots ,n,\text {{A}}, \text {{B}}\}\) satisfy (5). Therefore, we have shown that \(P(x,y) = 0\) iff the equations in (4) have a solution. \(\square \)
. Furthermore, the right-hand side equations of (4) guarantee that such matrices \(Z_i\), for \(i \in \{1,\dots ,n,\text {{A}}, \text {{B}}\}\) satisfy (5). Therefore, we have shown that \(P(x,y) = 0\) iff the equations in (4) have a solution. \(\square \)
Observe that, in general, if \((m_{\!\!\,1}, m_{\!\!\,2}, m_{\!\!\,3}, w_{\!\!\,1}, w_{\!\!\,2}, w_{\!\!\,3}, n)\) are the parameters of the original encoding, our negated transformation will produce an encoding with parameters \(\bar{n} = n{+}2\) and:
Note that, although the negated encoding may seem to have a much larger size compared to the original one, the matrices associated to the new encoding are actually very sparse and thus, our transformation will barely impact the performance of the ABE scheme build from the negated encoding.
Furthermore, note that our generic negation is compatible with the promising dynamic pair encoding composition technique very recently proposed by Attrapadung [6]. We believe our new transformation complements his work which could only achieve non-monotone formulae composition in a semi-generic (but dynamic) manner, since the composition had to rely on encodings for which a negated version was available.
6 Consequences of Our Results
Since Attrapadung introduced the notion of pair encoding schemes and the modular framework for constructing fully secure ABE from them [4], there have been several works [1, 2, 6] refining this framework and proposing new encoding schemes for different predicates, that sometimes enjoy extra properties (e.g., constant ciphertext size). The community has made a significant effort on building the negated version of most of the encodings from the literature, which in some cases is significantly more involved. However, there are still encodings for which not negation is known. Our generic transformation puts an end to this situation, since we can now take any encoding and immediately obtain its negated counterpart. A relevant example of a PES with (previously) unknown negation is the case of doubly spatial encryption.
6.1 PES for Negated Doubly Spatial Encryption
Doubly spatial encryption [20] is an important primitive that generalizes both spatial encryptionFootnote 8 [13] and negated spatial encryption, defined by Attrapadung and Libert [8]. It can be used to capture complex predicates and build flexible revocation systems. Its relevance is evidenced by the fact that a variant of it, called key-policy over doubly spatial encryption (defined by Attrapadung [4]), generalizes KP-ABE and leads to efficient unbounded KP-ABE schemes with large universes and KP-ABE with short ciphertexts. Given a field K, the doubly spatial predicate, over sets  and
and  , \(P((\varvec{x},X),(\varvec{y},Y))\), is defined as 1 if and only if the affine spaces \(\varvec{x} + \mathrm{span}(X)\) and \(\varvec{y} + \mathrm{span}(Y)\) intersect.
, \(P((\varvec{x},X),(\varvec{y},Y))\), is defined as 1 if and only if the affine spaces \(\varvec{x} + \mathrm{span}(X)\) and \(\varvec{y} + \mathrm{span}(Y)\) intersect.
In the same way that negated spatial encryption generalizes spatial encryption and serves as its revocation analogue, unifying existing primitives (for example, it subsumes non-zero-mode IPE), negated doubly spatial encryption is a more expressive and very powerful primitive that deserves our attention. However, to the best of our knowledge, there does not exist a general pair encoding scheme for negated doubly spatial encryption in the literature. Attrapadung [4] provided a pair encoding for doubly spatial encryption and a negated version, for which he had to restrict one of the attributes (originally the ciphertext attribute) to be confined to just a vector instead of a general affine space. This encoding gave birth to the first fully-secure negated spatial encryption scheme, but it is not the negated version of doubly spatial encryption. In the rest of this section, we describe how to obtain the first, to the best of our knowledge, pair encoding scheme for negated doubly spatial encryption without restrictions.
We start from the following PES for doubly spatial encryption (over \(\mathbb {Z}_N\)) from [4]. (With \(m_1 = 1\), \(m_2 = 0\), \(m_3 = \ell '{+}1\) and \(w_1 = 1\), \(w_2 = 0\), \(w_3 = \ell {+}1\).)

We refer to [4] for a proof of security and reconstructability.
In order to apply our negated transformation to this encoding, we first need to modify it so that it satisfies our structural assumption (see the first paragraph of our Sect. 4). For this, we can apply the conversion defined by Attrapadung [6, Section 4]. If we do so, we will get and encoding with \(m_1 = 2\), \(m_2 = 0\), \(m_3 = \ell '{+}1\) and \(w_1 = 2\), \(w_2 = 0\), \(w_3 = \ell {+}2\) that looks as follows (after renaming some variables):

Applying our negation transformation to the above encoding, we obtain the pair encoding described in Fig. 3 (presented in Appendix A), where we have renamedFootnote 9 some common variables for the sake of readability. In Appendix A.1 we show how we can slightly simplify the encoding from Fig. 3 and derive the encoding that we present in Fig. 2. Our Theorem 2 guarantees that it is a valid encoding for the negated doubly spatial encryption predicate, but we provide an independent proof in Appendix A.2.
The process of applying our generic negation by hand may seem tedious (but it seems necessary if we want to give an explicit description of an encoding that is parametric in size, like the one for negated doubly spatial encryption). However, notice that this process can be easily delegated to a computer, which does not need to have an explicit definition of the negated encoding. Instead, it can start from the non-negated encoding and apply the negation on the fly.
6.2 Other Implications of Our Transformation
Expressivity of Pair Encoding Schemes. A very important and long-standing open question about pair encoding schemes is how expressive they really are. They have led to breakthrough constructions such as constant-size ciphertext KP-ABE (with large universes) [4], fully-secure functional encryption for regular languages [4], completely-unbounded KP-ABE for non-monotone span programs (NSP) over large universes [6]. However, it is still unknown where their limit is. We believe our results bring new insight to answer this question and improve our understanding of pair encodings and their expressivity.
For example, there exist pair encodings for regular languages, where key attributes represent deterministic finite-state automata (DFSA), ciphertext attributes represent (arbitrarily long) words, and the predicate is defined as 1 iff the automaton accepts the word. However, building ABE for context-free languages (CFL) from pairings is still an important open problem, so it would be desirable to understand whether CFL can be constructed from pair encoding schemes. Our results imply that:
The set of predicates that can be expressed with PES is closed under negation.
This tells us new non-trivial information about what predicates can be expressed with a PES. In particular, it suggests that building PES for context-free languages may be harder than we think or even impossible. Note that context-free languages are not closed under complementation [21] and, consequently, if we can build a PES for CFL, we could build a PES for a predicate class that is strictly more powerful than CFL (at least the union of CFL and coCFLFootnote 10). Of course, this reasoning does not allow us to roundly conclude anything, but it serves as an evidence of the difficulty of this problem.
Potential Performance Improvements. Not only does our generic transformation broaden the class of predicates that can be captured by pair encoding schemes, but it also can lead to efficiency improvements in actual ABE constructions. Observe the peculiar structure of the negated encodings produced with our transformation from Fig. 1. All of the matrices associated to common variables, \(\bar{B}_i\) and \(\bar{B}'_i\), have a fixed structure that is independent of the key attribute and the ciphertext attribute respectively (only the part associated to lone variables is dependent on the attributes). Furthermore, observe that they are arguably sparse. We can conclude that all pair encoding schemes admit a representation (an encoding for the same predicate) in this form, since we can always apply our transformation twice, leveraging the fact that the negation is an involution. However, in many cases it may be simpler to arrive at the mentioned structure more directly, by simply applying linear combinations and variable substitutions. What is important is that such a representation always exists.
This observation opens the possibility of splitting the computation of ciphertexts and secret keys into an offline part (before the attribute value is known) and an online part (once the attribute has been determined). Observe that such a strategy can bring significant performance improvements, given that operations involving common variables require a group exponentiation per matrix coefficient (since the common variables are available in the master public key in the form of group elements, with unknown discrete logarithm)Footnote 11, whereas operations involving lone variables can be batched together, reducing the number of exponentiations (one can do linear algebra over the field \(\mathbb {Z}_N\) and perform one single exponentiation at the end). This is because the value of lone variables is freshly sampled during the computation and, therefore, known. This approach would not only reduce the online encryption and key generation time, but also the total time, since the offline computation can be reused for different attributes after it has been computed once.
7 Conclusions and Future Work
Pair encodings are a simple, yet powerful, tool for building complex fully secure attribute-based encryption schemes. In this work, we have presented a generic transformation that takes any pair encoding scheme and negates its predicate. This construction finally solves a problem that was open since 2015 [10] and that has been considered to be non-obvious by several recent works [2, 6]. Along the way, we have defined new results that improve our understanding of pair encodings and can be of independent interest, including a new encoding (previously unknown) for negated doubly spatial encryption, obtained with our transformation.
We propose several directions for future work. On the theoretical side, it would be interesting to explore whether our negation transformation can lead to simpler encodings as in [3]. In their work, Ambrona et al. show how, applying their negation to an encoding for monotone span programs [22] and after performing some simplifications, the new encoding is more compact and leads to an ABE that is twice as fast as the original one. The fact that the encoding is negated does not spoil its usage, since span programs are closed under negation and can be tweaked to implement the original functionality. The same technique of negating the encoding also results into a successful simplification in the case of arithmetic span programs. We believe the same kind of phenomenon can occur when negating pair encodings with our technique, potentially producing simpler encodings.
A very recent work [9] provides a new framework for constructing ABE schemes that support unbounded and dynamic predicate compositions whose security is proven under the standard matrix Diffie-Hellman assumption (generalizing the result by Attrapadung [6], which achieved the same kind of composition under the q-ratio assumption). The work by Attrapadung and Tomida [9] enables generic conjunctive and disjunctive compositions (which lead to monotone Boolean formula compositions). Extending their techniques in order to design a generic negation under standard assumptions is a very appealing direction for future work. (Note that the negation that we have provided in this work is applicable to the framework of Agrawal and Chase [2], thus it also relies on the less standard q-ratio assumption.)
On the practical side, it would be interesting to implement and evaluate the performance improvements that we propose in Sect. 6.2, exploiting the singular structure of the encodings produced by our transformation.
Notes
- 1.
In fact, it is known that predicate encodings are a subclass of pair encodings [3].
- 2.
In some literature, the number of non-lone ciphertext variables is defined as \(w_1{+}1\), since the special variable \(s_0\) is treated separately. Observe that our vector of non-lone variables ranges from \(s_0\) to \(s_{w_1{-}1}\), this is for the sake of notation in further sections.
- 3.
Recall that
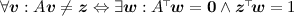 for all compatible A and \(\varvec{z}\).
for all compatible A and \(\varvec{z}\). - 4.
That way, the witness of non-reconstructability can be used as the linear combination for decryption (reconstructability) in the negated encoding and vice versa: the solution for reconstructability can be used as the witness of security in the negated encoding.
- 5.
An easy way of arguing that this is w.l.o.g. is to apply the generic dual transformation defined in [10] twice. (Note that the dual operation is an involution and a double application of it would preserve the original predicate.).
- 6.
Recall that we are assuming, without loss of generality, that the first polynomial produced by \(\mathsf{EncKey}\) is \(\alpha + r_1b_1\) and that \(\alpha \) does not appear anywhere else.
- 7.
To see why, set the matrices in Lemma 2 to
 ,
,  , for \(i \in [n]\) and
, for \(i \in [n]\) and 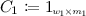 ,
,  for \(j \in [2,n]\). Also,
for \(j \in [2,n]\). Also,  and
and 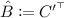 .
. - 8.
Spatial encryption is already a quite powerful predicate, that generalizes hierarchical identity-based encryption (HIBE).
- 9.
Before applying the transformation, we rename \(b_0 \mapsto t\), \(b_{d{+}1} \mapsto u\), \(b_{d{+}2} \mapsto v\). After the transformation, the two new common variables are named \(b_0\) and w respectively.
- 10.
We denote by coCFL the class of languages whose complement is context-free.
- 11.
See the ABE compiler from PES described in Appendix B.2.
References
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part II. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_10
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 627–656. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_22
Ambrona, M., Barthe, G., Schmidt, B.: Generic transformations of predicate encodings: constructions and applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 36–66. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_2
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Attrapadung, N.: Dual system encryption framework in prime-order groups via computational pair encodings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 591–623. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_20
Attrapadung, N.: Unbounded dynamic predicate compositions in attribute-based encryption. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 34–67. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_2
Attrapadung, N., Imai, H.: Dual-policy attribute based encryption. In: Abdalla, M., Pointcheval, D., Fouque, P.-A., Vergnaud, D. (eds.) ACNS 2009. LNCS, vol. 5536, pp. 168–185. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01957-9_11
Attrapadung, N., Libert, B.: Functional encryption for inner product: achieving constant-size ciphertexts with adaptive security or support for negation. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 384–402. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_23
Attrapadung, N., Tomida, J.: Unbounded dynamic predicate compositions in ABE from standard assumptions. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020, Part III. LNCS, vol. 12493, pp. 405–436. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64840-4_14
Attrapadung, N., Yamada, S.: Duality in ABE: converting attribute based encryption for dual predicate and dual policy via computational encodings. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 87–105. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_5
Beimel, A.: Secret-sharing schemes: a survey. In: Chee, Y.M., et al. (eds.) IWCC 2011. LNCS, vol. 6639, pp. 11–46. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20901-7_2
Boneh, D., Boyen, X.: Efficient selective identity-based encryption without random oracles. J. Cryptol. 24(4), 659–693 (2011)
Boneh, D., Hamburg, M.: Generalized identity based and broadcast encryption schemes. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 455–470. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_28
Chatterjee, S., Mukherjee, S., Pandit, T.: CCA-secure predicate encryption from pair encoding in prime order groups: generic and efficient. In: Patra, A., Smart, N.P. (eds.) INDOCRYPT 2017. LNCS, vol. 10698, pp. 85–106. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-71667-1_5
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Chen, J., Wee, H.: Dual system groups and its applications – compact HIBE and more. Cryptology ePrint Archive, Report 2014/265 (2014). http://eprint.iacr.org/2014/265
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. Available as Cryptology ePrint Archive Report 2006/309
Hamburg, M.: Spatial encryption. Cryptology ePrint Archive, Report 2011/389 (2011). http://eprint.iacr.org/2011/389
Hopcroft, J.E., Ullman, J.D.: Introduction to Automata Theory, Languages and Computation. Addison-Wesley, Boston (1979)
Karchmer, M., Wigderson, A.: On span programs. In: Proceedings of Structures in Complexity Theory, pp. 102–111 (1993)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Kim, J., Susilo, W., Guo, F., Au, M.H.: A tag based encoding: an efficient encoding for predicate encryption in prime order groups. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 3–22. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_1
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_27
Lewko, A., Waters, B.: Unbounded HIBE and attribute-based encryption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 547–567. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_30
Lewko, A.B., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_12
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Ning, P., De Capitani di Vimercati, S., Syverson, P.F. (eds.) ACM CCS 2007, pp. 195–203. ACM Press, October 2007
Rouselakis, Y., Waters, B.: Practical constructions and new proof methods for large universe attribute-based encryption. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 463–474. ACM Press, November 2013
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Waters, B.: Functional encryption for regular languages. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 218–235. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_14
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Acknowledgment
I would like to express my sincere gratitude to Nuttapong Attrapadung, for very fruitful discussions at the early stages of this project, and for pointing out that the transformation described herein would lead to an encoding for negated doubly spatial encryption. I would also like to thank Mehdi Tibouchi, for his help with the formulation of Lemma 1, which led to a simple proof for Lemma 2; and Elena Gutiérrez, for her advice on automata theory, and for all her feedback. Finally, I would like to thank the anonymous reviewers of PKC 2021, for their valuable time and multiple suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Pair Encoding for Negated Doubly Spatial Encryption
1.1 A.1 Building the Encoding
A direct application of our negated transformation (Fig. 1) to the encoding for doubly spatial encryption from [4] (after minor modifications so that it satisfies our structural constraints) leads to the encoding from Fig. 3. This encoding can be simplified, as the following reasoning shows that not all the polynomials are needed for reconstructability.
The only way to get polynomial \(s_0r_1b_0\) (and consequently \(\alpha s_0\)) as a linear combination of polynomials from \(L = \varvec{s} \otimes \varvec{k} \,\cup \, \varvec{c} \otimes \varvec{r}\) is through the two first polynomials in the key (multiplied by \(s_0\)): \(s_0r_1b_0 + s_0r_1w\) and \(s_0r_1b_0 + s_0r_1t\). For that, we need to express monomial \(s_0r_1w\) or monomial \(s_0r_1t\) as a linear combination of other polynomials in L. The former is impossible to obtain (since monomial \(s_0r_1w\) does not appear in any other polynomial in L). The latter can be achieved only through polynomial \(r_1s_0t - r_1\hat{s}_1 \in L\). Again, that requires to arrive at polynomial \(r_1\hat{s}_1\), which is present only in \(r_1s_1v - r_1\hat{s}_1\). Furthermore, \(r_1s_1v\) can only be (additionally) found in \(s_1r_1v + s_1\hat{r}_1\). However, \(s_1\hat{r}_1\) is present in several polynomials in L, namely: \(s_1r_2u + s_1\hat{r}_1\) and \(s_1(Y_j\hat{\varvec{r}}' + r_2b_{j} + \hat{r}_1 {y}_j)_{j \in [d]}\). The former contains a monomial, \(s_1r_2u\), that only additionally appears in \(r_2s_1u - r_2\hat{s}_2\), but \(r_2\hat{s}_2\) is only present in polynomials \(r_2(X_j\hat{\varvec{s}}' - s_1 b_{j} + \hat{s}_2 {x}_j)_{j \in [d]}\). Consequently, reconstructability will be possible if there exist coefficients \(\beta _j\) and \(\gamma _j\) for all \(j \in [0,d]\) such that:

Considering the different monomials in both sides of the equation, we deduce:

Consequently, reconstructability is possible if there exist coefficients \(\beta _j\) for all \(j \in [d]\) such that:

But this is equivalent to \(\varvec{y}-\varvec{x} \notin \mathrm{span}(Y) \cup \mathrm{span}(X)\) (see Lemma 1) which holds if and only if the predicate is true, as needed.
All the polynomials in the key and the ciphertext which have not been used for reconstructability can be eliminated. Figure 2 describes the resulting encoding after this simplification.
1.2 A.2 Arguing Security
Our Theorem 2 guarantees that the encoding from Fig. 3 is secure. Note that removing polynomials cannot change security (only spoil reconstructability), so the simpler scheme presented in the main body (Fig. 2) must also be secure. Nevertheless, we provide an independent proof of its security, for the sake of completeness.
Proof
(Security of the encoding from Fig. 2). Assume the predicate is false, i.e., the affine spaces \(\varvec{x} + \mathrm{span}(X)\) and \(\varvec{y} + \mathrm{span}(Y)\) intersect. Let \(\varvec{z} \in \mathbb {Z}_N^{d}\) be a vector in their intersection and let \(\varvec{z_x} \in \mathbb {Z}_N^{\ell }\) and \(\varvec{z_y} \in \mathbb {Z}_N^{\ell '}\) be such that:
Observe that all the polynomials in \(\mathsf{EncKey}(N,(\varvec{y},Y))\) and \(\mathsf{EncCt}(N, (\varvec{x},X))\) (see Fig. 2) evaluate to zero on the following substitution:
but polynomial \(\alpha s_0\) evaluates to \(-1\) (\(\ne 0\)). As explained in Example 1, this is an evidence of the security of the encoding.
B Additional Definitions
1.1 B.1 Security of Attribute-Based Encryption
An ABE scheme is adaptively secure if there exists a negligible \(\epsilon \) such that for all PPT adversaries \(\mathcal{A}\), and all sufficiently large \(\lambda \in \mathbb {N}\), \(\mathsf{Adv}_{\mathcal{A}}^\mathsf{ABE}(\lambda ) < \epsilon (\lambda )\), where:

where the advantage is defined to be zero if some of the queries y made by \(\mathcal{A}\) to the \(\mathsf{KeyGen}\) oracle violates the condition \(P(x^\star ,y) = 0\).
1.2 B.2 Attribute-Based Encryption from Pair Encodings
In order to explain how to build attribute-based encryption from pair encodings, we need to introduce the notion of dual system groups (DSG) [2, 16, 17], since the compilers from pair encodings into ABE [1, 5] rely on DSG in a black-box way.
Dual System Groups
A dual system group is a tuple of six efficiently computable algorithms:
-
\(\mathsf{SampP}(1^\lambda , 1^n)\): on input the security parameter and an integer n, outputs public parameters \(\mathsf {pp}\) and secret parameters \(\mathsf {sp}\) such that:
- \(\circ \):
-
The public parameters, \(\mathsf {pp}\), include a triple of abelian groups \((\mathsf{G},\mathsf{H},\mathsf{G}_{\mathsf{t}})\) (that are \(\mathbb {Z}_p\)-modules for some \(\lambda \)-bits prime p), a non-degenerate bilinear map \(e : \mathsf{G}\times \mathsf{H}\rightarrow \mathsf{G}_{\mathsf{t}}\), an homomorphism \(\mu \) (defined over \(\mathsf{H}\)) and additional parameters required by \(\mathsf{SampP}\) and \(\mathsf{SampH}\).
- \(\circ \):
-
Given \(\mathsf {pp}\), it is possible to uniformly sample to \(\mathsf{H}\).
- \(\circ \):
-
The secret parameters, \(\mathsf {sp}\), include a distinguished element \(h^* \in \mathsf{H}\) (different from the unit) and additional parameters required by
 and
and  .
.
-
\(\mathsf{SampG}(\mathsf {pp})\) and
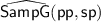 output an element from \(\mathsf{G}^{n{+}1}\).
output an element from \(\mathsf{G}^{n{+}1}\). -
\(\mathsf{SampH}(\mathsf {pp})\) and
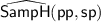 output an element from \(\mathsf{H}^{n{+}1}\).
output an element from \(\mathsf{H}^{n{+}1}\). -
\(\mathsf{SampGT}\) is a function defined from \(\mathrm{Im}(\mu )\) to \(\mathsf{G}_{\mathsf{t}}\).
Additional conditions are required for correctness and security:
-
projective: For all public parameters, \(\mathsf {pp}\), every \(h \in \mathsf{H}\) and all coin tosses \(\sigma \), it holds \(\mathsf{SampGT}(\mu (h); \sigma ) = e(g_0, h)\), where \((g_0, g_1,\dots ,g_n) \leftarrow \mathsf{SampG}(\mathsf {pp}; r)\).
-
associative: Let \((g_0,g_1,\dots ,g_n) \leftarrow \mathsf{SampG}(\mathsf {pp})\), \((h_0,h_1,\dots ,h_n) \leftarrow \mathsf{SampH}(\mathsf {pp})\), it holds \(e(g_0, h_i) = e(g_i, h_0)\) for every \(i \in [n]\).
-
\(\mathsf{H}\)-subgroup: \(\mathsf{SampH}(\mathsf {pp})\) is the uniform distribution over a subgroup of \(\mathsf{H}^{n{+}1}\).
-
orthogonality: \(h^* \in \mathrm{Kernel}(\mu )\).
-
non-degeneracy: For every \((h_0,h_1,\dots ,h_n) \leftarrow \mathsf{SampH}(\mathsf {pp})\), \(h^* \in \langle h_0 \rangle \). Furthermore, for every
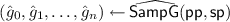 ,
, 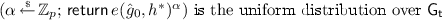 .
. -
left-subgroup indistinguishability: \((\mathsf {pp},\, \varvec{g}) \approx _{c}(\mathsf {pp},\, \varvec{g}{\cdot } \varvec{\hat{g}})\).
-
right-subgroup indistinguishability: \((\mathsf {pp},\, h^*,\, \varvec{g} {\cdot } \varvec{\hat{g}},\, \varvec{h}) \approx _{c}(\mathsf {pp},\, h^*,\, \varvec{g} {\cdot } \varvec{\hat{g}},\, \varvec{h} {\cdot } \varvec{\hat{h}})\).
-
parameter-hiding: \((\mathsf {pp},\, h^*,\, \varvec{\hat{g}},\, \varvec{\hat{h}}) \equiv (\mathsf {pp},\, h^*,\, \varvec{\hat{g}}{\cdot }\varvec{\hat{g}'},\, \varvec{\hat{h}}{\cdot }\varvec{\hat{h}'})\).
Where, \(\approx _{c}\) denotes a distinguishing probability upper-bounded by a negligible function on \(\lambda \) and, for any \(n \in \mathbb {N}\), the above elements are sampled as:

for  .
.
Remark. Observe that we have presented the version of dual system groups defined in [15]. Other works consider slightly different conditions (e.g., the non-degeneracy of [1]). However, the widely used instantiation of DSG from k-lin given in [15] also satisfies the properties of those variations.
ABE from Pair Encodings
Given a pair encoding scheme \(\{\mathsf{Param}, \mathsf{EncKey}, \mathsf{EncCt}, \mathsf{Pair}\}\) (see Definition 2) for a predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\) indexed by \(\kappa = (N,\mathsf{par})\) (let \(\lambda = |N|\)), an attribute-based encryption scheme can be constructed as follows:
-
\(\mathsf{Setup}(1^\lambda ,\mathcal{X}_{\kappa },\mathcal{Y}_{\kappa })\): let \(n \leftarrow \mathsf{Param}(\mathsf{par})\) and run the DSG generation algorithm \(\mathsf{SampP}(1^\lambda , 1^n)\) to obtain \(\mathsf {pp}\) and \(\mathsf {sp}\). Let
 and
and  . Output \((\mathsf {mpk}, \mathsf {msk})\).
. Output \((\mathsf {mpk}, \mathsf {msk})\). -
\(\mathsf{Enc}(\mathsf {mpk}, x)\): run \(\mathsf{EncCt}(N,x)\) to obtain polynomials \(\varvec{c}_x(\varvec{s},\varvec{\hat{s}},\varvec{b})\). For every \(\ell \in [w_3]\), let the \(\ell \)-th polynomial in \(\varvec{c}_x\) be
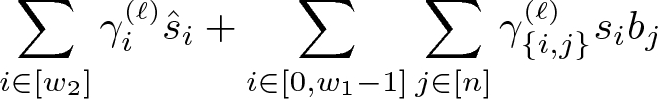
for some coefficients
 and
and 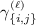 in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampG}\) to produce $$\begin{aligned} (\hat{g}_{\{i,0\}}, \hat{g}_{\{i,1\}},\dots ,\hat{g}_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [w_2] \\ (g_{\{i,0\}}, g_{\{i,1\}},\dots ,g_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [0,w_1{-}1] \\ (g_{\{0,0\}}, g_{\{0,1\}},\dots ,g_{\{0,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}; \sigma ) \end{aligned}$$
in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampG}\) to produce $$\begin{aligned} (\hat{g}_{\{i,0\}}, \hat{g}_{\{i,1\}},\dots ,\hat{g}_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [w_2] \\ (g_{\{i,0\}}, g_{\{i,1\}},\dots ,g_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [0,w_1{-}1] \\ (g_{\{0,0\}}, g_{\{0,1\}},\dots ,g_{\{0,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}; \sigma ) \end{aligned}$$Observe that we have made explicit the coin tosses, \(\sigma \), used in the last sampling. Setup
 and define the symmetric encryption key as
and define the symmetric encryption key as 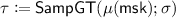 , where
, where  for every \(i \in [0,w_1{-}1]\); and for every \(\ell \in [w_3]\),
for every \(i \in [0,w_1{-}1]\); and for every \(\ell \in [w_3]\),  is computed as
is computed as 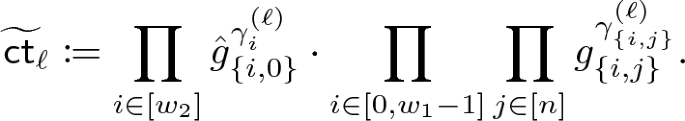
Output \((\mathsf {ct}_x, \tau )\).
-
\(\mathsf{KeyGen}(\mathsf {msk},y)\): run \(\mathsf{EncKey}(N,y)\) to obtain polynomials \(\varvec{k}_y(\varvec{r},\varvec{\hat{r}},\varvec{b})\). For every \(\ell \in [m_3]\), let the \(\ell \)-th polynomial in \(\varvec{k}_y\) be
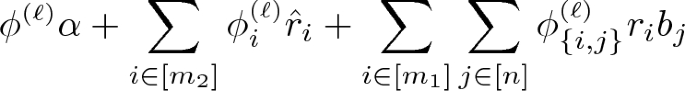
for some coefficients
 ,
,  and
and  in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampH}\) to produce $$\begin{aligned} (\hat{h}_{\{i,0\}}, \hat{h}_{\{i,1\}},\dots ,\hat{h}_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_2] \\ (h_{\{i,0\}}, h_{\{i,1\}},\dots ,h_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_1] \end{aligned}$$
in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampH}\) to produce $$\begin{aligned} (\hat{h}_{\{i,0\}}, \hat{h}_{\{i,1\}},\dots ,\hat{h}_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_2] \\ (h_{\{i,0\}}, h_{\{i,1\}},\dots ,h_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_1] \end{aligned}$$Define the secret key as
 , where
, where  for every \(i \in [m_1]\); and for every \(\ell \in [m_3]\),
for every \(i \in [m_1]\); and for every \(\ell \in [m_3]\),  is computed as
is computed as 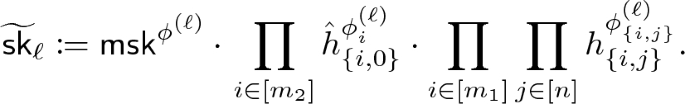
Output \(\mathsf {sk}_y\).
-
\(\mathsf{Dec}(\mathsf {mpk},\mathsf {sk}_y,\mathsf {ct}_x,x)\): run \(\mathsf{Pair}(N,x,y)\) to obtain matrices \(E, E'\) (note that y is assumed to be extractable from \(\mathsf {sk}_y\), whereas x is explicitly included as an input to \(\mathsf{Dec}\)). Define:
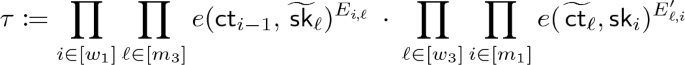
Output the symmetric encryption key \(\tau \).
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Ambrona, M. (2021). Generic Negation of Pair Encodings. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)





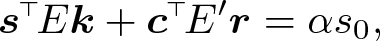
 , where
, where 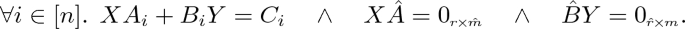
 ,
,  such that
such that 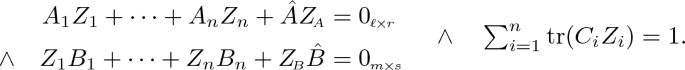
 run
run  run
run  run
run  find matrices
find matrices  .
. .
. run
run  run
run 

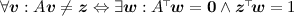 for all compatible A and
for all compatible A and  ,
,  , for
, for 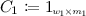 ,
,  for
for  and
and 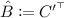 .
.
 and
and  .
.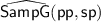 output an element from
output an element from 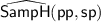 output an element from
output an element from 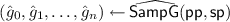 ,
, 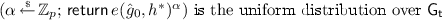 .
. and
and  . Output
. Output 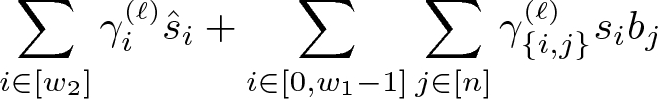
 and
and 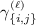 in
in  and define the symmetric encryption key as
and define the symmetric encryption key as 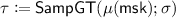 , where
, where  for every
for every  is computed as
is computed as 
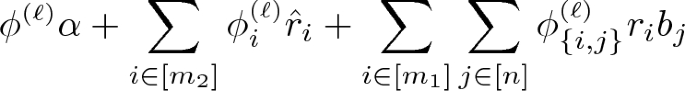
 ,
,  and
and  in
in 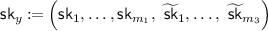 , where
, where  for every
for every  is computed as
is computed as