Abstract
In classical modal logic, necessity \({\mathop {\Box } A}\), possibility \({\mathop {\Diamond } A}\), impossibility \({\mathop {\Box } \lnot A}\) and non-necessity \({\mathop {\Diamond } \lnot A}\) form a Square of Oppositions (SO) whose corners are interdefinable using classical negation. The relationship between these modalities in intuitionistic modal logic is a more delicate matter since negation is weaker. Intuitionistic non-necessity \({\mathop {\boxminus }}\) and impossibility  , first investigated by Došen, have received less attention and—together with their positive counterparts \({\mathop {\Box }}\) and \({\mathop {\Diamond }}\)—form a square we call the Došen Square. Unfortunately, the core property of constructive logic, the Disjunction Property (DP), fails when the modalities are combined and, interpreted in birelational Kripke structures à la Došen, the Square partially collapses. We introduce the constructive logic \(\mathsf {CKD}\), whose four semantically independent modalities \({\mathop {\Box }}\), \({\mathop {\Diamond }}\), \({\mathop {\boxminus }}\),
, first investigated by Došen, have received less attention and—together with their positive counterparts \({\mathop {\Box }}\) and \({\mathop {\Diamond }}\)—form a square we call the Došen Square. Unfortunately, the core property of constructive logic, the Disjunction Property (DP), fails when the modalities are combined and, interpreted in birelational Kripke structures à la Došen, the Square partially collapses. We introduce the constructive logic \(\mathsf {CKD}\), whose four semantically independent modalities \({\mathop {\Box }}\), \({\mathop {\Diamond }}\), \({\mathop {\boxminus }}\),  prevent the Došen Square from collapsing under the effect of intuitionistic negation while preserving DP. The model theory of \(\mathsf {CKD}\) involves a constructive Kripke frame interpretation of the modalities. A Hilbert deduction system and an equivalent cut-free sequent calculus are presented. Soundness, completeness and finite model property are proven, implying that \(\mathsf {CKD}\) is decidable. The logics \({\mathsf {HK} {\mathop {\boxminus }}}\), \({\mathsf {HK} {\mathop {\Box }}}\),
prevent the Došen Square from collapsing under the effect of intuitionistic negation while preserving DP. The model theory of \(\mathsf {CKD}\) involves a constructive Kripke frame interpretation of the modalities. A Hilbert deduction system and an equivalent cut-free sequent calculus are presented. Soundness, completeness and finite model property are proven, implying that \(\mathsf {CKD}\) is decidable. The logics \({\mathsf {HK} {\mathop {\boxminus }}}\), \({\mathsf {HK} {\mathop {\Box }}}\),  and
and  of Došen and other known theories of intuitionistic modalities are syntactic fragments or axiomatic extensions of \(\mathsf {CKD}\) .
of Došen and other known theories of intuitionistic modalities are syntactic fragments or axiomatic extensions of \(\mathsf {CKD}\) .
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Such negative modalities have been considered in the literature on FDE and Routley semantics as ways of capturing forms of negation [17,18,19, 28, 36] often called ‘constructible’ or ‘strong’ negation [26, 37]. We do not suggest that the role of
 and \({\mathop {\boxminus }}\) in the logic \(\mathsf {CKD}\) is to capture forms of negation; rather, we are simply interested in how they behave in a constructive setting (i.e. in which the Disjunction Property holds) as modal operators.
and \({\mathop {\boxminus }}\) in the logic \(\mathsf {CKD}\) is to capture forms of negation; rather, we are simply interested in how they behave in a constructive setting (i.e. in which the Disjunction Property holds) as modal operators. - 2.
Our claim is that the doubly quantified truth conditions are a neat way out of the bind, not that they are necessary in order to provide a logic which combines \(\Box \), \({\mathop {\Diamond }}\),
 and \({\mathop {\boxminus }}\) interpreted with respect to the same relation.
and \({\mathop {\boxminus }}\) interpreted with respect to the same relation. - 3.
As usual, we can take \(\top =_{\scriptstyle {df}}p \rightarrow p\) for a variable \(p \in Var \). Interestingly, also absurdity \(\bot \) is representable, viz. as the non-necessity of truth, i.e., \({\bot =_{\scriptstyle {df}}\mathop {\boxminus } \top }\). First, \(\mathfrak {M}, s \,\models \, \bot \) implies \({\mathfrak {M}, s \,\models \, \mathop {\boxminus } \top }\) since by definition there is no \(s'\) with \({s \sqsubseteq s'}\). Second, if \({\mathfrak {M}, s \,\models \, \mathop {\boxminus } \top }\) and \(s \not \!\in \, F\) we would have \({s \sqsubseteq s}\) and so by the truth condition for \({\mathop {\boxminus }}\) there must be \(s''\) with \(s \mathrel {R} s''\) and
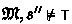 . This is impossible, hence \(s \in F\) and so \(\mathfrak {M}, s \,\models \, \bot \).
. This is impossible, hence \(s \in F\) and so \(\mathfrak {M}, s \,\models \, \bot \). - 4.
- 5.
A frame is weakly functional if \({\forall s \in S \setminus F.\, \exists s'.\ s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s'}\) and \( \forall s, s_1', s_2'.\, s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s_1' \& s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s_2' \Rightarrow s_1' \cong s_2'\), where \(s_1' \cong s_2'\) iff \(s_1' \le s_2'\) and \(s_2' \le s_1'\). The frame is functional if the existence condition holds in the stronger form \({\forall s \in S.\, \exists s'.\, s \mathrel {{\sqsubseteq }{;}{\mathrel {R}}} s'}\).
References
Acclavio, M., Catta, D., Straßburger, L.: Towards a denotational semantics for proofs in constructive modal logic. arXiv preprint arXiv:2104.09115 (2021)
Arisaka, R., Das, A., Straßburger, L.: On nested sequents for constructive modal logics. Logical Methods in Computer Science 11 (2015)
Bellin, G., de Paiva, V., Ritter, E.: Extended Curry-Howard correspondence for a basic constructive modal logic. In: Methods for Modalities II (2001)
Benton, N., Bierman, G., de Paiva, V.: Computational types from a logical perspective. J. Funct. Program. 8(2), 177–193 (1998)
Blamey, S., Humberstone, L.: A perspective on modal sequent logic. Publ. Res. Inst. Math. Sci. 27, 763–782 (1991)
Božić, M., Došen, K.: Models for normal intuitionistic modal logics. Studia Logica 43(3), 217–245 (1984)
Cabalar, P., Odintsov, S.P., Pearce, D.: Logical foundations of well-founded semantics. In: P.D. et al. (ed.) Proceedings of International Conference on Knowledge Representation and Reasoning (2006)
Dalmonte, T., Grellois, C., Olivetti, N.: Intuitionistic non-normal modal logics: a general framework. J. Philos. Logic 49, 833–882 (2020)
Došen, K.: Negation in the light of modal logic. In: Gabbay, D.M., Wansing, H. (eds.) What is Negation?, pp. 77–86. Springer, Heidelberg (1999). https://doi.org/10.1007/978-94-015-9309-0_4
Došen, K.: Negative modal operators in intuitionistic logic. Publications de L’Institut Mathématique 35(49), 3–14 (1984)
Došen, K.: Negation as a modal operator. Rep. Math. Logic 20(1986), 15–27 (1986)
Dragalin, A.G.: Mathematical Intuitionism: Introduction to Proof Theory. American Mathematical Society (1988)
Drobyshevich, S.: Double negation operator in logic \({N}^\star \). J. Math. Sci. 205(3) (2015)
Drobyshevich, S.A., Odintsov, S.P.: Finite model property for negative modalities. Sibirskie Elektronnye Matematicheskie Izvestiia 10 (2013)
Drobyshevich, S.A.: Composition of an intuitionistic negation and negative modalities as a necessity operator. Algebra Logic 52, 1–19 (2013). https://doi.org/10.1007/s10469-013-9235-8
Drobyshevich, S.: On classical behavior of intuitionistic modalities. Logic Log. Philos. 24(1), 79–104 (2015)
Dunn, J.M.: Star and perp: two treatments of negation. Philos. Perspect. 7, 331–357 (1993)
Dunn, J.M.: Negation, a notion in focus, vol. 7, chap. Generalized Ortho Negation, pp. 3–26. Walter de Gruyter Berlin (1996)
Dunn, J.M., Zhou, C.: Negation in the context of gaggle theory. Studia Logica 80(2–3), 235–264 (2005). https://doi.org/10.1007/s11225-005-8470-y
Fairtlough, M., Mendler, M.: Propositional lax logic. Inf. Comput. 137(1), 1–33 (1997)
Fitting, M.: Basic modal logic. In: Gabbay, D.M., Hogger, C.J., Robinson, J.A. (eds.) Handbook of Logic in Artificial Intelligence and Logic Programming, vol. 1, pp. 368–448. Oxford University Press, New York (1993)
Mendler, M., Scheele, S.: Towards constructive DL for abstraction and refinement. J. Autom. Reason. 44(3), 207–243 (2010). https://doi.org/10.1007/s10817-009-9151-8
Mendler, M., Scheele, S.: Cut-free Gentzen calculus for multimodal CK. Inf. Comput. 209(12), 1465–1490 (2011)
Mendler, M., Scheele, S.: On the computational interpretation of CK\(_n\). Fundamenta Informaticae 130, 1–39 (2014)
Mendler, M., de Paiva, V.: Constructive CK for contexts. In: Proceedings of the First Workshop on Context Representation and Reasoning, CONTEXT 2005 (2005)
Nelson, D.: Constructible falsity. J. Symb. Logic 14(1), 16–26 (1949)
Odintsov, S., Wansing, H.: Routley star and hyperintensionality. J. Philos. Logic 50, 33–56 (2020)
Odintsov, S.P.: Combining intuitionistic connectives and Routley negation. In: Siberian Electronic Mathematical Reports (2005)
Plotkin, G., Stirling, C.: A framework for intuitionistic modal logics. In: Halpern, J. (ed.) Theoretical Aspects of Reasoning About Knowledge, pp. 399–406. Monterey (1986)
Poggiolesi, F.: Gentzen Calculi for Modal and Propositional Logic. Springer, Heidelberg (2011). https://doi.org/10.1007/978-90-481-9670-8
Popkorn, S.: First Steps in Modal Logic. Cambridge University Press, Cambridge (1994)
Sato, M.: A study of Kripke-type models for some modal logics by Gentzen’s sequential method. Publ. Res. Inst. Math. Sci. 13, 381–468 (1977)
Scheele, S.: Model and Proof Theory of Constructive ALC, Constructive Description Logics. Ph.D. thesis, University of Bamberg (2015)
Simpson, A.K.: The proof theory and semantics of intuitionistic modal logic. Ph.D. thesis, University of Edinburgh, Scottland (1994)
Sotirov, V.H.: Modal theories with intuitionistic logic. In: Proceedings of the Conference on Mathematical Logic, Sophia, pp. 139–171 (1980)
Speranski, S.O.: Negation as a modality in a quantified setting. J, Logic Comput. (2021)
Wansing, H.: On split negation, strong negation, information, falsification, and verification. In: Bimbó, K. (ed.) J. Michael Dunn on Information Based Logics. OCL, vol. 8, pp. 161–189. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29300-4_10
Westerståhl, D.: On the Aristotelian square of opposition. Kapten Mnemos Kolumbarium, en festskrift med anledning av Helge Malmgrens (2005)
Wijesekera, D.: Constructive modal logic I. Ann. Pure Appl. Logic 50, 271–301 (1990)
Wolter, F., Zakharyaschev, M.: Intuitionistic modal logics as fragments of classical bimodal logics. Logic at work, pp. 168–186 (1997)
Wolter, F., Zakharyaschev, M.: The relation between intuitionistic and classical modal logics. Algebra Logic 36(2), 73–92 (1997)
Wolter, F., Zakharyaschev, M.: Intuitionistic modal logic. In: Cantini, A., Casari, E., Minari, P. (eds.) Logic and Foundations of Mathematics, pp. 227–238. Springer, Heidelberg (1999). https://doi.org/10.1007/978-94-017-2109-7_17
Acknowledgements
The authors would like to thank the anonymous referees and the PC, who provided useful and detailed comments on the submission version of the paper, and Stanislav Speranski, for sharing thoughts on constructive negation as a modality.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Mendler, M., Scheele, S., Burke, L. (2021). The Došen Square Under Construction: A Tale of Four Modalities. In: Das, A., Negri, S. (eds) Automated Reasoning with Analytic Tableaux and Related Methods. TABLEAUX 2021. Lecture Notes in Computer Science(), vol 12842. Springer, Cham. https://doi.org/10.1007/978-3-030-86059-2_26
Download citation
DOI: https://doi.org/10.1007/978-3-030-86059-2_26
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-86058-5
Online ISBN: 978-3-030-86059-2
eBook Packages: Computer ScienceComputer Science (R0)


 and
and  and
and 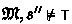 . This is impossible, hence
. This is impossible, hence