Abstract
Broadcast Encryption (BE) is a cryptosystem that allows a sender to specify recipients so that only the specified recipients can perform decryption. Anonymity, which is one of additional but important security requirements of BE, guarantees that no information of the designated recipients is leaked from ciphertexts, and several BE schemes with anonymity (ANO-BE) have been proposed so far.
Kiayias and Samari (IH 2013) analyzed a lower bound on the ciphertext size required for ANO-BE. In their analysis, they derived the lower bound under the assumption that ANO-BE schemes meets a special property. However, it is unclear whether the special property holds for existing ANO-BE schemes. In other words, their analysis is insufficient to show that the existing ANO-BE schemes achieve the optimal ciphertext size.
In this paper, we derive a lower bound on the ciphertext size in ANO-BE, assuming only properties that most existing ANO-BE schemes satisfy. In our analysis, we newly define several properties abstracted from existing (even non-anonymous) BE schemes and carefully analyze them to replace the Kiayias–Samari assumption with ours. As a result, we show that the existing ANO-BE schemes achieve the optimal ciphertext size. We further show that our analysis can be extended to the authentication setting. Specifically, we first derive a lower bound on the authenticator size required for anonymous broadcast authentication.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
There is another notion of “outsider anonymity” [6], weaker than both anonymity and full anonymity. We do not deal with the notion in this paper.
- 3.
Kiayias and Samari also derived lower bounds on the ciphertext sizes \(\varOmega \left( N + \kappa \right) \) required for any full-ANO-BE [9, Lemma 2]. However, it is unclear whether the lower bound is asymptotically tight, because no full-ANO-BE construction attains it.
- 4.
Although \(\mathsf{Join}\) behaves probabilistically, we can realize \(\mathsf{Join}\) as a deterministic algorithm by pseudo-random function.
- 5.
The “other elements” indicate, e.g., signatures for atomic ciphertexts (found in [11]).
References
Agrawal, S., Wichs, D., Yamada, S.: Optimal broadcast encryption from LWE and pairings in the standard model. In: Pass, R., Pietrzak, K. (eds.) TCC 2020. LNCS, vol. 12550, pp. 149–178. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64375-1_6
Agrawal, S., Yamada, S.: Optimal broadcast encryption from pairings and LWE. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12105, pp. 13–43. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45721-1_2
Barth, A., Boneh, D., Waters, B.: Privacy in encrypted content distribution using private broadcast encryption. In: Di Crescenzo, G., Rubin, A. (eds.) FC 2006. LNCS, vol. 4107, pp. 52–64. Springer, Heidelberg (2006). https://doi.org/10.1007/11889663_4
Boneh, D., Gentry, C., Waters, B.: Collusion resistant broadcast encryption with short ciphertexts and private keys. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 258–275. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_16
Boneh, D., Waters, B., Zhandry, M.: Low overhead broadcast encryption from multilinear maps. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 206–223. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_12
Fazio, N., Perera, I.M.: Outsider-anonymous broadcast encryption with sublinear ciphertexts. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 225–242. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_14
Gay, R., Kowalczyk, L., Wee, H.: Tight adaptively secure broadcast encryption with short ciphertexts and keys. In: Catalano, D., De Prisco, R. (eds.) SCN 2018. LNCS, vol. 11035, pp. 123–139. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98113-0_7
Gentry, C., Waters, B.: Adaptive security in broadcast encryption systems (with short ciphertexts). In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 171–188. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_10
Kiayias, A., Samari, K.: Lower bounds for private broadcast encryption. In: Kirchner, M., Ghosal, D. (eds.) IH 2012. LNCS, vol. 7692, pp. 176–190. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36373-3_12
Li, J., Gong, J.: Improved anonymous broadcast encryptions. In: Preneel, B., Vercauteren, F. (eds.) ACNS 2018. LNCS, vol. 10892, pp. 497–515. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93387-0_26
Libert, B., Paterson, K.G., Quaglia, E.A.: Anonymous broadcast encryption: adaptive security and efficient constructions in the standard model. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 206–224. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_13
Naor, D., Naor, M., Lotspiech, J.: Revocation and tracing schemes for stateless receivers. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 41–62. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_3
Watanabe, Y., Yanai, N., Shikata, J.: Anonymous broadcast authentication for securely remote-controlling IoT devices. In: Barolli, L., Woungang, I., Enokido, T. (eds.) AINA 2021. LNNS, vol. 226, pp. 679–690. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-75075-6_56
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Zhang, L., Wu, Q., Mu, Y.: Anonymous identity-based broadcast encryption with adaptive security. In: Wang, G., Ray, I., Feng, D., Rajarajan, M. (eds.) CSS 2013. LNCS, vol. 8300, pp. 258–271. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03584-0_19
Acknowledgements
This research was conducted under a contract of “Research and development on IoT malware removal/make it non-functional technologies for effective use of the radio spectrum” among “Research and Development for Expansion of Radio Wave Resources (JPJ000254),” which was supported by the Ministry of Internal Affairs and Communications, Japan.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Anonymous Broadcast Authentication
We define Anonymous Broadcast Authentication (ABA) and its security notions. In this paper, we assume that the maximum number of recipients N is determined at the time of setup and an arbitrary set of recipients can be specified at the time of authentication.
Syntax. An Anonymous Broadcast Authentication scheme \(\varPi ^{\mathsf{ABA}}\) consists of four algorithms \(( \mathsf{Setup}, \mathsf{Join}, \mathsf{Auth}, \mathsf{Vrfy} )\).
-
1.
\(\mathsf{ak}\leftarrow \mathsf{Setup}(1^{\kappa },N,\ell )\): a probabilistic algorithm for setup. It takes a security parameter \(1^{\kappa }\), the maximum number of recipients \(N\in \mathbb {N}\), the maximum number of recipients \(\ell \) designated at once as input, and outputs authentication key \(\mathsf{ak}\).
-
2.
\(\mathsf{vk}_{\mathsf{id}} \leftarrow \mathsf{Join}(\mathsf{ak}, \mathsf{id})\): a verification key generation algorithm. It takes \(\mathsf{ak}\) and an identifier \(\mathsf{id}\in \mathcal {ID}\), as input, and outputs verification key \(\mathsf{vk}_{\mathsf{id}}\) for \(\mathsf{id}\). Here, \(\mathcal {ID}\) is a set of all possible identifiers, and \(|\mathcal {ID}| := \mathsf {poly}( \kappa )\) for some polynomial \(\mathsf {poly}( \cdot )\).
-
3.
\(\mathsf{cmd}_{\mathcal {S}} \leftarrow \mathsf{Auth}(\mathsf{ak}, \mathsf {m}, \mathcal {S}; \mathsf {r})\): an authentication algorithm. It takes \(\mathsf{ak}\), a message \(\mathsf {m}\in \mathcal {M}\), a randomness \(\mathsf {r}\in \mathcal {R}\), and a privileged set \(\mathcal {S}\subseteq \mathcal {ID}\) as input, and outputs ciphertext \(\mathsf{cmd}_{\mathcal {S}}\), where \(\mathcal {M}\) is a message space and \(\mathcal {R}\) is a randomness space. It is also possible to omit \(\mathsf {r}\) from the input.
-
4.
\(\mathsf {m}\leftarrow \mathsf{Vrfy}(\mathsf{vk}_{\mathsf{id}},\mathsf{cmd}_{\mathcal {S}})\): a verification algorithm. It takes \(\mathsf{vk}_{\mathsf{id}}\) and \(\mathsf{cmd}_{\mathcal {S}}\) as inputs, and outputs \(\mathsf {m}\in \mathcal {M}\) (accept) or \(\bot \) (reject).
To describe properties of the existing ABA scheme, we regard \(\mathsf{Join}\) as a deterministic algorithm in this paper.
Correctness. For all \(\kappa ,N \in \mathbb {N}\), all \(\ell \) such that \(1\le \ell \le N\), all \(\mathsf{ak}\leftarrow \mathsf{Setup}(1^{\kappa },N,\ell )\), all \(\mathsf {m}\in \mathcal {M}\), all \(\mathsf {r}\in \mathcal {R}\), and all \(\mathcal {S}\subseteq \mathcal {ID}\) such that \(|\mathcal {S}| \le \ell \), if \(\mathsf{id}\in \mathcal {S}\), then \(\mathsf {m}\leftarrow \mathsf{Vrfy}(\mathsf{Join}(\mathsf{ak}, \mathsf{id}), \mathsf{Auth}(\mathsf{ak}, \mathsf {m},\mathcal {S}))\) holds with overwhelming probability. Otherwise, \(\bot \leftarrow \mathsf{Vrfy}(\mathsf{Join}(\mathsf{ak}, \mathsf{id}), \mathsf{Auth}(\mathsf{ak}, \mathsf {m},\mathcal {S}))\) holds with overwhelming probability
Anonymity. We define two kinds of anonymity for ABA, full anonymity (full-ANO) and anonymity (ANO).
Let \(\mathsf {A}\) be any PPT adversary against full-ANO security. We consider an experiment \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANO}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa , N, \ell )\) between a challenger \(\mathsf {C}\) and \(\mathsf {A}\).

\(\mathsf {C}\) randomly chooses \(b\in \{ 0,1 \} \). \(\mathsf {C}\) runs \(\mathsf{Setup}(1^{\kappa },N,\ell )\) to get \(\mathsf{ak}\) and randomly chooses \(b\in \{ 0,1 \} \). Let \(\mathcal {D}, \mathcal {CD}\) be a empty sets. We denote \(\mathcal {D}\) as a set of recipients currently participating in the protocol, and \(\mathcal {CD}\) as a set of identifiers of recipient from which \(\mathsf {A}\) obtained its verification key, respectively. \(\mathsf {A}\) may adaptively issue the following queries to \(\mathsf {C}\).
-
Key-generation Query: Upon a query \(\mathsf{id}\in \mathcal {ID}\) from \(\mathsf {A}\), \(\mathsf {C}\) adds \(\mathsf{id}\) to \(\mathcal {D}\) and generates \(\mathsf{vk}_{\mathsf{id}} \leftarrow \mathsf{Join}(\mathsf{ak},\mathsf{id})\). Note that \(\mathsf {A}\) obtains nothing, and that \(\mathsf {A}\) is allowed to make this query at most N times.
-
Corruption Query: Upon a query \(\mathsf{id}\in \mathcal {D}\) from \(\mathsf {A}\), \(\mathsf {C}\) adds \(\mathsf{id}\) to \(\mathcal {CD}\), and returns \(\mathsf{vk}_{\mathsf{id}}\) to \(\mathsf {A}\).
-
Challenge Query: Upon a query \((\mathsf {m},\mathcal {S}_0,\mathcal {S}_1)\in \mathcal {M}\times \left( 2^{\mathcal {D}}_{\le \ell }\right) ^2\) from \(\mathsf {A}\), \(\mathsf {C}\) runs \(\mathsf{cmd}_{\mathcal {S}_b} \leftarrow \mathsf{Auth}(\mathsf{ak}, \mathsf {m},\mathcal {S}_b)\) and returns \(\mathsf{cmd}_{\mathcal {S}_b}\) to \(\mathsf {A}\). \(\mathsf {A}\) is allowed to make this query only once under the restriction that
 .
.
At some point, \(\mathsf {A}\) outputs \(b'\). If \(b'=b\), \(\mathsf {C}\) then sets 1 as the output of \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANO}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell )\). Otherwise, \(\mathsf {C}\) then sets 0. \(\mathsf {C}\) terminates the experiment.
We can also define ANO with an experiment \(\mathsf {Exp}^{\mathsf{ANO}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell )\) which is the same as \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANO}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell )\) except for the following additional condition of the restriction for challenge query: \(|\mathcal {S}_0| = |\mathcal {S}_1|\).
Definition 5 (Anonymity)
We say \(\varPi ^{\mathsf{ABA}}\) is X secure (X \(\in \) {full-ANO, ANO}) if for any PPTA \(\mathsf {A}\), for all sufficiently-large \(\kappa \in \mathbb {N}\), all \(N \in \mathbb {N}\) and all \(\ell \, (\le N)\), it holds that \(\mathsf {Adv}^{X}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa , N, \ell ) < \mathsf {negl}( \kappa )\), where \(\mathsf {Adv}^{X}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa , N, \ell ) := |\Pr [\mathsf {Exp}^{X}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell ) \rightarrow 1] - \frac{1}{2}|\).
B Atomic Broadcast Authentication
In this section, we give a formal syntax of Atomic Broadcast Authentication (AtBA) to formally describe properties satisfied by the existing ABA scheme. These properties are used to formalize existing properties of ABA and derive lower bounds. We further provide security definitions for ABA covered with AtBA.
1.1 B.1 Syntax of AtBA
Our AtBA describes authentication and verification for each recipient in a designated set performed inside \(\mathsf{Auth}\) and \(\mathsf{Vrfy}\) algorithms of ABA. We define a model for Atomic BA  as follows.
as follows.
-
1.
 : a probabilistic algorithm for setup. It takes a security parameter \(1^{\kappa }\), the maximum number of receivers \(N\in \mathbb {N}\), the maximum number of receivers \(\ell \) designated at once as input, and outputs authentication key \(\mathsf{ak}\) consisting of \(|\varDelta |\) atomic authentication keys \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta }\).
: a probabilistic algorithm for setup. It takes a security parameter \(1^{\kappa }\), the maximum number of receivers \(N\in \mathbb {N}\), the maximum number of receivers \(\ell \) designated at once as input, and outputs authentication key \(\mathsf{ak}\) consisting of \(|\varDelta |\) atomic authentication keys \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta }\). -
2.
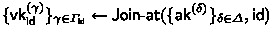 : a verification key generation algorithm. It takes \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta }\) and an identifier \(\mathsf{id}\in \mathcal {ID}\), as input, and outputs verification key \(\mathsf{vk}_{\mathsf{id}}\) for \(\mathsf{id}\) consisting of \(|\varGamma _{\mathsf{id}}|\) atomic verification keys \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}}\).
: a verification key generation algorithm. It takes \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta }\) and an identifier \(\mathsf{id}\in \mathcal {ID}\), as input, and outputs verification key \(\mathsf{vk}_{\mathsf{id}}\) for \(\mathsf{id}\) consisting of \(|\varGamma _{\mathsf{id}}|\) atomic verification keys \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}}\). -
3.
 : an atomic authenticate algorithm. It takes \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta '}\), a message \(\mathsf {m}\in \mathcal {M}\), a privileged set \(\mathcal {S}\subseteq \mathcal {ID}\), an identifier \(\mathsf{id}\in \mathcal {ID}\) and randomness \(\mathsf {r}\in \mathcal {R}\) as input, and outputs an atomic authenticator \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\), where \(\varDelta ' \subseteq \varDelta \).
: an atomic authenticate algorithm. It takes \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta '}\), a message \(\mathsf {m}\in \mathcal {M}\), a privileged set \(\mathcal {S}\subseteq \mathcal {ID}\), an identifier \(\mathsf{id}\in \mathcal {ID}\) and randomness \(\mathsf {r}\in \mathcal {R}\) as input, and outputs an atomic authenticator \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\), where \(\varDelta ' \subseteq \varDelta \). -
4.
 : an atomic verification algorithm. It takes a subset of atomic verification keys \(\{\mathsf{sk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}'}\), and \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\) as input, and outputs a message \(\mathsf {m}\)(accept) or \(\bot \)(reject), where \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\).
: an atomic verification algorithm. It takes a subset of atomic verification keys \(\{\mathsf{sk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}'}\), and \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\) as input, and outputs a message \(\mathsf {m}\)(accept) or \(\bot \)(reject), where \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\).
 and
and  are essentially equivalent to \(\mathsf{Setup}\) and \(\mathsf{Join}\) in ABA respectively, except for difference that authentication and verification keys are explicitly divided into multiple sub-elements. As in the case of \(\mathsf{Join}\) in BE, we regard
are essentially equivalent to \(\mathsf{Setup}\) and \(\mathsf{Join}\) in ABA respectively, except for difference that authentication and verification keys are explicitly divided into multiple sub-elements. As in the case of \(\mathsf{Join}\) in BE, we regard  as being a deterministic algorithm. We require a natural property for AtBA that an atomic authenticator \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\) contained in authenticator \(\mathsf{cmd}_{\mathcal {S}}\) will be correctly verified by a verification key \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}}\) of a recipient \(\mathsf{id}\in \mathcal {S}\) as follows:
as being a deterministic algorithm. We require a natural property for AtBA that an atomic authenticator \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\) contained in authenticator \(\mathsf{cmd}_{\mathcal {S}}\) will be correctly verified by a verification key \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}}\) of a recipient \(\mathsf{id}\in \mathcal {S}\) as follows:
Atomic Correctness. For all \(\kappa ,N \in \mathbb {N}\), all \(\ell \) such that  , all
, all  , all \(\mathsf{id}\in \mathcal {ID}\), all \(\mathsf {m}\in \mathcal {M}\), all
, all \(\mathsf{id}\in \mathcal {ID}\), all \(\mathsf {m}\in \mathcal {M}\), all  , all \(\mathcal {S}\subseteq \mathcal {ID}\) such that \(|\mathcal {S}| \le \ell \), all
, all \(\mathcal {S}\subseteq \mathcal {ID}\) such that \(|\mathcal {S}| \le \ell \), all  , for some \(\varDelta ' \subseteq \varDelta \) and \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\), for all
, for some \(\varDelta ' \subseteq \varDelta \) and \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\), for all  , if \(\mathsf{id}\in \mathcal {S}\), then
, if \(\mathsf{id}\in \mathcal {S}\), then  with overwhelming probability. Otherwise,
with overwhelming probability. Otherwise,  with overwhelming probability.
with overwhelming probability.
1.2 B.2 Security Definitions for ABA Covered with AtBA
We define anonymity for ABA covered with AtBA in the same way as in BE. In the following, we give definitions of full anonymity (full-ANOat) and anonymity (ANOat).
Security games for ABA covered with AtBA are the same as those for ABA except that an attacker obtains verification keys and a challenge authenticator is explicitly devided into multiple sub-elements. Essentially, there is no difference between anonymity for ABA and AtBA in that information attackers obtain. Therefore, we consider AnonymityAt defined below to be the same security as Anonymity.
Let \(\mathsf {A}\) be any PPT adversary against full-ANOat security. We consider an experiment \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANOat}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa , N, \ell )\) between a challenger \(\mathsf {C}\) and \(\mathsf {A}\). Let \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANOat}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}\) be the experiment with the following changes to Key-generation Query and Corruption Query in experiment \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANO}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}\).
-
Key-generation Query: Upon a query \(\mathsf{id}\in \mathcal {ID}\) from \(\mathsf {A}\), \(\mathsf {C}\) adds \(\mathsf{id}\) to \(\mathcal {D}\) and generates
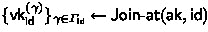 , not \(\mathsf{vk}_{\mathsf{id}} \leftarrow \mathsf{Join}(\mathsf{ak},\mathsf{id})\).
, not \(\mathsf{vk}_{\mathsf{id}} \leftarrow \mathsf{Join}(\mathsf{ak},\mathsf{id})\). -
Corruption Query: Upon a query \(\mathsf{id}\in \mathcal {D}\) from \(\mathsf {A}\), \(\mathsf {C}\) adds \(\mathsf{id}\) to \(\mathcal {CD}\), and returns \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}}\) to \(\mathsf {A}\), not \(\mathsf{vk}_{\mathsf{id}}\).
We also define ANOat with an experiment \(\mathsf {Exp}^{\mathsf{ANOat}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell )\) which is the same as \(\mathsf {Exp}^{\mathsf{full}\text {-}\mathsf{ANOat}}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell )\) except for the following additional condition of the restriction for challenge query: \(|\mathcal {S}_0| = |\mathcal {S}_1|\).
Definition 6 (Anonymity for AtBA)
We say \(\varPi ^{\mathsf{ABA}}\) is X secure (X \(\in \) full-ANOat, ANOat) if for any PPTA \(\mathsf {A}\), for all sufficiently-large \(\kappa \in \mathbb {N}\), all \(N \in \mathbb {N}\) and all \(\ell \, (\le N)\), it holds that \(|\mathsf {Adv}^{X}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa , N, \ell )| < \mathsf {negl}( \kappa )\), where \(\mathsf {Adv}^{X}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa , N, \ell ) := |\Pr [\mathsf {Exp}^{X}_{\varPi ^{\mathsf{ABA}},\mathsf {A}}(\kappa ,N,\ell ) \rightarrow 1] - \frac{1}{2}|\).
C Properties in An Existing ABA Scheme
In this section, we describe four properties that holds for an existing ABA scheme. The four properties is as follows.
Property 5
Authenticator \(\mathsf{cmd}_{\mathcal {S}}\) output from \(\varPi ^{\mathsf{ABA}}.\mathsf{Auth}\) algorithm consists of atomic authenticator \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\) obtained by  algorithm, and other elements. In other words, let a set of atomic authenticators contained in \(\mathsf{cmd}_{\mathcal {S}}\) be \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}}\), and let union of \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}}\) and some elements contained in \(\mathsf{cmd}_{\mathcal {S}}\) be \(\{\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}}]}\), it holds that \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}} \subseteq \{\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}}]} \subseteq \mathsf{cmd}_{\mathcal {S}}\). Here, a randomness \(\mathsf {r}\) input to
algorithm, and other elements. In other words, let a set of atomic authenticators contained in \(\mathsf{cmd}_{\mathcal {S}}\) be \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}}\), and let union of \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}}\) and some elements contained in \(\mathsf{cmd}_{\mathcal {S}}\) be \(\{\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}}]}\), it holds that \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}} \subseteq \{\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}}]} \subseteq \mathsf{cmd}_{\mathcal {S}}\). Here, a randomness \(\mathsf {r}\) input to  is the same when generating \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}}\) respectively. Also, inside ABA’s \(\varPi ^{\mathsf{ABA}}.\mathsf{Vrfy}\) algorithm,
is the same when generating \(\{\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\}_{\mathsf{id}\in \mathcal {S}}\) respectively. Also, inside ABA’s \(\varPi ^{\mathsf{ABA}}.\mathsf{Vrfy}\) algorithm,  algorithm takes atomic authenticator and a set of atomic verification key as input, and outputs a message. If \(\mathsf{cmd}_{\mathcal {S}}\) is valid authenticator, then there is an atomic authenticator \(\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\) in \(\mathsf{cmd}_{\mathcal {S}}\) that can be verified using a subset of atomic verification keys of a recipient \(\mathsf{id}\) in \(\mathcal {S}\). Formally, we require the following property for ABA \(\varPi ^{\mathsf{ABA}}\):
algorithm takes atomic authenticator and a set of atomic verification key as input, and outputs a message. If \(\mathsf{cmd}_{\mathcal {S}}\) is valid authenticator, then there is an atomic authenticator \(\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\) in \(\mathsf{cmd}_{\mathcal {S}}\) that can be verified using a subset of atomic verification keys of a recipient \(\mathsf{id}\) in \(\mathcal {S}\). Formally, we require the following property for ABA \(\varPi ^{\mathsf{ABA}}\):
For all \(\kappa ,N \in \mathbb {N}\), all \(\ell \) such that \(1 \le \ell \le N\), all \(\mathsf{ak}\leftarrow \varPi ^{\mathsf{ABA}}.\mathsf{Setup}(1^{\kappa },N,\ell )\), all \(\mathsf {m}\in \mathcal {M}\), all \(\mathcal {S}\subseteq \mathcal {ID}\) such that \(|\mathcal {S}| \le \ell \), all \(\mathsf{id}\in \mathcal {ID}\), all  , all
, all  , all \(\{\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}}]} \subseteq \mathsf{cmd}_{\mathcal {S}} \) \(\leftarrow \varPi ^{\mathsf{ABA}}.\mathsf{Auth}(\mathsf{ak}, \mathsf {m}, \mathcal {S}; \mathsf {r})\), if \(\mathsf{id}\in \mathcal {S}\), then for some \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\), there exists \(\theta \in [\beta _{\mathcal {S}}]\) such that
, all \(\{\mathsf{cmd}_{\mathcal {S}}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}}]} \subseteq \mathsf{cmd}_{\mathcal {S}} \) \(\leftarrow \varPi ^{\mathsf{ABA}}.\mathsf{Auth}(\mathsf{ak}, \mathsf {m}, \mathcal {S}; \mathsf {r})\), if \(\mathsf{id}\in \mathcal {S}\), then for some \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\), there exists \(\theta \in [\beta _{\mathcal {S}}]\) such that  . If \(\mathsf{id}\notin \mathcal {S}\), then for all \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\), there is no \(\theta \in [\beta _{\mathcal {S}}]\) such that
. If \(\mathsf{id}\notin \mathcal {S}\), then for all \(\varGamma _{\mathsf{id}}' \subseteq \varGamma _{\mathsf{id}}\), there is no \(\theta \in [\beta _{\mathcal {S}}]\) such that  .
.
Property 6
When generating \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\) such that  for some \(\gamma \in \varGamma _{\mathsf{id}}'\), let \(\varDelta ^*_{\mathsf{id}, \mathcal {S}, \mathsf {m}}\) be a minimum subset of atomic authentication keys required for the input to
for some \(\gamma \in \varGamma _{\mathsf{id}}'\), let \(\varDelta ^*_{\mathsf{id}, \mathcal {S}, \mathsf {m}}\) be a minimum subset of atomic authentication keys required for the input to  . In this case, \(\varDelta ^*_{\mathsf{id}, \mathcal {S}, \mathsf {m}}\) is uniquely determined by pairs of the recipient’s identifier, the message, and the set \((\mathsf{id}, \mathsf {m}, \mathcal {S})\) to input to
. In this case, \(\varDelta ^*_{\mathsf{id}, \mathcal {S}, \mathsf {m}}\) is uniquely determined by pairs of the recipient’s identifier, the message, and the set \((\mathsf{id}, \mathsf {m}, \mathcal {S})\) to input to  .
.
Property 7
When  holds, let \(\varGamma _{\mathsf{id}, \mathcal {S}}^*\) be a minimum subset of atomic verification keys required for the input to
holds, let \(\varGamma _{\mathsf{id}, \mathcal {S}}^*\) be a minimum subset of atomic verification keys required for the input to  . In this case, \(\varGamma _{\mathsf{id}, \mathcal {S}}^*\) is uniquely determined by pairs of the recipient’s identifier, and the set \((\mathsf{id}, \mathcal {S})\) to input to
. In this case, \(\varGamma _{\mathsf{id}, \mathcal {S}}^*\) is uniquely determined by pairs of the recipient’s identifier, and the set \((\mathsf{id}, \mathcal {S})\) to input to  when generating \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\).
when generating \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}\).
Property 8
For all \((\mathsf{ak}, \{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta }) \leftarrow \mathsf{Setup}(1^{\kappa },N,\ell ), \mathsf{id}, \mathsf{id}' \in \mathcal {ID}\), all \(\mathcal {S}\) such that \(\{\mathsf{id}, \mathsf{id}'\} \subseteq \mathcal {S}\), all \(\mathsf {m}\in \mathcal {M}, \mathsf {r}\in \mathcal {R}\), all 
 , if \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}= \mathsf{cmd}_{\mathcal {S}, \mathsf{id}'}\) holds, then we have \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}, \mathcal {S}, \mathsf {m}}} = \{\mathsf{ak}^{\left( {\delta '}\right) } \}_{\delta ' \in \varDelta ^*_{\mathsf{id}', \mathcal {S}, \mathsf {m}}}\) with overwhelming probability.
, if \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}= \mathsf{cmd}_{\mathcal {S}, \mathsf{id}'}\) holds, then we have \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}, \mathcal {S}, \mathsf {m}}} = \{\mathsf{ak}^{\left( {\delta '}\right) } \}_{\delta ' \in \varDelta ^*_{\mathsf{id}', \mathcal {S}, \mathsf {m}}}\) with overwhelming probability.
Here, we can see that the existing ABA scheme [13] satisfy the above properties in a similar way in Sect. 3.2.
D Lower Bounds of authenticator Size in ABA
1.1 D.1 A Property of ANO-BA and Full-ANO-BA
In order to derive lower bounds for ANO-BA and full-ANO-BA, we assume a property that “a minimum subset of atomic verification keys used to verify authenticators is uniquely determined by a subset of authentication keys used to generate the authenticator.” Specifically, we consider the following property for ANO-BA and full-ANO-BA:
Assumption 3. When \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta } \leftarrow \mathsf{Setup}(1^{\kappa },N,\ell )\) is generated, we denote \(\mathcal {AK}^*\) as a set of all authentication keys, namely \(\mathcal {AK}^* := \{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta }\). And, when \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}}} \leftarrow \mathsf{Join}(\mathsf{ak}, \mathsf{id})\) is generated, \(\mathcal {VK}^*\) denotes a set of a minimum subset of atomic verification keys to be input to  , namely \(\mathcal {VK}^* := \{\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) }\}_{\gamma \in \varGamma _{\mathsf{id}, \mathcal {S}}^*}\}_{\mathsf{id}\in \mathcal {ID}, \mathcal {S}\subseteq \mathcal {ID}}\). Here, we note that \(\mathcal {VK}^*\) is uniquely determined, since \(\mathsf{Join}-at\) is a deterministic algorithm. At this time, for all \(\mathsf{id}\in \mathcal {ID}\), all \(\mathcal {S}\subseteq \mathcal {ID}\), all \(\mathsf {m}\in \mathcal {M}\), all \(\mathsf {r}\in \mathcal {R}\), all \(\mathsf{ak}' \in 2^{\mathcal {AK}^*}\), all
, namely \(\mathcal {VK}^* := \{\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) }\}_{\gamma \in \varGamma _{\mathsf{id}, \mathcal {S}}^*}\}_{\mathsf{id}\in \mathcal {ID}, \mathcal {S}\subseteq \mathcal {ID}}\). Here, we note that \(\mathcal {VK}^*\) is uniquely determined, since \(\mathsf{Join}-at\) is a deterministic algorithm. At this time, for all \(\mathsf{id}\in \mathcal {ID}\), all \(\mathcal {S}\subseteq \mathcal {ID}\), all \(\mathsf {m}\in \mathcal {M}\), all \(\mathsf {r}\in \mathcal {R}\), all \(\mathsf{ak}' \in 2^{\mathcal {AK}^*}\), all  , a set of atomic verification keys \(\mathsf{vk}_{}' \in \mathcal {VK}^*\cup \{\bot \}\) such that
, a set of atomic verification keys \(\mathsf{vk}_{}' \in \mathcal {VK}^*\cup \{\bot \}\) such that  is uniquely determined by the set of atomic authentication keys \(\mathsf{ak}'\).
is uniquely determined by the set of atomic authentication keys \(\mathsf{ak}'\).
The above property holds for Watanabe et al.’s ANO-BA and full-ANO-BA schemes [13], which is a generic construction using message authentication code and pseudo-random function. Since it can be shown that they satisfies the above property in the same way as ANO-BE scheme of Libert et al. [11], we omit a detailed discussion here.
1.2 D.2 Lower Bounds in ANOat Secure ABA
First, we show two lemmas, Lemmas 4 and 5, for ANOat secure ABA with Properties 5, 6, 7 and 8 described in Section C. In Lemma 4, we show that “if ABA is ANOat secure, then for authenticators with a set \(\mathcal {S}_0, \mathcal {S}_1\) whose size is equal, sets of atomic verification keys used by a receipient \(\mathsf{id}\) for each verification is equal.” Then, in Lemma 5, we show that “if ABA is ANOat secure, then for any set \(\mathcal {S}\) with more than two elements, recipients \(\mathsf{id}, \mathsf{id}' \in \mathcal {S}\) must not share a set of atomic verification keys used to verify \(\mathsf{cmd}_{\mathcal {S}}\).”
Then, for ANOat secure ABA with the property described in Assumption 3, we will derive a lower bound on authenticator-size by Theorem 5.
Lemma 4
If ABA \(\varPi ^{\mathsf{ABA}}\) is ANOat secure, for all \(\mathsf{id}\in \mathcal {ID}\), all \(\mathcal {S}_0, \mathcal {S}_1\) such that \(\mathsf{id}\in \mathcal {S}_0 \cap \mathcal {S}_1\) and \(|\mathcal {S}_0|=|\mathcal {S}_1|\), we have \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}_0}} = \{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}_1}}\).
Proof
We show this lemma by contraposition. Suppose \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}_0}}\ne \{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}_1}}\) for some \(\mathsf{id}\in \mathcal {ID}\) and some \(\mathcal {S}_0, \mathcal {S}_1\) such that \(\mathsf{id}\in \mathcal {S}_0 \cap \mathcal {S}_1, |\mathcal {S}_0|=|\mathcal {S}_1|\). We will construct PPT adversary against ANOat security as follows. Let \(\mathsf{id}^*\) be \(\mathsf{id}\) as above. Initially, the adversary guesses sizes of \(\mathcal {S}_0, \mathcal {S}_1\) as  . Next, the adversary guesses \(\mathsf{id}^*, \mathcal {S}_0\), and \(\mathcal {S}_1\). A probability that the adversary succeeds in guessing is \(\frac{1}{|\mathcal {ID}|} \cdot \frac{1}{\ell } \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) ^{-1} \cdot \left( \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) - 1 \right) ^{-1}\). The adversary also issues Key-Generation queries for all \(\mathsf{id}\) in \(\mathcal {S}_0 \cup \mathcal {S}_1\) and Corruption queries for \(\mathsf{id}^*\) to obtain verification key \(\{\mathsf{vk}_{\mathsf{id}^*}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}^*}}\). Then, the adversary issues a challenge query \((\mathsf {m}, \mathcal {S}_0, \mathcal {S}_1)\) to obtain \(\{\mathsf{cmd}_{\mathcal {S}_b}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}_b}]} \subseteq \mathsf{cmd}_{\mathcal {S}_b}\). Finally, the adversary outputs \(b'=0\) if there exists \(\theta \in [\beta _{\mathcal {S}_b}]\) such that
. Next, the adversary guesses \(\mathsf{id}^*, \mathcal {S}_0\), and \(\mathcal {S}_1\). A probability that the adversary succeeds in guessing is \(\frac{1}{|\mathcal {ID}|} \cdot \frac{1}{\ell } \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) ^{-1} \cdot \left( \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) - 1 \right) ^{-1}\). The adversary also issues Key-Generation queries for all \(\mathsf{id}\) in \(\mathcal {S}_0 \cup \mathcal {S}_1\) and Corruption queries for \(\mathsf{id}^*\) to obtain verification key \(\{\mathsf{vk}_{\mathsf{id}^*}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma _{\mathsf{id}^*}}\). Then, the adversary issues a challenge query \((\mathsf {m}, \mathcal {S}_0, \mathcal {S}_1)\) to obtain \(\{\mathsf{cmd}_{\mathcal {S}_b}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}_b}]} \subseteq \mathsf{cmd}_{\mathcal {S}_b}\). Finally, the adversary outputs \(b'=0\) if there exists \(\theta \in [\beta _{\mathcal {S}_b}]\) such that  , and \(b'=1\) otherwise. In this case, the adversary can output \(b'\) such that \(b=b'\) with probability \(\frac{1}{2}\left( \frac{1}{|\mathcal {ID}|} \cdot \frac{1}{\ell } \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) ^{-1} \cdot \left( \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) - 1 \right) ^{-1} + 1 \right) \). \(\square \)
, and \(b'=1\) otherwise. In this case, the adversary can output \(b'\) such that \(b=b'\) with probability \(\frac{1}{2}\left( \frac{1}{|\mathcal {ID}|} \cdot \frac{1}{\ell } \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) ^{-1} \cdot \left( \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell ^* -1\end{array}}\right) - 1 \right) ^{-1} + 1 \right) \). \(\square \)
Lemma 5
If ABA \(\varPi ^{\mathsf{ABA}}\) is ANOat secure, for all \(\mathsf{id}, \mathsf{id}' \in \mathcal {ID}\), all \(\mathcal {S}\subseteq \mathcal {ID}\) such that \(\{\mathsf{id}, \mathsf{id}'\} \subseteq \mathcal {S}, |\mathcal {S}| \ge 2\), we have \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}}} \ne \{\mathsf{vk}_{\mathsf{id}'}^{\left( {\gamma '}\right) } \}_{\gamma ' \in \varGamma ^*_{\mathsf{id}', \mathcal {S}}}\).
Proof
Assume on the contrary that we have \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}}} = \{\mathsf{vk}_{\mathsf{id}'}^{\left( {\gamma '}\right) } \}_{\gamma ' \in \varGamma ^*_{\mathsf{id}', \mathcal {S}}}\) for some \(\mathsf{id}, \mathsf{id}' \in \mathcal {ID}\) and some \(\mathcal {S}\subseteq \mathcal {ID}\) such that \(\{\mathsf{id}, \mathsf{id}'\} \subseteq \mathcal {S}, |\mathcal {S}| \ge 2\). Then, we will show that it contradicts correctness of ABA with AtABA structure (see Section C, Property 5). First, we choose \(\mathcal {S}'\) such that \(\mathsf{id}\in \mathcal {S}', \mathsf{id}' \notin \mathcal {S}', |\mathcal {S}|=|\mathcal {S}'|\). In this case, since \(\mathsf{id}\in \mathcal {S}'\), we have  . And, since \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}'}} = \{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}}}\) from Lemma 4, we have
. And, since \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}'}} = \{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}}}\) from Lemma 4, we have  . Here, since \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}}} = \{\mathsf{vk}_{\mathsf{id}'}^{\left( {\gamma '}\right) } \}_{\gamma ' \in \varGamma ^*_{\mathsf{id}', \mathcal {S}}}\) from the assumption, we have
. Here, since \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}}} = \{\mathsf{vk}_{\mathsf{id}'}^{\left( {\gamma '}\right) } \}_{\gamma ' \in \varGamma ^*_{\mathsf{id}', \mathcal {S}}}\) from the assumption, we have  . However, by \(\mathsf{id}' \not \in \mathcal {S}'\), the above contradicts Property 5. \(\square \)
. However, by \(\mathsf{id}' \not \in \mathcal {S}'\), the above contradicts Property 5. \(\square \)
In the following, we derive a lower bound on authenticator-size in ANOat secure ABA with the property described in Assumption 3. Specifically, we show the statement: When there exists a set \(\mathcal {S}\) such that the number of atomic authenticators \(\mathsf{cmd}_{\mathcal {S}}\) contained in \(\mathsf{cmd}_{\mathcal {S}}\) is less than \(|\mathcal {S}|\), a contradiction occurs for Lemma 5.
Theorem 5
If ABA with the property shown in Assumption 3 is ANOat secure, the size of authenticator with any recipient set \(\mathcal {S}\subseteq \mathcal {ID}\) is \(\varOmega (|\mathcal {S}| \cdot k)\), where  .
.
Proof
For some set of recipients \(\mathcal {S}^*\), we assume \(\beta _{\mathcal {S}^*} < |\mathcal {S}^*|\), and then show that this contradicts Lemma 5. Now, from \(\beta _{\mathcal {S}^*}\ge 1\), we consider that \(|\mathcal {S}^*|\ge 2\) holds. From \(\beta _{\mathcal {S}^*} < |\mathcal {S}^*|\), for a set of atomic authenticators \(\{\mathsf{cmd}_{\mathcal {S}^*}^{{({\theta })}}\}_{\theta \in \beta _{\mathcal {S}^*}}\), there exists at least one atomic authenticator \(\mathsf{cmd}_{\mathcal {S}^*}^{{({\theta ^*})}}\) that can be verified by two recipients \(\mathsf{id}, \mathsf{id}' \in \mathcal {S}^*\). That is, for \(\mathsf{id}, \mathsf{id}' \in \mathcal {S}^*\) and for any \(\mathsf {m}\in \mathcal {M}, \mathsf {r}\in \mathcal {R}\), it holds that \(\mathsf{cmd}_{\mathcal {S}^*}^{{({\theta ^*})}} = \mathsf{cmd}_{\mathcal {S}, \mathsf{id}}= \mathsf{cmd}_{\mathcal {S}, \mathsf{id}'}\), when \(\mathsf{cmd}_{\mathcal {S}, \mathsf{id}}, \mathsf{cmd}_{\mathcal {S}, \mathsf{id}'}\) is generated by

Therefore, by Property 8, we have \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}, \mathcal {S}^*, \mathsf {m}}} = \{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}', \mathcal {S}^*, \mathsf {m}}}\).
In addition, we have the following by Atomic Correctness:


In this case, a set of atomic authentication keys used to authenticate \(\mathsf{cmd}_{\mathcal {S}^*}^{{({\theta ^*})}}\) is \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}, \mathcal {S}^*, \mathsf {m}}} = \{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}', \mathcal {S}^*, \mathsf {m}}}\). Then, by Assumption 3, a set of a minimum subset of atomic verification keys used to verify \(\mathsf{cmd}_{\mathcal {S}^*}^{{({\theta ^*})}}\) is uniquely determined by \(\{\mathsf{ak}^{\left( {\delta }\right) } \}_{\delta \in \varDelta ^*_{\mathsf{id}, \mathcal {S}^*, \mathsf {m}}}\). Therefore, in order that (3) and (4) holds, the following must hold true: \(\{\mathsf{vk}_{\mathsf{id}}^{\left( {\gamma }\right) } \}_{\gamma \in \varGamma ^*_{\mathsf{id}, \mathcal {S}^*}} = \{\mathsf{vk}_{\mathsf{id}'}^{\left( {\gamma '}\right) } \}_{\gamma ' \in \varGamma ^*_{\mathsf{id}', \mathcal {S}^*}}\). However, the above equality contradicts Lemma 5. \(\square \)
1.3 D.3 Lower Bounds in full-ANOat secure ABA
First, we show Lemma 6 that states “if ABA is full-ANOat secure, then for all privileged set \(\mathcal {S},\mathcal {S}'\), \(\beta _{\mathcal {S}} = \beta _{\mathcal {S}'}\) holds , where \(\beta _{\mathcal {S}}, \beta _{\mathcal {S}'}\) are the number of atomic authenticators in \(\mathsf{cmd}_{\mathcal {S}}, \mathsf{cmd}_{\mathcal {S}'}\), respectively.” Then, we derive a lower bound on authenticator size in Theorem 6 for full-ANOat secure ABA with the property described in Assumption 3, using Lemma 6 and Theorem 5.
Lemma 6
If ABA \(\varPi ^{\mathsf{ABA}}\) is full-ANOat secure, we have \(\beta _{\mathcal {S}} = \beta _{\mathcal {S}'}\) for all \(\mathcal {S}, \mathcal {S}'\).
Proof
We show the statement: If \(\beta _{\mathcal {S}} \ne \beta _{\mathcal {S}'}\) for some set \(\mathcal {S}, \mathcal {S}'\), then we can construct a PPT adversary that breaks the full-ANOat security.
the adversary guesses the size of \(\mathcal {S}, \mathcal {S}'\) as  , respectively. We then randomly select a set whose size is \(\ell _0, \ell _1\). Here, the probability that the adversary can obtain the set \(\mathcal {S}, \mathcal {S}'\) such that \(\beta _{\mathcal {S}} \ne \beta _{\mathcal {S}'}\) is \({\ell }^{-1} \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell _0\end{array}}\right) ^{-1} \cdot {\ell }^{-1} \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell _1\end{array}}\right) ^{-1}\). Then, the adversary issues \((\mathsf {m}, \mathcal {S}, \mathcal {S}')\) as a challenge query, and obtains \(\{\mathsf{cmd}_{\mathcal {S}_b}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}_b}]}\). If \(\beta _{\mathcal {S}_b} = \ell _0\), the adversary outputs \(b'=0\), otherwise \(b'=1\). \(\square \)
, respectively. We then randomly select a set whose size is \(\ell _0, \ell _1\). Here, the probability that the adversary can obtain the set \(\mathcal {S}, \mathcal {S}'\) such that \(\beta _{\mathcal {S}} \ne \beta _{\mathcal {S}'}\) is \({\ell }^{-1} \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell _0\end{array}}\right) ^{-1} \cdot {\ell }^{-1} \cdot \left( {\begin{array}{c}|\mathcal {ID}|\\ \ell _1\end{array}}\right) ^{-1}\). Then, the adversary issues \((\mathsf {m}, \mathcal {S}, \mathcal {S}')\) as a challenge query, and obtains \(\{\mathsf{cmd}_{\mathcal {S}_b}^{{({\theta })}}\}_{\theta \in [\beta _{\mathcal {S}_b}]}\). If \(\beta _{\mathcal {S}_b} = \ell _0\), the adversary outputs \(b'=0\), otherwise \(b'=1\). \(\square \)
Theorem 6
If ABA with the property shown in Assumption 3 is full-ANOat secure, the size of authenticator with an arbitrary recipient set \(\mathcal {S}\subseteq \mathcal {ID}\) is \(\varOmega (N \cdot k)\), where  .
.
Proof
We assume \(\beta _{\mathcal {S}} < N\) for some \(\mathcal {S}\), and show a contradiction. First, if \(\mathcal {S}^* := [N]\), then \(\beta _{\mathcal {S}^*} = \beta _{\mathcal {S}} < N\) holds from Lemma 6. On the other hand, since a full-ANOat secure ABA meets ANOat security, we have \(\beta _{\mathcal {S}^*} \ge N\) by Theorem 5, but it contradicts \(\beta _{\mathcal {S}^*} < N\). \(\square \)
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Kobayashi, H., Watanabe, Y., Shikata, J. (2021). Asymptotically Tight Lower Bounds in Anonymous Broadcast Encryption and Authentication. In: Paterson, M.B. (eds) Cryptography and Coding. IMACC 2021. Lecture Notes in Computer Science(), vol 13129. Springer, Cham. https://doi.org/10.1007/978-3-030-92641-0_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-92641-0_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-92640-3
Online ISBN: 978-3-030-92641-0
eBook Packages: Computer ScienceComputer Science (R0)


 .
. : a probabilistic algorithm for setup. It takes a security parameter
: a probabilistic algorithm for setup. It takes a security parameter 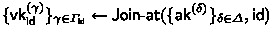 : a verification key generation algorithm. It takes
: a verification key generation algorithm. It takes  : an atomic authenticate algorithm. It takes
: an atomic authenticate algorithm. It takes  : an atomic verification algorithm. It takes a subset of atomic verification keys
: an atomic verification algorithm. It takes a subset of atomic verification keys 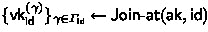 , not
, not