Counteracting Active Attacks in Social Network Graphs

Abstract

The growing popularity of social networks has generated interesting data analysis problems. At the same time, it has raised important privacy concerns, because social networks contain personal and sensitive information. Consequently, social graphs, which express the relations between the actors in a social network, ought to be sanitized or anonymized before being published. Most work on privacy-preserving publication of social graphs has focused on dealing with passive attackers while active attackers have been largely ignored. Active attackers can affect the structure of the social network graphs actively and use structural information, as a passive attacker does, to re-identify a user in a social graph. In this article we propose, to the best of our knowledge, the first anonymization method that resists to active attacks.

1 Introduction

Human interaction and socialization has changed as communication and information technology evolves. Emotions, feelings, thoughts, can all be shared instantly by simply pressing a button in one’s favorite social network application. This adds a degree of freedom to what we share and how we show it in comparison to, for example, face-to-face communication. While the latter is confined to a bounded physical space and builds upon the subtleties of human physical interaction, online social networks make it easier to disclose personal feelings as users are typically hidden behind a computer screen.

A social graph is a static representation of a social network; a sort of snapshot. Every vertex corresponds to a user who connects to other users through edges representing social links, e.g., friendship, co-authorship, and financial exchange. Researchers rely on graph theory and methods from modern sociology to extract useful knowledge by means of community detection, link prediction, identification of prominent actors, etc.

People tend to appreciate the discovery and revelation of new knowledge, but when it comes to personal information, one immediately perceives a privacy risk. Social graph analysis, although useful, may indeed jeopardize an individual’s privacy. An adversary could identify a user in a published social graph and learn sensitive information such as political and religious preferences. Ergo, social graphs ought to be sanitized or anonymized before making them available for analysis.

A fundamental anonymization technique consists in removing identifying attributes from the social graph, such as name, email address, and social security number [8]. Other types of attributes, often called quasi-identifiers, which in combination may uniquely identify an individual, ought to be removed as well. This makes it harder to identify the user behind a node in a social graph, which is often call re-identification. The challenge is that even a simple graph without attributes attached to its vertices can be subject to re-identification attacks. For example, an adversary who knows the number of social links of a target victim can identify the victim as a hub ¹ in the social network. The re-identification can be made more precise if the number of connections is unique in the network.

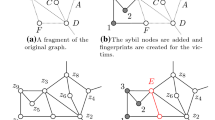
Re-identification attacks to social graphs are typically categorized as passive or active. In a passive attack the adversary attempts to re-identify the victim only after the social graph has been published. In an active attack, instead, the adversary proactively inserts sybil nodes in the network and tries to establish links with the targeted victims. The links are made in such a way that every victim connects to the set of sybil nodes in a unique and re-identifiable manner. Once the social graph is released, the adversary identifies his own set of sybil nodes, which are used to re-identify users by using their connections to the set of sybil nodes [1, 13].

Active attacks are by definition stronger than passive attacks, yet little attention has been paid to counteract this type of privacy attack. The first privacy notion that accounts for such active privacy attacks has been proposed just recently in [10]. This notion, which is called $(k,\ell )$-anonymity, expresses that a user cannot be re-identified with probability higher than 1 / k by an active attacker able to introduce $\ell$ sybil nodes in the graph. It has been shown in [10] that real-life social graphs tend to be (1, 1)-anonymous, which is the lowest privacy level possible. Indeed, in terms of offered privacy, $(k,\ell )$-anonymity forms a lattice (a square grid) where (1, 1)-anonymity is the minimum. This leads to the question whether it is possible to define privacy-preserving transformation techniques that defy active attacks by transforming a graph with low anonymity into a graph with higher anonymity that can be published without risking re-identification. In this paper, we take a first stab at defining such transformations. In particular, we will study the transformation of a graph into a graph with higher anonymity than (1, 1)-anonymity, while only adding edges.

Contributions: In this article we propose, to the best of our knowledge, the first privacy-preserving anonymization approach that resists active attacks. We use the privacy measure $(k,\ell )$-anonymity as proposed in [10] and provide an efficient method to transform a graph G into another graph $G'$ such that $G'$ is not (1, 1)-anonymous. That is to say, the obtained graph $G'$ satisfies $(k,\ell )$-anonymity with $k > 1$ or $\ell > 1$. Our anonymization method is based on edge addition operations only. As such, it preserves the original number of vertices in the graph. We provide a theoretical bound on the number of edges that our method needs to add in order to transform a graph into one that is not (1, 1)-anonymous. Finally, we provide empirical results showing the impact of our transformational approach in terms of resistance to well-known active attacks such as the walk-based attack [1].

Structure of the Paper: Section 2 explains in detail passive and active privacy attacks in social graphs. Definitions and useful notions used throughout this article are provided in Sect. 3. Section 4 presents and proves properties of (1, 1)-anonymous graphs, which form the theoretical foundation of the proposed anonymization approach (also introduced in Sect. 4). Section 5 consists of empirical evaluations of the proposed method on random graphs. Conclusions are drawn in Sect. 6.

2 Related Work

Most privacy notions for social graphs are based on k-anonymity [9], which was originally proposed as a privacy measure for microdata. We thus start this section by briefly depicting the role of k-anonymity in microdata, and how it has been adapted to social graphs in order to resist passive attacks. Related work on active attacks is provided at the end of this section.

k -anonymity in microdata. A pioneer study on re-identification attacks was published in 2002 by Sweeney [9]. Sweeney estimated that $87\,\%$ of the population in United States can be uniquely identified by combining seemingly innocuous attributes such as gender, date of birth and zip code.

Background knowledge is what makes a privacy attacker stronger. Either through public sources (e.g., census data) or by malicious actions, an adversary harvests information about a target victim which is used later to re-identify the victim in other databases. Hence, the challenge is how to publish data in such a way that users cannot be re-identified, regardless of the adversary’s background knowledge. A property known as k-anonymity gives a possible solution approach [8].

A dataset is said to satisfy k-anonymity if every record is indistinguishable from $k-1$ other records with respect to a given adversary’s background knowledge. Consequently, k-anonymity ensures that the considered adversary cannot pinpoint the user behind a record with probability higher than 1 / k. Moreover, a k-anonymous dataset can still be considered useful for analysis; researchers are interested in aggregate data describing the general behavior of a population rather than in the characteristics of a single individual.

k -anonymity in social graphs. While Sweeney’s revelation mainly concerns relational databases, later in 2009 Narayanan et al. showed that one third of social network users in Flickr and Twitter can be re-identified by a simple passive attack on the anonymized Twitter graph with only $12\,\%$ error rate [6]. Several notions of k-anonymity have been consequently proposed in order to mitigate the impact of passive attacks in social graphs.

Privacy notions based on k-anonymity rely on a proper definition of the adversary’s background knowledge. In microdata this knowledge consists of a set of quasi-identifiers, while in social graphs it is normally defined as a structural property on the graph, e.g., vertex degree or distance. Two vertices are said to be indistinguishable if they are structurally equivalent with respect to the considered structural property. For example, Liu et al. [4] considered an adversary who knows the degree of the victim node. This simple structural property leads to the notion of k-degree anonymity, which is satisfied if for every vertex there exist $k-1$ other vertices with the same degree.

A privacy notion strictly stronger than k-degree anonymity is k-neighbourhood anonymity [14]. This property requires that for every vertex v in the graph there exist at least $k-1$ other nodes $v_1,...v_{k-1}$ such that the subgraph induced by v’s neighbours is isomorphic to the subgraph induced by $v_i$’s neighbours, for every $i \in \{1, \ldots , k-1\}$. This notion was soon generalized to k-automorphism [3, 15]. Two vertices u and v are equivalent if there exists an isomorphism from the graph to itself where u maps to v [3]. The problem, however, is that real-life social graphs can hardly satisfy k-anonymity with respect to automorphism [15].

Active attacks. The privacy notions described above do not account for an adversary with the ability to actively manipulate the structure of the social network. That would allow the adversary to influence the structural property of a victim node, which is actually stronger than just knowing structural information.

Backstrom et al. were the first to show the impact of active privacy attacks in social networks [1]. They propose an attack where the adversary plants a well-constructed and uniquely identifiable subgraph in the social network graph. The nodes in the adversary’s subgraph are used to establish links with the victim nodes (e.g., by sending friendship requests), in such a way that every victim has a unique fingerprint of links to the adversary’s subgraph. Once the social graph is released, the adversary retrieves the planted subgraph and re-identifies those nodes that preserve the expected fingerprint.

A recent improvement over the methods in [1] is the Seed-and-Grow attack proposed by Wei et al. [13]. They combine the creation of a uniquely identifiable subgraph with a progressive and self-reinforcing strategy, which starts with the initial fingerprint and extends to other new vertices by using the knowledge acquired during the re-identification procedure.

Preventing active attacks is challenging. Indeed, none of the privacy notions described above [3, 4, 14, 15] is well-suited to counteract active attacks. To the best of our knowledge, the first privacy measure to evaluate the resistance of social graphs to active attacks was proposed just recently in [10]. Trujillo-Rasua and Yero model the adversary’s background knowledge as the distance vector of a vertex with respect to the adversary’s subgraph. This leads to the privacy notion $(k, \ell )$-anonymity [10].

In this article we take a first step on defining graph transformations aimed at improving privacy in terms of ($k,\ell$)-anonymity. Therefore, we provide in the next section a formal definition for this privacy concept and introduce various notations that we use throughout the article.

3 Preliminaries

We model a social graph $G=(V,E)$ as a simple graph where V represents individuals and E their relationships. The distance $d_{G}(v,u)$ between two vertices v and u in G is the number of edges in the shortest path connecting them. Often we simply write d(v, u) if it does not lead to ambiguity. The degree of a vertex is the number of edges connected to it. An end-vertex is a vertex with degree one. The eccentricity $\epsilon _G(v)$ of a vertex v in a connected graph G is the greatest number of edges in a shortest path between v and any other vertex in G. We call a shortest path an eccentricity path for v if its length is equal to $\epsilon _G(v)$.

Definition 1

(Metric representation). The metric representation of a vertex v with respect to an ordered subset of vertices $S=\{u_1,...,u_t\}$ in a graph G = (V, E) is the vector $r(v|S) = (d_G(v,u_1),\ldots ,d_G(v,u_t))$.

The metric representation is the structural property used in [10] to represent the adversary’s background knowledge in active attacks.

Definition 2

( k -antiresolving set). Let $G = (V, E)$ be a simple connected graph and let $S = \{u_1,\cdots , u_{t}\}$ be a subset of vertices of G. The set S is called a k-antiresolving set if k is the greatest positive integer such that for every vertex $v \in V-S$ there exist at least $k-1$ different vertices $v_1, \cdots , v_{k-1} \in V-S$ with $r(v|S) = r(v_1|S) = \cdots = r(v_{k-1}|S)$.

As an example, consider the star graph in Fig. 1. The distance from $v_1$ to any other vertex in the graph is 1, thus $\{v_1\}$ is a 4-antiresolving set. On the other hand, any set $\{v_i\}$ with $i \in \{2,3,4,5\}$ is a 1-antiresolving set because $r(v_1|\{v_i\}) = (1)$ while $r(v_j|\{v_i\}) = (2)$ for every $j \in \{2,3,4,5\}$ and $j \ne i$. Finally, we consider the subset $\{v_1, v_5\}$. We observe that $r(v_2|\{v_1, v_5\}) = r(v_3|\{v_1, v_5\}) = r(v_4|\{v_1, v_5\}) = (1, 2)$, implying that $\{v_1, v_5\}$ is a 3-antiresolving set.

Fig. 1.

A star graph.

Definition 3

( k -metric antidimension). The k-metric antidimension of a simple connected graph $G = (V, E)$ is the minimum cardinality amongst the k-antiresolving sets in G.

Considering again the star graph depicted in Fig. 1, we observe that $\{v_2\}$ is a 1-antiresolving set with cardinality 1. Ergo, the 1-metric antidimension of this graph is 1. Determining the 2-metric antidimension is a bit more troublesome. We should first notice that $v_1$ should be included in any 2-antiresolving set, while $\{v_1\}$ itself is a 4-antiresolving set. Therefore, the 2-metric antidimension of the star graph is greater than or equal to 2. However, the subset $\{v_1, v_i\}$ for every $i \in \{2, 3, 4, 5\}$ is a 3-antiresolving rather than a 2-antiresolving set. Consequently, the 2-metric antidimension of the graph in Fig. 1 is 3, given that $\{v_5, v_1, v_3\}$ is a 2-antiresolving set. We refer the interested reader to [2] and [11] for results on the metric dimension and the k-metric antidimension, respectively.

Definition 4

(( $k,\ell$ )-anonymity). A graph G is said to meet $(k,\ell )$-anonymity if k is the smallest positive integer such that the k-metric antidimension of G is lower or equal than $\ell$.

A graph G satisfying ($k,\ell$)-anonymity ensures that every subset of vertices with cardinality at most $\ell$ is a $k'$-antiresolving set for some $k' \ge k$. Thus, every vertex in G is indistinguishable from at least $k-1$ other vertices with respect to their metric representation to any subset of vertices of cardinality at most $\ell$.

4 Protecting (1, 1)-anonymous Graphs

In this section we provide theoretical properties of (1, 1)-anonymous graphs, and use them to prove convergence of our anonymization method.

4.1 Properties of (1, 1)-anonymous Graphs

If G contains a 1-antiresolving set, say $\{v\}$, then there exists a vertex u such that $d(v, u) \ne d(v, w)$ for every $w \in V - \{v,u\}$. Following terminology from [10], we call such a vertex u a 1-resolvable vertex, in particular, we say that u is 1-resolvable by $\{v\}$. It follows that containing a 1-resolvable vertex is a sufficient and necessary condition for a graph G to be (1, 1)-anonymous.

Proposition 1

A simple connected graph $G=(V,E)$ satisfies (1, 1)-anonymity if and only if it contains a 1-resolvable vertex.

Proof

If G contains a 1-resolvable vertex v, then there exists a vertex u in G such that $\{u\}$ is a 1-antiresolving set. Ergo G is (1, 1)-anonymous.

Now, let us assume that G is (1, 1)-anonymous and that there does not exist a 1-resolvable vertex in G. This implies that there does not exist a 1-antiresolving set of cardinality 1 in G. Therefore, if a 1-antiresolving set in G exists then G is $(1, \ell )$-anonymous for some $\ell > 1$, otherwise G is $(k, \ell )$-anonymous for some $k > 1$. In either case G is not (1, 1)-anonymous, which is a contradiction.    $\square$

Because the presence of 1-resolvable vertices implies (1, 1)-anonymity, we are interested in finding those vertices in the graph which are 1-resolvable. A first trivial result in this direction is the following.

Lemma 1

For every end-vertex v in a graph $G = (V,E)$ it holds that v’s neighbour is 1-resolvable by {v}.

Proof

We should first notice that if $|V| = 2$ then both v and v’s neighbour are 1-resolvable. Thus, let us assume that $|V| > 2$ and let u be v’s neighbour. Because any path to v passes through u, we obtain that $d(w, v) = d(w, u) + d(u, v) > d(u, v) = 1$ for every $w \in V - \{v, u\}$. Therefore, $\{v\}$ is a 1-antiresolving set and u is a vertex 1-resolvable by $\{v\}$.    $\square$

A consequence of Lemma 1 is that every graph with end-vertices is (1, 1)-anonymous. Hereinafter we thus assume that social graphs do not contain end-vertices; they can be either removed from the social network or connected to other nodes. It is also worth remarking that, if v is an end-vertex, then v’s neighbor lies in every eccentricity path of v. We prove next that, indeed, every vertex 1-resolvable by $\{v\}$ lies in an eccentricity path of v.

Lemma 2

Let G be a simple connected graph, let $\{v\}$ be a 1-antiresolving set in G, and let $v_1 \cdots v_m$ be an eccentricity path of v, i.e., $v_1 = v$. For every vertex u that is 1-resolvable by $\{v\}$ there exists $i \in \{1, \ldots , m\}$ such that $u = v_i$.

Proof

Let us assume that $u \ne v_i \ \forall i \in \{1, \ldots , m\}$. By definition, the eccentricity of v satisfies that $\epsilon (v)\ge d(v,w)$ for every $w\in V(G)$ and, in particular, $\epsilon (v) \ge d(v,u)$. Given that $d(v, v_m) = \epsilon (v) \ge d(v, u)$, there must exist $i \in \{1, \ldots , m\}$ such that $d(v, u) = d(v, v_i)$ (see Fig. 2 left). Consequently, either $u = v_i$ or u is not 1-resolvable by $\{v\}$, which both lead to a contradiction.    $\square$

The next result is rather simple, yet it is the core of our anonymization approach. It provides a necessary condition for a vertex to be not 1-resolvable by vertices within a cycle of odd order.

Proposition 2

A cycle graph $C_n$ of odd order satisfies (2, 1)-anonymity.

Proof

Every vertex v in $C_n$ has two diametral vertices (see Fig. 2 right), ergo $\{v\}$ is a 2-antiresolving set.    $\square$

Fig. 2.

Left: An eccentricity path $v_1-v_i-v_m$ and a vertex u located out of that path. Right: A cycle of odd order. A vertex (in Black) has the same distance to both diametral vertices (in Gray).

4.2 A Graph Transformation Approach

Our elimination approach of 1-resolvable vertices is based on Proposition 2 and Lemma 2. We aim at including all 1-resolvable vertices lying in a given eccentricity path into a cycle of odd order by adding a single edge. This transformation is defined as follows.

Definition 5

( v -transformation). Let v be a vertex in a graph $G = (V, E)$ such that $\{v\}$ is a 1-antiresolving set, and let $v_1 \cdots v_m$ be an eccentricity path of v where $v_1 = v$. Let i and j be the lowest and largest positive integers, respectively, such that $v_i$ and $v_j$ are 1-resolvable by v in G. A v-transformation results in the graph $(V,E \cup \{(v_{i-1}, v_j)\})$ if $j-i$ is odd, otherwise in $(V,E \cup \{(v_{i-2}, v_j)\})$.

The remaining results within this section are aimed at proving properties of a v-transformation in a graph.

Theorem 1

Let $G=(V,E)$ be a simple connected graph, $\{v\}$ a 1-antiresolving set, and $G'$ the graph resulting from a v-transformation in G. Let S be the set of vertices in G contained in an eccentricity path of v in G. Every $w \in S$ is not 1-resolvable by $\{v\}$ in $G'$.

Proof

Let $v_1 \cdots v_m$ be an eccentricity path where $v_1 = v$. Let i and j be the lowest and largest positive integers, respectively, such that $v_i$ and $v_j$ are 1-resolvable by v in G. $G_1$ and $G_2$ denote the v-transformation of G when $j-i$ is odd and even, respectively. Next, we consider a vertex $w \in \{v_1, \ldots , v_m\}$ and analyze different cases regarding the position of w in the eccentricity path $v_1 \cdots v_m$. Figure 3 depicts the three scenarios.

Fig. 3.

An eccentricity path $v_1-v_m$ within the graph G. The dashed edge $G_1$ (resp. $G_2$) represents the $v_1$-transformation if $j-i$ is odd (resp. even).

Case 1

( $w \in \{v_1, \ldots , v_{i-2}\}$ ). In this case w is not 1-resolvable by $\{v_1\}$ in G. Therefore, let $w' \in V -\{v_1, \ldots , v_m\}$ such that $d_G(v_1, w) = d_G(v_1, w')$. We choose $k \in \{1, \ldots , m\}$ to be the largest positive integer such that $d_G(v_1, w') = d_G(v_1, v_k)+d_G(v_k, w')$. On the one hand, it holds that $d_G(v_k, w') = d_{G_1}(v_k, w') = d_{G_2}(v_k, w')$. On the other hand, it is easy to note that $k < i-1$, otherwise $d_G(v_1, w') \ge i-1 > d_G(v_1, w)$. This implies that $d_G(v_1, v_k) = d_{G_1}(v_1, v_k) = d_{G_2}(v_1, v_k)$ and, thus, $d_{G}(v_1, w) = d_{G_1}(v_1, w) = d_{G_2}(v_1, w) = d_{G}(v_1, w') = d_{G_1}(v_1, w') = d_{G_2}(v_1, w')$. Ergo, w is not 1-resolvable by $\{v\}$ in $G_1$ and $G_2$.

Case 2

( $w \in \{v_{i-1}, \ldots , v_{j}\}$ ). Now consider that $w \in \{v_{i-1}, \ldots , v_{j}\}$, which means that w is contained in the cycles $v_{i-1}v_i\cdots v_j v_{i-1}$ and $v_{i-2}v_i\cdots v_j v_{i-2}$ from $G_1$ and $G_2$, respectively. Considering Proposition 2, we obtain that if $j-i$ is odd then w is not 1-resolvable by $\{v\}$ in $G_1$, otherwise w is not 1-resolvable by $\{v\}$ in $G_2$.

Case 3

( $w \in \{v_{j+1}, \ldots , v_{m}\}$ ). Finally, consider that $w \in \{v_{j+1}, \ldots , v_{m}\}$. In this case we obtain the following.

$$\begin{aligned} d_{G_1}(v_1, w)&= d_{G_1}(v_1, v_{i-1})+d_{G_1}(v_{i-1}, v_j) + d_{G_1}(v_j, w) \nonumber \\&= d_{G}(v_1, w) - (j - i) \end{aligned}$$

(1)

Similarly we obtain:

$$\begin{aligned} d_{G_2}(v_1, w)&= d_{G}(v_1, w) - (j - i+1) \end{aligned}$$

(2)

On the other hand, $d_{G_1}(v_1, w') = d_{G_1}(v_1, v_k)+d_{G_1}(v_k, w')$ and $d_{G_2}(v_1, w') = d_{G_1}(v_1, v_{k'})+d_{G_1}(v_{k'}, w')$ for some $k, k' \in \{1, \ldots , m\}$. We notice that $d_{G_1}(v_k, w') = d_{G}(v_k, w')$ and $d_{G_1}(v_1, v_k) \ge d_{G}(v_1, v_k) - (j-i)$, which gives the following inequality.

$$\begin{aligned} d_{G_1}(v_1, w') \ge d_{G}(v_1, v_k) +d_G(v_k, w') - (j-i) \end{aligned}$$

(3)

Analogously we obtain:

$$\begin{aligned} d_{G_2}(v_1, w') \ge d_{G}(v_1, v_{k'}) +d_G(v_{k'}, w') - (j-i+1) \end{aligned}$$

(4)

Moreover, $d_{G}(v_1, v_k)+d_{G}(v_k, w') \ge d_{G}(v_1, w') = d_{G}(v_1, w)$ and $d_{G}(v_1, v_{k'})+d_{G}(v_{k'}, w') \ge d_{G}(v_1, w') = d_{G}(v_1, w)$, which applied to Eqs. 3 and 4 gives:

$$\begin{aligned} d_{G_1}(v_1, w')&\ge d_{G}(v_1, w) - (j-i) \nonumber \\ d_{G_2}(v_1, w')&\ge d_{G}(v_1, w) - (j-i+1). \end{aligned}$$

(5)

Finally, Eqs. 1 and 2 together with the inequalities in 5 give that $d_{G_1}(v_1, w') \ge d_{G_1}(v_1, w)$ and $d_{G_2}(v_1, w') \ge d_{G_2}(v_1, w)$. Therefore, there exists a vertex $w''$ in the $v_1-w'$ path such that $d_{G_1}(v_1, w'') = d_{G_1}(v_1, w)$. We observe that $w'' \ne w$, given that $d_G(v_1, w') \ge d_{G_1}(v_1, w') \ge k$ implying that $d_G(v_1, w)$ must be greater or equal than k as well. We conclude that w is not 1-resolvable by $\{v\}$ in $G_1$. We draw the same conclusion for $G_2$ by following an analogous reasoning.

We conclude this proof by recalling Lemma 2, which states that every 1-resolvable vertex by $\{v\}$ lies in the path $v_1 \cdots v_m$. This means that i and j are unique amongst all eccentricity paths of v in G.    $\square$

Theorem 1 states that a v-transformation $G'$ satisfies that all vertices in G which are included in an eccentricity path of v are not 1-resolvable by $\{v\}$ in $G'$. Consider, for example, the vertex $v_i$ in Fig. 3. While $d_G(v_1, v_i) \ne d_G(v_1, u)$ for every vertex u in G, it is easy to see that $d_{G_1}(v_1, v_i) = d_{G_1}(v_1, v_j)$ and $d_{G_2}(v_1, v_i) = d_{G_2}(v_1, v_{j-1})$. We next determine sufficient conditions by which a vertex not contained in an eccentricity path of v is not 1-resolvable by $\{v\}$ in a v-transformation.

Theorem 2

Let $G=(V,E)$ be a simple connected graph, $\{v\}$ a 1-antiresolving set, and $G'$ the graph resulting from a v-transformation in G. Let S be the set of vertices in G contained in an eccentricity path of v in G. Let $v_1 \cdots v_m$ an eccentricity path of v where $v_1 = v$. For a given vertex $w \in V-S$ let $k \in \{1, \ldots , m\}$ be the largest positive integer such that $d_G(v_1, w) = d_G(v_1, v_k)+d_G(v_k, w)$. Then $k < i$ or $k \ge j$ implies that w is not 1-resolvable by $\{v\}$ in $G'$.

Proof

As above, we use $G_1$ and $G_2$ to denote the v-transformation of G when $j-i$ is odd and even, respectively, where i and j are the lowest and largest positive integers, respectively, such that $v_i$ and $v_j$ are 1-resolvable by v in G.

First, consider that $k < i$, in which case $d_G(v_1, w) < d_G(v_1, v_i)$, otherwise there exists $w' \in V-\{v_1, \ldots , v_m\}$ such that $d_G(v_1, w') = d_G(v_1, v_i)$, a contradiction. This means that $d_G(v_1, w) \le i-2$. Because $G_1$ and $G_2$ result from the addition of one edge to G, then $d_{G_1}(v_1, w) \le d_G(v_1, w) \le i-2$ and $d_{G_2}(v_1, w) \le d_G(v_1, w) \le i-2$. If $d_G(v_1, w) = i-2$, then $v_{i-1}$ and $v_{j}$ satisfy that $d_{G_1}(v_1, w) = d_{G_1}(v_1, v_{i-1}) = i-2$ and $d_{G_2}(v_1, w) = d_{G_2}(v_1, v_{j}) = i-2$ in $G_1$ and $G_2$, respectively. If $d_G(v_1, w) < i-2$, then $d_{G_1}(v_1, w) = d_{G_1}(v_1, v_{l}) = d_{G_2}(v_1, v_{l})$ where $l = d_G(v_1, w)+1$. We conclude that in both $G_1$ and $G_2$ the vertex w is not 1-resolvable by $\{v\}$.

Next, consider that $k \ge j$. Given that $G_1$ and $G_2$ result from the addition of the edge $(v_{i-1}, v_j)$ and $(v_{i-2}, v_j)$, respectively, to G, we obtain that $d_{G}(v_j, w) = d_{G_1}(v_j, w) = d_{G_1}(v_j, w)$. Therefore, we obtain the following equalities.

$$\begin{aligned} d_{G}(v_1, w)&= d_{G}(v_1, v_j)+d_{G}(v_j, w) \\ d_{G_1}(v_1, w)&= d_{G_1}(v_1, v_j)+d_{G}(v_j, w) \\ d_{G_2}(v_1, w)&= d_{G_2}(v_1, v_j)+d_{G}(v_j, w) \end{aligned}$$

Let $v_{l}$ be the vertex in $v_1 \cdots v_m$ such that $d_{G}(v_1, v_l) = d_{G}(v_1, w)$. It should be noticed that $l > j$ and $d_{G}(v_1, v_l) = d_{G}(v_1, v_j)+d_{G}(v_j, v_l)$, hence $d_{G}(v_j, w) = d_{G}(v_j, v_l)$. As before, we obtain that $d_{G}(v_j, v_l) = d_{G_1}(v_j, v_l) = d_{G_1}(v_j, v_l)$. Because $d_{G}(v_j, w) = d_{G}(v_j, v_l)$, we can rewrite the equalities above as follows.

$$\begin{aligned} d_{G}(v_1, w)&= d_{G}(v_1, v_j)+d_{G}(v_j, w) \\ d_{G_1}(v_1, w)&= d_{G_1}(v_1, v_j)+d_{G_1}(v_j, v_l) \\ d_{G_2}(v_1, w)&= d_{G_2}(v_1, v_j)+d_{G_2}(v_j, v_l) \end{aligned}$$

Consequently, $d_{G_1}(v_1, w) = d_{G_1}(v_1, v_l)$ and $d_{G_2}(v_1, w) = d_{G_2}(v_1, v_l)$, implying that in both $G_1$ and $G_2$ the vertex w is not 1-resolvable by $\{v\}$.    $\square$

We observe that even if $i \le k < j$ a vertex w can still remain not 1-resolvable by $\{v\}$ in a v-transformation. This is the case, for example, in the $v_1$-transformation shown by Fig. 4. We thus provide next a sufficient condition for a vertex w to be not 1-resolvable by $\{v\}$ in a v-transformation regardless of the position of k with respect to i and j.

Fig. 4.

An example showing that a v-transformation may create new 1-resolvable vertices.

Proposition 3

Let $G=(V,E)$ be a simple connected graph, $\{v\}$ a 1-antiresolving set, $G'$ the graph resulting from a v-transformation in G, and $v_1 \cdots v_m$ an eccentricity path of v where $v_1 = v$. For every $w \in V - \{v_1, \ldots , v_m\}$ it holds that $d_{G}(v_1, w) \le m-j+i-1$ implies that w is not 1-resolvable in $G'$.

Proof

Let $v_1 \cdots v_m$ be an eccentricity path where $v_1 = v$. Let i and j be the lowest and largest positive integers, respectively, such that $v_i$ and $v_j$ are 1-resolvable by v in G. We call $G_1$ and $G_2$ to the v-transformation of G when $j-i$ is odd and even, respectively.

If $d_{G_1}(v_1, v_m) \ge d_{G_1}(v_1, w)$ then w is not 1-resolvable by $\{v_1\}$ in $G_1$. It is easy to note that $d_{G_1}(v_1, v_m) = d_{G_1}(v_1, v_{i-1}) + d_{G_1}(v_{i-1}, v_j)+d_{G_1}(v_j, v_m) = i-1+m-j$ and analogously $d_{G_2}(v_1, v_m) = i-2+m-j$. Given that $d_{G_1}(v_1, w) \le d_{G}(v_1, w)$ and $d_{G_2}(v_1, w) \le d_{G}(v_1, w)$ we conclude that if $d_{G}(v_1, w) \le m-j+i-1$ then w is not 1-resolvable by $\{v_1\}$ in $G_1$. Similarly, we can conclude that if $d_{G}(v_1, w) \le m-j+i-2$ then w is not 1-resolvable by $\{v_1\}$ in $G_2$.    $\square$

Finally, we provide a convergence result for our approach.

Theorem 3

Let G be a simple graph. We define a sequence of graphs $G_i$ (for $i\ge 0$) inductively as follows:

• $G_0 = G$.

• If there exists a 1-antiresolving set $\{v\}$ in $G_{i}$ then $G_{i+1}$ is the result of applying a v-transformation to $G_{i}$.

• Otherwise, $G_{i+1} = G_{i}$.

Let $S_i$ be the set of vertices in $G_i$ such that $v \in S_i$ implies that $\{v\}$ is a 1-antiresolving set in $G_i$. Then $S_j$ is empty for $j \ge \sum _{\forall v \in V} \epsilon _{G_0}(v) - |V|$.

Proof

Consider $G_{i-1} = (V_{i-1}, E_{i-1})$ and $G_i = (V_{i}, E_{i})$ where $G_{i-1} \ne G_i$. That is to say, $G_i$ results from a v-transformation to $G_{i-1}$ where $\{v\}$ is a 1-antiresolving set in $G_{i-1}$. Let $v_1 \cdots v_m$ be the eccentricity path of v in $G_{i-1}$, i.e., $v_1 = v$, such that $G_{i} = (V_{i-1}, E_{i-1} \cup \{(v_i, v_j)\})$ for some $i,j \in \{1, \ldots , m\}$.

On the one hand, $d_{G_{i}}(v_1, v_m) = d_{G_{i}}(v_1, v_i)+ d_{G_{i}}(v_i, v_j)+d_{G_{i}}(v_j, v_m) = d_{G_{i-1}}(v_1, v_i)+ 1+d_{G_{i-1}}(v_j, v_m)$. On the other hand, by definition of a v-transformation the edge $(v_i, v_j)$ satisfies that $j - i \ge 2$. Therefore, $d_{G_{i-1}}(v_i, v_j) \ge 2$, which implies that $d_{G_{i-1}}(v_1, v_m) > d_{G_{i}}(v_1, v_m)$. We conclude then that $\epsilon _{G_i}(v) < \epsilon _{G_{i-1}}(v)$.

The result above states that every v-transformation from $G_{i-1}$ to $G_i$ makes the eccentricity of v to decrease. Because an eccentricity path cannot be shorter than 1, the maximum number of v-transformations that can be applied to $G_0$ is bounded by $\epsilon _{G_0}(v)-1$. Considering that every vertex could potentially form a 1-antiresolving set, we obtain the following upper bound: $\sum _{\forall u \in V} \epsilon _{G_0}(v) - |V|$. Consequently, the graph $G_i$ with $i = \sum _{\forall v \in V} \epsilon _{G_0}(v) - |V|$ does not contain 1-resolvable vertices.    $\square$

Our anonymization approach simply consists of the successive application of v-transformations until a graph without 1-resolvable vertices is found. The number of v-transformations depends on how fast these transformations converge to a graph without 1-resolvable vertices. According to Theorem 3, this number is upper bounded by $\sum _{\forall v \in V} \epsilon _{G}(v) - |V|$, which is higher than or equal to $|V|(\epsilon _G - 1)$ where $\epsilon _G$ is the eccentricity of G. Considering that finding the shortest path between every pair of vertices in a graph has computational complexity $\mathcal {O}(|V|^3)$, we obtain that the computational complexity of our method is $\mathcal {O}(|V|^4(\epsilon _G-1))$.

We end this section by remarking that the upper bound provided in Theorem 3 is tight. That is, there exists a graph $G = (V, E)$ such that the number of edges added by our method is equal to $\sum _{\forall v \in V} \epsilon _{G}(v) - |V|$. Moreover, such an upper bound corresponds to the minimum number of edges required to transform G into $G'$ through edge addition operations only and such that $G'$ is not (1, 1)-anonymous. The graph G we are referring to can be constructed as follows.

Consider the complete graph $C_n = (V, E)$ with n vertices $V = \{v_1, \ldots , v_n\}$. Given a vertex $v_{n+1}$, G is defined by $G = (V \cup \{v_{n+1}\}, E \cup \{(v_n, v_{n+1})\})$ (see Fig. 5). On the one hand, any edge added to G has the form $(v_{n+1}, v_{i})$ for some $i \in \{1, \ldots , n\}$, which makes the distance between $v_{n+1}$ and $v_i$ to become 1. On the other hand, if the edge $(v_{n+1}, v_{i})$ for some $i \in \{1, \ldots , n\}$ is not added to G, then the distance between $v_{n+1}$ and $v_i$ remains equal to 2, implying that $v_{n+1}$ is 1-resolvable by $\{v_i\}$. Therefore, there exists only one transformation of G into a graph that is not (1, 1)-anonymous, that is, the transformation to the complete graph $C_{n+1}$. This requires n additional edges, which is equal to $\sum _{\forall v \in V} \epsilon _{G}(v) - |V| = \epsilon _{G}(v_n) + \sum _{\forall v \in V-\{v_n\}} \epsilon _{G}(v) - |V| = 1 + 2n - (n+1) = n$.

Fig. 5.

An example graph.

5 Experiments

In this section we evaluate the proposed anonymization method in terms of privacy and utility loss². Privacy is measured as the resistance of a graph to the walk-based attack introduced in [1], while utility loss is measured as the number of added edges.

5.1 The Walk-Based Attack

Given a social graph $G = (V, E)$, the walk-based attack consists of inserting new nodes $X = \{x_1,\ldots ,x_n\}$ into G, resulting in the graph $G' = (V\cup X, E)$. The attacker chooses an arbitrary set $Y=\{y_1,\ldots , y_m\}$ of users in G as the target of the attack. For each vertex $y_i \in Y$, a subset $N_i \subseteq X$ is designated as the fingerprint of $y_i$, such that $i \ne j \implies N_i \ne N_j \ \forall i, j \in \{1, \ldots , m\}$. The fingerprint is created by connecting each vertex $y_i \in Y$ to all vertices in $N_i$. It is worth remarking that such a fingerprint is nothing but the metric representation of the vertex $y_i \in Y$ with respect to X, i.e., $r(y_i | X)$.

The goal of the attacker is to re-identify the set of vertices X in an anonymized version of $G'$, which is used to re-identify the set of targeted vertices Y by considering their unique fingerprints with respect to X. To do so, the attacker creates random internal connections between the vertices in X by adding the edge $(x_i,x_j)$ with probability 1/2 for every $i \ne j \in \{1, \ldots , n\}$. We use G(X) to denote the sub-graph in $G'$ induced by the vertices in X. Once $G'$ is released, the attacker computes the set $\mathcal {X}$ containing all sub-graphs in $G'$ isomorphic to G(X). Assuming that G(X) does not have a trivial automorphism as advocated in [1], the adversary determines for each fingerprint $N_i$ with $i \in \{1, \ldots , m\}$ the candidate set $V_i = \{v \in V | u \in N_i \iff d_{G'}(v, u) = 1\}$ containing all vertices in V whose fingerprint to G(X) is determined by $N_i$. We consider that the adversary succeeds if all vertices in Y are correctly re-identified. Therefore, the probability of success of the attack is:

$$ \frac{\sum _{G(X) \in \mathcal {X}}\prod _{1\le i \le m} p_i}{|\mathcal {X}|} \quad \text {where} \quad p_i =\left\{ \begin{array}{ll} 1/|V_i| \quad &{} \quad \text {if} \quad y_i \in V_i\\ 0 \quad &{} \quad \text {otherwise.} \end{array} \right. $$

5.2 Empirical Evaluation on Random Graphs

In order to validate the performance of the proposed anonymization method we ran experiments on random graphs with different density values. We fix 50 as the number of vertices in each random graph, implying that every density value corresponds to a fixed number of edges. A random graph is thus created by adding random edges, i.e., connecting random pairs of vertices, until the desired number of edges is reached.

The density values range in $\{0.1, \ldots , 1\}$, while we considered attacks with 1 and 4 sybil nodes. For each density value and a given number of sybil nodes, we build a random graph G with the previously mentioned density. In order to simulate the walk-based attack, G is transformed into $G'$ by adding the sybil nodes and their connections to the victim nodes. Two anonymized versions of $G'$ are considered: $G_{1}'$ and $G_{2}'$ corresponding to our anonymization method and a random approach, respectively. The random approach consists in adding random edges to $G'$. The particularity is that the random approach adds as many edges as our approach, i.e., the number of edges in $G_{1}'$ is equal to the number of edges in $G_{2}'$. Doing so, both approaches perform equally in terms of utility loss. Their performance in terms of privacy are depicted in Fig. 6.

Fig. 6.

Two charts depicting the average probability of success of the walk-based attack in three types of graphs: random graphs (“Original”), random graphs anonymized by our method (“Our approach”), and random graphs anonymized by the random approach (“Random approach”). Left: the adversary can enrol a single node in the network. Right: the adversary can enrol four nodes. (Color figure online)

Figure 6 shows the average probability of success of the walk-based attack in 250, 000 random graphs, and their corresponding anonymization versions by our method and the random approach. Both anonymization approaches improve the resistance to the walk-based attack with respect to the original graph. Indeed, this attack succeeds with probability close to 1 on the original graphs for all density values above 0.2. Amongst the two anonymization approaches, ours performs significantly better for most density values. In particular, our method ensures that the probability of success of an adversary with the capability to insert a single attacker node into the network is 0.

The pronounced non-monotonic behaviour of the curves in Fig. 6 corresponds to the same type of behaviour of the curves in Fig. 7, which shows the average number of added edges by both our method and the random approach. It is indeed an open question what would be the trend of a curve depicting the minimum number of edges needed to transform a graph into another that is not (1, 1)-anonymous for different density values. We observe that, for example, 1 and 2 edges need to be added to a path graph of odd and even order, respectively. This means that such minimum number of edges does not depend on the graph density only.

Fig. 7.

Two charts depicting the average number of edges added by our method, referred to as “Our approach”. The charts also show the upper-bound as determined in Theorem 3 (“Upper-bound”) and the maximum number of edges that can be added (“Maximum”). Left: the adversary can enrol a single node in the network. Right: the adversary can enrol four nodes. (Color figure online)

Figure 7 shows, as sketched in the previous section, that the minimum number of edges added by our method, the upper bound provided by Theorem 3, and the maximum number of edges that can be added, meet when the density of the random graph is 1 and the adversary adds a single node to the graph. This leads to the type of graph shown in Fig. 5. For other density values, the upper bound in Theorem 3 is clearly above the actual number of edges added by our technique.

6 Conclusions

In this article we have proposed, to the best of our knowledge, the first privacy-preserving transformation method for social graphs that counteracts active attacks. The proposed method is theoretically sound and outputs a graph that satisfies $(k, \ell )$-anonymity with $k > 1$ or $\ell > 1$. We provide a theoretical upper-bound on the utility loss, in terms of number of added edges, of our approach. And we prove that such upper-bound is tight. Experiments on random graphs show that the proposed method effectively counteracts active attack even when the adversary is able to insert more than one sybil node in the network.