Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Preoperative planning of a safe and efficient trajectory for a Deep Brain Stimulation (DBS) electrode is a crucial and challenging task which usually requires a long experience. The path is usually chosen as the best compromise between multiple placement rules that may be contradictory, such as accurate targeting, avoidance of various sensitive structures or zones, or compliance with standards.

Most of the automatic trajectory planning techniques that have been proposed in the literature for DBS are based on mono-objective approaches [1, 2, 5, 7, 11]. They combine the rules into a single aggregative weighted sum and minimize it to find an optimal solution. This approach is intuitive, and sounds close to the current decision making process. However, the optimization community has shown that using such mono-criteria approaches for solving multi-criteria optimization problems can lead to an under-detection of the optimal solutions in a given solution space: it often produces poorly distributed solutions and does not find optimal solutions in non-convex regions [6].

If multi-criteria methods are already widely used for radiation therapy planning [3], it’s only recently that a few groups started to consider Pareto-optimality techniques for path planning in minimally invasive surgery. For example, a non-dominance based optimization was described in [9, 10] for radiofrequency ablation of tumors. But to our knowledge, no such method has been used in DBS.

The purpose of this work is to better understand and quantify the capacities and limits of different approaches to detect optimal solutions in the case of preoperative DBS path planning. We introduce to this context an optimality quantification approach based on dominance with the computation of a Pareto front. We compare it to a classical aggregative method based on a weighted sum. For both methods, within a uniform distribution of candidate entry points, optimal solutions are proposed and the difference is studied. These approaches are described in detail in Sect. 2. Then in Sect. 3, we describe the experiment performed by an experienced neurosurgeon on 14 patients cases, in order to quantify the loss of relevant trajectories missed by the aggregative approach.

2 Materials and Methods

In this section, we detail both quality quantification approaches that were compared. Then, we describe the GUI proposed to facilitate the navigation within the solutions, and present the data and experiment used for comparison.

2.1 Method 1: Pareto Front (\(\mathcal {M}_{PF}\))

Method \(\mathcal {M}_{PF}\) is a multi-objective method based on a Pareto ranking scheme. It consists in analyzing the mutual non-dominance of candidate entry points in an initial set \(\mathcal {S}\). We define the strict dominance relationship dom between two individuals x and y of the solution space \(\mathcal {S}\) for a set of n objective functions \(f_i\) as follows:

$$\begin{aligned} \forall x,y\in \mathcal {S} \quad x \quad dom \quad y \quad \iff \quad \forall i \in [1..n], \quad f_i(x) < f_i(y) \end{aligned}$$

A solution x is Pareto-optimal if it is not dominated by any other solution in the solution space \(\mathcal {S}\).

$$\begin{aligned} x \in \mathcal {S}\quad \text {is}\,\, Pareto\,\, \text {optimal} \quad \iff \quad \forall y \in \mathcal {S}, \quad \lnot (y \quad dom \quad x) \end{aligned}$$

The set of all Pareto-optimal solutions is called a Pareto front. Let us denote \(\mathcal {S}_{PF}\) the subset of points of \(\mathcal {S}\) that belong to the Pareto front. Inside the front, no solution dominates another.

$$\begin{aligned} x \in \mathcal {S}_{PF} \quad \iff \quad \forall y \in \mathcal {S}_{PF}, \quad \lnot (y \quad dom \quad x) \quad \wedge \quad \lnot (x \quad dom \quad y) \end{aligned}$$

\(\mathcal {S}_{PF}\) represents the Pareto-optimal points of \(\mathcal {S}\) that can be reached using \(\mathcal {M}_{PF}\). They are computed by comparing point of the sampling in pairs and keeping only the points that satisfy the above property.

2.2 Method 2: Weighted Sum Exploration (\(\mathcal {M}_{WSE}\))

The weighted sum is a mono-objective approach for quantifying the quality of a solution based on the representation of all of the n objective functions \(f_i\) by a single aggregative cost function f to minimize. A weight \(w_i\) is associated to each \(f_i\) as follows:

$$\begin{aligned} f(\mathbf {x}) = \sum _{i=1}^{n}w_i . f_i(\mathbf {x}) , \quad \mathbf {x} \in \mathbb {R}^N \end{aligned}$$

where: \(0<w_i<1\) and \(\varSigma w_i=1\) (weights condition), and \(\mathbf {x}\) represents the trajectory associated to a candidate entry point.

For a fixed combination of weights \(W={w_1, ..., w_n}\), we can quantify the quality of each candidate entry point \(p_j \in \mathcal {S}\) of the initial set by evaluating \(f(\mathbf {x_j})\), where \(\mathbf {x_j}\) is the trajectory corresponding to \(p_j\). Then, the optimal entry point for combination W is the point of \(\mathcal {S}\) with a minimal evaluation of f.

When varying weights \(w_i\) in W, different entry points of \(\mathcal {S}\) minimizing f can be obtained. An exploration by varying systematically a high number of different combinations of weights is the most widely-used approach to approximate a Pareto front: the maximal coverage of this method \(\mathcal {M}_{WSE}\) is the subset \(\mathcal {S}_{WSE}\) of all the points of \(\mathcal {S}\) that can be found as optimal with this method.

To achieve this, a stochastic sampling of the n weights \(w_i\) satisfying the above-mentioned weights condition is built. A Dirichlet distribution [8] allows to obtain a uniform sampling of 20,000 different combinations of weights. Note that different combinations can lead to the same optimal entry point within a predefined finite set of candidate entry points.

2.3 Discretization of the Solution Space

Usual automatic trajectory planning techniques involve the search of the best entry point thanks to an optimization phase converging to solutions optimizing the chosen quality measurement. However, optimization methods would differ for mono- and multi-objective cases: classical derivative-free optimization techniques are appropriate for mono-objective, while evolutionary approaches are more suitable and most frequently used for multi-objective techniques. The choice of such different optimizers could bias the comparison of the quality measurement method, as their convergence may differ. In order to have a fair comparison, we chose to avoid the use of optimizers, and focused on comparing only the quality measurement methods on a selection of candidate entry points.

To do so, we computed a discretization of the solution space by choosing a uniform distribution \(\mathcal {S}\) of points over the surface of the feasible entry points, i.e. the points leading to a safe trajectory not crossing any forbidden anatomical structure or zone. The precision of the distribution was chosen such that we have one candidate trajectory per degree, if the center of rotation is the center of the targeted structure, which corresponds to approximately to one entry point every millimeter. This precision was assessed as sufficiently spaced by our expert neurosurgeon. An example of a distribution of candidate points over a surface of feasible points is shown on Fig. 1d.

2.4 Evaluation Study

The objective of the test was (1) to compare the two methods on their coverage over the surface of candidate entry points, and their ability to find the maximal set of optimal solutions, and (2) to check whether the points found as optimal by one method and not by the other one were likely to be chosen by neurosurgeons.

To this end, a retrospective study was performed on 14 datasets from 7 patients who underwent a bilateral Deep Brain Stimulation of the Subthalamic Nucleus (STN) to treat Parkinson’s disease. Each dataset was composed of preoperative 3T T1 and T2 MRI with a resolution of 1.0 mm \(\times \) 1.0 mm \(\times \) 1.0 mm, and a 3D brain model containing triangular surface meshes of the majority of cerebral structures, segmented and reconstructed from the preoperative images using the pyDBS pipeline described in [4]. Among the 3D structures, we have the STN, a patch delineated on the skin as a search area for the entry points, the ventricles and the sulci that neurosurgeon try to avoid. The T1, T2 and 3D meshes were registered in the same coordinates system.

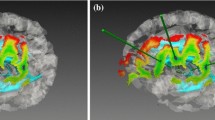
A second pipeline was implemented and executed on the 3D scenes. First a discretization \(\mathcal {S}\) of the search space, as described in Sect. 2.3, was performed. The distribution contained between 0.93 and 1.29 point per mm\(^2\) (average 1.07), representing an average of 2,320 sample points per case on an average surface of 2,158 mm\(^2\). Then we computed the subsets \(\mathcal {S}_{WSE}\) and \(\mathcal {S}_{PF}\) of points labeled as optimal respectively by methods \(\mathcal {M}_{WSE}\) and \(\mathcal {M}_{PF}\), as described in Sects. 2.1 and 2.2. Examples of subsets of optimal points proposed by both methods are presented on Figs. 1a and b. We marked for each case the difference set \(\mathcal {D}\) of points found by one method and not by the other \(\mathcal {D}_{WSE} = \mathcal {S}_{WSE} - (\mathcal {S}_{WSE} \cap \mathcal {S}_{PF})\) and \(\mathcal {D}_{PF} = \mathcal {S}_{PF} - (\mathcal {S}_{WSE} \cap \mathcal {S}_{PF})\), and computed their cardinality.

Fig. 1.
figure 1

Case #12: area of feasible entry points, with solutions of \(\mathcal {M}_{WSE}\) in blue, solutions of \(\mathcal {M}_{PF}\) in red, and the trajectory chosen with \(\mathcal {M}_{MP}\) in green.

Full size image

Finally, an experienced neurosurgeon was asked to perform a test in 4 steps.

  • Step 1: “Manual planning \(\mathcal {M}_{MP}\) ”. This phase consisted in selecting interactively the target point and the entry point on the 2D T1/T2 slices. The chosen trajectory \(T_{MP}\) could be visualized and assessed in the 3D view to check if the position was satisfying. Let’s denote this method \(\mathcal {M}_{MP}\).

  • Step 2: “Planning using method \(\mathcal {M}_{WSE}\) ”. In this phase, the target point chosen in step 1 was kept, and the surgeon had to choose an entry point among the ones proposed by \(\mathcal {M}_{WSE}\).

  • Step 3: “Planning using method \(\mathcal {M}_{PF}\) ”. In this phase, the target point chosen in step 1 was also kept, and the surgeon had to choose an entry point among the ones proposed by method \(\mathcal {M}_{PF}\).

  • Step 4: “Trajectories ranking”. This phase consisted in ranking the three trajectories \(T_{MP}\), \(T_{WSE}\) and \(T_{PF}\) chosen in steps 1–3. The ranking was blind as the three trajectories were randomly assigned a color, and the surgeon ranked the colors. An illustration of this step is shown on Fig. 1c, where the colors have been set to match Figs. 1a and b for readability purposes. The ranking could be zero if the trajectory was finally marked as being really worse than the others and rejected. Trajectories could be equally ranked if they were identical or estimated to have a similar quality.

The trajectory planning is submitted to a number of surgical rules. We have chosen to represent three of them, that seemed to be among the most commonly accepted rules, as objective functions for our experiment. Function \(f_1\) represents the proximity to a standard trajectory defined by expert neurosurgeons and commonly used in the commercial platforms: \(30^{\circ }\) anterior and \(30^{\circ }\) lateral. Function \(f_2\) represents the distance from the electrode to the sulci where the vessels are most often located, and that the surgeons try to avoid at best. Function \(f_3\) represents the distance from the electrode to the ventricles, to avoid as well.

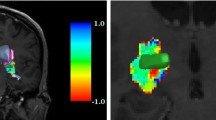
In order to assist the navigation through the solutions proposed by each method, we displayed visual clues controlled by sliders. For method \(\mathcal {M}_{WSE}\), a slider i allows the surgeon to assign a value to weight \(w_i\). Modifying the slider position updates a color map representing f for a particular set of weights, to help in the selection of a candidate. Its use is optional, and the visualization of all candidates in \(\mathcal {S}_{WSE}\) is not affected. In the case of method \(\mathcal {M}_{PF}\), the implemented filtering sliders were inspired by those proposed in [9] for radiofrequency tumor ablation. A slider i assigns a threshold \(\theta _i\) for the value of \(f_i\): point \(p \in \mathcal {S}_{PF}\) is displayed only if \(f_i(p) < \theta _i\), and hidden otherwise. Sliders range from 1 (all solutions displayed) to 0 (no solution displayed). Their use is also optional.

The experiment has been performed on an Intel Core i7 running at 2.67 GHz with 8 GB RAM workstation. For all cases, the positions of the target/entry points, the final ranking, and the times required for each step were recordedFootnote 1.

3 Results and Discussion

For all the cases, \(\mathcal {S}_{WSE} \subset \mathcal {S}_{PF}\). Average cardinalities are \(|\mathcal {S}_{WSE}|=26\) and \(|\mathcal {S}_{PF}|=190\). Difference set \(\mathcal {D}_{WSE}\) was always empty, meaning that all points found as optimal by \(\mathcal {M}_{WSE}\) were also proposed by \(\mathcal {M}_{PF}\). On the contrary, \(\mathcal {M}_{PF}\) always found more points than \(\mathcal {M}_{WSE}\). The chart on Fig. 2 shows the number of points in \(\mathcal {S}_{WSE}\) and \(\mathcal {S}_{PF}\). The average cardinality of the difference \(\mathcal {D}_{PF}\) is 164, which represents 86.41 % of the average number of points of \(\mathcal {M}_{PF}\).

Fig. 2.
figure 2

Number of points in \(\mathcal {S}_{WSE}\) (in blue) and \(\mathcal {S}_{PF}\) (in red) for the 14 cases

Full size image

In order to determine if the points missed by \(\mathcal {M}_{WSE}\) were interesting points likely to be chosen by a surgeon, we analyzed the data recorded during the test. First, we could observe that \(\mathcal {M}_{MP}\) ranked first in 2/14 cases, method \(\mathcal {M}_{WSE}\) ranked first in 5/14 cases, and method \(\mathcal {M}_{PF}\) ranked first in 6/14 cases. In the remaining case, the entry points chosen using \(\mathcal {M}_{WSE}\) and \(\mathcal {M}_{PF}\) coincided, so both methods were equally ranked in first position.

Let us note that the risk of being biased towards one solution picked right before is significantly reduced by the random color coding, the protocol pipeline (14 plannings with \(\mathcal {M}_{MP}\), then 14 with \(\mathcal {M}_{WSE}\) then 14 with \(\mathcal {M}_{PF}\), before the 14 rankings), and the absence of any visual clue when ranking.

The fact that \(\mathcal {M}_{WSE}\) ranked first 5 times does not mean \(\mathcal {M}_{WSE}\) outperformed \(\mathcal {M}_{PF}\) in 5 cases, as \(\mathcal {S}_{WSE} \subset \mathcal {S}_{PF}\). On the contrary, when \(\mathcal {M}_{PF}\) ranked first we observed that none of the entry points were also part of \(\mathcal {M}_{WSE}\). Therefore, we can state that method \(\mathcal {M}_{PF}\) is superior to \(\mathcal {M}_{WSE}\) in the sense that it finds preferred solutions that \(\mathcal {M}_{WSE}\) does not propose, while the opposite is not true. Presumably, the best possible solution was not available in \(\mathcal {S}_{WSE}\) so a sub-optimal alternative was chosen.

In order to see whether, in these kind of cases, reasonably close alternatives would be available in \(\mathcal {S}_{WSE}\), we computed the distances between entry points selected in \(\mathcal {S}_{PF}\) and the closest point of \(\mathcal {S}_{WSE}\). Results are shown on the left part of Table 1. It can be observed that in one case over six (#12), the distance is higher than 16 mm, which means that no point was proposed by \(\mathcal {S}_{WSE}\) within the region of the selected entry point. This case is also the one having the highest difference in terms of coverage of optimal points between the two methods. We chose to display this particular case in Fig. 1 to highlight that such cases may happen quite often due to the mathematical specificity of the weighted sum approach. In two other cases, the distance is higher than 4.8 mm, which is still far from the preferred location. For the other 3 cases, the distance ranges between 1.6 mm and 2.05 mm which may correspond to relatively reasonable alternatives.

Table 1. Distances in mm between entry points selected with methods \(\mathcal {M}_{PF}\) and \(\mathcal {M}_{MP}\) and the closest alternative point in other automatic methods
Full size table

It is also interesting to observe that for the two cases where \(\mathcal {M}_{MP}\) was ranked first (#7 and #13), the distance between the manually proposed entry point and the closest point of \(\mathcal {S}_{PF}\) (resp. 1.16 and 0.87 mm) was always lower than the closest point of \(\mathcal {S}_{WSE}\) (resp. 2.83 and 1.49 mm).

The average times taken for each of the three methods of selection were respectively 155 s. for \(\mathcal {M}_{MP}\), 38 s. for \(\mathcal {M}_{WSE}\), and 42 s. for \(\mathcal {M}_{PF}\). Of course, this measurement is biased because the target selection time is included only in \(\mathcal {M}_{MP}\), as steps 2 and 3 consisted in only selecting an entry point. We did not record separately the time required to select the entry point, because in step 1 we chose to let the surgeon go back and forth between target and entry point position refinement to have a good accuracy. However, even considering that planning the target point took half of the time in step 1, steps 2 and 3 were still much faster. Besides, the improvement of speed was not at the cost of accuracy, as an automatically proposed entry point was ranked first in 12/14 cases. This experiment confirms the overall interest of automatic assistance to preoperative trajectory planning for Deep Brain Stimulation.

Finally, we can notice that in 5 cases the surgeon did not choose the same point using PF and WS even though the preferred point was available in both. We hypothesize that the display might have to be improved for \(\mathcal {M}_{PF}\), for instance by using a color scheme for the objectives.

4 Conclusion

The automatic trajectory planning techniques that have been proposed for DBS in the literature are based on mono-objective optimization approaches that combine different criteria through weighted sums. Unfortunately, theory shows that such techniques cannot find concavities in Pareto fronts, meaning that some Pareto-optimal solutions cannot be reached.

This paper shows that methods using a quantification of the trajectories quality based on Pareto-optimality can find more optimal propositions than the current state of the art algorithms using weighted sums. The evaluation study we conducted involving a blind ranking, highlighted that the extra propositions can often be chosen as more accurate by a neurosurgeon, and that some of them did not have any reasonably close alternative proposed by the weighted sum method. Finally, the recorded times indicated that the automatic assistance was, in 12 cases over 14, both faster and more accurate than a manual planning, which further confirms the overall interest of automatic assistance to preoperative trajectory planning for Deep Brain Stimulation.