Abstract
We construct a functional encryption scheme for circuits which simultaneously achieves and improves upon the security of the current best known, and incomparable, constructions from standard assumptions: reusable garbled circuits by Goldwasser, Kalai, Popa, Vaikuntanathan and Zeldovich (STOC 2013) [GKP+13] and predicate encryption for circuits by Gorbunov, Vaikuntanathan and Wee (CRYPTO 2015) [GVW15]. Our scheme is secure based on the learning with errors (LWE) assumption. Our construction implies:
-
1.
A new construction for reusable garbled circuits that achieves stronger security than the only known prior construction [GKP+13].
-
2.
A new construction for bounded collusion functional encryption with substantial efficiency benefits: our public parameters and ciphertext size incur an additive growth of \(O(Q^2)\), where Q is the number of permissible queries (We note that due to a lower bound [AGVW13], the ciphertext size must necessarily grow with Q). Additionally, the ciphertext of our scheme is succinct, in that it does not depend on the size of the circuit. By contrast, the prior best construction [GKP+13, GVW12] incurred a multiplicative blowup of \(O(Q^4)\) in both the public parameters and ciphertext size. However, our scheme is secure in a weaker game than [GVW12].
Additionally, we show that existing LWE based predicate encryption schemes [AFV11, GVW15] are completely insecure against a general functional encryption adversary (i.e. in the “strong attribute hiding” game). We demonstrate three different attacks, the strongest of which is applicable even to the inner product predicate encryption scheme [AFV11]. Our attacks are practical and allow the attacker to completely recover \(\mathbf {x}\) from its encryption \(\mathsf{Enc}(\mathbf {x})\) within a polynomial number of queries. This illustrates that the barrier between predicate and functional encryption is not just a limitation of proof techniques. We believe these attacks shed significant light on the barriers to achieving full fledged functional encryption from LWE, even for simple functionalities such as inner product zero testing [KSW08, AFV11].
Along the way, we develop a new proof technique that permits the simulator to program public parameters based on keys that will be requested in the future. This technique may be of independent interest.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The last decade has witnessed important progress in the field of computing on encrypted data. Several sophisticated generalizations of encryption, such as Identity Based Encryption [BF01, Coc01, GPV08], Attribute Based Encryption [GPSW06, BSW07, GGH+13c, GVW13], Predicate Encryption [KSW08, AFV11, GVW15], Fully Homomorphic Encryption [Gen09, BV11, GSW13, BV14], Property Preserving Encryption [PR12] have burst onto the scene, significantly advancing the capabilities of modern cryptography.
These generalizations aim to provide the capability of computing “blind-folded” – namely, given an encryption of some data \(\mathbf {a}\), an untrusted party should be able to perform computations on \(\mathsf{Enc}(\mathbf {a})\) so that the resultant ciphertext may be decrypted meaningfully. The notion of fully homomorphic encryption permits arbitrary computation on encrypted data, but restricts decryption to be all-or-nothing, namely, the holder of the secret key may decrypt the resultant ciphertext to learn the result of the computation, but the same key also decrypts the original ciphertext revealing \(\mathbf {a}\). For applications that require restricted access to results of the computation, the notion of functional encryption (FE) is more suitable. In functional encryption, a secret key is associated with a function, typically represented as a circuit C, denoted by \(\mathsf {SK}_C\) and a ciphertext with some input \(\mathbf {a}\) from the domain of C, denoted by \(\mathsf {CT}_\mathbf {a}\). Given \(\mathsf {SK}_C\) and \(\mathsf {CT}_\mathbf {a}\), the user may run the decryption procedure to learn the value \(C(\mathbf {a})\). Security of the system guarantees that nothing beyond \(C(\mathbf {a})\) can be learned from \(\mathsf {CT}_\mathbf {a}\) and \(\mathsf {SK}_C\). Functional encryption was formalized by Boneh et al. [BSW11] to unify and extend the notions of Identity Based Encryption, Attribute Based Encryption and Predicate Encryption, which had already appeared in the literature.
There has been considerable progress in the last several years towards constructing FE for advanced functionalities [BF01, Coc01, BW06, BW07, GPV08, CHKP10, ABB10, GPSW06, BSW07, KSW08, LOS+10, AFV11, Wat12, GVW13, GGH+13c, GGH+13b, GVW15]. For the most powerful notion of “full-fledged” functional encryption, that allows the evaluation of arbitrary efficiently-computable functions and is secure against general adversaries, the only known constructions rely on multilinear maps [GGHZ14] or indistinguishability obfuscation (iO) [GGH+13b]. However, all known candidate multi-linear map constructions [GGH13a, CLT13, GGH15] as well as some candidates of iO have been recently broken [CHL+15, CGH+15, HJ15, CJL, CFL+16, MSZ16].
From standard assumptions, the best known constructions do support general functionalities, but achieve restricted notions of security. Currently, the state-of-the-art comprises two incomparable constructions:
-
The reusable garbled circuits construction of Goldwasser et al. [GTKP+13], which supports all polynomial sized Boolean circuits but restricts the attacker to only obtain a single secret key, for any circuit C of her choice. This construction can be compiled with the bounded collusion FE construction of [GVW12] to obtain a scheme which supports q queries, for any a-priori bounded q, and with a ciphertext size that grows by a multiplicative factor of \(O(q^4)\). Note that the ciphertext size here does not depend on the size of the circuit C, and is thus succinct.
-
The recent predicate encryption (PE) for circuits construction of Gorbunov et al. [GVW15], which also supports all polynomial sized Boolean circuits but restricts the attacker to only acquire keys for circuits \(C_i\) such that \(C_i(\mathbf {a})=0\), when \(\mathbf {a}\) is the vector of challenge attributes. He may not request any keys \(C_j\) such that \(C_j(\mathbf {a})=1\). We will refer to the former as 0-keys and the latter as 1-keys. This restricted game of security is often referred to as weak attribute hiding in the literature.
Both constructions natively achieve the restricted selective notion of security, which forces the attacker to output the challenge in the very first step of the game, before seeing the public parameters.
Note that both constructions provide the functionality demanded by functional encryption, but fall short in security. Covering the distance from the restricted security definitions acheived by these constructions to full fledged functional encryption is a much sought-after goal, and one that must contend with several thorny technical issues. The former construction relies on the use of garbled circuits for decryption, which restricts the number of supported keys to 1, or, using the additional machinery of [GVW12], to some a-priori bounded q. The use of garbled circuits is central to this construction, and surmounting the bounded key limitation appears to require entirely new techniques. On the other hand, the second construction does support an unbounded number of queries, but restricts them to belong to the 0-set. It is unclear how to support even a single 1-query in this case, due to various technical hurdles that arise from the proof techniques (more on this below). Whether these techniques may be extended to support the full-fledged security game of functional encryption is an important open question, and the one we study in this work.
1.1 Our Contributions
In this work, we provide a new construction for functional encryption which simultaneously achieves and improves upon the security of the current best known, and incomparable, constructions from standard assumptions [GKP+13, GVW15]. Our scheme is secure based on the learning with errors (LWE) assumption. Our construction implies:
-
1.
A new construction for reusable garbled circuits that achieves stronger security than the only prior construction by Goldwasser et al. (STOC 2013) [GKP+13]. In our construction, the attacker may additionally request an unbounded number of 0 keys in addition to the single arbitrary key allowed by the standard definition of reusable garbled circuits. Additionally, our construction achieves semi-adaptive security as against selective [GKP+13].
-
2.
A new construction for bounded collusion functional encryption where the adversary is restricted to making an a-priori fixed number of queries. The ciphertext of our scheme is succinct, in that it does not depend on the size of the circuit. Our public parameters and ciphertext size incur an additive growth of \(O(Q^2)\), where Q is the number of permissible queries. By contrast, the prior best construction [GKP+13, GVW12] incurred a multiplicative blowup of \(O(Q^4)\) in both the public parameters and ciphertext size. However, our construction is secure in a weaker game than best known [GKP+13, GVW12].
Additionally, we show that existing LWE based predicate encryption schemes [AFV11, GVW15] are completely insecure against a general functional encryption adversary (i.e. in the “strong attribute hiding” game). We demonstrate three different attacks, the strongest of which is applicable even to the inner product predicate encryption scheme [AFV11]. Our attacks are practical and allow the attacker to completely recover \(\mathbf {a}\) from its encryption \(\mathsf{Enc}(\mathbf {a})\) within a polynomial number of queries. This illustrates that the barrier between predicate and functional encryption is not just a limitation of proof techniques. We believe these attacks shed significant light on the barriers to achieving full fledged functional encryption for circuits from standard assumptions.
Along the way, we develop a new proof technique that permits the simulator to program public parameters based on keys that will be requested in the future. This technique may be of independent interest.
1.2 Our Techniques
Our work builds upon the constructions of Goldwasser et al. [GTKP+13] and Gorbunov et al. [GVW15]. Both these systems begin with the idea that the public attributes in an attribute based encryption scheme (ABE) may be hidden, and yet remain amenable to computation, if they are encrypted using fully homomorphic encryption. Recall that in an attribute based encryption scheme [GPSW06], a ciphertext is associated with a public attribute vector \(\mathbf {a}\) and plaintext bit \(\mu \), and it hides \(\mu \), but not \(\mathbf {a}\).
To hide \(\mathbf {a}\), one may encrypt it using FHE to obtain \(\widehat{\mathbf {a}}\), and treat this encryption as the public attribute in an ABE system. Since an ABE scheme for circuits [GVW13, BGG+14] allows for a key \(\mathsf {SK}_C\) to evaluate an arbitrary circuit C on the attribute, the decryptor may now homomorphically compute on \(\widehat{\mathbf {a}}\) using the FHE evaluation circuit. Then, given a key corresponding to the circuit \(\mathsf {FHE}.\mathsf{Eval}(C, \cdot )\), the decryptor may run the ABE decryption procedure to learn the FHE encryption of \(C(\mathbf {a})\), namely \(\widehat{C(\mathbf {a})}\).
This is not yet enough, as the goal is for the decryptor to learn \(C(\mathbf {a})\) in the clear. To achieve this, FHE decryption must be performed on \(\widehat{C(\mathbf {a})}\) in a manner that does not permit decryption of any ciphertext other than \(\widehat{C(\mathbf {a})}\). The scheme of Goldwasser et al. [GTKP+13] resolves this difficulty by employing a single use garbled circuit for the FHE decryption function and using ABE to provide labels corresponding to input \(\widehat{C(\mathbf {a})}\). This constrains FHE decryption, but restricts the resultant FE scheme to only be secure against a single key request. The scheme of Gorbunov et al. [GVW15] resolves this difficulty by making use of two nicely matching asymmetries:
-
1.
The asymmetry in computation. To compute \(C(\mathbf {a})\) using the above method, the bulk of the computation is to be performed on FHE ciphertext, namely \(\mathsf {FHE}.\mathsf{Eval}(C, \widehat{\mathbf {a}})\), where \(\widehat{\mathbf {a}}\) can be public. The remainder of the computation, namely running the FHE decryption circuit on \(\widehat{C(\mathbf {a})}\), is a relatively lightweight circuit.
-
2.
The asymmetry in attribute hiding in the ABE scheme of [BGG+14]. There is an inherent asymmetry in the homomorphic multiplication procedure of the ABE scheme [BGG+14], so that computing a product of two ciphertexts wth attributes \(\mathbf {a}_1\) and \(\mathbf {a}_2\) respectively, only necessitates revealing one attribute (say \(\mathbf {a}_1\)) while the other (\(\mathbf {a}_2\)) can remain hidden (for addition, both \(\mathbf {a}_1\) and \(\mathbf {a}_2\) may remain hidden). This property is leveraged by [GVW15] to construct partially hiding predicate (or attribute) encryption (PHPE), which allows computation of an inner product of a public attribute vector corresponding to \(\mathsf {FHE}.\mathsf{Eval}(C, \widehat{\mathbf {a}})\) and a private attribute vector, corresponding to the FHE secret key. Since inner product loosely approximates FHE decryption, this allows the decryptor to obtain a plaintext value corresponding to \(C(\mathbf {a})\) as desired.
While the predicate encryption scheme [GVW15] can handle an unbounded number of 0-queries from the adversary, it runs into at least three difficulties when faced with a 1-query:
-
1.
The proof of security in the PHPE scheme uses a trapdoor puncturing technique [ABB10] in the simulation, so that the simulator has a trapdoor to sample keys for 0-queries but this trapdoor vanishes for 1-queries, disabling the simulator.
-
2.
Given a PHPE ciphertext \(\mathsf {CT}_{\widehat{\mathbf {a}}}\) with public attributes \(\widehat{\mathbf {a}}\), key homomorphism [BGG+14, GVW15] enables the evaluation of a circuit C on the PHPE ciphertext resulting in a PHPE ciphertext \(\mathsf {CT}_{C(\;\widehat{\mathbf {a}}\;)}\) with attributes \(C(\;\widehat{\mathbf {a}}\;)\). By construction, this resultant ciphertext is an LWE sample with an error term which is fixed and public linear combination of the error terms used to construct \(\mathsf {CT}_{\widehat{\mathbf {a}}}\). This error is learned by the adversary upon decryption, which creates leakage that cannot be simulated. Indeed, this leakage, when sufficient, can completely break LWE security and allow the adversary to learn \(\mathbf {a}\) in the clear (see Sect. 3 for details).
-
3.
Recall that the FHE decryption operation is a lightweight operation conducted using PHPE with the FHE secret key as the private attribute vector. While FHE decryption is lightweight, it is still not lightweight enough to be performed in its entirety while maintaining the privacy of the FHE secret. FHE decryption is an inner product followed by a threshold function, of which only the inner product can be performed securely by PHPE. The authors overcome this hurdle by making use of the “lazy OR” trick, which roughly allows the decryptor to learn not the threshold inner product, but the pure inner product, which leaks sensitive information about the noise used while encrypting \(\mathbf {a}\). Again, this leakage cannot be simulated, and when sufficiently high, can lead to complete recovery of the FHE secret key.
Attacks. Interestingly, all of the above difficulties in proving security translate to polynomial time attacks that lead to complete message recovery in a game where 1-keys are permitted. Our first and strongest attack is related to the first difficulty, and is effective even against the inner product predicate encryption scheme of Agrawal et al. [AFV11]. Recall that the inner product zero test functionality of [AFV11] permits the decryptor to test whether the inner product of a vector \(\mathbf {x}\in \mathbb {Z}_p^\ell \) in the ciphertext and vector \(\mathbf {v}\in \mathbb {Z}_p^\ell \) in the key is zero or non-zero. We demonstrate that by requesting keys for linearly dependent functions, the attacker can construct a short basis for a matrix \(\mathbf {F}\) (say) which is related to the LWE matrices used in the challenge ciphertext. By manipulating the challenge ciphertext, the attacker may recover an LWE sample of the form \(\mathbf {F}^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathsf {noise}\). This LWE sample unresistingly reveals all its secrets given a trapdoor for \(\mathbf {F}\), which in turn allow the attacker to recover the entire message \(\mathbf {x}\) from the challenge ciphertext.
We believe this attack sheds significant light on the barriers to obtaining full fledged functional encryption even for a simple functionality such as inner product zero testing [KSW08, AFV11]. Note that full security has been achieved for a functionality that computes the inner product of two vectors \(\mathbf {x},\mathbf {v}\in \mathbb {Z}_p^\ell \) given \(\mathsf {CT}(\mathbf {x})\) and \(\mathsf {SK}(\mathbf {v})\), but it appears quite challenging to extend these techniques for the case of inner product zero testing. Intuitively, this is because the inner product zero test functionality is non-linear: 0 keys reveal almost nothing about \(\mathbf {x}\) while 1 keys reveal much more. This is in contrast to the inner product computation functionality, in which all function queries, whether type 0 or type 1, reveal proportionate information about \(\mathbf {x}\). Constructing functional encryption with full fledged security even for the simple functionality of [KSW08, AFV11] from lattice based assumptions appears to require fundamental new techniques.
Our second attack is against the Partially Hiding Predicate Encryption system for circuits [GVW15] and stems from the second difficulty above. This attack exploits the fact that the decryptor, given a 1-key, learns a public linear function of the error terms used in encryption. By requesting sufficient 1-keys, the attacker can solve this linear system to recover the errors used in encryption, which lead to recovery of the predicate \(\mathbf {a}\) even when functionality reveals much less.
Our third attack is against the Predicate Encryption (PE) system for circuits [GVW15]. As discussed in the third difficulty above, the PE decryption key, which wishes to provide the decryptor with a threshold inner product value, instead can only provide the exact inner product value, leaving the decryptor to compute the threshold herself. This leads to an attacker learning linear equations in the errors used to construct the FHE encryption \(\widehat{\mathbf {a}}\), which, when sufficiently many, let her recover the FHE secret, which in turn lets her recover \(\mathbf {a}\).
We emphasize that our attacks are entirely practical and also apply to the weaker indistinguishability based security game of functional encryption [BSW11] but do not work in the “weak attribute hiding” security game considered by [AFV11, GVW15]. This suggests that using predicate encryption systems in scenarios where even a small number of arbitrary users collude is insecure in practice.
“Very-Selective” \((1,{{\mathrm{poly}}})\) -Functional Encryption. We provide a construction that overcomes the above vulnerabilities for the case of a single arbitrary key, whether 1 or 0, and continues to support an unbounded number of 0-keys. By restricting the attacker to any single query, this yields an alternate construction for reusable garbled circuits [GTKP+13]. We summarize the main ideas here. For clarity of exposition, we omit many details; we refer the reader to Sects. 4, 5 and 6 for the formal construction and proof.
Our starting point is the predicate encryption scheme of [GVW15], which we will hereby refer to as \((0,{{\mathrm{poly}}})\)-FE, as it supports zero 1-queries and any polynomial number of 0-queries. The construction for \((0,{{\mathrm{poly}}})\)-FE makes use of two components as described above, namely, \((0,{{\mathrm{poly}}})\)-partially hiding predicate encryption (PHPE) and fully homomorphic encryption (FHE). Our construction for \((1,{{\mathrm{poly}}})\)-FE follows the same high level template as [GVW15], and as our first step, we require \((1,{{\mathrm{poly}}})\)-PHPE. Note that the \((0,{{\mathrm{poly}}})\)-PHPE scheme does allow the key generator to release an unbounded number of both 0 and 1 queries, but as mentioned above, the proof of security breaks down if the adversary requests a 1-key. This is because the secret key corresponding to a circuit C is a low norm matrix \(\mathbf {K}\) satisfying an equation of the following form:
where the matrices \(\mathbf {A}, \mathbf {P}\) are fixed and public, and the matrix \(\mathbf {A}_C\) is computed by executing a homomorphic evaluation procedure [BGG+14, GVW15] corresponding to the circuit C on some public matrices. In the real system, the key generator has a trapdoor for \(\mathbf {A}\), which allows it to sample \(\mathbf {K}\) using known techniques [CHKP10, ABB10]. In the simulation, the matrix \(\mathbf {A}_C\) has a special form, namely \(\mathbf {A}_C = [\mathbf {A}\mathbf {R}_C - C(\mathbf {a})\cdot \mathbf {G}]\) for some low norm matrix \(\mathbf {R}_C\) and fixed public matrix \(\mathbf {G}\). The simulator has a trapdoor for \(\mathbf {G}\) which enables it to sample the required \(\mathbf {K}\) also using known techniques but only when \(C(\mathbf {a}) \ne 0\) [ABB10]. When \(C(\mathbf {a}) = 0\), \(\mathbf {G}\) vanishes along with its trapdoor, and the simulator has no method by which to sample \(\mathbf {K}\) Footnote 1.
To overcome this, we note that if the circuit C is known before the public key is generated, the simulator can instead sample \(\mathbf {K}\) first and set \(\mathbf {P}\) to satisfy the above equation. This is a standard trick in LWE based systems [GPV08, Pei13], and yields the same distribution of the pair \((\mathbf {K}, \mathbf {P})\) as in the real world. This allows us to take a step forwardFootnote 2, but the adversary’s view remains distinguishable from the real world, because decryption leaks correlated noise which is un-simulatable, as discussed in difficulty #2 above. To overcome this, we must choose the noise in the challenge ciphertext with care so that the noise yielded by the decryption equation is statistically close to fresh and independently chosen noise. Put together, these tricks enable us to build a \((1,{{\mathrm{poly}}})\)-PHPE.
However, \((1,{{\mathrm{poly}}})\)-PHPE does not immediately yield \((1,{{\mathrm{poly}}})\)-FE due to difficulty #3 above, namely, leakage on FHE noise. To handle this, we modify the circuit for which the PHPE key is provided so that the FHE ciphertext \(\widehat{C(\mathbf {a})}\) is flooded with large noise before the inner product with the FHE secret key is computed. Now, though the attacker learns the exact noise in the evaluated FHE ciphertext \(\widehat{C(\mathbf {a})}\) as before, this noise is independent of the noise used to generate \(\widehat{\mathbf {a}}\) and no longer leaks any sensitive information. Note that care is required in executing the noise flooding step, since correctness demands that the FHE modulus be of polynomial size and the noise to be added may be super-polynomial. To ensure this, we flood the FHE ciphertext before the FHE “modulus reduction” step. Now, we have at our disposal a \((1,{{\mathrm{poly}}})\)-FE scheme, albeit one that is secure according to a very restricted definition of security, which requires the attacker to commit to both the challenge messages and the single arbitrary function in the first step of the game. This “very selective” definition can be upgraded to semi-adaptive, as described next.
Upgrading Very-Selective to Semi-Adaptive. We provide a method for compiling our function-selective secure PHPE construction to one that satisfies semi-adaptive security, in which the attacker may see the public parameters before revealing the challenge. Our transformation is generic – it applies to all constructions that satisfy certain structural properties. In more detail, we require that: (1) the PHPE ciphertext \(\mathsf {CT}_\mathbf {a}\) be decomposable into \(|\mathbf {a}|\) components \(\mathsf {CT}_i\), where \(\mathsf {CT}_i\) depends only on \(\mathbf {a}[i]\), and (2) \(\mathsf {CT}_i\) is a fixed and public linear function of the message \(\mathbf {a}[i]\) and randomness chosen for encryption.
Concretely, consider the ciphertext in the \((0,{{\mathrm{poly}}})\)-PHPE of [GVW15]. For \(i \in [\ell ]\),
Clearly condition (1) is satisfied – the \(i^{th}\) component of \(\mathbf {a}\) influences only \(\mathbf {u}_i\). Additionally, note that
Here, the first vector is a fixed public vector that is known to the key generator, while the second vector is made up of components all of which are known to the encryptor.
Given these two conditions, we construct a semi-adaptive PHPE for the circuit class \(\mathcal{C}\), denoted by \({\textsf {SaPH}}\), using two ingredients:
-
1.
A single key fully secureFootnote 3 functional encryption scheme, denoted by \({\textsf {FuLin}}\), for the inner product functionality defined as:
$$ F_{(\mathbf {V}_1, \ldots ,\mathbf {V}_k)} (\mathbf {a}_1, \ldots ,\mathbf {a}_k) = \underset{i \in [k]}{\sum }\; \mathbf {V}_i \cdot \mathbf {a}_i\;\mod q $$Such a scheme was recently constructed by Agrawal et al. [ALS16].
-
2.
A \((1,{{\mathrm{poly}}})\) selectively secure PHPE scheme for the circuit class \(\mathcal{C}\), which we denote by \({\textsf {VSelPH}}\).
Intuitively, the idea is to nest the selective PHPE system for \(\mathcal{C}\) within an adaptive FE system for inner products, so that the latter is used to generate ciphertexts of the former on the fly. In more detail, the public parameters of \({\textsf {SaPH}}\) are set as the public parameters of \({\textsf {FuLin}}\), the secret key corresponding to C, namely \({\textsf {SaPH}}.\mathsf {SK}(C)\) is the tuple \(\big (\;{\textsf {VSelPH}}.\mathsf {MPK}, \;{\textsf {FuLin}}.\mathsf {SK}(\;[\;\mathbf {A}_i^{\scriptscriptstyle \mathsf {T}},\; 1,\; 1\;]\;),\; {\textsf {VSelPH}}.\mathsf {SK}(C)\; \big ) \) and the ciphertext is \({\textsf {SaPH}}.\mathsf {CT}= {\textsf {FuLin}}.\mathsf {CT}\big ([\;\mathbf {s},\; \mathbf {a}[i]\cdot \mathbf {G}^{\scriptscriptstyle \mathsf {T}}\mathbf {s},\; \mathsf {noise}_i\;]\big )\). Now, the ciphertext \({\textsf {FuLin}}.\mathsf {CT}\big ([\;\mathbf {s},\; \mathbf {a}[i]\cdot \mathbf {G}^{\scriptscriptstyle \mathsf {T}}\mathbf {s},\; \mathsf {noise}_i\;]\big )\) and secret key component \({\textsf {FuLin}}.\mathsf {SK}(\;[\;\mathbf {A}_i^{\scriptscriptstyle \mathsf {T}},\; 1,\; 1\;]\;)\) may be decrypted to obtain the \({\textsf {VSelPH}}\) ciphertext, which may be decrypted using \({\textsf {VSelPH}}.\mathsf {SK}(C)\). Some care is required in ascertaining that \({\textsf {FuLin}}\) is only invoked for a single secret key, but this can be ensured by taking multiple copies of the \({\textsf {FuLin}}\) scheme, and using the same randomness to generate multiple copies of the same key.
The advantage to the above strategy is that the public parameters of the \({\textsf {SaPH}}\) scheme are now set as the public parameters of the \({\textsf {FuLin}}\) scheme, and the public parameters of the \({\textsf {VSelPH}}\) scheme are moved into the secret keys of \({\textsf {SaPH}}\) scheme. This enables the simulator of the \({\textsf {SaPH}}\) scheme to provide the public parameters using the (adaptive/full) simulator for the \({\textsf {FuLin}}\) scheme, and delay programming the \(\mathsf{PHPE}\) public parameters until after the challenge is received, as required by the \({\mathsf {VSelPH}}\) simulator. Thus, very-selective security may be upgraded to semi-adaptive security for the circuit class \(\mathcal{C}\), by leveraging adaptive security of the simpler inner product functionality. For more details, please see Sect. 5.
Generalising to Q Queries. To construct \((Q,{{\mathrm{poly}}})\)-FE, we again begin by constructing \((Q,{{\mathrm{poly}}})\)-PHPE, which in turn is constructed from \((1,{{\mathrm{poly}}})\)-PHPE. The \((1,{{\mathrm{poly}}})\)-PHPE scheme has the following structure: it encodes the message \(\mathbf {b}\) within an LWE sample \({\varvec{\beta }}_0 = \mathbf {P}^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathsf {noise}+ \mathbf {b}\). Given other components of the ciphertext, the decryptor is able to compute a ciphertext \(\mathbf {c}_\mathsf{Eval}\) and key generator provides as the key a short matrix \(\mathbf {K}\), where
By computing \(\mathbf {K}^{\scriptscriptstyle \mathsf {T}}\mathbf {c}_\mathsf{Eval}- {\varvec{\beta }}_0\) and rounding the result, the decryptor recovers \(\mathbf {b}\).
To generalize the above to handle Q queries, a natural approach would be to encode the message Q times, using Q distinct matrices \(\mathbf {P}_1,\ldots ,\mathbf {P}_Q\) and have the \(i^{th}\) key \(\mathbf {K}_i\) be a short matrix satisfying \([\;\mathbf {A}\;|\;\mathbf {A}_{C_i}\;] \;\mathbf {K}_i = \mathbf {P}_i \mod q\). Then, the key generator can pick \(\mathbf {P}_i\) for the \(i^{th}\) key, and sample the corresponding \(\mathbf {K}_i\) as the secret key. However, this straightforward idea would require the key generator to keep track of how many keys it has produced so far and would make the key generator stateful, which is undesirable.
To get around this, we make use of a trick using cover free sets [GVW12]. The idea is to enable the key generator to generate a fresh matrix \(\mathbf {P}_i^*\) for the \(i^{th}\) key in a stateless manner, as follows. We publish a set of matrices \(\{\mathbf {P}_1,\ldots , \mathbf {P}_k\}\) in the public key, for some parameter k. The key generator chooses a random subset \(\varDelta _i \subset [k]\) s.t. \(|\varDelta _i| = v\) for some suitably chosen v, and computes \(\mathbf {P}^*_i = \underset{j \in \varDelta _i}{\sum } \mathbf {P}_j\). It then samples \(\mathbf {K}_i\) so that
If we choose (v, k) as functions of the security parameter \(\kappa \) and number of queries Q in a way that the Q subsets \(\varDelta _1, \ldots , \varDelta _Q\) are cover free with high probability, then this ensures that the matrices \(\mathbf {P}^*_1,\ldots , \mathbf {P}^*_Q\) are independent and uniformly distributed, which will enable the simulator to sample the requisite keys. This idea can be converted to a secure scheme with only an additive blowup of \(O(Q^2)\) in the public key and ciphertext size. However, security is proven in a game which is weaker than [GVW12] in which the attacker may not request the \(1\text {-}\)keys adaptively, but must announce them all at once after seeing the public parameters.
This gives us a \((Q,{{\mathrm{poly}}})\)-PHPE but constructing \((Q,{{\mathrm{poly}}})\)-FE requires some more work. Instead of flooding the evaluated ciphertext with a single piece of noise, we must now encode at least Q pieces of noise, to flood the ciphertext for Q decryptions. Fortunately, this can be ensured by leveraging cover-free sets again, so that the decryptor is forced to add a random cover-free subset sum of noise terms to the ciphertext before decryption. This ensures that each decryption lets the decryptor learn a fresh noise term which wipes out any troublesome noise leakage. Details are in the full version [Agr16].
Additional Related Work. We note that in an independent and concurrent work, Goyal et al. [GKW16] provide a generic method to compile selective security to semi-adaptive security for functional encryption schemes. We note that this result does not apply to our setting as-is, since our starting-point security definition is even more restricted than selective. See Sect. 2.1 for more details. In another work, Brakerski and Vaikuntanathan [BV16] achieved semi-adaptive security for “Attribute Based Encryption” using specialized techniques – these also do not apply black box to our construction.
Organization of the Paper. The paper is organized as follows. Preliminaries are provided in Sect. 2. In Sect. 3, we describe our three attacks using 1-keys against existing predicate encryption systems. In Sect. 4 we provide our construction for \((1,{{\mathrm{poly}}})\) partially hiding predicate encryption. This is upgraded to achieve semi-adaptive security in Sect. 5. In Sect. 6 we provide our \((1,{{\mathrm{poly}}})\) FE scheme. The generalization to \((q, {{\mathrm{poly}}})\) FE is provided in the full version of the paper [Agr16].
2 Preliminaries
In this section we provide the preliminaries required for our work. For definitions of lattices and the LWE problem, we refer the reader to the full version of the paper [Agr16].
2.1 Functional Encryption
In this section, we provide the definition of functional encryption.
Definition 2.1
A functional encryption scheme \(\mathsf {FE}\) for an input universe \(\mathcal{X}\), a circuit universe \(\mathcal{C}\) and a message space \(\mathcal{M}\), consists of four algorithms \(\mathsf {FE}=(\mathsf { FE.Setup}, \mathsf { FE.Keygen},\) \(\mathsf { FE.Enc}, \mathsf { FE.Dec})\) defined as follows.
-
\(\mathsf { FE.Setup}(1^\kappa )\) is a p.p.t. algorithm takes as input the unary representation of the security parameter and outputs the master public and secret keys \(({\mathsf {PK}}, \mathsf {MSK})\).
-
\(\mathsf { FE.Keygen}(\mathsf {MSK}, C)\) is a p.p.t. algorithm that takes as input the master secret key \(\mathsf {MSK}\) and a circuit \(C \in \mathcal{C}\) and outputs a corresponding secret key \(\mathsf {SK}_C\).
-
\(\mathsf { FE.Enc}\big ({\mathsf {PK}}, (\mathbf {a}, \mu )\big )\) is a p.p.t. algorithm that takes as input the master public key \({\mathsf {PK}}\) and an input message \((\mathbf {a}, \mu ) \in \mathcal{X}\times \mathcal{M}\) and outputs a ciphertext \(\mathsf {CT}_{\mathbf {a}}\).
-
\(\mathsf { FE.Dec}(\mathsf {SK}_C, \mathsf {CT}_\mathbf {a})\) is a deterministic algorithm that takes as input the secret key \(\mathsf {SK}_C\) and a ciphertext \(\mathsf {CT}_\mathbf {a}\) and outputs \(\mu \) iff \(C(\mathbf {a})=1\), \(\bot \) otherwise.
Note that our definition is a slightly modified, albeit equivalent version of the standard definition for FE [BSW11]. For compatibility with the definition of predicate encryption [GVW15], we define our functionality to incorporate a message bit \(\mu \) which is revealed when \(C(\mathbf {a}) =1\).
Correctness. Next, we define correctness of the system.
Definition 2.2
(Correctness). A functional encryption scheme \(\mathsf {FE}\) is correct if for all \(C \in \mathcal {C}_\kappa \) and all \(\mathbf {a}\in \mathcal{X}_\kappa \),
-
If \(C(\mathbf {a})=1\)
$$ \Pr \bigg [\begin{array}{ll}({\mathsf {PK}},\mathsf {MSK}) \leftarrow \mathsf { FE.Setup}(1^\kappa ); \\ \mathsf { FE.Dec}\Big (\mathsf { FE.Keygen}(\mathsf {MSK},C), \mathsf { FE.Enc}\big ({\mathsf {PK}},(\mathbf {a},\mu )\big )\Big ) \ne \mu \end{array}\bigg ] = {{\mathrm{negl}}}(\kappa ) $$ -
If \(C(\mathbf {a})=0\)
$$ \Pr \bigg [\begin{array}{ll}({\mathsf {PK}},\mathsf {MSK}) \leftarrow \mathsf { FE.Setup}(1^\kappa ); \\ \mathsf { FE.Dec}\Big (\mathsf { FE.Keygen}(\mathsf {MSK},C), \mathsf { FE.Enc}\big ({\mathsf {PK}},(\mathbf {a},\mu )\big )\Big ) \ne \bot \end{array}\bigg ] = {{\mathrm{negl}}}(\kappa ) $$
where the probability is taken over the coins of \(\mathsf { FE.Setup}\), \(\mathsf { FE.Keygen}\), and \(\mathsf { FE.Enc}\).
Security. Next, we define simulation based security for functional encryption. Note that simulation based security is impossible for functional encryption against an adversary that requests even a single key after seeing the challenge ciphertext [BSW11], or an unbounded number of keys before seeing the challenge ciphertext [AGVW13]. However, against an adversary who only requests an a-priori bounded number of keys before seeing the challenge ciphertext, simulation based security is possible but causes the ciphertext size to grow with the number of requested keys [AGVW13].
For the application of reusable garbled circuits, it suffices to construct a functional encryption scheme that supports a single key request made before seeing the challenge ciphertext. We generalize this definition to subsume the notion of predicate encryption, where an attacker can make an unbounded number of function queries \(C_i\) so long as it holds that the function keys do not decrypt the challenge ciphertext \(\mathsf {CT}(\mathbf {a}, \mu )\) to recover \(\mu \). Thus, it holds that \(C_i(\mathbf {a})=0\) for all requested \(C_i\). We shall refer to such \(C_i\) as 0-keys, and any C such that \(C(\mathbf {a})=1\) as a 1-key. In our definition, the adversary can request a single arbitrary (i.e. 0 or 1) key followed by an unbounded polynomial number of 0-keys. We refer to this security notion as \((1, {{\mathrm{poly}}})\) simulation security. The notion we achieve is semi-adaptive, in that the adversary must declare the challenge message after receiving the public key.
Definition 2.3
( \((1, {{\mathrm{poly}}})\text {-}\mathsf {SA\text {-}SIM}\) Security). Let \(\mathsf {FE}\) be a functional encryption scheme for a Boolean circuit family \(\mathcal {C}\). For every p.p.t. adversary \(\mathsf {Adv}\) and a stateful p.p.t. simulator \({\mathsf {Sim}}\), consider the following two experiments:

We say an adversary \(\mathsf {Adv}\) is admissible if:
-
1.
For a single query \(C^*\), it may hold that \(C^*(\mathbf {a})=1\) or \(C^*(\mathbf {a})=0\).
-
2.
For all other queries \(C_i \ne C^*\), it holds that \(C_i(\mathbf {a}) = 0\).
In the ideal experiment, the simulator \({{\mathsf {Sim}}}\) is traditionally given access to an oracle \(U_{(\mathbf {a}, \mu )}(\cdot )\), which upon input C returns \(\bot \) if \(C(\mathbf {a})=0\) and \(\mu \) if \(C(\mathbf {a})=1\). However, we note that our simulator does not require access to an oracle because an admissible adversary may only make a single 1 query \(C^*\), which is provided explicitly to the simulator. Every other query \(C_i\) made by the adversary is a 0 query, hence the simulator can compare each query \(C_i\) with \(C^*\), and set \(C_i(\mathbf {a})=0\) when the equality does not hold.
The functional encryption scheme \(\mathsf {FE}\) is then said to be \((1,{{\mathrm{poly}}})\)-\(\mathsf {SA\text {-}SIM}\)-secure if there is an admissible stateful p.p.t. simulator \({\mathsf {Sim}}\) such that for every admissible p.p.t. adversary \(\mathsf {Adv}\), the following two distributions are computationally indistinguishable.
For the \((Q,{{\mathrm{poly}}})\) version of the above game, we merely replace each occurrence of \(C^*\) with a tuple \(C^*_1, \ldots , C^*_Q\).
2.2 Partially Hiding Predicate Encryption
A Partially-Hiding Predicate Encryption scheme \(\mathsf{PHPE}\) for a pair of input-universes \(\mathcal{X},\mathcal{Y}\), a predicate universe \(\mathcal{C}\), a message space \(\mathcal{M}\), consists of four algorithms \(({\mathsf {PH}}.\mathsf{Setup}, {\mathsf {PH}}.\mathsf{Enc}, {\mathsf {PH}}.\mathsf{KeyGen}, {\mathsf {PH}}.\textsf {Dec})\):
-
\({\mathsf {PH}}.\mathsf{Setup}(1^\kappa , \mathcal{X}, \mathcal{Y}, \mathcal{C},\mathcal{M}) \rightarrow ({\mathsf {PH}}.{\mathsf {PK}}, {\mathsf {PH}}.\mathsf {MSK})\). The setup algorithm gets as input the security parameter \(\kappa \) and a description of \((\mathcal{X}, \mathcal{Y}, \mathcal{C}, \mathcal{M})\) and outputs the public parameter \({\mathsf {PH}}.{\mathsf {PK}}\), and the master key \({\mathsf {PH}}.\mathsf {MSK}\).
-
\({\mathsf {PH}}.\mathsf{Enc}({\mathsf {PH}}.{\mathsf {PK}},(\mathbf {x}, \mathbf {y}), \mu ) \rightarrow \mathsf {CT}_\mathbf {y}\). The encryption algorithm gets as input \({\mathsf {PH}}.{\mathsf {PK}}\), an attribute pair \((\mathbf {x}, \mathbf {y}) \in \mathcal{X}\times \mathcal{Y}\) and a message \(\mu \in \mathcal{M}\). It outputs a ciphertext \(\mathsf {CT}_\mathbf {y}\).
-
\({\mathsf {PH}}.\mathsf{KeyGen}({\mathsf {PH}}.\mathsf {MSK}, C) \rightarrow \mathsf {SK}_C\). The key generation algorithm gets as input \({\mathsf {PH}}.\mathsf {MSK}\) and a predicate \(C \in \mathcal{C}\). It outputs a secret key \(\mathsf {SK}_C\).
-
\({\mathsf {PH}}.\textsf {Dec}((\mathsf {SK}_C , C),(\mathsf {CT}, \mathbf {y})) \rightarrow \mu \vee \bot \). The decryption algorithm gets as input the secret key \(\mathsf {SK}_C\), a predicate C, and a ciphertext \(\mathsf {CT}_\mathbf {y}\) and the public part \(\mathbf {y}\) of the attribute vector. It outputs a message \(\mu \in \mathcal{M}\) or \(\bot \).
Correctness. We require that for all \(({\mathsf {PH}}.{\mathsf {PK}}, {\mathsf {PH}}.\mathsf {MSK}) \leftarrow {\mathsf {PH}}.\mathsf{Setup}(1^\kappa , \mathcal{X}, \mathcal{Y}, \mathcal{C}, \mathcal{M}) \), for all \((\mathbf {x}, \mathbf {y}, C) \in \mathcal{X}\times \mathcal{Y}\times \mathcal{C}\) and for all \(\mu \in \mathcal{M}\),
-
For 1-queries, namely \(C(\mathbf {x}, \mathbf {y}) =1\),
$$ \Big [ {\mathsf {PH}}.\textsf {Dec}\big ((\mathsf {SK}_C, C), (\mathsf {CT}_\mathbf {y}, \mathbf {y})\big ) = \mu \Big ] \ge 1- {{\mathrm{negl}}}(\kappa ) $$ -
For 0-queries, namely \(C(\mathbf {x}, \mathbf {y}) =0\),
$$ \Big [ {\mathsf {PH}}.\textsf {Dec}\big ((\mathsf {SK}_C, C), (\mathsf {CT}_\mathbf {y}, \mathbf {y})\big ) = \bot \Big ] \ge 1- {{\mathrm{negl}}}(\kappa ) $$
Semi Adaptive SIM Security. Below, we define the \(\mathsf {SA\text {-}SIM}\) security experiment for partially hiding predicate encryption (PHPE) that supports a single 1-query and an unbounded number of 0-queries. We denote such a scheme by \((1, {{\mathrm{poly}}})\)-PHPE scheme. We note that the scheme of Gorbunov et al. [GVW15] is a \((0, {{\mathrm{poly}}})\)-PHPE scheme.
Definition 2.4
( \((1, {{\mathrm{poly}}})\)-\(\mathsf {SA\text {-}SIM}\) Security). Let \(\mathsf {PHPE}\) be a partially hiding predicate encryption scheme for a circuit family \(\mathcal {C}\). For every stateful p.p.t. adversary \(\mathsf {Adv}\) and a stateful p.p.t. simulator \({\mathsf {Sim}}\), consider the following two experiments:

We say an adversary \(\mathsf {Adv}\) is admissible if:
-
1.
For the single query \(C^*\), it may hold that \(C^*(\mathbf {x}, \mathbf {y})=1\) or \(C^*(\mathbf {x}, \mathbf {y})=0\).
-
2.
For all queries \(C \ne C^*\), it holds that \(C(\mathbf {x}, \mathbf {y}) = 0\).
In the ideal experiment, the simulator \({{\mathsf {Sim}}}\) is traditionally given access to an oracle \(U_{(\mathbf {x}, \mathbf {y}, \mu )}(\cdot )\), which upon input C returns \(\bot \) if \(C(\mathbf {x}, \mathbf {y})=0\) and \(\mu \) if \(C(\mathbf {x}, \mathbf {y})=1\). However, since in our case \({{\mathsf {Sim}}}\) is provided \(C^*\) explicitly, and this is the only possible 1-query, the simulator can check whether \(C_i = C^*\) for any query \(C_i\), and if not, set \(C_i(\mathbf {x},\mathbf {y})=0\). Hence, to simplify notation, we omit the oracle in the ideal experiment above.
The partially hiding predicate encryption scheme \(\mathsf {PHPE}\) is said to be \((1, {{\mathrm{poly}}})\)-attribute hiding if there exists a p.p.t. simulator \({\mathsf {Sim}}\) such that for every admissible p.p.t. adversary \(\mathsf {Adv}\), the following two distributions are computationally indistinguishable:
Very Selective SIM Security. Next, we define a “very” selective variant of the above game, in which the adversary must announce the challenge messages as well as the challenge function \(C^*\) in the very first step of the game.
Definition 2.5
( \((1, {{\mathrm{poly}}})\) \(\mathsf {VSel}\text {-}\mathsf {SIM}\) Security). Let \(\mathsf {PHPE}\) be a partially hiding predicate encryption scheme for a circuit family \(\mathcal {C}\). For every p.p.t. adversary \(\mathsf {Adv}\) and a stateful p.p.t. simulator \({\mathsf {Sim}}\), consider the following two experiments:

The admissibility of the adversary \(\mathsf {Adv}\), the notes about the simulator and the required indistinguishability of distributions are as in Definition 2.4.
For the definition of \((Q,{{\mathrm{poly}}})\)-PHPE, where an adversary may request Q decrypting queries, we merely replace each occurence of \(C^*\) with a tuple \(C^*_1, \ldots , C^*_Q\) in both the games above.
2.3 Full Security for Single Key Linear FE
Definition 2.6
( \(\mathsf {FULL}\text {-}\mathsf {SIM}\) security). Let \(\mathsf {FE}\) be a single key functional encryption scheme for a circuit family \(\mathcal {C}\). For every p.p.t. adversary \(\mathsf {Adv}\) and a stateful p.p.t. simulator \({\mathsf {Sim}}\), consider the following two experiments:

The functional encryption scheme \(\mathsf {FE}\) is then said to be \(\mathsf {FULL}\text {-}\mathsf {SIM}\)-secure if there is a stateful p.p.t. simulator \({\mathsf {Sim}}\) such that for every p.p.t. adversary \(A=(A_1,A_2)\), the following two distributions are computationally indistinguishable.
2.4 Algorithms Used by Our Constructions
The following algorithms will be used crucially in our construction and proof.
Trapdoor Generation. Below, we discuss two kinds of trapdoors that our construction and proof will use.
Generating Random Lattices with Trapdoors. To begin, we provide an algorithm for generating a random lattice with a trapdoor.
Theorem 2.7
[Ajt99, GPV08, MP12]. Let q, n, m be positive integers with \(q \ge 2\) and \(m \ge 6n \lg q\). There is a probabilistic polynomial-time algorithm \(\mathsf{TrapGen}(q,n,m)\) that with overwhelming probability (in n) outputs a pair \((\mathbf {A}\in \mathbb {Z}_q^{n \times m}, \ \mathbf {T}\in \mathbb {Z}^{m \times m})\) such that \(\mathbf {A}\) is statistically close to uniform in \(\mathbb {Z}_q^{n \times m}\) and \(\mathbf {T}\) is a basis for \(\varLambda _q^{\perp }({(\mathbf {A})})\) satisfying

The Primitive Matrix \(\mathbf {G}\) and its Trapdoor. The matrix \(\mathbf {G}\in \mathbb {Z}_q^{n \times m}\) is the “powers-of two” matrix (see [MP12, Pei13] for the definition). The matrix \(\mathbf {G}\) has a public trapdoor \(\mathbf {T}_\mathbf {G}\) such that \(\Vert \mathbf {T}_\mathbf {G}\Vert _\infty =2\). Let \(\mathbf {G}^{-1}: \mathbb {Z}_q^{n \times m} \rightarrow \mathbb {Z}_q^{n \times m}\) denote a deterministic algorithm which outputs a short preimage \(\tilde{\mathbf {A}}\) so that \(\mathbf {G}\cdot \tilde{\mathbf {A}} = \mathbf {A}\mod q\).
Three Ways of Generating a Distribution. Let \(\mathbf {F}= [\;\mathbf {A}|\mathbf {A}\mathbf {R}+ \gamma \cdot \mathbf {G}\;]\) where \(\mathbf {A}\leftarrow \mathbb {Z}_q^{n \times m}\), \(\mathbf {R}\leftarrow \{-1,1\}^{m \times m}\), \(\mathbf {G}\) is the primitive matrix defined above and \(\gamma \in \mathbb {Z}_q\) is arbitrary (in particular, it can be 0). We are interested in the distribution \((\mathbf {F}, \mathbf {K}, \mathbf {P}) \in \mathbb {Z}_q^{n \times 2m} \times \mathbb {Z}_q^{2m \times m} \times \mathbb {Z}_q^{n \times m}\) satisfying \(\mathbf {F}\; \mathbf {K}= \mathbf {P}\mod q\).
Given \(\mathbf {F}\), we provide three different ways of sampling \((\mathbf {K}, \mathbf {P})\) so that the same resultant distribution is obtained.
-
1.
The first method is to sample \(\mathbf {P}\leftarrow \mathbb {Z}_q^{n \times m}\) randomly and use a trapdoor for the left matrix of \(\mathbf {F}\), namely \(\mathbf {A}\) to sample a low norm \(\mathbf {K}\). We let \(\mathbf {B}\triangleq \mathbf {A}\mathbf {R}+ \gamma \cdot \mathbf {G}\) and \(\mathbf {p}\) denote a column of \(\mathbf {P}\).
Algorithm \(\mathsf {SampleLeft}(\mathbf {A}, \mathbf {B}, \mathbf {T}_{\mathbf {A}}, \mathbf {p}, \sigma )\) [CHKP10, ABB10]:
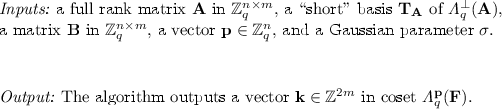 (2.1)
(2.1)
Its distribution is analyzed in the following theorem.
Theorem 2.8
([ABB10, Theorem 17], [CHKP10, Lemma 3.2]). Let \(q>2,\ m > n\) and  . Then \(\mathsf {SampleLeft}(\mathbf {A}, \mathbf {B}, \mathbf {T}_\mathbf {A}, \mathbf {p}, \sigma )\) taking inputs as in (2.1), outputs a vector \(\mathbf {k}\in \mathbb {Z}^{2m}\) distributed statistically close to \({\mathcal D}_{{\varLambda _q^{{\mathbf {p}}}({\mathbf {F}})},{\sigma }}\) where \(\mathbf {F}\mathrel {\mathop :}=(\mathbf {A}\ \Vert \ \mathbf {B})\).
. Then \(\mathsf {SampleLeft}(\mathbf {A}, \mathbf {B}, \mathbf {T}_\mathbf {A}, \mathbf {p}, \sigma )\) taking inputs as in (2.1), outputs a vector \(\mathbf {k}\in \mathbb {Z}^{2m}\) distributed statistically close to \({\mathcal D}_{{\varLambda _q^{{\mathbf {p}}}({\mathbf {F}})},{\sigma }}\) where \(\mathbf {F}\mathrel {\mathop :}=(\mathbf {A}\ \Vert \ \mathbf {B})\).
-
2.
The second method is to again sample \(\mathbf {P}\leftarrow \mathbb {Z}_q^{n \times m}\) and use a trapdoor for the right matrix \(\mathbf {G}\) (when \(\gamma \ne 0\)) to sample \(\mathbf {K}\).
Algorithm \(\mathsf {SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}, \mathbf {T}_{\mathbf {G}}, \mathbf {p}, \sigma )\) :
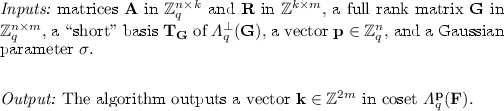 (2.2)
(2.2)
Often the matrix \(\mathbf {R}\) given to the algorithm as input will be a random matrix in \(\{1,-1\}^{m \times m}\). Let \(S^{m}\) be the m-sphere \(\{\mathbf {x} \in \mathbb {R}^{m+1} \ :\ ||\mathbf {x} || = 1\}\). We define  .
.
Theorem 2.9
([ABB10, Theorem 19]). Let \(q>2, m > n\) and  . Then \(\mathsf {SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}, \mathbf {T}_\mathbf {G}, \mathbf {p}, \sigma )\) taking inputs as in (2.2) outputs a vector \(\mathbf {k}\in \mathbb {Z}^{2m}\) distributed statistically close to \({\mathcal D}_{{\varLambda _q^{{\mathbf {p}}}({\mathbf {F}})},{\sigma }}\) where \(\mathbf {F}\mathrel {\mathop :}=(\mathbf {A}\ \Vert \ \mathbf {A}\mathbf {R}+ \gamma \cdot \mathbf {G})\).
. Then \(\mathsf {SampleRight}(\mathbf {A}, \mathbf {G}, \mathbf {R}, \mathbf {T}_\mathbf {G}, \mathbf {p}, \sigma )\) taking inputs as in (2.2) outputs a vector \(\mathbf {k}\in \mathbb {Z}^{2m}\) distributed statistically close to \({\mathcal D}_{{\varLambda _q^{{\mathbf {p}}}({\mathbf {F}})},{\sigma }}\) where \(\mathbf {F}\mathrel {\mathop :}=(\mathbf {A}\ \Vert \ \mathbf {A}\mathbf {R}+ \gamma \cdot \mathbf {G})\).
-
3.
The final method is to sample \(\mathbf {K}\leftarrow \big ({\mathcal D}_{{\mathbb {Z}^{2m}},{\sigma }}\big )^m\) and set \(\mathbf {P}= \mathbf {F}\cdot \mathbf {K}\mod q\). We note that this method works even if \(\gamma = 0\). As argued by [GPV08, Lemma 5.2], this produces the correct distribution.
Lemma 2.10
Assume the columns of \(\mathbf {F}\) generate \(\mathbb {Z}_q^n\) and let \(\sigma \ge \omega (\sqrt{n \log q})\). Then, for \(\mathbf {k}\leftarrow {\mathcal D}_{{\mathbb {Z}^{2m}},{\sigma }}\), the distribution of the vector \(\mathbf {p}= \mathbf {F}\cdot \mathbf {k}\mod q\) is statistically close to uniform over \(\mathbb {Z}_q^n\). Furthermore, fix \(\mathbf {p}\in \mathbb {Z}_q^n\) and let \({\mathbf {t}}\) be an arbitrary solution s.t. \(\mathbf {F}\cdot {\mathbf {t}}= \mathbf {p}\mod q\). Then, the conditional distribution of \(\mathbf {k}\leftarrow {\mathcal D}_{{\mathbb {Z}^{2m}},{\sigma }}\) given \(\mathbf {F}\cdot \mathbf {k}= \mathbf {p}\mod q\) is \({\mathbf {t}}+ \mathcal{D}_{{\varLambda ^\perp (\mathbf {F}),}{\sigma ,}{-{\mathbf {t}}}}\), which is precisely \({\mathcal D}_{{\varLambda _q^{{\mathbf {p}}}({\mathbf {F}})},{\sigma }}\).
Public Key and Ciphertext Evaluation Algorithms. Our construction will make use of the public key and ciphertext evaluation algorithms from [BGG+14, GVW15]. Since these algorithms can be used as black boxes for our purposes, we only state their input/output behavior and properties. These algorithms were constructed by Boneh et al. [BGG+14] in the context of attribute based encryption, and extended by Gorbunov et al. [GVW15] to the setting of partially hiding predicate encryption. In this setting, the attributes are divided into a private component \(\mathbf {x}\) and a public component \(\mathbf {y}\), and the functionality supports computation of a lightweight inner product composed with a heavy circuit \(\widehat{C}\). Formally, [GVW15] construct algorithms \(\mathsf{PHPE}.\mathsf{Eval}_\mathsf {MPK}\) and \(\mathsf{PHPE}.\mathsf{Eval}_\mathsf {CT}\) to support the following circuit family:
They make crucial use of the fact that \(\mathsf{PHPE}.\mathsf{Eval}_\mathsf {CT}\) does not need \(\mathbf {x}\) for its execution since the computation involving \(\mathbf {x}\) is an inner product. To compute the inner product, the multiplication may be carried out keeping \(\mathbf {x}\) private and letting \(\widehat{C}(\mathbf {y})\) be public, and addition may be carried out keeping both attributes private. Additionally, the circuit \(\widehat{C}\) operates entirely on public attributes \(\mathbf {y}\).
In more detail, [GVW15, Sect. 3.2] demonstrate the existence of the following efficient algorithms:
-
1.
\(\mathsf{Eval}_\mathsf {MPK}\) takes as input \(\ell +t\) matrices \(\{\mathbf {A}_i\},\;\{\mathbf {B}_j\} \in \mathbb {Z}_q^{n \times m}\) and a circuit \({\widehat{C} \circ \mathsf {IP}}\in \mathcal{C}\) and outputs a matrix \(\mathbf {A}_{{\widehat{C} \circ \mathsf {IP}}} \in \mathbb {Z}_q^{n \times m}\).
-
2.
\(\mathsf{Eval}_\mathsf {CT}\) takes as input \(\ell +t\) matrices \(\{\mathbf {A}_i,\}\{\mathbf {B}_j\} \in \mathbb {Z}_q^{n \times m}\), \(\ell +t\) vectors \(\{\mathbf {u}_i\}, \{\mathbf {v}_j\}\), the public attribute \(\mathbf {y}\in \{0,1\}^\ell \) and a circuit \({\widehat{C} \circ \mathsf {IP}}\in \mathcal{C}\), and outputs a vector \(\mathbf {u}_{\widehat{C} \circ \mathsf {IP}}\in \mathbb {Z}_q^m\).
-
3.
\(\mathsf{Eval}_{\mathsf{R}}\) takes as input \(\ell +t\) matrices \(\{\mathbf {R}_i\}, \{\mathbf {R}_j'\} \in \mathbb {Z}_q^{m \times m}\), the matrix \(\mathbf {A}\), the public attribute vector \(\mathbf {y}\in \{0,1\}^\ell \) and a circuit \({\widehat{C} \circ \mathsf {IP}}\in \mathcal{C}\) and outputs a matrix \(\mathbf {R}_{{\widehat{C} \circ \mathsf {IP}}} \in \mathbb {Z}_q^{m \times m}\).
such that the following properties hold:
When
Additionally, we may bound the norms as:
2.5 Fully Homomorphic Encryption
A leveled symmetric key fully homomorphic scheme is a tuple of P.P.T algorithms \(\mathsf {FHE}.\mathsf{KeyGen}\), \(\mathsf {FHE}.\textsf {Enc}\), \(\mathsf {FHE}.\mathsf{Eval}\) and \(\mathsf {FHE}.\textsf {Dec}\):
-
\(\mathsf {FHE}.\mathsf{KeyGen}(1^\kappa , 1^d, 1^k):\) This is a probabilistic algorithm that takes as input the security parameter, the depth bound for the circuit, the message length and outputs the secret key \(\mathsf {FHE}.\mathsf {SK}\).
-
\(\mathsf {FHE}.\textsf {Enc}(\mathsf {FHE}.\mathsf {SK}, \mu ):\) This is a probabilistic algorithm that takes as input the secret key and message and produces the ciphertext \(\mathsf {FHE}.\mathsf {CT}\).
-
\(\mathsf {FHE}.\mathsf{Eval}(C, \mathsf {FHE}.\mathsf {CT})\): This is a deterministic algorithm that takes as input a Boolean circuit \(C: \{0,1\}^k \rightarrow \{0,1\}\) of depth at most d and outputs another ciphertext \(\mathsf {FHE}.\mathsf {CT}'\).
-
\(\mathsf {FHE}.\textsf {Dec}(\mathsf {FHE}.\mathsf {SK}, \mathsf {FHE}.\mathsf {CT})\): This is a deterministic algorithm that takes as input the secret key and a ciphertext and produces a bit.
Correctness. Let \(\mathsf {FHE}.\mathsf {SK}\leftarrow \mathsf {FHE}.\mathsf{KeyGen}(1^\kappa , 1^d, 1^k)\) and C be a circuit of depth d. Then we require that
Security. Security is defined as the standard semantic security. Let \(\mathcal{A}\) be an efficient, stateful adversary and \(d, k = {{\mathrm{poly}}}(\kappa )\). The semantic security game is defined as follows.
-
1.
\(\mathsf {FHE}.\mathsf {SK}\leftarrow \mathsf {FHE}.\mathsf{Setup}(1^\kappa , 1^d, 1^k)\)
-
2.
\((\mu _0, \mu _1) \leftarrow \mathcal{A}(1^\kappa , 1^d, 1^k)\)
-
3.
\(b \leftarrow \{0,1\}\)
-
4.
\(\mathsf {FHE}.\mathsf {CT}\leftarrow \mathsf {FHE}.\textsf {Enc}(\mathsf {FHE}.\mathsf {SK}, \mu _b)\)
-
5.
\(b' \leftarrow \mathcal{A}(\mathsf {FHE}.\mathsf {CT})\)
We require that the advantage of \(\mathcal{A}\) in the above game be negligible, namely
Instantiating FHE from Learning with Errors. We make use of the following instantiation of FHE from LWE.
Theorem 2.11
[BV11, BGV12, GSW13, BV14, AP14]. There is an FHE scheme based on the LWE assumption such that, as long as \(q \ge O(\kappa ^2)\):
-
1.
\(\mathsf {FHE}.\mathsf {SK}\in \mathbb {Z}_q^t\) for some \(t \in {{\mathrm{poly}}}(\kappa )\).
-
2.
\(\mathsf {FHE}.\mathsf {CT}(\mu ) \in \{0,1\}^\ell \) where \(\ell = {{\mathrm{poly}}}(\kappa , k,d,\log q)\).
-
3.
\(\mathsf {FHE}.\mathsf{{Eval}}\) outputs a ciphertext \(\mathsf {FHE}.\mathsf {CT}' \in \{0,1\}^{\ell }\).
-
4.
There exists an algorithm \(\mathsf {FHE}.{\mathsf{Scale}}(q, p)\) which reduces the modulus of the FHE ciphertext from q to p.
-
5.
For any Boolean circuit of depth d, \(\mathsf {FHE}.\mathsf{{Eval}}(C, \cdot )\) is computed by a Boolean circuit of depth \({{\mathrm{poly}}}(d, \kappa , \log q)\).
-
6.
\(\mathsf {FHE}.\textsf {Dec}\) on input \(\mathsf {FHE}.\mathsf {SK}\) and \(\mathsf {FHE}.\mathsf {CT}'\) outputs a bit \(b \in \{0,1\}\). If \(\mathsf {FHE}.\mathsf {CT}'\) is an encryption of 1, then
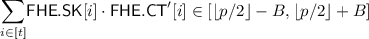
for some fixed \(B = {{\mathrm{poly}}}(\kappa )\). If \(\mathsf {FHE}.\mathsf {CT}'\) is an encryption of 0, then

-
7.
Security relies on \(\mathsf {LWE}_{\Theta (t),q,\chi }\).
3 Insecurity of Predicate Encryption Schemes Against General Adversaries
In this section, we demonstrate that known LWE based predicate encryption constructions [AFV11, GVW15] are insecure against an adversary that requests 1-keys.
3.1 Attack #1 on [AFV11] Using \(1\text {-}\)Keys.
Warmup Attack. To begin, we show a warmup attack that results from an adversary requesting the same key multiple times. Since the key generation algorithm is stateless, requesting many keys for the same function results in fresh, independent keys, which may be combined to fully recover the message.
An observant reader may notice that our warmup attack may be easily prevented by derandomizing key generation (using a PRF, say) so that multiple requests of the same circuit result in the same key. However, as we show in the full version [Agr16], the attack may be generalized to an adversary requesting non-identical functions against which derandomization does not work; the warmup attack is only the simplest application of the technique.
We now describe the attack in detail. The construction of [AFV11] is described here at a high level, for more details we refer the reader to the paper.
Say the attacker requests many keys for the vector \(\mathbf {v}\) such that \(\langle \mathbf {x},\mathbf {v} \rangle = 0\). Let \(\mathbf {A}_\mathbf {v}= \sum v_i \mathbf {A}_i\). Now by construction of keys in [AFV11], we have:
Thus, we have a short vector in the lattice \(\varLambda _q^{\perp }({\mathbf {A}|\mathbf {A}_{\mathbf {v}}})\). By making many queries for the same \(\mathbf {v}\), the attacker may recover a full trapdoor basis for \(\varLambda _q^{\perp }({\mathbf {A}|\mathbf {A}_{\mathbf {v}}})\). Now, note that the ciphertext contains \(\mathbf {A}^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathsf {noise}\) as well as \(\big (\;\mathbf {A}_i + \mathbf {x}[i] \mathbf {G}\;\big )^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathsf {noise}\). Since \(\langle \mathbf {x},\mathbf {v} \rangle = 0\), we can follow the decryption procedure as:
This in turn allows the attacker to recover
for which he now has a trapdoor. Using the trapdoor, he can now recover the noise terms to get exact linear equations in the LWE secret \(\mathbf {s}\), completely breaking LWE security. Note that by functionality, the attacker should only have been able to learn a single bit of information, namely \(\langle \mathbf {x}, \;\mathbf {v}\rangle =0\).
The reason this attack works given 1-keys, i.e. in the strong attribute hiding setting, is that a particular linear relation needs to be satisfied to enable decryption, which, given a decrypting key, can be exploited to carry out the attack. Specifically, in the above attack, the decryption procedure allows the attacker to recover \([\mathbf {A}\;|\mathbf {A}_{\mathbf {v}}]^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathsf {noise}\) which would not be possible if the decryption condition did not hold, i.e. given only 0-keys.
The generalization of the above attack, as well as the second and third attack are provided in the full version of the paper [Agr16].
4 \((1, {{\mathrm{poly}}})\) Very Selective PHPE
In this section, we show that the partially hiding predicate encryption system \(\mathsf{PHPE}\) of [GVW15] satisfies a stronger definition than described in [GVW15], namely \((1,{{\mathrm{poly}}})\)-\(\mathsf {VSel}\text {-}\mathsf {SIM}\) security (see Definition 2.5). We emphasize that in addition to a single query of any kind, PHPE supports an unbounded number of 0-queries, as in [GVW15].
4.1 Construction
The construction of our \((1, {{\mathrm{poly}}})\)-\(\mathsf{PHPE}\) scheme is the same as in [GVW15], except the setting of certain parameters described in the full version [Agr16]. The main novelty is in the proof, which shows that in the restricted game of Definition 2.5, the attacker can obtain a key for any circuit of his choice. As in [GVW15], he can also obtain an unbounded number of 0 keys, resulting in a \((1, {{\mathrm{poly}}})\)-\(\mathsf{PHPE}\) scheme.
For completeness, we describe the construction below.
-
\({\mathsf {PH}}.\mathsf{Setup}(1^\kappa , 1^t, 1^\ell , 1^d):\) Given as input the security parameter \(\kappa \), the length of the private and public attributes, t and \(\ell \) respectively, and the depth of the circuit family d, do the following:
-
1.
Choose random matrices
$$\mathbf {A}_i \in \mathbb {Z}_q^{n \times m} \text { for } i \in [\ell ],\;\mathbf {B}_i \in \mathbb {Z}_q^{n \times m} \text { for }i \in [t],\;\mathbf {P}\in \mathbb {Z}_q^{n \times m}$$To simplify notation, we denote by \(\{\mathbf {A}_i\}\) the set \(\{\mathbf {A}_i\}_{i \in [\ell ]}\) and by \(\{\mathbf {B}_i\}\) the set \(\{\mathbf {B}_i\}_{i \in [t]}\).
-
2.
Sample \((\mathbf {A}, \mathbf {T}) \leftarrow \mathsf{TrapGen}(1^m, 1^n, q)\).
-
3.
Let \(\mathbf {G}\in \mathbb {Z}_q^{n \times m}\) be the powers of two matrix with public trapdoor \(\mathbf {T}_\mathbf {G}\).
-
4.
Output the public and master secret keys.
$$ {\mathsf {PH}}.{\mathsf {PK}}= \big ( \{\mathbf {A}_i\}, \{\mathbf {B}_i\},\mathbf {A}, \mathbf {P}\big ),\;\;{\mathsf {PH}}.\mathsf MSK= ({\mathsf {PH}}.{\mathsf {PK}}, \mathbf {T})$$
-
1.
-
\({\mathsf {PH}}.\mathsf{KeyGen}({\mathsf {PH}}.\mathsf MSK, {\widehat{C} \circ \mathsf {IP}_\gamma }):\) Given as input the circuit and the master secret key, do the following:
-
1.
Let \(\mathbf {A}_{\widehat{C} \circ \mathsf {IP}}= \mathsf{Eval}_\mathsf {MPK}\big ( \{\mathbf {A}_i\}, \{\mathbf {B}_i\},{\widehat{C} \circ \mathsf {IP}}\big )\).
-
2.
Sample \(\mathbf {K}\) such that
$$\begin{aligned}{}[\mathbf {A}|\;\mathbf {A}_{\widehat{C} \circ \mathsf {IP}}+\gamma \cdot \mathbf {G}]\;\cdot \mathbf {K}= \mathbf {P}\mod q \end{aligned}$$using \(\mathbf {K}\leftarrow \mathsf{SampleLeft}(\mathbf {A}, \mathbf {A}_{\widehat{C} \circ \mathsf {IP}}+ \gamma \cdot \mathbf {G}, \mathbf {T}, \mathbf {P}, s)\). Here s is the standard deviation of the Gaussian being sampled (see [Agr16] for the parameters).
-
3.
Output \(\mathsf {SK}_{{\widehat{C} \circ \mathsf {IP}_\gamma }} = \mathbf {K}\).
-
1.
-
\({\mathsf {PH}}.\mathsf{Enc}\big ( {\mathsf {PH}}.\mathsf PK, (\mathbf {x}, \mathbf {y}), \mu \big ):\) Given as input the master public key, the private attributes \(\mathbf {x}\), public attributes \(\mathbf {y}\) and message \(\mu \), do the following:
-
1.
Sample \(\mathbf {s}\leftarrow {\mathcal D}_{{\mathbb {Z}^n},{s_B}}\) and error terms \(\mathbf {e}\leftarrow {\mathcal D}_{{\mathbb {Z}^m},{s_B}}\) and \(\mathbf {e}' \leftarrow {\mathcal D}_{{\mathbb {Z}^m},{s_D}}\).
-
2.
Let \(\mathbf {b}= [0,\ldots ,0,\lceil q/2\rceil \mu ]^{\scriptscriptstyle \mathsf {T}}\in \mathbb {Z}_q^m\). Set
$$\begin{aligned} {\varvec{\beta }}_0 = \mathbf {A}^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathbf {e},\;\;\; {\varvec{\beta }}_1 = \mathbf {P}^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathbf {e}' + \mathbf {b}\end{aligned}$$ -
3.
For \( i \in [\ell ]\), compute
$$\mathbf {u}_i = (\mathbf {A}_i + \mathbf {y}_i \cdot \mathbf {G})^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ \mathbf {R}_i^{\scriptscriptstyle \mathsf {T}}\mathbf {e}$$where \(\mathbf {R}_i \leftarrow \{-1,1\}^{m \times m}\).
-
4.
For \( i \in [t]\), compute
$$\mathbf {v}_i = (\mathbf {B}_i + \mathbf {x}_i \cdot \mathbf {G})^{\scriptscriptstyle \mathsf {T}}\mathbf {s}+ (\mathbf {R}'_i)^{\scriptscriptstyle \mathsf {T}}\mathbf {e}$$where \(\mathbf {R}'_i \leftarrow \{-1,1\}^{m \times m}\).
-
5.
Output the ciphertext
$$\mathsf {CT}_{\mathbf {y}} = \big ( \mathbf {y}, {\varvec{\beta }}_0, {\varvec{\beta }}_1, \{\mathbf {u}_i\}, \{\mathbf {v}_j\}\big )$$for \(i \in [\ell ]\), \(j \in [t]\).
-
1.
-
\({\mathsf {PH}}.\textsf {Dec}\big ( \mathsf {SK}_{\widehat{C} \circ \mathsf {IP}_\gamma }, \mathsf {CT}_{\mathbf {y}} \big )\): Given as input a secret key and a ciphertext, do the following:
-
1.
Compute
$$ \mathbf {u}_{{\widehat{C} \circ \mathsf {IP}}} = \mathsf{Eval}_\mathsf {CT}\big ( \{\mathbf {A}_i, \mathbf {u}_i\}, \{\mathbf {B}_j, \mathbf {v}_j\}, {\widehat{C} \circ \mathsf {IP}}, \mathbf {y}\big )$$ -
2.
Compute
$$ {\varvec{\nu }}= {\varvec{\beta }}_1 - \mathbf {K}^{\scriptscriptstyle \mathsf {T}}\left( \begin{array}{c} {\varvec{\beta }}_0 \\ \mathbf {u}_{{\widehat{C} \circ \mathsf {IP}}} \end{array}\right) $$ -
3.
Round each coordinate of \({\varvec{\nu }}\) and if \(\big [\mathsf{Round}({\varvec{\nu }}[1]), \ldots , \mathsf{Round}({\varvec{\nu }}[m-1])\big ] = \mathbf {0}\) then set \(\mu =\mathsf{Round}({\varvec{\nu }}[m])\).
-
4.
Output \(\mu \).
-
1.
In the full version [Agr16], we show that the scheme is correct.
4.2 Proof of Security
Next, we argue that the above construction is secure against an adversary who requests a single key of any kind and an unbounded number of 0-keys.
Theorem 4.1
The partially hiding predicate encryption scheme described in Sect. 4.1 is secure according in the very-selective game defined in Definition 2.5.
Proof
We define a p.p.t. simulator \({{\mathsf {Sim}}}\) and argue that its output is computationally indistinguishable (under the LWE assumption) from the output of the real world. Let \(b =\mu \) if \({\widehat{C}^* \circ \mathsf {IP}}_\gamma (\mathbf {x},\mathbf {y})=1\), \(\bot \) otherwise.
Simulator. \({{\mathsf {Sim}}}(\mathbf {A}_{\widehat{C}^* \circ \mathsf {IP}}, \mathbf {y}, 1^{|\mathbf {x}|}, b)\) :
-
1.
It generates all public parameters as in the real \({\mathsf {PH}}.\mathsf{Setup}\) except \(\mathbf {P}\). To generate \(\mathbf {P}\), it computes \(\mathbf {A}_{\widehat{C}^* \circ \mathsf {IP}}= \mathsf{Eval}_\mathsf {MPK}\big ( \{\mathbf {A}_i\}, \{\mathbf {B}_i\},{\widehat{C}^* \circ \mathsf {IP}}\big )\), samples \(\mathbf {K}^* \leftarrow \big ({\mathcal D}_{{\mathbb {Z}^{2m}},{s}}\big )^m\) and sets:
$$\begin{aligned} \mathbf {P}= [\mathbf {A}\;|\; \mathbf {A}_{\widehat{C^*}\circ \mathsf {IP}} + \gamma \cdot \mathbf {G}]\;\mathbf {K}^* \end{aligned}$$(4.1) -
2.
It generates all keys using the real \({\mathsf {PH}}.\mathsf{KeyGen}\) except the key for \({\widehat{C}^* \circ \mathsf {IP}}_\gamma \), which is set as \(\mathbf {K}^*\) sampled above.
-
3.
\({{\mathsf {Sim}}}.\textsf {Enc}\big (\widehat{C^*} \circ \mathsf {IP}_\gamma , \mathbf {y}, 1^{|\mathbf {x}|}, b \big )\): It takes as input the challenge circuit \(\widehat{C^*} \circ \mathsf {IP}_\gamma \), the public attributes \(\mathbf {y}\), the size of the private attributes \(\mathbf {x}\), and the message \(b = \mu \) if \({\widehat{C}^* \circ \mathsf {IP}}_\gamma (\mathbf {x},\mathbf {y})=1\), \(\bot \) otherwise. It constructs the challenge ciphertext as follows.
-
It samples \({\varvec{\beta }}_0, \mathbf {u}_i, \mathbf {v}_i\) independently and uniformly from \(\mathbb {Z}_q^m\). If \(b = \bot \), it samples \({\varvec{\beta }}_1\) also randomly from \(\mathbb {Z}_q^m\).
-
If \(b = \mu \), it computes \({\varvec{\beta }}_1\) to satisfy the decryption equation corresponding to \({\widehat{C}^* \circ \mathsf {IP}}_\gamma \) as follows.
-
Let \(\mathbf {u}_{{\widehat{C^*} \circ \mathsf {IP}}} = \mathsf{Eval}_\mathsf {CT}\big ( \{\mathbf {A}_i, \mathbf {u}_i\}, \{\mathbf {B}_i, \mathbf {v}_i\}, {{\widehat{C^*} \circ \mathsf {IP}}}, \mathbf {y}\big )\).
-
Sample \(\mathbf {e}'' \leftarrow {\mathcal D}_{{\mathbb {Z}^m},{s_D}}\)
-
Set \({\varvec{\beta }}_1 = (\mathbf {K}^*)^{\scriptscriptstyle \mathsf {T}}\left( \begin{array}{c} {\varvec{\beta }}_0 \\ \mathbf {u}_{{\widehat{C^*} \circ \mathsf {IP}}} \end{array}\right) + \mathbf {e}'' + \mathbf {b}\) where \(\mathbf {b}= [ 0\ldots ,0,\lceil q/2 \rceil \mu ]^{\scriptscriptstyle \mathsf {T}}\in \mathbb {Z}_q^m\).
-
-
It outputs the challenge ciphertext
$$\mathsf {CT}^* = \Big (\;\{\mathbf {u}_i\}_{i \in [\ell ]}, \{\mathbf {v}_i\}_{i \in [t]}, \mathbf {y}, {\varvec{\beta }}_0, {\varvec{\beta }}_1 \;\Big )$$
-
We argue that the output of the simulator is distributed indistinguishably from the real world. Intuitively, there are only two differences between the real world and simulated distribution. The first is that instead of choosing \(\mathbf {P}\) first and sampling \(\mathbf {K}^*\) to satisfy Eq. 4.1, we now choose \(\mathbf {K}^*\) first and set \(\mathbf {P}\) accordingly. This is a standard trick in LWE based systems (see the survey [Pei13], where this is trick 1), its first use that we are aware of appears in [GPV08].
The second difference is in how the challenge ciphertext is generated. In our challenge ciphertext the elements \(({\varvec{\beta }}_0, \mathbf {u}_i, \mathbf {v}_i)\) are sampled uniformly at random while \({\varvec{\beta }}_1\) which is computed using the elements \(({\varvec{\beta }}_0, \mathbf {u}_i, \mathbf {v}_i)\) and \(\mathbf {K}^*\) in order to satisfy the decryption equation for a 1 key. We note that \({\varvec{\beta }}_1\) is the only ciphertext element that is generated differently from the challenge ciphertext in the simulator of [GVW15]. In the [GVW15] simulator, \({\varvec{\beta }}_1\) is also sampled at random, whereas in our case, it is generated to satisfy the decryption equation involving \(\mathsf {CT}^*\) and \(\mathsf {SK}({\widehat{C}^* \circ \mathsf {IP}}_\gamma )\) when \({\widehat{C}^* \circ \mathsf {IP}}_\gamma (\mathbf {x}, \mathbf {y}) = 1\). Enforcing this relation is necessary, as it is dictated by the correctness of the systemFootnote 4.
The formal proof is provided in the full version of the paper [Agr16].
5 Upgrading Very Selective to Semi Adaptive Security for PHPE
In this section, we show how to construct a \((1,{{\mathrm{poly}}})\)-Partially Hiding Predicate Encryption scheme for circuit class \(\mathcal{C}\) satisfying semi adaptive security according to Definition 2.4. Our construction, which we denote by \({\textsf {SaPH}}\), will make use of two ingredients:
-
1.
A single keyFootnote 5, \(\mathsf {FULL}\text {-}\mathsf {SIM}\) secure functional encryption scheme for the following functionality:
$$ F_{(\mathbf {V}_1, \ldots ,\mathbf {V}_k)} (\mathbf {a}_1, \ldots ,\mathbf {a}_k) = \underset{i=1}{\sum }\; \mathbf {V}_i \cdot \mathbf {a}_i\;\mod q $$where \(\mathbf {V}_i \in \mathbb {Z}_q^{m \times m}\) and \(\mathbf {a}_i \in \mathbb {Z}_q^m\) for \(i \in [k]\). The parameters k, q, m are input to the setup algorithm. Such a scheme was recently constructed by [ALS16]Footnote 6. We will denote this scheme by \({\textsf {FuLin}}\).
-
2.
A \((1,{{\mathrm{poly}}})\) very selectively secure PHPE scheme for the circuit class \(\mathcal{C}\), as provided in Sect. 4. We will denote this scheme by \({\textsf {VSelPH}}\).
Our construction is described below.
-
\({\textsf {SaPH}}.\mathsf{Setup}(1^\kappa , 1^t, 1^\ell , 1^d)\): Given as input the circuit and the master secret key, do the following:
-
1.
For \(i \in [\ell ]\), let \( (\mathsf {FuLin.PK}_i, \mathsf {FuLin.MSK}_i) \leftarrow {\textsf {FuLin}}.\mathsf{Setup}\big (1^\kappa , (\mathbb {Z}_q^m)^3\big )\).
-
2.
For \(j \in [t]\), let \( (\mathsf {FuLin.PK}'_j, \mathsf {FuLin.MSK}'_j) \leftarrow {\textsf {FuLin}}.\mathsf{Setup}\big (1^\kappa , (\mathbb {Z}_q^m)^3\big )\).
-
3.
Let \((\mathsf {FuLin.PK}_0, \mathsf {FuLin.MSK}_0) \leftarrow {\textsf {FuLin}}.\mathsf{Setup}\big (1^\kappa , (\mathbb {Z}_q^m)^2\big )\).
-
4.
Let \((\mathsf {FuLin.PK}'_0, \mathsf {FuLin.MSK}'_0) \leftarrow {\textsf {FuLin}}.\mathsf{Setup}\big (1^\kappa , (\mathbb {Z}_q^m)^3\big )\).
-
5.
Let \(\{\mathsf{PRG}\}_{s \in \{0,1\}^\kappa }\) be a family of PRGs with polynomial expansion. Sample a PRG seed, denoted by \(\mathsf{seed}\).
-
6.
Output
$$\begin{aligned} {\mathsf {PH}}.{\mathsf {PK}}&= \big \{\mathsf {FuLin.PK}_0,\; \mathsf {FuLin.PK}'_0,\; \{\mathsf {FuLin.PK}_i\}_{i \in [\ell ]},\;\{\mathsf {FuLin.PK}'_j\}_{j \in [t]}\big \}\\ {\mathsf {PH}}.\mathsf {MSK}&= \big \{\mathsf{seed},\;\mathsf {FuLin.MSK}_0,\; \mathsf {FuLin.MSK}'_0,\; \{\mathsf {FuLin.MSK}_i\}_{i \in [\ell ]},\;\{\mathsf {FuLin.MSK}'_j\}_{j \in [t]}\big \} \end{aligned}$$
-
1.
-
\({\textsf {SaPH}}.\mathsf{Enc}\big ( {\mathsf {PH}}.{\mathsf {PK}}, (\mathbf {x}, \mathbf {y}), \mu \big ):\) Given as input the master public key, the private attributes \(\mathbf {x}\), public attributes \(\mathbf {y}\) and message \(\mu \), do the following:
-
1.
Sample \(\mathbf {s}\leftarrow {\mathcal D}_{{\mathbb {Z}^n},{s_B}}\) and error terms \(\mathbf {e}\leftarrow {\mathcal D}_{{\mathbb {Z}^m},{s_B}}\) and \(\mathbf {e}' \leftarrow {\mathcal D}_{{\mathbb {Z}^m},{s_D}}\).
-
2.
Let \(\mathbf {b}= [0,\ldots ,0,\lceil q/2\rceil \mu ]^{\scriptscriptstyle \mathsf {T}}\in \mathbb {Z}_q^m\).
-
3.
Sample \(\mathbf {R}_i \leftarrow \{-1,1\}^{m \times m}\) for \(i \in [\ell ]\) and \(\mathbf {R}'_j \leftarrow \{-1,1\}^{m \times m}\) for \(j \in [t]\).
-
4.
SetFootnote 7
$$\begin{aligned} \hat{{\varvec{\beta }}}_0&= {\textsf {FuLin}}.\textsf {Enc}\big (\; \mathbf {s}, \mathbf {e}\;\big ), \;\;&\hat{\mathbf {u}}_i = {\textsf {FuLin}}.\textsf {Enc}\big (\;\mathbf {s},\; \mathbf {y}[i]\cdot \mathbf {G}^{\scriptscriptstyle \mathsf {T}}\mathbf {s},\; \mathbf {R}_i^{\scriptscriptstyle \mathsf {T}}\mathbf {e}\;\big ),\\ \hat{{\varvec{\beta }}}_1&= {\textsf {FuLin}}.\textsf {Enc}\big (\;\mathbf {s}, \mathbf {e}', \mathbf {b}\;\big ), \;\;&\hat{\mathbf {v}}_j = {\textsf {FuLin}}.\textsf {Enc}\big (\;\mathbf {s},\; \mathbf {x}[j]\cdot \mathbf {G}^{\scriptscriptstyle \mathsf {T}}\mathbf {s},\; {\mathbf {R}'}_j^{\scriptscriptstyle \mathsf {T}}\mathbf {e}\;\big ) \end{aligned}$$ -
5.
Output the ciphertext
$$\mathsf {CT}_{\mathbf {y}} = \big ( \mathbf {y}, \hat{{\varvec{\beta }}}_0, \hat{{\varvec{\beta }}}_1, \{\hat{\mathbf {u}}_i\}, \{\hat{\mathbf {v}}_j\}\big )$$for \(i \in [\ell ]\), \(j \in [t]\).
-
1.
-
\({\textsf {SaPH}}.\mathsf{KeyGen}({\mathsf {PH}}.\mathsf {MSK}, {\widehat{C} \circ \mathsf {IP}_\gamma }):\) Given as input the circuit and the master secret key, do the following:
-
1.
Use \(\mathsf{PRG}(\mathsf{seed})\) to generate sufficient randomness \(\mathsf{rand}\) for the \({\mathsf {VSelPH}}.\mathsf{Setup}\) algorithm as well as \(\{\mathsf{rand}_i\}\), \(\{\mathsf{rand}'_j\}\), \(\mathsf{rand}_0\), \(\mathsf{rand}_0'\) for the \({\textsf {FuLin}}.\mathsf{KeyGen}\) algorithms.
-
2.
Sample \(({\mathsf {VSelPH}}.\mathsf {MPK}, {\mathsf {VSelPH}}.\mathsf {MSK}) \leftarrow {\mathsf {VSelPH}}.\mathsf{Setup}\big (1^\kappa ,1^t, 1^\ell , 1^d, \mathsf{rand}\big )\).
Parse \({\mathsf {VSelPH}}.\mathsf {MPK}= \big (\{\mathbf {A}_i\},\; \{\mathbf {B}_j\},\; \mathbf {A},\; \mathbf {P}\;\big )\).
-
3.
LetFootnote 8
$$\begin{aligned} \mathsf {FuLin.SK}_i&\leftarrow {\textsf {FuLin}}.\mathsf{KeyGen}\big (\;\mathsf {FuLin.MSK}_i, (\mathbf {A}_i^{\scriptscriptstyle \mathsf {T}}, 1,1),\; \mathsf{rand}_i\; \big )&\forall i\in [\ell ] \\ \mathsf {FuLin.SK}'_j&\leftarrow {\textsf {FuLin}}.\mathsf{KeyGen}\big (\;\mathsf {FuLin.MSK}'_j, (\mathbf {B}^{\scriptscriptstyle \mathsf {T}}_j,1,1),\;\mathsf{rand}'_j\; \big )&\forall j \in [t]\\ \mathsf {FuLin.SK}_0&\leftarrow {\textsf {FuLin}}.\mathsf{KeyGen}\big (\;\mathsf {FuLin.MSK}_0, (\mathbf {A}^{\scriptscriptstyle \mathsf {T}},1),\;\mathsf{rand}_0\; \big )\\ \mathsf {FuLin.SK}'_0&\leftarrow {\textsf {FuLin}}.\mathsf{KeyGen}\big (\;\mathsf {FuLin.MSK}'_0, (\mathbf {P}^{\scriptscriptstyle \mathsf {T}},1,1),\;\mathsf{rand}'_0\; \big ) \end{aligned}$$ -
4.
Let \({\mathsf {VSelPH}}.\mathsf {SK}({\widehat{C} \circ \mathsf {IP}_\gamma }) \leftarrow {\mathsf {VSelPH}}.\mathsf{KeyGen}\big (\;{\mathsf {VSelPH}}.\mathsf {MSK}, {\widehat{C} \circ \mathsf {IP}_\gamma }\;\big )\).
-
5.
Output
$$\begin{aligned} {\mathsf {VSelPH}}.\mathsf {SK}({\widehat{C} \circ \mathsf {IP}_\gamma })=\Big (&\big ({\mathsf {VSelPH}}.\mathsf {MPK},\; {\mathsf {VSelPH}}.\mathsf {SK}({\widehat{C} \circ \mathsf {IP}_\gamma })\;\big ),\;\\&\big (\;\{\mathsf {FuLin.SK}_i\},\; \{\mathsf {FuLin.SK}'_j\},\; \mathsf {FuLin.SK}_0,\; \mathsf {FuLin.SK}'_0 \;\big )\Big ) \end{aligned}$$
-
1.
-
\({\textsf {SaPH}}.\textsf {Dec}\big ( \mathsf {SK}_{\widehat{C} \circ \mathsf {IP}_\gamma }, \mathsf {CT}_{\mathbf {y}} \big )\): Given as input a secret key and a ciphertext, do the following:
-
1.
Let
$$\begin{aligned}&{\varvec{\beta }}_0 = {\textsf {FuLin}}.\textsf {Dec}(\mathsf {FuLin.SK}_0, \hat{{\varvec{\beta }}}_0), \;&\mathbf {u}_i = {\textsf {FuLin}}.\textsf {Dec}(\mathsf {FuLin.SK}_i, \hat{\mathbf {u}}_i), \\&{\varvec{\beta }}_1 = {\textsf {FuLin}}.\textsf {Dec}(\mathsf {FuLin.SK}'_0, \hat{{\varvec{\beta }}}_1), \;&\mathbf {v}_j = {\textsf {FuLin}}.\textsf {Dec}(\mathsf {FuLin.SK}'_j, \hat{\mathbf {v}}_j) \end{aligned}$$Let \({\mathsf {VSelPH}}.\mathsf {CT}= \big (\;{\varvec{\beta }}_0, \;{\varvec{\beta }}_1,\; \{\mathbf {u}_i\}, \;\{\mathbf {v}_j\},\; \mathbf {y}\;\big )\).
-
2.
Output \(\mu \leftarrow {\mathsf {VSelPH}}.\textsf {Dec}\big (\;{\mathsf {VSelPH}}.\mathsf {MPK}, \;{\mathsf {VSelPH}}.\mathsf {CT}, {\mathsf {VSelPH}}.\mathsf {SK}\;\big )\).
-
1.
Correctness. Correctness may be argued using the correctness of \({\textsf {FuLin}}\) and \({\textsf {VSelPH}}\).
By correctness of \({\textsf {FuLin}}\), the tuple \(({\varvec{\beta }}_0,\; {\varvec{\beta }}_1,\;\{\mathbf {u}_i\},\;\{\mathbf {v}_j\})\) produced in the first step of decryption is precisely the ciphertext of the \({\mathsf {VSelPH}}\) scheme. More formally, we get:

Let \({\mathsf {VSelPH}}.\mathsf {CT}= \big (\;{\varvec{\beta }}_0, \;{\varvec{\beta }}_1,\; \{\mathbf {u}_i\}, \;\{\mathbf {v}_j\},\; \mathbf {y}\;\big )\). Then, by correctness of \({\textsf {VSelPH}}\), the following is correct
In the full version of the paper [Agr16], we prove the following theorem.
Theorem 5.1
Assume that \({\mathsf {VSelPH}}\) satisfies \(\mathsf {VSel}\text {-}\mathsf {SIM}\) attribute hiding (Definition 2.5) and that \({\textsf {FuLin}}\) satisfies \(\mathsf {FULL}\text {-}\mathsf {SIM}\) security (Appendix 2.3). Then the scheme \({\textsf {SaPH}}\) satisfies \(\mathsf {SA\text {-}SIM}\) attribute hiding (Definition 2.4).
6 \((1,{{\mathrm{poly}}})\)-Functional Encryption
In this section, we construct our \((1, {{\mathrm{poly}}})\)-functional encryption scheme. The ciphertext of the construction is succinct, providing a unification of the results [GKP+13, GVW15]. Our construction of \((1, {{\mathrm{poly}}})\)-functional encryption uses \((1,{{\mathrm{poly}}})\)-partially hiding predicate encryption and fully homomorphic encryption in a manner similar to [GVW15, Sect. 4].
6.1 Construction
We begin with an overview of the main ideas in the construction. Let us recall the \((0,{{\mathrm{poly}}})\)-FE scheme constructed by [GVW15]. The scheme makes use of two ingredients, namely, a \((0,{{\mathrm{poly}}})\)-PHPE scheme for circuits, and a fully homomorphic encryption scheme for circuits. The ciphertext of \((0,{{\mathrm{poly}}})\)-FE corresponding to an attribute \(\mathbf {a}\) is a PHPE ciphertext corresponding to \((\widehat{\mathbf {a}}, {\mathbf {t}})\) where \( \widehat{\mathbf {a}}\) is the FHE encryption of \(\mathbf {a}\), and corresponds to the public attributes in PHPE, while \({\mathbf {t}}\) is the FHE secret key and corresponds to the private attributes in PHPE.
The secret key corresponding to circuit C in the \((0,{{\mathrm{poly}}})\)-FE scheme is a set of PHPE secret keys  where:
where:
The decryptor executes the homomorphic ciphertext evaluation procedure for circuit \(\mathsf {FHE}.\mathsf{Eval}(\cdot , C)\) on the attributes \(\widehat{\mathbf {a}}\) embedded in the PHPE ciphertext as in [BGG+14] to obtain a ciphertext corresponding to public attributes \(\widehat{C(\mathbf {a})}\), where \(\widehat{C(\mathbf {a})}\) is an FHE encryption of \(C(\mathbf {a})\). Now, when \(C(\mathbf {a})=1\), then by correctness of FHE, there exists a noise term  such that \(\big \langle \; {\mathbf {t}}, \widehat{C(\mathbf {a})}\; \big \rangle = \gamma \). The decryptor tries keys corresponding to all possible \(\gamma \) within the aforementioned range to ascertain whether \({\widehat{C} \circ \mathsf {IP}_\gamma }(\widehat{\mathbf {a}}, {\mathbf {t}}) = 1\). Note that this step makes it crucial that the FHE decryption range be polynomial in size. Fortunately, as noted by [GVW15], this can be ensured by the modulus reduction technique in FHE schemes [BGV12, GSW13, BV14], which allows a superpolynomial modulus to be scaled down to polynomial size.
such that \(\big \langle \; {\mathbf {t}}, \widehat{C(\mathbf {a})}\; \big \rangle = \gamma \). The decryptor tries keys corresponding to all possible \(\gamma \) within the aforementioned range to ascertain whether \({\widehat{C} \circ \mathsf {IP}_\gamma }(\widehat{\mathbf {a}}, {\mathbf {t}}) = 1\). Note that this step makes it crucial that the FHE decryption range be polynomial in size. Fortunately, as noted by [GVW15], this can be ensured by the modulus reduction technique in FHE schemes [BGV12, GSW13, BV14], which allows a superpolynomial modulus to be scaled down to polynomial size.
The first idea in building \((1,{{\mathrm{poly}}})\)-FE is to replace the use of \((0,{{\mathrm{poly}}})\)-PHPE in the above transformation by the \((1,{{\mathrm{poly}}})\) PHPE constructed in Sect. 4. However, as discussed in Attack #3, Sect. 3, such a straightforward adaptation leads to vulnerabilities. This is because decryption using a 1-key allows the decryptor to learn the exact inner product of the FHE ciphertext \(\widehat{C(\mathbf {a})}\) and the FHE secret key \({\mathbf {t}}\) rather than the threshold inner product corresponding to FHE decryption. This lets her obtain leakage on the noise terms used to construct \(\widehat{\mathbf {a}}\), which is problematic. We will denote the noise used in the construction of the FHE ciphertext \(\widehat{\mathbf {a}}\) by \(\mathsf{Noise}(\;\widehat{\mathbf {a}}\;)\).
Overcoming Leakage on FHE Noise. For a single 1-key, there is a natural way out, via “noise flooding” or “noise smudging” [Gen09, GKPV10, AJLA+12]. To prevent leakage on \(\mathsf{Noise}(\;\widehat{\mathbf {a}}\;)\), we may augment the FHE evaluation circuit with a “flooding” operation, which, after computing \(\mathsf{{FHE}.\mathsf{Eval}}( \widehat{\mathbf {a}}, C)\) adds to it an encryption of 0 with large noise \(\eta \) to drown out the effects of \(\mathsf{Noise}(\;\widehat{\mathbf {a}}\;)\). This idea is complicated by the fact that our construction of \((1, {{\mathrm{poly}}})\)-FE must use an FHE scheme whose final modulus is polynomial in size, whereas \(\eta \) must be chosen to satisfy:
so that it drowns the effects of \(\mathsf{Noise}(\;\widehat{\mathbf {a}}\;)\). The above constraint may necessitate \(\eta \), and hence the FHE modulus, to be superpolynomial in the security parameter.
Fortunately, we can work around this difficulty by performing FHE modulus reduction after flooding. Then, \(\eta \) can be superpolynomial in the security parameter to obliterate the dependency of the revealed noise on the initial noise, while letting the final FHE modulus still be polynomial. Another method is to use the “sanitization” operation [DS16], which will result in better parameters for this step – however, since it does not improve our overall parameters, we do not discuss this.
Formally, we require a \(\mathsf{PHPE}\) scheme for the circuit family \(\mathcal{C}_\mathsf{PHPE}\) where \({\widehat{C} \circ \mathsf {IP}}\in \mathcal{C}_\mathsf{PHPE}\) is defined as follows. Let the private attributes \(\mathbf {x}= {\mathbf {t}}\) where \({\mathbf {t}}\) is the FHE secret, and public attributes \(\mathbf {y}= (\widehat{\mathbf {a}}, \widehat{0})\), where \(\widehat{0}\) is an FHE encryption of the bit 0, with large noise \(\eta \). Then, define:
Above, \(\mathsf {FHE}.\mathsf{Eval}\) is the FHE ciphertext evaluation algorithm, and \(\mathsf {FHE}.\mathsf{Scale}\) is the modulus reduction algorithm described in Sect. 2.5. Recall that \({\mathsf {FHE}}.{\mathsf{Scale}}_{q,p}\) takes as input an FHE ciphertext that lives modulo q and reduces it to a ciphertext that lives modulo p. For the sake of brevity, we abuse notation and do not explicitly include the inputs (q, p) in the inputs to \({\widehat{C} \circ \mathsf {IP}}\).
Construction. We now proceed to describe the construction.
-
\(\mathsf { FE.Setup}(1^\kappa , 1^k, 1^d)\): The setup algorithm takes the security parameter \(\kappa \), the attribute length k and the function depth d and does the following:
-
1.
Choose the FHE modulus q in which \(\mathsf {FHE}.\mathsf{Eval}(\cdot , \cdot )\) will be computed and the FHE modulus \(p \in {{\mathrm{poly}}}(\kappa )\) in which decryption will be performed as per Sect. 2.5.
-
2.
Invoke the setup algorithm for the PHPE scheme for family \(\mathcal{C}_\mathsf{PHPE}\) to get:
$$({\mathsf {PH}}.{\mathsf {PK}}, {\mathsf {PH}}.\mathsf {MSK}) \leftarrow {\mathsf {PH}}.\mathsf{Setup}(1^\kappa , 1^t, 1^\ell , 1^{d'}) $$where length of private attributes \(t= |\mathsf {FHE}.\mathsf {SK}| \), length of public attributes \(\ell \) is the length of an FHE encryption of \(k+1\) bits corresponding to the attributes \(\mathbf {a}\) and 0, i.e. \(\ell = (k+1) \cdot |\mathsf {FHE}.\mathsf {CT}|\) and \(d'\) is the bound on the augmented FHE evaluation circuit.
-
3.
Output \(({\mathsf {PK}}= {\mathsf {PH}}.{\mathsf {PK}}, \;\mathsf {MSK}= {\mathsf {PH}}.\mathsf {MSK})\).
-
1.
-
\(\mathsf { FE.Keygen}(\mathsf {MSK}, C):\) The key generation algorithm takes as input the master secret key \(\mathsf {MSK}\) and a circuit C. It does the following:
-
1.
Let
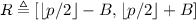 . Compute the circuit \({\widehat{C} \circ \mathsf {IP}_\gamma }\) as described above for \(\gamma \in R\).
. Compute the circuit \({\widehat{C} \circ \mathsf {IP}_\gamma }\) as described above for \(\gamma \in R\). -
2.
For \(\gamma \in R\), compute
$$ {\mathsf {PH}}.\mathsf {SK}_{{\widehat{C} \circ \mathsf {IP}_\gamma }} \leftarrow {\mathsf {PH}}.\mathsf{KeyGen}({\mathsf {PH}}.\mathsf {MSK}, {\widehat{C} \circ \mathsf {IP}_\gamma })$$ -
3.
Output the secret key as \(\mathsf {SK}_C = \{{\mathsf {PH}}.\mathsf {SK}_{{\widehat{C} \circ \mathsf {IP}_\gamma }}\}_{\gamma \in R}\).
-
1.
-
\(\mathsf { FE.Enc}({\mathsf {PK}}, \mathbf {a}, \mu )\): The encryption algorithm does the following:
-
1.
Sample a fresh FHE secret key \(\mathsf {FHE}.\mathsf {SK}\), and denote it by \({\mathbf {t}}\).
-
2.
Compute an FHE encryption of \(\mathbf {a}\) to get \(\widehat{\mathbf {a}} = \mathsf {FHE}.\textsf {Enc}(\;{\mathbf {t}}, \mathbf {a}\;)\).
-
3.
Sample \(\eta \) to satisfy Eq. 6.1 and compute an FHE encryption of 0 with noise \(\eta \) as \(\widehat{0}\).
-
4.
Set public attributes \(\mathbf {y}= (\widehat{\mathbf {a}}, \widehat{0})\) and private attributes \(\mathbf {x}= {\mathbf {t}}\).
-
5.
Compute \({\mathsf {PH}}.\mathsf {CT}_{\widehat{\mathbf {a}}, \widehat{0}} = {\mathsf {PH}}.\mathsf{Enc}\big (\;{\mathsf {PH}}.{\mathsf {PK}}, (\mathbf {x}, \mathbf {y}), \mu \big )\).
-
6.
Output \(\mathsf {CT}_\mathbf {a}= \big (\;\widehat{\mathbf {a}}, \widehat{0}, {\mathsf {PH}}.\mathsf {CT}_{\widehat{\mathbf {a}}, \widehat{0}}\; \big )\).
-
1.
-
\(\mathsf { FE.Dec}(\mathsf {SK}_C, \mathsf {CT}_\mathbf {a})\): Do the following:
-
1.
Parse \(\mathsf {SK}_C\) as the set \(\{{\mathsf {PH}}.\mathsf {SK}_{{\widehat{C} \circ \mathsf {IP}_\gamma }}\}_{\gamma \in R}\).
-
2.
For \(\gamma \in R\), let \(\tau _\gamma = {\mathsf {PH}}.\textsf {Dec}\big (\;\mathsf {CT}_\mathbf {a}, {\mathsf {PH}}.\mathsf {SK}_{{\widehat{C} \circ \mathsf {IP}_\gamma }}\;\big )\). If there exists some value \(\gamma '\) for which \(\tau _{\gamma '} \ne \bot \), then output \(\mu = \tau _{\gamma '}\), else output \(\bot \).
-
1.
Correctness. Correctness follows from correctness of PHPE and properties of FHE (see Sect. 2.5). Please see the full version [Agr16] for details.
6.2 Proof of Security
Next, we argue that the above scheme satisfies semi-adaptive security.
Theorem 6.1
The \((1,{{\mathrm{poly}}})\) functional encryption scheme described above is secure according to Definition 2.3.
Proof
We construct a simulator \(\mathsf {FE}.{{{\mathsf {Sim}}}}\) as required by Definition 2.3 as follows.
Simulator \(\mathsf {FE}.{{{\mathsf {Sim}}}}(1^\kappa )\) . The simulator is described as follows.
-
1.
It invokes \( \mathsf{PHPE}.{{{\mathsf {Sim}}}}(1^\kappa )\) to obtain the public parameters and returns these.
-
2.
The \(\mathsf {FE}\) adversary outputs \((\mathbf {a}, \mu , C^*)\) upon which, \(\mathsf {FE}.{{{\mathsf {Sim}}}}\) obtains \((1^{|\mathbf {a}|}, \mu , C^*)\). It does the following:
-
(a)
It samples an FHE secret key \(\mathsf {FHE}.\mathsf {SK}\) and sets \(\widehat{\mathbf {a}} = \mathsf {FHE}.\mathsf{Enc}(\mathsf {FHE}.\mathsf {SK}, \mathbf {0})\) and \(\widehat{0} = \mathsf {FHE}.\mathsf{Enc}(\mathsf {FHE}.\mathsf {SK}, 0)\).
-
(b)
It samples \(\gamma _q\) to satisfy Eq. 6.1. Let \(\gamma \) denote its scaled down version modulo p. It computes \({\widehat{C}^* \circ \mathsf {IP}}_\gamma \) as described above.
-
(c)
It invokes \( \mathsf{PHPE}.{{{\mathsf {Sim}}}}\big (\;(\widehat{\mathbf {a}}, \widehat{0}), \; 1^{|\mathsf {FHE}.\mathsf {SK}|},\; {\widehat{C}^* \circ \mathsf {IP}}_\gamma ,\; \mu \;\big )\) to obtain \(\big (\;{\mathsf {PH}}.\mathsf {CT},\; {\mathsf {PH}}.\mathsf {SK}({\widehat{C}^* \circ \mathsf {IP}}_\gamma )\;\big )\).
-
(d)
For \(\rho \in R \setminus \gamma \), it constructs \(\widehat{C}^* \circ \mathsf {IP}_\rho \) and sends these queries to \(\mathsf{PHPE}.{{{\mathsf {Sim}}}}\). It receives \({\mathsf {PH}}.\mathsf {SK}(\widehat{C}^* \circ \mathsf {IP}_\rho )\).
-
(e)
It outputs \(\big (\;{\mathsf {PH}}.\mathsf {CT}, \;\{{\mathsf {PH}}.\mathsf {SK}(\widehat{C}^* \circ \mathsf {IP}_\rho )\}_{\rho \in R}\;\big )\).
-
(a)
-
3.
When \(\mathsf {Adv}\) makes any query C, \(\mathsf {FE}.{{{\mathsf {Sim}}}}\) transforms it into \(\{\widehat{C} \circ \mathsf {IP}_\rho \}_{\rho \in R}\) and sends this to \(\mathsf{PHPE}.{{{\mathsf {Sim}}}}\). It returns the set of received keys to \(\mathsf {Adv}\). Note that these are 0-keys.
-
4.
When \(\mathsf {Adv}\) outputs \(\alpha \), output the same.
We argue that the simulator is correct in the full version of the paper [Agr16].
We note that the above construction is shown secure in a game which allows a single arbitrary query and other 0 queries. Circuit privacy may be obtained by using symmetric key encryption \(\mathsf{SKE}\) to hide the key and augmenting the function circuit with \(\mathsf{SKE}\) decryption, exactly as in [GKP+13]. The details as well as the generalization to the bounded collusion setting is provided in the full version of the paper [Agr16].
Notes
- 1.
The careful reader may observe that the simulator is disabled when \(C(\mathbf {a})=0\), not when \(C(\mathbf {a})=1\), though we have claimed that [AFV11, GVW15] can support 0-queries and not 1 queries. This is because, traditional functional encryption literature defines decryption to be permitted when the function value is 1, and defines the function value to be 1 when \(C(\mathbf {a})=0\). We follow this flip to be consistent with prior work.
- 2.
This is presently a weak security game which we term as very-selective where the circuit C as well as the challenge message is announced before the parameters are generated. This restriction will be removed subsequently.
- 3.
Please see Appendix 2.3 for the definition of full security.
- 4.
Note that the step of “programming” \({\varvec{\beta }}_1\) forces the simulator to use its knowledge of \(\mathbf {y}\). On the other hand, the simulator in [GVW15] does not need to use \(\mathbf {y}\) for simulation, implying that even \(\mathbf {y}\) is hidden when the attacker does not request 1-keys. Since the real decryption procedure needs \(\mathbf {y}\) in order to decrypt, this (in our opinion) further illustrates the weakness of the weak attribute hiding definition.
- 5.
More precisely, we require that the adversary may request the same single function any number of times, but multiple requests for the same function result in the same key.
- 6.
While the construction in [ALS16] has stateful \(\mathsf{KeyGen}\) against a general adversary, we only need the single key version which is clearly stateless.
- 7.
Note that we are abusing notation slightly, since the message space of \({\textsf {FuLin}}\) was set as \(\mathbb {Z}_q^m\) but \(\mathbf {s}\in \mathbb {Z}_q^n\). However, since \(n < m\), we can pad it with zeroes to make it match. We do not explicitly state this for the sake of notational convenience.
- 8.
Here, 1 is used to denote the \(m \times m\) identity matrix.
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_28
Agrawal, S., Freeman, D.M., Vaikuntanathan, V.: Functional encryption for inner product predicates from learning with errors. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 21–40. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25385-0_2
Agrawal, S.: Stronger security for reusable garbled circuits, general definitions and attacks. Eprint 2016/654 (2016)
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_28
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_29
Ajtai, M.: Generating hard instances of the short basis problem. In: Wiedermann, J., Emde Boas, P., Nielsen, M. (eds.) ICALP 1999. LNCS, vol. 1644, pp. 1–9. Springer, Heidelberg (1999). doi:10.1007/3-540-48523-6_1
Agrawal, S., Libert, B., Stehle, D.: Fully secure functional encryption for linear functions from standard assumptions. In: CRYPTO (2016)
Alperin-Sheriff, J., Peikert, C.: Faster bootstrapping with polynomial error. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 297–314. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_17
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_13
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_30
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (Leveled) fully homomorphic encryption without bootstrapping. In: ITCS (2012)
Bethencourt, J., Sahai, A., Waters, B.: Ciphertext-policy attribute-based encryption. In: IEEE Symposium on Security and Privacy (2007)
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: FOCS (2011)
Brakerski, Z., Vaikuntanathan, V.: Lattice-based FHE as secure as PKE. In: ITCS (2014)
Brakerski, Z., Vaikuntanathan, V.: Circuit-ABE from LWE: unbounded attributes and semi-adaptive security. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 363–384. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53015-3_13
Boyen, X., Waters, B.: Anonymous hierarchical identity-based encryption (without random oracles). In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 290–307. Springer, Heidelberg (2006). doi:10.1007/11818175_17
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_29
Cheon, J.H., Fouque, P.-A., Lee, C., Minaud, B., Ryu, H.: Cryptanalysis of the new CLT multilinear map over the integers. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 509–536. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_20
Coron, J.-S., Gentry, C., Halevi, S., Lepoint, T., Maji, H.K., Miles, E., Raykova, M., Sahai, A., Tibouchi, M.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: CRYPTO (2015)
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_27
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_1
Cheon, J.H., Jeong, J., Lee, C.: An algorithm for NTRU problems and cryptanalysis of the GGH multilinear map without a low level encoding of zero. Eprint 2016/139
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_26
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). doi:10.1007/3-540-45325-3_32
Ducas, L., Stehlé, D.: Sanitization of FHE ciphertexts. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 294–310. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_12
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC, pp. 169–178 (2009)
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013). http://eprint.iacr.org/
Garg, S., Gentry, C., Halevi, S., Sahai, A., Waters, B.: Attribute-based encryption for circuits from multilinear maps. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 479–499. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_27
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_20
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Fully secure functional encryption without obfuscation. In: IACR Cryptology ePrint Archive, vol. 2014, p. 666 (2014)
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: STOC, pp. 555–564 (2013)
Goldwasser, S., Kalai, Y.T., Peikert, C., Vaikuntanathan, V.: Robustness of the learning with errors assumption. In: ITCS (2010)
Goyal, R., Koppula, V., Waters, B.: Semi-adaptive security and bundling functionalities made generic and easy. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 361–388. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_14
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: CCS (2006)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC (2008)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_5
Goldwasser, S., Kalai, Y.T., Popa, R., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Proceedings of STOC (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute based encryption for circuits. In: STOC (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_25
Hu, Y., Jia, H.: Cryptanalysis of GGH map. Cryptology ePrint Archive: Report 2015/301 (2015)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_9
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_4
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_41
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_22
Peikert, C.: Lattices.. to cryptography (2013). http://web.eecs.umich.edu/~cpeikert/pubs/slides-visions.pdf
Pandey, O., Rouselakis, Y.: Property preserving symmetric encryption. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 375–391. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_23
Waters, B.: Functional encryption for regular languages. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 218–235. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_14
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Agrawal, S. (2017). Stronger Security for Reusable Garbled Circuits, General Definitions and Attacks. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)





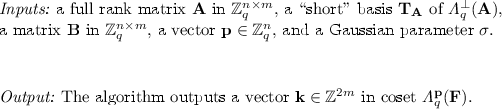
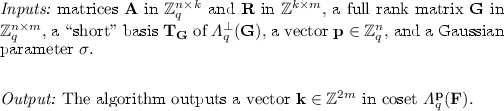
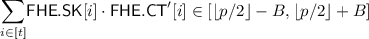

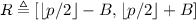 . Compute the circuit
. Compute the circuit 