Severity Estimation of Stator Winding Short-Circuit Faults Using Cubist

Abstract

In this paper, an approach to estimate the severity of stator winding short-circuit faults in squirrel-cage induction motors based on the Cubist model is proposed. This is accomplished by scoring the unbalance in the current and voltage waveforms as well as in Park’s Vector, both for current and voltage. The proposed method presents a systematic comparison between models, as well as an analysis regarding hyper-parameter tunning, where the novelty of the presented work is mainly associated with the application of data-based analysis techniques to estimate the stator winding short-circuit severity in three-phase squirrel-cage induction motors. The developed solution may be used for tele-monitoring of the motor condition and to implement advanced predictive maintenance strategies.

1 Introduction

The three-phase squirrel-cage induction motor (SCIM) is the most used kind of electric motor due to its relatively low cost, good efficiency and high availability - representing about 85–90% of the electric motors installed in the industry [1]. Although the probability of breakdowns of electric motors is very low [2], these motors are critical to the industry. Since an unexpected failure can have high costs associated [3], the investment in maintenance practices that improve the efficiency and availability of electrical motors is very attractive to the industry. Stator winding short circuits are the most frequent electrical faults, forming 26% of the faults in electrical motors and in low power motors can go up to 90% [3].

1.1 Stator Winding Short-Circuits

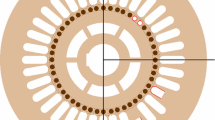
The SCIM, illustrated in Fig. 1, can be mainly decomposed in a stator and a rotor. The stator is composed by coils, each coil having a number of turns, which generates a rotating magnetic field that makes the rotor rotate.

Fig. 1.

A three-phase squirrel-cage induction motor. From: goo.gl/M8J6Ax

Short-circuits are phenomenona that can occur in the stator windings in three forms: inter-turn short circuit, inter-winding short circuit and earth fault. Following the scheme in Fig. 2, an inter-turn short-circuit fault is one such as the one that is happening in the Phase C’s winding. These faults appear between the turns of the same coil, and therefore the faulty current is not much.

Fig. 2.

Types of insulation faults.

This small faulty current is enough to start degrading the surrounding turns (due to thermal and electromagnetic stress), increasing the faulty current and letting the fault evolve to an inter-winding fault, where an adjacent winding (Phase B’s winding) of the faulty winding (phase C’s winding) starts to degrade. This fault will decrease the created magnetic field, which will deteriorate the motor’s efficiency since it will now produce less mechanical energy. If not timely detected, it can degenerate into an earth short-circuit (also shown in Fig. 2). It is known that the time between the onset of the fault and a degradation that causes the motor to enter in fault state depends mainly on the initial number of shorted turns and the initial fault loop resistance, among others factors.

1.2 Stator Winding Short-Circuit Detection and Estimation

It is possible to detect stator winding short-circuits through model based or data based approaches, or even a combination of both [4]. A data based approach provides several advantages over model based approaches, such as non-ideal assumptions about the motor, learning of the sensors behavior [5] and can be used to classify or estimate the state of the motor without the need of complex physical models [4]. The problem of detecting Stator Winding Short Circuit faults is vastly studied in the literature, where both model based [6, 7] as well as data based strategies are proposed [8,9,10].

Nevertheless, techniques to complement the detection of the Stator Winding Short-Circuit by estimating its severity are still limited. The simple detection of the fault is not enough, once it does not provide any indication of the fault’s degradation and, per si, does not allow for an adequate and realistic maintenance plan. Therefore, it is important to achieve an early estimation of the severity of the Stator Winding Short-Circuit.

To approach the problem of Stator Winding Short-Circuit’s severity estimation, [11] proposed a model-based approach to estimate the percentage of shorted turns ($\mu$) and the value of the winding shorted portion’s insulation resistance ($r_f$). This is done by measuring the current and voltage, calculate the negative sequence component both for current and voltage and the two target variables ($\mu$ and $r_f$) are derived from the estimation of one parameter by means of using an equality constraint on fault parameters and a nonlinear Kalman Filter. The authors test the proposed methodology with short-circuits with a percentage of shorted-turns between 10% and 16%, and a $r_f$ between 20 $\Omega$ and 10 $\Omega$.

In [12, 13], a model-based approach is proposed where the percentage of shorted turns is estimated. To achieve that, [12] measures the currents and voltages in the motor’s terminal box (1.4 kHz sample frequency) and a model of a motor in short-circuit state is derived. Using Linear Matrix Inequalities theory and an observer, the percentage of shorted turns is estimated (as well as other properties). In [13], a model for short-circuit is derived and by estimating the model’s parameters, the percentage of shorted turns is estimated.

In [14], the authors derive a model based strategy based on a dynamic Induction Motor model, where through the sequence component analysis it is possible to estimate a severity factor which is given by Eq. 1, where $I_{nom}$ is the nominal current of the motor, and $\mu _{dq}i_f$ is the obtained fault signal.

$$\begin{aligned} SI = \frac{| \mu _{dq}i_f |}{\sqrt{2}I_{nom}} \end{aligned}$$

(1)

In [14], the authors test the proposed methodology with short-circuits in phase A of the motor. The emulated short-circuits are of two types: 3 shorted turns of the phase winding (which winding contains 300 turns) and 3 shorted turns with a very low faulty current. The authors show that the proposed severity index estimation is robust for such cases.

1.3 Proposed Method

In this work, which is an extension of the work developed in [10], a data based approach is proposed where a model is developed using the Cubist algorithm to estimate a severity factor that depends on the percentage of shorted turns (per phase) and the percentage of faulty current (per rated current). The input for the Cubist is the result of a feature extraction process that takes place in the raw data, as well as in the d-q space. The d-q space is the output space of the Park’s transformation function, which is explained in Subsect. 3.2. In the d-q space, by applying Principal Component Analysis (PCA), the components are used to score the unbalance. The Cubist model was chosen after a systematic comparison with other models, and went through a process of fine-tunning. To acquired the data, several experiments were made to emulate different short-circuits. To do so, a special motor was used to generated the short-circuit data while a data logger monitored the line currents and voltage of the motor.

1.4 Outline

The presented paper is structured in the following way - Sect. 2 describes the data generation process, presents the available data for this work and explains the proposed severity index; Sect. 3 shows the proposed extracted features in the raw space as well as in the d-q space, explains the process used to take into account the variations of the supply current; Sect. 4 presents the experiments done as well as the evaluation process to choose the proposed Cubist model; Sect. 5 presents the authors’ conclusion of the presented work.

2 Data Generation Process

For the experiments, a special 400-V, 50-Hz, 4-pole, 2.2-kW delta-connected SCIM (nominal current of 4.5 A), with reconfigurable stator windings through external access to the terminals of all the coils was used. The stator core has 36 slots, and the stator winding has two sets of coils, each with 6 coils per phase.

The currents and line-to-neutral voltages waveforms of the three phases (R, S and T; 50-Hz), have been acquired at a 1-kHz sampling rate (which is relatively low), using a commercial datalogger (InMonitor). Each minute, five cycles are acquired and from those cycles an averaged cycle is computed - resulting on 20 points, representing 20 ms. The average waveform is a way to mitigate some noise and/or interference transients during the data acquisition process. The averaged cycle is sent via Wi-Fi to a database, where the data is finally recorded.

To emulate the stator winding short-circuits, an external resistance has been connected to the external terminals. Data have been collected for different motor states, namely, healthy with and without load, 2.5-A short-circuit on all the paired coil terminals in each phase, with and without load, and 1.5-, 1.0-, 0.25-A short-circuits in one coil of a given phase. Table 1 shows the number of cycles generated given the phase in fault, the number of coils in fault, the fault current and the motor condition. When one coil is short-circuited (total of 50 turns) it represents a short-circuit of 16.7% of the total number of turns per phase (total of 300 turns), whereas when half a coil is short circuited (total of 25 turns) it represents a short-circuit of 8.3% of the total number of turns per phase. Table 1 presents the severity index for the generated data.

Table 1. Proposed severity index (SI) in the generated data given the shorted turns and short circuit (SC) current, plus the number of cycles per severity.

As referred in Subsect. 1.1, the two main contributors for the degradation of the fault are the number of shorted turns and the fault loop resistance (which is related to the short-circuited current). Therefore, we proposes a severity index which is composed by the percentage of shorted turns given the total of turns per phase (50%) and the percentage of generated faulty current given the rated current of the motor (50%), as stated in Eq. 2 - where SI is the Severity Index, STP is Shorted Turns Percentage and SCC is Short Circuit Current (A).

$$\begin{aligned} SI = STP*0.5 + SCC*0.5 \end{aligned}$$

(2)

A projection of the raw data over time can be seen in Fig. 3, where Fig. 3a shows the current of a healthy motor’s cycle (with a duration of 0.02 s). When the motor is healthy, any phase of the three-phase current system has approximately the same peak value and approximately the same distance between the adjacent phases - condition which is known by a balance in the phases of the current. An unbalance condition appears when the motor presents a stator short-circuit, as it is shown in Fig. 3b. Comparing Fig. 3a and b, it is possible to observe the existence of an unbalance on the phases in Fig. 3b.

Fig. 3.

Performance on validation and test set.

3 Feature Extraction

Before extracting any feature, each signal (current phase A, B, C and voltage A, B, C) is normalized by the nominal value of the motor. This normalization allows for a certain generalization to estimate the severity for other machines of the same power type. The averages are a way to take into account the variations of the supply current which may happen due to external factors.

The features that will be extracted are: (a) the first Principal Components (PC) coordinates both for current and voltage in d-q space, (b) eccentricity for both current and voltage in d-q space using the two PCs, (c) averages of the previous 6 record’s first PC coordinates of the current and voltage in d-q space, (d) averages of the previous 6 records’s eccentricity of the PCs of the current and voltage in d-q space, (e) score of the three phase currents and voltages unbalance, (f) average of the RMS current and voltage phases’ value, (g) average of the previous 6 records’s score of the three phase currents and voltages unbalance, (h) root mean square value for each phase current and voltage, and (i) averages of the RMS value of the previous 6 records for each phase current and voltage.

3.1 Raw Data

The features obtained from the raw data are (e)–(i), forming a total of 18 features. To score the three-phase unbalance (for currents and voltages), the current RMS value for each phase ($I_A$, $I_B$, $I_C$) is calculated and then the current unbalance was calculated according to (3).

$$\begin{aligned} \begin{gathered} unb_I = \left( \frac{max\left( |I_A - avg| , |I_B - avg| , |I_C - avg| \right) }{avg} \right) \\ avg = \frac{I_A + I_B + I_C}{3} \end{gathered} \end{aligned}$$

(3)

3.2 Park’s Vector

For each record, the Park’s Transform is applied to the currents and voltages, resulting into the Park’s Vector, which, over an entire period, results into a circle (symmetrical condition) or an ellipse containing some ripple (asymmetrical condition). The instantaneous values of the direct (d) and quadrature (q) vectors, $i_d$ and $i_q$, resulting from the application of the Park Transform to the instantaneous values of the three line currents, $i_a$, $i_b$ and $i_c$, are given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} i_d = \sqrt{\frac{2}{3}}i_a - \sqrt{\frac{1}{6}}i_b - \sqrt{\frac{1}{6}}i_c \\ i_q = \sqrt{\frac{1}{2}}i_b - \sqrt{\frac{1}{2}}i_c \end{array}\right. } \end{aligned}$$

(4)

This is an intermediate step so that the PCA can be applied. In the Park’s Vector there are several characteristics that allow the determination of several short-circuit faults. From the resultant ellipse’s format, it is possible to associate its eccentricity (Fig. 4) with the severity of the fault.

Fig. 4.

Principal components of the Park’s Vector with eigen-value (d-q space).

3.3 PCA Transform

The features obtained from the d-q space are (a)–(d). PCA is a widely used method (a linear orthogonal transformation) which yields directions of maximum variance. For this reason, this method is normally employed for dimension reduction, given that the directions that have a greater data variance are those that describe better the data.

As a result, PCA is able to provide the main directions of the given data on the space-vector and, when applied to the elliptical form of the Park’s Vector, the two first components correspond to the major and minor axis (as shown in Fig. 4). From here, an unbalance score is calculated as an eccentricity:

$$\begin{aligned} score = 1 - e_2/e_1 \end{aligned}$$

(5)

where $e_2$ is the eigen-value of the second principal component and the $e_1$ is the eigen-value of the first principal component.

4 Modeling and Evaluation

The modeling and evaluation were made using R (version 3.3.1) under macOS Sierra. The caret [15] package (version 6.0-73) was used since it simplifies the task of experimenting a set of models and simplifies the interface of the training pipeline. The modeling stages consisted on selecting the better candidates from a set of selected models (Sect. 4.2) and only the best two of this stage were further analyzed (Sect. 4.3). After the training stage, the two models are evaluated in both validation set and test set.

4.1 Cubist

The Cubist is a rule-based regression model which follows the principles of an M5 Model Tree [16]. A tree is grown and in the leaf nodes, instead of classes or values, they contain a linear regression model which is based on the predictors used in the activation path of the rule. Also, each intermediate node also has a linear regression model with the predictors that were activated from the root until the node. These regressions are used to smooth the results, which are taken into account together with the leaf node’s linear regression model result.

The final result of the Cubist can also be adjusted by the k parameter, which indicates that the result should be averaged with the k most identical instances in the training set. The technique used to identify the most similar instances in the training set is the k-NN, where the Manhattan distance is used [17].

The Cubist model can also make use of the boosting strategy, which is an ensemble technique that can reduce both bias and variance. This strategy consists on iteratively learning weak classifiers of the same model with respect to a dataset, where the next model’s learning will depend on the performance of the previous model - points where the previous model had a higher error associated will be more important than the others for the next model. When weak learners are joined, they are typically weighted in a way that is usually related to the weak learner’s performance - low performance learners have low weight, while high performance learners have high weights. To output the result, the Cubist with ensemble calculates an average of the learners as the final result.

4.2 Selecting Promising Models

An experiment to study the performance of a set of models was assessed. The chosen models for this experiment were k-NN, Stochastic Gradient Boosting, Random Forest, Cubist, Support Vector Machine (SVM) with Radial Basis Function Kernel and Artificial Neural Networks (ANN). Since the goal is not to study a final model but rather have a general perception of the models’ performance, the train process was a rather simple one. The dataset was randomly split in train set (70%) and test set (30%), and for each train model a bootstrap resample with 10 repeats was considered.

The k-NN parameters were combinations of $k = [15,31,49]$, $distance = [0.5,1,2]$ and $kernel = [$rectangular, gaussian, cosine]. The Stochastic Gradient Boosting parameters were combinations of $n.trees =$ [100, 150, 250], $interac.deep =$ [1, 3, 10], $reduction.stepsize =$ [0.1, 0.5, 1] and $min.observs =$ [10, 15, 30]. The Random Forest parameters were combinations of $n.trees = 500$ and $mtry = [1..10]$. The Cubist model parameters were combinations of $neighbors = [1,3,6,9]$ and $committes = [1,20,35,50,80,90,100]$. The SVM parameters were combinations of C$= [0.5, 1, 4, 8, 32, 128]$ and $sigma = [0.01, 0.02, 0.06, 0.1]$. The ANN parameters were combinations of $hidden.size = [2, 8, 10, 14, 16]$ and $decay = [0,0005, 0,001, 0,002, 0,005, 0,01]$.

To evaluate the performance of the model’s instances, two metrics were used: Mean Absolute Error (MAE, Eq. 6) and Root Mean Square Log Error (RMSLE, Eq. 7). In both equations n is the size of the sample, $\hat{y}$ is the estimated value and y is the true value.

$$\begin{aligned} MAE = \frac{\sum _{i=1}^{n}| y - \hat{y}|}{n} \end{aligned}$$

(6)

$$\begin{aligned} RMSLE = \sqrt{\frac{\sum _{i=1}^{n} ( log(\hat{y} + 1) - log(y + 1) )^2 }{n}} \end{aligned}$$

(7)

In this experiment, it was noticeable that the great majority of instances of Cubist and k-NN were systematically better than the rest of the models, and therefore the chosen models for further study were the Cubist and k-NN.

4.3 Model Training

After the pre-selection of two machine learning models, another assessment regarding the influence of meta-parameters in the models (resample technique used, chosen metric to chose the best model during the resample process, type of preprocess applied to data) was made. The data was randomly divided in train set (50%), validation set (20%) and test set (30%).

The tested pre-process techniques were Yeo-Johnson Transformation, center, scale, range, Box-Cox Transformation and Spatial Sign Transform.

The Spatial Sign transformation is a multidimensional normalization which is defined as follows:

$$\begin{aligned} \varvec{x}^{*spa-sign} = {\left\{ \begin{array}{ll} \frac{\varvec{x}}{||\varvec{x}||} &{}\quad \text {if} \varvec{x} \ne \text {0} \\ 0 &{}\quad \text {if} \varvec{x} = \text {0} \end{array}\right. } \end{aligned}$$

(8)

where $\varvec{x}^{*spa-sign}$ represents the transformed vector by the spatial sign transformation, $\varvec{x}$ is the input vector that represents the instance, and $||\varvec{x}||$ represent the vector’s euclidean norm. This transformation has an output domain of [0, 1] [18].

The tested resample techniques were bootstrap (50 and 25 repeats), bootstrap632 (50 and 25 repeats), repeated cross validation (6 folds and 10 repeats; 3 folds and 10 repeats), cross validation (6 and 3 folds). The tested metrics during the resample process were MAE (Eq. 6) and RMSLE (Eq. 7). The Cubist and k-NN parameters were the same as the previous experiment.

4.4 Evaluation

After training the two models with all the configurations, they were evaluated in both validation and test set by using MAE and RMSLE. Figure 5 shows an overview of the models’ performance on the validation set.

Fig. 5.

K-NN and Cubist performance on validation set (MAE and RMSLE).

Figure 5 is composed by two rows and two columns - the first row for the RMSLE and the second row MAE; the first column for Cubist and the second column for k-NN. It is possible to verify that, in Fig. 5, the best k-NN instance is better than the best Cubist instance, either for MAE as well as for RMSLE.

Regarding MAE, it is noticeable that for all the pre-process techniques, the best k-NN instance is better than the best Cubist instance - being the best Cubist instance associated with the Spatial Sign Transform. It is also shown that the k-NN scores a lower MAE but an equivalent RMSLE when comparing to the Cubist with a Spatial Sign Transform.

Regarding RMSLE, the only pre-process that leads the Cubist to a performance close to the k-NN is the Spatial Sign Transformation, whereas the k-NN presents instances that can achieve low RMSLE independent of the pre-process.

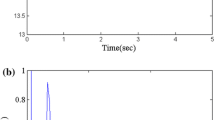
This means that most of the time the k-NN will produce an estimate that is closer to the truth than the Cubist estimation, but there are times where the k-NN estimate will be way further away than the Cubist. In other words, in this dataset the Cubist model have a more reliable estimation than the k-NN due to the error-variation in the estimation, as it can be seen in Fig. 6.

Figure 6 shows the predictions of the Cubist (Fig. 6(a)) and k-NN (Fig. 6(b)) for the validation set. In this figure the miss-estimations of the k-NN are noticeable higher than the miss-estimations of the Cubist, in spite of the Cubist present more miss-estimations than the k-NN - making the error-variation of the k-NN higher than the Cubist’s.

In the test set results, the same observation was made regarding the error-variation in the estimation between the Cubist with Spatial Sign Transformation and any k-NN group. It was noticeable that both MAE and RMSLE of test set are a little higher when compared to the MAE and RMSLE of the validation set. At this point, it can be concluded that the Spatial Sign Transformation is the transformation that brings better results both for Cubist and for k-NN models.

Fig. 6.

Performance on validation and test set.

After inspecting the parameters of the best models given the Spatial Sign Transformation, it was possible to notice that the resample technique was indifferent. Regarding the metric used during resample, there was a slight incidence of MAE metric over the other, but all of the tested metrics appeared.

Regarding model parameter configuration for k-NN model, only instances with a rectangular kernel appeared, all of them with the $k = 49$ and the distance parameter were whether 0.5 or 2.

Regarding model parameter configuration for Cubist, there great majority of the instances had a committee quantity greater than 30, existing some instances with a committee quantity of 1 and 10. The number of neighbors varied from 1 to 9, with no visible incidence.

At the end of the evaluation process, the Cubist model is chosen due to two factors: it presents an ensemble model, and therefore is more robust than the k-NN, and due to the observation that when the k-NN miss-estimate the predictions, those miss-estimations are way worse than the Cubist’s miss-estimations. At the end of the day, the Cubist model predictions will present a lower error-estimate variation than the ones predicted by k-NN which can be seen in Fig. 6.

5 Conclusions

This work presents a practical way for industrial condition monitoring, given that the goal is to apply the presented method to thousands of motors to complement the detection of stator-winding inter-turns short-circuit detection. The data-based nature of the proposed technique makes it a good fit for the industrial scale, and the shown robustness of the estimation of the proposed severity index allows for a severity fault monitoring which can provide early insights on the state of the motor, allowing to a timely maintenance plan. It is important to remind that the emulated short-circuits were generated with and without load.

The presented work can be improved by acquiring data associated with undervoltage, overvoltage and unbalanced voltage conditions. A database of more motors presenting a more vast short-circuits severity would also be beneficial to ensure the robustness of the estimator.