Convexity-Preserving Rigid Motions of 2D Digital Objects

Abstract

Rigid motions on $\mathbb {R}^2$ are isometric and thus preserve the geometry and topology of objects. However, this important property is generally lost when considering digital objects defined on $\mathbb {Z}^2$, due to the digitization process from $\mathbb {R}^2$ to $\mathbb {Z}^2$. In this article, we focus on the convexity property of digital objects, and propose an approach for rigid motions of digital objects which preserves this convexity. The method is extended to non-convex objects, based on the concavity tree representation.

1 Introduction

Rigid motions (i.e., transformations based on translations and rotations) in $\mathbb {R}^n$ are well-known topology- and geometry-preserving operations. They are frequently used in image processing and image analysis. Due to digitization effects, these important properties are generally lost when considering digital images defined on $\mathbb {Z}^n$, as illustrated in Fig. 1.

A part of these problems, topological preservation, was studied for 2D images under rigid transformations [19]. In a similar context, we investigate the geometrical issue, in particular convexity, in this article.

Fig. 1.

Convexity alterations under rotation: (a) a convex digital object in 2D, and (b) its non-convex transformed image by a rotation; (c) a convex digital object in 3D, and (d) its non-convex transformed image by a rotation.

Fig. 2.

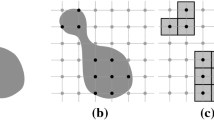
(a–b) Convexity defined on $\mathbb {R}^n$ is not applicable to $\mathbb {Z}^n$ due to the digitization. (a) A convex continuous object defined on $\mathbb {R}^2$ and the grid $\mathbb {Z}^2$, (b) its digital image represented by pixels. The segments in red and blue belong fully to (a) but not to (b) H-convex (c) and non H-convex (d) objects. Red polygons are their convex hulls. (Color figure online)

Convexity plays an important role in geometry. This notion is well studied and understood in the continuous space. A convex object in $\mathbb {R}^n$ is defined as a region such that the segment joining any two points within the region is also within the region. Nevertheless, this notion is not adapted to $\mathbb {Z}^n$, due to the digitization process required to convert continuous objects to digital objects, as illustrated in Fig. 2.

In the literature, several definitions have been proposed for convexity defined on $\mathbb {Z}^n$, namely digital convexity, such as MP-convexity [18], S-convexity [22], D-convexity [12], H-convexity [12]. The latter will be used in this article due to its simplicity and usefulness. Roughly speaking, a digital object $\mathsf {X} \subset \mathbb {Z}^2$ is H-convex if its convex hull does contain exactly the points of $\mathsf {X}$ (see Fig. 2(c–d)).

In this article, we propose a method allowing us to preserve the H-convexity of digital objects under any rigid motions. Such a method relies on a representation of an H-convex digital object by half-planes. The rigid motion is then applied on such half-plane representation and followed by a digitization. Furthermore, we investigate the condition under which the H-convexity of digital objects is preserved by arbitrary rigid motions.

The paper is organized as follows. After recalling in Sect. 2 basic notions about rigid motions on digital objects, Sect. 3 presents a representation of digital object, well-adapted to H-convexity recognition. A convexity-preserving method for digital objects under rigid motions is then proposed in Sect. 4. Section 5 investigates the problem of rigid motions of non-convex digital objects and opens perspectives summarized in the conclusion.

2 Digital Objects and Rigid Motions on $\mathbb {Z}^2$

2.1 Objects and Rigid Motions on $\mathbb {R}^2$

Let us consider an object ${\mathrm X}$ in the Euclidean plane $\mathbb {R}^2$ as a closed connected finite subset of $\mathbb {R}^2$. Rigid motions on $\mathbb {R}^2$ are defined by a mapping:

$$\begin{aligned} \left| \begin{array}{lllll} {\mathfrak T}&{} : &{} \mathbb {R}^2 &{} \rightarrow &{} \mathbb {R}^2 \\ &{} &{} {\mathrm x}&{} \mapsto &{} R {\mathrm x}+ {t}\end{array} \right. \end{aligned}$$

(1)

where $R$ is a rotation matrix and ${t}\in \mathbb {R}^2$ is a translation vector. Such bijective transformation ${\mathfrak T}$ is isometric and orientation-preserving. Thus, ${\mathfrak T}({\mathrm X})$ has the same shape (i.e., the same geometry and topology) as ${\mathrm X}$.

2.2 Digitization of Objects and Topology Preservation

As the digitization process may cause topological alterations, conditions for guaranteeing the topology of shape boundaries have been studied [16, 20].

Definition 1

An object ${\mathrm X}\subset \mathbb {R}^2$ is r-regular if for each boundary point of ${\mathrm X}$, there exist two tangent open balls of radius r, lying entirely in ${\mathrm X}$ and its complement $\overline{{\mathrm X}}$, respectively.

This notion, based on classical concepts of differential geometry, establishes a topological link between a continuous shape and its digital counterpart as follows.

Proposition 1

([20]). An r-regular object ${\mathrm X}\subset \mathbb {R}^2$ has the same topological structure as its digitized version ${\mathrm X}\cap \mathbb {Z}^2$ if $r \ge \frac{\sqrt{2}}{2}$.

Note that the digitization defined by the intersection of a continuous object ${\mathrm X}$ and $\mathbb {Z}^2$ is called Gauss digitization [15]. It was shown that the digitization process of an r-regular object yields a well-composed shape [16], whose definition relies on the following concepts of digital topology (see e.g., [15]). Given a point ${\mathsf p}\in \mathbb {Z}^2$, the k-neighborhood of ${\mathsf p}$ is defined by ${\mathcal N}_{k}({\mathsf p}) = \{ {\mathsf q}\in \mathbb {Z}^2 : \Vert {\mathsf p}- {\mathsf q}\Vert _{\ell } \le 1 \}$ for $k=4$ (resp. 8) where $\ell = 1$ (resp. $\infty$). We say that a point ${\mathsf q}$ is k-adjacent to ${\mathsf p}$ if ${\mathsf q}\in {\mathcal N}_{k}({\mathsf p}) \setminus \{ {\mathsf p}\}$. From the reflexive-transitive closure of this k-adjacency relation on a finite subset ${\mathsf S}\subset \mathbb {Z}^2$, we derive the k-connectivity relation on ${\mathsf S}$. The k-connectivity relation on ${\mathsf S}$ is an equivalence relation. If there is exactly one equivalence class for this relation, namely ${\mathsf S}$, then we say that ${\mathsf S}$ is k-connected.

Definition 2

([16]). A finite subset ${\mathsf S}\subset \mathbb {Z}^2$ is well-composed if each 8-connected component of ${\mathsf S}$ and of its complement $\overline{{\mathsf S}}$ is also 4-connected.

This definition implies that the boundary¹ of ${\mathsf S}$ is a set of 1-manifolds whenever ${\mathsf S}$ is well-composed. As stated above, there exists a strong link between r-regularity and well-composedness.

Proposition 2

([16]). If an object ${\mathrm X}\subset \mathbb {R}^2$ is r-regular with $r \ge \frac{\sqrt{2}}{2}$, then ${\mathrm X}\cap \mathbb {Z}^2$ is well-composed.

We define a digital object $\mathsf {X}$ as a connected finite subset of $\mathbb {Z}^2$. In the context of topological coherence of shape boundary, we hereafter assume that $\mathsf {X}$ is well-composed, and thus 4-connected.

2.3 Problem of Point-by-Point Rigid Motions on $\mathbb {Z}^2$

If we simply apply a rigid motion ${\mathfrak T}$ of Eq. (1) to every point in $\mathbb {Z}^2$, we generally have ${\mathfrak T}(\mathbb {Z}^2) \not \subset \mathbb {Z}^2$. In order to get the points back on $\mathbb {Z}^2$, we then need a digitization operator ${\mathfrak D}: \mathbb {R}^2 \rightarrow \mathbb {Z}^2$, commonly defined as a standard rounding function. A discrete analogue of ${\mathfrak T}$ is then obtained by ${\mathcal T}_{point} = {\mathfrak D}\circ {\mathfrak T}_{\mid \mathbb {Z}^2}$, so that the discrete analogue of the point-by-point rigid motion of a digital object $\mathsf {X}$ on $\mathbb {Z}^2$ is given by ${\mathcal T}_{point}(\mathsf {X})$.

Figure 3 illustrates some examples of ${\mathcal T}_{point}$ of digital lines with different thicknesses. These examples show that the topology and geometry of digital objects are not always preserved, even when the initial shapes are very simple. If a digital line is sufficiently thick, then it preserves topology, but not always geometry. This led us to consider a digital counterpart of regularity condition for guaranteeing topology during point-by-point rigid motions on $\mathbb {Z}^2$ [19]. However, finding rigid motions on $\mathbb {Z}^2$ preserving geometry is still an open problem. In this article, we focus on one important geometrical property, namely convexity. We present a new method for rigid motions on $\mathbb {Z}^2$ that preserves convexity.

Fig. 3.

Well-composed digital lines (a, c) with different thicknesses, which remain well-composed (d) or not (b) after a point-by-point digitized rigid motion ${\mathcal T}_{point}$. In both cases, the convexity of the digital lines is lost by ${\mathcal T}_{point}$.

3 Digital Convexity

In $\mathbb {R}^2$, an object ${\mathrm X}$ is said to be convex if and only if for any pair of points ${\mathrm x}, {\mathrm y}\in {\mathrm X}$, every point on the straight line segment joining ${\mathrm x}$ and ${\mathrm y}$, defined by $[{\mathrm x}, {\mathrm y}] = \{\lambda {\mathrm x}+ (1 - \lambda ) {\mathrm y}\mid 0 \le \lambda \le 1 \},$ is also within ${\mathrm X}$. This continuous notion, however, cannot be directly applied to digital objects $\mathsf {X}$ in $\mathbb {Z}^2$ since for ${\mathsf p}, {\mathsf q}\in \mathsf {X}$, we generally have $[{\mathsf p}, {\mathsf q}] \not \subset \mathbb {Z}^2$. In order to tackle this issue, several extensions of the notion of convexity from $\mathbb {R}^2$ to $\mathbb {Z}^2$ have been proposed.

3.1 Definitions

First of all, we introduce the definition of Minsky and Papert [18], called MP-convexity, which is a straightforward extension of the continuous notion.

Definition 3

A digital object $\mathsf {X}$ is MP-convex if for any pair of points ${\mathsf p}, {\mathsf q}\in \mathsf {X}$, $\forall {\mathsf r}\in [{\mathsf p}, {\mathsf q}] \cap \mathbb {Z}^2$, ${\mathsf r}\in \mathsf {X}$.

Sklansky proposed a different definition based on digitization process [22], called S-convexity.

Definition 4

A digital object $\mathsf {X}$ is S-convex if there exists a convex object ${\mathrm X}\subset \mathbb {R}^2$ such that $\mathsf {X} = {\mathrm X}\cap \mathbb {Z}^2$.

Later, Kim gave a geometrical definition that is based on convex hull [12], named H-convexity. The convex hull of $\mathsf {X}$ is defined by

$$ {\mathcal Conv}(\mathsf {X}) = \biggr \{ {\mathrm x}\in \mathbb {R}^2 \; \biggr \vert \; {\mathrm x}= \sum _{i=1}^{|\mathsf {X} |} \lambda _i {\mathsf p}_i \; \wedge \; \sum _{i=1}^{|\mathsf {X} |} \lambda _i = 1 \; \wedge \; \lambda _i \ge 0 \; \wedge \; {\mathsf p}_i \in \mathsf {X} \biggr \}. $$

Definition 5

A digital object $\mathsf {X}$ (connected, by definition) is H-convex if $\mathsf {X} = {\mathcal Conv}(\mathsf {X}) \cap \mathbb {Z}^2$.

Kim also showed the equivalence between MP-convexity and H-convexity for 4-connected digital objects [12, Theorem 5]. Similar results under the assumption of 8-connectivity can be found in [10] via the chord property, which relates the MP- and H-convexities to another digital convexity notion based on digital lines, called D-convexity [13]. On the other hand, discussing the relation between S-convexity and H-convexity requires some conditions. An element ${\mathsf p}$ of a digital object $\mathsf {X}$ is said to be isolated if $|{\mathcal N}({\mathsf p}) \cap \mathsf {X} |\le 1$. Under the condition that $\mathsf {X}$ has no isolated element, it was proven that $\mathsf {X}$ is H-convex if and only if $\mathsf {X}$ is S-convex [12, Theorem 4]. A detailed description of various notions of digital convexity can be found in [5, Chap. 9]. In this article, we adopt the H-convexity notion, as it allows us to propose a method for rigid motions of digital objects which preserves H-convexity thanks to the half-plane representation (see Sect. 4).

It should be also mentioned that a similar property to the intersection property known from ordinary convex sets, is preserved; a proof based on an approach of the chord property can be found in [5, Corollary 3.5.1].

Property 1

Let $\mathsf {X}$ and $\mathsf {Y}$ be two digital objects. If $\mathsf {X}$ and $\mathsf {Y}$ are H-convex and $\mathsf {X} \cap \mathsf {Y}$ is connected, then $\mathsf {X} \cap \mathsf {Y}$ is H-convex.

Let us remark that convexity does not imply connectivity in $\mathbb {Z}^2$ by contrast to $\mathbb {R}^2$. This is a reason why an additional connectivity condition is reasonable in the discrete setting.

3.2 Digital Half-Plane Representation

If a digital object $\mathsf {X}$ consists of more than two elements, then the convex hull ${\mathcal Conv}(\mathsf {X})$ ² is a convex polygon whose vertices are some points of $\mathsf {X}$. As these vertices are grid points, ${\mathcal Conv}(\mathsf {X})$ is thus represented by the union of closed half-planes with integer coefficients such that

$$ {\mathcal Conv}(\mathsf {X}) = \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathrm H}, $$

where ${\mathcal R}(P)$ is the minimal set of closed half-planes that constitute a convex polygon P and each ${\mathrm H}$ is a closed half-plane in the following form:

$$\begin{aligned} {\mathrm H}= \{ (x,y) \in \mathbb {R}^2 \mid a x + b y + c \le 0, \; a, b, c \in \mathbb {Z}, \; \gcd (a,b)=1 \}. \end{aligned}$$

(2)

Note that the integer coefficients of ${\mathrm H}$ are uniquely obtained by the pairs of the corresponding consecutive vertices of ${\mathcal Conv}(\mathsf {X})$, denoted by ${\mathsf u}, {\mathsf v}\in \mathbb {Z}^2$, which are in the clockwise order, such that $(a, b) = \frac{1}{\gcd (w_x, w_y)} (-w_y, w_x)$, and $c = (a, b) \cdot {\mathsf u}$ where $(w_x, w_y) = {\mathsf v}- {\mathsf u}\in \mathbb {Z}^2$.

Therefore, from Definition 5, if $\mathsf {X}$ is H-convex, then we have

$$\begin{aligned} \mathsf {X} = \biggr ( \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathrm H}\biggr ) \cap \mathbb {Z}^2 = \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} \biggr ( {\mathrm H}\cap \mathbb {Z}^2 \biggr ) \end{aligned}$$

(3)

where each ${\mathrm H}\cap \mathbb {Z}^2$ is called a digital half-plane. It is obvious that any digital half-plane is H-convex. An example of an H-convex digital object with its half-plane representation is illustrated in Fig. 4.

Fig. 4.

Example of the digital half-plane representation of a digital object. Left: Digital object and its convex hull (convex hull vertices are in red). Right: Digital half-planes extracted from this convex hull. (Color figure online)

3.3 Verification and Recognition Algorithms

To determine if a digital object is H-convex, several discrete methods were proposed with different approaches. In particular, they are based on the observation of the 8-connected curve corresponding to the inner contour of digital object.

In [6], a linear algorithm determines if a given polyomino is convex and, in this case, it returns its convex-hull. It relies on the incremental digital straight line recognition algorithm [7], and uses the geometrical properties of leaning points of maximal discrete straight line segments on the contour. The algorithm scans the contour curve and decomposes it into discrete segments whose extremities must be leaning points. The tangential cover of the curve [11] can be used to obtain this decomposition. Then, the half-planes corresponding to Eq. (3) are directly deduced from the characteristics of discrete segments obtained in the curve decomposition. Similar approaches [8, 21] were used to decompose a discrete shape contour into a faithful polygonal representation respecting convex and concave parts.

On the other hand, a combinatorial approach presented in [4] uses tools of combinatorics on words to study contour words: the linear Lyndon factorization algorithm [9] and the Christoffel words. A linear time algorithm verifies convexity of polyominoes and can also compute the convex hull of a digital object. It is presented as a discrete version of the classical Melkman algorithm [17]. This latter can also be used to compute the convex hull of a digital object, so that the half-planes of ${\mathcal R}({\mathcal Conv}(\mathsf {X}))$ of a digital object $\mathsf {X}$ are then deduced from the consecutive vertices (see Eq. (2)). Note that ${\mathcal R}(P)$ is the minimal set of half-planes whose support lines are the edges of a convex polygon P. Then, the H-convexity is tested with elementary operations (see Eq. (3)).

4 Convexity-Preserving Rigid Motions of Digital Objects

In order to preserve the H-convexity of a given H-convex digital object $\mathsf {X}$, we will not apply rigid motions to each grid point of $\mathsf {X}$, as discussed in Sect. 2.3, but to each half-plane ${\mathrm H}$ of ${\mathcal R}({\mathcal Conv}(\mathsf {X}))$ according to Eq. (3). We first explain how to perform a rigid motion of a closed integer half-plane. Then, we propose a method for rigid motions of the whole H-convex digital object.

4.1 Rational Rigid Motions of a Digital Half-Plane

A notion of rigid motion of a digital half-plane ${\mathrm H}\cap \mathbb {Z}^2$ is given by:

$$\begin{aligned} {\mathcal T}_{{\mathcal Conv}} ({\mathrm H}\cap \mathbb {Z}^2) := {\mathfrak T}({\mathrm H}) \cap \mathbb {Z}^2 \end{aligned}$$

(4)

where ${\mathfrak T}({\mathrm H})$ is defined analytically as follows.

Digital objects and digital half-planes involve exact computations with integers. Thus, we assume hereafter that all the parameters R and ${t}$ of rigid motions ${\mathfrak T}$ are rational. More precisely, we consider $R = \frac{1}{r} \left( \begin{array}{cc} p &{} - q \\ q &{} p \end{array} \right)$ where $p, q, r \in \mathbb {Z}$ constitute a Pythagorean triple, i.e.,  $p^2 + q^2 = r^2$, $r \ne 0$, and ${t}= (t_x, t_y) \in \mathbb {Q}^2$. This assumption is reasonable, as we can always find rational parameter values sufficiently close to any real values (see [2] for finding such a Pythagorean triple).

An integer half-plane ${\mathrm H}$ defined by Eq. (2) is transformed by such ${\mathfrak T}$ to the rational half-plane:

$$\begin{aligned} {\mathfrak T}({\mathrm H}) = \{ (x,y) \in \mathbb {R}^2 \mid \alpha x + \beta y + \gamma \le 0, \; \alpha , \beta , \gamma \in \mathbb {Q}\}, \end{aligned}$$

(5)

whose coefficients $\alpha$, $\beta$, $\gamma$ are given by $\left( \begin{array}{c} \alpha \\ \beta \end{array} \right) = R \left( \begin{array}{c} a \\ b \end{array} \right)$ and $\gamma = c + \alpha t_x + \beta t_y$.

Note that any rational half-plane can be easily rewritten as an integer half-plane in the form of Eq. (2).

4.2 Rigid Motions of H-convex Digital Objects

In the previous subsection, we showed how to transform a digital half-plane with Eq. (4) via Eq. (5). Since an H-convex digital object $\mathsf {X}$ is represented by a finite set of digital half-planes ${\mathsf H}$, as shown in Eq. (3), we can define a rigid motion of $\mathsf {X}$ on $\mathbb {Z}^2$ using its associated digital half-planes such that

$$\begin{aligned} {\mathcal T}_{{\mathcal Conv}}(\mathsf {X}) := {\mathfrak T}\biggr ( \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathrm H}\biggr ) \cap \mathbb {Z}^2 = \biggr (\bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathfrak T}( {\mathrm H}) \biggr ) \cap \mathbb {Z}^2. \end{aligned}$$

(6)

For each ${\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))$, we obtain ${\mathfrak T}({\mathrm H})$ by Eq. (5), and then re-digitize the transformed convex polygon $P = \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathfrak T}( {\mathrm H})$.

We now show that ${\mathcal T}_{{\mathcal Conv}}(\mathsf {X})$ is H-convex under a condition on the transformed convex polygon P, called quasi-r-regularity. Thanks to Property 1, what we need here is to characterize convex polygons P whose re-discritization $P \cap \mathbb {Z}^2$ preserves the 4-connectivity since any digital half-plane is H-convex.

Property 2

Let P be a (closed) convex polygon in $\mathbb {R}^2$. If P includes a (closed) ball of diameter $\sqrt{2}$, then $P \cap \mathbb {Z}^2$ is not empty.

This property is trivial due to the fact that we work on the grid $\mathbb {Z}^2$ of size 1. From a morphological point of view, it can be reformulated as follows.

Property 3

If the erosion of P by a ball $B_{\frac{\sqrt{2}}{2}}$ of radius $\frac{\sqrt{2}}{2}$ is not empty, namely, $P \ominus B_{\frac{\sqrt{2}}{2}} \ne \emptyset$, then $P \cap \mathbb {Z}^2$ is not empty.

Indeed, if $P \ominus B_{\frac{\sqrt{2}}{2}} \ne \emptyset$, then the opening $(P \ominus B_{\frac{\sqrt{2}}{2}}) \oplus B_{\frac{\sqrt{2}}{2}}$ is the $(\frac{\sqrt{2}}{2})$-regular part of P, noted ${\mathcal Reg}(P)$. Its digitization with grid interval 1 is guaranteed to have the same topological structure of P (see Proposition 1). In this context, the regular part of P is defined by

$$ {\mathcal Reg}(P) = (P \ominus B_{\frac{\sqrt{2}}{2}}) \oplus B_{\frac{\sqrt{2}}{2}}, $$

and $P \setminus {\mathcal Reg}(P)$ is called non-regular part. If, for each boundary half-plane of ${\mathrm H}\in {\mathcal R}(P)$, there exists a ball $B_{\frac{\sqrt{2}}{2}} \subset P$ being tangent to ${\mathrm H}$, then we can define the corner parts of P as $P \setminus {\mathcal Reg}(P)$. More precisely, each connected component of $P \setminus {\mathcal Reg}(P)$ corresponds to a corner part of P. In other words, the set of the corner parts is defined by ${\mathcal Cor}(P) = {\mathcal C}(P \setminus {\mathcal Reg}(P))$ where ${\mathcal C}$ is the (continuous) connected component function (see Fig. 5).

Fig. 5.

Convex polygons P, which are quasi-($\frac{\sqrt{2}}{2}$)-regular (a) and not (b-c): (b) there is a vertex of P with angle $<\frac{\pi }{2}$; (c) there is an half-plane ${\mathrm H}\in {\mathcal R}(P)$ where no ball $B_{\frac{\sqrt{2}}{2}} \subset P$ exists such that ${\mathrm H}$ is tangent to $B_{\frac{\sqrt{2}}{2}}$. In the figures, P are in blue, $B_{\frac{\sqrt{2}}{2}}$ are in red, $P \ominus B_{\frac{\sqrt{2}}{2}}$ is in yellow, ${\mathcal Reg}(P)$ are in pink, and ${\mathcal Cor}(P)$ are in green. (Color figure online)

Property 4

Let us consider a corner part $A \in {\mathcal Cor}(P)$. If the angle $\theta (A)$ at the corresponding vertex of P verifies $\theta (A) \ge \frac{\pi }{2}$ and $A \cap \mathbb {Z}^2$ is not empty, then any point ${\mathsf p}\in A \cap \mathbb {Z}^2$ has at least one 4-adjacent point in ${\mathcal Reg}(P)$.

Proof

As the Euclidean distance from ${\mathsf p}$ to ${\mathcal Reg}(P)$ cannot be higher than $\frac{\sqrt{2}}{2}$, thus inferior to 1, the circle of radius 1 whose center is ${\mathsf p}$ always has a non-empty intersection with ${\mathcal Reg}(P)$. Due to the angle condition of $\theta (A)$, this intersection forms a circular arc whose central angle is not less than $\frac{\pi }{2}$. The 4-neighbours of ${\mathsf p}$ are on the circle of radius 1 and at least one of them appears on this circular-arc intersection with ${\mathcal Reg}(P)$. Therefore, there always exists at least one of the 4-neighbours of ${\mathsf p}$ in ${\mathcal Reg}(P)$.

Let us now introduce the notion of quasi-regularity.

Definition 6

A convex polygon P is quasi-r-regular if $\forall {\mathrm H}\in {\mathcal R}(P)$, $\exists B_{r} \subset P$ such that ${\mathrm H}$ is tangent to $B_{r}$, and if $\forall A \in$ ${\mathcal Cor}(P)$, $\theta (A) \ge \frac{\pi }{2}$.

From Property 4, we then obtain the following lemma.

Lemma 1

Let $\mathsf {X}$ be an H-convex digital object. If ${\mathcal Conv}(\mathsf {X})$ is quasi-$(\frac{\sqrt{2}}{2})$-regular, then ${\mathcal T}_{{\mathcal Conv}}(\mathsf {X})$ is 4-connected.

Finally, we obtain the main proposition from this lemma and Property 1.

Proposition 3

Let $\mathsf {X}$ be an H-convex digital object. If ${\mathcal Conv}(\mathsf {X})$ is quasi-$(\frac{\sqrt{2}}{2})$-regular, then ${\mathcal T}_{{\mathcal Conv}}(\mathsf {X})$ is H-convex.

Moreover, the transformed convex polygon $P = \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathfrak T}( {\mathrm H})$ generally does not correspond to the convex hull $P^{\prime }$ of ${\mathcal T}_{{\mathcal Conv}}(\mathsf {X})$, i.e.,  $P^{\prime } = {\mathcal Conv}{(P \cap \mathbb {Z}^2)}$. However, we always have the following inclusion relation.

Property 5

Let $\mathsf {X}$ be an H-convex digital object. Let us consider the two convex polygons such that $P = \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {X}))} {\mathfrak T}( {\mathrm H})$ and $P^{\prime } = {\mathcal Conv}({\mathcal T}_{{\mathcal Conv}}(\mathsf {X}))$. Then, we always have $P^{\prime } \subseteq P$.

5 Rigid Motions of a Non-convex Digital Object

In the previous section, we showed how to carry out rigid motions of H-convex digital objects with preservation of their H-convexity under the quasi-$(\frac{\sqrt{2}}{2})$-regular condition. In this section, we first present a hierarchical representation of a non-convex digital objects based on convex hulls, called a concavity tree [23]. Then, we show how to perform rigid motions of a non-convex digital object via this concavity-tree representation.

5.1 Concavity Tree of a Digital Object

A concavity tree, initially introduced in [23], is a hierarchical representation of the convex and concave parts of the contour of a digital object, with different levels of detail. This tree structure has been used, e.g., for minimum-perimeter polygon computation [14, 23], hierarchical shape analysis [3], polygonal approximation [1]. The root of the tree corresponds to a given digital object. Then, each node corresponds to a concavity part of its parent. Note that each concavity part $\mathsf {X}^{\prime }$ of a digital object $\mathsf {X}$ is obtained as a connected component of the subtraction of $\mathsf {X}$ from the digitized convex hull ${\mathcal Conv}(\mathsf {X}) \cap \mathbb {Z}^2$. This is written by $\mathsf {X}^{\prime } \in {\mathfrak C}( ( {\mathcal Conv}(\mathsf {X}) \cap \mathbb {Z}^2 ) \setminus \mathsf {X} )$ where ${\mathfrak C}({\mathsf S})$ denotes the set of all connected components of a finite set ${\mathsf S}\in \mathbb {Z}^2$. In other words, we have

$$\begin{aligned} \mathsf {X} = \biggr ( {\mathcal Conv}(\mathsf {X}) \bigcap \mathbb {Z}^2 \biggr ) \setminus \biggr ( \bigcup \limits _{\mathsf {X}^{\prime } \in {\mathfrak C}( ( {\mathcal Conv}(\mathsf {X}) \cap \mathbb {Z}^2 ) \setminus \mathsf {X} )} \mathsf {X}^{\prime } \biggr ), \end{aligned}$$

(7)

where each concavity part $\mathsf {X}^{\prime }$ is recursively replaced by the subtraction of the concavity parts of $\mathsf {X}^{\prime }$ from ${\mathcal Conv}(\mathsf {X}^{\prime }) \bigcap \mathbb {Z}^2$ until no concavity part is found. An illustration of concavity tree is given in Fig. 6.

Fig. 6.

(a) A digital object. (b) The convex and concave parts of (a) with their convex hulls. (c) The concavity tree of (a) where each colored node corresponds to a concavity part of its parent and the root (in orange) corresponds to (a). (Color figure online)

5.2 Digital Object Rigid Motions Using Concavity Tree

As observed in Eq. (7), a digital object $\mathsf {X}$ can be decomposed into the set of digitized convex hulls of hierarchical concavity parts, ${\mathcal Conv}(\mathsf {X}) \cap \mathbb {Z}^2$, ${\mathcal Conv}(\mathsf {X}^{\prime }) \cap \mathbb {Z}^2$, $\ldots$, via the subtraction operations. As we are rather interested in such a hierarchical decomposition by digitized convex polygons, we consider a concavity tree such that each node corresponds to the half-plane representation of the convex hull of a concavity part $\mathsf {Y}$, ${\mathcal Conv}(\mathsf {Y}) = \bigcap \limits _{{\mathrm H}\in {\mathcal R}({\mathcal Conv}(\mathsf {Y}))} {\mathrm H}$, instead of $\mathsf {Y}$ itself. Once the hierarchical object decomposition is obtained, we simply apply ${\mathcal T}_{{\mathcal Conv}}$ to each digitized convex polygon ${\mathcal Conv}(\mathsf {Y}) \cap \mathbb {Z}^2$, as shown in the previous section, and then carry out the set subtraction operations guided by the tree. Figure 7 illustrates comparisons between applications of point-by-point transformation ${\mathcal T}_{point}$ and convexity-preserving transformation ${\mathcal T}_{{\mathcal Conv}}$ using concavity tree to non-convex digital objects.

From Proposition 3, we can preserve the H-convexity of each digitized convex polygon in the tree if the convex polygon is quasi-$(\frac{\sqrt{2}}{2})$-regular. Practically, such hypothesis is not satisfied in general (see Fig. 6(b)). However up-sampling strategies on the digital objects can allow us to generate convex polygons which guarantee the quasi-$(\frac{\sqrt{2}}{2})$-regularity. This subject is one of our perspectives.

Fig. 7.

Original digital objects (a, d) with their point-by-point digital rigid motions (b, e) and their convex-preserving digital rigid motions using concavity tree (d, f).

6 Conclusion

In this article, we proposed a method for rigid motions of digital objects which preserves the H-convexity. The method is based on the half-plane representation of H-convex digital objects. In order to guarantee the H-convexity, we introduced the notion of quasi-r-regularity for convex polygons, and showed that the H-convexity is preserved under rigid motions if the convex hull of an initial H-convex digital object is quasi-$(\frac{\sqrt{2}}{2})$-regular. The necessity of such condition is caused by the fact that the convexity does not imply the connectivity in $\mathbb {Z}^2$ contrary to $\mathbb {R}^2$. As we need to re-discretize the transformed convex polygon at the end, it is natural to have a similar notion of the r-regularity of continuous objects, which guarantees the topology after its digitization. The method was also extended to non-convex digital objects using the hierarchical object representation.

The proposed method works only with digital objects satisfying the quasi-($\frac{\sqrt{2}}{2}$)-regular condition on the convex hull. In practice, this condition is difficult to obtain, and this would limit the direct use of the proposed method. However, an up-sampling approach would provide a promising strategy to guarantee the quasi-($\frac{\sqrt{2}}{2}$)-regularity of the convex hull of any digital object. It is also observed that the quasi-($\frac{\sqrt{2}}{2}$)-regularity is sufficient but not necessary for the H-convexity preservation. It would be one of our perspectives to find such a sufficient and necessary condition. Another perspective would be to extend the method into higher dimensions.