Abstract
In this chapter, we devote our attention to establishing mathematical properties concerning the electromagnetic fields that are governed by the time-dependent Maxwell equations. For that, we investigate a number of physical properties of the electromagnetic fields exhibited in Chap. 1, using the mathematical tools introduced in Chaps. 2, 3 and 4. We focus mainly on four items.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See Remark 5.1.2 on how to take into account the boundary condition on the magnetic field.
- 2.
Since one can choose where to put the artificial boundary Γ A , it is a reasonable assumption. Also, because Γ A is smooth, one has
$$\displaystyle \begin{aligned} \boldsymbol{H}^{1/2}_\parallel(\varGamma_A)=\boldsymbol{H}^{1/2}_\perp(\varGamma_A)=\boldsymbol{H}^{1/2}_t(\varGamma_A),\mbox{ where }\boldsymbol{H}^{1/2}_t(\varGamma_A):=\boldsymbol{L}^{2}_t(\varGamma_A)\cap\boldsymbol{H}^{1/2}(\varGamma_A), \end{aligned}$$and similarly for the dual spaces, \(\boldsymbol {H}^{-1/2}_\parallel (\varGamma _A)=\boldsymbol {H}^{-1/2}_\perp (\varGamma _A)=\boldsymbol {H}^{-1/2}_t(\varGamma _A)\).
- 3.
If ∂Γ P ∩ ∂Γ A = ∅, one still needs to address the possible lack of regularity of the artificial boundary (see Remark 5.1.6). This corresponds to configurations 2 and 3 of Γ A in the study below.
- 4.
One applies the Lax-Milgram Theorem 4.2.8 to the equivalent variational form:
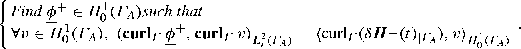
If Γ A is not a connected set, one chooses—instead of \(H^1_0(\varGamma _A)\)—the space
$$\displaystyle \begin{aligned} \{ f\in H^1(\varGamma_A)\ :\ f_{\mid{\partial\varGamma_A^0}}=0,\ f_{\mid{\partial\varGamma_A^k}}=cst_k,\ 1\le k\le K_A\}, \end{aligned}$$where \((\varGamma _A^k)_{k=0,K_A}\) are the (maximal) connected components of Γ A .
- 5.
For \( \underline \psi = \underline \psi ^++\sqrt {{\mu }/{\varepsilon }} \underline \psi ^-\), we have: \( \underline \psi \in H^{1/2}(\varGamma _A)\), \(\varDelta _\varGamma \underline \psi =0\) in Γ A , \(t_{\boldsymbol {\nu }}( \operatorname {\mathrm {\mathbf {grad}}}_\varGamma \underline \psi )=0\). In this case, we are looking for singular solutions (with at least H 1∕2-regularity) to the Laplace-Beltrami problem with homogeneous Neumann boundary condition and right-hand side. Completely similar analyses can be carried out for \( \underline \psi \): they yield the same results as for \( \underline \phi \).
- 6.
More precisely, we recall that, if \( \underline \phi \) belongs to H 1(Γ A ) with \( \underline \phi { }_{\mid {\partial \varGamma _A}}=0\), we apply the integration by parts (5.23) to find that
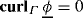 . If one replaces \( \underline \phi \) with \( \underline \phi '= \underline \phi +c\) with c≠0, then the technique still applies (even though \( \underline \phi '{ }_{\mid {\partial \varGamma _A}}\ne 0\)), because \(\varDelta _\varGamma \underline \phi '=0\). So, the local constant behavior can be neglected.
. If one replaces \( \underline \phi \) with \( \underline \phi '= \underline \phi +c\) with c≠0, then the technique still applies (even though \( \underline \phi '{ }_{\mid {\partial \varGamma _A}}\ne 0\)), because \(\varDelta _\varGamma \underline \phi '=0\). So, the local constant behavior can be neglected. - 7.
See footnote 5, p. 12.
- 8.
- 9.
- 10.
The situation is different for time-harmonic problems (see Chap. 8).
References
S. Abarbanel, D. Gottlieb, A mathematical analysis of the PML method. J. Comput. Phys. 134, 357–363 (1997)
S. Abarbanel, D. Gottlieb, J.S. Hestaven, Non-linear PML equations for time-dependent electromagnetics in three dimensions. J. Sci. Comput. 28, 125–137 (2006)
G. Amendola, On the asymptotic behavior for an electromagnetic system with a dissipative boundary condition. IMA J. Appl. Math. 70, 270–292 (2005)
F. Assous, P. Ciarlet, Jr., S. Labrunie, Theoretical tools to solve the axisymmetric Maxwell equations. Math. Methods Appl. Sci. 25, 49–78 (2002)
H. Barucq, M. Fontes, Well-posedness and exponential stability of Maxwell-like systems coupled with strongly absorbing layers. J. Math. Pures Appl. 87, 253–273 (2007)
H. Barucq, B. Hanouzet, Asymptotic behavior of solutions to Maxwell’s system in bounded domains with absorbing Silver-Müller’s condition on the exterior boundary. Asymptot. Anal. 15, 25–40 (1997)
E. Bécache, S. Fauqueux, P. Joly, Stability of perfectly matched layers, group velocities and anisotropic waves. J. Comput. Phys. 188, 399–433 (2003)
E. Bécache, P. Joly, On the analysis of Bérenger’s perfectly matched layers for Maxwell’s equations. Math. Model. Numer. Anal. 36, 87–119 (2002)
A. de la Bourdonnaye, Décomposition de \(H_{div}^{-1/2}(\varGamma )\) et nature de l’opérateur de Steklov-Poincaré du problème extérieur de l’électromagnétisme. C. R. Acad. Sci. Paris Ser. I 316, 369–372 (1993)
A. Buffa, Hodge decompositions on the boundary of nonsmooth domains: the multi-connected case. Math. Models Methods App. Sci. 11, 147–176 (2001)
A. Buffa, P. Ciarlet, Jr., On traces for functional spaces related to Maxwell’s equations. Part II: Hodge decompositions on the boundary of Lipschitz polyhedra and applications. Math. Methods Appl. Sci. 24, 31–48 (2001)
A. Buffa, M. Costabel, C. Schwab, Boundary element methods for Maxwell’s equations on non-smooth domains. Numer. Math. 92, 679–710 (2002)
M. Cassier, P. Joly, M. Kachanovska, Mathematical models for dispersive electromagnetic waves: an overview. Comput. Math. Appl. 74, 2792–2830 (2017)
P.G. Ciarlet, P. Ciarlet, Jr., Another approach to linearized elasticity and Korn’s inequality. C. R. Acad. Sci. Paris Ser. I 339, 307–312 (2004)
M. Costabel, M. Dauge, S. Nicaise, Singularities of Maxwell interface problems. Modél. Math. Anal. Numér. 33, 627–649 (1999)
J. Diaz, P. Joly, An analysis of higher order boundary conditions for the wave equation. SIAM J. Appl. Math. 65, 1547–1575 (2005)
M. Fabrizio, A. Morro, Electromagnetism of Continuous Media (Oxford University Press, Oxford, 2003)
P. Grisvard, Singularities in Boundary Value Problems. RMA, vol. 22 (Masson, Paris, 1992)
T. Hagstrom, A. Mar-Or, D. Givoli, High-order local absorbing conditions for the wave equation: extensions and improvements. J. Comput. Phys. 227, 3322–3357 (2007)
A.D. Ioannidis, G. Kristensson, I.G. Stratis, On the well-posedness of the Maxwell system for linear bianisotropic media. SIAM J. Math. Anal. 44, 2459–2473 (2012)
J.-C. Nédélec, Acoustic and Electromagnetic Equations. Applied Mathematical Sciences, vol. 144 (Springer, New York, 2001)
K.D. Phung, Controllability and stabilization of electromagnetic waves. ESAIM Control Optim. Calc. Var. 5, 87–137 (2000)
F. Poupaud, M. Remaki, Existence et unicité des solutions du système de Maxwell pour des milieux hétérogènes non réguliers. C. R. Acad. Sci. Paris Ser. I 330, 99–103 (2000)
M. Remaki, Méthodes numériques pour les équations de Maxwell instationnaires en milieu hétérogène, PhD Thesis, Ecole des Ponts et Chaussées, Paris, France, 1999 (in French)
G.F. Roach, I.G. Stratis, A.N. Yannacopoulos, Mathematical Analysis of Deterministic and Stochastic Problems in Complex Media Electromagnetics (Princeton University Press, Princeton, 2012)
M. Slodicka, S. Durand, Fully discrete finite element scheme for Maxwell’s equations with non-linear boundary condition. J. Math. Anal. Appl. 375, 230–244 (2011)
I. Terrasse, Résolution mathématique et numérique des équations de Maxwell instationnaires par une méthode de potentiels retardés, PhD Thesis, Ecole Polytechnique, Palaiseau, France, 1993 (in French)
V. Vinoles, Problèmes d’interface en présence de métamatériaux : modélisation, analyse et simulations, PhD Thesis, Université Paris-Saclay, France, 2016 (in French)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Assous, F., Ciarlet, P., Labrunie, S. (2018). Analyses of Exact Problems: First-Order Models. In: Mathematical Foundations of Computational Electromagnetism. Applied Mathematical Sciences, vol 198. Springer, Cham. https://doi.org/10.1007/978-3-319-70842-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-70842-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70841-6
Online ISBN: 978-3-319-70842-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


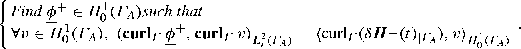
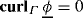 . If one replaces
. If one replaces