A Multiscale Bezier-Representation for Time Series that Supports Elastic Matching

Abstract

Common time series similarity measures that operate on the full series (like Euclidean distance or Dynamic Time Warping DTW) do not correspond well to the visual similarity as perceived by a human. Based on the interval tree of scale, we propose a multiscale Bezier representation of time series, that supports the definition of elastic similarity measures that overcome this problem. With this representation the matching can be performed efficiently as similarity is measured segment-wise rather than element-wise (as with DTW). We effectively restrict the set of warping paths considered by DTW and the results do not only correspond better to the analysts intuition but improve the accuracy in the standard 1NN time series classification.

1 Introduction

Time series analysis almost always starts with inspecting plots. But does a visually perceived similarity correspond to the similarity determined by common measures? We consider this as important whenever a domain expert, who has familiarized herself with the data earlier, wants to match her own knowledge and own expectations to the results of some data mining process or an exploratory analysis. Prominent approaches to time series similarity do not care that much about this correspondence and the results may thus be misinterpreted easily.

With this problem in mind, a new multiscale representation of time series is proposed, not to compress the series in the first place, but to capture its characteristic traits. It simplifies the definition of a notion of similarity that corresponds to our cognition. While we will showcase its usefulness in the context of classification, we see it as a versatile and helpful representation that enables new and carries over to existing approaches. As an example, a new efficient elastic similarity measure is derived directly from this representation. Although we focus on the series as a whole here – rather than subsequences as with shapelets or bag-of-words approaches – the representation may nevertheless be used as a starting point for a meaningful segmentation and subpattern-based approaches.

The main contribution of this paper is a new Bezier spline-based, multiscale time series representation, which (a) encodes many different, continuous representations of the same series, thereby capturing many possible alternative views and mimicking the ambiguity in human perception. (b) It directly supports (no need to access the raw data) elastic similarity measures, which can be computed efficiently and finally (c) performs more than competitive to DTW.

The paper is organized as follows. In the next section we briefly review some existing time series representations and also dynamic time warping as the most prominent elastic similarity measure. We recall the so-called Interval Tree of Scales (IToS), which serves as a basis for the new time series representation. Then, in Sect. 3 we identify two drawbacks shared by most elastic measures and how we intend to use the IToS to overcome these problems. The new representation is presented in Sect. 4, including a proposal how to use it for an elastic similarity measure. The representation is evaluated, amongst others, on time series classification problems in Sect. 5.

2 Related Work

2.1 Similarity Measures and Time Series Representations

Similarity Measures. Given two series $\mathbf{x}$ and $\mathbf{y}$, Euclidean distance $d^2(\mathbf{x},\mathbf{y})=\sum _i (x_i-y_i)^2$ assumes a perfect alignment of both series as only values with the same time index are compared. If the series are not aligned, $x_i$ might be better compared with some $y_{m(i)}$ where $m:{\mathbb {N}}\rightarrow {\mathbb {N}}$ is a monotonic index mapping. With dynamic time warping (DTW) [2] the optimal warping path m, that minimizes the Euclidean distance of $\mathbf{x}$ to a warped version of $\mathbf{y}$, is determined. An example warping path m is shown in Fig. 2(left): Two series are shown along the two axes; $\mathbf{x}$ on the left, $\mathbf{y}$ at the bottom. The matrix enclosed by both series encodes the warping path: an index pair (i, j) on the warping path denotes that $x_i$ is mapped to $y_j=y_{m(i)}$. All pairs (i, j) of the warping path, starting at index pair (0, 0) and leading to (m, m), contribute to the overall DTW distance. Despite the fact that DTW is rather old, recent studies [14] still recommend it as the best measure on average over a large range of datasets.

Time Series Representations. While a time series may consist of many values (high-dimensional), consecutive values typically correlate strongly. So we may seek for a more compact representation, such as piecewise polynomials. This requires a segmentation of the whole series, which may be adaptive (segments of varying length to approximate the data best) or static (subdivide the series into equal-length segments) [14]. Symbolic approaches may replace (short segments of) numeric values by a symbol, shifting the problem into the domain of strings (e.g. SAX [8]). Bag of words representations consider the series as a set of substrings as in text retrieval, but do not allow a reconstruction of an approximation of the original series as all positional information gets lost. While most approaches focus on approximation quality, compression rate, or bounding of the Euclidean distance, a few explicitly care about the perception of time series. The Landmark Model focuses on the extrema of time series to define similarity that is consistent with human intuition [11]. The extrema are also considered as important points in [12]. With noisy data, both approaches skip some extrema based on a priori defined thresholds. This is typical for smoothing operations, but it is difficult to come up with such a fixed threshold, because different degrees of smoothing may be advisable for different parts of the series. Too much smoothing bears the danger of smearing out important features, too little smoothing may draw off the attention from the relevant features.

Bezier Curves. Time series representations usually approximate the raw series. Polynomials are most frequently used, e.g. piecewise constant segments [8], linear segments [9], cubic segments or splines. The polynomials are defined as functions of time t or time series index i, such that (t, f(t)) resembles the approximation.

Bezier curves are common in computer graphics but not in data analysis. They are used to represent arbitrary curves in the plane and thus are not necessarily functional. A Bezier curve $(B_\mathbf{t}(\tau ),B_\mathbf{q}(\tau ))$ is a $\tau$-parameterized 2D-curve, $\tau \in [0,1]$, defined by two cubic polynomials (separately for the time and value domain). For given coefficients $\mathbf{c}=(c_0,c_1,c_2,c_3)\in {\mathbb {R}}^4$, $B_\mathbf{c}(\tau )$ is defined as

$$\begin{aligned} B_\mathbf{c}(\tau )= & {} (1-\tau )^3c_0+3(1-\tau )^2\tau c_1+3(1-\tau )\tau ^2c_2+\tau ^3c_3 \end{aligned}$$

(1)

2.2 Interval Tree of Scales (IToS)

The relevance of extrema has been recognized early and by many authors. Extrema are, however, also introduced by noise, so we have to find means to distinguish extrema of different importance. Witkin was one of the first who recognized the usefulness of a scale-space representation of time series [15]. The scale s denotes the degree of smoothing (std. dev. of Gaussian filter) that is applied to the time series. The scale-space representation of a series depicts the location of extrema (or inflection points) as the scale s increases (cf. Fig. 1(left) for the time series shown at the bottom). An extremum can be tracked from the original series ($s\approx 0$) to the scale s at which it vanishes (where it gets smoothed away), indicating its persistence against smoothing.

Fig. 1.

Left: Depending on the variance of a Gaussian smoothing filter (vertical axis, logarithmic) the number and position of zero crossings in the first derivative varies. Mid: The zero-crossings of the first derivative (extrema in the original series) vanish pairwise. Right: Interval tree of scales obtained from left figure.

Zero-crossings vanish pairwise, three consecutive segments (e.g. increasing, decreasing, increasing) turn into a single segment (e.g. increasing), cf. Fig. 1(middle). The scale-space representation can thus be understood as a ternary tree of time series segments where the location of zero-crossings determine the temporal extent of the segment and the (dis-) appearance of zero-crossings limit the (vertical) extent or lifetime of a segment. By tracing the position of an extrema in the scale-space back to the position at $s\approx 0$ we can compensate the displacement caused by smoothing itself. We construct a so-called interval tree of scales [15] (cf. Fig. 1(right)), where the lifetime of a monotonic time series segment is represented by a box in the scale-space: its horizontal extent denotes the position of this segment in the series, the vertical extent denotes the stability or resistance against smoothing. The tree represents the time series at multiple scales and allows to take different views on the same series. It can be obtained by applying Gaussian filters or by means of the wavelet transform à trous [10].

We found the IToS already useful in a visualization technique to highlight discriminating parts of a class of time series [13]. But all comparisons had to be conducted directly on the raw data, which was time-consuming. Here, we propose a new general and efficient representation that supports various notions of elastic similarity (and also speeds up [13]). In the remainder of this work, we refer to the elements of the tessellation (rectangles) as tiles. A tile v covers a temporal range $[t_1^v,t_2^v]$ ($t_1^v<t_2^v$) and a scale range $[s_1^v,s_2^v]$ ($s_1^v<s_2^v$) and has an orientation $o\in \{\text{ increasing },\text{ decreasing }\}$. By $\mathbf{x}|_v$ we denote the segment $\mathbf{x}|_{[t_1^v,t_2^v]}$ from the original series $\mathbf{x}$ covered by tile v.

3 Visual Perception of Series – Problems and Motivation

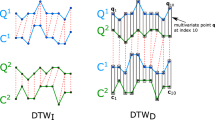
We want to draw the reader’s attention to two problems with measures of the DTW-kind, the most prominent representative of elastic measures. In Fig. 2(middle) we have two similar series (linearly decreasing, incr., decr. segments), depicted in red and green. Both series are also shown on the x- and y-axis in the leftmost figure, together with the warping path. How the warping maps points of both series is also indicated in the middle by dotted lines. All series were standardized, which is common practice in the literature.

Fig. 2.

Behaviour of time warping distances. Left: warping path of two time series (also shown in green and red in the middle). Mid and right: examples series; dotted lines indicate the DTW assignment. Right: Pair of blue and red series; structurally different, but with the same distance as green and red series. (Color figure online)

Problems of Existing Elastic Approaches. First, elastic time series similarity measures treat value and time differently: while a monotone but otherwise arbitrary transformation of time is allowed (with DTW), the values are usually not adapted to the comparison but are transformed a priori and uniformly (via standardization). But once we warp a time series locally, this also affects the value distribution and thus mean and variance: The local maximum of the red curve is mapped to many points of the green curve (cf. dotted assignment), so its local maximum occurs more often in the warped path than in the original red series. The initial mean and variance do not have much in common with the mean and variance of the warped curve, so why use the a priori values anyway?

Second, elastic measures allow almost arbitrary (monotonic) warping, which may lead to some surprising results. If we would ask a human to align the red and green series in Fig. 2, an alignment of the local extrema would be natural, revealing the high similarity of both series as they behave identically between the local extrema. The local maximum m of the red curve (near $t=60$), however, lies below the local maximum of the green curve, so all DTW approaches assign the red maximum to all points of the green curve above m. As a consequence, if we shuffle or reorder the green data above m (cf. rightmost subfigure, blue curve), neither the assignment nor the distance changes. This is in contrast to the human perception, we would never consider the blue series being as similar to the red series as the green.

Envisaged Use of the IToS. So we focus on two problems: (1) emphasis of local temporal scaling but ignorance of local vertical scaling, (2) arbitrary warping paths instead of warping that matches landmarks.

Regarding (2) we propose to utilize the IToS as a regularizer. We consider the IToS as a representation of all possible perceptions of a time series. Taking a finer or coarser look at some part of the series corresponds to selecting different tiles within the same time range but at different scales. Consider for example Fig. 3(right): If we intentionally ignore some fine-grained details of the series in the gray box we perceive it only as a single decreasing segment. By choosing tiles (from the IToS below the series) at different scales ($b_4$ rather than $b_3 b_5 b_6$) we adjust the level of detail and either ignore or consider local extrema. Any sequence of tiles (adjacent in time and covering the whole series) corresponds to a different perception of the series. Instead of allowing an arbitrary (monotonic) assignment of data points as with DTW, we propose to assign tiles to each other. In case of Fig. 3 we may choose perception $a_0,a_1,a_2,a_4$ for the left and $b_1,b_4,b_7,b_8$ for the right series and match them accordingly ($a_0:b_1, a_1:b_4, \ldots$).

Fig. 3.

The IToS for two time series. One possible perception of each time series is marked by circles. Matching time series is then accomplished by matching adjacent tiles subsequently.

Regarding (1) we propose to apply linear scaling to the temporal domain and the value domain. Continuing our example, we may match (decreasing) tiles $a_1$ and $b_4$. We align both start times and linearly rescale time to match the temporal extent of both tiles. This is justified by the observations of different authors [5,6,7] that arbitrary warping is seldomly justified but linear warping suffices. In the same fashion we align the starting values and linearly rescale the vertical axis (replacing standardization) to have the same value range as illustrated at the bottom of Fig. 3. Once this alignment has taken place, we may measure the Euclidean distance between both series. This procedure limits the warping capabilities to perceptually meaningful paths and focuses on the shape of the tiles rather than (questionable) standardized absolute values. In contrast to other landmark approaches we want to keep the ambiguity in the perception of a time series by sticking to the multiscale representation.

4 A New Time Series Representation

The IToS just captures the temporal and vertical extent of monotone segments. In this section, we extend the IToS such that it fully represents the underlying series. The goal is to have all information readily available to measure similarity.

4.1 Multiscale Bezier-Representation of Time Series

We propose to attach a compact representation of an appropriately smoothed time series to each tile. This is shown in Fig. 4 for one series from the Beef dataset. At the top, the IToS is depicted. The light blue and red colors indicate increasing and decreasing segments. At the bottom, the original time series is shown, but this is hardly recognizable because for each tile from the IToS above we show an approximation of the corresponding segment (each in different color). Note that the segments connect seamlessly: for any sequence of adjacent tiles in the IToS we find a corresponding, smooth representation of the time series (a possible perception of the series, cf. Sect. 3).

Fig. 4.

Interval Tree of Scales for one series from the Beef dataset together with Bezier spline approximations. (Color figure online)

To achieve such a representation we cannot simply apply standard curve fitting to $\mathbf{x}|_v$, because that would ignore our background knowledge: By definition the tile boundaries mark local extrema of the series, so each segment has to be monotonic. From this alone a polynomial of degree 3 is uniquely determined (cf. [11]). However, one can actually think of many different shapes for an increasing segment, with a uniquely determined polynomial we would not be able to distinguish different shapes like those in Fig. 5 from one another. To better adapt to the data, we settle on Bezier curves, which are widely used in computer graphics. A Bezier curve (of degree 3) allows us to define a polynomial for both dimensions, the value domain as well as the time domain, which gives us the desired flexibility to adapt the approximations to the data as shown in Fig. 5.

These constraints are a strong regularizer of the fit. Note the last large peak on the right in Fig. 4 and the Bezier segments that correspond to the upmost two tiles in the IToS: Due to the constraints on monotonicity and start/end point the curve essentially ignores the peak to approximate the remaining data best. This is desired as the upmost tiles correspond to a smoothing level where the peak no longer exists. The associated Bezier curve does not contain this peak but still represent the original data well. This is quite different from a series we would obtain by actually smoothing the data (features would be smeared out and displaced).

The proposed time series representation is therefore as follows: Given a time series $\mathbf{x}$ and its IToS. The Interval Tree of Bezier Segments (IToBS) representation of $\mathbf{x}$ is a set V of tiles $v=(t_1,t_4,s_1,s_2,y_1,y_2,t_2,t_3,\sigma )\in V$, where $[t_1,t_4]$ denotes the temporal range of the tile, $[s_1,s_2]$ the scale range (both from the IToS) and $[y_1,y_1,y_2,y_2]$ / $[t_1,t_2,t_3,t_4]$ denote the parameters of the Bezier curve that approximates $\mathbf{x}|_v$ with standard deviation $\sigma$ of the residuals. The reason why the coefficients of $B_\mathtt{v}(\cdot )$ require only the two values $y_1$ and $y_2$ will be explained in Sect. 4.3. The definition of a tile in the IToBS as a 9-tuple is convenient, but it is also highly redundant. Tiles v and w adjacent in time share one point in time $t_4^v=t_1^w$ and value $y_2^v=y_1^w$. For tiles v and w adjacent in scale (w is child-node of v) we have $s_2^v=s_1^w$. The values $t_2,t_3$ will be discretized and replaced by a code later (with a small number of possible values). When serializing the IToBS to disk, we need to store only one time point, one scale, one y-value, $\sigma$ and the shape-code per tile.

Fig. 5.

Monotonically increasing Bezier curves with parameters $[0,0,1,1]/[0,\frac{i}{10},1-\frac{j}{10},1]$. For each spline the value of i/j is shown in the center. The dashed, red curves indicate parameter configurations that lead to non-monotonic or non-functional curves. (Color figure online)

4.2 Euclidean Tile Distance

The key idea of the tile distance (Sect. 3 and Fig. 3) was to rescale the content, i.e. the corresponding time series segments which will now be represented by Bezier segments, such that they fit into the same bounding box. We have not yet decided which size of the bounding box we actually want to use. But for any two functions f(t) and g(t) representing fitted segments, an affine transformation of values leads to a linearly scaled Euclidean distance (area between curves):

$$ \int _{t_0}^{t_1} \left| (a\cdot f(t)+b)-(a\cdot g(t)+b)\right| dt = |a| \cdot \int _{t_0}^{t_1} |f(t)-g(t)| dt $$

The same holds for an affine transformation of time (integration by substitution). Thus, regardless of the bounding box we choose, whether we fit f to the original frame of g, the other way round or any other bounding box, we convert distances for different bounding boxes by applying linear scaling factors. So we determine reference distances using $[0,1]^2$ as the default bounding box (and use them to derive distances for any other bounding box).

We thus consider distances of Bezier segments rescaled to the unit square only. Applying such an affine transformation (in value and time) to a Bezier segment is simple: we have to apply the affine transformation to the Bezier curve coefficients. To rescale a monotonically increasing Bezier curve $[t_1,t_2,t_3,t_4]/[y_1,y_1,y_2,y_2]$ to the unit square, we obtain the coefficients as $\left[ 0,\tau _2,\tau _3,1\right] /\left[ 0,0,1,1\right]$ with $\tau _2=\frac{t_2}{t_4-t_1}$, $\tau _3=\frac{t_3}{t_4-t_1}$. For a decreasing segment, the value coefficients would be [1, 1, 0, 0]. From our intended application in Sect. 3 it makes only sense to compare tiles of the same orientation (both increasing or both decreasing), so the value coefficients of both Bezier segments to be compared will be either [0,0,1,1] or [1,1,0,0]. Switching between these two configurations again corresponds to an affine value transformation $1-y$, the curve gets mirrored on the horizontal axis. The Euclidean distance between the curves is thus unaffected by this mirroring (scaling factor 1), so whenever we want to calculate the tile distance of two decreasing splines we could as well consider their mirrored, increasing counterparts and obtain the same distance.

At this point we know that it is sufficient to consider distances in the unit square for increasing curves. If we have efficient means to calculate tile distances for this case, we can provide arbitrary tile distances for arbitrary bounding boxes. While measuring Euclidean distance is a cheap operation on indexed time series (as $x_i$ is aligned with $y_i$), it is an expensive operation with Bezier curves, because the temporal component $B_\mathbf{t}(\tau )$ of tile v from series $\mathbf{x}$ is not necessarily aligned with that of tile w from series $\mathbf{y}$. Due to different cubic polynomials for $\mathbf{t}_v$ and $\mathbf{t}_w$ in the temporal dimension, we first have to identify parameters $\tau '$ and $\tau ''$ such that $B_{\mathbf{t}_v}(\tau ')$ and $B_{\mathbf{t}_w}(\tau '')$ refer to the same point in time. We cannot afford to perform such expensive operations whenever we need to calculate a tile distance (it becomes a core operation in the similarity measure). We therefore suggest to discretize the possible values of $\tau _2$ and $\tau _3$ (say, consider values $0, 0.05, \ldots , 1$) and pre-calculate all possible tile distances offline. At a resolution of $R=0.05$ we have about 500 possible pairs of $\tau _2 / \tau _3$, so a lookup table that stores the tile distances between any two tiles consists of roughly 250.000 entries, which is small enough to fit into main memory. From this lookup table we can immediately return the distance of any two tiles on any chosen bounding box.

4.3 Determine the Bezier Segments

In this section we discuss how to obtain the Bezier parameters needed for the IToBS. While piecewise monotone approximations have been investigated for polynomials (e.g. [4]), this does not seem to be the case for Bezier curves. We assume that a monotonic time series segment with observations $\mathbf{s}=(x_i,y_i)_{1\le i\le n}$ is given. We seek coefficients $\mathbf{t},\mathbf{q}\in {\mathbb {R}}^4$ of a (cubic) Bezier curve $(B_\mathbf{t}(\tau ),B_\mathbf{q}(\tau ))_{\tau \in [0,1]}$ (cf. Eq. (1)) to approximate $\mathbf{s}$. First, we determine the Bezier coefficients $\mathbf{q}=(q_0,q_1,q_2,q_3)$ for the value domain. We want to preserve the extrema of the original function and thus require $B_\mathbf{q}(0)=y_1$ and $B_\mathbf{q}(1)=y_n$ and obtain $q_0=y_1$ and $q_3=y_n$. Furthermore we know that $y_1$ and $y_n$ are the extrema of the segment – so the gradient vanishes at $t=0$ and $t=1$: $B'_\mathbf{q}(0)=0=B'_\mathbf{q}(1)$:

$$\begin{aligned} B'_\mathbf{q}(0)= & {} 3(q_1-q_0)=0 \quad \Rightarrow \quad q_1=q_0 \;(=y_1) \\ B'_\mathbf{q}(1)= & {} 3(q_3-q_2)=0 \quad \Rightarrow \quad q_2=q_3 \;(=y_n) \end{aligned}$$

So $\mathbf{q}$ is fully determined as $\mathbf{q}=(y_1,y_1,y_n,y_n)$. (As already mentioned we have no degrees of freedom to adopt the Bezier spline $B_\mathbf{q}(\tau )$ to the data at hand.)

Second, we determine coefficients $\mathbf{t}=(t_0,t_1,t_2,t_3)$ for the time domain. Similar arguments as above lead us quickly to $t_0=x_1$ and $t_3=x_n$. By means of $t_1$ and $t_2$ we can adopt the shape of the Bezier curve to the time series segment. As $B_\mathbf{q}(\tau )$ is already fixed, we first identify a series $\tau _i$ such that $B_\mathbf{q}(\tau _i)=y_i$. The value $\tau _i$ may be found by solving a cubic equation or by a bisection method. There is a solution to this equation because for all i we have $y_i\in B_\mathbf{q}([0,1])=[y_1,y_n]$. To optimize the fit we now seek a vector $\mathbf{t}$ that warps the temporal domain, that is, $B_\mathbf{t}(\tau _i)$ approximates $x_i$. So we deal with a regression problem that minimizes

$$\begin{aligned} f(\mathbf{t}\,|\,\mathbf{s})=\sum _i (B_\mathbf{t}(\tau _i)-x_i)^2 \end{aligned}$$

(2)

where $\mathbf{t}$ has only two degrees of freedom left ($t_1$ and $t_2$). Introducing the abbreviations $\delta _{ij}:=t_i-t_j$, i.e., $t_1=t_0+\delta _{10}$, $t_2=t_0+\delta _{10}+\delta _{21}$, the optimal fit is then obtained from the linear equation system (with unknowns $\delta _{10}, \delta _{21}$):

$$\begin{aligned} \begin{array}{llll} 0&{}=&{}\sum _i 3(\tau _i^4-2\tau _i^5+\tau _i^6)\delta _{21}+3(\tau _i^3-2\tau _i^4+\tau _i^5)\delta _{10}\\ &{}&{} +(\tau _i^5-\tau _i^6)\delta _{30}+(\tau _i^2-\tau _i^3)t_0+(\tau _i^3-\tau _i^2)x_i \\ 0&{}=&{}\sum _i 3(\tau _i^3-2\tau _i^4+\tau _i^5)\delta _{21}+3(\tau _i^2-2\tau _i^3+\tau _i^4)\delta _{10}\\ &{}&{} +(\tau _i^4-\tau _i^5)\delta _{30}+(\tau _i-\tau _i^2)t_0+(\tau _i^2-\tau _i)x_i \end{array} \end{aligned}$$

(3)

Functional Curves. The regression problem provides us the global minimizer for the missing parameters $\delta _{10}$ and $\delta _{21}$, but the solution to the regression problem may not fit our needs: In order to model a time series segment, the temporal component $B_\mathbf{t}(\tau )$ must be strictly increasing, otherwise the resulting Bezier spline $(B_\mathbf{t}(\tau ),B_\mathbf{q}(\tau ))$ might not be functional (cf. red cases in Fig. 5). Rather than an unconstrained optimization we actually have to impose a constraint on the monotonicity of $B_\mathbf{t}(\tau )$ within [0, 1]. We require a non-negative first derivative

$$ \frac{1}{3} B'_\mathbf{t}(\tau ) = (\delta _{30}-3\delta _{21})\cdot \tau ^2+2(\delta _{21}-\delta _{10})\cdot \tau +\delta _{10}\ge 0 \quad \text{ for } \tau \in [0,1]. $$

We find the solution to this constrained problem by solving the unconstrained problem first (cf. Eq. (3)) and then, if it does not yield a monotonic $B_\mathbf{t}(\tau )$, find the minimizers of (2) among all boundary cases where $B'_\mathbf{t}(\tau )$ vanishes for some $\tau '\in [0,1]$. From the continuity of $B'_\mathbf{t}(\tau )$ and the fact that it must not become negative, we can conclude that either $\tau '$ has to be at the boundary of its valid range [0, 1], that is $\tau \in \{0,1\}$, or $B'_\mathbf{t}(\tau ')$ must be a saddle point.

From $\tau \in \{0,1\}$ we can conclude (by straightforward considerations, dropped due to lack of space) that either $\delta _{10}=0$, $\delta _{21}=\delta _{30}/3$, or $\delta _{21}=\delta _{30}-2\delta _{10}$, which yields three linear regression problems with a single parameter only. In case of a saddle point we can conclude $\delta _{21}^2=\delta _{10}\delta _{30}$, which does unfortunately not lead to a linear regression problem. Instead of solving a quadratic optimization problem, we take the resolution at which the Bezier curves will be considered in the lookup-table into account, so we simply explore the possible values (according to the resolution R) for $\delta _{10}$, set $\delta _{21}=\sqrt{\delta _{10}\delta _{30}}$ and finally pick the best boundary solution. This is done for all time series to turn the raw series into the IToBS representation, which is then stored to disk and for the subsequent operations we do not access the raw data.

4.4 A Tile Distance to Mimic Perceived Similarity

We can conveniently lookup tile distances on arbitrary bounding boxes, but to employ it in other contexts we have to settle on a concrete distance. Trying to mimic the human perception we take as much information into account as provided by the IToBS. But it is heuristic in nature and many other definitions are possible. The first aspect is the shape of both tiles: Let $d_{US}(v,w)$ denote the Euclidean distance between the tiles v and w in the unit square (retrieved from a lookup-table). To include the goodness-of-fit of both approximations we include their standard deviations $\sigma _v+\sigma _w$ (as obtained in the unit square). As the term $d_{US}(v,w)+\sigma _v+\sigma _w$ is independent of the tile dimensions (projection to the unit square), we choose a bounding box with the maximum of both tile durations and the maximum of both value ranges. This ensures that longer segments yield (potentially) larger distances than shorter segments and also establishes symmetry (by taking the maximum extent of both tiles). By $\max _{\varDelta t}$ we denote the maximum temporal extent of both tiles, analogously for $\min$ and index y (value range) and s (scale). As already discussed, we obtain the distance in this bounding box by multiplying with the extents of the box ($\text {max}_{\varDelta t}, \text {max}_{\varDelta y}$):

$$\begin{aligned} \text {max}_{\varDelta t}\cdot \text {max}_{\varDelta y}\cdot (d_{US}(v,w)+\sigma _v+\sigma _w) \end{aligned}$$

(4)

So far we account for the shape and approximation quality. But after rescaling, a flat and short segment may appear similar to a tall and long segment – but visually we would not perceive them as similar. Therefore we include penalty factors for differences in duration, vertical extent and stability, that is, their persistence against smoothing in the scale space. The latter is an aspect of similarity that is unique to multiscale approaches such as IToS. We penalize distances by a factor of 2 if one segment is twice as long, tall, or important (persistent) as the other:

$$ TD(v,w) = \text {max}_{\varDelta t}\cdot \text {max}_{\varDelta y}\cdot (d_{US}(v,w)+\sigma _v+\sigma _w) \cdot \frac{\max _{\varDelta t}}{\min _{\varDelta t}}\cdot \frac{\max _{\varDelta y}}{\min _{\varDelta y}}\cdot \frac{\max _{\varDelta s}}{\min _{\varDelta s}} $$

4.5 Elastic Measure Based on IToBS

Once we have settled on a tile distance, we finally approach the definition of a distance for full time series. From a series $\mathbf{x}$ we obtain all of its tiles $V^{\mathbf{x}}$. (As long as only one time series is involved in the discussion, we drop the superscript $\mathbf{x}$.) Based on the tiles we can build a graph $G=(V,E)$ by connecting adjacent tiles (we have an edge $v\rightarrow w$, $v,w\in V$, iff $t_4^v = t_1^w$). We define a subset $V_S\subseteq V$ (resp. $V_E\subseteq V$) that contains all start-tiles (resp. end-tiles), that is, tiles which do not have a predecessor (resp. successor) in the graph. In the example of Fig. 6, the interval tree of the series on the left (resp. bottom) consists of 7 (resp. 9) tiles. The graphs are superimposed on the interval tree. Nodes belonging to $V_S$ (or $V_E$) are connected to the virtual node S (or E). From these examples we find two perception for the left series ($(a_0,a_1,a_2,a_4)$ and $(a_0,a_1,a_2,a_3,a_5,a_6)$) and several for the bottom series (e.g. $(b_0,b_2,b_4,b_7,b_8)$).

Among all perceptions of series $\mathbf{x}$ and $\mathbf{y}$ we want to identify those that lead to the smallest overall accumulated tile distance. As with DTW this requires a mapping $m(\cdot )$ of a tile $v^\mathbf{x}$ from the perception of series $\mathbf{x}$ to a tile $w^\mathbf{y}$ from a perception of series $\mathbf{y}$: $m(v^\mathbf{x})=w^\mathbf{y}$. Unlike DTW we do not allow $m(\cdot )$ to skip tiles. When perceiving all details (path near the bottom of the interval tree), both series may not match structurally in the number of tiles: In Fig. 6 the series $\mathbf{x}$ (left) contains a landmark at the end (peak at $a_5,a_6$) while the other series $\mathbf{y}$ (bottom) does not. To perceive them as similar, we switch to a coarser scale for $\mathbf{x}$ ($a_4$ instead of $a_3,a_5,a_6$). Finding the path through both graphs $G_{\mathbf{x}}$ and $G_{\mathbf{y}}$, such that the tiles in both sequences correspond to each other best, corresponds to a structural comparison of the series.

Fig. 6.

Two series (left and bottom), represented by their interval tree and respective graph (slope is color-coded). The matrix in the center encodes the assignment of nodes from both graphs, a match of perceptions from both series is thus a path from the bottom left to top right edge of the matrix. (Color figure online)

The alignment-task is solved using dynamic programming (cf. Fig. 7), very much in the fashion of DTW. The classic DTW solution uses a distance matrix D[i, j] to store the lowest accumulated cost of a warping path that matches $\mathbf{x}|_{1:i}$ to $\mathbf{y}|_{1:j}$. The subscripts refer to the time indices of the series. Now tiles take the role of points – but it is not possible to match arbitrary tiles, they have to have the same orientation and they must be adjacent in the graph. In Fig. 6 the hatched entries in the matrix denote illegal assignments due to incompatible tile orientation. An associative array L plays the role of a distance matrix in Fig. 7, line 2. To identify the minimal cost to reach an arbitrary pair $(v^\mathbf{x},w^\mathbf{y})$ of tiles we have to consider how these tiles were reached: We need a predecessor $r^\mathbf{x}$ of $v^\mathbf{x}$ and a predecessor $s^\mathbf{y}$ of $w^\mathbf{y}$. Among all possible predecessor-pairs $(r^\mathbf{x},s^\mathbf{y})$ leading to $(v^\mathbf{x},w^\mathbf{y})$ we determine the one with minimal cost and add the tile distance between $v^\mathbf{x}$ and $w^\mathbf{y}$ (line 6). We have to make sure that all predecessors $(r^\mathbf{x},s^\mathbf{y})$ have been evaluated earlier, which is easily achieved by sorting the tiles by their start-point in time (line 1). A predecessor of a tile must end before the new tile starts, so if we deal with a tile starting at t all possible predecessors must have started at $t'<t$ and were processed earlier. Finally, the matching of both series is complete if we reach the end of both series, so we find the minimal cost at pairs $(v^\mathbf{x},w^\mathbf{y})\in V_E^\mathbf{x}\times V_E^\mathbf{y}$ (line 9). The complexity of the algorithm is $O(n\cdot m)$, n and m being the number of tiles in the resp. graph (rather than number of points as in DTW). Only a fraction of the $n\cdot m$ tile combinations will be considered (cf. hatched elements of Fig. 6). The tile distances need not be stored in D but may be calculated when needed as they are calculated in O(1) thanks to the lookup-table of Sect. 4.2. We use the distance of Sect. 4.4, but the algorithm in Fig. 7 does not depend on a particular tile distance. To deal with series that start with different orientations ($\mathbf{x}$ starts only with increasing and $\mathbf{y}$ only with decreasing segments) we include virtual tiles of opposite orientation in $V_S$ and $V_E$, which are considered as being of constant value y for distance calculations (where $y=y_1$ for virtual tiles in $V_S$ and $y=y_n$ in $V_E$).

Fig. 7.

Dynamic programming solution.

Fig. 8.

Frequency of used shapes (as shown in Fig. 5) in the Adiac and Plane dataset.

Fig. 9.

Correlation of distances: (1) raw vs BS distances, (2) raw vs BSN distances (cf. text).

5 Evaluation

5.1 Sensitivity of Discretized Bezier Segments

The Bezier curves have been selected to keep the representation simple (polynomial of degree 3) but still flexible enough to adapt to the data. To increase efficiency, we consider only a discretized subset of all possible Bezier segments (cf. Fig. 5). Is this setting sensitive enough to capture differences in time series? The matrices of Fig. 8 show for each of the (discretized) segment types how often they occur in a specific dataset (Adiac and Plane [3]) at a resolution of 0.05. We can recognize that the frequency of segment types varies significantly in these datasets and the IToBS can thus capture differences between sets of time series.

5.2 Approximation of Euclidean Distance

Next we consider the approximation quality by the Bezier segments. We have calculated distances for valid pairs of tiles using (a) the Euclidean distance on the original time series segments without any approximation [raw], (b) the Euclidean distance using the approximated Bezier segments and the lookup table [BS] and (c) the Euclidean distance from a lookup-table including the standard deviation (as in Eq. (4)) [BSN]. Figure 9 shows how these distances typically correlate for some UCR datasets (cor. of (a) vs (b) in column 1, (a) vs (c) in column 2). The results show the (expected) loss in approximation quality when switching from the Euclidean distance on the raw data to the approximation by Bezier segments as the approximation eliminates details (column 1). But when including the approximation error in the tile distance the correlation coefficients increase and may get very close to 1 (column 2).

5.3 Utility of Elastic Measure Based on IToBS

We demonstrate the utility of the IToBS/elastic measure in the standard 1-NN time series classification setting. We have performed cross-validated (CV) experiments with datasets from the UCR repository [3]. Figure 11 shows how the proposed approach (IToBS-D) compares against DTW [2] on two datasets. To eliminate the effect of the sample size in k-fold CV (one fold is used as training data, $k-1$ folds for testing), experiments were run over a full range of values for k. Both figures are examples where IToBS-D performs better than DTW for all k. Figure 10 shows the Texas Sharp Shooter plot [1] to demonstrate that the performance gain¹ over DTW obtained on the training set (x-axis) correlates with the gain for the test set (y-axis). Non-artificial UCR-datasets below 2 MB size were included in this figure. The number of folds was chosen such that the training set contained 5 examples from each class. For many cases near the center both measures perform comparable, but the top right quadrant (IToBS-D is better) contains more cases than the bottom left quadrant (DTW is better). The best performance is obtained for datasets where series from different classes have structural differences. If series are extremely similar across different classes, as it is the case with a few spectrogram datasets, very tiny differences must be exploited to distinguish the classes. These tiny differences may get lost in the Bezier approximation.

Compression was not our interest in the first place. Using a simple serialization, series with little noise use between $\frac{1}{3}$ and $\frac{1}{2}$ of the original disk space. As long as we store all tiny nodes of the IToBS, noisy series may use more than twice as much disk space. Future work includes pruning of the IToBS.

Fig. 10.

Texas Sharp Shooter plot for the proposed elastic measure versus DTW.

Fig. 11.

X-validated 1NN performance

6 Conclusions

Guided by the interpretability of time series similarity, we have employed the extrema of time series, nicely summarized in an Interval Tree of Scale, to guide the elastic matching of time series. We have thereby restricted the full flexibility of dynamic time warping to meaningful, interpretable warping paths. Regarding the value range, we allow for the same linear scaling of time series values as in the temporal domain. Different warping paths are motivated from the multiscale structure of the series itself. To support such operations efficiently, we approximate segments of the series (tiles of the interval tree) by monotone Bezier segments, for which a look-up table of distances has been demonstrated to provide sufficient accuracy. A first tentative elastic measure, based on this representation, delivered very promising results compared to dynamic time warping. Future work includes pruning of the IToBS and the use of subtrees (or subsequences of tiles) as the basis for elastic shapelet- or bag of word approaches that directly connect to the visual perception.