Attributed Graph Clustering with Unimodal Normalized Cut

Abstract

Graph vertices are often associated with attributes. For example, in addition to their connection relations, people in friendship networks have personal attributes, such as interests, age, and residence. Such graphs (networks) are called attributed graphs. The detection of clusters in attributed graphs is of great practical relevance, e.g., targeting ads. Attributes and edges often provide complementary information. The effective use of both types of information promises meaningful results. In this work, we propose a method called UNCut (for Unimodal Normalized Cut) to detect cohesive clusters in attributed graphs. A cohesive cluster is a subgraph that has densely connected edges and has as many homogeneous (unimodal) attributes as possible. We adopt the normalized cut to assess the density of edges in a graph cluster. To evaluate the unimodality of attributes, we propose a measure called unimodality compactness which exploits Hartigans’ dip test. Our method UNCut integrates the normalized cut and unimodality compactness in one framework such that the detected clusters have low normalized cut and unimodality compactness values. Extensive experiments on various synthetic and real-world data verify the effectiveness and efficiency of our method UNCut compared with state-of-the-art approaches. Code and data related to this chapter are available at: https://www.dropbox.com/sh/xz2ndx65jai6num/AAC9RJ5PqQoYoxreItW83PrLa?dl=0.

1 Introduction

Real-world graphs (networks) tend to have attributes associated with vertices. For example, in social networks such as Facebook, Google+ and Twitter, users have their personal information, e.g., interests, ages, living places, and etc., in addition to their friendship relationships. Proteins in a protein-protein internation network may be associated with gene expressions in addition to their interaction relations. Such graphs are referred to as attributed graphs in which vertices represent entities, edges represent their relations and attributes describe their own characteristics. Often the attributes and edges provide complementary information [11]. Neither can we infer vertex relationships from their attributes nor vice versa. Nevertheless, both types of information can be valuable for the detection of clusters in attributed graphs. Traditional methods for attributed graph clustering consider all attributes to compute the similarity. However, some attributes may be irrelevant to the edge structure and thus clusters only exist in the subsets (subspaces) of attributes. Currently, several methods have been proposed to detect subspace clusters in attributed graphs, such as CoPaM [11] and SSCG [3]. CoPaM uses various pruning strategies to find maximal cohesive patterns in the subspaces of attributes. One major problem with CoPaM is that it outputs a large number of clusters which have few vertices or attributes and which overwhelm data analysts. As for SSCG, it needs to eigen-decompose the graph Laplacian matrix and to update the subspace dependent weight matrix in every iteration, which is not scalable for large-scale graphs. How to effectively find clusters in attributed graphs remains a big challenge.

Fig. 1.

An example social network. (Color figure online)

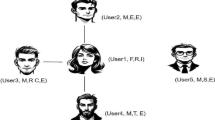
In this work, we develop an effective and efficient method to find cohesive clusters in attributed graphs. A cohesive cluster is a subgraph that has densely connected edges and has as many homogeneous (unimodal) attributes as possible. Why do we prefer to find cohesive clusters? One proper answer is that the more cohesive a graph cluster is, the more information it can reveal. For example, in social networks, if social networking advertisers know more characteristics of the people, they can do targeting ads more precisely. Figure 1 demonstrates an example social network with three attributes (age, sport time per week, and studying time per week) associated to each vertex. The task is to divide the network into two distinct parts which have as many homogenerous (unimodal) attributes as possible. In this example social network, we have two candidate partitions, i.e., by the orange dashed line and by the blue dashed line. The orange dashed line divides the network into two cohesive clusters $\mathcal {C}_1=\{0,1,2,3,4,5,6\}$ that is cohesive on the attribute studying time and $\mathcal {C}_2=\{7,8,9\}$ that is cohesive on all the attributes. The blue dashed line divides the network into another two cohesive clusters $\mathcal {C}_3=\{0,1,2,3,4\}$ which is cohesive on all the attributes and $\mathcal {C}_4=\{5,6,7,8,9\}$ which is cohesive on the attributes age and sport time. Compared with clusters $\mathcal {C}_1$ and $\mathcal {C}_2$, clusters $\mathcal {C}_3$ and $\mathcal {C}_4$ are more cohesive. Although the normalized cut value increases a little bit from 0.536 to 0.559, the unimodality compactness (see Sect. 3) value of attributes dramatically decreases from 3.289 to 1.230. The unimodal normalized cut (see Sect. 3) value of the partition by the blue dashed line is 0.895 and that of the partition by the orange dashed line is 1.913. Thus, we prefer clusters $\mathcal {C}_3$ and $\mathcal {C}_4$ to clusters $\mathcal {C}_1$ and $\mathcal {C}_2$.

Our contributions can be summarized as follows,

• We introduce the univariate statistic hypothesis test called Hartigans’ dip test [4] to the problem of attributed graph clustering.

• We achieve the cohesive cluster detection by developing an objective function which integrates the proposed measure unimodality compactness with the normalized cut. The unimodality compactness takes advantage of Hartigans’ dip test to measure the degree of the unimodality of attributes in a graph cluster.

• We show the effectiveness and efficiency of our method UNCut by conducting extensive experiments on synthetic and real-world graphs.

The paper is organized as follows: We continue in Sect. 2 with a review of preliminaries. Section 3 covers the core ideas and theory behind our approach UNCut, including the unimodality compactness and algorithmic details. Using synthetic and real-world data, Sect. 4 compares UNCut to related techniques. Section 5 discusses the related work and Sect. 6 gives concluding remarks.

2 Preliminaries

2.1 Notation

In this work, we use lower-case Roman letters (e.g. a, b) to denote scalars. We denote vectors (column) by boldface lower case letters (e.g. $\mathbf {x}$). Matrices are denoted by boldface upper case letters (e.g. $\mathbf {{X}}$). We denote entries in a matrix by non-bold lower case letters, such as $x_{i j}$. Row i of matrix $\mathbf {{X}}$ is denoted by the vector $\mathbf {x}_{i \cdot }$, column j by the vector $\mathbf {x}_{\cdot j}$. A set is denoted by calligraphic capital letters (e.g. $\mathcal {S}$). An undirected attributed graph is denoted by $\mathsf {G}=(\mathcal {V},\mathcal {E}, \mathbf {{F}})$, where $\mathcal {V}$ is a set of graph vertices with number $n=|\mathcal {V}|$ of vertices, $\mathcal {E}$ is a set of graph edges with number $m=|\mathcal {E}|$ of edges and $\mathbf {{F}}\in \mathbb {R}^{n \times d}$ is a data matrix of attributes associated to vertices, where d is the number of attributes. An adjacency matrix of vertices is denoted by $\mathbf {A}\in \mathbb {R}^{n\times n}$ with $a_{i j}=1$ if the vertices $v_i$ and $v_j$ are connected, and $a_{i j}=0$ otherwise. The degree matrix $\mathbf {D}$ is a diagonal matrix associated with $\mathbf {A}$ with $d_{i i}=\sum _j a_{i j}$. The random walk transition matrix $\mathbf {W}$ is defined as $\mathbf {D}^{-1}\mathbf {A}$. The Laplacian matrix is denoted as $\mathbf {L}=\mathbf {I}-\mathbf {W}$, where $\mathbf {I}$ is an identity matrix. A graph cluster is a subset of vertices $\mathcal {S}\in \mathcal {V}$. The indicator function is denoted by $\mathbb {1}(x)$.

2.2 Normalized Cut

The definition of the widely used normalized cut [16] objective function is:

$$\begin{aligned} \text {NCut}(\mathcal {S})=\frac{\text {cut}(\mathcal {S},\overline{\mathcal {S}})}{\text {vol}(\mathcal {S})}. \end{aligned}$$

(1)

where $\text {cut}(\mathcal {S},\overline{\mathcal {S}})=\sum _{v_i\in \mathcal {S},v_j\in \overline{\mathcal {S}}}a_{i j}$ and $\text {vol}(\mathcal {S})=\sum _{v_i\in \mathcal {S},v_j\in \mathcal {V}}a_{i j}$.

Equation 1 can be equivalently rewritten as (for a more detailed explanation, please refer to [18]):

$$\begin{aligned} \text {NCut}(\mathcal {S})=\mathbf {u}^\intercal \mathbf {L}\mathbf {u}, s.t. \; \mathbf {u}^\intercal \mathbf {D}\mathbf {u}=\text {vol}(\mathsf {G}), \; \mathbf {D}\mathbf {u}\perp \mathbf 1 . \end{aligned}$$

(2)

where $\mathbf {u}$ is the cluster indicator vector and $\mathbf {u}^\intercal \mathbf {L}\mathbf {u}$ is the cost of the cut and $\mathbf 1$ is a constant vector whose entries are all 1. Note that finding the optimal solution is known to be NP-hard [19] when the values of $\mathbf {u}$ are constrained to $\{1,-1\}$. But if we relax the objective function to allow it take values in $\mathbb {R}$, a near optimal partition of the graph $\mathsf {G}$ can be derived from the second smallest eigenvector of $\mathbf {L}$. More generally, k eigenvectors with the k smallest eigenvalues partition the graph into k subgraphs with near optimal normalized cut value.

2.3 The Dip Test

In this paper, we apply a univariate statistic hypothesis test for unimodality called Hartigans’ dip test [4] on the vertex attributes to measure the degree of the unimodality of a graph cluster. The dip test has been successfully used in detecting clusters in a sea of noise [10]. The dip measures the departure of a distribution from unimodality. Before introducing the concept of the dip test, let us first introduce the concepts of the greatest convex minorant (g.c.m) and the least concave majorant (l.c.m.). The g.c.m of F(x) in $(-\infty ,x_l]$ is sup G(x) for $x\le x_l$, where the sup is taken over all functions G that are convex in $(-\infty ,x_l]$ and nowhere greater than F(x). The l.c.m. of F(x) in $[x_u, \infty )$ is inf L(x) for $x\ge x_u$, where the inf is taken over all functions L that are concave in $[x_u, \infty )$ and nowhere less than F(x). Let $\mathcal {U}$ be the set of all unimodal distributions, the dip test of the distribution function F(x) is computed as follows,

$$\begin{aligned} D(F)=\inf _{H\in \mathcal {U}}\sup _x|F(x)-H(x)| \end{aligned}$$

(3)

The dip test is the infimum among the supremum computed between the cumulative distribution function (CDF) of F and the CDF of H from the set of unimodal distributions. The computation of the dip test is: Let F(x) be an empirical distribution function for the sorted samples $x_1,\dots ,x_n$. There are $n\cdot (n-1)/2$ candidate modal intervals. Compute for each candidate $[x_i, x_j], i\le j\le n$ the g.c.m. of F(x) in $(-\infty ,x_i]$ and the l.c.m. of F(x) in $[x_j, \infty )$ and let $d_{ij}$ be the maximum distance of F to these computed curves (g.c.m. and l.c.m.). Finally, it selects the modal interval with the maximum distance which is the twice of the dip test. For more details, please refer to [4, 6].

As pointed out in [4], the class of uniform distributions U is the most suitable for the null hypothesis, because their dip test values are stochastically larger than those of other unimodal distributions. The p-value for the unimodality test is then computed by comparing D(F) with $D(U^r)$ b times, each time with a different n observations from U, and the proportion $\sum _{1\le r\le b}\mathbb {1}(D(F)\le D(U^r))/b$ is the p-value. If the p-value is greater than a significance level $\alpha$, say 0.05, the null hypothesis that F is unimodal is accepted.

3 Unimodal Normalized Cut

Our objective is to detect cohesive graph clusters which have densely connected edges (low normalized cut value) and have as many homogeneous (unimodal) attributes as possible (low unimodality compactness value). To achieve the goal, we need to take both the edge structure and attribute information into account. If we eigen-decompose the Laplacian matrix associated with the edge structure to generate n eigenvectors, the k eigenvectors associated with the k smallest eigenvalues near optimally partition the graph into k subgraphs. However, the procedure does not consider the attribute information. Since each eigenvector bisects the graph into two clusters, our idea is to develop a measure to simultaneously evaluate the density of the edge structure and the homogeneity of vertex attributes of a graph cluster derived from the eigenvector. To this end, we first propose a measure called unimodality compactness to assess the homogeneity of attributes of a graph cluster. Then we integrate it with the normalized cut and call the combination unimodal normalized cut. We select k eigenvectors associated with the k smallest unimodal normalized cut values to partition the graph. In the following, we describe our idea in detail. But first let us give the definitions as follows,

Definition 1

A unimodal graph cluster is defined as a set of vertices with at least one attribute following unimodal distributions.

To compute the degree of the unimodality of a graph cluster, we devise a measure called unimodality compactness using the dip test on each attribute of the cluster.

Definition 2

Given a cluster of vertices $\mathcal {S}$ with number $c>0$ of unimodal attributes, the unimodality compactness is defined as,

$$\begin{aligned} \text {UC}(\mathcal {S})=\log _2\frac{d}{c}+\frac{1}{c}\sum _{i=1}^cD(F_i) . \end{aligned}$$

(4)

where d is the number of attributes, $F_i$ is the empirical distribution function of the i-th unimodal attribute of $\mathcal {S}$ and $D(F_i)$ is the dip test of $F_i$.

The first summand measures the number of unimodal attributes of a cluster. The second summand measures the average dip test of these unimodal attributes. This measure prefers the cluster that has more unimodal attributes with lower average dip test. Note that the multimodal (irrelevant) attributes are not considered in the computation. If a graph cluster only has one unimodal attribute, its unimodality compactness is close to $\log _2d$ because the second summand in Eq. 4 is very low. If there is no unimodal attribute in a cluster, we simply set its unimodality compactness to $2\log _2d$. When d is large and $c=1$, the value of $\frac{d}{c}$ is also large. To reduce the effect of $\frac{d}{c}$, we introduce $\log _2$ in the definition. We do not use the sigmoid function $S(x)=\frac{1}{1+\exp (-x)}$ here because its resolution is not good, for example $S(\frac{8}{1})=0.9997$ and $S(\frac{8}{2})=0.9820$. Also note that a graph cluster will be more cohesive if it has more unimodal attributes.

A cohesive graph cluster is defined as follows,

Definition 3

A cohesive graph cluster is a subgraph that has densely connected edges and has as many homogeneous (unimodal) attributes as possible. The density of edges is measured by the normalized cut, and the homogeneity of attributes is measured by the unimodality compactness.

To detect cohesive graph clusters, our objective function integrates the normalized cut and unimodality compactness in one framework which is given as follows,

$$\begin{aligned} \text {UNCut}(\mathcal {S})=(1-\omega )\cdot \text {NCut}(\mathcal {S})+\omega \cdot \text {UC}(\mathcal {S}) . \end{aligned}$$

(5)

where $\omega (0\le \omega \le 1)$ is a weight parameter to adjust the importance between the unimodality compactness value and the normalized cut value of a graph cluster.

As said above, we can first eigen-decompose $\mathbf {L}$ to get some eigenvectors. Then, for each eigenvector, we apply 2-means (k-means with the input number of clusters two) to bisect the graph into two clusters and compute our objective function (Eq. 5). Finally, we select the k eigenvectors associated with the k smallest unimodal normalized cut values. However, the time complexity to eigen-decompose $\mathbf {L}$ is $\mathcal {O}(n^3)$ which is impractical for large-scale attributed graphs. Instead, in this work, we use the power iteration method [8] to compute a number, say $10\cdot k$, of pseudo-eigenvectors (approximate eigenvectors) and then choose k pseudo-eigenvectors associated with the k smallest unimodal normalized cut values.

The power iteration is a fast method to compute the dominant eigenvector of a matrix. Note that the k largest eigenvectors of $\mathbf {W}$ are also the k smallest eigenvectors of $\mathbf {L}$. The power iteration method starts with a randomly generated vector $\mathbf {v}^0$ and iteratively updates as follows,

$$\begin{aligned} \mathbf {v}^t=\frac{\mathbf {W}\mathbf {v}^{t-1}}{||\mathbf {W}\mathbf {v}^{t-1} ||_1} . \end{aligned}$$

(6)

Suppose $\mathbf {W}$ has eigenvectors $\mathbf {U}=[\mathbf {u}_1;\mathbf {u}_2;\cdots ;\mathbf {u}_n]$ with eigenvalues $\mathbf {\Lambda }=[\lambda _1,\lambda _2,\cdots ,\lambda _n]$, where $\lambda _1=1$ and $\mathbf {u}_1$ is constant. We have $\mathbf {W}\mathbf {U}=\mathbf {\Lambda }\mathbf {U}$ and in general $\mathbf {W}^t\mathbf {U}=\mathbf {\Lambda }^t\mathbf {U}$. When ignoring renormalization, Eq. (6) can be written as

$$\begin{aligned} \begin{aligned} \mathbf {v}^t&=\mathbf {W}\mathbf {v}^{t-1}=\mathbf {W}^2\mathbf {v}^{t-2}=\cdots =\mathbf {W}^t\mathbf {v}^0 \\&=\mathbf {W}^t\left( c_1\mathbf {u}_1+c_2\mathbf {u}_2+\cdots +c_n\mathbf {u}_n\right) \\&=c_1\mathbf {W}^t\mathbf {u}_1+c_2\mathbf {W}^t\mathbf {u}_2+\cdots +c_n\mathbf {W}^t\mathbf {u}_n \\&=c_1\lambda _1^t\mathbf {u}_1+c_2\lambda _2^t\mathbf {u}_2+\cdots +c_n\lambda _n^t\mathbf {u}_n . \end{aligned} \end{aligned}$$

(7)

where $\mathbf {v}^0$ can be denoted by $c_1\mathbf {u}_1+c_2\mathbf {u}_2+\cdots +c_n\mathbf {u}_n$ which is a linear combination of all the original eigenvectors. By generating different starting vectors, we can get diverse linear combinations. If we let the power iteration method run enough time, it will converge to the dominant eigenvector $\mathbf {u}_1$ which is of little use in clustering. We define the velocity at t to be the vector $\varvec{\delta }^t=\mathbf {v}^t-\mathbf {v}^{t-1}$ and define the acceleration at t to be the vector $\varvec{\epsilon }^t=\varvec{\delta }^t-\varvec{\delta }^{t-1}$ and stop the power iteration when $||\varvec{\epsilon }^t||_{max}$ is below a threshold $\hat{\epsilon }$.

Algorithm 1 gives the pseudo-code to find k clusters with the smallest k unimodal normalized cut values.

Complexity analysis. Lines 5–10 in Algorithm 1 use the power iteration method to compute one pseudo-eigenvector, whose time complexity is $\mathcal {O}(m)$ [9], where m is the number of graph edges. Line 11 uses 2-means on each pseudo-eigenvector, whose time complexity is $\mathcal {O}(n)$. At line 12, we compute the unimodal normalized cut which is dominated by the complexity of computing the unimodality compactness of clusters. We first need to sort each attribute before computing the dip test, which costs $\mathcal {O}\left( n\cdot \log (n)\right)$. The computation of dip test on each attribute costs $\mathcal {O}(n)$ [4]. Thus, the time complexity of lines 4–12 is $\mathcal {O}\left( \left( m+n\cdot \log (n) \cdot d\right) \cdot k \right)$. Line 13 uses k-means on the selected k pseudo-eigenvector, whose time complexity is $\mathcal {O}(n\cdot k^2)$. The total time complexity of Algorithm 1 is $\mathcal {O}\left( m\cdot k+n\cdot \log (n)\cdot d\cdot k+n\cdot k^2\right)$, which is superlinear in the number of vertices n, linear in the numbers of edges m and attributes d, and quadratic in the number of clusters k.

4 Experimental Evaluation

In this section, we compare our method UNCut with state-of-the-art methods from the attributed graph clustering field. As pointed out in [3], the comparison with the overlapping clustering approaches [2, 11] would always be biased to one of the paradigms due to their completely different objective from those of paititioning clustering approaches. Thus, following [3] we compare UNCut with the partitioning clustering methods SA-cluster [21], SSCG [3] and NNM [17]. We use the synthetic and real-world data to evaluate the clustering performance. All the experiments are run on the same machine with an Intel Core Quad i7-3770 with 3.4 GHz and 32 GB RAM. We set $\omega =0.5$ for our method UNCut on all the synthetic and real-world data. The parameters for the competitors are set according to their original papers. For every method, we use the same number of cluster on each dataset. For the evaluation of clustering on synthetic data, we use the Normalized Mutual Information (NMI) and Adjusted Rand Index (ARI) [5] as clustering quality measures. The higher these clustering measures are, the better the clustering is. Because we do not have the ground truth for the real-world data, we use the normalized cut and our unimodality compactness to evaluate the clustering performance and interprete the results. The code and all the synthetic and real-world data are publicly available at the website¹.

4.1 Synthetic Data

Cluster Quality. We generate synthetic graphs with varying number of vertices n and attributes d. For the case of varying n, we fix the attribute dimension $d=20$. For the case of varying d, we fix the number of vertices $n=2000$. All the graphs are generated based on a benchmark graph generator [7], which makes the degree and cluster size follow power law distributions that reflect the real properties of vertices and clusters found in real networks. To add vertex attributes, for each graph cluster, we choose 20% attributes as relevant attributes and generate their values according to a Gaussian distribution with mean value of each attribute randomly sampled from the range $\left[ 0,100\right]$ and variance value of each attribute randomly sampled from the range $\left( 0, 0.1\right)$. To render the other attributes of clusters irrelevant to the edge structure, we randomly permute the cluster labels and generate each cluster’s irrelevant attribute values according to a Gaussian distribution with mean 0 and variance 1. For each experiment, we test all the methods on the generated ten attributed graphs differing in the edge structure and attribute values and report the average performance of each method.

Figures 2(a) and 3(a) show the performance of all the methods when varying the number of attributes, where we can see that UNCut is superior to its competitors. Compared with SA-cluster and NNM, both UNCut and SSCG exceed them with large margins. UNCut and SSCG are subspace clustering methods, while SA-cluster and NNM are full-space clustering methods which are easily deceived by “the curse of dimensionality”. Figures 2(b) and 3(b) present the performance of all the methods when varying the number of graph vertices. SSCG has a comparable performance when the number of vertices is 1000. However, our method UNCut beats SSCG when increasing the vertex number. Note that subspace clustering methods UNCut and SSCG are still better than the full-space clustering methods SA-cluster and NNM.

Fig. 2.

Quality evaluation (NMI).

Fig. 3.

Quality evaluation (ARI).

Scalability. We still use the above attributed graph generation method to generate synthetic graphs for the evaluation of the runtime of each method. Figure 4(a) shows the runtime when varying the number of attributes (the number of vertices is fixed to 2000). We can see that NNM is the fastest method and SSCG is the slowest method. SSCG needs to update its subspace dependent weight matrix in every iteration, which is very time consuming. Figure 4(b) demonstrates the runtime when varying the number of vertices (the number of attributes is fixed to 20). NNM still performs the best and SSCG performs the worst. Our method UNCut is the second. Because UNCut is linear in the number of edges, a drop in the runtime when increasing the number of vertices from 4000 to 6000 can be interpreted as caused by the drop in the number of edges.

Fig. 4.

Runtime evaluation.

Stability. In this section, we study how the parameter $\omega$ affects the clustering performance. Figure 5(a) gives the clustering performance of UNCut on the synthetic graph with 100 attributes and 2000 vertices when varying $\omega$. And Fig. 5(b) gives the clustering performance of UNCut on the synthetic graph with 20 attributes and 1000 vertices when varying $\omega$. From Fig. 5(a), we can see that UNCut achieves the best result when the value of $\omega$ is 0.5. From Fig. 5(b), we can see that UNCut achieves the best result when the value of $\omega$ is 0.1. For different graphs with different edge structure and attribute values, the values of the best $\omega$ are different.

Fig. 5.

Varying the parameter $\omega$.

4.2 Real-World Data

In this section, we evaluate UNCut and its competitors on six real-world datasets Disney [12], DFB [3], ARXIV [3], PolBlogs [13], 4area [13] and Patents [3]. The statistics of the real-world data are given in Table 1. The normalized cut and unimodality compactness values achieved by each algorithm are listed in Table 2.

We can see from Table 2 that our method UNCut achieves the best results on the datasets Disney, DFB and ARXIV in terms of both the normalized cut and unimodality compactness values. On the dataset PolBlogs, SSCG achieves the best normalized cut value. However, the unimodality compactness value achieved by UNCut is much lower than those of its competitors. On the dataset 4area, SA-cluster achieves the best results. Although SSCG is a method detecting subspace clusters, it is defeated by SA-cluster on the datasets Disney, ARXIV and 4area in terms of the unimodality compactness values. For the dataset Patents, all the competitors fail due to their much consumption of the memory. Our method UNCut is scalable for large-scale networks. To examine whether UNCut can achieve differing results to those of its competitors, as did in [3], we compute NMI between the results of UNCut and its competitors. A low NMI value indicates that UNCut is able to detect novel cluster insights, without implying that the results of the competitors are worse or meaningless. The NMI values are given in Table 3. From Table 3, we can see that UNCut can find novel cluster insights different from the competitors, especially on the 4area dataset. The NMI values between the results of UNCut and its competitors are near 0, which means totally different insights. For case studies, we interprete the detected clusters of all the methods on the datasets Disney and PolBlogs. The results are plotted in Figs. 6 and 7 by the Python toolbox Networkx.

Table 1. Statistics of datasets.

Table 2. Normalized cut and unimodality compactness values. (N/A means the results are not available due to the runout of memory.)

Table 3. NMI between the results of UNCut and its competitors. (N/A means the results are not available due to the runout of memory.)

Fig. 6.

Clustering results on Disney. (Color figure online)

Fig. 7.

Clustering results on PolBlogs. (Color figure online)

Disney. Disney is a subgraph of the Amazon copurchase network. Each movie (vertex) is described by 28 attributes, such as “average vote”, “product group”, “price” and etc. The green cluster has 14 movies, which is rated as PG (Parental Guidance Suggested) and attributed as “Action & Adventure”. It contains movies such as “Spy Kids”, “Inspector Gadget” and “Mighty Joe Young”. The purple cluster includes 9 read-along movies, which is rated as G (General Audience) and attributed as “Kids & Family”. It has movies such as “Beauty and the Beast”, “Lilo and Stitch”, “Toy Story 2”, “The Little Mermaid”, and “Monsters, Inc.”. The purple cluster has three multimodal attributes “review frequency”, “rating of review with most votes”, and “rating of most helpful rating”. In other words, the movies in the purple cluster are similar in the subspace spanned by the other attributes. The clusters found by our method UNCut are subspace clusters which are cohesive on as many attributes as possible. SSCG splits our purple cluster into two clusters and our green clusters into two clusters. SA-cluster splits our green cluster into two clusters. NNM groups the most of the movies together (yellow cluster), which leads to the highest unimodality compactness value as shown in Table 2.

PolBlogs. PolBlogs is the citation network among a collection of online blogs that discuss political issues. Attributes are the keywords in their text. If a keyword appears in the text, the attribute value is set to 1, otherwise 0. Thus, each attribute only has binary values. The red cluster contains 70 blogs. The top five frequent keywords of the red cluster are “London”, “Iraq”, “government”, “work”, and “American”. The orange cluster contains 23 blogs. The top six frequent keywords of the orange cluster are “act”, “bush”, “conservative”, “court”, “justice”, and “law”. The blue cluster includes 53 blogs. The top eight frequent keywords of the blue cluster are “people”, “post”, “right”, “political”, “issue”, “media”, “president”, and “public”. For SSCG and SA-cluster, the sizes of the two main clusters are very big, i.e., the red and green clusters found by SSCG totally have 312 vertices and the blue and green clusters found by SA-cluster totally have 335 vertices. For NNM, the most of the blogs belong to the green cluster which has 306 vertices. Thus, the sizes of the most clusters detected by the competitors are small, which leads to the high probability of having multimodal attributes as proved by the much higher unimodality compactness values in Table 2.

5 Related Work and Discussion

Compared with massive works on the plain graph clustering, there are relatively less work on the attributed graph clustering. Differing from the plain graph clustering that groups vertices only considering the edge structure, the attributed graph clustering achieves grouping vertices with dense edge connectivity and homogeneous attribute values into clusters. NNM [17] first develops a measure called normalized network modularity and then proposes a spectral method that combines the costs of clustering numerical vectors and normalized network modularity into an eigen-decomposition problem. BAGC (Bayesian Attributed Graph Clustering) [20] develops a Bayesian probabilistic model for attributed graphs, which captures both structure and attribute aspects of a graph. Clustering is accomplished by an efficient variational inference method. BAGC is only capable of categorical attributes. PICS [1] groups vertices into disjoint clusters satisfying that vertices in the same cluster exhibit similar connectivity and feature coherence. It exploits the Minimum Description Length (MDL) principle to automatically select the parameters such as the cluster number. PICS is only capable of graphs with binary feature vectors. SA-cluster [21] designs a unified neighborhood random walk distance to measure the vertex similarity on an augmented graph. It uses k-medoids to partition the graph into clusters with cohesive intra-cluster structures and homogeneous attribute values.

However, the above methods which take all attributes into consideration may fail because there may be attributes irrelevant to the edge structure. Now more researches focus on detecting subspace clusters to which only subsets of attributes are assigned. CoPaM [11] exploits various pruning strategies to efficiently find maximal cohesive patterns in the subspace of feature vectors. GAMer [2] determines sets of vertices which have high similarity in the subsets of attributes and are densely connected as well by combining the paradigms of subspace clustering and dense subgraph mining together. The twofold clusters are optimized by exploiting various pruning strategies considering the density, size and number of relevant attributes. CoPaM and GAMer exploit the notion of quasi-cliques which poses strong restrictions on the feature range and diameter of the clusters. CoPaM generates a huge number of redundant overlapping clusters. To reduce the redundancy, GAMer introduces additional parameters which are difficult to set for the real-world data. Differing from CoPaM and GAMer, our partitioning method UNCut does not suffer from redundancy. SSCG [3] presents a solution for an objective function called Minimum Normalized Subspace Cut, which integrates spectral clustering to the problem of subspace clustering for attributed graphs. It detects an individual set of relevant features for each cluster. Our method UNCut only considers the relevant attributes to the edge structure, i.e., irrelevant attributes are excluded from the computation of the unimodality compactness. In other words, UNCut detects subspace clusters with as many unimodal attributes as possible.

Recently, a new research trend is to detect community outliers in attributed graphs. MAM (maximization of attribute-aware modularity) [14] develops attribute compactness to quantify the relevance of the attributes, which is then combined with the conventional modularity for the robust graph clustering with respect to irrelevant attributes and outliers. ConSub (congruent subspace selection) [15] defines a measure to assess the degree of congruence between a set of attributes and the edge structure, which is then used for the statistical selection of the congruent subspaces. FocusCO [13] defines a new graph clustering problem which incorporates the user’s preference into graph mining. Given a set of examplar nodes of user’s interest, FocusCO infers user’s preference by applying a distance metric learning method. New nodes are carefully added to the set of examplar nodes by checking the weighted conductance. Differing from the conventional attributed graph clustering methods, FocusCO performs a local clustering of interest to the user rather than the global partitioning of the entire graph.

6 Conclusion

In this paper, we have proposed UNCut to detect cohesive clusters in attributed graphs. To this end, we develop a measure called unimodality compactness, which is then combined with the normalized cut to elegantly search for cohesive clusters. Since the complexity of the eigen-decomposition of the graph Laplacian matrix is high, we adopt the power iteration method to approximately compute the eigenvectors. We have tested our method UNCut on various synthetic and real-world data, which verifies that UNCut achieves better results than its competitors. Since in social networks people may belong to multiple groups, an interesting challenge for the future work is to develop a method to detect overlapping cohesive clusters in attributed graphs.