Keywords

1 Introduction

Connected components labeling (CCL) in the binary image is a fundamental step in many fields such as image segmentation [1], computer vision, graph coloring, object recognition, etc. As the development of image techniques, number of pixels in a natural image increases dramatically. Consequently, number of objects in an image is also increasing and fast CCL algorithms have drawn attention of many researchers. Existing CCL algorithms can be classified into three categories: pixel-based algorithms, block-based algorithms and run-based algorithms.

Early researches about CCL were mainly focused on iterative pixel-based algorithm [2]. In [3], Suzuki et al. introduced a labeling algorithm whose execution time is linear with the number of total pixels. In [4, 5], an implementation of pixel-based algorithm was designed for applications where FPGA was used. In [6] Rosenfeld and Pfaltz proposed a two-scan algorithm. To save the memory allocated to the equivalent-label table, Lumia Rosenfeld et al. proposed an algorithm which only needs to store the equivalent labels in the current and last rows [7]. Through the analysis of values of adjacent pixels, He et al. used the Karnaugh map to design an efficient procedure in assigning the provisional labels in the first scan [8]. Instead of checking values of four adjacent pixels in [8], algorithm in [9] only needs to check three. In [10] Chang et al. introduced a contour-tracing algorithm. The above algorithms are all characterized by checking values of adjacent pixels of the current pixel. They have advantages of saving storage and operation simplicity. However, these algorithms need to scan all the pixels one by one, which is inefficient. Moreover, many of them need to scan the whole image more than twice.

To cope with the low efficiency of pixel-based algorithms, in [11], a labeling algorithm scanning the whole image through the two-by-two blocks was introduced. A decision tree was built to determine the provisional label of the current block. Based on [11], algorithm in [12] uses the information of checked pixels to avoid the same pixels are checked for multiple times. Similarly, two-by-one block-scanning was also introduced in algorithm in [13]. Instead of checking all the 16 pixels in the adjacent blocks, in [14] Chang et al. designed an algorithm which only needs to check 4 pixels to determine the provisional label of the current block. In [15], Santiago et al. gave three labeling algorithms which all scan the whole image through the two-by-two blocks. Recently in [16], several state-of-the-art CCL algorithms were compared with each other on synthetic images and public datasets. Average results show that the BBDT [12], CCIT [14], and CTB [13] are the fastest three algorithms. Nevertheless, the weakness of these algorithms is that they are complex to implement and hard to be executed in parallel.

In addition to the two types of labeling algorithms mentioned above, there is another type which is efficient while simple to implement. They are based on the run. As defined in [17], a run is a segment of contiguous foreground pixels in a row. In [17], He et al. introduced a run-based two-scan labeling algorithm. However, the mergences of the equivalent-label sets in this algorithm are time-consuming. Besides, it needs to find the smallest label in each merged set, which is inefficient. Similar to [17], a run-based one-scan algorithm was proposed in [18], which essentially needs to scan the whole image twice. In [19], He et al. introduced a one and a half scan algorithm which only checks the foreground pixels in the second scan.

It should be noted that all the run-based algorithms above scan only one row of pixels at each time and they all need to dynamically adjust the equivalent-label sets. These weaknesses lead to a reduction of time efficiency. Therefore, to overcome these shortcomings, we introduce a new run-based algorithm which scans double rows of pixels at each time. Besides, the Dulmage-Mendelson (DM) decomposition is applied to search for the equivalent-label sets in linear time.

2 Proposed Algorithm

2.1 The First Scan

In the following discussions, component connectivity is defined in the sense of eight-adjacent regions in binary images. The proposed algorithm contains the first scan, equivalent-label sets searching and the second scan. Detail implementations are stated as follows.

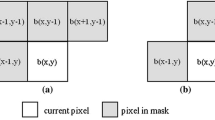
In the first scan, unlike the existing run-based algorithms, the run in our algorithm is defined in double rows, which consists of a succession of two-by-one pixel blocks. Each block contains one foreground pixel at least. For example, runs in the double rows in Fig. 1(a) as the red bold boxes show. Under the above definition, it is easy to see that all the foreground pixels in the same run are connected to each other. So, we give each run a single label. Then a record table is built to record the row numbers, start column numbers, end column numbers and provisional labels of all the runs, as shown in Fig. 1(b). For each run, we give it a provisional label according to its connectivity to runs in the last two rows. Through analysis we conclude that there are three cases when two runs are considered to be connected to each other, as shown in Fig. 2, from which we can see that if there is one pair of connected pixels between two runs, both runs are connected to each other. According to Fig. 2, we summarize the detail computation procedures of the provisional label in Table 1. In Table 1, \( \left\{ {s_{i} } \right\},\left\{ {e_{i} } \right\},i = 1,2, \cdots ,K \) are the start and end column number sets, where \( K \) is the number of runs in the last two rows. \( s \) and \( e \) are the start and end column numbers of the current run. \( L_{i} \) represents the \( i{\text{th}} \) run in the last two rows. \( L_{i} \left[ {1,j} \right] \) and \( L_{i} \left[ {2,j} \right] \) are the two pixels with column number \( j \) in \( L_{i} \). \( C\left[ {1,j} \right] \) and \( C\left[ {2,j} \right] \) are the two pixels with column number \( j \) in the current run. MAX and MIN are functions calculating the maximum and minimum numbers.

Fig. 1.
figure 1

Runs in double rows and the record table. (Color figure online)

Full size image
Fig. 2.
figure 2

Three cases of connected runs.

Full size image
Table 1. Pseudocode for computing the provisional label.
Full size table

In determining the provisional label of the current run, if multiple runs in the last two rows are connected to the current run, the provisional label of the current run will be the same as the first connected run. If there are no runs in the last two runs being connected to the current run, then a new label will be assigned to the current run. In Table 1 we also point out how to build the equivalent-label table. In the last two rows, if there are more than one runs being connected to the current run, the provisional labels of these runs are considered to be equivalent and stored in a two-column equivalent-label table. In each row of the equivalent-label table, the first member is the provisional label of the first connected run, and the second member is a provisional label of one of other connected runs. For an example, in Fig. 3(a) there are three connected runs with provisional labels \( l_{1} \), \( l_{2} \) and \( l_{3} \) respectively, so \( l_{1} \) will be given as the provisional label to the current run. \( l_{1} \), \( l_{2} \) and \( l_{3} \) are considered to be equivalent and two pairs \( \left( {l_{1} ,l_{2} } \right) \), \( \left( {l_{1} ,l_{3} } \right) \) are stored in the equivalent-label table as shown in Fig. 3(b).

Fig. 3.
figure 3

Building the equivalent-label table

Full size image

Compared with the conventional run-based algorithms, the proposed algorithm has two advantages. First, the number of runs to store is reduced, which reduces the subsequent processing time. This can be seen by Fig. 1(a), for which in conventional one-row scan algorithms it needs to store seven runs while in ours it only needs to store three. Second, as the example in the third run in Fig. 1(a) shows, the size of the equivalent-label table is reduced because different runs in one row are unified into a run due to the usage of double-row scan. Since the time spent on the subsequent steps is directly proportional to the sizes of record table and the equivalent-label table, the proposed algorithm is time efficient. The time complexity of the first scan in the proposed algorithm is \( O\left( {W^{2} H} \right) \), where \( W \) and \( H \) are the width and height of the input image.

The primary goal of the first scan is to build the record table and equivalent-label table. Since the order of labels in both tables has no effect on the subsequent steps, the first scan can be executed in parallel. A simple way is to divide the image into several parts and scan them simultaneously, and then combine all the record tables and equivalent-label tables respectively, to obtain the whole record table and equivalent-label table.

2.2 Equivalent-Label Sets Searching

After getting the equivalent-label table, the key step is to find out all the equivalent-label sets. In these sets, none of them contains the same label with other sets. Based on the provisional labels, an adjacent matrix can be built as Fig. 4(a) shows. The number of provisional labels in Fig. 4(a) is 9. If two labels are equivalent, then the element on the cross position is set to be 1, otherwise 0. The adjacent matrix is symmetric and generally sparse. It has been proved that a symmetric matrix can be decomposed into a block triangular form using the DM decomposition [20,21,22]. As Fig. 4(b) shows, vertices in the same block are connected to each other while disconnected with all the vertices in other blocks. Therefore, the equivalent-label sets can be obtained through the extraction of vertices from these triangular blocks.

Fig. 4.
figure 4

Procedures of equivalent-label sets searching. (a) Adjacent matrix. (b) Block triangular form. (c) Extraction of equivalent-label sets.

Full size image

An implementation of the DM decomposition using the bipartite graph was proposed in [23], while it was used for system reduction. Here, we design a new algorithm in Table 2 to search for the equivalent-label sets. Suppose the number of the provisional labels is \( M \), and \( T \) denotes the equivalent-label table. \( V \) represents the vertex set \( \{ 1,2, \cdots ,M\} \) and \( M^{\prime} \) is the number of rows in the equivalent-label table. Detail implementations are summarized in Table 2.

Table 2. Equivalent-label sets searching algorithm.
Full size table

Because the adjacent matrix is generally sparse, to save the memory space, only the 1 s in the adjacent matrix are stored. Execution time spent on the step1, step2 and step4 in Table 2 are all linear with \( M \). The time complexity of step3 is \( O\left( {M + M^{\prime}} \right) \) [24]. Since \( M^{\prime} \) is close to \( M \) when the adjacent matrix is sparse, the time complexity of the whole procedure of equivalent-label sets searching is about \( O\left( M \right) \).

2.3 The Second Scan

In the second scan, a number from 1 is assigned to each equivalent-label set. For example, in Fig. 4(c) three numbers 1, 2, and 3, are given to the equivalent-label sets respectively. Here, we use an array \( R \) as a lookup table to relate the provisional labels to the numbers. For each provisional label we have

$$ R\left[ i \right] = the\;number\;for\;the\;equivalent - label\;set\;which\;contains\;i\,. $$

Then all the foreground pixels in the \( i{\text{th}} \) run are labeled with \( R\left[ i \right] \).

As shown in Fig. 1, all the runs are independent with each other. So, the labeling procedure in the second scan can be executed in parallel. The time complexity of the second scan is \( O\left( S \right) \), where \( S \) is the number of foreground pixels.

3 Experimental Results

In the following experiments, all the algorithms are accomplished by C++ on a PC with 8 Intel Core i7-6700 CPUs, 3.4 GHz, 8 GB RAM, and a single core is used for the processing. We compare our algorithm with four state-of-the-art algorithms BBDT [12], CCIT [14], CTB [13], and RBTS [17], among which the first three algorithms are block-based and the last one is run-based with single-row scan. First, we compare the efficiency of five algorithms on 19 \( 4096 \times 4096 \) synthetic images with different densities of foreground pixels. The densities range from 0.05 to 0.95. The number of connected components in each image is fixed to 900. The result in Fig. 5(a) shows that our algorithm outperforms the other algorithms when the density is lower than about 0.8. We also tested 19 \( 2048 \times 2048 \) synthetic images with different densities of foreground pixels and the result was similar.

Fig. 5.
figure 5

Algorithm performance on synthetic images. (a) Execution time per image on images with different densities of foreground pixels. (b) Execution time per image on images with different number of connected components.

Full size image

To study the relationship between the time efficiency of the five algorithms and the number of connected components, 22 \( 4096 \times 4096 \) synthetic images with different number of connected components are tested. Here, the density of foreground pixels in each image is fixed to 0.49. N is the number of connected components. The result is shown in Fig. 5(b), from which we can see that the proposed algorithm outperforms the other algorithms when the number of connected components is lower than about 10^4. Combining Figs. 5(a) and (b), we can conclude that when the foreground pixels are sparse and the number of connected components is small, the proposed algorithm will perform best.

In natural images, generally the region of interest (ROI) consists of several connected components. While the number of ROIs is small, the number of foreground pixels may be considerable. To study the performance of the proposed algorithm further, four real image datasets introduced in [16] and two additional datasets are tested. These datasets include the MIRflickr dataset [25], Hamlet dataset, Tobacco800 dataset [26], 3DPeS dataset [27], Medical dataset [28] and the Fingerprints dataset [29]. Images in these datasets are of various sizes and foreground pixel densities. Samples in each dataset as Fig. 6 shows.

Fig. 6.
figure 6

Sample images in six datasets

Full size image

Table 3 presents the average execution time of the five algorithms. From the table we can see that our algorithm outperforms the other algorithms on Hamlet, Tobacco-800, 3DPeS, and Medical datasets. While on MIRflickr and Fingerprints datasets, it is inferior to BBDT and CCIT. The reason why the proposed algorithm is less efficient on these two datasets is that the foreground pixels in images of both datasets are dense, which leads to a large size of record table. On the other side, in BBDT and CCIT there are no use of record table, so when the foreground pixels are dense, BBDT and CCIT run faster. Nevertheless, compared with the conventional run-based algorithm RBTS, our algorithm keeps ahead all the time. In addition, our algorithm can be easily executed in parallel, both in the first scan and the second scan. While for block-based algorithms such as BBDT, CCIT and CTB, parallel execution is difficult to be conducted in the first scan since the steps in the first scan in these algorithms are closely linked and interdependent. Therefore, easy parallelism is another advantage of our algorithm.

Table 3. Execution time per image on real datasets (ms).
Full size table

4 Conclusions

A new run-based CCL algorithm is proposed in this paper. Compared with the conventional algorithms, it reduces the sizes of record table and the equivalent-label table using double-row scan. In addition, a fast equivalent-label sets searching method using the sparse matrix decomposition is designed to improve the time efficiency. Since all the runs are independent with each other, both the first scan and the second scan can be executed in parallel. Comparative experiments are conducted on synthetic images and real image datasets. Results demonstrate that our algorithm outperforms the state-of-the-art algorithms, especially when the foreground pixels are sparse and the number of connected components in the image is small. Future work will focus on the optimization of the current algorithm.