Semiconductor Heterostructures and Low-Dimensional Quantum Structures

Abstract

In Chap. 4, we have introduced the basic concepts and formalism of quantum mechanics. In Chap. 0, we have determined the energy spectrum, or energy-momentum or E–k relations, for electrons in a crystal which governs their interaction with external forces and fields. Moreover, we saw that the quantum behavior of particles is best observed in small, typically nanometer scale (one billionth of a meter or 10⁻⁹ m) dimension structures, as illustrated in the example of a particle in a 1D box.

Problems

• 1. In this chapter, we used the effective mass of the electron in the Schrödinger equation. Explain why it was necessary to do so, whereas it was not necessary in the infinite and finite potential well in Chap. 4.

• 2. Give an expression (an integral) for the total number of electrons in the conduction band of a bulk three-dimensional semiconductor and then in the first subband of a quantum well of width L in terms of the density of states and the Fermi function (assume box eigenstates in the confined direction). If at T = 0 K we dope the first subband in the conduction band and we fill all the states in the first subband, how many electrons do we need per unit area?

• 3. Consider a 50 Å GaAs and 300 Å Al_0.6Ga_0.4As layers forming a quantum well structure.

  

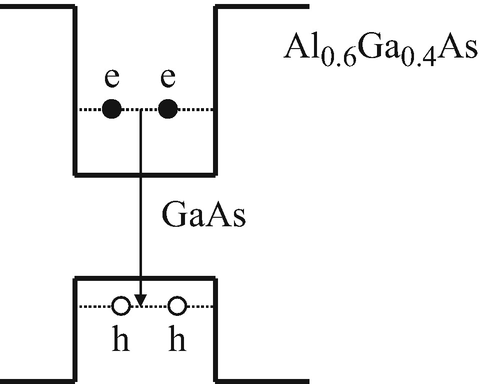
The electrons are all located at the first energy state (e), and holes are at (h). The general expression of the first energy state is determined as E₁ = ℏ²π²/2m^∗a², where a is the width of the quantum well and m* is the effective mass of the particle considered (for holes, consider the heavy-hole effective mass).

What is the photon energy of the light emitted when the electron and the hole recombine as shown in the above figure?

• 4. Let us assume a quantum dot which is spherical. The electrons or holes are confined at energy states with the following expression: E_nl = (ℏ²/2m^∗)(α_nl/R)², where m* is the effective mass of the electron or hole and the value of α_nl is given by α₁₀ = π, α₁₁ = 4.49, α₁₂ = 5.76, α₂₀ = 6.28, α₂₁ = 7.72, and α₂₂ = 9.09. Now consider the very small GaAs quantum dots of radius 10 nm. If the electron drops from the second state (α₁₁) to the first state (α₁₀), what is the photon energy of the light emitted from this transition?

  Draw the energy diagram for GaAs quantum dots with radius 5 nm, 10 nm, and 15 nm. How does the first energy state change as a function of radius?

• 5. Density of States of an Ideal Two-Dimensional Electron Gas

  Using the infinite barrier approximation, derive an expression for the density of states for electrons in a quantum well in terms of the well width L and electron effective mass m*.

• 6. Fermi Energy of an Ideal Two-Dimensional Electron Gas

  Consider a structure consisting of two GaAs quantum wells that have been grown far apart in Al_xGa_1-xAs with the same Al composition x (x ≤ 0.3). In well A the GaAs thickness is L, while in well B, it is 2L. Now, approximate the conduction bands in wells A and B by ideal quantum wells between infinitely high potential barriers. Suppose that the quantum wells contain electrons and that both wells have the same Fermi energy,${E}_{\mathrm{F}}=3{F}_1^{\mathrm{A}}$ where ${E}_1^{\mathrm{A}}$ is the lowest quantized energy level in well A.

  • (a) How many subbands in each well contain electrons at zero temperature?

  • (b) What is the two-dimensional charge density N_A and N_B in each well?

  Give the answer in terms of known physical quantities such as ℏ and L.

• 7. The Graphic of the Two-Dimensional Density of States

  Figure 15 shows the density of states of a quantum well. The confinement energy of the lowest level (E₁) is 17 meV, and the first excited state (E₂) has a confinement energy of 30 meV. The Fermi level is located 50 meV above the bottom of the conduction band. Determine the number of electrons contained in the well.

• 8. The two-dimensional potential which confines the electrons in a quantum wire made of GaAs is assumed to be parabolic, and the subband separation is given as ℏω₀ = 12 meV. If the Fermi energy is E_F = 37 meV as measured from the bottom of the lowest subband, calculate the number of electron per unit length at 0 K including spin degeneracy.

• 9. The Moss-Burstein Shift in Absorption Spectra

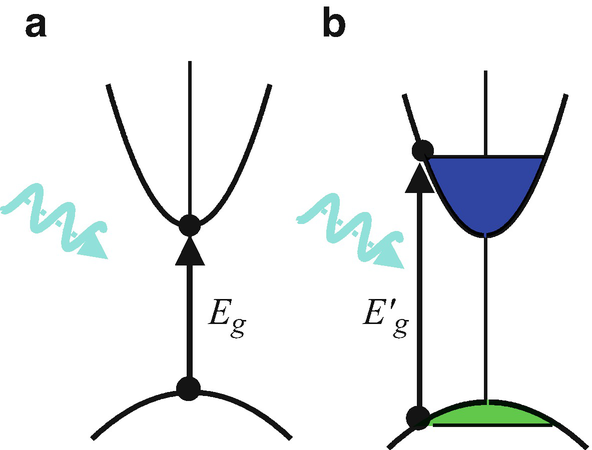
  The “band filling” or Moss-Burstein shift effect occurs in all heavily doped three-dimensional semiconductors. It is a consequence of the fact that electrons are fermions, and therefore it is impossible (by the Pauli exclusion principle) to optically excite an electron into a same spin k-state, which is already occupied. In the case of strongly degenerate n⁺-doped sample, this has the effect of prohibiting any interband transition into electron states below the Fermi energy leading to an upward shift in the effective absorption edge, ${E}_{\mathrm{g}}^{\prime }$ (see figure below). The Moss-Burstein shift (ΔE) is defined as the difference between the effective absorption edge and the energy gap (E_g) of the material, i.e., $\Delta E={E}_{\mathrm{g}}^{\prime }-{E}_{\mathrm{g}}$.

  • (a) Calculate the Burstein shift in the absorption edge of a direct semiconductor with parabolic bands due to the heavy doping (n-type) at very low temperature (T ≈ 0 K). The carrier concentration is n_e. Neglect excitons. Note that the shift is not simply the Fermi energy of the electrons and involves the mass of both conduction and valence bands.

  • (b) Calculate the Moss-Burstein shift for the GaAs material doped with 1 × 10¹⁸ electrons/cm³. What should happen to the shape of the absorption edge? Assume ${m}_{\mathrm{e}}^{\ast }=0.067\kern0.24em {m}_0$ and ${m}_{\mathrm{h}}^{\ast }=0.45\kern0.24em {m}_0$ where m₀is the electron rest mass.

    

Allowed optical transitions in direct-gap semiconductors: (a) undoped material, absorption threshold of E_g; (b) n⁺-doped material, absorption threshold blue shifted to ${E}_{\mathrm{g}}^{\prime }$ by the Moss-Burstein shift

• 10. Critical Radius of a Spherical Quantum Dot with Finite Barrier Height

  Assume that a quantum dot has a spherical shape with radius R and is surrounded by a medium of higher bandgap such as AlGaAs. The potential barrier at the conduction band is ΔE_c at all points in the surface of the sphere. The potential well is a square well of height, ΔE_c, for r > R and is 0 for r < R. Let us consider the simplest case of zero angular momentum (l = 0), and then it follows that the wavefunctions $\Psi \left(\overrightarrow{r}\right)$ depends only on the radial part. When l = 0 and $\Psi \left(\overrightarrow{r}\right)=R(r)=\phi (r)/r$, Eq. (15.56) reduces to:

  $$ \left\{\begin{array}{ll}-\frac{{\mathrm{\hslash}}^2}{2{m}^{\ast }}\frac{d^2\phi (r)}{dr^2}+\Delta {E}_{\mathrm{c}}\phi (r)= E\phi (r)& \left(r>R\right)\\ {}-\frac{{\mathrm{\hslash}}^2}{2{m}^{\ast }}\frac{d^2\phi (r)}{dr^2}= E\phi (r)& \left(r<R\right)\end{array}\right. $$

The solution of the above equation is the same as the one with a one-dimensional finite potential well. Find the critical radius below which there is no bound state of one electron in the quantum dot.