1 Introduction

Markov decision processes (MDPs) have their roots in operations research and stochastic control theory. They are frequently used for stochastic and dynamic optimization problems and are widely applicable, see e.g., [151]. For instance, in 1957 Bellman [23] introduced MDPs by considering the following problem: a machine can produce either perfect or defective items and can breakdown requiring repair. Breakdowns and producing defective items are random phenomena, e.g., depending on the machine’s age. When to decide whether to inspect the machine for a failure, or to just wait until a defective item is produced? If a defective item is produced, does one repair, inspect other sources of failure, or order new machine parts? These decisions depend amongst other on the costs of repair, inspection, and producing defective parts. This setting is naturally modelled as an MDP: the number of items produced so far is the state, breakdowns and producing defective or perfect items are probabilistic moves, inspections and repairs are decisions (a.k.a.: actions), and costs are modelled as rewards associated to actions in a given state.

The central problem for MDPs [74] is to find a policy (or strategy) required to determine what action to take in the light of what is known about the system at the time of choice. The typical aim is to optimize a given objective, such as minimizing expected cost until a given number of repairs, maximizing the probability of a system being operational for a large number of steps or minimizing the long-run average costs. The former two are known as finite horizon objectives, the latter as infinite time horizon objectives. These optimization problems can be cast as dynamic programming problems—Bellman equations—that are typically solved by value or policy iteration [133], or reinforcement learning [142].

This paper surveys approaches to tackle MDP problems from the perspective of probabilistic model checking (PMC) [17, 107, 113]. It determines for an MDP \(\mathcal{M}\) and a property specification \(\varphi \), typically expressed as a formula in mathematical logic or as a finite-state automaton, whether \(\mathcal{M}\) satisfies \(\varphi \). Under the hood, it uses graph algorithms, value or policy iteration, compact data structures, etc. so as to achieve a fully automated procedure. The use of logics enables to express the classical finite and infinite time-horizon MDP objectives, but also (new) intricate and complex objectives, or even mixtures thereof.

The power of PMC is that no matter how complex the logical guarantee, it is automatically checked which states in the MDP satisfy it. Neither manual manipulations of MDPs (or their high-level descriptions) are needed, nor expertise on any of its analysis techniques is required. Effective abstraction, reduction, and symbolic techniques curb the “curse of dimensionality” problem. Diagnostic feedback is provided in case \(\mathcal{M}\) does not satisfy \(\varphi \), giving useful insight in the reason of the refutation. More importantly though, is that PMC automatically obtains an optimal policy for the specification \(\varphi \) as a by-product of the verification procedure. PMC thus offers a flexible and powerful framework for MDP analysis.

In addition to the original application areas of MDP analysis such as operations research and stochastic control theory, MDP model checking is employed in several areas of computer science. Examples are randomized distributed algorithms, robotics, security and communication protocols, dynamic resource management, multimedia protocols and many more. We briefly give an idea for the first two.

For the class of randomized distributed algorithms, randomization provides an elegant way to break the symmetry between identical processes. This is perhaps best illustrated by the consensus problem: how to get a distributed network of processors to agree on a common bit. In the setting where processors communicate in an asynchronous manner and only one processor might crash, there is no distributed algorithm that solves this problem. This is the well-known FLP impossibility result [77]. If, however, a process can make a decision based on its internal state, its messages, and some coin-flip mechanism, consensus in this setting is almost surely possible [24]. Randomized mutual exclusion and leader-election algorithms naturally can be modelled as MDPs in which non-determinism naturally models the concurrent evolution of processes [147].

Another emerging application area of MDP model checking is the field of robotics. Robots have to perform tasks in uncertain environments (possibly involving humans) and may operate with errors in their sensing and actuation resulting in uncertainty when detecting and responding to its current state. Robot movements are modelled as being non-deterministic, and planning amounts to find an optimal control policy such that the robot achieves certain tasks (like picking up objects in a given order) while traversing a safe trajectory. A specification \(\varphi \) formally specifies which tasks are to be executed. In contrast to simulation, PMC offers formal guarantees about robot behaviour by providing bounds on how likely the robot satisfies its specification. As a by-product of the model checking, an optimal robot strategy is synthesized that can be used to construct controllers. PMC is applied in this context e.g., to analyze the probabilistic behavior of a robot operating with errors in its sensing and actuation [103] or to check whether robot swarms indeed behave as required [112]. More advanced applications of PMC include the analysis and repair of control policies using parametric probabilistic models [131] and the generation of policies using multi-objective model checking that ensure to achieve several objectives in a given order of priority: maximize the probability of finishing a task; maximize progress towards completion, if this is not possible; and minimize the expected time or cost required [119].

Purpose and Organization of This Paper. This paper reflects on the developments in MDP model checking and surveys its state-of-the-art. It is impossible to give a complete treatment of all works and developments on MDP model checking; this paper reflects the main directions and achievements from the perspective of the authors. The paper is written in an informal manner; numerous citations are provided to more detailed literature.

Section 2 introduces MDPs and the central problem in MDP model checking: determining reachability probabilities. Section 3 discusses several facets of MDPs such as costs, parametric probabilities, MDPs with intervals, MDPs with random delays, and MDPs whose state is only partially observable. Section 4 presents the kind of property specifications that can be treated by MDP model checking. Section 5 gives some insight in the techniques in tackling the state-space explosion problem in MDP model checking. Finally, Sect. 6 concludes this survey paper.

2 MDP Model Checking in a Nutshell

2.1 What are MDPs?

Markov decision processes (MDPs [102, 133]) are transition systems in which in any state a non-deterministic choice between a finite set of probability distributions exists. On reaching a state s in an MDP, non-deterministically a distribution \(\mu \in \mathcal{D}(s)\) is selected, where \(\mathcal{D}(s)\) is the set of available distributions (over the MDP’s state space) in s. The next state is determined according to \(\mu \). That is, state \(s'\) is selected with probability \(\mu (s')\). It is assumed that \(\mathcal{D}(s) \ne \emptyset \) for each state s. Every MDP for which \(| \mathcal{D}(s) | = 1\) in every state s, is a Markov chain (MC, for short). Paths in an MDP are infinite alternating sequences of pairs of states and distributions: \((s_i, \mu _i)\) where \(\mu _i \in \mathcal{D}(s_i)\) and \(\mu _i(s_{i+1}) > 0\), for each i. A probability measure \(\mathrm {Pr}\) on such paths can be defined using the cylinder set construction provided for each state \(s_i\) it is known which distribution \(\mu _i\) has been selected. This decision maker is a policy, also referred to as scheduler or adversary, that in state \(s_i\) selects a distribution \(\mu \in \mathcal{D}(s_i)\). Several types of policies do exist. Two ingredients are relevant: on the basis of which information does a policy make a decision, and does it use randomization to do so, or not. Positional policies decide solely on the current state \(s_i\) and not on the history, i.e., the prefix of the path until reaching \(s_i\). Randomized positional policies select \(\mu \in \mathcal{D}(s_i)\) with a certain probability. Deterministic policies select a fixed distribution from \(\mathcal{D}(s_i)\). History-dependent policies base their decision on the prefix \(s_0 \mu _0 s_1 \mu _1 \cdots \mu _{i-1} s_i\). Such policies may thus depend on e.g., the states visited so far, the actions taken so far, the frequency of visiting states, and the order in which states have been visited. As a policy resolves the non-determinism in an MDP, it yields an (possibly infinite-state) MC.

2.2 Reachability

One of the elementary questions in MDP analysis is whether a certain set T of target states can be reached almost surely, i.e., with probability one. As the likelihood to reach T depends on how the non-determinism is resolved, one considers minimal, or dually, maximal probabilities. Let \(\mathrm {Pr}^{\max }_s(\Diamond \, T)\) denote the maximal probability to reach some state in T starting from s. That is, \(\mathrm {Pr}^{\max }_s(\Diamond \, T)\) is the supremum over all possible policies to reach T under such policy. A graph analysis suffices to determine all states s for which this probability equals one. It does so by iteratively eliminating all states for which \(\mathrm {Pr}^{\max }_s(\Diamond \, T) < 1\). First all states that cannot reach T are removed as well as their incoming transitions. All states without outgoing transitions are then deleted. This is repeated as long as no change is possible anymore. Also all states for which \(\mathrm {Pr}^{\max }_s(\Diamond \, T) = 0\) can be obtained by a polynomial-time graph analysis, and similar applies to minimal reachability probabilities. Graph algorithms also suffice for checking whether any \(\omega \)-regular property holds almost surely [147].

Quantitative reachability amounts to check whether the probability to reach T exceeds a threshold different from one, like \(\nicefrac {4}{7}\). For a finite-state MDP, let variable \(x_s = \mathrm {Pr}^{\max }_s (\Diamond T)\) for state s. The following recursive characterization will be helpful. If T is not reachable from s, then \(x_s = 0\); if \(s \in T\), then \(x_s =1\). For all other cases:

$$ x_s \ = \ \max \, \Bigl \{ \ \sum _{t \in S} \, \mathbf {P}(s,\mu ,t) \cdot x_t \ \mid \ \mu \in \mathcal{D}(s) \ \Bigr \} $$

where \(\mathbf {P}(s,\mu ,t)\) denotes the probability to move from state s to t when selecting distribution \(\mu \) in s. This is an instance of the Bellman equation. It is well known that for every finite MDP, a deterministic positional policy does exist that attains \(\mathrm {Pr}^{\max }_s(\Diamond T)\). Value or policy iteration, and linear programming are computational techniques to obtain these policies. Linear inequation systems are thus key for reachability objectives in finite-state MDPs. Value iteration can be mildly amended such that it halts at the correct moment, i.e., when the iteratively computed probabilities truly converge [88].

Example 1

Consider the following stochastic job scheduling problem: complete n jobs on k identical processors under a pre-emptive scheduling policy. Once a job completes, all k processors can be assigned any of the m remaining jobs. Pre-empted jobs need to be started from scratch. When \(n-m\) jobs are finished, this yields \(m \atopwithdelims ()k\) non-deterministic choices. A property of interest is: what is the minimal expected time to complete all jobs? Or: what is the maximal probability to complete all jobs within 10,000 steps? We consider the scenario as given in [40] where the service time of job i is given by a negative exponential distribution with rate \(\lambda _i\). (Here, we do not consider the timing yet; only the branching probabilities induced by these dealsy matter.) This job-shop scheduling problem can be naturally modelled as an MDP, where a state corresponds to the jobs that still need to be executed, scheduling decisions are actions, and the discrete probability distributions \(\mathcal{D}(s)\) in state s are determined by the rates of the service times of the jobs that are being scheduled. The MDP for four jobs and two machines is indicated in Fig. 1. The initial state (left) contains all jobs, the rightmost state represents the completion of all four jobs. Each transition corresponds to a selection of two jobs that are scheduled. Probabilities are determined as follows. If one of the scheduled jobs, say job i, finishes in a situation where m jobs have not been processed yet, an event that happens with probability \(p_{i,j} = \frac{\lambda _i}{\lambda _i + \lambda _j}\) (where j is the number of the other selected, but unfinished job), \(m-1\) jobs remain, and a new selection is made. It is known that the largest-expected-service-time-first-policy is optimal to minimize the expected time to complete all jobs [40].

Fig. 1.
figure 1

Possible schedules for 4 jobs on 2 machines, modelled as an MDP.

Full size image

3 The Manifold Facets of MDPs

This section considers several features of MDPs: costs (where each transition incurs a certain cost), parameters (where probabilities are unknowns and given as e.g., polynomials over a set of variables), partial observability (where the state of an MDP is only partially visible), and continuous time (where state residence times are governed by negative exponential distributions).

3.1 Costs

Already in Bellman’s treatment [23], MDPs have been equipped with rewards (a.k.a.: gains), or dually costs. Costs are associated to transitions and are constant non-negative real values that are incurred on taking a transition. Thus, on selecting distribution \(\mu \) in state s a reward \(c(s,\mu )\) is earned. The cumulative reward of a finite path fragment in an MDP is the sum of all transition costs of the transitions on that path fragment. Typical MDP objectives are the maximal expected cost to reach a state in T (provided T can almost surely be reached), the maximal long-run average cost, and so forth. These objectives can be easily cast as Bellman equations and can be achieved by deterministic positional policies. If a constraint is imposed on the cumulative cost, e.g., what is the minimal probability to reach a bad state with a cumulative reward below a given threshold, finite-memory policies that keep track of the cumulative cost up to the decision point, i.e., the current state, are needed. A simple cost function associates cost one to each transition; in fact, the property “what is the maximal probability to complete all jobs within 10,000 steps?” in Example 1 refers to the cumulative cost in that case.

3.2 Parameters

In various circumstances, certain system quantities such as failure probabilities, packet loss ratios, etc. are often not—or at the best partially—known. In that setting, parametric MDPs where transition probabilities are specified as polynomials over real-valued parameters are useful. The problem of parameter synthesis is: Given a finite-state parametric MDP, what are all the parameter values for which a given property exceeds (or is below) a given fixed threshold? For the job-shop scheduling problem, an example of a synthesis problem is to determine the unknown job durations such that all jobs can be completed with a total expected duration of two days, say. Parameter synthesis typically amounts to partition the parameter space into safe and unsafe regions. A safe region contains all parameter valuations for which the property-of-interest is satisfied, while the unsafe region is its complement. In practise, typically not a full coverage can be achieved, but a large (say, >95%) coverage is aimed for. Existing parameter synthesis techniques use heuristics and sampling [89], or obtain over-approximations by replacing parametric transitions by non-deterministic choices over extremal parameter values resulting in a two-player stochastic game that is analyzed using standard means [134]. If for certain parameter regions, the result is inconclusive, the region is refined, and the procedure is repeated until a certain coverage is achieved. Parameter synthesis for parametric MDP models of about 100,000 states and two to four parameters have been reported [134]. Recently, geometric programming has been proposed to treat parameter synthesis for multi-objective parametric MDPs [51]; this provides a polynomial-time algorithm to obtain approximations that are arbitrarily close. Several instances of parametric Markovian models have been discussed in the literature, such as bounded-parameter MDPs [83] and interval MDPs [96],[?], MDPs where the transition probabilities are known to lie within certain upper and lower bounds. This model is rooted in interval Markov chains introduced by Jonsson and Larsen [104] in the context of a specification theory for probabilistic systems.

3.3 Partial Observability

Partially observable MDP (POMDPs, for short) models generalize MDPs by relaxing the assumption that the state of the system is completely observable. POMDPs play an important role in, e.g., mobile robot navigation, probabilistic planning and multi-agent systems where each agent can access its own variables, but cannot view the variables and locations of the other agents. A POMDP models a decision process in which it is assumed that the system dynamics are determined by an MDP, but the policy cannot directly observe the underlying state. Instead a policy considers equivalence classes of states, states for which the observations are equal, and base their decision on these equivalence classes rather than on the states themselves. A POMDP thus is an MDP \(\mathcal{M}\) equipped with an equivalence relation over its states. de Alfaro [59] has shown that checking whether for some policy the POMDP stays within a set T of target states is positive, is EXPTIME-complete. Many other model-checking problems for POMDPs have shown to be undecidable using reductions from the emptiness (or other undecidable problems) for probabilistic language acceptors, which can be seen as “fully blind” POMDPs where all states have the same observable [6, 12, 123]. Let us give some simple examples for undecidable problems for POMDPs. Checking the existence of a policy where the expected cost until reaching a goal state exceeds some threshold is undecidable, and so are other policy-existence problems for alternative expected cost criteria such as discounted or long-run average cost objectives [123]. These results have been shown using reductions from the emptiness problem for probabilistic finite automata. The inapproximability results for probabilistic finite automata carry over to POMDPs with expected total or long-run average costs [123]. However, there are several algorithms for the analysis of POMDPs under finite-horizon objectives as well as approximation algorithms for infinite-horizon discounted cost objectives [122] or expected cost objectives for POMDPs with positive cost functions [46]. The decidability of the value 1 problem that asks whether there are policies under which a reachability property holds with probability arbitrarily close to 1, has been established for a subclass of POMDPs [81].

Qualitative verification problems for MDPs, such as the problem to decide the existence of a policy ensuring that a goal state will be visited infinitely often almost surely, only depend on the graph structure of the MDP, but not on the precise transition probabilities. This facilitates efficient graph algorithms for checking qualitative verification problems in MDPs, possibly in combination with automata-based approach to represent complex path properties. The situation in POMDPs is different as such qualitative properties can depend on the transition probabilities. Indeed, the policy-existence problem for qualitative repeated reachability properties where the task is to check whether for some policy some state in T is visited infinitely often with positive probability is undecidable. This has been shown using reductions from the emptiness problem for probabilistic Büchi automata [6, 12]. However, decidability and EXPTIME-completeness has been established for qualitative verification problems against \(\omega \)-regular specifications when restricting to finite-memory policies [47].

3.4 Exponential Delays

Continuous-time MDPs [85] (CTMDPs, for short) are MDPs in which the state residence time is governed by a negative exponential distribution. The rate of this exponential distribution depends on the current state and the probability distribution \(\mu \) that is used to determine the next state. Accordingly, the average residence time in state s under taking distribution \(\mu \) is given by \(\nicefrac {1}{r(s,\mu )}\). Rate \(r(s,\mu )\) thus determines the random residence time in state s provided distribution \(\mu \) is selected in s by the policy. Paths in CTMDPs are infinite sequence of triples \((s_i,t_i,\mu _i)\) where \(t_i\) denotes the residence time in state \(s_i\) given that distribution \(\mu _i\) has been selected. Policies in CTMDPs can decide on the basis of the states visited and the selected distributions so far, but may also exploit the elapsed time (in every state). This gives rise to uncountably many policies. It for instance, makes a difference whether a policy decides on entering a state (early) or on leaving a state (late) after delaying in that state. A categorisation of the class of policies for CTMDPs is given in [127]. Costs can be added to CTMDPs in the same vein as for MDPs except that the incurred cost linearly depends on the state residence time. That is, on selecting action \(\mu \) after residing t time units in state s with cost rate \(c(s,\mu )\), the cost \(c(s,\mu ){\cdot }t\) is incurred.

Example 2

Consider the stochastic job scheduling problem again (see Example 1). Rather than considering time-abstract properties such as minimizing the expected completion time, we are now interested in: what is the maximal/minimal probability to finish all jobs within a given deadline. This requires to considering the timing behaviour of the job scheduling. Note that if jobs i and j are currently being scheduled, and i finishes first, then the elapsed time is determined by the rate \(\lambda _i\). Due to the memoryless property of the exponential distribution, the remaining execution time of the pre-empted job j remains exponentially distributed with rate \(\lambda _j\).

Other Forms of Stochastic Delays. Probabilistic extensions of timed automata exist [129]; they are known as probabilistic timed automata (PTA). Their edges are discrete probability distributions over states. PTA are finite symbolic representations of uncountable MDPs—as clock valuations are real values. Non-determinism is inherited from timed automata. Computing reachability probabilities in PTA is decidable via a region graph-like construction. Whereas in PTA clocks are deterministic, stochastic timed automata [25] (STA) provide a stochastic interpretation to clocks. In STA, unbounded clocks are interpreted as negative exponential distributions, whereas bounded clocks obey a uniform distribution. Stochastic interpretations of TA are also used in statistical model checking [55].

4 The Manifold MDP Properties

This section considers a spectrum of properties that can be addressed by MDP model checking: probabilistic CTL, various variations of reachability objectives (expected cost until reaching a target state, total cost until reaching such state, quantiles, reachability with time deadlines, repeated reachability etc.), multiple objectives that need to be fulfilled simultaneously, mean payoff and long-run objectives, as well as energy/weight objectives, conditional probabilities. We also briefly discuss obtaining permissive policies, and counterexample generation.

4.1 Probabilistic CTL

PCTL [27, 93] is a variant of the well-known computation tree logic (CTL). It replaces the universal and existential quantification over paths by an operator that expresses a bound on the probability of all paths satisfying a path-formula. In the setting for MDPs, the formula \(\varPhi =\mathbb {P}_{> p}(\varphi )\) asserts that regardless of the resolution of the non-determinism, the likelihood of the set of paths satisfying \(\varphi \) exceeds p. Formally, \(s\, \models \,\mathbb {P}_{> p}(\varphi )\) if and only if for all policies it holds that \(\mathrm {Pr}^{\sigma }_s(\varphi ) > p\), where \(\mathrm {Pr}^{\sigma }\) refers to the probability measure under the policy \(\sigma \) at hand. Stated differently, PCTL-formula \(\mathbb {P}_{> p}(\varphi )\) holds in state s whenever \(\mathrm {Pr}^{\min }_s(\varphi )\) exceeds p. Here, \(\mathrm {Pr}^{\min }_s(\varphi )\) denotes the infimum of the probability of the set of \(\varphi \)-paths under all policies. For finite MDPs, this corresponds to the minimum over all policies, as a finite-memory policy suffices. A dual formulation holds for \(\mathbb {P}\)-formulas that have a probability upper bound. The model checking of a finite MDP against a PCTL-formula \(\varPhi \) can be done using a recursive descent over the parse tree of \(\varPhi \). For each sub-formula of \(\varPhi \) the set of states is determined that satisfy this sub-formula. For reachability objectives, and until-formulas—reach a \(\varPhi _2\)-state via \(\varPhi _1\)-states only—this can be done using solving a linear equation system whose size is proportional to the number of states in the MDP. This yields a model-checking algorithm that is polynomial in the size of the MDP \(\mathcal{M}\) and linear in the size of the PCTL-formula \(\varPhi \); for details we refer to [17, Chap. 10.6].

4.2 Expected Costs Until Reaching a Target

For an MDP equipped with costs, a natural objective is to consider the expected cost until reaching some target state in T. For an infinite path through an MDP, let the cumulative cost until reaching T be defined as the sum of all costs until reaching some state in T for the first time, and undefined in case such state does not exist, i.e., the path does never reach T. A policy \(\sigma \) is said to be proper if T will be reached almost surely under \(\sigma \), i.e., \(\mathrm {Pr}^{\sigma }_s(\Diamond T)=1\) for all states s. The expected reward for a state s under a given proper policy \(\sigma \) from which T will almost surely be reached is then the weighted sum over all \(\sigma \)-paths from s to T of their cumulative cost up to reaching T times their probability. If there is at least one proper policy and all costs are non-negative, the minimal expected cumulative costs are achieved by a deterministic positional policy and are computable in much the same way as extremal reachability probabilities by linear programming techniques, policy or value iteration [26, 58]. The supremum of the expected cumulative costs until reaching T over all proper policies might be infinite. If the costs are non-negative then the latter can be checked in polynomial time. If the supremum is finite then a deterministic positional policy maximizing the expected cumulative costs until reaching T exist and is computable again using similar techniques as for extremal reachability probabilities [58].

4.3 Cost-Bounded Reachability

Whereas positional policies suffice for reachability (and long run) objectives, step- or cost-bounded reachability objectives require finite-memory policies [97]. The same applies to \(\omega \)-regular properties. For \(\Diamond \, \!^{\le k} \, T\), i.e., can a state in T be reached while the accumulated costs are bounded by k, this can be intuitively understood as follows. Consider a state with two choices: one that almost surely leads to T but with high costs, and one that may lead to T directly with low costs, but with a certain probability ends up in a state from which T can never be reached. Then, depending on the cost bound left to reach T, an optimal policy will decide for the (first) safe choice, whereas the remaining cost bound to reach T is small, it picks the (second) unsafe strategy. Computing policies maximizing the probability for a cost-bounded event \(\Diamond \, \!^{\le k} \, T\) is known to be computationally hard, namely PSPACE-hard even for acyclic MDPs [86]. An exponential-time algorithm is obtained by using an iterative approach that successively computes the values \(p_{s,i}\) for the maximal probability to reach T with cost-bound i from state s for \(i=0,1,\ldots ,k\). For this, we can rely on a variant of the Bellman equations

$$ p_{s,i} \ = \ \max \, \Bigl \{ \ \sum _{t \in S} \, \mathbf {P}(s,\mu ,t) \cdot p_{t,\max \{i-c(s,\mu ),0\}} \ \mid \ \mu \in {\mathcal D}(s) \ \Bigr \} $$

for \(s\notin T\) and T reachable from s. If \(0 < c(s,\mu )\) is positive then the values \(p_{t,\max \{i-c(t,\mu ),0\}}\) have been computed in a previous iteration. Zero-cost actions can be treated using linear programming techniques [9].

4.4 Quantiles

In quantile objectives, one considers computing the minimal cost bound k such that with probability at least p the target set T will be reached before the cumulative costs exceeds k. Qualitative quantile objectives (i.e., \(p=0\) or \(p=1\)) can be determined in polynomial time, whereas an exponential-time algorithm for quantitative quantile objectives (where p belongs to the open interval (0, 1)) exists that relies on the successive computation of cost-bounded reachability probabilities [9, 146]. Quantile objectives for MDPs with multiple cost functions for several pay-off criteria have been considered in [137].

4.5 Timed Reachability

In CTMDPs, policies that base their decision on the current state as well as the total cumulative time so far, the so-called total-time positional deterministic policies are optimal for timed reachability objectives—given a set T of target states and a deadline d, what is the maximal probability to reach T within d? This is the continuous counterpart of a policy in MDPs for bounded reachability \(\Diamond \, \!^{\le k} \, T\) where the total number of steps taken so far is needed to achieve optimality. PMC algorithms for timed reachability determine \(\epsilon \)-close approximations of the optimal total-time positional deterministic policy. Timed reachability objectives can be tackled via a discretization yielding an MDP on which a corresponding step-bounded reachability problem is solved using value iteration. The smallest number of steps needed in the discretized MDP to guarantee an accuracy of \(\epsilon \) is \(\frac{\lambda ^2{\cdot }d^2}{2\epsilon }\), where \(\lambda \) is the largest rate of a state residence time in the CTMDP at hand [128]. In a similar way, minimal timed reachability probabilities can be obtained as well as their corresponding policies. Tighter bounds with slightly different discretization techniques have been obtained in [42, 136]. A comparative empirical study shows that a simple greedy algorithm, originally developed for uniform models [16], can be lifted to the general setting, where it often outperforms all other approaches [44]. The duality between costs (at states) and time is discussed in [15] thereby enabling the use of algorithms for timed reachability for the purpose of computing cost-bounded reachability. Optimal policies for multi-cumulative cost reachability properties in CTMDPs are treated in [79].

Example 3

Consider timed reachability for the job-shop scheduling problem of Example 1 with exponential service times. That is, we focus on what is the probability to complete all jobs within a given deadline d? The results of applying this discretization on the example with 4 jobs and two machines is shown in Fig. 2 where the deadline d is given on the x-axis and the reachability probability on the y-axis. For equally distributed job durations, the maximal and minimal probabilities coincide. Otherwise, the probabilities depend on the scheduling policy. It turns out that the \(\epsilon \)-optimal policy that maximizes the reachability probabilities adheres to the SEPT (shortest expected processing time first) strategy; moreover, the optimal \(\epsilon \)-policy for the minimum probabilities obeys the LEPT (longest expected processing time first) strategy.

Fig. 2.
figure 2

Minimal and maximal reachability probabilities for finishing 4 jobs on 2 machines under a pre-emptive scheduling strategy.

Full size image

4.6 Beyond Reachability

Repeated reachability events or persistence probabilities can be obtained by considering maximal end-components [50, 56], the MDP counterpart to bottom strongly connected components in Markov chains. An end component \({\mathcal E}\) of an MDP \(\mathcal{M}\) is a sub-MDP of \(\mathcal{M}\) whose induced graph is strongly connected. \({\mathcal E}\) is called maximal if there is no other end component \({\mathcal E}'\) that contains \({\mathcal E}\). A crucial observation made by de Alfaro [56] is that under each policy \(\sigma \), the limit of almost all \(\sigma \)-paths constitutes an end component. Here, the limit of an infinite path \(\pi \) is the set of state-distribution pairs that occur infinitely often in \(\pi \). Thus, maximal probability for a repeated reachability condition \(\Box \Diamond T\) (“infinitely often T”) is computable as the maximal probability to reach a maximal end component containing at least one T-state.

Determining the maximal probability of an \(\omega \)-regular property \(\varphi \) in an MDP \(\mathcal{M}\) amounts to determining the maximal probability to reach an accepting end component in the product of \(\mathcal{M}\) with a deterministic \(\omega \)-automaton for \(\varphi \) [21, 50, 56]. An accepting end component is an end component that satisfies the acceptance condition of the deterministic \(\omega \)-automaton at hand. This procedure involves a double-exponential blow-up caused by (1) transforming an LTL formula into an \(\omega \)-automaton, and (2) determinizing this automaton. In fact, no algorithm of lower complexity can be expected as the question, whether \(\mathrm {Pr}^{\max }_{\mathcal {M},s_0}(\varphi ) = 1\) for a given MDP \(\mathcal{M}\) with initial state \(s_0\) and LTL-formula \(\varphi \), is 2EXPTIME-complete [50]. Recent practical advancements on converting LTL, an important temporal logic for expressing a large class of \(\omega \)-regular properties, into deterministic \(\omega \)-automata have been reported in [70].

4.7 Fairness

When using MDPs as an interleaving model for systems composed by several probabilistic processes, establishing liveness properties often requires fairness assumptions for the resolution of nondeterministic choices that rule out pathological cases where, e.g., one process never performs an action. In this context, one considers only fair policies, i.e., policies where a certain fairness assumption holds almost surely. The analysis of MDPs under fair policies has been considered in the context of LTL and PCTL-like logics [14, 21, 148]. Suppose \( fair \) is a realizable fairness assumption in the sense that there exists a fair policy \(\tau \) such that \( fair \) holds with probability 1 from each state under this policy \(\tau \). Then, a fair policy maximizing the probability to reach a target T under all fair policies is obtained by first computing a positional (possibly unfair) policy \(\sigma \) maximizing the probability for \(\Diamond T\) from each state where the maximum is taken over all policies. We then modify \(\sigma \) to a fair policy \(\nu \) that behaves as \(\sigma \) until reaching T, in which case it switches mode and behaves as \(\tau \) from then on. Thus, \(\sup _{{\tiny \sigma \ \text {fair}}}\mathrm {Pr}^{\sigma }_s(\Diamond T) \ \ = \ \ \max _{{\tiny \sigma \ \text {fair}}}\mathrm {Pr}^{\sigma }_s(\Diamond T) \ \ = \ \ \mathrm {Pr}^{\max }_s(\Diamond T)\), which shows that realizable fairness is irrelevant for maximizing reachability probabilities. This does not hold when the task to find a fair policy minimizing the probability for reaching T. Consider, for example, an MDP with a state s that has two nondeterministic alternatives: either stay in s via action \(\alpha \) or to move to a target state \(t\in T\) via action \(\beta \) (both with probability one). If we suppose strong fairness for action \(\beta \), i.e., each fair policy that visits s infinitely often with positive probability needs to take eventually action \(\beta \) in state s. Then, the probability to reach T from s is one under each fair policy, while \( \mathrm {Pr}^{\min }_s(\Diamond T)=0\). However, a fair policy minimizing the probability for reaching T can be obtained using the following fact (again we suppose realizability of the fairness condition):

$$ \min _{{\small \sigma \ \text {fair}}} \mathrm {Pr}^{\sigma }_s(\Diamond T) \ \ = \ \ 1- \mathrm {Pr}^{\max }_s(\lnot T \, \mathsf{U}\,F) $$

where F denotes the set of states u such that \(\mathrm {Pr}^{\sigma }_u(\Diamond T)=0\) for some fair policy \(\sigma \) and where \(\, \mathsf{U}\,\) denotes the until operator. This set F is computable using an analysis of the end components of the MDP and PCTL model-checking techniques. Notions of fairness have also been used as an approximation of probabilistic executions and used in the context of proof systems for establishing qualitative linear-time properties for MDP-like models [132].

4.8 Mean Payoff and Other Long-Run Averages

Given a weighted MDP, i.e., an MDP with a cost function assigning (possibly negative) integers, called weights, to the state-distribution pairs \((s,\mu )\) with \(\mu \in {\mathcal D}(s)\), the mean payoff \(\mathrm {MP}(\pi )\) of an infinite path \(\pi \) is defined as the limit superior of the sequence \( wgt (\pi ,n)/n\) where \( wgt (\pi ,n)\) denotes the accumulated weight of the first n state-distribution pairs in \(\pi \). In finite-state MDPs, minimal and maximal expected mean payoff always exist and are achieved by deterministic positional policies. The minimal and maximal expected mean payoff are computable in polynomial-time using linear programming techniques that encode the long-run frequencies of the state-distribution pairs in randomized positional policies [106, 133]. MDPs with multiple mean-payoff objectives have been studied in [34]. Other forms of long-run averages have been proposed by de Alfaro [57] where finite-state automata serve to trigger so-called experiments that monitor finite fragments of the paths generated by the MDP and evaluate them in terms of a reward value. He presents polynomial-time algorithms to check whether there is a policy \(\sigma \) ensuring that almost all \(\sigma \)-paths satisfy a threshold condition for the long-run average reward, defined as the mean payoff, but the limit average is taken over the number of experiments rather than the number of transitions. These concepts have been further developed for reasoning about long-run ratios in MDPs and related synthesis problems using standard and fractional linear programming techniques [56, 149].

4.9 Multiple Objectives

The properties discussed so far focused on single objectives such as reachability, timed/bounded reachability, expected costs, and long-run averages. In practice, a system is subject to multiple objectives that are mutually influencing each other, like quickly reaching a target is more costly. Multi-objective model checking aims at achieving multiple objectives on MDPs at once and to facilitate trade-off analysis by obtaining Pareto curves. Multi-objective decision making for MDPs with discounting and long-run objectives has been well investigated; for a recent survey, see [138]. Etessami et al. [72] consider verifying finite MDPs with multiple \(\omega \)-regular objectives. Other multiple objectives include expected rewards under worst-case reachability [41, 78], quantiles, long-run ratio objectives, and conditional probabilities [10], multiple discounted rewards [49], mean payoffs and stability [38], long-run objectives [33] and total average discounted rewards under PCTL [143]. Combinations of safety properties and expected cost objectives have been considered for MDPs with unknown cost function [105].

Fig. 3.
figure 3

Approximate Pareto curve for stochastic job scheduling.

Full size image

Example 4

Consider again the job-shop scheduling problem. In addition to requiring that all jobs need to be completed within a given deadline with a high probability, let us impose extra constraints, e.g., requiring a high probability to finish a batch of c jobs within a tight deadline (to accelerate their post-processing), or having a low average waiting time. Figure 3, e.g., shows the results of CTMDP multi-objective model checking for 12 jobs and 3 processors. It approximates the set of points (t, p) for schedules achieving that (1) the expected time to complete all jobs is at most t and (2) the probability to finish half of the jobs within an is at least p. The red area indicates the set of points (t, p) that cannot be attained by any policy, whereas the green area indicates the set of points that are achievable by some policy; the white area is the “unknown” area, due to the \(\epsilon \)-approximation. Whereas for MDP model checking [72], the set of achievable points is a convex area with finitely many corner points, for CTMDPs the convex area may have infinitely many corner points [135]. This is why approximations of Pareto curves are obtained. Novel techniques for multi-objective model checking and robust strategy synthesis of MDPs with uncertain transition probabilities have also been discussed recently [91, 139].

4.10 Energy and Other Weight Objectives

There is a close relation between the mean payoff and the energy objective, which again is closely related to the termination condition in one-counter systems. The energy condition imposes the constraint that the total cumulative weight never drops below 0 (or another constant) and is typically considered in conjunction with other \(\omega \)-regular or weight conditions. In the case of MDPs the task is then to find a policy \(\sigma \) such that almost all \(\sigma \)-paths satisfy both the energy condition and the additional \(\omega \)-regular or weight conditions. Energy-parity objectives in MDPs are solvable in pseudo-polynomial time and the decision problem is in \(\mathrm {NP}\,\cap \,\mathrm {coNP}\) [48, 125]. Even the pure energy objective is known to be reducible to (non-probabilistic) two-player mean-payoff games [32], for which no polynomial-time algorithms are known. Energy-MDPs with other side conditions have been studied, e.g., in [39] where multiple expected mean payoff constraints have been considered.

MDPs with the energy condition can also be seen as infinite-state MDPs that operate with a counter [36], or equivalently, with stacks over an unary stack alphabet, which again is closely related to the model of recursive MDPs [35, 73]. Although reasoning about temporal properties with weight constraints is in general undecidable, even in the non-probabilistic case [29], the maximal or minimal probabilities for LTL formulas with constraints for the weight accumulated in windows of a fixed length are computable using a reduction to standard LTL [19].

4.11 Conditional Probabilities

Reasoning about conditional probabilities (rather than unconditional ones) is natural when the task is to analyze a system in specific (possibly rare) scenarios. For example, to analyze the impact and cost of error-handling mechanisms, selected error scenarios can be used as conditions. For another example, conditional probabilities and expectations are used to define the semantics of probabilistic programs in terms of weakest pre-expectations or to define conditional termination times [108]. They have also been used to formalize a notion of anonymity [3] by the requirement that the probability for an observable does not depend on the secret.

In purely probabilistic models, such as MC, conditional probabilities are computable directly by their definition \(\mathrm {Pr}(\varphi | \psi ) = \mathrm {Pr}(\varphi \wedge \psi )/\mathrm {Pr}(\psi )\) as quotient of “standard” probabilities. Such a simple approach is, however, not applicable in MDPs when the task is to find a policy maximizing the probabilities for \(\varphi \), under the condition of a temporal property \(\psi \). Suppose, e.g., that \(\varphi = \Diamond \, T\) and \(\psi = \Diamond \, A\) are reachability properties. A crucial observation to construct an optimal policy is that after having reached T (resp. A), optimal policies maximize the probability to reach A (resp. T) [4, 18]. This observation allows to transform the given MDP \(\mathcal {M}\) into a normal form MDP, which allows to assume that \(T \subseteq A\). Suppose now \(s_0\) is the initial state of \(\mathcal {M}\). By adding “reset transitions” \(s \rightarrow s_0\) for all states s in \(\mathcal {M}\) with \(\mathrm {Pr}^{\min }_{\mathcal {M},s}(\Diamond A)=0\) as additional nondeterministic alternatives, we obtain an MDP \(\mathcal {N}\) such that the maximal conditional probability for \(\Diamond T\), given \(\Diamond A\), in \(\mathcal {M}\) from \(s_0\) equals \(\mathrm {Pr}^{\max }_{\mathcal {N},s_0}(\Diamond T)\). Intuitively, the reset transition serve to “discard” all paths violating the condition \(\Diamond A\) and “re-distributing” their probability mass to the paths satisfying \(\Diamond A\). Thus, maximal conditional reachability probabilities are reducible to maximal (unconditional) reachability probabilities. This approach can be generalized for the case where the objective \(\varphi \) and the condition \(\psi \) are \(\omega \)-regular properties using deterministic \(\omega \)-automata for \(\varphi \) and \(\psi \).

The techniques for maximal or minimal expected costs until reaching target states sketched above seek for the optimum under all proper policies, i.e., policies under which the target will be reached almost surely. However, such policies need not to exist. Computing maximal conditional expected costs until reaching a target under the condition that the target will indeed be reached is more involved as positional policies are no longer powerful enough. [20] presents an exponential-time algorithm to compute maximal conditional expected costs until reaching a target and proves PSPACE-completeness for the threshold problem in acyclic MDPs that asks whether the maximal conditional expectation meets a given lower or upper bound.

4.12 Permissive Policies

Whereas MDP model checking typically generates a single policy that is optimal with respect to a given objective, recently this has been extended to obtaining multi-policies [66]. Such multi-policies specify multiple possible actions rather than a single possible action. The aim is to synthesize multi-policies that are as permissive as possible, which one can quantify by assigning penalties to actions. These are incurred when a multi-policy disallows (does not make available) a given action. Permissive controller synthesis aims to generate a multi-policy that minimises these penalties, whilst guaranteeing the satisfaction of a specified property \(\varphi \). Randomised multi-policies are strictly more powerful than deterministic ones, and the permissive controller synthesis problem is NP-hard for either class with upper bounds in NP and PSPACE, respectively. Practical methods for synthesising multi-policies exploit mixed integer linear programming (MILP).

4.13 Counterexamples

If model checking MDP \(\mathcal{M}\) against specification \(\varphi \) with upper bound p, say, yields an affirmative result, then a formal guarantee is obtained that \(\mathcal{M}\) satisfies \(\varphi \) with probability at most p, regardless of how the non-determinism is resolved. As a by-product, most model checkers offer the possibility to obtain a policy that maximizes the likelihood of ensuring \(\varphi \). If however, the model checking procedure yields a negative answer, then some diagnostic feedback would be useful. PMC techniques have been therefore extended with the possibility to obtain counterexamples. Such techniques obtain a sub-MDP of \(\mathcal{M}\) whose maximal probability to satisfy \(\varphi \) exceeds p. Whereas obtaining such sub-MDP of minimal size is computationally hard (the corresponding decision problem is NP-hard [45]) for \(\omega \)-regular properties, good practical results have been obtained using MILP [154].

5 Curbing State-Space Explosion

The often excessive size of the state space spanned by a concrete verification problem is a major impediment to practicality across the entire spectrum of verification methods, see e.g. [2, 92]. This problem of state-space explosion also affects negatively the basic probabilistic model checking procedures we discussed thus far. A recent approach circumvents it by nevertheless explicitly enumerating all states and transitions, but keeping only a minor portion thereof in main memory at any time of the computation, storing the remainder almost exclusively in secondary storage (usually an attached hard disk) [94]. Other, more conceptual approaches consider abstraction and compression techniques for MDP models. They indeed form an important area of probabilistic model checking research. We can only present an abridged survey here, more detailed accounts can be found for instance in [62]. Abstraction and compression techniques remove details from concrete models provided these are not relevant to the property of interest. In many cases, only this makes the analysis of the model feasible or at least speeds up verification considerably. For real-world problems, abstraction and compression is a prerequisite for successful verification.

5.1 Compress

Bisimulation Minimization. A popular compression technique is bisimulation minimization [31]. Here, the states of the compressed system represent equivalence classes with respect to a bisimulation equivalence, ensuring that the compressed system, the quotient, is guaranteed to preserve all relevant properties. The basis thereof is an algorithm to decide the respective relation, which in the MDP setting is probabilistic bisimulation, a concept introduced by Larsen and Skou [120] in the early nineties, and adapted to MDPs by Segala [141]. Probabilistic bisimulation can be decided in polynomial time [11], and this extends to interval MDPs [96, 98] with bounded nondeterminism, as well as to weak variations of bisimulation, i.e., to variations where internal steps are considered compressable [145]. Minimality of the quotient construction requires some care in the presence of probability, depending on the particular strong or weak bisimulation employed [68].

Compositional Minimization. The relevant bisimulations are congruence relations, in the sense that they are compatible with the usual variants of parallel composition and other composition operators. This enables the application of bisimulation minimization to components, which can turn out to be extremely effective. Non-trivial examples are known where state spaces with 1.6 billion states and 7 billion transitions can be compressed to a very small minimal MDP [76] prior to model checking.

Distribution-Based Bisimulation. Weaker equivalences lead to better model compression since they induce coarser partitions of the state space, but might come with higher algorithmic complexity. Weak distribution bisimulation is coarser than the aforementioned relations [69]. It is not defined as a relation between states, but instead between probability distributions on states. Exponential-time algorithms deciding distribution-based bisimulations have been proposed [67, 99, 140].

Symmetry. On the other hand, strong bisimulation equivalence is often induced by symmetries in the model, which in turn are generally easier to identify directly [65, 115] instead of running a dedicated decision algorithm, albeit at the price of a possibly non-minimal result.

5.2 Be Symbolic

In non-probabilistic systems, symbolic data structures such as binary decision diagrams (BDDs) have been investigated successfully [43] to mitigate the state explosion phenomenon. For probabilistic systems, multi-terminal binary decision diagram (MTBDDs) [80], also called algebraic decision diagrams [5], have been introduced as a data structure for representing and manipulating functions from a finite set to values in an algebraic structure. In the context of probabilistic systems, they have been first used for computing steady-state probabilities [87] and PCTL model checking [8] for Markov chains and later extended for MDPs [60]. Among others, [60] demonstrate that model construction and reachability-based model checking is possible in a matter of seconds for certain classes of systems consisting of up to 10\(^{30}\) states. While [60] follows a purely symbolic approach, which causes the problem that the MTBDD-representation of the probability vector can degenerate to a tree-like structure, [114, 130] introduces a hybrid approach using an MTBDD-representation of the MDP and an explicit representation of the probability vector.

Symblicit Analysis. For certain problems, the benefits of explicit and of symbolic analysis steps can be exploited in carefully crafted combinations, so-called symblicit analysis approaches [28, 90, 153].

Tool Support. The probabilistic model checkers PRISM [114, 116] and storm [63] both support the hybrid approach, but also offer a purely symbolic MTBDD-based engine, a purely explicit engine, as well as a sparse engine that generates the model symbolically, but carries out the numerical computations using sparse data structures. The storm model checker [63] also implements bisimulation-based minimization algorithms applicable to MDPs.

5.3 Abstract Safely

Most abstraction schemes are based on grouping states that are not necessarily bisimilar. Abstract and original models are then no longer bisimilar but they are related by a simulation relation. Abstraction is typically conservative in the sense that affirmative verification results for abstract models carry over to concrete models. That is to say, if the abstract model satisfies a property, the concrete one does so too. Probabilistic simulation preserves a safe fragment of PCTL [100]. The converse does not apply, as spurious negative results may occur due to over-approximation in the abstraction. This however can be detected by checking the result on the concrete model, which in turn can be exploited for refining the abstract model.

Abstraction-Refinement. The use of abstraction-refinement for probabilistic systems has been pioneered by D’Argenio and coworkers [52, 53]. In this approach a first attempt is made to prove a reachability property on the coarsest imaginable abstraction of the system. If that verification fails, the system is successively refined until a conclusive answer can be given.

Predicate and Game-Based Abstraction. The above concept has been taken up in combination with predicate abstraction and counterexample guided refinement [45, 101], so as to form probabilistic counterexample-guided abstraction-refinement. Another important variation of this concept employs game-based abstraction [110, 150]. Here, one player is representing the non-determinism that is inherent in the MDP, while the other player controls the non-determinism introduced by the abstraction, i.e., by the grouping of states into sets. The analysis of the resulting two-player stochastic game yields lower and upper bounds for the reachability properties of the MDP. The tightness of these bounds indicate the quality of the abstraction and form the basis of refinement. This typically relies on disagreeing strategies for the individual players to make the abstraction more precise when required. Magnifying-lens abstraction [61] uses a similar scheme, but rather considers the concrete states contained in an abstract state in each step, thereby magnifying the state as needed.

Three-Valued Abstraction. Three-valued semantics, i.e., an interpretation in which a formula evaluates to either true, false, or indefinite may help out. In this setting, abstraction is conservative for both positive and negative verification results. Only if the verification of the abstract model yields an indefinite answer (“don’t know”), the validity in the concrete model is unknown. This has been adopted to interval MDPs [109]. For a queueing system from performance evaluation, (hand-crafted) three-valued abstraction shows that \(10^{278}\) concrete states (calculated analytically) can be reduced to 1.2 million states, while preserving six decimals accuracy for timed reachability probabilities [111].

Other Approaches. A prominent technique to construct safe abstractions while possibly working with an explicit-state representation is partial-order reduction. This has effectively been lifted to the probabilistic setting [13, 54, 82] where it exhibits similarities with confluence reduction approaches [95]. Another approach to perform abstraction for probabilistic automata [64] uses may and must modalities, inspired by modal transition systems [121].

Fig. 4.
figure 4

Explicit MDP model checking

Full size image

Example 5

We provide a glimpse of the effectiveness of several of the approaches mentioned above, especially symbolic representations and bisimulation-based compression.

Figure 4 provides a log-log scale plot of the total time (i.e., MDP construction from a high-level description plus the MDP model checking time) against the number of MDP states. It indicates the maximal size of the MDP that can be constructed and solved within 10,000 s when using an explicit engine, i.e., sparse matrix representations of the MDP. The results are obtained for all MDP case studies taken from the PRISM benchmark [117] suite. All MDPs model randomized distributed algorithms as indicated in the legend. The largest solved MDP instance within 10,000 s has about \(130\cdot 10^6\) states. The specifications are (minimal and maximal) reachability probability and expected reward objectives. Figure 5 provides a similar plot when carrying out the MDP model checking in a fully symbolic manner using MTBDDs. All experimental results are obtained using the storm model checker with accuracy \(10^{{-}6}\) [63].

Fig. 5.
figure 5

Symbolic MDP model checking

Full size image

For most cases, the best results are obtained using a mixture of symbolic and explicit engines—this is also referred to as hybrid or symblicit. In that case, operations that can be done more efficiently using an explicit representation are done explicitly, whereas remaining operations are done on a symbolic representations. Figure 6 indicates the model sizes that can be treated within 10,000 s. The hybrid engine solves the largest problem instance of \(2\cdot 10^9\) states within 26 min.

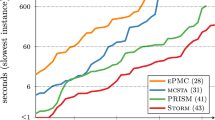
As mentioned before, another important technique to curb the state-space explosion problem is bisimulation minimization. The effect of this technique on the MDP benchmark is indicated in Fig. 7. The reduction factor depends on the specification \(\varphi \). For some qualitative specifications even models of one state remain. Reductions up to factor 10,000 are obtained. As indicated, for various MDPs the minimization could not be completed within 10,000 s (TO) and 16 GB RAM (MO).

Fig. 6.
figure 6

Hybrid MDP model checking

Full size image
Fig. 7.
figure 7

MDP reduction by bisimulation

Full size image

6 Epilogue

The previous sections surveyed various techniques for the analysis of MDPs and related policy synthesis questions. This survey is by far not complete and there are many other research directions addressing the analysis of MDP-like models. Let us mention a few more recent developments.

A promising new direction is to combine verification and learning techniques. On the one hand, model checking examines all possible behaviours, in particular, certain corner cases are detected. An interesting question is if this information can be leveraged to train AI models in the sense that these corner cases are considered for the observed data. On the other hand, employing learning techniques could improve PMC’s scalability. Initial results are promising. For instance, [37] exploits reinforcement learning so as to avoid treating fragments of the state space that do almost not contribute to the probability of interest. For a mutual exclusion protocol with \(10^{13}\) states only less than 2,000 are visited by the method ensuring a precision of \(10^{-6}\). Another example is the iterative combination of PMC and reinforcement learning to synthesize a safe policy whose expected cost is low for an MDP with unknown costs [105] as well as in the context of the compositional analysis of MDPs [75]. Learning has also been applied to continuous-time MDP (using gradient ascent) [22]. The use of automata learning techniques for probabilistic models [124] is also an interesting future direction.

Another future direction is the use of parallelization to exploit the presence of multiple cores in modern computers for MDP model checking. It is fair to say that this is still at its infancy. So far, determining maximal end components in MDPs has been parallelized on GPGPUs [152], but apart from some initial investigations in the setting of Markov chains [30], probabilistic computations on MDPs seem not yet to be parallelized.

The treatment in this paper has primarily focused on finite-state MDPs. A large variety of generalizations of infinite-state MDPs have been (and still are) investigated. Timed automata equipped with discrete branching probabilities give rise to uncountably large MDPs due to real-valued clocks. Using the region construction technique from timed automata [1], the standard algorithms for finite MDPs suffice for the analysis [118]. Model checking of (discrete-time) uncountable MDPs is treated in [144]. Countably infinite variants of MDPs include probabilistic lossy channel systems [7] where message losses have a probabilistic behavior while the component finite-state processes behave nondeterministically, one-counter MDPs [36], MDPs equipped with counters that can be arbitrarily negative or positive, and recursive MDPs [71, 73] (that subsume one-counter MDPs). Recursive MDPs are equivalent to push-down MDPs. Deciding whether there is a policy that yields termination probability one is undecidable for recursive MDPs. Whereas in the finite-state setting, the least fixed point (least non-negative) solution to a monotone system of linear equations is key to MDP model checking, for termination probabilities of recursive MDPs these equations are polynomial. Infinite MDPs are a natural operational model for probabilistic programming with non-determinism [84, 126].