Efficient Cardinality/Mean-Variance Portfolios

Abstract

We propose a novel approach to handle cardinality in portfolio selection, by means of a biobjective cardinality/mean-variance problem, allowing the investor to analyze the efficient tradeoff between return-risk and number of active positions. Recent progress in multiobjective optimization without derivatives allow us to robustly compute (in-sample) the whole cardinality/mean-variance efficient frontier, for a variety of data sets and mean-variance models. Our results show that a significant number of efficient cardinality/mean-variance portfolios can overcome (out-of-sample) the naive strategy, while keeping transaction costs relatively low.

Luís Vicente: Support for this research was provided by FCT under the grant PTDC/MAT/098214/2008.

1 Introduction

One knows since the pioneer work of Markowitz [19] that a rational investor has typically two goals in mind: to maximize the portfolio return (given, e.g., by the portfolio expected return) and to minimize the portfolio risk (described, e.g., by the portfolio variance). Traditionally, the Markowitz mean-variance optimization model is taken as a quadratic program (QP), intended to minimize the portfolio risk (variance) for a given level of expected return, over a set of feasible portfolios. By varying the level of expected return, the Markowitz model determines the so-called efficient frontier, as the set of nondominated portfolios regarding the two goals (variance and mean of the return). The rational investor can thus make choices, by analyzing the tradeoff between expected return and variability of the investment, over a set of appropriate portfolios.

Several modifications to the classical Markowitz model or alternative methodologies have since then been proposed. One resulting from a simple observation was suggested in an article by DeMiguel, Garlappi, and Uppal [14]. These authors analyzed a number of methodologies inspired on the classic model of Markowitz and showed that none were able to significantly and consistently overcome the naive strategy, that is to say, the one in which the available investor’s wealth is divided equally among the available securities. One possible explanation is related to the ill conditioning of the objective function of the Markowitz model (given by the variance of the return).

One of the important issues to consider in portfolio selection is how to handle transaction costs. There are well known modifications that can be made in the Markowitz model to incorporate transaction costs, such as to bound the turnover, which basically amount to further linear constraints in the QP. A recent technique to keep transaction costs low consists of selecting sparse portfolios, i.e., portfolios with few active positions, by imposing a cardinality constraint. Such a constraint, however, changes the classical QP into a MIQP (mixed-integer quadratic programming), which can no longer be solved in polynomial time.

In this paper, we suggest an alternative approach to the cardinality constrained Markowitz mean-variance optimization model, reformulating it directly as a biobjective problem, allowing the investor to analyze the tradeoff between cardinality and mean-variance, in a general scenario where short-selling is permitted. Such an approach allows us to find the set of nondominated points of biobjective problems in which an objective is smooth and combines mean and variance and the other is nonsmooth (the cardinality or $\ell _0$ norm of the vector of portfolio positions). The mean-variance objective function can take a number of forms. A parameter free possibility is given by profit per unity of risk (a nonlinear function obtained by dividing the expected return by its variance).

Given the lack of derivatives of the cardinality function, we decided then to apply a directional derivative-free algorithm for the solution of the biobjective optimization problem. Such methods do not require derivatives, although their convergence results typically assume some weak form of smoothness such as Lipschitz continuity. Direct multisearch is a derivative-free multiobjective methodology for which one can show some type of convergence in the discontinuous case. More importantly, it exhibited excellent numerical performance on a comparison to a number of other multiobjective optimization solvers. We applied direct multisearch to determine (in-sample) the set of efficient or nondominated cardinality/mean-variance portfolios.

To illustrate our approach, we gathered several data sets from the FTSE 100 index (for returns of single securities) and from the Fama/French benchmark collection (for returns of portfolios), computed the efficient cardinality/mean-variance portfolios using (in-sample) optimization, and measured their out-of-sample performance using a rolling-sample approach. We found that a large number of sparse portfolios for the FTSE 100 data sets, among the efficient cardinality/mean-variance ones, consistently overcome the naive strategy in terms of out-of-sample performance measured by the Sharpe ratio. This effect is also clearly visible for the FF data sets, where the performance of a large portion of the cardinality/mean-variance efficient frontier outperforms, in most of the instances, the naive strategy. The transactions costs are shown to be relatively low for all efficient cardinality/mean-variance portfolios, with a moderate increase with cardinality.

The organization of our paper is as follows. In the next section, we formulate the classical Markowitz model for portfolio selection, describe the naive strategy, and formulate the problem with cardinality constraint. In Sect. 3, we reformulate the cardinality constrained Markowitz mean-variance optimization model as a biobjective problem for application of multiobjective optimization. In Sect. 4, we present the empirical results. Finally, in Sect. 5 we summarize our findings and discuss future research.

2 Portfolio Selection Models

2.1 The Classical Markowitz Mean-Variance Model

Portfolios consist of securities (shares or bonds, for example, or classes or indices of the same). Suppose the investor has a certain wealth to invest in a set of $N$ securities. The return of each security $i$ is described by a random variable $R_i$, whose average can be computed (from estimation based on historical data). Let $\mu _i=E(R_i)$, $i=1,\ldots ,N$, denote the expected returns of the securities. Let also $w_i$, $i=1,\ldots ,N$, represent the proportions of the total investment to allocate in the individual securities. The portfolio return is assumed linear in $w_1,\ldots ,w_N$, and thus the portfolio expected return can be written as

$$ E(R) \; = \; E(w_iR_1+\cdots +w_NR_N) \; = \; w_1\mu _1+\cdots +w_N\mu _N \; = \; \mu ^\top w\nonumber $$

with

$$ \mu \; = \; (\mu _1,\ldots ,\mu _N)^\top \quad \mathrm {and}\quad w \; = \; (w_1,\ldots ,w_N)^\top . $$

The portfolio variance, in turn, is calculated by

$$V(R) \; = \; E\bigg (\bigg [\sum _{i=1}^{N}{w_iR_i}-E\bigg (\sum _{i=1}^{N}{w_iR_i}\bigg )\bigg ]^2\bigg ).$$

So,

$$V(R) \; = \; \sum _{i=1}^{N}\sum _{j=1}^{N}{E[(R_i-\mu _i)(R_j-\mu _j)]w_iw_j}.$$

Representing each entry $i,j$ of the covariance matrix $Q$ by

$$\sigma _{ij}=E[(R_i-\mu _i)(R_j-\mu _j)],$$

one has

$$V(R) \; = \; w^\top Qw,$$

where $Q$ is symmetric and positive semi-definite (and typically assumed positive definite). As said before, a portfolio is defined by an $N\times 1$ vector $w$ of weights representing the proportion of the total funds invested in the $N$ securities. This vector of weights is thus required to satisfy the constraint

$$\sum _{i=1}^{N}{w_i} \; = \; e^\top w \; = \; 1,$$

where $e$ is the $N\times 1$ vector of entries equal to $1$. Lower bounds on the variables, of the form $w_i \ge 0$, $i=1,\ldots ,n$, can be also considered if short selling is undesirable. In general, we will say that $L_i \le w_i \le U_i$, $i=1,\ldots ,N$, for given lower $L_i$ and upper $U_i$ bounds on the variables.

Markowitz’s model [19, 20] is based on the formulation of a mean-variance optimization problem. By solving this problem, we identify a portfolio of minimum variance among all which provide an expected return not below a certain target value $r$. The aim is thus to minimize the risk from a given level of return. The formulation of this problem can be described as:

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} w^\top Qw\\ {\text {subject to}} &{} \mu ^\top w \ge r,\\ &{} e^\top w=1, \\ &{} L_i \le w_i \le U_i, \quad i=1,\ldots ,N. \end{array} \end{aligned}$$

(1)

Problem (1) is a convex quadratic programming problem (QP), for which the first order necessary conditions are also sufficient for (global) optimality. See [12, 21] for a survey of portfolio optimization. The classical Markowitz mean-variance model can be seen as way of solving the biobjective problem which consists of simultaneously minimizing the portfolio risk (variance) and maximizing the portfolio profit (expected return)

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} w^\top Qw\\ \displaystyle \max _{w\in \mathbb {R}^N} &{} \mu ^\top w\\ {\text {subject to}} &{} e^\top w=1, \\ &{} L_i \le w_i \le U_i, \quad i=1,\ldots ,N. \end{array} \end{aligned}$$

(2)

In fact, it is easy to prove that a solution of (1) is nondominated, efficient or Pareto optimal for (2). Efficient portfolios are thus the ones which have the minimum variance among all that provide at least a certain expected return, or, alternatively, those that have the maximal expected return among all up to a certain variance. The efficient frontier (or Pareto front) is typically represented as a 2-dimensional curve, where the axes correspond to the expected return and the standard deviation of the return of an efficient portfolio.

2.2 The Naive Strategy $1/N$

The naive strategy is the one in which the available investor’s wealth is divided equally among the securities available

$$w_i = \frac{1}{N},\quad i=1,\ldots ,N.$$

This strategy has diversification as its main goal, it does not involve optimization, and it completely ignores the data.

Although a number of theoretical models have been developed in the last years, many investors pursuing diversification revert to the use of the naive strategy to allocate their wealth (see [4]). DeMiguel, Garlappi, and Uppal [14] evaluated fourteen models across seven empirical data sets and showed that none is consistently better than the naive strategy. A possible explanation for this phenomenon lies on the fact that the naive strategy does not involve estimation and promotes ‘optimal’ diversification. The naive strategy is therefore an excellent benchmarking strategy.

2.3 The Cardinality Constrained Markowitz Mean-Variance Model

Since the appearance of the classical Markowitz mean-variance model, a number of methodologies have been proposed to render it more realistic. The classical Markowitz model assumes a perfect market without transaction costs or taxes, but such costs are an important issue to consider as far as the portfolio selection is concerned, especially for small investors. Recently, it has been studied the addition of a constraint that sets an upper bound on the number of active positions taken in the portfolio, in an attempt to improve performance and reduce transactions costs. Such a cardinality constraint is defined by limiting ${{\mathrm{card}}}(x)= | \{i \in \{ 1,...,N \}: x_i\ne 0\}|$ and leads to cardinality constrained portfolio selection problems. In particular, the cardinality constrained Markowitz mean-variance optimization problem has the form:

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} w^\top Qw\\ {\text {subject to}} &{} \mu ^\top w\ge r,\\ &{} {{\mathrm{card}}}(w)\le K, \\ &{} e^\top w=1, \\ &{} L_i \le w_i \le U_i, \quad i=1,\ldots ,N, \end{array} \end{aligned}$$

(3)

where $K \in \{1,\ldots ,N\}$. Although ${{\mathrm{card}}}(x)$ is not a norm, it is frequently called the $\ell _0$ norm in the literature, $\Vert x\Vert _0={{\mathrm{card}}}(x)$. By introducing binary variables, one can rewrite the problem as a mixed-integer quadratic programming (MIQP) problem:

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w,y\in \mathbb {R}^N} &{} w^\top Qw\\ {\text {subject to}} &{} \mu ^\top w\ge r,\\ &{}e^\top y \le K,\\ &{}e^\top w=1, \\ &{} L_i y_i \le w_i \le U_i y_i, \quad i=1,\ldots ,N, \\ &{} y_i \in \{0,1\}, \quad i=1,\ldots ,N. \end{array} \end{aligned}$$

(4)

However such MIQPs are known to be hard combinatorial problems. The number of sparsity patterns in $w$ (i.e., number of different possibilities of having $K$ nonzeros entries) is $\left( {\begin{array}{c}N\\ K\end{array}}\right) =N!/[(N-K)!K!]$. Although there are exact algorithms for the solution of MIQPs (see [5–7, 25]), many researchers and portfolio managers prefer to use heuristics approaches (see [3, 9, 11, 15, 17, 26]). Some of these heuristics vary among evolutionary algorithms, tabu search, and simulated annealing (see [15, 26]).

Promotion of sparsity is also used in the field of signal and imaging processing, where a new technique called compressed sensing has been intensively studied in the recent years. Essentially one aims at recovering a desired signal or image with the least possible amount of basis components. The major developments in compressed sensing have been achieved by replacing the $\ell _0$ norm by the $\ell _1$ one, the latter being a convex relation of the former and known to also promote sparsity. The use of the $\ell _1$ norm leads to recovering optimization problems solvable in polynomial time (in most of the cases equivalent to linear programs), and a number of sparse optimization techniques have been developed for the numerical solution of such problems. These ideas have already been used in portfolio selection primarily to promote regularization of ill conditioning (of the estimation of data or of the variance of the return itself). DeMiguel et al. [13] constrained the Markowitz classical model by imposing a bound on the $\ell _1$ norm of the vector of portfolio positions, among other possibilities. Brodie et al. [8] focus on a modification to the Markowitz mean-variance classical model by the incorporation of a term involving a multiple of the $\ell _1$ norm of the vector of portfolio positions. Inspired by sparse reconstruction (see, for instance, [7]), they also proposed an heuristic for the solution of the problem.

3 The Cardinality/Mean-Variance Biobjective Model

Although the cardinality constrained Markowitz mean-variance model described in (3) provides an alternative to the classical Markowitz model in the sense of realistically limiting the number of active positions in a portfolio, it is dependent on the parameter $K$, the maximum number of such positions. Thus, one has to vary $K$ to obtain various levels of cardinality or sparsity, and for each value of $K$ solve an MIQP of the form (4).

The alternative suggested in this paper is to consider the cardinality function as an objective function itself. At a first glance, one could see the problem as a triobjective optimization problem by minimizing the variance of the return, maximizing the expected return, and minimizing the cardinality over the set of feasible portfolios. Such a framework was taken into account in the studies [1, 2, 10, 18]. However, these authors did not investigate the effects of cardinality constraints on portfolio models in terms of out-of-sample performance, a subject still poorly analyzed in the literature. On the other hand, investors may find it useful to directly analyze the tradeoff between cardinality and mean-variance. A parameter-free possibility is to consider a Sharpe ratio type objective function, by maximizing expected return per variance and minimizing the cardinality, over the set of feasible portfolios. In this case, the cardinality/mean-variance biobjective optimization problem is posed as

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} -\frac{\mu ^\top w}{w^ \top Q w}\\ \displaystyle \min _{w\in \mathbb {R}^N} &{} {{\mathrm{card}}}(w)\\ {\text {subject to}} &{} e^\top w=1, \\ &{} L_i \le w_i \le U_i, \quad i=1,\ldots ,N. \end{array} \end{aligned}$$

(5)

By solving (5), we identify a cardinality/mean-variance efficient frontier. A portfolio in this frontier is such that there exists no other feasible one which simultaneously presents a lower cardinality and a lower mean-variance measure. Given such an efficient frontier and a mean-variance target, an investor may directly find the answers to the questions of what is the optimal (lowest) cardinality level that can be chosen and what are the portfolios leading to such a cardinality level. Problem (5) has two objective functions and linear constraints. The first objective $f_1(w)=-\mu ^\top w / w^ \top Q w$ is nonlinear but smooth. However, the second objective function $f_2(w)={{\mathrm{card}}}(w)= | \{i \in \{ 1,...,N \}: w_i\ne 0\}|$ is piecewise linear discontinuous, consequently nonlinear and nonsmooth. We have thus decided to solve the biobjective optimization problem (5) using a derivative-free solver, based on direct multisearch.

4 Empirical Performance of Efficient Cardinality/Mean-Variance Portfolios

Now we report a number of experiments made to numerically determine and assess the efficient cardinality/mean-variance frontier. We applied direct multisearch to determine the Pareto front or efficient frontier of the biobjective optimization problem (5) (according to Appendix A). We tested three data sets collected from the FTSE 100 index and three others from the Fama/French benchmark collection (see Subsect. 4.1). The efficient frontiers obtained by the initial in-sample optimization are given in Subsect. 4.2.

The out-of-sample performance of the cardinality/mean-variance efficient portfolios, measured by a rolling-sample approach, is described in Subsect. 4.3. In Subsect. 4.4 we measure the out-of-sample performance by the Sharpe ratio, in Subsubsect. 4.5 we report the proportional transaction costs, and in Subsect. 4.6 we measure the out-of-sample performance by the Sharpe ratio of returns net of transaction costs, all of this for each cardinality/mean-variance efficient portfolio. To better assess the robustness of our results, we also considered, using the FTSE 100 data, a sample including the financial crisis years 2008–2010, and the corresponding results are reported in Subsect. 4.7. The section is ended with a discussion of the overall obtained results.

4.1 Data Sets

For the first three data sets we collected daily data for securities from the FTSE 100 index, from 01/2003 to 12/2007 (five years). Such data is public and available from the site http://www.bolsapt.com. The three data sets are referred to as DTS1, DTS2, and DTS3, and are formed by 12, 24, and 48 securities, respectively. The composition of these data sets is given in Table 1. We used the daily continuous returns for the in-sample optimization (estimation of $Q$ and $\mu$) and the daily discrete returns for the out-of-sample analysis. We also included in our experiments three data sets from the Fama/French benchmark collection (FF10, FF17, and FF48, with cardinalities 10, 17, and 48), using the monthly returns from 07/1971 to 06/2011 (forty years) given there for a number of industry security sectors. More information on these security sectors (or portfolios of securities) can be found in http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html.

Table 1. Composition of the three data sets from the FTSE 100 index. In brackets we indicate the data set to which each security belongs to.

Fig. 1.

Efficient frontier of the biobjective cardinality/mean-variance problem for DTS1.

Naive

Markowitz mean per variance $\blacksquare$ Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 2.

Efficient frontier of the biobjective cardinality/mean-variance problem for DTS2. See the caption of Fig. 1 for an explanation of the various symbols.

Fig. 3.

Efficient frontier of the biobjective cardinality/mean-variance problem for DTS3. See the caption of Fig. 1 for an explanation of the various symbols.

Fig. 4.

Efficient frontier of the biobjective cardinality/mean-variance problem for FF10.

Naive

Markowitz mean per variance $\blacksquare$ Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 5.

Efficient frontier of the biobjective cardinality/mean-variance problem for FF17. See the caption of Fig. 4 for an explanation of the various symbols.

Fig. 6.

Efficient frontier of the biobjective cardinality/mean-variance problem for FF48. See the caption of Fig. 4 for an explanation of the various symbols.

Fig. 7.

Out-of-sample performance for DTS1 measured by the Sharpe ratio over all the out-of-sample periods.

Naive

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 8.

Out-of-sample performance for DTS2 measured by the Sharpe ratio over all the out-of-sample periods. See the caption of Fig. 7 for an explanation of the various symbols and lines.

Fig. 9.

Out-of-sample performance for DTS3 measured by the Sharpe ratio over all the out-of-sample periods. See the caption of Fig. 7 for an explanation of the various symbols and lines.

Fig. 10.

Out-of-sample performance for FF10 measured by the Sharpe ratio over all the out-of-sample periods.

Naive

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 11.

Out-of-sample performance for FF17 measured by the Sharpe ratio over all the out-of-sample periods. See the caption of Fig. 10 for an explanation of the various symbols and lines.

Fig. 12.

Out-of-sample performance for FF48 measured by the Sharpe ratio over all the out-of-sample periods. See the caption of Fig. 10 for an explanation of the various symbols and lines.

Fig. 13.

Transaction costs of the efficient cardinality/mean-variance portfolios for DTS1.

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 14.

Transaction costs of the efficient cardinality/mean-variance portfolios for DTS2. See the caption of Fig. 13 for an explanation of the various symbols and lines.

Fig. 15.

Transaction costs of the efficient cardinality/mean-variance portfolios for DTS3. See the caption of Fig. 13 for an explanation of the various symbols and lines.

Fig. 16.

Transaction costs of the efficient cardinality/mean-variance portfolios for FF10.

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 17.

Transaction costs of the efficient cardinality/mean-variance portfolios for FF17. See the caption of Fig. 16 for an explanation of the various symbols and lines.

Fig. 18.

Transaction costs of the efficient cardinality/mean-variance portfolios for FF48. See the caption of Fig. 16 for an explanation of the various symbols and lines.

Fig. 19.

Out-of-sample performance for DTS1 measured by the Sharpe ratio over all the out-of-sample periods.

Naive

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 20.

Out-of-sample performance for DTS2 measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods.See the caption of Fig. 19 for an explanation of the various symbols and lines.

Fig. 21.

Out-of-sample performance for DTS3 measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods.See the caption of Fig. 19 for an explanation of the various symbols and lines.

Fig. 22.

Out-of-sample performance for FF10 measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods.

Naive

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 23.

Out-of-sample performance for FF17 measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods. See the caption of Fig. 22 for an explanation of the various symbols and lines.

Fig. 24.

Out-of-sample performance for FF48 measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods. See the caption of Fig. 22 for an explanation of the various symbols and lines.

Fig. 25.

Out-of-sample performance for DTS1, including the financial crisis years 2008–2010, measured by the Sharpe ratio over all the out-of-sample periods.

Naive

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 26.

Out-of-sample performance for DTS2, including the financial crisis years 2008–2010, measured by the Sharpe ratio over all the out-of-sample periods. See the caption of Fig. 25 for an explanation of the various symbols and lines.

Fig. 27.

Out-of-sample performance for DTS3, including the financial crisis years 2008–2010, measured by the Sharpe ratio over all the out-of-sample periods. See the caption of Fig. 25 for an explanation of the various symbols and lines.

Fig. 28.

Transaction costs of the efficient cardinality/mean-variance portfolios for DTS1, including the financial crisis years 2008–2010.

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 29.

Transaction costs of the efficient cardinality/mean-variance portfolios for DTS2, including the financial crisis years 2008–2010. See the caption of Fig. 28 for an explanation of the various symbols and lines.

Fig. 30.

Transaction costs of the efficient cardinality/mean-variance portfolios for DTS3, including the financial crisis years 2008–2010. See the caption of Fig. 28 for an explanation of the various symbols and lines.

Fig. 31.

Out-of-sample performance for DTS1, including the financial crisis years 2008–2010, measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods.

Naive

Markowitz mean per variance -.- Markowitz minimum variance

cardinality/mean-variance

cardinality constrained minimum variance (Color figure online)

Fig. 32.

Out-of-sample performance for DTS2, including the financial crisis years 2008–2010, measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods. See the caption of Fig. 31 for an explanation of the various symbols and lines.

Fig. 33.

Out-of-sample performance for DTS3, including the financial crisis years 2008–2010, measured by the Sharpe ratio of returns net of transaction costs over all the out-of-sample periods. See the caption of Fig. 31 for an explanation of the various symbols and lines.

Fig. 34.

Efficient frontier of the biobjective cardinality/mean-variance problem for FF100.

4.2 In-Sample Optimization

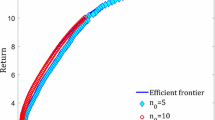
We then applied the solver dms (version 0.2) to compute the efficient frontier (or Pareto front) of the cardinality/mean-variance biobjective optimization problem (5). A few modifications to (5) were made before applying the solver as well as a few changes to the solver default parameters (the details are described in Appendix A). We present results for the initial in-sample optimization. For the FTSE 100 data sets this sample is from 01/2003 to 12/2006 and for the FF data sets is from 07/1971 to 06/1996. Figures 1, 2, 3, 4, 5, and 6 contain the plots of the efficient frontiers calculated for, respectively, the FTSE 100 and FF data sets. In all these plots we also marked three other portfolios. The first one is the $1/N$ portfolio corresponding to the naive strategy. A second one is obtained maximizing expected return per variance.

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} -\frac{\mu ^\top w}{w^\top Q w}\\ {\text {subject to}} &{} e^\top w=1. \end{array} \end{aligned}$$

(6)

This portfolio corresponds to the extreme point (of maximum cardinality) of the efficient frontier (or Pareto front) of the cardinality/mean-variance biobjective optimization problem (5). The third one is a classical Markowitz related portfolio and is obtained by minimizing variance under no short-selling

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} w^\top Qw\\ {\text {subject to}} &{} e^\top w \;= \; 1, \\ &{} w \ge 0. \end{array} \end{aligned}$$

(7)

This instance was solved using the quadprog function from the MATLAB [24] Optimization Toolbox. Regarding problem (7), it is known that not allowing short-sale has a regularizing effect on minimum-variance Markowitz portfolio selection (see [16]) and leads to portfolios of low cardinality.

Since we know that minimum variance portfolios outperform mean-variance portfolios (the estimate error of the expected returns is eliminated, see [16]), we considered the following cardinality constrained minimum variance model (instead of the one introduced in Sect. 2.3)

$$ \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} w^\top Qw\\ {\text {subject to}} &{} {{\mathrm{card}}}(w) \le K, \\ &{} e^\top w=1, \\ &{} L_i \le w_i \le U_i, \quad i=1,\ldots ,N. \end{array} $$

By introducing binary variables, one can rewrite this problem as a mixed-integer quadratic programming (MIQP) problem:

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w,y\in \mathbb {R}^N} &{} w^\top Qw\\ {\text {subject to}} &{}e^\top y \le K,\\ &{}e^\top w=1, \\ &{} L_i y_i \le w_i \le U_i y_i, \quad i=1,\ldots ,N, \\ &{} y_i \in \{0,1\}, \quad i=1,\ldots ,N. \end{array} \end{aligned}$$

(8)

We also mark in the plots the portfolios that result from solving problem (8) for each value of $K\in [1,N]$. For this purpose we used the solver cplexmiqp from ILOG IBM CPLEX for MATLAB [22].

4.3 Out-of-sample Performance

The analysis of out-of-sample performance relies on a rolling-sample approach. For the FTSE 100 data sets we considered 12 periods (months) of evaluation. We begin by computing the efficient frontier (or Pareto front) of the cardinality/mean-variance biobjective optimization problem (5) for the in-sample time window from 01/2003 to 12/2006 (see Subsect. 4.2). We then held fixed each portfolio and observed its returns over the next period (January 2007). Then we discarded January 2003 and brought January 2007 into the sample. We repeated this process until exhausting the 12 months of 2007. We applied the same rolling-sample approach to the FF data sets, considering an initial in-sample time window from 07/1971 to 06/1996 (see Subsect. 4.2) and 15 periods of evaluation (the 15 next years).

4.4 Out-of-sample Performance Measured by the Sharpe Ratio

In each period of evaluation, the out-of-sample performance was then measured by the Sharpe ratio

$$ S \; = \; \frac{m-r_f}{\sigma }, $$

where $m$ is the mean return, $r_f$ is the return of the risk-free asset¹, and $\sigma$ is the standard deviation. The results (over all the periods of evaluation) are given in Figs. 7, 8 and 9 for the FTSE 100 portfolios and in Figs. 10, 11 and 12 for the FF ones. Using IBM SPSS Statistics [23] we calculated the p-values for the statistical significance of the difference between Sharpe ratios of the benchmark naive portfolio and all the others computed portfolios. We did not report them here because they are not statistically significant.

4.5 Transaction Costs

Since one is rebalancing portfolios for each out-of-sample period, one can compute the transaction costs of such a trade. We set the proportional transaction cost equal to 50 basis points per transaction (as usually assumed in the literature). Thus the cost of a trade over all assets is given by

$$\begin{aligned} TC \; = \; \sum _{t=1}^{T-1} 0.5\,\% \sum _{i=1}^{N}\mid w_{i,t+1}-w_{i,t}\mid , \end{aligned}$$

(9)

with $T=12$ for the FTSE 100 data sets and $T=15$ for the FF data sets. The results are given in Figs. 13, 14 and 15 for the FTSE 100 portfolios and in Figs. 16, 17 and 18 for the FF ones.

4.6 Out-of-sample Performance Measured by the Sharpe Ratio of Returns Net of Transaction Costs

In the presence of transaction costs we calculated the Sharpe ratio of returns net of transaction costs

$$ SR \; = \; \frac{m-TC-r_f}{\sigma }, $$

where $m$ is the mean return, $TC$ is the proportional transaction cost in (9), $r_f$ is the return of the risk-free asset, and $\sigma$ is the standard deviation. The out-of-sample performance was then measured by the Sharpe ratio of returns net of transaction costs. The results are given in Figs. 19, 20 and 21 for the FTSE 100 portfolios and in Figs. 22, 23 and 24 for the FF ones.

4.7 Results Including the Financial Crisis Years 2008–2010

The FTSE 100 data set used covered the period 2003–2007. With the aim of testing the robustness of the results, we also tried a FTSE 100 data set that covers the time window 2003–2010 (including thus the financial crisis years 2008–2010). The data sets were formed as described in Sect. 4.1, but excluding British Airways (see Table 1) due to missing data during the period considered, and including Wolseley (following an arbitrary alphabetic order). We performed an out-of-sample analysis as described in Sect. 4.3. We used daily periods of evaluation. We began by computing the efficient frontier (or Pareto front) of the cardinality/mean-variance biobjective optimization problem (5) for the in-sample time window from 01/2003 to 12/2010 (using daily data). We then held fixed each portfolio and observed its returns over the next period (first trading day of January 2011). Then we discarded this first trading day of January 2011 and brought this into the sample. We repeated this process until exhausting the firsts 15 trading days of 2011.

The results of the out-of-sample performance measured by the Sharpe ratio² are given in Figs. 25, 26 and 27. The results of the proportional transaction costs, are given in Figs. 28, 29 and 30. The results of the out-of-sample performance measured by the Sharpe ratio of returns net of transaction costs, are given in Figs. 31, 32 and 33.

4.8 Discussion of the Results

Contrary to one could think, given the intractability of $f_2(w)={{\mathrm{card}}}(w)$ and the fact that no derivatives are being used for $f_1(w)=-\mu ^\top w / w^ \top Q w$, direct multisearch (the solver dms) was capable of quickly determining (in-sample) the efficient frontier for the biobjective optimization problem (5). For instance, for the data sets of roughly 50 assets, a regular laptop takes a few dozens of seconds to produce the efficient frontiers. We have a direct way of dealing with sparsity, which offers a complete determination of an efficient frontier for all cardinalities. According to a priori preferences, one could choose (in-sample) the desired cardinality. For the portfolios constructed using the FTSE 100 index data (portfolios of individual securities), a large number of our sparse portfolios, among the efficient cardinality/mean-variance ones, consistently overcame the naive strategy and at least one of the two related classical Markowitz models, in terms of out-of-sample performance measured by the Sharpe ratio. This effect has even happened for the largest data set (DTS3 with 48 securities), where the demand for sparsity is more relevant. For the portfolios constructed using the Fama/French benchmark collection (where securities are portfolios rather than individual securities), the scenario is different since the behavior of the naive strategy is even more difficult to outperform. Still, a large number of sparse efficient cardinality/mean-variance portfolios consistently overcame the naive strategy.

In both cases, FTSE 100 and FF data, the transaction costs of the efficient cardinality/mean-variance portfolios are lower than the mean per variance portfolio (solution of problem (6)) and higher than the minimum-variance portfolio (solution of problem (7)). Note that the minimum-variance portfolio does not allow short-selling, and so the weights at the outset are much more limited, thus leading to better results. Evaluating the performance out-of-sample by the Sharpe ratio of returns net of transaction costs (take into account the transaction costs), the efficient cardinality/mean-variance portfolios do not overcame the naive strategy for FTSE 100 data, but for FF data a large number of sparse efficient cardinality/mean-variance portfolios still consistently overcame the naive strategy. When we compare the performance results between the efficient cardinality/mean-variance portfolios and the cardinality constrained minimum variance portfolios (solution of (8)), without considering the transaction costs, we observed better results for the FTSE 100 and worse for the FF. The MIQP performed better in terms of Sharpe ratio of returns net of transaction costs since the cost of transaction costs are lower, one possible explanation for this is the fact of not taking into account the estimation of the expected returns. Moreover, our cardinality/mean-variance portfolios are truly efficient whereas the cardinality constrained minimum variance do not necessarily exhibit Pareto efficiency. For the FTSE 100 data set, the analysis including the financial crisis years 2008–2010 shows that the results are robust. Finally, we also computed the cardinality/mean-variance efficient frontier for the data set FF100, where portfolios are formed on size and book-to-market (see Fig. 34). (This time we needed a budget of the order of $10^7$ function evaluations, see Appendix A.) We remark that FF48 and FF100 are the data sets also used in [8]. In this paper, as we said before, the authors focus on a modification to the Markowitz classical model by the incorporation of a term involving a multiple of the $\ell _1$ norm of the vector of portfolio positions. Despite the different sparse-oriented techniques and different strategies for evaluating out-of-sample performance, in both approaches (theirs and ours), sparse portfolios are found overcoming the naive strategy. In our approach one computes sparse portfolios satisfying an efficient or nondominant property and one does it directly and in single run, whereas in [8], there is a need to vary a tunable parameter and select the portfolios according to some criterion to be met (for example, sparsity). It is unclear what sort of efficient or nondominant property their portfolios satisfy. Moreover, we provide results for all cardinality values (from 1 to 48 in FF48 and from 1 to 100 in FF100), while in [8] the authors report results for cardinality values from 4 and 48 (FF48) and from 3 to 60 (FF100). We therefore claim to have a more direct way of dealing with sparsity, which offers a complete determination of an efficient frontier for all cardinalities.

5 Conclusions and Perspectives for Future Work

In this paper we have developed a new methodology to deal with the computation of mean-variance Markowitz portfolios with pre-specified cardinalities. Instead of imposing a bound on the maximum cardinality or including a penalization or regularization term into the objective function (in classical Markowitz mean-variance models), we took the more direct approach of explicitly considering the cardinality as a separate goal. This led us to a cardinality/mean-variance biobjective optimization problem (5) whose solution is given in the form of an efficient frontier or Pareto front, thus allowing the investor to tradeoff among these two goals when having transaction costs and portfolio management in mind. In addition, and surprisingly, a significant portion of the efficient cardinality/mean-variance portfolios (with cardinality values considerably lower than the number $N$ of securities) have exhibited superior out-of-sample performance (under reasonably low transaction costs that only increase moderately with cardinality). We solved the biobjective optimization problem (5) using a derivative-free solver running direct multisearch. Direct-search methods based on polling are known in general to be slow but extremely robust due their directional properties. Such a feature is crucial given the difficulty of the problem (one discontinuous objective function, the cardinality, and discontinuous Pareto fronts). We have observed the robustness of direct multisearch, in other words, its capability of successfully solving a vast majority of the instances (all in our case) even if at the expense of a large budget of function evaluations. Direct multisearch was applied off-the-shelf to determine the cardinality/mean-variance efficient frontier. The structure of problem (5), or of its practical counterpart (10), was essentially ignored. One can use the fact that the first objective function is smooth and of known derivatives to speed up the optimization and reduce even further the budget of function evaluations. Moreover, we also point out that it is trivial to run the poll step of direct multisearch in a parallel mode.

The use of derivative-free single or multiobjective optimization opens the research range of future work in sparse or dense portfolio selection. In fact, since derivative-free algorithms only rely on zero order information, they are applicable to any objective function of black-box type. One can thus use any measure to quantify the profit and risk of a portfolio. The classical Markowitz model assumes that the return of a portfolio is a linear combination of the returns of the individual securities. Also, it implicitly assumes a Gaussian distribution for the return, letting its variance be a natural measure of risk. However, it is known from the analysis of stylized facts that the distribution for the return of securities exhibits tails which are fatter than the Gaussian ones. Practitioners consider other measures of risk and profit better tailored to reality. Our approach to compute the cardinality/mean-variance efficient frontier is ready for application in such general scenarios.

A Using Direct Multisearch to Determine Efficient Cardinality/Mean-Variance Portfolios

A few modifications to problem (5) were required to make it solvable by a multiobjective derivative-free solver, in particular by a direct multisearch one. In practice the first modification to (5) consisted of approximating the true cardinality, by introducing a tolerance $\epsilon$,

$$ \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{}-\frac{\mu ^\top w}{w^ \top Q w}\\ \displaystyle \min _{w\in \mathbb {R}^N} &{} \sum _{i=1}^N 1\!\!1_{ \{|w_i| > \epsilon \}}\\ {\text {subject to}} &{} e^\top w=1, \\ &{} L_i \le w_i \le U_i, \quad i=1,\ldots ,N. \end{array} $$

chosen as $\epsilon = 10^{-8}$ ($1\!\!1$ represents the indicator function). Secondly, we selected symmetric bounds on the variables $L_i=-b$ and $U_i=b$,

$$ \begin{array}{ll} \displaystyle \min _{w\in \mathbb {R}^N} &{} -\frac{\mu ^\top w}{w^ \top Q w}\\ \displaystyle \min _{w\in \mathbb {R}^N} &{} \sum _{i=1}^N 1\!\!1_{ \{|w_i| > \epsilon \} }\\ {\text {subject to}} &{} e^\top w \;= \; 1,\\ &{} - b \; \le \; w_i \; \le \; b, \quad i=1,\ldots ,N, \end{array} $$

setting $b=10$. Finally, we eliminated the constraint $e^\top w = 1$ since direct search methods do not cope well with equality constraints. The version fed to the dms solver was then

$$\begin{aligned} \begin{array}{ll} \displaystyle \min _{w(1:N-1)\in \mathbb {R}^{N-1}} &{} -\frac{\mu ^\top w}{w^ \top Q w} \\ \displaystyle \min _{w(1:N-1)\in \mathbb {R}^{N-1}} &{} \sum _{i=1}^{N-1} 1\!\!1_{ \{ |w_i| > \epsilon \} }\\ {\text {subject to}} &{} - b \; \le \; w_i \; \le \; b, \quad i=1,\ldots ,N-1,\\ &{} -b \; \le \; 1-\sum _{i=1}^{N-1} w_i \; \le \; b, \end{array} \end{aligned}$$

(10)

where $w_N$ in $-\mu ^\top w/ w^ \top Q w$ was replaced by $1-\sum _{i=1}^{N-1} w_i$.

We used a ll the default parameters of dms (version 0.2) with the following four exceptions. First, we needed to increase the maximum number of function evaluations allowed (from 20000 to 2000000 for $N(=n)$ up to 50) given the dimension of our portfolios, as well as to require more accuracy by reducing the step size tolerance from $10^{-3}$ to $10^{-7}$. Then we turned off the use of the cache of previously evaluated points to make the runs faster (the default version of dms keeps such a list to avoid evaluating points too close to those already evaluated). Lastly, we realized that initializing the list of feasible nondominated points with a singleton led to better results than initializing it with a set of roughly $N$ points as it happens by default. Thus, we set the option list of dms to zero, which, given the bounds on the variables, assigns the origin to the initial list.