Protecting Against Multidimensional Linear and Truncated Differential Cryptanalysis by Decorrelation

Abstract

The decorrelation theory provides a different point of view on the security of block cipher primitives. Results on some statistical attacks obtained in this context can support or provide new insight on the security of symmetric cryptographic primitives. In this paper, we study, for the first time, the multidimensional linear attacks as well as the truncated differential attacks in this context. We show that the cipher should be decorrelated of order two to be resistant against some multidimensional linear and truncated differential attacks. Previous results obtained with this theory for linear, differential, differential-linear and boomerang attacks are also resumed and improved in this paper.

1 Introduction

In the last 25 years many statistical attacks have been proposed and implemented on different symmetric key cryptographic primitives. Nowadays, new symmetric primitives are not considered secure until evaluation by the community. But it is often difficult to evaluate the security of a cipher due to the large number of known attacks.

In 1998, Vaudenay [18, 21] introduced the decorrelation theory to prevent this long and tedious security evaluation. When a cipher is designed and proved secure up to a certain degree of decorrelation, it is secure against a wide range of statistical attacks. Among statistical attacks, differential cryptanalysis [8], linear cryptanalysis [17] and their generalizations have been prominent. For instance, we know that a cipher decorrelated of order two is resistant to the classical differential and linear cryptanalysis. Recently [7], it has been shown that the primitives should be decorrelated of order four to be protected against differential-linear [3, 13] and boomerang [22] attacks.

Understanding the similitude of the different statistical attacks is of great importance to simplify the security analysis of the symmetric cryptographic primitives. While different works in that direction have been presented in the last couple of years [4, 9, 10, 16], part of this unification can also be obtained by determining the order of decorrelation of the new presented attacks. However, the question of measuring the advantage of taking the information from different differentials or linear approximations has not yet been studied in the context of decorrelation theory. In this paper, we study the decorrelation order of the multidimensional linear and truncated differential attacks. In particular, we show that a cipher is protected against multidimensional linear attacks if it is decorrelated of order two. Some elements of the proof are related to the link between multidimensional linear attacks and truncated differential attacks which was discovered by Blondeau and Nyberg [9, 10]. Using the result obtained for a special truncated differential distinguisher, we have been able to determine that the truncated differential attacks involving a large number of input differences are also decorrelated of order two. Using the decorrelation theory, in this paper, we provide for the first time an intuition on the power of truncated differential and multidimensional linear attacks as a function of the number of involved differential or linear approximations used in the attack.

Outline. In Sect. 2, we recall some basic definitions and previous works in the context of the decorrelation theory. In Sect. 3 we study the multidimensional linear attack in this context. In Sect. 4, we study the decorrelation order of the truncated differential attack. In Sect. 5, we provide some improvement of the previous results for the well known differential, linear, differential-linear and boomerang attacks. Section 6 concludes this paper.

2 Preliminaries

2.1 Statistical Attacks

We recall in this section some basic definitions related to the statistical attacks studied in this paper.

Linear cryptanalysis [17] uses a linear relation between bits from plaintexts, corresponding ciphertexts, and the encryption key. Given a permutation $\mathsf {Enc}$ over $\{0,1\}^\ell$, the strength of the linear relation is measured by its correlation. The correlation of a function $\mathsf {Enc}:\mathbb {F}_2^{\ell }\rightarrow \mathbb {F}_2^{\ell }$ at point $(\alpha ,\beta )\in \mathbb {F}_2^{\ell }\times \mathbb {F}_2^{\ell }$ is defined as

$$\begin{aligned} \mathsf {cor}(\alpha ,\beta ) = 2^{-\ell } \Big [&\# \left\{ x\in \mathbb {F}_2^{\ell }|\alpha \cdot x \oplus \beta \cdot \mathsf {Enc}(x)=0 \right\} - \\&\# \left\{ x\in \mathbb {F}_2^{\ell }| \alpha \cdot x \oplus \beta \cdot \mathsf {Enc}(x)= 1 \right\} \Big ], \end{aligned}$$

where the quantity within brackets can be computed as the Walsh transform of $\alpha \cdot x \oplus \beta \cdot \mathsf {Enc}(x)$ evaluated at zero.

Through this paper, the square correlation at point $v=(\alpha ,\beta )\in \mathbb {F}_2^{2\ell }$ will be denoted by $\mathsf {LP}^\mathsf {Enc}(v)$ and corresponds to $\mathsf {LP}^\mathsf {Enc}(v)=\mathsf {cor}^2(\alpha ,\beta )$.

For the generalizations of linear cryptanalysis, such as multidimensional linear cryptanalysis [14], a quantity C, called capacity, is used for evaluating the non-uniformity of the set of linear approximations.

The capacity corresponds to the sum of the square correlations of the involved linear approximations. We let $V\subset \mathbb {F}_2^{2\ell }$ be the vector space spanned by different $(\alpha _j,\beta _j)$ masks. In the context of multidimensional linear attacks, we define the capacity

$$ \mathsf {cap}_\mathsf {Enc}(V)=\sum _{v\in V,v\ne 0}\mathsf {LP}^\mathsf {Enc}(v). $$

In the following of this paper, we denote by k the dimension of V.

In differential cryptanalysis [8], the attacker is interested in finding and exploiting non-uniformity in occurrences of plaintext and ciphertext differences. Given the differences $\varDelta \in \mathbb {F}_2^{\ell }$ and $\varGamma \in \mathbb {F}_2^{\ell }$, the probability $\mathsf {DP}^\mathsf {Enc}(\varDelta ,\varGamma )$ of the differential $(\varDelta ,\varGamma )$ is defined as

$$ \mathsf {DP}^\mathsf {Enc}(\varDelta ,\varGamma )= 2^{-\ell }\# \{ x\in \mathbb {F}_2^{\ell }\,|\, \mathsf {Enc}(x)\oplus \mathsf {Enc}(x \oplus \varDelta ) = \varGamma \}. $$

The power of the generalization of differential cryptanalysis involving multiple differentials is measured by a sum or average of these probabilities. For the truncated differential attacks [15] with differences $(\varDelta ,\varGamma )$ in the vector space $V^\perp \subset \mathbb {F}_2^{2\ell }$ we define

$$ {P^\mathsf {STD}_\mathsf {Enc}}(V^\perp ) =2^{-2\ell }\# \{ (x,x')\in \mathbb {F}_2^{\ell }\times \mathbb {F}_2^{\ell } \,|\, \left( x\oplus x', \mathsf {Enc}(x)\oplus \mathsf {Enc}(x') \right) \in V^\perp \}. $$

We can show that,

$$ {P^\mathsf {STD}_\mathsf {Enc}}(V^\perp ) =2^{-\ell } \sum _{(\varDelta ,\varGamma )\in V^\perp } \mathsf {DP}^\mathsf {Enc}(\varDelta ,\varGamma ). $$

Derived from the general link between differential probability and linear correlations [12], the authors of [10, 11] show a general link between multidimensional linear attacks and truncated differential attacks. To derive in Sect. 3 the decorrelation order of a multidimensional linear attack, we will use this link. Using our notations, Theorem 1 of [11] corresponds to the following one.

Theorem 1

Let $V^\perp$ be the set of all u such that $u\cdot v=0$ for all $v\in V$. Using the previous notation, we obtain the following relation between ${P^\mathsf {STD}_\mathsf {Enc}}(V^\perp )$ and $\mathsf {cap}_\mathsf {Enc}(V)$:

$$\begin{aligned} 2^{-k}\mathsf {cap}_\mathsf {Enc}(V)= p^\mathsf {STD}_\mathsf {Enc}(V^\perp )-2^{-k}. \end{aligned}$$

Proof

We provide the proof with our settings. We have

$$\begin{aligned} 1+\mathsf {cap}_\mathsf {Enc}(V)= & {} \sum _{v\in V}\mathsf {LP}^\mathsf {Enc}(v) \\= & {} \sum _{v\in V}2^{-\ell }\sum _u(-1)^{u\cdot v}\mathsf {DP}^\mathsf {Enc}(u) \\= & {} 2^{-\ell }\sum _u\mathsf {DP}^\mathsf {Enc}(u)\sum _{v\in V}(-1)^{u\cdot v}. \end{aligned}$$

Since $v\mapsto u\cdot v$ is a group homomorphism from V to $\mathbf{Z}_2$, either it is balanced, or identically equal to 0 (when $u\in V^\perp$, by definition). We have

$$ 1+\mathsf {cap}_\mathsf {Enc}(V) = 2^{k-\ell }\sum _{u\in V^\perp }\mathsf {DP}^\mathsf {Enc}(u). $$

So, $p^\mathsf {STD}_\mathsf {Enc}(V^\perp )= 2^{-k}+2^{-k}\mathsf {cap}_\mathsf {Enc}(V)$.    $\square$

Splitting the space $V^\perp$ of involved differentials to the spaces $V_\mathsf {in}^\perp$ and $V_\mathsf {out}^\perp$ of input and output differences, we can define the truncated differential probability ${P^\mathsf {TD}_\mathsf {Enc}}$ as follows

$$ {P^\mathsf {TD}_\mathsf {Enc}}(V^\perp )= 2^{-\ell }\dfrac{1}{|V_\mathsf {in}^{\perp }|} \sum _{\varDelta \in V_\mathsf {in}^\perp } \#\{ x\in \mathbb {F}_2^{\ell } \,|\, \mathsf {Enc}(x)\oplus \mathsf {Enc}(x \oplus \varDelta )\in V_\mathsf {out}^\perp \}. $$

Differential-Linear Cryptanalysis. Differential and linear attacks were used together for the first time by Langford and Hellman [13]. This was differential-linear cryptanalysis. The basic idea is to split the cipher under consideration into a composition of two parts. The split should be such that, for the first part of the cipher there should exist a strong truncated differential with input difference $\varDelta$ and for the second part there should exist a strongly biased linear approximation with output mask $\beta$. In [13], the particular case where the differential over the first part holds with probability one has been introduced. Later on, Biham et al. [3] generalized this attack using a probabilistic truncated differential on the first rounds of the distinguisher. In [11], Blondeau et al. presented a general model for this attack.

$$ p^\mathsf {DL}_{\mathsf {Enc}}(\varDelta ,\beta ) =2^{-\ell } \# \left\{ x \; | \; \beta \cdot \left( {\mathsf {Enc}}(x)\oplus {\mathsf {Enc}}(x\oplus \varDelta ) \right) =0 \right\} . $$

Boomerang Attack. In the boomerang attack, introduced in 1999 by Wagner [22], the advantage is taken from both the encryption and decryption. Given a difference $\varDelta$ between two plaintexts x and $x'$, the attacker is taking advantage of the probability

$$ p^\mathsf {Boo}_{\mathsf {Enc}}(\varDelta ,\nabla ) =2^{-\ell }\# \left\{ x \; |\; \mathsf {Enc}^{-1}\left( \mathsf {Enc}(x)\oplus \nabla \right) \oplus \mathsf {Enc}^{-1} \left( \mathsf {Enc}(x\oplus \varDelta )\oplus \nabla \right) =\varDelta \right\} , $$

where $\nabla$ is a ciphertext difference.

2.2 The Decorrelation Theory

We consider a permutation $\mathsf {Enc}$ over $\{0,1\}^\ell$. Sometimes, $\mathsf {Enc}$ will be a random permutation with uniform distribution and will be denoted by $C^*$. Sometimes, it will be a permutation defined by a random key K and will be denoted by $C_K$.

Decorrelation was first presented in [18]. The non-adaptive (resp. adaptive) decorrelation of $C_K$ of order d is denoted by $\Vert [C_K]^d-[C^*]^d\Vert _{\infty }$ (resp. $\Vert [C_K]^d-[C^*]^d\Vert _a$). It is the $\Vert \cdot \Vert _{\infty }$- (resp. $\Vert \cdot \Vert _a$-) distance between the matrices $[C_K]^d$ and $[C^*]^d$. Given a random $\mathsf {Enc}$, we define $[\mathsf {Enc}]^d$, the d-wise distribution matrix by

$$ [\mathsf {Enc}]^d_{(x_1,\ldots ,x_d),(y_1,\ldots ,y_d)}= \Pr [y_1=\mathsf {Enc}(x_1),\ldots ,y_d=\mathsf {Enc}(x_d)]. $$

The $\Vert \cdot \Vert _{\infty }$-norm is defined by

$$ \Vert M\Vert _{\infty }= \max _{x_1,\ldots ,x_d}\sum _{y_1,\ldots ,y_d} |M_{(x_1,\ldots ,x_d),(y_1,\ldots ,y_d)}|. $$

A random variable can be considered as a random function from a set of cardinality 1, so its d-wise distribution matrix is a row vector and the $\Vert \cdot \Vert _{\infty }$ matrix-norm corresponds to the $\Vert \cdot \Vert _1$ vector-norm. For distributions, the $\Vert \cdot \Vert _1$-distance is also called the statistical distance. The $\Vert \cdot \Vert _a$-norm was defined in [20] by

$$ \Vert M\Vert _a= \max _{x_1}\sum _{y_1}\cdots \max _{x_d}\sum _{y_d} |M_{(x_1,\ldots ,x_d),(y_1,\ldots ,y_d)}|. $$

Here is the fundamental link between the best advantage of a distinguisher and decorrelation.

Theorem 2

(Best advantage and decorrelation, Theorem 10–11 of [21]). The $\Vert \cdot \Vert _{\infty }$-decorrelation of order d of $C_K$, $\Vert [C_K]^d-[C^*]^d\Vert _{\infty }$, is twice the best advantage of a non-adaptive unbounded distinguisher between $C_K$ and $C^*$ which is allowed to make d encryption queries.

The $\Vert \cdot \Vert _a$-decorrelation of order d of $C_K$, $\Vert [C_K]^d-[C^*]^d\Vert _a$, is twice the best advantage of an adaptive unbounded distinguisher between $C_K$ and $C^*$ which is allowed to make d encryption queries.

We say $C_K$ is decorrelated if its decorrelation is small. We have perfect decorrelation when the decorrelation is 0. I.e., $[C_K]^d=[C^*]^d$, meaning

$$ \Pr [y_1=C_K(x_1),\ldots ,y_d=C_K(x_d)]= \Pr [y_1=C^*(x_1),\ldots ,y_d=C^*(x_d)] $$

for all $x_1,\ldots ,x_d,y_1,\ldots ,y_d$.

For instance, decorrelation of order $d=2$ corresponds to that $\Pr [y_1=C_K(x_1),y_2=C_K(x_2)]$ is always close to $\frac{1}{2^\ell (2^\ell -1)}$ for $x_1\ne x_2$ and $y_1\ne y_2$. This is the notion of pairwise independence by Wegman and Carter [23].

Given a permutation $\mathsf {Enc}$ over $\{0,1\}^\ell$, we define $Q_\mathsf {Enc}$, a function from $\{0,1\}\times \{0,1\}^\ell$ to $\{0,1\}^\ell$ by

$$ Q_\mathsf {Enc}(0,x)=\mathsf {Enc}(x) \quad \text {and}\quad Q_\mathsf {Enc}(1,y)=\mathsf {Enc}^{-1}(y). $$

To study distinguishers which can make encryption and decryption queries, we just consider the decorrelation of $Q_\mathsf {Enc}$ instead of the decorrelation of $\mathsf {Enc}$. For this, we study the distance between $[Q_{C_K}]^d$ and $[Q_{C^*}]^d$.

We review some general security results below.

Non-adaptive iterated distinguisher of order d. Given an encryption function $\mathsf {Enc}$, a non-adaptive iterated distinguisher of order d (Distinguisher Iter) is characterized by a distribution D and two Boolean functions T and f. With n iterations, it works as follows:

For such distinguisher, the following results have been derived in [19].

Theorem 3

(Advantage of Iter bounded by decorrelation [19], Theorem 18 of [21]). For the Boolean function T, we have

$$\begin{aligned} E(p^\mathsf {Iter}_{C_K})-E(p^\mathsf {Iter}_{C^*}) \le&5\root 3 \of { n^2 \left( 2\delta + \frac{5d^2}{2\times 2^\ell }+ \frac{3}{2}\Vert [C_K]^{2d}-[C^*]^{2d}\Vert _{\infty } \right) } \\&+n\Vert [C_K]^{2d}-[C^*]^{2d}\Vert _{\infty } \end{aligned}$$

where $\delta$ is an upper bound on the probability that the distinguisher picks a plaintext in common between any two iterations. I.e., $\delta =\Pr [\exists i,j\quad x_i=x'_j: (x_1,\ldots ,x_d)\leftarrow D,(x'_1,\ldots ,x'_d)\leftarrow D]$.

Note that it was proven in [6, 7] that we cannot have a general security result when $\delta$ is high or when we only have a decorrelation of order $2d-1$.

Theorem 3 was generalized in [19] to the case where the range of T has s elements instead of 2:

Theorem 4

(Advantage of Iter bounded by decorrelation, Theorem 7 of [19]). If T maps onto a set of s elements, we have

$$\begin{aligned} E(p^\mathsf {Iter}_{C_K})-E(p^\mathsf {Iter}_{C^*})\le&3s\root 3 \of { n^2 \left( 2\delta + \frac{2d^2}{2^\ell }+ \frac{d^3}{2^\ell (2^\ell -d)}+ \frac{3}{2}\Vert [C_K]^{2d}-[C^*]^{2d}\Vert _{\infty } \right) }\\&+\frac{ns}{2}\Vert [C_K]^{2d}-[C^*]^{2d}\Vert _{\infty } \end{aligned}$$

where $\delta$ is an upper bound on the probability that the distinguisher picks a plaintext in common between any two iterations. I.e., $\delta =\Pr [\exists i,j\quad x_i=x'_j: (x_1,\ldots ,x_d)\leftarrow D,(x'_1,\ldots ,x'_d)\leftarrow D]$.

Adaptive iterated distinguisher of order d. Theorem 3 was generalized in [5, 7] to adaptive plaintext-ciphertext iterated distinguishers (i.e., distinguishers which make in each iteration some adaptive queries and can also make chosen ciphertext queries): Given an encryption function $\mathsf {Enc}$, an adaptive plaintext-ciphertext iterated distinguisher of order d (Distinguisher AIter) is characterized by $d-1$ functions $q_1,\ldots ,q_{d-1}$, and two Boolean functions T and f. With n iterations, it works as follows:

Theorem 5

(Advantage of AIter bounded by decorrelation [5], Theorem 5 of [7]). We have

$$\begin{aligned} E(p^\mathsf {AIter}_{C_K})-E(p^\mathsf {AIter}_{C^*})\le&5\root 3 \of { n^2 \left( 2\delta + e^{8d^22^{-\ell }}+ \frac{2d^2}{2^\ell }+ \frac{3}{2}\Vert [Q_{C_K}]^{2d}-[Q_{C^*}]^{2d}\Vert _{\infty } \right) }\\&+n\Vert [Q_{C_K}]^{2d}-[Q_{C^*}]^{2d}\Vert _{\infty } \end{aligned}$$

where $\delta$ is an upper bound on the probability that the distinguisher picks a query in common between any two iterations.

In what follows we give tighter results for specific classes of iterated attacks for which we can get rid of $\delta$ and sometimes rely on a lower decorrelation order.

2.3 Previous Results in the Context of Decorrelation Theory

To obtain the decorrelation order as well as the order of the different statistical attacks we have to describe the distinguishers we are working with. In this section, we describe the differential, linear, differential-linear and boomerang attacks, and recall the different results obtained for these distinguishers. A comparison with the results obtained for the multidimensional linear and truncated differential attacks will be presented later in this paper.

Differential Cryptanalysis. Given an encryption function $\mathsf {Enc}$, a differential distinguisher (Distinguisher DC) is characterized by two differences $\varDelta$ and $\varGamma$ and a Boolean function f. With n iterations, it works as follows:

This is a non-adaptive iterated attack of order 2.

Theorem 6

(Advantage of DC bounded by decorrelation, Theorem 13 of [21]). For the function $f(b_1,\ldots ,b_n)=\max _ib_i$, we have

$$ E(p^\mathsf {DC}_{C_K})-E(p^\mathsf {DC}_{C^*})\le \frac{n}{2^\ell -1}+ \frac{n}{2}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }. $$

Linear Cryptanalysis. Given an encryption function $\mathsf {Enc}$, a linear distinguisher (Distinguisher LC) is characterized by two masks $\alpha$ and $\beta$, and a Boolean function f. With n iterations, it works as follows:

This is a non-adaptive iterated attack of order 1.

Theorem 7

(Advantage of LC bounded by decorrelation, Theorem 17 of [21]). We have

$$ E(p^\mathsf {LC}_{C_K})-E(p^\mathsf {LC}_{C^*})\le 3\root 3 \of { n\Vert [C_K]^2-[C^*]^2\Vert _{\infty }+\frac{n}{2^\ell -1} }+ 3\root 3 \of { \frac{n}{2^\ell -1} }. $$

Differential-Linear Cryptanalysis. Given a function $\mathsf {Enc}$, a differential-linear distinguisher is characterized by a difference $\varDelta$, a mask $\beta$, and a Boolean function f. With n iterations, it works as follows:

This is a non-adaptive iterated attack of order 2.

Theorem 8

(Advantage of DL bounded by decorrelation, Theorem 7 of [7]). We have

$$\begin{aligned} E(p^\mathsf {DL}_{C_K})-E(p^\mathsf {DL}_{C^*})\le&3\root 3 \of { n\Vert [C_K]^4-[C^*]^4\Vert _{\infty }+ n\frac{2\times 2^\ell -5}{(2^\ell -1)(2^\ell -3)} }+ \\&3\root 3 \of { n\frac{2\times 2^\ell -5}{(2^\ell -1)(2^\ell -3)} }. \end{aligned}$$

This results say that if a cipher is decorrelation to the order 4, it is protected against differential- linear cryptanalysis. It was further proven in [1, pp. 77–78] that some ciphers decorrelated to the order 3 can have a high advantage with DL. Which means that the decorrelation of order 4 is really what is needed.

Remark 9

The result from [7] was stated for a function f based on a counter $b_1+\cdots +b_n$ but it is easy to see that the proof holds for a more general f as it is very similar to that of Theorem 7.

Boomerang Cryptanalysis. Given an encryption function $\mathsf {Enc}$, a boomerang distinguisher is characterized by two differences $\varDelta$ and $\nabla$ and a Boolean function f. With n iterations, it works as follows:

This is an adaptive plaintext-ciphertext iterated attack of order 4.

Theorem 10

(Advantage of Boo bounded by decorrelation, Theorem 8 of [7]). For the function $f(b_1,\ldots ,b_n)=\max _ib_i$, we have

$$ E(p^\mathsf {Boo}_{C_K})-E(p^\mathsf {Boo}_{C^*})\le n\frac{2\times 2^\ell -5}{(2^\ell -1)(2^\ell -3)}+ \frac{n}{2}\Vert [C_K]^4-[C^*]^4\Vert _a. $$

It was further proven in [1, pp. 79–80] that some ciphers decorrelated to the order 3 can have a high advantage with Boo. We deduce that decorrelation of order 4 is really what is needed.

A summary of the results presented in this section (and new ones) is given in Table 1.

3 Multidimensional Linear Cryptanalysis

In this section we study the multidimensional linear (ML) attack. To do so we consider the following multidimensional linear distinguisher (Distinguisher ML):

I.e., we look at the observed distribution of the bits $(b_{1,1},\ldots ,b_{n,k})$ and we take a decision by following a function f. According to this algorithm, this attack looks like a non-adaptive iterated attack of order 1, except that a vector $b_i$ is kept instead of a bit at each iteration. We want to bound the advantage of this distinguisher for any function f. We let $p^\mathsf {ML}_\mathsf {Enc}$ be the probability (over the selection of the random x’s) to output 1 by using the fixed function $\mathsf {Enc}$. We want to bound

$$\begin{aligned} E(p^\mathsf {ML}_{C_K})-E(p^\mathsf {ML}_{C^*}) \end{aligned}$$

where K is a random key, $C_K$ is the encryption under the key K, and $E(p^\mathsf {ML}_{C_K})$ is the expected value over the distribution of K, and where $C^*$ is a uniformly distributed random permutation and $E(p^\mathsf {ML}_{C^*})$ is the expected value over the distribution of $C^*$.

For $\mathsf {Enc}$ fixed, all vectors $b_i$ are independent and identically distributed. We let $D_\mathsf {Enc}$ be the distribution of the vector $b_i$.

We let V be the vector space spanned by the $(\alpha _j,\beta _j)$ masks. We recall that k denotes the dimension of V.

We could apply Theorem 4 with $d=1$, $s=2^k$, $\delta =2^{-\ell }$, and obtain

$$\begin{aligned} E(p^\mathsf {ML}_{C_K})-E(p^\mathsf {ML}_{C^*})\le&3\times 2^k\root 3 \of { n^2 \left( \frac{4}{2^\ell }+ \frac{1}{2^\ell (2^\ell -1)}+ \frac{3}{2}\Vert [C_K]^2-[C^*]^2\Vert _{\infty } \right) }\\&+\frac{n2^k}{2}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }. \end{aligned}$$

With a negligible decorrelation, we would obtain a security for a data complexity n up to approximately $2^{\frac{\ell }{2}-3k}$. Nevertheless, this is meaningless when the dimension k of V is such that $k>\frac{\ell }{6}$. With the technique to develop in this section, we aim at $n\approx 2^{\frac{\ell -k}{2}}$. This makes sense until k is close to $\ell$.

We note that if $k>\ell$, there exists a Boolean function $\mathsf {bit}(y)$ on the ciphertext and a mapping from $b_i=(b_{i,1},\ldots ,b_{i,k})$ to $(x,\mathsf {bit}(y))$. For n relatively small, the vectors $(b_1,\ldots ,b_n)$ uniquely identify the key K. So, there exists a function f (maybe with high complexity) leading to a very high advantage. Hence, we cannot prove any security without assuming any complexity on f.

For $k=\ell -\mathsf {cste}$, we could have cases in which there is a mapping from $b_i$ to $(x_1,\ldots ,x_{k-1},\mathsf {bit}(y))$ so $2^{\mathsf {cste}+1}$ possible values for x. We can eliminate keys for which none of these x lead to $\mathsf {bit}(y)$. This eliminates a fraction $2^{-2^{\mathsf {cste}+1}}$ of the keys. So, for n within the order of magnitude of $2^{2^{\mathsf {cste}+1}}$, we uniquely determine the key. So, no information-theoretic security is feasible for these values of n.

Remark 11

(Relation with [14] and [10, 11]). In [14], the function f used to evaluate the multidimensional linear approximation is based on $\mathrm {LLR}$ or $\chi ^2$ statistical test. In [10, 11], where the relation between the truncated differential and multidimensional linear key-recovery attacks is derived, the function f is based on the $\chi ^2$ test.

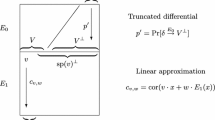
To provide a bound on $p^\mathsf {ML}_\mathsf {Enc}-p^\mathsf {ML}_{\mathsf {Enc}^*}$ we consider the following distinguisher, which is a special truncated differential (STD) distinguisher:

This distinguisher is a known plaintext truncated differential distinguisher using only one pair of samples. It corresponds to a non-adaptive attack using two queries.

Let $p^\mathsf {STD}_\mathsf {Enc}$ be the probability that the output is 1 with $\mathsf {Enc}$ fixed. Clearly, as given in Sect. 2.1, we have

$$ p^\mathsf {STD}_\mathsf {Enc}= \sum _{(\varDelta ,\varGamma )\in V^\perp } 2^{-\ell }\mathsf {DP}^\mathsf {Enc}(\varDelta ,\varGamma ). $$

Lemma 12

(Euclidean distance vs. capacity). We let U be the uniform distribution. We have

$$\begin{aligned} \Vert D_\mathsf {Enc}-U\Vert _2^2=2^{-k}\mathsf {cap}_\mathsf {Enc}(V). \end{aligned}$$

Proof

If $v\in V$, we can write $v=\sum _j\lambda _j(\alpha _j,\beta _j)$. Then,

$$\begin{aligned} \mathsf {LP}^\mathsf {Enc}(v)= & {} \left( E\left( (-1)^{v\cdot (x,\mathsf {Enc}(x))} \right) \right) ^2 \\= & {} \left( E\left( (-1)^{\sum _j\lambda _j(\alpha _j,\beta _j)\cdot (x,\mathsf {Enc}(x))} \right) \right) ^2 \\= & {} \left( E\left( (-1)^{\sum _j\lambda _jb_j} \right) \right) ^2 \\= & {} E\left( (-1)^{\sum _j\lambda _j(b_j+b'_j)} \right) \end{aligned}$$

so,

$$ \sum _{v\in V}\mathsf {LP}^\mathsf {Enc}(v) = 2^k\Pr [b_1=b'_1,\ldots ,b_k=b'_k] = 2^k\sum _{b_1,\ldots ,b_k}\Pr [b_1,\ldots ,b_k]^2 $$

from which we deduce

$$ \sum _{v\in V,v\ne 0}\mathsf {LP}^\mathsf {Enc}(v)=2^k\Vert D_\mathsf {Enc}-U\Vert _2^2. $$

   $\square$

Lemma 13

(Statistical distance of iterated distribution). Let n be an integer and $D_\beta$ be a probability distribution for $\beta \in \{0,1\}$. Let $D_\beta ^{\otimes n}$ be the distributions of vectors of n independent samples following $D_\beta$. We have

$$\begin{aligned} \Vert D_0^{\otimes n}-D_1^{\otimes n}\Vert _1\le n\Vert D_0-D_1\Vert _1. \end{aligned}$$

Proof

We use

$$\begin{aligned} aa'-bb'=(a-b)\frac{a'+b'}{2}+(a'-b')\frac{a+b}{2}. \end{aligned}$$

We have

$$\begin{aligned} \Vert D_0^{\otimes n}-D_1^{\otimes n}\Vert _1= & {} \frac{1}{2}\sum _{u,v} |D_0(u)D_0^{\otimes (n-1)}(v)-D_1(u)D_1^{\otimes (n-1)}(v)| \\\le & {} \frac{1}{2}\sum _u|D_0(u)-D_1(u)| \sum _v\frac{D_0^{\otimes (n-1)}(v)+D_1^{\otimes (n-1)}(v)}{2}+ \\&\frac{1}{2}\sum _v|D_0^{\otimes (n-1)}(v)-D_1^{\otimes (n-1)}(v)| \sum _u\frac{D_0(u)+D_1(u)}{2} \\= & {} \Vert D_0-D_1\Vert _1+\Vert D_0^{\otimes (n-1)}-D_1^{\otimes (n-1)}\Vert _1. \end{aligned}$$

We conclude by proving the result by induction.    $\square$

Lemma 14

(Advantage of ML vs. Euclidean distance). For any fixed $\mathsf {Enc}$ and $\mathsf {Enc}^*$, we have

$$ p^\mathsf {ML}_\mathsf {Enc}-p^\mathsf {ML}_{\mathsf {Enc}^*} \le \frac{n2^{\frac{k}{2}}}{2}\Vert D_\mathsf {Enc}-D_{\mathsf {Enc}^*}\Vert _2. $$

Proof

Thanks to Theorem 2, we have $p^\mathsf {ML}_\mathsf {Enc}-p^\mathsf {ML}_{\mathsf {Enc}^*}\le \frac{1}{2}\Vert D_\mathsf {Enc}^{\otimes n}-D_{\mathsf {Enc}^*}^{\otimes n}\Vert _1$. Then, we have $\Vert D_\mathsf {Enc}^{\otimes n}-D_{\mathsf {Enc}^*}^{\otimes n}\Vert _1\le n\Vert D_\mathsf {Enc}-D_{\mathsf {Enc}^*}\Vert _1$ due to Lemma 13. Next, we use $\Vert D_\mathsf {Enc}-D_{\mathsf {Enc}^*}\Vert _1\le 2^{\frac{k}{2}}\Vert D_\mathsf {Enc}-D_{\mathsf {Enc}^*}\Vert _2$ due to the Cauchy-Schwarz Inequality.    $\square$

Remark 15

For $k=1$ (linear cryptanalysis), we have $\mathsf {cap}_\mathsf {Enc}(V)=\mathsf {LP}^\mathsf {Enc}(\alpha _1,\beta _1)$. From Lemma 12 and Lemma 14, we obtain

$$ |p^\mathsf {ML}_\mathsf {Enc}-p^\mathsf {ML}_{\mathsf {Enc}^*}|\le \frac{n}{2}\sqrt{\mathsf {LP}^\mathsf {Enc}(\alpha _1,\beta _1)}+ \frac{n}{2}\sqrt{\mathsf {LP}^{\mathsf {Enc}^*}(\alpha _1,\beta _1)} $$

for any fixed $\mathsf {Enc}$ and $\mathsf {Enc}^*$. From [21, Lemma 15], we know that there is a constant $p_0$ such that for any fixed $\mathsf {Enc}$, we have $|p^\mathsf {ML}_\mathsf {Enc}-p_0|\le 2\sqrt{n\mathsf {LP}^\mathsf {Enc}(\alpha _1,\beta _1)}$. So,

$$ |p^\mathsf {ML}_\mathsf {Enc}-p^\mathsf {ML}_{\mathsf {Enc}^*}|\le 2\sqrt{n\mathsf {LP}^\mathsf {Enc}(\alpha _1,\beta _1)}+ 2\sqrt{n\mathsf {LP}^{\mathsf {Enc}^*}(\alpha _1,\beta _1)}. $$

As we can see, the bound obtained from Lemma 14 is not tight in the case where $k=1$. We are loosing a factor $\sqrt{n}$. The loss comes from Lemma 13 which is far from being tight.

Lemma 16

(Link between ML and STD). For any fixed $\mathsf {Enc}$ and $\mathsf {Enc}^*$, we have

$$ p^\mathsf {ML}_{\mathsf {Enc}}-p^\mathsf {ML}_{\mathsf {Enc}^*} \le \frac{n2^{\frac{k}{2}}}{2}\sqrt{p^\mathsf {STD}_{\mathsf {Enc}}-2^{-k}}+ \frac{n2^{\frac{k}{2}}}{2}\sqrt{p^\mathsf {STD}_{\mathsf {Enc}^*}-2^{-k}}. $$

Proof

We apply Theorem 1, Lemma 12, Lemma 14, and the triangular inequality $\Vert D_\mathsf {Enc}-D_{\mathsf {Enc}^*}\Vert _2\le \Vert D_\mathsf {Enc}-U\Vert _2+\Vert D_{\mathsf {Enc}^*}-U\Vert _2$.    $\square$

Lemma 17

(Using decorrelation in STD). We have

$$ E(p^\mathsf {STD}_{C_K})\le E(p^\mathsf {STD}_{C^*})+\frac{1}{2}\Vert [C_K]^2-[C^*]^2\Vert _\infty . $$

Proof

$E(p^\mathsf {STD}_{C_K})-E(p^\mathsf {STD}_{C^*})$ expresses as the advantage of $\mathsf {STD}$, a non-adaptive distinguisher limited to two queries. We conclude by using Theorem 2.    $\square$

Lemma 18

(The ideal case in STD). We have

$$ E(p^\mathsf {STD}_{C^*}-2^{-k})\le 2^{-\ell }\frac{1-2^{-k}}{1-2^{-\ell }}. $$

Assuming that all $\alpha _j$ are linearly independent and that all $\beta _j$ are linearly independent, we further have

$$ E(p^\mathsf {STD}_{C^*}-2^{-k})= 2^{-\ell }\frac{1-2^{-k}}{1-2^{-\ell }}. $$

Proof

From Theorem 1, we have

$$ p^\mathsf {STD}_\mathsf {Enc}= 2^{-k}+2^{-k}\sum _{v\in V,v\ne 0}\mathsf {LP}^\mathsf {Enc}(v). $$

There are exactly $2^k-1$ vectors v which are non-zero. When all $\alpha _j$ resp. all $\beta _j$ are linearly independent, neither the left half nor the right half of v is zero. Based on [21, Lemma 14], we deduce $E(\mathsf {LP}^{C^*}(v))=\frac{1}{2^\ell -1}$ and obtain

$$ E(p^\mathsf {STD}_{C^*})=2^{-k}+2^{-k}\frac{2^k-1}{2^\ell -1}. $$

Without the assumption of independence, there are some of the vectors $v\ne 0$ such that either the left half or the right half is zero but not both. Therefore, we have $\mathsf {LP}^{C^*}(v)=0$. Since this satisfies $E(\mathsf {LP}^{C^*}(v))\le \frac{1}{2^\ell -1}$, we still have

$$ E(p^\mathsf {STD}_{C^*})\le 2^{-k}+2^{-k}\frac{2^k-1}{2^\ell -1}. $$

   $\square$

Theorem 19

(Advantage of ML bounded by decorrelation). We have

$$ E(p^\mathsf {ML}_{C_K})-E(p^\mathsf {ML}_{C^*})\le n\sqrt{2^{k-\ell }+2^{k-1}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }}. $$

Proof

We first apply Lemma 16. Then, since $\sqrt{\cdot }$ is concave, the Jensen inequality says that

$$ E\left( \sqrt{p^\mathsf {STD}_\mathsf {Enc}-2^{-k}}\right) \le \sqrt{E(p^\mathsf {STD}_\mathsf {Enc}-2^{-k})}. $$

By using Lemma 17 and Lemma 18, we obtain

$$ E(p^\mathsf {ML}_{C_K})-E(p^\mathsf {ML}_{C^*})\le n\sqrt{ 2^{k-\ell }\frac{1-2^{-k}}{1-2^{-\ell }} +2^{k-1}\Vert [C_K]^2-[C^*]^2\Vert _{\infty } }. $$

The bound in Theorem 19 is trivial for $k>\ell$. For $k\le \ell$, we bound $\frac{1-2^{-k}}{1-2^{-\ell }}\le 1$ and conclude.    $\square$

4 Truncated Differential Attack

As in [10, 11], we restrict to V of form $V_\mathsf {in}\times V_\mathsf {out}$ with $V_\mathsf {in}$ and $V_\mathsf {out}$ subspaces of $\{0,1\}^\ell$ of dimension s and q, respectively. We have $V^\perp =V_\mathsf {in}^\perp \times V_\mathsf {out}^\perp$. The dimension of $V^\perp$ is $2\ell -k=\ell -s+\ell -q$. We consider the following distinguisher:

The function f which computes the output depending on the vector b is left arbitrary. For instance, with $f(b_1,\ldots ,b_n)=b_1\cdots b_n$, this captures impossible differentials [2]. This is a non-adaptive iterated attack of order 2.

Lemma 20

(Link between TD and STD). For any fixed $\mathsf {Enc}$ and $\mathsf {Enc}^*$, we have

$$ |p^\mathsf {TD}_{\mathsf {Enc}}-p^\mathsf {TD}_{\mathsf {Enc}^*}| \le n2^s|p^\mathsf {STD}_{\mathsf {Enc}}-p^\mathsf {STD}_{\mathsf {Enc}^*}|. $$

Proof

We let $p^1$ denote the best distinguisher with same D and $n=1$. We apply Lemma 13 and we obtain

$$ |p^\mathsf {TD}_{\mathsf {Enc}}-p^\mathsf {TD}_{\mathsf {Enc}^*}| \le n|p^1_\mathsf {Enc}-p^1_{\mathsf {Enc}^*}|. $$

Clearly, depending on the sign of $p^1_\mathsf {Enc}-p^1_{\mathsf {Enc}^*}$, either $p^1$ is the probability that a differential is found, or it is the probability that it is not found. In any case, we have $2^{-s}|p^1_\mathsf {Enc}-p^1_{\mathsf {Enc}^*}|= |p^\mathsf {STD}_\mathsf {Enc}-p^\mathsf {STD}_{\mathsf {Enc}^*}|$, and we obtain the result.    $\square$

Theorem 21

(Advantage of TD bounded by decorrelation). For the TD differential distinguisher described in this section, we have

$$ E(p^\mathsf {TD}_{C_K})-E(p^\mathsf {TD}_{C^*}) \le n2^{1+s-\ell }\frac{1-2^{-k}}{1-2^{-\ell }}+ n2^{s-1}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }. $$

Proof

Due to Lemma 20, we have

$$\begin{aligned} p^\mathsf {TD}_{\mathsf {Enc}}-p^\mathsf {TD}_{\mathsf {Enc}^*}\le & {} n2^s|p^\mathsf {STD}_{\mathsf {Enc}}-2^{-k}|+ n2^s|p^\mathsf {STD}_{\mathsf {Enc}^*}-2^{-k}| \\= & {} n2^s\left( p^\mathsf {STD}_{\mathsf {Enc}}-2^{-k}\right) + n2^s\left( p^\mathsf {STD}_{\mathsf {Enc}^*}-2^{-k}\right) \end{aligned}$$

since we know from Theorem 1 that $p^\mathsf {STD}_{\mathsf {Enc}}-2^{-k}$ is positive. Based on Lemma 17, we have, $E(p^\mathsf {STD}_{C_K})-E(p^\mathsf {STD}_{C^*})\le \frac{1}{2}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }$. So,

$$ E(p^\mathsf {TD}_{C_K})-E(p^\mathsf {TD}_{C^*}) \le 2n2^s\left( E(p^\mathsf {STD}_{C^*})-2^{-k}\right) + n2^{s-1}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }. $$

Due to Lemma 18, we obtain the result.    $\square$

Remark 22

The critical term for ML in Theorem 19 is $n^22^{k-1}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }$. The one for TD in Theorem 21 is $n2^{s-1}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }$. Presumably, we have lost a factor n in Theorem 19 and the difference between ML and TD should only be k vs. s, the dimension of V vs. the one of $V_\mathsf {in}$.

Remark 23

For $s=\ell -1$ and $q=1$, $V_\mathsf {in}^\perp$ has a single non-zero vector (which can be seen as a difference vector $\varDelta$) and $V_\mathsf {out}$ has a single non-zero vector (which can be seen as a mask $\varGamma$). However, our bound is useless in that case since $2^{1+s-\ell }=1$. Here, we used again the loose bound of Lemma 13, but changing n into $\sqrt{n}$ would not change this fact. Actually, TD becomes equivalent to DL in this case, and it is known that 4-decorrelation is needed to protect against DL [1]. Since our TD-security results uses 2-decorrelation, improving this bound to get a more useful one in the case of DL would require to use 4-decorrelation. Except for the equivalence to DL, these observations extend to all values of q.

5 Improvement of Previous Results

5.1 Improvement in the Linear and Differential-Linear Contexts

If $\Vert [C_K]^2-[C^*]^2\Vert _{\infty }\approx 2^{-\ell }$, the bound derived in Theorem 7, for linear attacks, is approximately equal to $3(1+\root 3 \of {2})\root 3 \of {n2^{-\ell }}$ and is useful only if the attacker can take advantage of up to $2^\ell /311$ plaintext-ciphertext pairs. For a 64-bit cipher, it would corresponds to attacks with data complexity less than $2^{55.71}$. In this section we provide a new bound, for linear attacks, useful for n up to $2^\ell /24$ which is $2^{59.42}$.

Theorem 7, which is given in Sect. 2.1, has been originally derived in 2003 [21]. The following result consists of an improvement of the upper bound of $E(p^\mathsf {LC}_{C_K})-E(p^\mathsf {LC}_{C^*})$. This improvement is obtained thanks to the Jensen equality.

Theorem 24

(Advantage of LC bounded by decorrelation, improvement of Theorem 7 ). For the linear distinguisher of Sect. 2.3, we have

$$ E(p^\mathsf {LC}_{C_K})-E(p^\mathsf {LC}_{C^*})\le 2\sqrt{ n\Vert [C_K]^2-[C^*]^2\Vert _{\infty }+\frac{n}{2^\ell -1} }+ 2\sqrt{ \frac{n}{2^\ell -1} }. $$

Proof

Based on [21, Lemma 15], we know that there is some $p_0$ such that for every $\mathsf {Enc}$, we have $|p^\mathsf {Enc}-p_0|\le 2\sqrt{n\mathsf {LP}^\mathsf {Enc}(a,b)}$.

To prove Theorem 7, the method used in [21] consisted in getting for any A that¹ $E(p^\mathsf {LC}_\mathsf {Enc})-p_0\le 2\cdot A \sqrt{n}+\frac{1}{A^2}E(\mathsf {LP}^\mathsf {Enc}(\alpha ,\beta ))$ and then in minimizing the sum in terms of A. In [21], $A=n^{-\frac{1}{6}}\root 3 \of {E(\mathsf {LP}^\mathsf {Enc}(\alpha ,\beta ))}$ was taken, to get $E(p^\mathsf {LC}_\mathsf {Enc})-p_0\le 3\root 3 \of {nE(\mathsf {LP}^\mathsf {Enc}(\alpha ,\beta ))}$.

To derive the improved bound, instead, we use the Jensen inequality to obtain $|E(p^\mathsf {Enc})-p_0|\le 2\sqrt{nE(\mathsf {LP}^\mathsf {Enc}(\alpha ,\beta ))}$.

We consider the elementary non-adaptive distinguisher picking x and $x'$ and checking if $\alpha \cdot (x\oplus x')= \beta \cdot \left( \mathsf {Enc}(x)\oplus \mathsf {Enc}(x')\right)$. The probability of the equality is $p^2+(1-p)^2=\frac{1}{2}(2p-1)^2+\frac{1}{2}$ where $p=\Pr [\alpha \cdot x=\beta \cdot \mathsf {Enc}(x)]$. Therefore, it is $\frac{1}{2}\mathsf {LP}^\mathsf {Enc}(\alpha ,\beta )+\frac{1}{2}$ and $\mathsf {LP}^\mathsf {Enc}(\alpha ,\beta )$ expresses the advantage of a non-adaptive distinguisher using two queries. From Theorem 2, we have $E(\mathsf {LP}^{C_K}(\alpha ,\beta ))\le E(\mathsf {LP}^{C^*}(\alpha ,\beta ))+\Vert [C_K]^2-[C^*]^2\Vert _{\infty }$. From [21, Lemma 14] we obtain that

$$\begin{aligned} E(\mathsf {LP}^{C^*}(\alpha ,\beta ))=\frac{1}{2^\ell -1}. \end{aligned}$$

   $\square$

In the same way the bound derived for the differential-linear attack, in Theorem 8 is approximately equal to $3(\root 3 \of {3}+\root 3 \of {2})\root 3 \of {n2^{-\ell }}$ and is useful for an attacker which can take advantage to up to $2^\ell /532$ plaintext-ciphertext pairs. Using the same technique, meaning the Jensen inequality, we can improve Theorem 8 and derive a new bound in the differential-linear context which is valid for any attack using up to $2^{\ell }/39$ plaintext-ciphertext pairs.

Theorem 25

(Advantage of DL bounded by decorrelation, improvement of Theorem 8 ). For the differential-linear distinguisher of Sect. 2.3, we have

$$\begin{aligned} E(p^\mathsf {DL}_{C_K})-E(p^\mathsf {DL}_{C^*})\le&2\sqrt{ n\Vert [C_K]^4-[C^*]^4\Vert _{\infty }+ n\frac{2\times 2^\ell -5}{(2^\ell -1)(2^\ell -3)} }+ \\&2\sqrt{ n\frac{2\times 2^\ell -5}{(2^\ell -1)(2^\ell -3)} }. \end{aligned}$$

5.2 In the Context of Differential and Boomerang Attacks, Extension of Theorems 6 and 10

Before providing, in this section, an extension of Theorem 6 and 10, we present an extension of [21, Lemma 15] for the following iterative distinguisher:

Lemma 26

. Let $p_\mathsf {Enc}$ be a probability depending on a cipher $\mathsf {Enc}$. We have $|E(p^\mathsf {Dist}_\mathsf {C_K})-E(p^\mathsf {Dist}_\mathsf {C^*})| \le n.\max (E(p_{C_K}),E(p_{C^*}))$.

Proof

If $f(0,\ldots ,0)=0$, then $p^\mathsf {Dist}_\mathsf {Enc}\le np_\mathsf {Enc}$ and $E(p^\mathsf {Dist}_{C_K})-E(p^\mathsf {Dist}_{C^*})\le E(p^\mathsf {Dist}_{C_K})\le nE(p_{C_K})$. Similarly, we have $E(p^\mathsf {Dist}_{C^*})-E(p^\mathsf {Dist}_{C_K})\le E(p^\mathsf {Dist}_{C^*})\le nE(p_{C^*})$, and the result holds in this case.

If $f(0,\ldots ,0)=1$, we change f to $1-f$ without changing $|E(p^\mathsf {Dist}_{C^*})-E(p^\mathsf {Dist}_{C_K})|$ and go back to the previous case.    $\square$

Differential Distinguisher. In Sect. 2.1, the differential distinguisher is defined for a given Boolean function f corresponding to $f(b_1,\cdots b_n)=\max _ib_i$. In practice, for many differential attacks more than one valid pair is necessary to distinguish the cipher from a random permutation. In this section we generalize this distinguisher to any Boolean function f.

Theorem 27

(Advantage of DC bounded by decorrelation, improved Theorem 6 ). For the distinguisher DC, we have

$$ E(p^\mathsf {DC}_{C_K})-E(p^\mathsf {DC}_{C^*})\le \frac{n}{2^\ell -1}+ \frac{n}{2}\Vert [C_K]^2-[C^*]^2\Vert _{\infty }. $$

Proof

The proof is similar to the proof of Theorem 6 which can be found in [21, Theorem 13]. The difference is that we use Lemma 26 to get rid of the arbitrary f.

Boomerang Distinguisher. In the same way, we can improve the boomerang distinguisher by considering any Boolean function f. As for Theorem 10, we can prove the following result.

Theorem 28

(Advantage of Boo bounded by decorrelation, improved Theorem 10 ). For the distinguisher Boo, we have

$$ E(p^\mathsf {Boo}_{C_K})-E(p^\mathsf {Boo}_{C^*})\le n\frac{2\times 2^\ell -5}{(2^\ell -1)(2^\ell -3)}+ \frac{n}{2}\Vert [C_K]^4-[C^*]^4\Vert _a. $$

6 Conclusion

In this paper, we studied the multidimensional linear and truncated differential attacks in the context of the decorrelation theory. We showed that these attacks are non-adaptive iterated attacks of order 2. Table 1 summarizes the considered attacks. In particular, we obtained three types of results:

• we improved the bounds for the linear and differential-linear distinguishers (Theorems 7 and 8 are improved by Theorems 24 and 25, respectively);

• we generalized the differential and boomerang distinguishers to allow an arbitrary function f (Theorems 6 and 10 are improved by Theorems 27 and 28, respectively);

• we proved the security for multidimensional linear and truncated differential with decorrelation (Theorems 19 and 21).

We let as open problems the seek for an improved Lemma 13 with $\sqrt{n}$ instead of n as suggested in Remark 15. This would allow for better bounds in Theorem 19 and 21. We shall also find better bounds based on a higher order of decorrelation, in particular to link Theorem 21 to Theorem 25 (see Remark 23).

Table 1. The decorrelation order of some statistical attacks.