Expressive Equivalence and Succinctness of Parametrized Automata with Respect to Finite Memory Automata

Abstract

We compare parametrized automata, a class of automata recently introduced by the authors, against finite memory automata with non-deterministic assignment, an existing class of automata used to model services. We prove that both classes have the same expressive power, while parametrized automata can be exponentially succinct in some cases. We then prove that deciding simulation preorder for parametrized automata is EXPTIME-complete, extending an earlier result showing it in EXPTIME.

1 Introduction

The simple and powerful formalism of finite automata (FAs in short) is widely used for service specification and verification. Considerable efforts have been devoted to extend finite automata to infinite alphabets: data automata [6], finite memory automata [11], usage automata [7], fresh-variable automata [2] and parametrized automata (PAs in short) [3, 4], only to cite a few (see [12] for a survey). They have been applied recently to formal verification, see e.g. [8]. When developing formalisms over infinite alphabets, the main challenge is to preserve as much as possible useful properties such as compositionality (i.e. closure under basic operations) and decidability of basic problems such as nonemptiness, membership, universality, language containment, simulation, etc.

Our interest for simulation preorders is motivated by the composition synthesis problem for web services in which the agents (i.e. client and the available services) exchange data ranging over an infinite domain. One of the most successful approaches to composition amounts to abstract services as finite-state automata and synthesize a new service satisfying the given client requests from an existing community of services (e.g. [5, 13]). This amounts to computing a simulation relation of the client by the community of the available services, e.g. [5]. Simulation preorder can also be employed to efficiently underapproximate the language containment relation (e.g. [9]), which has applications in verification.

Akroun et al. have used such classes of automata over infinite alphabet to model verification and synthesis problems for Web Services, and give a detailed study in [1]. Parametrized automata, a class of automata introduced by the authors, is shown to be equivalent to finite memory automata with non-deterministic reassignment (NFMAs) [11] in terms of the class of languages they can represent. We have shown in our previous works [2, 3] how to extend the automata-based service composition approach to the case of infinite alphabets, also showing an EXPTIME solution for solving simulation preorder. Akroun et al. [1] further demonstrate that it is EXPTIME-complete. However, we also provide a simpler proof of the EXPTIME-completeness claim in this paper.

Contributions. In this paper, we first compare the expressiveness of PAs and NFMAs, in Sect. 3, proving their expressive equivalence. However, we claim and prove, that for many languages, PAs provide a succinct representation against NFMAs. We prove this by showing a class of languages for which the smallest NFMA that recognize them are exponentially large as compared to smallest PA that recognize the same.

We then prove, in Sect. 4, the EXPTIME-completeness of deciding whether one PA can be simulated by other, extending the result from [3], where its membership in EXPTIME was shown. We do this by providing a proof for the EXPTIME-hardness in this paper using reduction from Countdown Games, which were introduced and shown to be EXPTIME-complete by Jurdzinski et al. in [10].

2 Preliminaries

Before introducing formally the class of PAs, let us first explain the main ideas behind them. The transitions of a PA are labeled with letters or variables ranging over an infinite set of letters. Transitions can also be labeled with a guard, a conjunction of equalities and disequalities that permits to fire the transition only when the guard is true. We emphasize that while reading a guarded transition some variables of the guard might be free and we need to guess their value. Finally, some variables are refreshed in some states, that is, variables can be freed in these states so that new letters can be assigned to them. In other words, once a letter is assigned to a variable, this variable can not get another letter unless it is refreshed.

2.1 Technical Preliminaries

Let $\mathcal {X}$ be a finite set of variables, $\varSigma$ an infinite alphabet of letters. A substitution $\sigma$ is an idempotent mapping $\{x_1\mapsto \alpha _1,\ldots ,x_n\mapsto \alpha _n\}\cup \bigcup _{a\in \varSigma }\{{a \mapsto a}\}$ with variables $x_1, \ldots , x_n$ in $\mathcal {X}$ and $\alpha _1, \ldots , \alpha _n$ in $\mathcal {X} \cup \varSigma$, for some $n \in \mathbb {N}$. We call $\{{x_1,\ldots ,x_n}\}$ its proper domain, and denote it by $dom(\sigma )$. We denote by $Dom(\sigma )$ the set $dom(\sigma ) \cup \varSigma$, and by $codom(\sigma )$ the set $\{{a\in \varSigma \;\;|\;\;\exists x \in dom(\sigma ) \text { s.t. } \sigma (x)=a}\}$. If all the $\alpha _i,i=1\ldots n$ are letters then we say that $\sigma$ is ground. The empty substitution (i.e., with an empty proper domain) is denoted by $\emptyset$. The set of substitutions from $\mathcal {X}\cup \varSigma$ to a set A is denoted by $\zeta _{\mathcal {X},A}$, or by $\zeta _{\mathcal {X}}$, or simply by $\zeta$ if there is no ambiguity. If $\sigma _1$ and $\sigma _2$ are substitutions that coincide on the domain $dom(\sigma _1)\cap dom(\sigma _2)$, then $\sigma _1 \cup \sigma _2$ denotes their union in the usual sense. If $dom(\sigma _1)\cap dom(\sigma _2)=\emptyset$ then we denote by $\sigma _1 \uplus \sigma _2$ their disjoint union. We define the function $\mathcal {V}:\varSigma \cup \mathcal {X} \longrightarrow \mathcal {P}(\mathcal {X})$ by $\mathcal {V}(\alpha )=\{{\alpha }\}$ if $\alpha \in \mathcal {X}$, and $\mathcal {V}(\alpha )=\emptyset$, otherwise. For a function $F: A \mathop {\rightarrow }\limits ^{} B$, and $A'\subseteq A$, the restriction of F on $A'$ is denoted by $F_{|A'}$. For $n \in \mathbb {N}^{+}$, we denote by [n] the set $\{1,\ldots ,n\}$.

2.2 Parametrized Automata

Firstly, we introduce the syntax and semantics of guards.

Definition 1

The set $\mathbb {G}$ of guards over $\varSigma \cup \mathcal {X}$, where $\varSigma$ is an infinite set of letters and $\mathcal {X}$ is a finite set of variables, is inductively defined as follows:

$$\begin{aligned} G \; :=\; \mathtt {true} \;\;|\;\;\alpha =\beta \;\;|\;\;\alpha \ne \beta \;\;|\;\;G \wedge G, \end{aligned}$$

where $\alpha ,\beta \in \varSigma \cup \mathcal {X}$. We write $\sigma \models g$ if a substitution $\sigma$ satisfies a guard g.

Note that a disjunction of guard expressions here is equivalent to multiple parallel edges, with those guards, as a result of Non-determinism.

For a guard g, we denote the set of variables used in g with $\mathcal {V}(g)$ and the set of constants used in g with $\varSigma _g$, which can be defined inductively over guard expressions. Substitutions can be applied similarly, inductively, and we write $\sigma \vdash g$ if there exists a substitution $\gamma$ s.t. $\sigma \uplus \gamma \models g$.

The formal definition of PAs follows.

Definition 2

A PA is a tuple $\mathcal {A}=\langle \varSigma ,\mathcal {X},Q,Q_0,\delta ,F,\kappa \rangle$ where

• $\varSigma$ is an infinite set of letters,

• $\mathcal {X}$ is a finite set of variables,

• Q is a finite set of states,

• $Q_0\subseteq Q$ is a set of initial states,

• $\delta :Q \times (\varSigma _{\mathcal {A}} \cup \mathcal {X} \cup \{{\varepsilon }\}) \times \mathbb {G}\rightarrow 2^{Q}$ is a transition function where $\varSigma _{\mathcal {A}}$ is a finite subset of $\varSigma$,

• $F\subseteq Q$ is a set of accepting states, and

• $\kappa : \mathcal {X} \rightarrow 2^Q$ is called the refreshing function.

The run of a PA is defined over configurations. A configuration is defined as a pair $(\gamma ,q)$ where $\gamma$ is a substitution such that for all variables x in $dom(\gamma )$, $\gamma (x)$ can be interpreted as the current value of x, and $q \in Q$ is a state of the PA.

Intuitively, when a PA $\mathcal {A}$ is in state q, and $(\gamma ,q)$ is the current configuration, and there is a transition $q \mathop {\rightarrow }\limits ^{\alpha ,g} q'$ in $\mathcal {A}$ then:

• (i) if $\alpha$ is a free variable (i.e. $\alpha \in \mathcal {X} \setminus dom(\gamma )$) then $\alpha$ stores the input letter and some values for all the other free variables of $\gamma (g)$ are guessed such that $\gamma (g)$ holds, and $\mathcal {A}$ enters the state $q' \in \delta (q,\alpha ,g)$,

• (ii) if $\alpha$ is a bound variable or a letter (i.e. $\alpha \in Dom(\gamma )$) and $\gamma (\alpha )$ is equal to the input letter l then some values for all the free variables of $\gamma (g)$ are guessed such that $\gamma (g)$ holds, and $\mathcal {A}$ enters the state $q'\in \delta (q,\alpha ,g)$.

Fig. 1.

Two PAs $\mathcal {A}_1$ and $\mathcal {A}_2$ where the variable $y_1$ is refreshed in the state p, and the variables $x_2,y_2$ are refreshed in the state q.

Example 1. Let $\mathcal {A}_1$ and $\mathcal {A}_2$ be the PAs depicted above in Fig. 1 where the variable $y_1$ is refreshed in the state p, and the variables $x_2,y_2$ are refreshed in the state q. That is, $\mathcal {A}_1=\langle \varSigma , \{{x_1,y_1}\}, \{{p,p'}\}, \{{p}\}, \delta _1, \{{p'}\},\kappa _1 \rangle$ with

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta _1(p,y_1,(y_1 \ne x_1))=\{{p}\} \text { and }\delta _1(p,x_1,\texttt {true})=\{{p'}\}, \text { and }\\ \kappa _1(y_1)=\{{p}\} \end{array}\right. } \end{aligned}$$

And $\mathcal {A}_2=\langle \varSigma , \{{x_2,y_2}\}, \{{q,q'}\}, \{{q}\}, \delta _2, \{{q'}\},\kappa _2 \rangle$ with

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta _2(q,x_2,\texttt {true})=\{{q'}\} \text { and }\delta _2(q',y_2,(y_2 \ne x_2))=\{{q}\}, \text { and }\\ \kappa _2(x_2)=\kappa _2(y_2)=\{{q}\}. \end{array}\right. } \end{aligned}$$

We notice that while making the first loop over the state p of $\mathcal {A}_1$, the variable $x_1$ of the guard $(y_1\ne x_1)$ is free and its value is guessed. Then the variable $y_1$ is refreshed in p, and at each loop the input letter should be different from the value of the variable $x_1$ already guessed. More precisely, the behaviour of $\mathcal {A}_1$ on an input word is as follows. Being in the initial state p, either

• the automaton makes the transition $p\mathop {\rightarrow }\limits ^{x_1} p'$ by reading the input symbol and binding the variable $x_1$ to this input symbol, then enters the state $p'$. Or,

• the automaton makes the transition $p\mathop {\longrightarrow }\limits ^{y_1, y_1\ne x_1} p$ by:

  • 1. reading the input symbol and binding the variable $y_1$ to it,

  • 2. guessing a symbol in $\varSigma$ that is different from the input symbol (i.e. the value of $x_1$) and binds the variable $y_1$ to the guessed symbol, then enters the state p,

  • 3. in the state p the variable $y_1$ is refreshed, that is, it is no longer bound to the input symbol. Then, start again.

We illustrate the run of $\mathcal {A}_1$ on the word $w=abbc$, starting from the initial configuration $(\emptyset ,p)$ as follows:

$$\begin{aligned} (\emptyset ,p) \mathop {\rightarrow }\limits ^{a} (\{{x_1 \mapsto c}\},p) \mathop {\rightarrow }\limits ^{b} (\{{x_1 \mapsto c}\},p) \mathop {\rightarrow }\limits ^{b} (\{{x_1 \mapsto c}\},p) \mathop {\rightarrow }\limits ^{c} (\{{x_1 \mapsto c}\},p') \end{aligned}$$

Notice that the variable $y_1$ does not appear in any of the configurations of this run since it is refreshed in the state p. Hence, the language $\mathcal {L}(\mathcal {A}_1)$ consists of all the words in $\varSigma ^{\star }$ in which the last letter is different from all the other letters. By following similar reasoning, we get $\mathcal {L}(\mathcal {A}_2)=\{w_1w'_1\cdots w_{n}w'_n \;\;|\;\;w_i, w'_i \in \varSigma , \, n\ge 1, \text { and }w_{i} \ne w'_{i}, \, \forall i \in [n]\}$. This language can be recognized by an NFMA [11] but not by a fresh-variable automaton [2].

3 Comparison Between PAs and NFMAs

In this section, we show that parametrized automata (PAs) and finite-memory automata with non-deterministic reassignment (NFMAs), which are discussed in [11], have the same expressive power (i.e. for any language over infinite alphabet, there exists an NFMA recognizing it iff there exists a PA that recognizes it), but there are languages for which PAs can be exponentially more succinct than NFMAs.

3.1 Expressiveness

We recall that an NFMA (as defined in [11]) is a 8-tuple $\mathcal {F}=\langle \varSigma ,k,Q,q_0,\varvec{u},\rho ,\delta ,F \rangle$ where $k\in \mathbb {N}^{+}$ is the number of registers, Q is a finite set of states, $q_0 \in Q$ is the initial state, $\varvec{u}: [k] \rightharpoonup \varSigma$ is a partial function called the initial assignment of the k registers, $\rho : \{{(p,q) : (p,\varepsilon ,q) \in \delta }\} \rightharpoonup [k]$ is a function called the non-deterministic reassignment, $\delta : Q\times ([k]\cup \{{\varepsilon }\}) \times Q$ is the transition relation, and $F \subseteq Q$ is the set of final states. Intuitively, if $\mathcal {F}$ is in state p, and there is an $\varepsilon$-transition from p to q and $\rho (p,q)=l$, then $\mathcal {F}$ can non-deterministically replace the content of the $l^\mathrm{{th}}$ register with an element of $\varSigma$ not occurring in any other register and enter state q. However, if $\mathcal {F}$ is in state p, and the input symbol is equal to the content of the $l^\mathrm{{th}}$ register and $(p,l,q) \in \delta$ then $\mathcal {F}$ may enter state q and pass to the next input symbol. An $\varepsilon$-transition $(p,\varepsilon ,q)\in \delta$ with $\rho (p,q)=l$, for a register $l \in [k]$, is denoted by $(p,\varepsilon \slash l, q)$.

Interpreting registers of the NFMAs as variables, the semantics of NFMAs can be given as a relation over configurations of the form $(q,\sigma )$ where q is a state of the NFMA and $\sigma$ is a substitution of registers with letters.

Fig. 2.

A translation schema of NFMA to PA. The registers of the NFMA $\mathcal {A}$ are $\{{1,\ldots ,k}\}$, they correspond to the variables $\{{x_1,\ldots ,x_k}\}$ of the PA $\mathcal {A}'$. The variable $x_l$ is refreshed in the state $\tilde{p}$ of $\mathcal {A}'$.

It is easy to see, as illustrated in Fig. 2, that any NFMA (with k registers) can be translated into a PA (with k variables) of linear size, that recognizes the same language. More precisely, as shown in Fig. 2: (i) a transition $(p,m,p')$ of the NFMA is translated as such, i.e. to $(p,x_m,p')$; and, (ii) a transition $(p,\varepsilon \slash l,p'')$ of the NFMA is translated to two transitions $(p,\varepsilon ,\tilde{p})$ and $(\tilde{p},(x_l,g),p'')$ where $g=\bigwedge _{i \in [k]\setminus \{{l}\}} (x_l \ne x_i)$ and $x_l$ is refreshed in state $\tilde{p}$.

Lemma 1

For any NFMA over $\varSigma$ with k registers and q states, there exists a corresponding PA with k variables and number of states linear in q, that recognizes the same language.

We show next that a PA can be translated into an NFMA recognizing the same language, by introducing an intermediary class of PAs, called $\overline{\text {PA}}$s, in which the variables should have distinct values. The idea is that the $\varepsilon$-transitions of the NFMA are used to encode the refreshing of the variables of the $\overline{\text {PA}}$s, which are translated into NFMA.

Definition 3

Let $\overline{\text {PA}}$s be the subclass of PAs such that every $\mathcal {A}$ in $\overline{\text {PA}}$s, verifies i) $\mathcal {A}$ has no constants, i.e. $\varSigma _{\mathcal {A}}=\emptyset$, and ii) for every reachable configuration $(\sigma ,q)$ of $\mathcal {A}$ and for all $x,y \in dom(\sigma )$, $\sigma (x) \ne \sigma (y)$.

It can be shown that PAs and $\overline{\text {PA}}$s recognize the same language, more precisely we have:

Lemma 2

For every PA $\mathcal {A}$ with k variables and n states there is a $\overline{\text {PA}}$ with $k+m$ variables and $O( n \cdot (k+m)!)$ states recognizing the same languages, where $m=|\varSigma _{\mathcal {A}}|$.

For the proof and construction of the same, let $\mathcal {X}$ and $\mathcal {X}'$ be two disjoint sets of variables, and let $\psi$ be a total function from $\mathcal {X}$ to ${\mathcal {X}'}$, and let g be a conjunction of equalities between variables in $\mathcal {X}$. Then define $g \sqsubset \psi$ iff there exists $x' \in \mathcal {X}'$ s.t. $\psi (x)=x'$ for all x in $\mathcal {V}(g)$. And let $\mathcal {A}=\langle \varSigma ,\mathcal {X},Q,Q_0,\delta ,F,\kappa \rangle$ be a PA with $\mathcal {X}=\{{x_1,\ldots ,x_k}\}$.

Firstly, we transform the PA $\mathcal {A}$ into a PA $\varvec{\mathcal {A}}$ recognizing the same language and in which each state is labeled with the set of variables being free in this state. We define $\varvec{\mathcal {A}}=\langle \varSigma ,\mathcal {X},\varvec{Q},\varvec{Q_0},\varvec{F},\varvec{\delta },\varvec{\kappa } \rangle$ by:

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{Q} &{}= \{{ (q,X) \,\vert \, q\in Q \text { and }X\subseteq \mathcal {X}}\}, \\ \varvec{Q_0} &{} = \{{ (q,\mathcal {X}) \,\vert \, q\in Q_0 }\}, \\ \varvec{F} &{}= \{{ (q,X) \,\vert \, q\in F \text { and }X\subseteq \mathcal {X} }\}. \end{array}\right. } \end{aligned}$$

The transition function $\varvec{\delta }$ is defined by $(q',X')\in \varvec{\delta }((q,X),\alpha ,g)$, where $\alpha \in \varSigma \cup \mathcal {X}$ and g is a guard, if and only if, $X'=(X\setminus (\{{\alpha }\}\cup \mathcal {V}(g)))\cup \kappa ^{-1}(q')$. Finally, the refreshing function $\kappa '$ is defined by $\varvec{\kappa }(x)= \{{(q,X) \,\vert \, q\in \kappa (x)}\}$.

Secondly, we can assume w.l.o.g. that $\varvec{\mathcal {A}}$ has no constants and the variables are refreshed only in the states preceded by $\varepsilon$-transitions. The constants can be replaced by additional variables that have to be initialized with the related constants using an $\varepsilon$-transition outgoing from the initial state. And, if some variables, say $X\subseteq \mathcal {X}$, are refreshed in a state, say $\varvec{q}$, then we add an $\varepsilon$-transition $\varvec{q}\mathop {\rightarrow }\limits ^{\varepsilon } \varvec{\tilde{q}}$ where the variables X are refreshed in $\varvec{\tilde{q}}$ instead of $\varvec{q}$ and the outgoing transitions of $\varvec{q}$ become the outgoing transitions of $\varvec{\tilde{q}}$. Thus, the guards of $\varvec{\mathcal {A}}$ are of the form $\phi \wedge \phi '$ where $\phi$ (resp. $\phi '$) is a conjunction of equalities (resp. inequalities) between variables.

Thirdly, we let $\varvec{\mathcal {A}}'$ to be the $\overline{\text {PA}}$ $\varvec{\mathcal {A}}'=\langle \varSigma ,\mathcal {X}',\varvec{Q}',\varvec{Q}'_0, \varvec{\delta }',\varvec{F}',\varvec{\kappa }' \rangle$ defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathcal {X}' &{} =\{{x'_1,\ldots ,x'_k}\} \\ \varvec{Q}' &{}= \varvec{Q} \times \mathcal {X}^{\mathcal {X}'} \\ \varvec{Q}'_0 &{} = \varvec{Q}_0 \times \mathcal {X}^{\mathcal {X}'} \\ \varvec{\kappa }' &{} = \kappa \times \mathcal {X}^{\mathcal {X}'} \end{array}\right. } \end{aligned}$$

and $\varvec{\delta }'$ is defined by [where g (resp. $g'$) is a conjunction of equalities (resp. inequalities)] :

$$\begin{aligned} ((q_1,X_1,\psi _1), (\alpha ,\psi _1(g\wedge g')), (q_2,X_2,\psi _1)) \in \varvec{\delta }' \text { iff } {\left\{ \begin{array}{ll} ((q_1,X_1),(\alpha ,g \wedge g'),(q_2,X_2)) \in \varvec{\delta } \text { and }\\ \alpha \ne \varepsilon \text { and }\\ g \sqsubset \psi _1 \text { and }\\ \mathcal {V}(g') = codom(\psi _1) \text { and }\\ \mathcal {V}(g\wedge g') \cap X_1 =\emptyset \end{array}\right. } \end{aligned}$$

And,

$$\begin{aligned} ((q_1,X_1,\psi _1), (\varepsilon , \psi _1(g \wedge g')), (q_2,X_2,\psi _2)) \in \varvec{\delta }' \text { iff } {\left\{ \begin{array}{ll} ((q_1,X_1),(\varepsilon , g \wedge g'),(q_2,X_2)) \in \varvec{\delta } \text { and }\\ \mathcal {V}(g') = codom(\psi _1) \text { and }\\ \mathcal {V}(g\wedge g') \subseteq X_1 \text { and }\\ \psi _2 = \psi _1 \cup \{{x \mapsto x_0 \;\;|\;\;x \in \mathcal {V}(g)}\} \cup \\ \quad \quad \quad \{{x \mapsto y_0 \;\;|\;\;x \in \mathcal {V}(g')}\} \\ x_0= get (X' \setminus codom(\psi _1)) \\ y_0= get \big (X' \setminus (codom(\psi _1) \cup \{{x_0}\})\big ) \end{array}\right. } \end{aligned}$$

Therefore having proved the expressive equivalence of $\overline{\text {PA}}$ and PA, we now show every $\overline{\text {PA}}$ can be turned into an NFMA recognizing the same languages by encoding the refreshing of the variables of the $\overline{\text {PA}}$s with $\varepsilon$-transitions. Hence,

Lemma 3

For every PA with k variables and n states there exists an NFMA with $n \cdot k!$ states recognizing the same languages.

Theorem 1

For every language L over $\varSigma$, there exists an NFMA $\mathcal {F}$ such that $\mathcal {L}(\mathcal {F}) = L$, if and only if there exists a PA $\mathcal {A}$ such that $\mathcal {L}(\mathcal {A}) = L$.

3.2 Succinctness of PAs over NFMAs

We next show that while PAs and NFMAs have the same expressive power, PAs can be exponentially succinct than NFMAs. That is, we prove that there exists a class of PAs such that any NFMA that recognizes the same language must be exponentially larger.

Theorem 2

There exists a countably infinite class of languages $\lbrace L_1, L_2, ...\rbrace$, such that for every n, there exists a PA $\mathcal {A}_n$, of size $\mathcal {O}(\log n)$, such that $\mathcal {L}(\mathcal {A}_n) = L_n$, but there does not exist any NFMA $\mathcal {F}$, of size o(n), such that $\mathcal {L}(\mathcal {F}) = L_n$.

We prove the existence by taking the class of languages $L_n = \lbrace a^n \rbrace$. We first argue in Lemma 4 the existence of a PA with $\mathcal {O}(\log n)$ states and $\mathcal {O}(\log n)$ variables, that recognizes $L_n$. Then we prove in Lemma 6 that any NFMA that accepts the language $L_n$ must have at least $\varOmega (n)$ states.

Lemma 4

For every $n \ge 1$, there exists a PA $\mathcal {A}_n$ with $\mathcal {O}(\log n)$ states and $\mathcal {O}(\log n)$ variables, such that $\mathcal {L}(\mathcal {A}_n) = L_n = \lbrace a^n\rbrace$.

It has already been shown in [3] that addition and comparison for bounded integers can be implemented in PAs, with constants to denote 0 and 1, in $\mathcal {O}(\log n)$ states and $\mathcal {O}(\log n)$ variables that encode bit representation of an integer. To construct a PA for the language $L_n = \lbrace a^n\rbrace$, we construct a PA that acts as a Counter, i.e. the value encoded by variables is incremented every time a is read, until $\bigwedge _{i=1,\ldots ,m} (x_i=c_i)$, which allows transition from the seed state to an accepting state, where $c_1c_2\ldots c_m$ is the binary representation of n.

Such a PA, acting as a Counter, recognizes only $L_n = \lbrace a^n\rbrace$, by counting till n using the variables for bit representation.

We now show that any NFMA that recognizes the $L_n = \lbrace a^n\rbrace$ must require at least $\mathcal {O}(n)$ states. Let us take an NFMA $\mathcal {F}$, with $\mathcal {L}(\mathcal {F}) = L_n$.

Since $\mathcal {F}$ accepts $a^n$, we know that there exists a configuration path

$$\begin{aligned} \wp = c_1 \rightarrow c_2 ... \rightarrow c_m = (q_1, \sigma _1) \rightarrow (q_2, \sigma _2) ... \rightarrow (q_m, \sigma _m) \end{aligned}$$

(1)

such that

$$\begin{aligned} trace(\wp ) = a^n \end{aligned}$$

(2)

where $\wp$ is a path over the set of configurations of $\mathcal {F}$, and $m \ge n$.

Since a is a constant, and $L_n$ includes only $a^n$, we argue that a must be stored in some NFMA register initially, which we can call without loss of generality $l_0$.

Lemma 5

$\wp$ (from Eq. (1), a path in $\mathcal {F}$ that accepts $a^n$) contains only $\varepsilon$-transitions and $l_0$-transitions.

Proof

It can be easily seen that $l_0$-transitions are the only non-$\varepsilon$-transitions in $\wp$. Since the trace contains only a’s, if on the contrary there was some $l_k$-transition for any $k\ne 0$, it would require $\sigma (l_k)= a$ at that transition. However, due to implicit dis-equality, since $\sigma _1(l_k) \ne a$, there must be some i such that $c_i \overset{\varepsilon / l_k}{\longrightarrow } c_{i+1}$, and $\sigma _i(l_{k'}) \ne a$ for all $k^\prime \ne k$, at which stage $l_k$ stored a.

But if this holds, then it is also possible for $l_k$ to get assigned to some completely different letter b, such that $b \ne \sigma _i(l_{k'})$ for any $k^\prime$, from the infinite alphabet $\varSigma$, at the $i^{th}$ transition. Since this would imply that $\mathcal {F}$ also accepts another string with some a’s in $trace(\wp )$ replaced with b’s, hence by contradiction, we know that $\wp$ only contains $\varepsilon$-transitions and $l_0$-transitions.

We observe $\forall i: \sigma _i(l_0) = a$, and therefore the sub-NFMA $\mathcal {F}^\prime$, with only the $\varepsilon$-transitions and $l_0$ labelled transitions of $\mathcal {F}$ is sufficient for recognizing the singleton language. In fact, all accepting paths in $\mathcal {F}$ are accepting paths in $\mathcal {F}^\prime$.

We now define the notion of strong bisimilarity for NFMAs to argue for an important assertion for our proof.

Definition 4

(NFMA Bisimulation). Two NFMA configurations $(q_1, \sigma _1)$ and $(q_2, \sigma _2)$ are said to be strongly bisimilar, i.e. $(q_1, \sigma _1) \sim (q_2, \sigma _2) \leftrightarrow (q_2, \sigma _2) \sim (q_1, \sigma _1)$, if

• 1. for all $\alpha \in \varSigma$, if there exists $(q_1^\prime , \sigma _1^\prime )$ with $(q_1, \sigma _1) \overset{\alpha }{\longrightarrow } (q_1^\prime , \sigma _1^\prime )$, then there must exist $(q_2^\prime , \sigma _2^\prime )$, such that $(q_2, \sigma _2) \overset{\alpha }{\longrightarrow } (q_2^\prime , \sigma _2^\prime )$ and $(q_2^\prime , \sigma _2^\prime ) \sim (q_1^\prime , \sigma _1^\prime )$. And vice versa.

• 2. if there exists $(q_1^\prime , \sigma _1^\prime )$ such that $(q_1, \sigma _1) \overset{\varepsilon }{\longrightarrow } (q_1^\prime , \sigma _1^\prime )$, then there must exist $(q_2^\prime , \sigma _2^\prime )$ with $(q_2, \sigma _2) \overset{\varepsilon }{\longrightarrow } (q_2^\prime , \sigma _2^\prime )$, such that $(q_2^\prime , \sigma _2^\prime ) \sim (q_1^\prime , \sigma _1^\prime )$. And vice versa.

Lemma 6

For an NFMA with all non-$\varepsilon$-transitions restricted to registers in a subset $\mathbb {L}$ of the set of registers, if $\sigma _1$ agrees with $\sigma _2$ over $\mathbb {L}$ then $(q, \sigma _1)$ is bisimilar to $(q, \sigma _2)$, for all states q.

This follows by observing that:

• for all transitions $(q, l_j, q^\prime ) \in \delta$, with 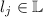and $\sigma _1(l_j) = \sigma _2(l_j)$, $(q, \sigma _1) \overset{\alpha }{\longrightarrow } (q^\prime , \sigma _1^\prime )$ if and only if $(q, \sigma _2) \overset{\alpha }{\longrightarrow } (q^\prime , \sigma _2^\prime )$, for any $\alpha \in \varSigma$.

• for all transitions $(q, \varepsilon / l_j, q^\prime )$, if $(q, \sigma _1) \overset{\varepsilon }{\longrightarrow } (q^\prime , \sigma _1^\prime )$, with $\sigma _1^\prime (l_j) = \beta$, for some $\beta \in \varSigma$ without loss of generality, then there exists $\sigma _2^\prime$, where $\sigma _2^\prime (l_j) = \beta$ and $\sigma _2^\prime (l_k) = \sigma _2(l_k)$ for all $k\ne j$, such that $(q, \sigma _2) \overset{\varepsilon }{\longrightarrow } (q^\prime , \sigma _2^\prime )$. And vice versa.

Now applying Lemma 6 to the $\mathcal {F}^\prime$ for which $\mathcal {L}(\mathcal {F}^\prime ) = L_n$ and contains only $\varepsilon$-transitions and $l_0$ labelled transitions, as argued above, we claim that $\mathcal {F}^\prime$ must contain $\varOmega (n)$ states.

Lemma 7

An NFMA $\mathcal {F}^\prime$ that recognizes $\lbrace a^n \rbrace$ has at least $n+1$ states.

Proof

Towards a contradiction, let us assume that there are less than $n+1$ states in $\wp$ (from Eq. (1)). Then we can argue that $\exists i \ne j : q_i=q_j$ and the trace from configuration $c_i$ to $c_j$ is $a^{n_1}$ for $n_1 > 0$. Since, otherwise, if there are no such i and j then there must be at least $n+1$ states.

Now, let the trace from $c_1$ to $c_i$ be $a^{n_0}$, from $c_i$ to $c_j$ be $a^{n_1}$, and $c_j$ to $c_m$ be $a^{n_2}$, with $n_0 , n_1 , n_2 > 0$. And thus $n_0 + n_1 + n_2 = n$.

But since $q_i = q_j$, thus the path from $c_j$ to $c_m$ can also be simulated from $c_i$, by Lemma 6, since the substitutions already agree on $l_0$. Hence the automata $\mathcal {F}$ also accepts $a^{(n_0 + n_2)}$, which is in contradiction to the language.

Hence by contradiction there are at least $n+1$ states in $\mathcal {F}$, which is exponential in the size of comparable PA, proving Theorem 2.

4 Complexity of Simulation Preorder over PAs

Theorem 3

Deciding the simulation preorder over PA is EXPTIME-complete.

An EXPTIME algorithm for deciding if a PA simulates another PA was given in [3], and we show that this problem is indeed EXPTIME-complete, by reduction from Countdown Games(CG) [10].

In [10], Jurdzinski et al. introduce Countdown Games (CG), and prove that the problem of deciding the winner for these games is EXPTIME-complete. We reduce the problem of deciding winner to deciding simulation of PA by giving a construction for PAs $\mathcal {A}_{\forall }$ and $\mathcal {A}_{\exists }$, for any CG, such that Eloise wins the game iff $\mathcal {A}_{\forall }$ is simulated by $\mathcal {A}_{\exists }$.

The countdown game is defined as a tuple $(Q, \rightarrowtail {}, q^0, k^{*})$ where Q is a finite set of states, $\rightarrowtail {}\subseteq Q \times \mathbb {N}\setminus \lbrace 0\rbrace \times Q$ is a transition relation, $q^0 \in Q$ is the initial state, and $k^{*}$ is the final value. We write $q \overset{\ell }{\rightarrowtail {}} r$ if $(q, \ell , r) \in \rightarrowtail {}$. A configuration of the game is an element $(q, k) \in Q \times \mathbb {N}$. The game starts in configuration $(q^0, 0)$ and proceeds in moves: if the current configuration is $(q, k) \in Q \times \mathbb {N}$, first Player 0 chooses a number $\ell$ with $0 < \ell \le k^{*} - k$ and $q \overset{\ell }{\rightarrowtail {}} r$ for at least one $r \in Q$; then Player 1 chooses a state $r \in Q$, with $q \overset{\ell }{\rightarrowtail {}} r$. The resulting new configuration is $(r, k + \ell )$. Player 0 wins if she hits a configuration from $Q \times \lbrace k^{*}\rbrace$, and she loses if she cannot move (and has not yet won).

We proceed by reducing this game to a Simulation game, played between a Duplicator (Eloise) and a Spoiler (Abelard). Thus, Abelard wins if he is able to make a transition on $\mathcal {A}_{\forall }$ which cannot be simulated on $\mathcal {A}_{\exists }$, and Eloise otherwise.

To explicitly describe the construction, we first define a function $\lambda : Q \rightarrow 2^{\mathbb {Z}^{+}}$, where for each state q, $\lambda (q) = \lbrace \ell \mid \exists q' : q \overset{\ell }{\rightarrowtail {}} q'\rbrace$ We also note that the number of positive integers that occur in a CG will be less than the number of edges, and thus cannot be superpolynomial in the size of the description of the game. Let us denote these integers that occur as labels by the set $\varLambda = \lbrace \ell _1, \ell _2, ... \rbrace = \underset{q \in Q}{\bigcup } \lambda (q)$

Now let us define $\mathcal {A}_{\forall }$, as a PA, with the set of states, $Q_{\forall } = \lbrace p_0, p_\bot , p_{\ell _1}, p_{\ell _2}, ...\rbrace$, with a state for each label in $\varLambda$, in addition to an initial state and a dump state. We associate a letter $\alpha _i$ from the infinite alphabet $\varSigma$, to every integer $\ell _i \in \varLambda$, and define the transitions as:

• For each $\ell _i \in \varLambda$, there is $p_0 \overset{\alpha _i}{\longrightarrow } p_{\ell _i}$ and $p_{\ell _i} \overset{+ \ell _i}{\longrightarrow } p_0$,

• And finally, we have $p_0 \overset{\beta , k = k^{*}}{\longrightarrow } p_\bot$, where $\beta \in \varSigma$ and is not equal to any $\alpha _i$

We now define $\mathcal {A}_{\exists }$ as a PA, given a corresponding CG with states Q. The states of $\mathcal {A}_{\exists }$ are $Q_\exists = Q \uplus \lbrace q_\top \rbrace \uplus (\rightarrowtail {})$, with the following transitions:

• For each $q \overset{\ell _j}{\rightarrowtail {}} q^\prime$ in the CG, we have $q \overset{\alpha _j}{\longrightarrow } (q, \ell _j, q^\prime )$ and $(q, \ell _j, q^\prime ) \overset{+ \ell _j}{\longrightarrow } q^\prime$

• For each $q_i \in Q$, we have $q_i \overset{x, x \in \varLambda \setminus \lambda (q_i)}{\longrightarrow } q_\top$

• For each $q_i \in Q$, we have $q_i \overset{x, k > k^{*}}{\longrightarrow } q_\top$

• And we ensure that $q_\top$ is a universal simulator, i.e. $q_\top$ can simulate any PA transition, by allowing $q_\top \overset{y}{\longrightarrow } q_\top$ and making it a refresh state for y.

Notice that the “macro” transitions $p_{\ell _i} \overset{+ \alpha _i}{\longrightarrow } p_0$ and $q_i \overset{x , k > k^{*}}{\longrightarrow } q_\top$ can be translated into a series of transitions of a PA of linear size, by implementing corresponding adders and comparators, using $log (k^{*})$ variables, as shown earlier in [3].

We now show that Player 0 wins the CG iff Abelard wins the corresponding simulation game. In fact, we prove that a configuration (q, k) of CG is a winning configuration for Player 0 iff $[\mathcal {A}_\forall : (p_0 , k), \mathcal {A}_\exists : (q, k)]$ is a winning configuration for Abelard in the simulation game.

We know that for any configuration of simulation game where $\mathcal {A}_\exists$ is at $q_\top$ will be a losing state for Abelard, by definition, since $q_\top$ can simulate all transitions. Similarly, any configuration of simulation game, where $\mathcal {A}_\forall$ is at $p_\bot$ and $\mathcal {A}_\exists$ is not at $q_\top$, will be a winning state for Abelard since Eloise cannot otherwise duplicate a $\beta$-transition.

Abelard wins in $[\mathcal {A}_\forall : (p_0 , k), \mathcal {A}_\exists : (q, k)]$ iff either $k=k^{*}$, since $p_\bot$ is then reachable with a $\beta$-transition, or $k < k^{*}$ and there exists an $\alpha _i$-transition to a winning state. However, for $\ell _i \notin \lambda (q)$, Eloise can move to $q_\top$, therefore if there exists an $\alpha _i$-transition to a winning state, then $\ell _i \in \lambda (q)$. Such a transition can be duplicated only by $q \overset{\alpha _i}{\longrightarrow } (q, \ell _i, q^\prime )$, by Eloise for some $q^\prime$, resulting in subsequent duplication of $p_{\ell _i} \overset{+ \ell _i}{\longrightarrow } p_0$ with $(q, \ell _i, q^\prime ) \overset{+ \ell _i}{\longrightarrow } q^\prime$. Thus, if $k < k^{*}$ then there exists an $\alpha _i$-transition to a winning state iff there is an $\ell _i \in \lambda (q)$ such that for all $q^\prime$ such that $q \overset{\alpha _i}{\longrightarrow } (q, \ell _i, q^\prime )$ (which iff $q \overset{\ell _j}{\rightarrowtail {}} q^\prime$ in CG), $[\mathcal {A}_\forall : (p_0 , k + \ell _i), \mathcal {A}_\exists : (q^\prime , k + \ell _i)]$ are all winning states.

Since Player 0 wins in configuration (q, k) iff $k=k^{*}$ or if $k < k^{*}$ and $\exists \ell _i \in \lambda (q) : \forall q^\prime : q \overset{\ell _j}{\rightarrowtail {}} q^\prime \implies (q^\prime , k+\ell _i)$ is a winning state, therefore we coinductively prove that Abelard wins in $[\mathcal {A}_\forall : (p_0 , k), \mathcal {A}_\exists : (q, k)]$ iff Player 0 wins in (q, k).

Therefore the problem of deciding a winner for any CG can be polynomially reduced to the problem of deciding the winner for the simulation game over PAs. This proves that deciding simulation preorder over PAs is EXPTIME-hard, which coupled with previous results, implies that simulation is EXPTIME-complete.

5 Conclusion

We have shown that PAs can be exponentially smaller than NFMAs for some languages and that simulation preorder over PAs is EXPTIME-complete. Finding a good lower bound for deciding simulation preorder over NFMAs, which has an upper bound of EXPTIME, will also reveal more about the relationship between the two models. It is easy to see that it is NP-hard, which also means that for languages where PAs are succinct with respect to NFMAs, while deciding simulation in NFMAs cannot possibly be done in polynomial time in n, checking the same over PAs would require time exponential in log(n), i.e. polynomial in n.

Further, it will be interesting to see if there are interesting subclasses of PAs, for which language containment is decidable or simulation preorder is efficiently decidable.