Abstract
Tracking bits through block ciphers and optimizing attacks at hand is one of the tedious task symmetric cryptanalysts have to deal with. It would be nice if a program will automatically handle them at least for well-known attack techniques, so that cryptanalysts will only focus on finding new attacks. However, current automatic tools cannot be used as is, either because they are tailored for specific ciphers or because they only recover a specific part of the attacks and cryptographers are still needed to finalize the analysis.
In this paper we describe a generic algorithm exhausting the best meet-in-the-middle and impossible differential attacks on a very large class of block ciphers from byte to bit-oriented, SPN, Feistel and Lai-Massey block ciphers. Contrary to previous tools that target to find the best differential / linear paths in the cipher and leave the cryptanalysts to find the attack using these paths, we automatically find the best attacks by considering the cipher and the key schedule algorithms. The building blocks of our algorithm led to two algorithms designed to find the best simple meet-in-the-middle attacks and the best impossible truncated differential attacks respectively. We recover and improve many attacks on AES, mCRYPTON, SIMON, IDEA, KTANTAN, PRINCE and ZORRO. We show that this tool can be used by designers to improve their analysis.
Patrick Derbez was partially supported by the CORE ACRYPT project from the Fond National de Recherche (Luxembourg).
© IACR 2016. This article is the final version submitted by the author to the IACR and to Springer-Verlag in June 2016, which appears in the proceedings of CRYPTO 2016.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
To explore the exponential space of differentials or linears characteristics, cryptanalysts usually implement some algorithms. Many tools have been proposed for ciphers or hash functions [BDF11, DF13, FJP13, Leu12] but most of the time they are not publicly available. Moreover, they are not very convenient for block cipher designers and are rarely used for many reasons. On the one hand, some tools have been designed to explore precise ciphers and it is not easy to adapt them for new designs. The main reason is that we hope that taking into account some particularities of the cipher, would lead to more efficient attacks. Consequently, some details of the analyzed ciphers are hard-coded into the tool and it is not easy to make any changes. On the other hand, only cryptanalysts can used such tools which are more computational-aid than real tools. Indeed, some tools allow to find some differential paths, but more work has to be done by cryptanalysts to find the best attack. However, this last part is usually not completely trivial and it is not always the best differential paths, that would lead to the best attacks. For instance, the best differential attack on DES does not use the best and longest differential path [BS93] on 15 rounds, but a 13 rounds differential path is used with meet-in-the-middle technique to extend this path, leading to the so-called 3R attack. The meet-in-the-middle step is rarely considered in tools while it is computationally difficult to exhaust the most efficient combination of say a differential path with the number of guesses. Indeed, once a differential path is found, attackers have to guess some key bits in order to be able to check the differential part. Consequently, the overall complexity of the attack depends on the number of guesses and the probability of the differential. The best attack has a complexity that is the maximum of both stages. The last step is a meet-in-the-middle technique and it is well-known that it allows to find the most efficient attack since bad key guesses are quickly rejected. As a conclusion, if we want to automatically find the best attack, we need to be able to automatically solve each stage: find many good differential paths and for each of them evaluate the cost of the meet-in-the-middle part.
Automatic Tools. Automatic search of symmetric attacks boils down to solving a system of equations in many variables as Shannon described in his seminal work in 1949 on Communication Theory of Secrecy Systems: Breaking a good cipher should require as much work as solving a system of simultaneous equations in a large number of unknowns of a complex type. Algebraic cryptanalysis can be traced back to him and some attacks on stream ciphers have been very efficient [CM03]. However, solving these equations is not always easy and cryptanalysts have to take into account the structure of such systems if they want to efficiently solve them. Indeed, Gröbner basis algorithms have been used, but they never endanger the security of real block ciphers [BPW06a, BPW06b]. Cryptographers have to closely analyze the involved systems depending on the number of variables, their degree, some symmetries in the equations if they want to find some attacks. The other well-known tool consists in writing boolean equations and feed them to a SAT solver such as CryptoMiniSAT [SNC09]. Black box use of these two well-known solvers never lead to efficient attacks. They can be used either on a very small number of rounds [MS13] or when attacks are described in order to speed up the search [SKPI07, MZ06]. Since solving a polynomial system of equations in many variables is a NP-hard problem [GJ79], some cryptanalysts try to better take into account the structure of these systems. Since block ciphers are built iteratively in many rounds and each of them use a linear part (diffusion) and a non-linear part (Sbox essentially), one of the most interesting research directions consists in writing linear equations by adding new variables for each Sbox [BDF11, KBN09]. Consequently, we can write the system as a linear system in variables x and S(x), where S is treated as an inert function. Such systems are not easy to solve because there is a relation between these two kinds of variables and classical gaussian technique does not work. In order to consider the system of equations, Bouillaguet et al. in [BDF11] have used well-known cryptographic techniques to solve such systems such as guess-and-determine and meet-in-the-middle. The consequence is that the tool is very versatile and solves any such systems by describing an algorithm to solve it with its average time/memory complexity. For instance, they were able to find attacks on MAC and stream-ciphers. However, it is not specific for block ciphers and it is not easy to search attacks involving many messages. This tool is nevertheless interesting since it is generic and for instance, Derbez and Fouque use it in [DF13] and Dinur and Jean in [DJ14].
Related Work. The original meet-in-the-middle attack [DS08] of Demirci and Selçuk against AES has been improved and generalized by many researchers and is nowadays well-understood. It relies on particular sets called \(\delta \)-sets, which were first introduced by Daemen et al. against the block cipher SQUARE. At ASIACRYPT 2010, Dunkelman et al. [DKS10] presented several improvements for the attack including the differential enumeration technique, a clever and powerful memory/data trade-off that does not change the time. Then at EUROCRYPT 2013, Derbez et al. [DFJ13] mainly showed that this technique leads to much better attacks than expected by Dunkelman et al., and reached the best known attacks against 7-round AES-128 and 9-round AES-256 in the single-key model. Next, at FSE 2013, Derbez and Fouque [DF13] generalized the attack of Demirci and Selçuk by searching a match on some equation and not only on the byte state, and showed that approximately \(2^{16}\) different attacks can be mounted against the AES. In order to find the best ones among them, they used the tool presented by Bouillaguet et al. [BDF11] at CRYPTO 2011 to take care of the key schedule relations between the subkey bytes involved in the attacks.
This kind of attacks is very efficient againsts round-reduced versions of the AES and actually it may also be efficient against non-SPN ciphers as showed by Li and Jia in [LJ14] where they successfully applied the technique against Camellia [AIK+00]. At ICISC 2013, Li et al. [LWWZ13] described an algorithm to find the best distinguishers one can use to mount a Demirci-Selçuk attack on a word-oriented block cipher. In particular, they showed that finding the distinguishers which have the least number of active cells can be turned into an integer linear program that they solved. As a result, they found new attacks against both Crypton-128 and mCrypton-96.
Our Contribution. Our first contribution is a new tool that allows to automatically find meet-in-the-middle and impossible differential attack. Contrary to other tools, this new one is publicly available and allows to recover differential paths and complete attacks by extending them using well-known meet-in-the-middle technique. One major contribution is that we determine specific problems that allow us to design a modular approach for our tool. Indeed, we will describe some building blocks that allow us to automatically find impossible differential attack, truncated differential path and meet-in-the-middle attacks when we combine them in a specific manner. Finally, we apply it on many block ciphers.
We show that our tool allows to discover automatically in a few seconds many of the best meet-in-the-middle and impossible differential attacks on some bit and byte oriented ciphers: CRYPTON, mCRYPTON, AES, SIMON, IDEA and XTEA. On SIMON, the tool allows to recover all the attacks found by hand by Boura et al. in [BNS14] and even improve them by one more round. Essentially, the tool was able to discover that we can save some guesses by guessing the xor of two key bits instead of each of the two bits. For IDEA, our results are noteworthy and we think it is a good example of bit-oriented cipher since it mixes various operations which prevent to use any larger field as in AES. This cipher has been unattacked during 10 years after its publications and in 2002, Biryukov and Demirci discovered a particular relation that allows them to break 2 rounds among the 8.5 rounds. About 10 years after, Biham, Dunkelman, Keller and Shamir use this relation to mount efficient meet-in-the-middle attacks [BDKS15]. In a few seconds, our tool was able to automatically recover the Biryukov-Demirci relation and to find all the attacks on 6 rounds [BDKS15]. On XTEA, the tool was also able to recover the best impossible differential path of [MHL+02] on 12 rounds. If we only want to recover differential path and not the complete attack, it is possible to ask it to the tool.
The main purpose of this tool is not only for cryptanalysis in order to find attacks, but also for designers in order to test their new ciphers. The ZORRO block cipher has been proposed by Gérard et al. at CHES 2013 [GGNS13] in order to be secure and efficient to mask. The main idea consists in using an easy to mask Sbox and to reduce the number of Sbox at each round since the overhead of masking comes from these two factors. The overall design is close to AES. However, many attacks have been discovered on this cipher including on the full number of rounds. Here, we exhaust using symmetries properties all the family of ZORRO ciphers and we show that some strategic positions of the Sboxes lead to stronger ciphers.
We describe a generic algorithm exhausting the best meet-in-the-middle and impossible differential attacks on a very large class of block ciphers. Unlike Li et al.’s algorithm, our is not restricted to word-oriented block ciphers and takes into account the key schedule relations to directly give as output the best attacks and their complexities. Actually, it is based on the tool of Bouillaguet et al. to estimate the complexity of the attacks. Thus our algorithm only requires as input a system of equations describing the targeted cipher and the type of each variable: plaintext, ciphertext, key or state. Incidentally, the building blocks of our algorithm led to two others algorithms designed to find the best simple meet-in-the-middle attacks and the best impossible truncated differential attacks respectively. Impossible differential cryptanalysis, which was simultaneously introduced by Knudsen [Knu98] and Biham et al. [BBS99], is a powerful technique against a large variety of block ciphers. While there are already algorithms designed to find impossible differential against various kind of block ciphers (for instance [WW12]), our is the first one which outputs the complexities of the best attacks. More precisely, our algorithm gives as output all the parameters required to compute the complexity according to the general formula given at ASIACRYPT 2014 by Boura et al. in [BNS14].
We implemented our algorithms in C++ and make them available at:
2 Preliminaries
First we present a generalization of the Demirci-Selçuk (GDS) meet-in-the-middle technique for iterated block ciphers. Then, we recall some definitions from Bouillaguet et al. [BDF11] about systems of AES-like equations.
The GDS attack is similar to the splice-and-cut technique [WRG+11] but works with differences rather than state values. Demirci-Selçuk attacks have been discovered for AES and first generalized by Derbez and Fouque in [DF13] to match on a byte relation involving many bytes rather than on one state byte. Here, we generalize it on iterated block ciphers.
2.1 Generalized Demirci-Selçuk (GDS) Attack
We illustrate GDS on an AES-like cipher and then we generalize it to other ciphers. The basic idea is the following and assume that we have a relation involving internal variables. It can be a linear relation between 5 active bytes in an AES computation around the MixColumn operation. On the second line of Fig. 1, we represent such a relation between two states. Once, the variables of this relation have been identified, we propagate them to the plaintext and ciphertext bits and we get, the bits that have to be guessed in the intermediate states from the ciphertext and plaintext. The main problem is that the number of bits that have to be guessed is very large as in the figure. The main trick to reduce them is to force some constraints on the differential path. They are described by the first line, where some conditions are proposed. We will search for plaintexts satisfying the differential path. It is classical in AES cryptanalysis to use the differential path with one transition from one byte to 4 active bytes after the MixColumn operation with probability one and we let it propagate to the plaintext and ciphertext part with probability one. Finally, we get a GDS attack on the third line that use the bytes in the intersection of the two sets used in each state.
More formally, the original attack of Demirci and Selçuk [DS08] mainly relies on two subcomponents: one truncated differential characteristic and one basic meet-in-the-middle attack. More precisely, let \(E = E_3 \circ E_2 \circ E_1\) be an encryption function splitted into three parts. For the first step we pick a truncated difference \(\varDelta _X\) with \(b_{i}\) active bits, propagate it through \(E_1^{-1}\) (resp. \(E_3 \circ E_2\)) with probability 1 and denote the set of active bits by \(I_{P}\) (resp. \(I_{C}\)). Then, for the second step, we mount a basic meet-in-the-middle attack against \(E = E_3 \circ (E_2 \circ E_1)\): let Y be the output state of \(E_2 \circ E_1\), we pick \(b_{o}\) bits of Y and denote by \(O_{P}\) (resp. \(O_{C}\)) the bits required to compute their difference in Y from the difference in the plaintexts (resp. ciphertexts).
To explain further the GDS attack we introduce the definition of a b-\(\delta \)-set:
Definition 1
( b - \(\delta \) -set). A b-\(\delta \)-set is a set of \(2^b\) states such that b bits are active and take all the possible value while the others bits are constant. We also assume that the states of a b-\(\delta \)-set are sorted according to differences (i.e. if \(\{x^0,x^1,\ldots \}\) is a valid order then the valid orders are \(\{x^i,x^{i+1},\ldots \}\) for \(0 \le i < 2^b\)).
The structure of the Generalized Demirci-Selçuk attack is the following:
-
Offline phase:
-
1.
Consider the encryption of a \(b_{i}\)-\(\delta \)-set \(\{x^0,x^1,\ldots \}\) corresponding to the truncated difference \(\varDelta _X\) through \(E_2\).
-
2.
Guess the value of \(I_{C} \cap O_{P}\) for \(x^0\).
-
3.
Deduce the differences in the \(b_{o}\) chosen bits of Y for the \(b_{i}\)-\(\delta \)-set.
-
4.
Store them as a sequence of \(2^{b_{i}} - 1\) \(b_{o}\)-bit values in a hash table.
-
1.
-
Online phase:
-
1.
Pick a plaintext P.
-
2.
Guess the value of \(I_{P}\) for P and identify a set \(\{P,P^1,P^2, \ldots \}\) leading to a \(b_{i}\)-\(\delta \)-set associated to \(\varDelta _X\).
-
3.
Ask for the corresponding ciphertexts.
-
4.
Guess the value of \(O_{C}\) and partially decrypt the ciphertexts to compute the differences in the \(b_{o}\) chosen bits of Y.
-
5.
Check whether the sequence belongs to the hash table. If not, discard the guess.
-
1.
The complexity of this procedure depends directly on how many values the sets \(I_P\) and \(I_{C} \cap O_{P}\) can assume, \(\mathcal {S}( I_{C} \cap O_{P})\), and on how fast all the possible values of sets \(I_P \cup O_C\) and \(I_C \cap O_P\) can be enumerated, \(\mathcal {T}(I_{P} \cup O_C)\):
-
Data: \((2^{b_{i}} - 1) \cdot \mathcal {S}(I_P)\) adaptively chosen plaintexts,
-
Time (online): \( 2^{b_{i}} \cdot \mathcal {T}(I_{P} \cup O_C) \) partial encryptions,
-
Memory: \(b_{o} \cdot (2^{b_{i}} - 1 ) \cdot \mathcal {S}( I_{C} \cap O_{P} )\) bits,
-
Time (offline): \( 2^{b_{i}} \cdot \mathcal {T}(I_{C} \cap O_{P}) \) partial encryptions.
At the end of this attack we expect \(\min (1, \mathcal {S}( I_{C} \cap O_{P} ) \cdot 2^{-b_{o}(2^{b_{i}} - 1)}) \cdot \mathcal {S}( I_{P} \cup O_C)\) candidates to remain for \(I_{P} \cup O_C\). Thus \(b_i\) and \(b_o\) have to be chosen such that they provide enough filtration, but expanding them also increases the size of the sets \(I_P\), \(I_C\), \(O_P\) and \(O_C\) which then may rise the complexity of the resulting attack.
Remarks:
-
In the case where the truncated difference \(\varDelta _X\) does not fully active \(\varDelta _P\), i.e. differences in some plaintext bits are null, the attack can be turned into a chosen-plaintext attack by starting by asking for a structure of plaintexts. Actually this is (almost) always better to do so since, in general, \((2^{b_{i}} - 1) \cdot \mathcal {S}(I_P)\) is higher than \(2^{\vert \varDelta _P \vert }\).
-
Some extra memory can be used to map each sequence to its corresponding value of \(I_{C} \cap O_{P}\).
-
Given two invertible matrices \(M_1\) and \(M_2\), we can rewrite the encryption function \(E = (E_3 \circ M_2^{-1}) \circ (M_2 \circ E_2 \circ M_1^{-1}) \circ (M_1 \circ E_1)\). Hence the sentences “with \(b_i\) active bits” or “pick \(b_o\) bits of Y” should be understood as “with \(b_i\) active linear combinations of bits” or “pick \(b_o\) linear combinations of bits of Y”.
2.2 Systems of AES-like Equations
In the sequel we recall some definitions of Bouillaguet et al. we will use in our algorithms. In particular, we detail the notion of linear variables that allows us to reduce variables. Indeed, in our system of equations that are linear in the variables x and S(x), when all the equations only depend on \(ax+bS(x)\) for specific value a and b, then we can replace the variable x by a new one in X that represents \(ax+bS(x)\), so that if we recover X, we will be able to find x. Then, the second important notion is that for a system of equations describing the computation of the block cipher, the system is triangular from the plaintext and key variables to the ciphertext variables and so, from the ciphertext and key variables to the plaintext variables.
Given a finite field \(\mathbb {F}_q\), where q is a power of a prime number, and a non-linear function \(S: \mathbb {F}_q \longrightarrow \mathbb {F}_q\), an AES-like equation is defined as follows.
Definition 2
(AES-like equation). An AES-like equation in variables \(\mathbf {X}= \{x_1,\ldots ,x_n\}\) is an equation of the form:
where \(a_1,\ldots ,a_n,b_1,\ldots ,b_n,c \in \mathbb {F}_q\).
AES-like equations enjoy some very interesting properties. First the set of all the AES-like equations in variables \(\mathbf {X}= \{x_1,\ldots ,x_n\}\) is a vector space over \(\mathbb {F}_q\). Indeed, this set is stable by the multiplication by a scalar and the sum of two AES-like equations is still an AES-like equation.
Definition 3
(AES-like system). We denote by \(\mathcal {V}\left( \mathbf {X} \right) \) the vector space spanned by all the AES-like equations in variable \(\mathbf {X}\). A system of AES-like equations in variables \(\mathbf {X}\) is a subspace of \(\mathcal {V}\left( \mathbf {X} \right) \).
Definition 4
(subsystem). Let \(\mathbb {E}\) be a system of AES-like equations in variables \(\mathbf {X}\) and let \(\mathbf {Y}\) be a subset of \(\mathbf {X}\). We denote by \(\mathbb {E}(\mathbf {Y})\) the subspace \(\mathbb {E}\cap \mathcal {V}\left( \mathbf {Y} \right) \). This subspace is the biggest subsystem of \(\mathbb {E}\) composed of AES-like equations in variables \(\mathbf {Y}\).
Definition 5
(linear variable). Let \(\mathbb {E}\) be a system of AES-like equations in variables \(\mathbf {X}\) and let be \(x \in \mathbf {X}\). The variable x is a linear variable if and only if \(\dim \mathbb {E}- \dim \mathbb {E}(\mathbf {X}- \{x\}) \le 1\). The set of all the linear variables is denoted by \(\textsc {Lin}\left( \mathbb {E} \right) \).
This definition may seem abstract and the following proposition clarifies it:
Property 1
Let \(\mathbb {E}\) be a system of AES-like equations in variables \(\mathbf {X}\) and let \(x \in \textsc {Lin}\left( \mathbb {E} \right) \). Then it exists \((a,b) \in \mathbb {F}_q^2\) such that each equation of \(\mathbb {E}\) involving the variable x involves in fact a multiple of \(ax + bS(x)\). In other words, if we replace \(ax + bS(x)\) by X in the system of equations then x and S(x) do not appear any more. In particular, \(\textsc {Lin}\left( \mathbb {E} \right) \cap \mathbf {Y} \subseteq \textsc {Lin}\left( \mathbb {E}(\mathbf {Y}) \right) \) for any subset \(\mathbf {Y}\) of \(\mathbf {X}\).
Linear variables are very important in the work of Bouillaguet et al., in particular when the following assumption about the number of solutions of system of AES-like equations holds, we can estimate the complexity of our algorithms:
Let us introduce a last definition related to linear variables:
Definition 6
Let \(\mathbb {E}\) be a system of AES-like equations in variables \(\mathbf {X}\) and let \(\mathbf {Y}\) be a subset of \(\mathbf {X}\). Consider the following sequences:
The sequence \(\left( \mathbb {E}_i\right) \) is decreasing and thus at some rank r it becomes constant. We denote by \(\textsc {Lin}\left( \mathbb {E},\mathbf {Y} \right) \) the set of all variables occurring in the system \(\mathbb {E}_r\).
3 New Set of Tools
In this section, we will first describe our generic GDS attack. Therefore, we need to explain how we can automatically find the useful relations (minimal equations) and how we automatically split the variables involved in these relations in order to perform an efficient meet-in-the-middle for instance in sets \(O_P\) and \(O_C\). Then, we have to explain how we automatically find the truncated differential path and the sets \(I_P\) and \(I_C\). Splitting variables in some sets appears to be quite obvious by hand when we consider the cipher round by round. However, using the system of equations, this task appears to be not easy. Moreover, we need to perform this split efficiently and without any redundancy since the number of splitting an equation involving n variables in two sets of k and \(n-k\) variables becomes quickly very large. Finally, the intersections of the set of variables in some sets (\(I_P,I_C,O_P,O_C\)) define our attack and we use Bouillaguet et al. algorithm in order to find the best attack taking into account the key schedule equations.
It turns out that our tool is modular in the following sense. The algorithm used to find the sets \(O_P,O_C\) from the minimal equation is very similar to the one used to find the set \(I_P,I_C\) in the truncated differential path. Moreover, the algorithm used to find the impossible differential path used in fact two executations for the truncated differential path algorithms and by computing the intersection of both sets, we can automatically discover impossible differentials.
3.1 Generic Attack on Simple Block Cipher
Our idea is to build a tool finding the best GDS attacks on a block cipher, but where the block cipher is given as a system \(\mathbb {E}\) of AES-like equations over \(\mathbb {F}_q\). The only information assumed in our possession is the type of involved variables: plaintext (\(\mathbf {P}\)), ciphertext (\(\mathbf {C}\)), key (\(\mathbf {K}\)) or state (\(\mathbf {X}\)). To be a valid block cipher we impose three conditions on the system of equations:
These conditions are natural as they translate the fact that all variables can be computed step by step from \(\mathbf {P}\) and \(\mathbf {K}\) and also from \(\mathbf {C}\) and \(\mathbf {K}\), that all the key variables can be computed step by step from a master key and that the plaintext has the same size than the ciphertext (i.e. the blocksize).
For each non-key variable y we define 4 particular sets:
-
\(O_P(y) := \textsc {Lin}\left( \mathbb {E}, \mathbf {P}\cup \mathbf {K}\cup \{y\} \right) - \mathbf {K}\)
-
\(O_C(y) := \textsc {Lin}\left( \mathbb {E}, \mathbf {C}\cup \mathbf {K}\cup \{y\} \right) - \mathbf {K}\)
-
\(I_P(y) := \{ x \in \mathbf {X}\cup \mathbf {P}\cup \mathbf {C}~ \vert ~ y \in O_C(x) \}\)
-
\(I_C(y) := \{ x \in \mathbf {X}\cup \mathbf {P}\cup \mathbf {C}~ \vert ~ y \in O_P(x) \}\)
The set \(O_P(y)\) (resp. \(O_C(y)\)) contains the state variables required to propagate the differences from the plaintexts (resp. ciphertexts) to both y and S(y), i.e. the state variables required to compute y that go through an Sbox. In another hand, the set \(I_P(y)\) (resp. \(I_C(y)\)) contains the state variables that are required to propagate a non-zero difference from y to the plaintext (resp. ciphertext). Those sets give us all the information we need about a block cipher. Interestingly, we distinguish two kinds of block ciphers: the SPNs for which \(O_P(y) = I_P(y)\) and \(O_C(y) = I_C(y)\) for all non-key variables y, and the other ones (Fig. 2).
We can now give our algorithm finding the best GDS attacks which relies on four sub-algorithms. The aim of the first algorithm is to find a minimal equation involving a given variable. The two next ones are based on the guess-and-determine technique and are designed to exhaust the best building blocks of GDS attacks. Finally, the last sub-algorithm is just a merging procedure which also computes the complexities of the GDS attacks and sorts them.
Finding a Minimal Equation. In next algorithms we need to be able to find a minimal equation involving a particular variable y. Here minimal means that there is no equation involving y and a smaller subset (for the inclusion) of variables. For a system of AES-like equations it is rather simple as showed by Algorithm 1.


Truncated Differential Search. Given a value b, our goal is to exhaust all the minimal truncated differential characteristics that come from a truncated differential \(\varDelta _X\) of dimension b (at least), propagated in both way with probability 1. More precisely, we are interested by the corresponding couples \((I_P,I_C)\) (defined in Sect. 2.1) that are minimal for the following partial order relation:
In other words, we would like to exhaust truncated differential characteristics for which the set of active bits is minimal for the inclusion.
To solve this problem we decided to use a guess-and-determine procedure. At the beginning each non-key variable has 3 possible states: it can belong to \(I_P\), to \(I_C\) or be constant. Those states are exclusive, i.e. a variable can only be in one of them at the same time. Then the state search is easy to update thanks to the following rules:
-
\(x \in I_P \Rightarrow I_P(x) \subseteq I_P \text { and } O_P(x) \cap I_C = \emptyset \).
-
\(x \in I_C \Rightarrow I_C(x) \subseteq I_C \text { and } O_C(x) \cap I_P = \emptyset \).
-
\(x \text { constant } \Rightarrow O_P(x) \cap I_C = \emptyset \text { and } O_C(x) \cap I_P = \emptyset \).
One could perform an exhaustive search using only those rules but this is not optimal. Instead we define two new subsets:
-
\(I^G_P := \{ x \in I_P ~ \vert ~ \forall y \in I_P - \{x \}, ~ x \notin I_P(y) \}\).
-
\(I^G_C := \{ x \in I_C ~ \vert ~ \forall y \in I_C - \{x \}, ~ x \notin I_C(y) \}\).
Those sets are somehow the generators of \(I_P\) and \(I_C\) respectively. Our idea is to begin by guessing one variable of \(I^G_P\) and then by flagging just enough variables to a non-constant state to ensure that the guessed one is truly non-constant. This is done by looking for minimal equations involving the guessed variable and only unset variables. Finally if the dimension of the zero differences is small enough then the couple \((I_P,I_C)\) is stored. Otherwise, another variable of \(I^G_P\) or \(I^G_C\) is guessed and the procedure is repeated. Furthermore, the variables can be sorted such that at each step only two cases are possible: either the variable belongs to \(I^G_P\) or it does not belong to \(I_P\). While being more generic, this is actually quite close than picking a round r, saying that variables of \(I_P\) belong to the first r rounds and then first guessing the state of variables of the r-th round. The whole procedure is described in an algorithmic manner in Algorithm 2 and 3.

Basic Meet-in-the-middle Attack Search. Our algorithm to find the best couples \((O_P,O_C)\) is quite similar to the previous one. Each non-key variable also has 3 possible states: it can belong to \(O_P\), to \(O_C\) or be unused. The upgrade rules become:
-
\(x \in O_P \Rightarrow O_P(x) \subseteq O_P \text { and } I_P(x) \cap O_C = \emptyset \).
-
\(x \in O_C \Rightarrow O_C(x) \subseteq O_C \text { and } I_C(x) \cap O_P = \emptyset \).
-
\(x \text { unused } \Rightarrow I_P(x) \cap O_C = \emptyset \text { and } I_C(x) \cap O_P = \emptyset \).
We also define two generators sets:
-
\(O^G_P := \{ x \in O_P ~ \vert ~ \forall y \in O_P - \{x \}, ~ x \notin O_P(y) \}\).
-
\(O^G_C := \{ x \in O_C ~ \vert ~ \forall y \in O_C - \{x \}, ~ x \notin O_C(y) \}\).
The search procedure begins by guessing a variable of \(O^G_P\). Then we look for a minimal equation involving it, at least one unset variable and no variables flagged as unused. Next, two cases are possible: either we set to unused one of the involved variables and go back to the previous step, or we set to \(O_P\) or \(O_C\) all the involved variables. In the last case if \((O_P,O_C)\) leads to enough equations we store it, otherwise we guess another variable of \(O^G_P\) or \(O^G_C\) and restart the procedure in order to increase the number of equations.
Merging Procedure. The merging procedure is quite simple and similar to the one used by Derbez et al. in [DF13]. In order to perform it we need to compute the number of values that the sets \(I_P \cup O_C \cup \mathbf {P}\cup \mathbf {C}\) and \(I_C \cap O_P\) can assume and the time required to enumerate them. Under the heuristic assumption of the number of solutions given in the previous section, the procedure described in Algorithm 4 can be used. This procedure takes as input a system of equations \(\mathbb {E}\) and a set \(\mathbf {Y}\) and gives as output a set \(\mathbf {Z}\) containing \(\mathbf {Y}\) such that the number of solutions of \(\mathbb {E}(\mathbf {Z})\) is minimal. Furthermore, as we only consider systems \(\mathbb {E}\) such that \(\textsc {Lin}\left( \mathbb {E},\emptyset \right) = \emptyset \) (i.e. systems that are triangular) then the time required to enumerate the solutions of a subsystem is equal to its number of solutions.

3.2 Extension to a Larger Class of Block Ciphers
While interesting the previous algorithm can only handle a limited amount of block ciphers as many of them cannot be represented by a system of AES-like equations. So our idea is to make it work on systems of the following kind of equations:
Indeed a very large variety of block ciphers can be written as systems of such equations and actually it is rather simple to extend our previous algorithms to handle them. The main difference is that instead of considering single variables we now have to consider set of variables. The notion of linear variable can be easily extended to set of variable as follows:
Definition 7
(linear set of variables). Let \(\mathbb {E}\) be a system of equations in variables \(\mathbf {X}\) and let be \(x_1, \ldots , x_n \in \mathbf {X}\). The set \(\{x_1, \ldots , x_n \}\) is a linear set of variables if and only if \(\dim \mathbb {E}- \dim \mathbb {E}(\mathbf {X}- \{x_1, \ldots , x_n\}) \le n\).
Obviously we do not consider all set of variables but only the ones which go through an Sbox. Also, two sets of variables can share some variables which may be a problem. To solve it we introduce new variables and equations as shown in the following example:
Finally, handling multi-variables S-boxes naturally leads to the particular case of AND and OR. While until now S-boxes were considered as black boxes, both those functions have a special property that we want to be properly handled. Indeed, the following equation holds for any variables x and y:
In particular, if \(\varDelta y = 0\) then \(\text {AND}(x,y) \oplus \text {AND}(x \oplus \varDelta x, y) = \text {AND}(\varDelta x, y)\), meaning that computing the difference after the AND requires \(\varDelta x\) and y but not the actual value of x. This is also true for the OR operator since \(\text {OR}(x,y) = \text {AND}(x,y) \oplus x \oplus y\). As a consequence, in the previous algorithms, we have to define new sets \(I_P'\), \(I_C'\), \(O_P'\) and \(O_C'\) containing the variables required to compute the differences in each variable of \(I_P\), \(I_C\), \(O_P\) and \(O_C\) respectively, and use them instead for the complexity computations.
3.3 Two Other Modes
The building blocks of the GDS search algorithm allow to make automatic search for two others kind of attacks.
Basic Meet-in-the-Middle Attack. It is actually one of the building block used in the GDS-attack search procedure and thus it can be used on itself to find very low data complexity attacks. Its application is quite marginal but it was successfully used during the PRINCE Challenge [Sem14] to win some of the contests and it automatically rediscovered the best attack on full KTANTAN [CDK09].
Impossible Differential Attack. Recently, Boura et al. [BNS14] proposed a generic vision of impossible differential attacks with the aim of simplifying and helping the construction and verification of this type of cryptanalysis. In particular, they provided a formula to compute the complexity of such an attack according to its parameters. To understand the formula we first briefly remain how an impossible differential attack is constructed. It starts by splitting the cipher in three parts: \(E = E_3 \circ E_2 \circ E_1\) and by finding an impossible differential \((\varDelta _X \nrightarrow \varDelta _Y)\) through \(E_2\). Then \(\varDelta _X\) (resp. \(\varDelta _Y\)) is propagated through \(E_1^{-1}\) (resp. \(E_3\)) with probability 1 to obtain \(\varDelta _{in}\) (resp. \(\varDelta _{out}\)). We denote by \(c_{in}\) and \(c_{out}\) the \(\log _2\) of the probability of the transitions \(\varDelta _{in} \rightarrow \varDelta _X\) and \(\varDelta _{out} \rightarrow \varDelta _Y\) respectively. Finally we denote by \(k_{in}\) and \(k_{out}\) the key materials involved in those transitions. All in all the attack consists in discarding the keys k for which at least one pair follows the characteristic through \(E_1\) and \(E_3\) and in exhausting the remaining ones. The complexity of doing so is the following:
-
data: \(C_{N_\alpha }\)
-
memory: \( N_\alpha \)
-
time: \( C_{N_\alpha } + \left( 1 + 2^{\left| k_{in} \cup k_{out} \right| - c_{in} - c_{out}} \right) N_{\alpha } C_{E^{\prime }} + 2^{\vert k \vert - \alpha } \)
where \(N_\alpha \) is such that \((1 - 2^{-c_{in} - c_{out}})^{N_\alpha } < 2^{-\alpha }\), \(C_{N_\alpha }\) is the number of chosen plaintexts required to generate \(N_\alpha \) pairs satisfying \((\varDelta _{in}, \varDelta _{out})\), \(\vert k \vert \) is the key size and \(C_{E^{\prime }}\) is the ratio of the cost of partial encryption to the full encryption.
As we already have an algorithm to find the kind of truncated differential characteristics used in impossible differential attack, making an automatic search for this kind of attacks is straightforward. The tool gives as output all the parameters used in the above formula.
3.4 Limitations and Usage
In this section we discuss the limitations of our tools and give some recommendations.
Generic VS Ad-Hoc. As our algorithms are very generic they are probably slower than an ad-hoc algorithm designed for a specific block cipher. In particular, we do not take into account the symmetries found in almost all modern ciphers. This could be a nice improvement of our algorithms and we are already thinking about such a feature.
ARX Ciphers. While in theory ARX ciphers are handled, in practice they are not. More precisely, fully describing all the modular additions to fit the expected representation leads to a lot of nested Sboxes and/or new variables which may make the search too slow. In such case, we recommend to describe them only for the 3-4 lower bits and to use black boxes for other ones as follows:
In our opinion the issue comes more from our implementation than from our algorithms and we are currently working on it.
Complex Key Schedule. Too complex key schedules may also make the search too slow. For instance, if it is very hard to retrieve a part of the master key without almost all the subkeys like for CLEFIA [SSA+07] or Camellia [AIK+00] then we recommend to remove the subkeys generation process from the system of equations. Our tools should see a key size larger than expected but the user can give bounds for data, time and memory complexities of attacks.
Exhaustive Search. Unfortunately, it is not always possible to fully perform the algorithms described in Sect. 3.1 in a reasonable time (say less than a month). In order to decrease the running time, one thing we considered was to slightly modify the partial order relation into the following one:
While in theory we may miss some of the best attacks, we never encounter a block cipher for which the building blocks of best attacks were not minimal for this order relation because the complexity of attacks is highly (but not fully) related to the number of variables to enumerate.
Differential Enumeration Technique. In [DKS10], Dunkelman et al. introduced a sophisticated trade-off for GDS attacks which reduces the memory without increasing the time complexity. The main idea is to add restrictions on the parameters used to build the table such that those restrictions can be checked (at least partially) during the online phase. More precisely, they impose that sequences stored come from a \(\delta \)-set containing a message m which belongs to a pair \((m,m')\) that follows a well-chosen differential path. Then the attacker first focus on finding such pair before identifying a \(\delta \)-set and finally building the sequence. This technique is very powerful and was used to reach the best attacks against the AES [DFJ13, DF13, LJW13]. We did not make an algorithm finding the best GDS attacks under this trade-off mainly because it may be complicated to compute the exact complexity of the resulting attack. However, we distinguish two cases:
-
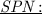 for an SPN block cipher the sets \(I_P(y)\) and \(O_P(y)\) (resp. \(I_C(y)\) and \(O_C(y)\)) are equal for all non-key variable y. Thus any GDS attack defined by the four sets \(I_P\), \(I_C\), \(O_P\) and \(O_C\) leads to only one truncated differential characteristic (say \(\varDelta \)) such that active variables are exactly the variables of \(I_P \cup (I_C \cap O_P) \cup O_C\). This is the natural candidate to use the differential enumeration technique. Then both the data and memory complexities are modified according to the probability of \(\varDelta \) and are easy to compute. However the time complexities of the online and the offline phases are more complicated to compute since in both cases we have to find the best algorithm to enumerate the solutions of a set of variables under the constraint of \(\varDelta \) (see [LJW13] for instance).
for an SPN block cipher the sets \(I_P(y)\) and \(O_P(y)\) (resp. \(I_C(y)\) and \(O_C(y)\)) are equal for all non-key variable y. Thus any GDS attack defined by the four sets \(I_P\), \(I_C\), \(O_P\) and \(O_C\) leads to only one truncated differential characteristic (say \(\varDelta \)) such that active variables are exactly the variables of \(I_P \cup (I_C \cap O_P) \cup O_C\). This is the natural candidate to use the differential enumeration technique. Then both the data and memory complexities are modified according to the probability of \(\varDelta \) and are easy to compute. However the time complexities of the online and the offline phases are more complicated to compute since in both cases we have to find the best algorithm to enumerate the solutions of a set of variables under the constraint of \(\varDelta \) (see [LJW13] for instance). -
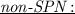 for non-SPN block ciphers there is no natural truncated differential characteristic to use, making the search of best attacks much more complicated. Furthermore, the technique is less powerful than against SPN but can still provide efficient attacks as shown by Li and Jia in [LJ14].
for non-SPN block ciphers there is no natural truncated differential characteristic to use, making the search of best attacks much more complicated. Furthermore, the technique is less powerful than against SPN but can still provide efficient attacks as shown by Li and Jia in [LJ14].
4 Applications
Our tools handle a very large class of block ciphers and we applied them on AES [NIS01], ARIA [KKP+03], CLEFIA [SSA+07], KLEIN [GNL11], KTANTAN [CDK09], LBlock [WZ11], PICCOLO [SIH+11], PRINCE [BCG+12], SIMON [BSS+13], TWINE [SMMK12], ZORRO [GGNS13] and more. In this section we present many applications highlighting some of the possibilities offered by our set of tools.
4.1 MCrypton
mCrypton is a 64-bit lightweight block cipher introduced in 2006 by Lim et al., which is a reduced version of Crypton. It is specifically designed for resource-constrained devices like RFID tags and sensors in wireless sensor networks. Like AES, mCrypton is also a SPN block cipher. According to key length, mCrypton has three versions namely mCrypton-64/96/128, which is in high accordance with AES-128/192/256. All the three versions have 12 rounds and each round consists of 4 transformations as follows:
-
Non-linear Substitution \(\gamma \) . This transformation consists of nibble-wise substitutions using four 4-bit S-boxes \(S_0\), \(S_1\), \(S_2\) and \(S_3\).
-
Bit Permutation \(\pi \) . The bit permutation transformation \(\pi \) has the same function than MixColumns transformation of AES: mixing each column of the state matrix. Operation \(\pi \) restricted to the i-th column is defined as follows:
$$ b = \pi _i(a) \Longleftrightarrow b[j] = \bigoplus _{k = 0}^3 (a[k]\, { \& }\, m_{i + j + k \text { mod } 4}),$$where \(m_0 = 1110\), \(m_1 = 1101\), \(m_2 = 1011\), \(m_3 = 0111\) and where&is the bitwise operation AND.
-
Column-To-Row Transposition \(\tau \) . This is simply the ordinary matrix transposition.
-
Key Addition \(\sigma \) . It is a simple bit-wise XOR operation and resembles the AddRoundKey operation of AES.
mCrypton also adds a linear operation \(\phi = \tau \circ \pi \circ \tau \) after the last round so that the whole encryption process is:
All best known attacks against mCrypton are GDS attacks combined to the differential enumeration technique. Hence it was a good target to check whether our tool could find better attacks. As a result, we found attacks on more rounds for the three standardized key lengths. We also found an attack against 11 rounds of Crypton-256 while the full version is composed of 12 rounds. Complexities of attacks are reported in Table 1.
Attack against 10-round mCrypton-128. Let us describe our GDS attack against 10 rounds of the 128-bit version of mCrypton, depicted on Fig. 3.
First we introduce some notations: \(x_i\) for the state just before the \(i-1\)-th \(\gamma \) operation, \(y_i\) for the state just after \(i-1\)-th \(\gamma \) operation and \(z_i\) for the state just after the \(i-1\)-th \(\pi \) operation. Given a state a, a[i] denotes the i-th nibble of a and \(a[i]_b\) the b-th bit of nibble a[i].
For this attack we consider \(\delta \)-sets of \(2^6\) messages such that nibbles \(y_1[2,3..7,10,12..15]\) and \(z_1[2,3..7,10,12..15]\) are constant, exploiting the fact that the branch number of the \(\pi \) operation is 4. Then, the meet-in-the-middle is performed on the 4 bit-equations between \(\varDelta y_6[1,3,9,11]\) and \(\varDelta z_6[1,3,9,11]\), exploiting again the same property of the \(\pi \) operation.
Given a \(\delta \)-set \(\{p^0,p^1, \ldots , p^{63}\}\), the ordered sequence
is fully determined by 42 nibbles, which can assume only \(2^{159}\) thanks to the key schedule relations. Furthermore, if we restrict ourself to the case where the pair \((p^0, p^1)\) follows the differential characteristic depicted on Fig. 3, the number of possible ordered sequences is reduced by a factor \(2^{56}\). Computing all these ordered sequences can be done using the same approach Derbez et al. used in [DFJ13]. On the other hand, the online phase requires to guess 42 state nibbles which can assume only \(2^{117}\) values thanks to 51 key schedule equations.
Given a pair which may follow the differential characteristic, the 42 nibbles of the online phase can assume only \(2^{117 - 32 + 6 - 64 + 4} = 2^{31}\) values. Enumerating those \(2^{31}\) values in roughly \(2^{31}\) is complicated but possible using a meet-in-the-middle procedure: the main idea is to compute all the possible values for involved nibbles of states \(x_0\) and \(x_1\) in one hand and all the possible values for involved nibbles of states \(x_7\), \(x_8\) and \(x_9\) in an other hand, and then to match those sets according to key schedule equations.
All in all, we need \(2^{23}\) structures of \(2^{32}\) messages to get one pair following the differential characteristic. The probability for a wrong pair to pass the test is \(2^{103-63*4} = 2^{-149}\) so we expect that only the right pair will pass it. Finally, the remaining key bits can be exhausted.
4.2 IDEA
IDEA was introduced by Lai and Massey in 1991 and became widely deployed due to its inclusion in the PGP package. It is a 64-bit, 8.5-round block cipher with 128-bit keys and it uses a composition of XOR operations, additions modulo \(2^{16}\), and multiplications over \(GF(2^{16}+ 1)\).
In order to apply our set of tools to IDEA, we chose to represent the multiplication by a black-box and to describe the modular addition only for the 4 least significant bits, other ones being handle by a black-box.
As a result, we automatically recovered the 6-round meet-in-the-middle attack described by Biham et al. in [BDKS15]. In particular, we retrieved the keyless Biryukov-Demirci relation, a linear equation involving the plaintext, the ciphertext, and several intermediate values computed during the IDEA encryption process. This equation is central in best known attacks against IDEA and was discovered only 15 years after IDEA was introduced.
4.3 XTEA
XTEA is an evolutionary improvement of TEA. XTEA makes essentially use of arithmetic and logic operations like TEA. New features of XTEA are to use two bits of \(\delta _i\) and the shift of 11. This adjustments cause the indexes of round keys to be irregular. We can describe the output \((Y_{i+1},Z_{i+1})\) of the i-th cycle of XTEA with the 64-bit input \((Y_i, Z_i)\) as follows:
where \(\delta _i\)’s are constants, \(K_i\)’s round keys and where round function F is defined by:
Partially Described Modular Addition. In that case our tools can handle a large number of rounds. Unfortunately, resulting attacks were far from best known ones, in term of complexity and broken rounds, due to the information lost in the representation of the modular addition.
Fully Described Modular Addition. In that case our tools were not able to search for attacks on more than 10 rounds, in the sense that the search takes too much time. The main issue comes from the huge number of sets of variables for which the tools have to compute the number of possible values in order to compute complexities of resulting attacks. However this does not make our set of tools useless. Indeed, our idea was to run the tool searching for impossible differential attacks but with a bound equals to 0 on the time complexity of searched attacks. In that case, it becomes a simpler tool which only looks for truncated impossible differentials. As a result, we were able to recover the longest ones on XTEA in few minutes.
4.4 ZORRO
At CHES 2013, Gerard et al. presented the block cipher ZORRO [GGNS13]. It is an AES-like block cipher but with a partial non-linear layer. The 128-bit plaintext initializes the internal state viewed as a \(4\times 4\) matrix of bytes as values in the finite field \(\mathbb {F}_{2^8}\). It has 24 rounds and the 128-bit master key is XORed with the internal state every four rounds. A round of ZORRO consists of 4 simple operations applied successively on the state matrix:
-
\(\mathbf{SubBytes}\) (\(\textsf {SB}^{*}\)) applies the same 8-bit to 8-bit invertible S-Box on each byte of the first row in parallel,
-
\(\mathbf{ShiftRows}\) (SR) shifts the i-th row left by i positions,
-
\(\mathbf{MixColumns}\) (MC) replaces each of the four column C of the state by \(M\times C\) where M is a constant \(4\times 4\) maximum distance separable matrix over \(\mathbb {F}_{2^8}\),
-
\(\mathbf{AddConstant}\) (AC) adds a constant on the first row.
Both the \(\mathbf{MixColumns}\) and \(\mathbf{ShiftRows}\) operations are the same than those used in the AES. The S-box however is different and was chosen in order to be easier to mask but in return has worse differential properties which were exploited by the differential attacks. In particular, ZORRO has been fully broken [GNPW13, BDD+14, RASA14] because of the existence of a high probability 4-round iterated differential (Fig. 4).
While ZORRO has been already broken, we will study it as a toy example to show how useful our tool can be to designers. Generalized Demirci-Selçuk attacks combined to the differential enumeration technique led to the best attacks on the three versions of the AES in the single-key setting and thus our idea was to study the resistance of ZORRO and its variants against such attacks. If the Sbox is applied on the same four bytes each round then there are 1820 variants of ZORRO. In order to not decrease the (already very low) resistance against differential cryptanalysis we considered only variants such that the S-box is applied on one byte per column and on one byte per diagonal, leading to 24 variants including the original one. Finally, and because of the symmetry in the structure of Zorro we focused on the 11 variants depicted on Fig. 5.
For each of those variants we wrote the corresponding system of equations and gave it to our tool. Interestingly, we found that the complexity and the number of rounds broken only depend on the number of rows having an S-box. More precisely, for all the variants with only one Sbox-free row we found that 16 rounds are secure against GDS attacks and 20 are fully secure against GDS attacks combined with the differential enumeration technique while 20 and 25 rounds are required to provide the same security for the variants with two or three Sbox-free rows. As a consequence, the designers of ZORRO did not choose the most secure variant and the number of rounds chosen was too low. Actually, this enforces the results of Bar-On et al. [BDD+15], stating that the design behind Zorro may lead to both secure and easy to mask block ciphers as long as we take care of its specificities.
Note that here fully secure against GDS attacks combined with the differential enumeration technique means that there is no GDS attack with a time complexity strictly smaller than \(2^k\) and a memory complexity strictly smaller than \(2^{k + n}\), where k is the keysize and n the blocksize, since, combined to the differential enumeration technique, such attack may (but not always) be turned into one with an overall complexity smaller than \(2^{k}\).
4.5 SIMON
SIMON [BSS+13] is family of lightweight block ciphers designed by the American National Security Agency (NSA) in 2013. It performs exceptionally well in both hardware and software, although SIMON is supposed to be more hardware-oriented. The SIMON family is based on a classical Feistel construction operating on two branches. The round function is composed of three simple operations: AND, XOR and rotations. More precisely, at each round the left branch is transformed using the following non-linear function:
Then, the output of F is XORed with the round key and the right branch to form the left branch of the next round. The SIMON family contains 10 ciphers and, in the sequel, we refer to them by SIMONn/k where n and k are respectively the blocksize and the keysize.
In [BNS14], Boura et al. described the best (in term of broken rounds) impossible differential attacks against all the versions of SIMON. However, after running our tool against SIMON we found that actually more rounds can be broken by using the exact same technique, highlighting how useful an automatic approach is.
20-Round Attack on SIMON32/64. To mount an impossible differential attack on 19-round SIMON32/64, Boura et al. used an impossible differential characteristic covering 11 rounds extended by 4 rounds in both directions such that \(4 + 11 + 4 = 19\) rounds of the cipher were attacked. In our case we also use an 11-round impossible differential but our tool found one (see Table 2) that can be extended by 3 + 6 rounds while still resulting in an attack faster than the exhaustive search according to the formula given Sect. 3.3.
The attack is depicted in Fig. 6. It can be seen that the difference in the plaintexts has to be zero in 16 bits and equals to 1 in 2 bits. Hence \(c_{in} + c_{out} = 13 + 31 = 44\) and thus \(N_\alpha \approx \alpha \cdot 2^{43.5}\). Given a structure of \(2^{14}\) plaintexts such that bits \(L_0[1..5,8..11,15]\) and \(R_0[0..3,7,9]\) are constant and such that \(L_0[12] = R_0[10]\), one can form \(2^{14 + 13 - 1} = 2^{26}\) pairs lying in the right space and thus \(C_{N_\alpha } = \alpha \cdot 2^{31.5}\). Finally, 70 subkey bits are involved in the attack (blue colored in Fig. 6) but they can assume only \(2^{62}\) values thanks to the key schedule (see Appendix A). All in all, the complexity of our attack is \(D = \alpha \cdot 2^{31.5}\), \(M = \alpha \cdot 2^{43.5}\) and \(T = \alpha \cdot 2^{31.5} + (1 + 2^{62 - 44})\cdot \alpha \cdot 2^{43.5} C_{E'} + 2^{64 - \alpha }\). As we estimate the ratio \(C_{E'}\) to \(70/(16\cdot 20)\), the value of \(\alpha \) minimizing the overall complexity is 4.17. However \(\alpha \) has to be smaller than \(2^{0.5}\) because of the data complexity and, for this particular value the complexity of our attack is:
which is similar to the complexity Boura et al. reached on 19 rounds (\(D = 2^{32}, ~ M = 2^{44} \text { and } T = 2^{62.5}\)).
Others Versions of SIMON. Running our tool against SIMON takes time (up to many days for the largest versions) so we did not exhaust all the best attacks yet. However, we found that SIMON32/64 is not the only version for which results of Boura et al. are suboptimal as, for instance, one more round can be broken for both SIMON48/64 and SIMON48/96.
5 Conclusion
In this paper we described powerful and versatile cryptanalysis tools handling a very large class of block ciphers. They are designed to find the best generalized Demirci-Selçk attacks, basic meet-in-the-middle attacks and impossible truncated differential attacks for a given target. They are publicly released, easy to use and their running time is reasonable (from few seconds for AES to many days for SIMON). Thus we believe they will be of great help for both designers and cryptanalysts. Furthermore, our approach is very generic and requires no a priori information about the targeted block cipher.
Future work will be to think about better algorithms/implementations, mainly in order to handle ARX ciphers faster. Including the last results concerning the differential enumeration technique would also be nice as well as handling systems from authenticated encryptions. Finally, currently we have to write code in order to generate the system of equations. It would be nice if we would be able to generate it from a C implementation.
References
Aoki, K., Ichikawa, T., Kanda, M., Matsui, M., Moriai, S., Nakajima, J., Tokita, T.: Camellia: A 128-bit block cipher suitable for multiple platforms - design and analysis. In: Stinson, D.R., Tavares, S. (eds.) SAC 2000. LNCS, vol. 2012, pp. 39–56. Springer, Heidelberg (2001)
Biham, E., Biryukov, A., Shamir, A.: Cryptanalysis of skipjack reduced to 31 rounds using impossible differentials. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 12–23. Springer, Heidelberg (1999)
Borghoff, J., Canteaut, A., Güneysu, T., Kavun, E.B., Knezevic, M., Knudsen, L.R., Leander, G., Nikov, V., Paar, C., Rechberger, C., Rombouts, P., Thomsen, S.S., Yalçın, T.: PRINCE – A low-latency block cipher for pervasive computing applications. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 208–225. Springer, Heidelberg (2012)
Bar-On, A., Dinur, I., Dunkelman, O., Lallemand, V., Tsaban, B.: Improved analysis of zorro-like ciphers. IACR Cryptology ePrint Archive 2014, 228 (2014)
Bar-On, A., Dinur, I., Dunkelman, O., Lallemand, V., Keller, N., Tsaban, B.: Cryptanalysis of SP networks with partial non-linear layers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 315–342. Springer, Heidelberg (2015)
Bouillaguet, C., Derbez, P., Fouque, P.-A.: Automatic search of attacks on round-reduced AES and applications. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 169–187. Springer, Heidelberg (2011)
Biham, E., Dunkelman, O., Keller, N., Shamir, A.: New attacks on IDEA with at least 6 rounds. J. Cryptol. 28(2), 209–239 (2015)
Boura, C., Naya-Plasencia, M., Suder, V.: Scrutinizing and improving impossible differential attacks: applications to CLEFIA, Camellia, LBlock and Simon. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 179–199. Springer, Heidelberg (2014)
Buchmann, J., Pyshkin, A., Weinmann, R.-P.: Block ciphers sensitive to gröbner basis attacks. In: Pointcheval, D. (ed.) CT-RSA 2006. LNCS, vol. 3860, pp. 313–331. Springer, Heidelberg (2006)
Buchmann, J., Pyshkin, A., Weinmann, R.-P.: A zero-dimensional Gröbner basis for AES-128. In: Robshaw, M. (ed.) FSE 2006. LNCS, vol. 4047, pp. 78–88. Springer, Heidelberg (2006)
Biham, E., Shamir, A.: Differential Cryptanalysis of the Data Encryption Standard. Springer, New York (1993)
Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B., Wingers, L.: The simon and speck families of lightweight block ciphers. Cryptology ePrint Archive, Report 2013/404 (2013). http://eprint.iacr.org/
De Cannière, C., Dunkelman, O., Knežević, M.: KATAN and KTANTAN — A family of small and efficient hardware-oriented block ciphers. In: Clavier, C., Gaj, K. (eds.) CHES 2009. LNCS, vol. 5747, pp. 272–288. Springer, Heidelberg (2009)
Courtois, N.T., Meier, W.: Algebraic attacks on stream ciphers with linear feedback. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 345–359. Springer, Heidelberg (2003)
Derbez, P., Fouque, P.-A.: Exhausting Demirci-Selçuk meet-in-the-middle attacks against reduced-round AES. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 541–560. Springer, Heidelberg (2014)
Derbez, P., Fouque, P.-A., Jean, J.: Improved key recovery attacks on reduced-round AES in the single-key setting. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 371–387. Springer, Heidelberg (2013)
Dinur, I., Jean, J.: Cryptanalysis of FIDES. In: Cid, C., Rechberger, C. (eds.) FSE 2014. LNCS, vol. 8540, pp. 224–240. Springer, Heidelberg (2015)
Dunkelman, O., Keller, N., Shamir, A.: Improved single-key attacks on 8-Round AES-192 and AES-256. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 158–176. Springer, Heidelberg (2010)
Demirci, H., Selçuk, A.A.: A meet-in-the-middle attack on 8-Round AES. In: Nyberg, K. (ed.) FSE 2008. LNCS, vol. 5086, pp. 116–126. Springer, Heidelberg (2008)
Fouque, P.-A., Jean, J., Peyrin, T.: Structural evaluation of AES and chosen-key distinguisher of 9-round AES-128. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 183–203. Springer, Heidelberg (2013)
Gérard, B., Grosso, V., Naya-Plasencia, M., Standaert, F.-X.: Block ciphers that are easier to mask: how far can we go? In: Bertoni, G., Coron, J.-S. (eds.) CHES 2013. LNCS, vol. 8086, pp. 383–399. Springer, Heidelberg (2013)
Garey, M.R., Johnson, D.S.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman, New York (1979)
Gong, Z., Nikova, S., Law, Y.W.: KLEIN: A new family of lightweight block ciphers. In: Juels, A., Paar, C. (eds.) RFIDSec 2011. LNCS, vol. 7055, pp. 1–18. Springer, Heidelberg (2012)
Guo, J., Nikolic, I., Peyrin, T., Wang, L.: Cryptanalysis of zorro. IACR Cryptology ePrint Archive 2013:713 (2013)
Hao, Y., Bai, D., Li, L.: A meet-in-the-middle attack on round-reduced mcrypton using the differential enumeration technique. In: Au, M.H., Carminati, B., Kuo, C.-C.J. (eds.) NSS 2014. LNCS, vol. 8792, pp. 166–183. Springer, Heidelberg (2014)
Khovratovich, D., Biryukov, A., Nikolic, I.: Speeding up collision search for byte-oriented hash functions. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 164–181. Springer, Heidelberg (2009)
Kang, J., Jeong, K., Sung, J., Hong, S., Lee, K.: Collision attacks on AES-192/256, crypton-192/256, mCrypton-96/128, anubis. J. Appl. Math. 2013, 713673:1–713673:10 (2013). Observation of strains
Kwon, D., et al.: New block cipher: ARIA. In: Lim, J.-I., Lee, D.-H. (eds.) ICISC 2003. LNCS, vol. 2971, pp. 432–445. Springer, Heidelberg (2004)
Knudsen, L.R.: Deal – a 128-bit block cipher. Technical Report Department of Informatics (1998)
Leurent, G.: Analysis of differential attacks in ARX constructions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 226–243. Springer, Heidelberg (2012)
Li, L., Jia, K.: Improved meet-in-the-middle attacks on reduced-round camellia-192/256. Cryptology ePrint Archive, Report 2014/292 (2014)
Li, L., Jia, K., Wang, X.: Improved meet-in-the-middle attacks on aes-192 and prince. Cryptology ePrint Archive, Report 2013/573 (2013)
Lin, L., Wu, W., Wang, Y., Zhang, L.: General model of the single-key meet-in-the-middle distinguisher on the word-oriented block cipher. In: Lee, H.-S., Han, D.-G. (eds.) ICISC 2013. LNCS, vol. 8565, pp. 203–223. Springer, Heidelberg (2014)
Moon, D., Hwang, K., Lee, W., Lee, S., Lim, J.: Impossible differential cryptanalysis of reduced round XTEA and TEA. In: Daemen, J., Rijmen, V. (eds.) FSE 2002. LNCS, vol. 2365, pp. 49–60. Springer, Heidelberg (2002)
Morawiecki, P., Srebrny, M.: A sat-based preimage analysis of reduced keccak hash functions. Inf. Process. Lett. 113(10–11), 392–397 (2013)
Mironov, I., Zhang, L.: Applications of SAT solvers to cryptanalysis of hash functions. In: Biere, A., Gomes, C.P. (eds.) SAT 2006. LNCS, vol. 4121, pp. 102–115. Springer, Heidelberg (2006)
NIST. Advanced Encryption Standard (AES), FIPS 197. Technical report, NIST, November 2001
Rasoolzadeh, S., Ahmadian, Z., Salmasizadeh, M., Aref, M.R.: Total break of zorro using linear and differential attacks. IACR Cryptology ePrint Archive 2014:220 (2014)
NXP Semiconductors. The PRINCE challenge (2014). https://www.emsec.rub.de/research/research_startseite/prince-challenge/
Shibutani, K., Isobe, T., Hiwatari, H., Mitsuda, A., Akishita, T., Shirai, T.: Piccolo: An ultra-lightweight blockcipher. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 342–357. Springer, Heidelberg (2011)
Sugita, M., Kawazoe, M., Perret, L., Imai, H.: Algebraic cryptanalysis of 58-Round SHA-1. In: Biryukov, A. (ed.) FSE 2007. LNCS, vol. 4593, pp. 349–365. Springer, Heidelberg (2007)
Suzaki, T., Minematsu, K., Morioka, S., Kobayashi, E.: TWINE: A lightweight block cipher for multiple platforms. In: Knudsen, L.R., Wu, H. (eds.) SAC 2012. LNCS, vol. 7707, pp. 339–354. Springer, Heidelberg (2013)
Soos, M., Nohl, K., Castelluccia, C.: Extending SAT solvers to cryptographic problems. In: Kullmann, O. (ed.) SAT 2009. LNCS, vol. 5584, pp. 244–257. Springer, Heidelberg (2009)
Shirai, T., Shibutani, K., Akishita, T., Moriai, S., Iwata, T.: The 128-bit blockcipher CLEFIA (Extended Abstract). In: Biryukov, A. (ed.) FSE 2007. LNCS, vol. 4593, pp. 181–195. Springer, Heidelberg (2007)
Wei, L., Rechberger, C., Guo, J., Wu, H., Wang, H., Ling, S.: Improved meet-in-the-middle cryptanalysis of KTANTAN (Poster). In: Parampalli, U., Hawkes, P. (eds.) ACISP 2011. LNCS, vol. 6812, pp. 433–438. Springer, Heidelberg (2011)
Wu, S., Wang, M.: Automatic search of truncated impossible differentials for word-oriented block ciphers. In: Galbraith, S., Nandi, M. (eds.) INDOCRYPT 2012. LNCS, vol. 7668, pp. 283–302. Springer, Heidelberg (2012)
Wu, W., Zhang, L.: LBlock: A lightweight block cipher. In: Lopez, J., Tsudik, G. (eds.) ACNS 2011. LNCS, vol. 6715, pp. 327–344. Springer, Heidelberg (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Key Schedule Equations Used in the 20-Round Attack Against SIMON32/64
A Key Schedule Equations Used in the 20-Round Attack Against SIMON32/64
Actually, all the 70 key bits are not required to perform the impossible differential attack described Sect. 4.5 since bits \(K_{1}[7] \oplus K_{0}[9]\), \(K_{1}[9] \oplus K_{0}[11]\), \(K_{15}[0] \oplus K_{16}[2]\) and \(K_{15}[2] \oplus K_{16}[4]\) can be used instead of the 8 bits \(K_{0}[9]\), \(K_{0}[11]\), \(K_{1}[7]\), \(K_{1}[9]\), \(K_{15}[0]\), \(K_{15}[2]\), \(K_{16}[2]\), \(K_{16}[4]\). This already saves 4 bits.
Then, in SIMON32/64, the subkeys are related by the following equations:
Switching \(K_r\) and \(K_{r+4}\) we can use this equation to express \(K_0\) as a linear combination of \(K_{16}\), \(K_{17}\), \(K_{18}\) and \(K_{19}\), and interestingly it has the following shape:
where f is a linear function. Finally, thanks to this equation, we deduce bits 1, 8, 10 and 15 of \(K_0\) from the same bits of \(K_{16}\) and the full subkeys \(K_{17}\), \(K_{18}\) and \(K_{19}\).
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Derbez, P., Fouque, PA. (2016). Automatic Search of Meet-in-the-Middle and Impossible Differential Attacks. In: Robshaw, M., Katz, J. (eds) Advances in Cryptology – CRYPTO 2016. CRYPTO 2016. Lecture Notes in Computer Science(), vol 9815. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53008-5_6
Download citation
DOI: https://doi.org/10.1007/978-3-662-53008-5_6
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53007-8
Online ISBN: 978-3-662-53008-5
eBook Packages: Computer ScienceComputer Science (R0)






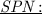 for an SPN block cipher the sets
for an SPN block cipher the sets 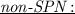 for non-SPN block ciphers there is no natural truncated differential characteristic to use, making the search of best attacks much more complicated. Furthermore, the technique is less powerful than against SPN but can still provide efficient attacks as shown by Li and Jia in [
for non-SPN block ciphers there is no natural truncated differential characteristic to use, making the search of best attacks much more complicated. Furthermore, the technique is less powerful than against SPN but can still provide efficient attacks as shown by Li and Jia in [


