Abstract
Functional encryption lies at the frontiers of current research in cryptography; some variants have been shown sufficiently powerful to yield indistinguishability obfuscation (IO) while other variants have been constructed from standard assumptions such as LWE. Indeed, most variants have been classified as belonging to either the former or the latter category. However, one mystery that has remained is the case of secret-key functional encryption with an unbounded number of keys and ciphertexts. On the one hand, this primitive is not known to imply anything outside of minicrypt, the land of secret-key crypto, but on the other hand, we do no know how to construct it without the heavy hammers in obfustopia.
In this work, we show that (subexponentially secure) secret-key functional encryption is powerful enough to construct indistinguishability obfuscation if we additionally assume the existence of (subexponentially secure) plain public-key encryption. In other words, secret-key functional encryption provides a bridge from cryptomania to obfustopia.
On the technical side, our result relies on two main components. As our first contribution, we show how to use secret key functional encryption to get “exponentially-efficient indistinguishability obfuscation” (XIO), a notion recently introduced by Lin et al. (PKC ’16) as a relaxation of IO. Lin et al. show how to use XIO and the LWE assumption to build IO. As our second contribution, we improve on this result by replacing its reliance on the LWE assumption with any plain public-key encryption scheme.
Lastly, we ask whether secret-key functional encryption can be used to construct public-key encryption itself and therefore take us all the way from minicrypt to obfustopia. A result of Asharov and Segev (FOCS ’15) shows that this is not the case under black-box constructions, even for exponentially secure functional encryption. We show, through a non-black box construction, that subexponentially secure-key functional encryption indeed leads to public-key encryption. The resulting public-key encryption scheme, however, is at most quasi-polynomially secure, which is insufficient to take us to obfustopia.
N. Bitansky—Supported by an IBM DARPA grant and an NJIT DARPA grant.
R. Nishimaki—This work was done in part while the author was visiting Northeastern University.
A. Passelègue—This work was done in part while the author was visiting Northeastern University. Supported in part by the Direction Générale de l’Armement.
D. Wichs—Supported in part by NSF grants CNS-1347350, CNS-1314722, CNS-1413964.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The concept of functional encryption [17, 45] extends that of traditional encryption by allowing the distribution of functional decryption keys that reveal specified functions of encrypted messages, but nothing beyond. This concept is one of the main frontiers in cryptography today. It offers tremendous flexibility in controlling and computing on encrypted data, is strongly connected to the holy grail of program obfuscation [3, 14, 44], and for many problems, may give superior solutions to obfuscation-based ones [28, 29]. Accordingly, recent years have seen outstanding progress in the study of functional encryption, both in constructing functional encryption schemes and in exploring different notions, their power, and the relationship amongst them (see for instance, [1, 2, 4, 5, 7, 11, 15, 16, 20, 21, 24–26, 32–36, 40, 42, 47, 49] and many more).
One striking question that has yet to be solved is the gap between public-key and secret-key functional encryption schemes. In particular, does any secret-key scheme imply a public-key one?
The answer to this question is nuanced and seems to depend on certain features of functional encryption schemes, such as the number of functional decryption keys and number of ciphertexts that can be released. For functional encryption schemes that only allow the release of an a-priori bounded number of functional keys (often referred to as bounded collusion), we know that the above gap is essentially the same as the gap between plain (rather than functional) secret-key encryption and public-key encryption, and should thus be as hard to bridge. Specifically, in the secret-key setting, such schemes supporting an unbounded number of ciphertexts can be constructed assuming low-depth pseudorandom generators (or just one-way functions in the single-key case) [34, 47]. These secret-key constructions are then converted to public-key ones, relying on (plain) public-key encryption (and this is done quite directly by replacing invocations of a secret-key encryption scheme with invocations of a public-key one.) The same state of affairs holds when reversing the roles and considering a bounded number of ciphertexts and an unbounded number of keys [34, 47]. In other words, in the terminology of Impagliazzo’s complexity worlds [38], if the number of keys or ciphertexts is a-priori bounded, then symmetric-key functional encryption lies in minicrypt, the world of one-way functions, and public-key functional encryption lies in cryptomania, the world of public-key encryption.
For functional encryption schemes supporting an unbounded (polynomial) number of keys and unbounded number of ciphertexts, which will be the default notion throughout the rest of the paper, the question is far less understood. In the public-key setting, such functional encryption schemes with subexponential security are known to imply indistinguishability obfuscation [3, 4, 14]. In contrast, Bitansky and Vaikuntanathan [14] show that their construction of indistinguishability obfuscation using functional encryption may be insecure when instantiated with a secret-key functional encryption scheme. In fact, secret-key functional encryption schemes (even exponentially secure ones) are not known to imply any cryptographic primitive beyond those that follow from one-way functions. As far as we know the two notions of functional encryption may correspond to opposite extremes of the complexity spectrum: on one side, public-key schemes correspond to obfustopia, the world where indistinguishability obfuscation exists, and on the other side secret-key schemes may lie in minicrypt where there is even no (plain) public-key encryption.
One piece of evidence that may support such a view of the world is given by Asharov and Segev [6] who show that there do not exist fully black-box constructions of plain public-key encryption from secret-key functional encryption, even if the latter is exponentially secure. Still, while we may hope that such secret-key schemes could be constructed from significantly weaker assumptions than needed for public-key schemes, so far no such construction has been exhibited — all known constructions live in obfustopia.
1.1 Our Contributions
In this work, we shed new light on the question of secret-key vs public-key functional encryption (in the multi-key, multi-ciphertext setting). Our main result bridges the two notions based on (plain) public-key encryption.
Theorem 1 (Informal)
Assuming secret-key functional encryption and plain public-key encryption that are both subexponentially secure, there exists indistinguishability obfuscation, and in particular, also public-key functional encryption.
In the terminology of Impagliazzo’s complexity worlds: secret-key functional encryption would turn cryptomania, the land of public-key encryption, into obfustopia. This puts in new perspective the question of constructing such secret-key schemes from standard assumptions — any such construction would lead to indistinguishability obfuscation from standard assumptions.
The above result still does not settle the question of whether secret-key functional encryption on its own implies (plain) public-key encryption. Here we show that assuming subexponentially-secure secret-key functional encryption and (almost) exponentially-secure one-way functions, there exists (polynomially-secure) public-key encryption.
Theorem 2 (Informal)
Assuming subexponentially-secure secret-key functional encryption and  -secure one-way functions, there exists (polynomially-secure) public-key encryption.
-secure one-way functions, there exists (polynomially-secure) public-key encryption.
The resulting public-key encryption is not strong enough to take us to obfustopia. Concretely, the constructed scheme is not subexponentially secure as required by our first theorem — it can be quasi-polynomially broken. Nevertheless, the result does show that the black-box barrier shown by Asharov and Segev [6], which applies even if the underlying secret-key functional encryption scheme and one-way functions are exponentially secure, can be circumvented. Indeed, our construction uses the functional encryption scheme in a non-black-box way (see further details in the technical overview section below).
1.2 A Technical Overview
We now provide an overview of the main steps and ideas leading to our results.
Key Observation: From SKFE to (Strong) Exponentially-Efficient IO. Our first observation is that secret-key functional encryption (or SKFE in short) implies a weak form of indistinguishability obfuscators termed by Lin, Pass, Seth, and Telang [43] exponentially-efficient indistinguishability obfuscation (XIO). Like IO, this notion preserves the functionality of obfuscated circuits and guarantees that obfuscations of circuits of the same size and functionality are indistinguishable. However, in terms of efficiency the XIO notion only requires that an obfuscation  of a circuit
of a circuit  is just mildly smaller than its truth table, namely
is just mildly smaller than its truth table, namely  , for some compression factor \(\gamma < 1\), and a fixed polynomial \(\mathrm {poly}\), rather than the usual requirement that the time to obfuscate, and in particular the size of
, for some compression factor \(\gamma < 1\), and a fixed polynomial \(\mathrm {poly}\), rather than the usual requirement that the time to obfuscate, and in particular the size of  , are polynomial in |C|. We show that SKFE implies a slightly stronger notion than XIO where the time to obfuscate C is bounded by \(2^{\gamma n}\cdot \mathrm {poly}(|C|)\). We call this notion strong exponentially-efficient indistinguishability obfuscation (SXIO). (We note that, for either XIO or SXIO, we shall typically be interested in circuits over some polynomial size domain, which could be much larger than the circuit itself, e.g., \(\{0,1\}^n\) where \(n = 100\log |C|\).)
, are polynomial in |C|. We show that SKFE implies a slightly stronger notion than XIO where the time to obfuscate C is bounded by \(2^{\gamma n}\cdot \mathrm {poly}(|C|)\). We call this notion strong exponentially-efficient indistinguishability obfuscation (SXIO). (We note that, for either XIO or SXIO, we shall typically be interested in circuits over some polynomial size domain, which could be much larger than the circuit itself, e.g., \(\{0,1\}^n\) where \(n = 100\log |C|\).)
Proposition 1 (Informal)
-
1.
For any constant \(\gamma <1\), there exists a transformation from SKFE to SXIO with compression factor \(\gamma \).
-
2.
For some subconstant \(\gamma =o(1)\), there exists a transformation from subexponentially-secure SKFE to polynomially-secure SXIO with compression factor \(\gamma \).
We add more technical details regarding the proof of the above SXIO proposition later on. Both of our theorems stated above rely on the constructed SXIO as a main tool. We next explain, still at a high-level, how the first theorem is obtained. We then dive into further technical details about the proof of this theorem as well as the proof of the second theorem.
From SXIO to IO Through Public-key Encryption. Subexponentially-secure SXIO (or even XIO) schemes with a constant compression factor (as in Proposition 1) are already shown to be quite strong in [43] — assuming subexponential hardness of Learning with Errors (LWE) [46], they imply IO.
Corollary 1
(of Proposition 1 and [43]). Assuming SKFE and LWE, both subexponentially secure, there exists IO.
We go beyond the above corollary, showing that LWE can be replaced with a generic assumption — the existence of (plain) public-key encryption schemes. The transformation of [43] from LWE and XIO to IO, essentially relies on LWE to obtain a specific type of public-key functional encryption (PKFE) with certain succinctness properties. We show how to construct such PKFE from public-key encryption and SXIO. More details follow.
Concretely, the notion considered is of PKFE schemes that support a single decryption key. Furthermore, the time complexity of encryption is bounded by roughly \(s^{\beta }\cdot d^{O(1)}\), where s and d are the size and depth of the circuit computing the function, and \(\beta <1\) is some compression factor. We call such schemes weakly succinct PKFE schemes. A weakly succinct PKFE for boolean functions (i.e., functions with a single output bit) is constructed by Goldwasser et al. [33] from (subexponentially-hard) LWE; in fact, the Goldwasser et al. construction has no dependence at all on the circuit size s (namely, \(\beta =0\)).
Lin et al. [43] then show a transformation, relying on XIO, that extends the class of functions also to functions with a long output, rather than just boolean ones. (Their transformation is stated for the case that \(\beta =0\) assuming any constant XIO compression factor \(\gamma <1\), but can be extended to also work for any sufficiently small constant compression factor \(\beta \) for the PKFE.) Such weakly-succinct PKFE schemes can then be plugged in to the transformations of [3, 14, 44] to obtain full-fledged IO.Footnote 1
We follow a similar blueprint. We first construct weakly-succinct PKFE for functions with a single output bit based on SXIO and PKE, rather than LWE (much of the technical effort in this work lies in this construction). We then bootstrap the construction to deal with multibit functions using (a slightly augmented version of) the transformation from [43].
Proposition 2 (Informal)
For any \(\beta =\varOmega (1)\), assuming PKE and SXIO with a small enough constant compression factor \(\gamma \), there exists a single-key weakly-succinct PKFE scheme with compression factor \(\beta \) (for functions with long output).
1.3 A Closer Look into the Techniques
We now provide further details regarding the proofs of the above Propositions 1 and 2 as well as the proof of Theorem 2.
SKFE to SXIO: The Basic Idea. To convey the basic idea behind the transformation, we first describe a construction of SXIO with compression \(\gamma = 1/2\). We then explain how to extend it to obtain the more general form of Proposition 1.
Recall that in an SKFE scheme, first a master secret key \(\mathsf {MSK}\) is generated, and can then be used to:
-
encrypt (any number of) plaintext messages,
-
derive (any number of) functional keys.
The constructed obfuscator \(\mathsf {sxi}\mathcal {O}\) is given a circuit C defined on domain \(\{0,1\}^{n}\), where we shall assume for simplicity that the input length is even (this is not essential), and works as follows:
-
For every \(x\in \{0,1\}^{n/2}\), computes a ciphertext \(\mathsf {CT}_x\) encrypting the circuit \(C_x(\cdot )\) that given input \(y\in \{0,1\}^{n/2}\), returns C(x, y).
-
For every \(y\in \{0,1\}^{n/2}\), derives a functional decryption key \(\mathsf {SK}_y\) for the function \(U_y(\cdot )\) that given as input a circuit D of size at most \(\max _{x}|C_x|\), returns D(y).
-
Outputs
 as the obfuscation.
as the obfuscation.
To evaluate  on input \((x,y)\in \{0,1\}^{n}\), simply decrypt
on input \((x,y)\in \{0,1\}^{n}\), simply decrypt
Indeed, the required compression factor \(\gamma =1/2\) is achieved. Generating each ciphertext is proportional to the size of the message \(|C_x|= \tilde{O}(|C|)\) and some fixed polynomial in the security parameter \(\lambda \). Similarly the time to generate each functional key is proportional to the size of the circuit \(|U_y|=\tilde{O}(|C|)\) and some fixed polynomial in the security parameter \(\lambda \). Thus overall, the time to generate  is bounded by \(2^{n/2} \cdot \mathrm {poly}(|C|,\lambda )\).
is bounded by \(2^{n/2} \cdot \mathrm {poly}(|C|,\lambda )\).
The indistinguishability guarantee follows easily from that of the underlying SKFE. Indeed, SKFE guarantees that for any two sequences \({\varvec{m}}=\left\{ m_i\right\} \) and \({\varvec{m}}' = \left\{ m'_i\right\} \) of messages to be encrypted and any sequence of functions \(\left\{ f_i\right\} \) for which keys are derived, encryptions of the \({\varvec{m}}\) are indistinguishable from encryptions of the \({\varvec{m}}'\), provided that the messages are not “separated by the functions”, i.e. \(f_j(m_i) = f_j(m'_i)\) for every (i, j). In particular, any two circuits C and \(C'\) that have equal size and functionality will correspond to such two sequences of messages \(\left\{ C_x\right\} _{x\in \{0,1\}^{n/2}}\) and \(\left\{ C'_x\right\} _{x\in \{0,1\}^{n/2}}\), whereas \(\left\{ U_y\right\} _{y\in \{0,1\}^n}\) are indeed functions such that \(U_y(C_x) =C(x,y)=C'(x,y) = U_y(C'_x)\) for all (x, y). (The above argument works even given a very weak selective security definition where all messages and functions are chosen by the attacker ahead of time.)
As said, the above transformation achieves compression factor \(\gamma =1/2\). While such compression is sufficient for example to obtain IO based on LWE, it will not suffice for our two Theorems 1 and 2 (for the first we will need \(\gamma \) to be a smaller constant, and for the second we will need it to even be slightly subconstant). To prove Proposition 1 in its more general form, we rely on a result by Brakerski, Komargodski, and Segev [20] that shows how to convert any SKFE into a t-input SKFE. A t-input scheme allows to encrypt a tuple of messages \((m_1,\dots ,m_t)\) each independently, and derive keys for t-input functions \(f(m_1,\dots ,m_t)\). In their transformation, starting from a multi-key SKFE results in a multi-key t-input SKFE.
The general transformation then follows naturally. Rather than arranging the input space in a 2-dimensional cube \(\{0,1\}^{n/2}\times \{0,1\}^{n/2}\) as we did before with a 1-input scheme, given a t-input scheme we can arrange it in a \((t+1)\)-dimensional cube \(\{0,1\}^{n/(t+1)}\times \cdots \times \{0,1\}^{n/(t+1)}\), and we will accordingly get compression \(\gamma =1/(t+1)\). The only caveat is that the BKS transformation incurs a security loss and blowup in the size of the scheme that can grow doubly exponentially in t. As long as t is constant the security loss and blowup are fixed polynomials. The transformation can also be invoked for slightly super-constant t (double logarithmic) assuming subexponential security of the underlying 1-input SKFE (giving rise to the second part of Proposition 1).
We remark that previously Goldwasser et al. [32] showed that t-input SKFE for polynomial t directly gives full-fledged IO. We demonstrate that even when t is small (even constant), t-input SKFE implies a meaningful obfuscation notion such as SXIO.
From SXIO and PKE to Weakly Succinct PKFE: Main Ideas. We now describe the main ideas behind our construction of a single-key weakly succinct PKFE. We shall focus on the main step of obtaining such a scheme for functions with a single output bit.Footnote 2
Our starting point is the single-key PKFE scheme of Sahai and Seyalioglu [47] based on Yao’s garbled circuit method [50]. Their scheme basically works as follows (we assume basic familiarity with the garbled circuit method):
-
The master public key
 consists of \(L\) pairs of public keys
consists of \(L\) pairs of public keys  for a (plain) public-key encryption scheme.
for a (plain) public-key encryption scheme. -
A functional decryption key \(\mathsf {SK}_f\) for a function (circuit) f of size \(L\) consists of the secret decryption keys \(\{\mathsf {SK}_i^{f_i}\}_{i\in L}\) corresponding to the above public keys, according to the bits of f’s description.
-
To encrypt a message m, the encryptor generates a garbled circuit \(\widehat{U}_m\) for the universal circuit \(U_m\) that given f, returns f(m). It then encrypts the corresponding input labels \(\{k_i^0,k_i^1\}_{i\in L}\) under the corresponding public keys.
-
The decryptor in possession of \(\mathsf {SK}_f\) can then decrypt to obtain the labels \(\{k_i^{f_i}\}_{i\in L}\) and decode the garbled circuit to obtain \(U_m(f) = f(m)\).
Selective security of this scheme (where the function f and all messages are chosen ahead of time) follows from the semantic security of PKE and the garbled circuit guarantee which says that \(\widehat{U}_m,\{k_i^{f_i}\}_{i\in L}\) can be simulated from f(m).
The scheme is indeed not succinct in any way. The complexity of encryption and even the size of the ciphertext grows with the complexity of f. Nevertheless, it does seem that the encryption process has a much more succinct representation. In particular, computing a garbled circuit is a decomposable process — each garbled gate in \(\widehat{U}_m\) depends on a single gate in the original circuit \({U}_m\) and a small amount of randomness (for computing the labels corresponding to its wires). Furthermore, the universal circuit \(U_m\) itself is also decomposable — there exists a small (say, \(\mathrm {poly}(\left| m\right| ,\log L)\)-sized) circuit that given i can output the i-th gate in \(U_m\) along with its neighbours. The derivation of randomness itself can also be made decomposable using a pseudorandom function. All in all, there exists a small (\(\mathrm {poly}(\left| m\right| ,\log L,\lambda )\)-size, for security parameter \(\lambda \)), decomposition circuit \(U_{m,K}^{\mathsf {de}}\) associated with a key \(K\in \{0,1\}^\lambda \) for a pseudorandom function that can produce the ith garbled gate/input-label given input i.
Yet, the second part of the encryption process, where the input labels \(\{k_i^0,k_i^1\}_{i\in L}\) are encrypted under the corresponding public keys \(\left\{ \mathsf {PK}_i^0,\mathsf {PK}_i^1\right\} _{i\in L}\), may not be decomposable at all. Indeed, in general, it is not clear how to even compress the representation of these 2L public-keys. In this high-level exposition, let us make the simplifying assumption that we have at our disposal a succinct identity-based-encryption (IBE) scheme. Such a scheme has a single public-key \(\mathsf {PK}\) that allows to encrypt a message to an identity \(\mathsf {id}\in \mathcal {ID}\) taken from an identity space \(\mathcal {ID}\). Those in possession of a corresponding secret key \(\mathsf {SK}_\mathsf {id}\) can decrypt and others learn nothing. Succinctness means that the complexity of encryption may only grow mildly in the size of the identity space. Concretely, by a factor of \(|\mathcal {ID}|^\gamma \) for some small constant \(\gamma <1\). In the body, we show that such a scheme can be constructed from (plain) public-key encryption and SXIO (the construction relies on standard “puncturing techniques” and is pretty natural).
Equipped with such an IBE scheme, we can now augment the Sahai-Seyalioglu scheme to make sure that the entire encryption procedure is decomposable. Concretely, we will consider the identity space \(\mathcal {ID}= [L]\times \{0,1\}\), augment the public key to only include the IBE’s public key \(\mathsf {PK}\), and provide the decryptor with the identity keys \(\{\mathsf {SK}_{(i,f_i)}\}_{i\in L}\). Encrypting the input labels \(\{k_i^0,k_i^1\}_{i\in L}\) will now be done by simply encrypting to the corresponding identities \(\{(i,0),(i,1)\}_{i\in L}\). This part of the encryption can now also be described by a small (say \(L^{\gamma }\cdot \mathrm {poly}(\lambda ,\log L)\)-size) decomposition circuit \(E^{\mathsf {de}}_{K,K',\mathsf {PK}}\) that has the PRF key K to derive input labels, the IBE public key \(\mathsf {PK}\), and another PRF key \(K'\) to derive randomness for encryption. Given an identity (i, b), it generates the corresponding encrypted input label.
At this point, a natural direction is to have the encryptor send a compressed version of the Sahai-Seyalioglu encryption, by first using SXIO to shield the two decomposition circuits \(E^{\mathsf {de}}_{K,K',\mathsf {PK}},U_{m,K}^{\mathsf {de}}\) and then sending the two obfuscations. Indeed, decryption can be done just as before by first reconstructing the expanded garbled circuit and input labels and then proceeding as before. Also, in terms of encryption complexity, provided that the IBE compression factor \(\gamma \) is a small enough constant, the entire encryption time will scale only sublinearly in the function’s size \(|f|=L\) (i.e., with \(L^{\beta }\) for some constant \(\beta <1\)).
The only question is of course security. It is not too hard to see that if the decomposition circuits \(E^{\mathsf {de}}_{K,K',\mathsf {PK}},U_{m,K}^{\mathsf {de}}\) are given as black-boxes then security is guaranteed just as before. The challenge is to prove security relying only on the indistinguishability guarantee of SXIO. A somewhat similar challenge is encountered in the work of Bitansky et al. [12] when constructing succinct randomized encodings. In their setting, they obfuscate (using standard IO rather than SXIO) a decomposition circuit \(C^{\mathsf {de}}_{x,K}\) (analogous to our \(U^{\mathsf {de}}_{m,K}\)) that computes the garbled gates of some succinctly represented long computation.
As already demonstrated in [12], proving the security of such a construction is rather delicate. As in the standard setting of garbled circuits, the goal is to gradually transition through a sequence of hybrids, from a real garbled circuit (that depends on the actual computation) to a simulated garbled circuit that depends just on the result of the computation. However, unlike the standard setting, here each of these hybrids should be generated by a hybrid obfuscated decomposition circuit and the attacker should not be able to tell them apart. As it turns out, “common IO gymnastics” are insufficient here, and we need to rely on the specific hybrid strategy used to transition between the different garbling modes is the proof of security for standard garbled circuits. One feature of the hybrid strategy which is dominant in this context is the amount of information that hybrid decomposition circuits need to maintain about the actual computation. Indeed, as the amount of this information grows so will the size of these decomposition circuits as will the size of the decomposition circuits in the actual construction (that will have to be equally padded to preserve indistinguishability).
Bitansky et al. show a hybrid strategy where the amount of information scales with the space of the computation (or circuit width). Whereas in their context this is meaningful (as the aim is to save comparing to the time of the computation), in our context this is clearly insufficient. Indeed, in our case the space of the computation given by the universal circuit \(U_m\) and the function f can be as large as f’s description. Instead, we invoke a different hybrid strategy by Hemenway et al. [37] that scales only with the circuit depth. Indeed, this is the cause for the polynomial dependence on depth in our single-key PKFE construction. Below, we further elaborate on the Hemenway et al. hybrid strategy and how it is imported into our setting.
Decomposable Garbling and Pebbling. The work of Hemenway et al. [37] provided a useful abstraction for proving the security of Yao’s garbled circuits via a sequence of hybrid games. The goal is to transition from a “real” garbled circuit, where each garbled gate is in “\(\mathsf {RealGate}\)” mode consisting of four ciphertexts encrypting the two labels \(k_c^0,k_c^1\) of the output wire c under the labels of the input wires, to a “simulated” garbled circuit where each garbled gate is in \(\mathsf {SimGate}\) mode consisting of four ciphertexts that all encrypt the same dummy label \(k_c^0\). As an intermediate step, we can also create a garbled gate in \(\mathsf {CompDepSimGate}\) mode consisting of four ciphertexts encrypting the same label \(k_c^{v(c)}\) where v(c) is the value going over wire c during the computation C(x) and therefore depends on the actual computation.
The transition from a real garbled circuit to a simulated garbled circuit proceeds via a sequence of hybrids where in each subsequent hybrid we can change one gate at a time from \(\mathsf {RealGate}\) to \(\mathsf {CompDepSimGate}\) (and vice versa) if all of its predecessors are in \(\mathsf {CompDepSimGate}\) mode or it is an input gate, or change a gate from \(\mathsf {CompDepSimGate}\) mode to \(\mathsf {SimGate}\) mode (and vice versa) if all of its successors are in \(\mathsf {CompDepSimGate}\) or \(\mathsf {SimGate}\) modes. The goal of Hemenway et al. was to give a strategy using the least number of gates in \(\mathsf {CompDepSimGate}\) mode as possible.Footnote 3 They abstracted this problem as a pebbling game and show that for circuits of depth d there exists a sequence of \(2^{O(d)}\) hybrids with at most O(d) gates in \(\mathsf {CompDepSimGate}\) mode in any single hybrid.
In our case, we can give a decomposable circuit for each such hybrid game consisting of gates in \(\mathsf {RealGate},\mathsf {SimGate},\mathsf {CompDepSimGate}\) modes. In particular, the decomposable circuit takes as input a gate index and outputs the garbled gate in the correct mode. We only need to remember which gate is in which mode, and for all gates in \(\mathsf {CompDepSimGate}\) mode we need to remember the bit v(c) going over the wire c during the computation C(x). It turns out that the configuration of which mode each gate is in can be represented succinctly, and therefore the number of bits we need to remember is roughly proportional to the number of gates in \(\mathsf {CompDepSimGate}\) mode in any given hybrid. Therefore, for circuits of depth d, the decomposable circuit is of size O(d) and the number of hybrid steps is \(2^{O(d)}\).
To ensure that the obfuscations of decomposable circuits corresponding to neighboring hybrids are indistinguishable we also need to rely on standard puncturing techniques. In particular, the gates are garbled using a punctured PRF and we show that in any transition between neighboring hybrids we can even give the adversary the PRF key punctured only on the surrounding of the gate whose mode is changed.
From SKFE to PKE: The Basic Idea. We end our technical exposition by explaining the basic idea behind the construction of public-key encryption (PKE) from SKFE. The construction is rather natural. Using subexponentially-secure SKFE and the second part of Proposition 1, we can obtain a \(\mathrm {poly}(\lambda )\)-secure SXIO with a subconstant compression factor \(\gamma =o(1)\); concretely, it can be for example \(O(1/ \log \log \lambda )\). We can now think about this obfuscator as a plain (efficient) indistinguishability obfuscator for circuits with input length at most \( \log \lambda \cdot \log \log \lambda \).
Then, we take a construction of public-key encryption from IO and one-way functions where the input-size of obfuscated circuits can be scaled down at the expense of strengthening the one-way functions. For instance, following the basic witness encryption paradigm in [27], the public key can be a pseudorandom string \(\mathsf {PK}={\mathsf {PRG}}(s)\) for a \(2^{n/\log \log n}\)-secure length-doubling pseudorandom generator with seed length \(n=\log \lambda \cdot \log \log \lambda \). Here the obfuscator is only invoked for a circuit with inputs in \(\{0,1\}^n\). An encryption of m is simply an obfuscation of a circuit that has \(\mathsf {PK}\) hardwired, and releases m only given a seed s such that \(\mathsf {PK}={\mathsf {PRG}}(s)\). Security follows essentially as in [27]. Note that in this construction, we cannot expect more than \(2^n\) security, which is quasi-polynomial in the security parameter \(\lambda \).
How Does the Construction Circumvent the Asharov-Segev Barrier? As noted earlier, Asharov and Segev [6] show that even exponentially secure SKFE cannot lead to public-key encryption through a fully black-box construction (see their paper for details about the exact model). The reason that our construction does not fall under their criteria lies in the transformation from SKFE to SXIO with subconstant compression, and concretely in the Brakerski-Komargodski-Segev [20] transformation from SKFE to t-input SKFE that makes non-black-box use in the algorithms of the underlying SKFE scheme.
Organization. In Sect. 2, we provide preliminaries and basic definitions used throughout the paper. In Sect. 3, we introduce the definition of SXIO and present our construction based on SKFE schemes. In Sect. 4, we introduce a notion of decomposable garbling. In Sect. 5, we present our construction of IO from PKE and SXIO. In Sect. 6, we present a polynomially-secure PKE scheme from SKFE schemes.
2 Preliminaries
2.1 Standard Computational Concepts
We rely on the standard notions of Turing machines and Boolean circuits.
-
We say that a (uniform) Turing machine is PPT if it is probabilistic and runs in polynomial time.
-
A polynomial-size (or just polysize) circuit family \({\mathcal {C}}\) is a sequence of circuits \({\mathcal {C}}=\left\{ C_\lambda \right\} _{\lambda \in \mathbb {N}}\), such that each circuit \(C_\lambda \) is of polynomial size \(\lambda ^{O(1)}\) and has \(\lambda ^{O(1)}\) input and output bits.
-
We follow the standard habit of modeling any efficient adversary strategy as a family of polynomial-size circuits. For an adversary \(\mathcal {A}\) corresponding to a family of polysize circuits \(\left\{ \mathcal {A}_\lambda \right\} _{\lambda \in \mathbb {N}}\), we often omit the subscript \(\lambda \), when it is clear from the context.
-
We say that a function \(f:\mathbb {N}\rightarrow \mathbb {R}\) is negligible if for all constants \(c > 0\), there exists \(N \in \mathbb {N}\) such that for all \(n > N\), \(f(n) < n^{-c}\).
-
If \(\mathcal {X}^{(b)}=\{X^{(b)}_{\lambda }\}_{\lambda \in \mathbb {N}}\) for \(b \in \{0,1\}\) are two ensembles of random variables indexed by \(\lambda \in \mathbb {N}\), we say that \(\mathcal {X}^{(0)}\) and \(\mathcal {X}^{(1)}\) are computationally indistinguishable if for all polysize distinguishers \(\mathcal {D}\), there exists a negligible function \(\nu \) such that for all \(\lambda \), \(|\Pr [\mathcal {D}(X^{(0)}_\lambda )=1] - \Pr [\mathcal {D}(X^{(1)}_\lambda )=1]| \le \nu (\lambda )\).
2.2 Functional Encryption
Definition 1
(Multi-input secret-key functional encryption). Let \(t(\lambda )\) be a function, \(\overline{{\mathcal {M}}}=\{\overline{{\mathcal {M}}}_\lambda ={\mathcal {M}}^{(1)}_\lambda \times \cdots \times {\mathcal {M}}^{(t(\lambda ))}_\lambda \}_{\lambda \in \mathbb {N}}\) be a product message domain, \({\mathcal {Y}}=\left\{ {\mathcal {Y}}_\lambda \right\} _{\lambda \in \mathbb {N}}\) a range, and \({\mathcal {F}}=\left\{ {\mathcal {F}}_\lambda \right\} _{\lambda \in \mathbb {N}}\) a class of t-input functions \(f:\overline{{\mathcal {M}}}_\lambda \rightarrow {\mathcal {Y}}_\lambda \). A t-input secret-key functional encryption (t-SKFE) scheme for \({\mathcal {M}},{\mathcal {Y}},{\mathcal {F}}\) is a tuple of algorithms \(\mathsf {SKFE}_t = (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) where:
-
\(\mathsf {Setup}(1^\lambda )\) takes as input the security parameter and outputs a master secret key \(\mathsf {MPK}\).
-
\(\mathsf {KeyGen}(\mathsf {MSK},f)\) takes as input the master secret \(\mathsf {MPK}\) and a function \(f\in {\mathcal {F}}\). It outputs a secret key \(\mathsf {SK}_f\) for f.
-
 takes as input the master secret key \(\mathsf {MPK}\), a message \(m\in {\mathcal {M}}^{(i)}_\lambda \), and an index \(i \in [t(\lambda )]\), and outputs a ciphertext \(\mathsf {CT}_i\).
takes as input the master secret key \(\mathsf {MPK}\), a message \(m\in {\mathcal {M}}^{(i)}_\lambda \), and an index \(i \in [t(\lambda )]\), and outputs a ciphertext \(\mathsf {CT}_i\). -
 takes as input the secret key \(\mathsf {SK}_f\) for a function \(f\in {\mathcal {F}}\) and ciphertexts \(\mathsf {CT}_1,\ldots ,\mathsf {CT}_t\), and outputs some \(y\in {\mathcal {Y}}\), or \(\bot \).
takes as input the secret key \(\mathsf {SK}_f\) for a function \(f\in {\mathcal {F}}\) and ciphertexts \(\mathsf {CT}_1,\ldots ,\mathsf {CT}_t\), and outputs some \(y\in {\mathcal {Y}}\), or \(\bot \).
Correctness: For all tuples \({\varvec{m}} = (m_1,\ldots ,m_t)\in \overline{{\mathcal {M}}}_\lambda \) and any function \(f\in {\mathcal {F}}_\lambda \), we have that

Definition 2
(Selectively-secure multi-key t -SKFE). We say that a tuple of algorithms \(\mathsf {SKFE}_t = (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) is a selectively-secure t-input secret-key functional encryption scheme for \(\overline{{\mathcal {M}}},{\mathcal {Y}},{\mathcal {F}}\), if it satisfies the following requirement, formalized by the experiment \(\mathsf {Expt}^{\mathsf {SKFE_{\text {t}}}}_{\mathcal {A}}(1^\lambda ,b)\) between an adversary \(\mathcal {A}\) and a challenger:
-
1.
The adversary submits challenge message tuples \(\left\{ (m_{i,1}^0,m_{i,1}^1,i)\right\} _{i\in [t]},\ldots ,\left\{ (m_{i,q}^0,m_{i,q}^1,i)\right\} _{i\in [t]}\) for all \(i \in [t]\) to the challenger where q is an arbitrary polynomial in \(\lambda \).
-
2.
The challenger runs \(\mathsf {MSK}\leftarrow \mathsf {Setup}(1^\lambda )\)
-
3.
The challenger generates ciphertexts \(\mathsf {CT}_{i,j}\leftarrow \mathsf {Enc}(\mathsf {MSK},m_{i,j}^b,i)\) for all \(i\in [t]\) and \(j\in [q]\), and gives \(\{\mathsf {CT}_{i,j}\}_{i\in [t],j\in [q]}\) to \(\mathcal {A}\).
-
4.
\(\mathcal {A}\) is allowed to make q function queries, where it sends a function \(f_{j}\in {\mathcal {F}}\) to the challenger for \(j\in [q]\) and q is an arbitrary polynomial in \(\lambda \). The challenger responds with \(\mathsf {SK}_{f_j}\leftarrow \mathsf {KeyGen}(\mathsf {MSK},f_j)\).
-
5.
\(\mathcal {A}\) outputs a guess \(b'\) for b.
-
6.
The output of the experiment is \(b'\) if the adversary’s queries are valid:
$$\begin{aligned}f_j(m_{1,j_1}^0,\dots ,m_{t,j_t}^0) = f_j(m_{1,j_1}^1,\dots ,m_{t,j_t}^1) \text { for all } j_1,\dots ,j_t,j \in [q].\end{aligned}$$Otherwise, the output of the experiment is set to be \(\bot \).
We say that the functional encryption scheme is selectively-secure if, for all polysize adversaries \(\mathcal {A}\), there exists a negligible function \(\mu (\lambda )\), such that

We further say that \(\mathsf {SKFE}_t\) is \(\delta \)-selectively-secure, for some concrete negligible function \(\delta (\cdot )\), if the above indistinguishability gap \(\mu (\lambda )\) is smaller than \(\delta (\lambda )^{\varOmega (1)}\).
We recall the following theorem by Brakerski, Komargodski, and Segev, which states that one can build selectively-secure t-SKFE from any selectively-secure 1-SKFE. The transformation induces a significant blowup and security loss in the number of inputs t. This loss is polynomial as long as t is constant, but in general grows doubly-exponentially in t.
Theorem 3
[20]
-
1.
For \(t=O(1)\), if there exists \(\delta \)-selectively-secure single-input SKFE for \(\mathsf {P}/\mathsf {poly}\), then there exists \(\delta \)-selectively-secure t-input SKFE for \(\mathsf {P}/\mathsf {poly}\).
-
2.
There exists a constant \(\varepsilon <1\), such that for \(t(\lambda )=\varepsilon \cdot \log \log (\lambda )\), \(\tilde{\lambda } = 2^{(\log \lambda )^{\varepsilon }}\), \(\delta (\tilde{\lambda }) = 2^{-\tilde{\lambda }^\varepsilon }\), if there exists \(\delta \)-selectively-secure single-input SKFE for \(\mathsf {P}/\mathsf {poly}\), then there exists polynomially-secure selectively-secure t-input SKFE for functions of size at most \(2^{O((\log \lambda )^{\varepsilon })}\). (Here \(\tilde{\lambda }\) is the single-input SKFE security parameter and \(\lambda \) is the t-input SKFE security parameter.)
Remark 1
(Dependence on circuit size in [20]). The [20] transformation incurs a \((s\cdot \tilde{\lambda })^{2^{O(t)}}\) blowup in parameters, where s is the size of maximal circuit size of supported functions, and \(\tilde{\lambda }\) is the security parameter used in the underlying single-input SKFE. In the main setting of parameters considered there, \(t=O(1)\), the security parameter \(\lambda \) of the t-SKFE scheme can be identified with \(\tilde{\lambda }\) and s can be any polynomial in this security parameter. (Accordingly, the dependence on s is implicit there, and the blowup they address is \(\lambda ^{2^{O(t)}}\).)
For the second part of the theorem, to avoid superpolynomial blowup in \(\lambda \), the security parameter \(\tilde{\lambda }\) for the underlying SKFE and the maximal circuit size s should be set to \(2^{O((\log \lambda )^{\varepsilon })}\).
Definition 3
(Public-key functional encryption). Let \({\mathcal {M}}=\left\{ {\mathcal {M}}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a message domain, \({\mathcal {Y}}=\left\{ {\mathcal {Y}}_\lambda \right\} _{\lambda \in \mathbb {N}}\) a range, and \({\mathcal {F}}=\left\{ {\mathcal {F}}_\lambda \right\} _{\lambda \in \mathbb {N}}\) a class of functions \(f:{\mathcal {M}}\rightarrow {\mathcal {Y}}\). A public-key functional encryption (PKFE) scheme for \({\mathcal {M}},{\mathcal {Y}},{\mathcal {F}}\) is a tuple of algorithms \(\mathsf {PKFE}= (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) where:
-
\(\mathsf {Setup}(1^\lambda )\) takes as input the security parameter and outputs a master secret key \(\mathsf {MSK}\) and master public key
 .
. -
 takes as input the master secret \(\mathsf {MSK}\) and a function \(f\in {\mathcal {F}}\). It outputs a secret key \(\mathsf {SK}_f\) for f.
takes as input the master secret \(\mathsf {MSK}\) and a function \(f\in {\mathcal {F}}\). It outputs a secret key \(\mathsf {SK}_f\) for f. -
 takes as input the master public key
takes as input the master public key  and a message
and a message  , and outputs a ciphertext c.
, and outputs a ciphertext c. -
 takes as input the secret key \(\mathsf {SK}_f\) for a function \(f\in {\mathcal {F}}\) and a ciphertext c, and outputs some \(y\in {\mathcal {Y}}\), or \(\bot \).
takes as input the secret key \(\mathsf {SK}_f\) for a function \(f\in {\mathcal {F}}\) and a ciphertext c, and outputs some \(y\in {\mathcal {Y}}\), or \(\bot \).
Correctness: For any message \(m\in {\mathcal {M}}\) and function \(f\in {\mathcal {F}}\), we have that

Definition 4
(Selectively-secure single-key PKFE). We say that a tuple of algorithm \(\mathsf {PKFE}= (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) is a selectively-secure single-key public-key functional encryption scheme for \({\mathcal {M}},{\mathcal {Y}},{\mathcal {F}}\), if it satisfies the following requirement, formalized by the experiment \(\mathsf {Expt}^{\mathsf {PKFE}}_{\mathcal {A}}(1^\lambda ,b)\) between an adversary \(\mathcal {A}\) and a challenger:
-
1.
\(\mathcal {A}\) submits the message pair \(m_0^*,m_1^* \in {\mathcal {M}}\) and a function f to the challenger.
-
2.
The challenger runs \((\mathsf {MSK},\mathsf {MPK})\leftarrow \mathsf {Setup}(1^\lambda )\), generates ciphertext \(\mathsf {CT}^*\leftarrow \mathsf {Enc}(\mathsf {MPK},m_b^*)\) and a secret key \(\mathsf {SK}_f \leftarrow \mathsf {KeyGen}(\mathsf {MSK},f)\). The challenger gives \((\mathsf {MPK},\mathsf {CT}^*,sk_f)\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) outputs a guess \(b'\) for b.
-
4.
The output of the experiment is \(b'\) if \(f(m_0^*) = f(m_1^*)\) and \(\bot \) otherwise.
We say that the public-key functional encryption scheme is selectively-secure if, for all PPT adversaries \(\mathcal {A}\), there exists a negligible function \(\mu (\lambda )\), such that
We further say that \(\mathsf {PKFE}\) is \(\delta \)-selectively secure, for some concrete negligible function \(\delta (\cdot )\), if for all polysize distinguishers the above indistinguishability gap \(\mu (\lambda )\) is smaller than \(\delta (\lambda )^{\varOmega (1)}\).
We now further define a notion of succinctness for functional encryption schemes as above.
Definition 5
(Weakly Succinct functional encryption). For a class of functions \({\mathcal {F}}=\left\{ {\mathcal {F}}_\lambda \right\} \) over message domain \({\mathcal {M}}=\left\{ {\mathcal {M}}_\lambda \right\} \), we let:
-
\(n(\lambda )\) be the input length of the functions in \({\mathcal {F}}\),
-
\(s(\lambda ) = \max _{f\in {\mathcal {F}}_\lambda }\left| f\right| \) be a bound on the circuit size of functions in \({\mathcal {F}}_\lambda \),
-
\(d(\lambda ) = \max _{f\in {\mathcal {F}}_\lambda }\mathsf {depth}(f)\) a bound on the depth, and
A functional encryption scheme is
-
weakly succinct [14] if the size of the encryption circuit is bounded by \(s^{\gamma }\cdot \mathrm {poly}(n,\lambda ,d)\), where \(\mathrm {poly}\) is a fixed polynomial, and \(\gamma <1\) is a constant. We call \(\gamma \) the compression factor.
The following result from [14, Sect. 3.2] states that one can construct an indistinguishability obfuscator from any single-key weakly succinct public-key functional encryption scheme.
Theorem 4
([14]). If there exists a subexponentially secure single-key weakly succinct PKFE scheme, then there exists an indistinguishability obfuscator.
2.3 Indistinguishability Obfuscation
Definition 6
(Indistinguishability obfuscator (IO) [8, 9]). A PPT machine \(\mathsf {i}\mathcal {O}\) is an indistinguishability obfuscator for a circuit class \(\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}\) if the following conditions are satisfied:
-
Functionality: for all security parameters \(\lambda \in \mathbb {N}\), for all \(C \in \mathcal {C}_\lambda \), for all inputs x, we have that \(\Pr [C'(x)=C(x) : C' \leftarrow \mathsf {i}\mathcal {O}(C)] = 1\).
-
Indistinguishability: for any polysize distinguisher \(\mathcal {D}\), there exists a negligible function \(\mu (\cdot )\) such that the following holds: for all security parameters \(\lambda \in \mathbb {N}\), for all pairs of circuits \(C_0, C_1 \in \mathcal {C}_\lambda \) of the same size and such that \(C_0(x) = C_1(x)\) for all inputs x, then
$$\begin{aligned} \left| \Pr \big [\mathcal {D}(\mathsf {i}\mathcal {O}(C_0))= 1\big ] - \Pr \big [\mathcal {D}(\mathsf {i}\mathcal {O}(C_1))= 1\big ] \right| \le \mu (\lambda ). \end{aligned}$$We further say that \(\mathsf {i}\mathcal {O}\) is \(\delta \)-secure, for some concrete negligible function \(\delta (\cdot )\), if for all polysize distinguishers the above indistinguishability gap \(\mu (\lambda )\) is smaller than \(\delta (\lambda )^{\varOmega (1)}\).
2.4 Succinct Identity-Based Encryption
We define identity-based encryption (IBE) [48] with a succinctness properties.
Definition 7
(Succinct IBE with \(\gamma \) -compression). Let \({\mathcal {M}}\) be some message space and \(\mathcal {ID}\) be an identity space. A succint IBE scheme with \(\gamma \) -compression for \({\mathcal {M}},\mathcal {ID}\) is a tuple of algorithms \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) where:
-
\(\mathsf {Setup}(1^\lambda )\) is takes as input the security parameter and outputs a master secret key \(\mathsf {MSK}\) and a master public key
 .
. -
 takes as input the master secret \(\mathsf {MSK}\) and an identity \(\mathsf {id}\in \mathcal {ID}\). It outputs a secret key \(\mathsf {SK}_\mathsf {id}\) for \(\mathsf {id}\).
takes as input the master secret \(\mathsf {MSK}\) and an identity \(\mathsf {id}\in \mathcal {ID}\). It outputs a secret key \(\mathsf {SK}_\mathsf {id}\) for \(\mathsf {id}\). -
\(\mathsf {Enc}(\mathsf {MPK},\mathsf {id},m)\) takes as input the public-parameter
 , an identity \(\mathsf {id} \in \mathcal {ID}\), and a message
, an identity \(\mathsf {id} \in \mathcal {ID}\), and a message  , and outputs a ciphertext c.
, and outputs a ciphertext c. -
\(\mathsf {Dec}(\mathsf {SK}_\mathsf {id},c)\) takes as input the secret key \(\mathsf {SK}_\mathsf {id}\) for an identity \(\mathsf {id}\in \mathcal {ID}\) and a ciphertext c, and outputs some \(m \in {\mathcal {M}}\), or \(\bot \).
We require the following properties:
Correctness: For any message \(m\in {\mathcal {M}}\) and identity \(\mathsf {id}\in \mathcal {ID}\), we have that
Succinctness: For any security parameter \(\lambda \in \mathbb {N}\), identity space \(\mathcal {ID}\), the size of the encryption circuit \(\mathsf {Enc}\), for messages of size \(\ell \), is at most \( |\mathcal {ID}|^{\gamma }\cdot \mathrm {poly}(\lambda ,\ell )\).
In this work, we shall consider the following selective-security.
Definition 8
(Selectively-secure IBE). A tuple of algorithms \(\mathsf {IBE}= (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) is a selectively-secure IBE scheme for \({\mathcal {M}},\mathcal {ID}\) if it satisfies the following requirement, formalized by the experiment \(\mathsf {Expt}^{\mathsf {IBE}}_{\mathcal {A}}(1^\lambda ,b)\) between an adversary \(\mathcal {A}\) and a challenger:
-
1.
\(\mathcal {A}\) submits the challenge identity \(\mathsf {id}^* \in \mathcal {ID}\) and the challenge messages \((m_0^*,m_1^*)\) to the challenger.
-
2.
The challenger runs \((\mathsf {MSK},\mathsf {MPK})\leftarrow \mathsf {Setup}(1^\lambda )\), generates ciphertext \(\mathsf {CT}^*\leftarrow \mathsf {Enc}(\mathsf {MPK},m_b^*)\) and gives \((\mathsf {MPK},\mathsf {CT}^*)\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) is allowed to query (polynomially many) identities \(\mathsf {id}\in \mathcal {ID}\) such that \(\mathsf {id} \ne \mathsf {id}^*\). The challenger gives \(\mathsf {SK}_\mathsf {id} \leftarrow \mathsf {KeyGen}(1^\lambda ,\mathsf {MSK},\mathsf {id})\) to the adversary.
-
4.
\(\mathcal {A}\) outputs a guess \(b'\) for b. The experiment outputs 1 if \(b'=b\), 0 otherwise.
We say the IBE scheme is selectively-secure if, for all PPT adversaries \(\mathcal {A}\), there exists a negligible function \(\mu (\lambda )\), it holds
We further say that \(\mathsf {IBE}\) is \(\delta \)-selectively secure, for some concrete negligible function \(\delta (\cdot )\), if for all polysize distinguishers the above indistinguishability gap \(\mu (\lambda )\) is smaller than \(\delta (\lambda )^{\varOmega (1)}\).
Theorem 5
For any \(\beta< \gamma < 1\), assuming there exists a \(\beta \)-compressing SXIO scheme for \(\mathsf {P}/\mathsf {poly}\) (defined in Sect. 3), a puncturable PRF, and a plain PKE scheme, there exists a succinct IBE scheme with \(\gamma \)-compression. Moreover, assuming the underlying primitives are \(\delta \)-secure so is the resulting IBE scheme.
We omit the proof of this theorem due to the limited space. See the full version of this paper [13].
We also omit the definition of puncturable PRF and (plain) PKE due to the limited space. Puncturable PRFs are constructed from OWFs [18, 19, 31, 39]. See the full version of this paper [13] or references therein.
3 Strong Exponentially-Efficient Indistinguishability Obfuscation
Lin, Pass, Seth, and Telang [43] propose a variant of IO that has a weak (yet non-trivial) efficiency, which they call exponentially-efficient IO (XIO). All that this notion requires in terms of efficiency is that the size of an obfuscated circuit is sublinear in the size of the corresponding truth table. They also refer to a stronger notion that requires that also the time to obfuscate a given circuit is sublinear in the size of the truth table. This notion, which we call strong exponentially-efficient IO (SXIO), serves as one of the main abstractions in our work.
Definition 9
(Strong exponentially-efficient indistinguishability obfuscation (SXIO) [43]). For a constant \(\gamma < 1\), a machine \(\mathsf {sxi}\mathcal {O}\) is a \(\gamma \)-compressing strong exponentially-efficient indistinguishability obfuscator (SXIO) for a circuit class \(\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}\) if it satisfies the functionality and indistinguishability in Definition 6 and the following efficiency requirements:
Non-trivial Time Efficiency: for any security parameter \(\lambda \in \mathbb {N}\) and circuit \(C \in \{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}\) with input length n, the running time of \(\mathsf {sxi}\mathcal {O}\) on input \((1^\lambda ,C)\) is at most \(2^{n\gamma }\cdot \mathrm {poly}(\lambda ,|C|)\).
3.1 SXIO from Single-Input SKFE
In this section, we show that we can construct SXIO from any selectively-secure t-input SKFE scheme. We recall that such a t-SKFE scheme can be constructed from any selectively-secure 1-SKFE scheme, as stated in Theorem 3.
Theorem 6
For any function \(t(\lambda )\), if there exists \(\delta \)-selectively-secure t-SKFE for \(\mathsf {P}/\mathsf {poly}\), then there exists \(\frac{1}{t+1}\)-compressing \(\delta \)-secure SXIO for \(\mathsf {P}/\mathsf {poly}\).
The idea of the construction of SXIO from SKFE is explained in the introduction.
We immediately obtain the following corollary from Theorems 3 and 6.
Corollary 2
-
1.
If there exists \(\delta \)-selectively-secure single-input SKFE for \(\mathsf {P}/\mathsf {poly}\), then there exists \(\gamma \)-compressing \(\delta \)-secure SXIO for \(\mathsf {P}/\mathsf {poly}\) where \(\gamma <1\) is an arbitrary constant.
-
2.
Let \(\varepsilon <1\) be a constant and \(\tilde{\lambda } = 2^{(\log \lambda )^{\varepsilon }}\). If there exists \(2^{-\tilde{\lambda }^{\varOmega (1)}}\)-selectively-secure single-input SKFE for \(\mathsf {P}/\mathsf {poly}\), then there exists polynomially-secure SXIO with compression factor \(\gamma (\lambda ) = O(1/\log \log \lambda )\) for circuits of size at most \(2^{O((\log \lambda )^{\varepsilon })}\). (Here \(\tilde{\lambda }\) is the single-input SKFE security parameter and \(\lambda \) is the SXIO security parameter.)
3.2 The Construction of SXIO
In what follows, given a circuit C, we identify its input space with \([N] =\left\{ 1,\dots ,N\right\} \) (so in particular, \(N= 2^n\) if C takes n-bit strings as input). Let \(\mathsf {SKFE}_t = (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) be a selectively-secure t-input secret-key functional encryption scheme.
Construction. We construct an SXIO scheme \(\mathsf {sxi}\mathcal {O}\) as follows.
\(\mathsf {sxi}\mathcal {O}(1^\lambda ,C)\): For every \(j \in [N^{1/(t+1)}]\):
-
let \(U_{j}\) be the t-input universal circuit that given \(j_1,\ldots ,j_{t-1} \in [N^{1/(t+1)}]\) and a t-input circuit D, returns \(D(j_1,\ldots , j_{t-1},j)\).
-
let \(C_{j}\) be the t-input circuit that given \(j_1,\ldots ,j_{t}\in [N^{1/(t+1)}]\) returns \(C(j_1,\ldots , j_{t},j)\).
-
1.
Generate \(\mathsf {MSK}\leftarrow \mathsf {Setup}(1^\lambda )\).
-
2.
Generate \(\mathsf {CT}_{t,j} \leftarrow \mathsf {Enc}(\mathsf {MSK},C_j,t)\) for \(j\in [N^{1/(t+1)}]\).
-
3.
Generate \(\mathsf {CT}_{i,j} \leftarrow \mathsf {Enc}(\mathsf {MSK},j,i)\) for \(i\in [t-1]\) and \(j\in [N^{1/(t+1)}]\).
-
4.
Generate \(\mathsf {SK}_{U_j} \leftarrow \mathsf {KeyGen}(\mathsf {MSK},U_j)\) for \(j\in [N^{1/(t+1)}]\)
-
5.
\(\mathsf {sxi}\mathcal {O}(C) =(\{\mathsf {CT}_{i,j}\}_{i\in [t],j\in [N^{1/(t+1)}]},\{\mathsf {SK}_{U_j}\}_{j\in [N^{1/(t+1)}]})\)
\(\mathsf {Eval}(\mathsf {sxi}\mathcal {O},x)\): To evaluate the obfuscated circuit, convert \(x \in [N]\) into \((j_1,\ldots , j_t,j_{t+1}) \in [N^{1/(t+1)}]^{(t+1)}\) and output \(\mathsf {Dec}(\mathsf {SK}_{U_{j_{t+1}}},\mathsf {CT}_{1,j_1},\ldots ,\mathsf {CT}_{t,j_t}).\)
We omit the proof due to the limited space. See the full version [13].
Remark 2
(SXIO from succinct single-key SKFE). To get t-input SKFE as required above from 1-input SKFE, via the [20] transformation, the original SKFE indeed has to support an unbounded polynomial number of functional keys. We note that a similar SXIO construction is possible from a 1-input SKFE that supports a functional key for a single function f, but is succinct in the sense that encryption only grows mildly with the complexity of f, namely with \(|f|^\beta \) for some constant \(\beta <1\).
In more detail, assume a (1-input) single-key SKFE with succinctness as above, where the time to derive a key for a function f is bounded by \(|f|^c\cdot \mathrm {poly}(\lambda )\) for some constant \(c \ge 1\). The SXIO will consist of a single key for the function f that given as input \(C_j\), as defined above, returns \(C_j(1),\dots ,C_j(N^{\frac{1}{c+1-\beta }})\), and encryptions of \(C_1,\dots ,C_{N^{c-\beta /c+1-\beta }}\). Accordingly we still get SXIO with compression factor \(\gamma = 1-\frac{1-\beta }{c+1-\beta }\). This does not lead to arbitrary constant compression (in contrast with the theorem above), since \(\frac{1}{2} \le \gamma < 1\). Yet, it already suffices to obtain IO, when combined with LWE (as in Corollary 1).
4 Yao’s Garbled Circuits Are Decomposable
In this section, we define the notion of decomposable garbled circuits. We can prove that the classical Yao’s garbled circuit construction satisfies our definition of decomposability (in some parameter regime) though we omit the details about the proof due to the limited space. We use a decomposable garbling scheme as a building block to construct a PKFE scheme in Sect. 5.1.
4.1 Decomposable Garbling
Circuit garbling schemes [10, 50] typically consist of algorithms \((\mathsf {Gar.CirEn},\mathsf {Gar.InpEn},\mathsf {Gar.De})\). \(\mathsf {Gar.CirEn}(C,K)\) is a circuit garbling algorithm that given a circuit \(C\) and secret key K, produces a garbled circuit \(\widehat{C}\). \(\mathsf {Gar.InpEn}(x,K)\) is an input garbling algorithm that takes an input \(x\) and the same secret key K, and produces a garbled input \(\widehat{x}\). \(\mathsf {Gar.De}(\widehat{C},\widehat{x})\) is a decoder that given the garbled circuit and input decodes the result y.
In this work, we shall particularly be interested in garbling decomposable circuits. A decomposable circuit \(C\) can be represented by a smaller circuit \(C_\mathsf{de}\) that can generate each of the gates in the circuit \(C\) (along with pointers to their neighbours). When garbling such circuits, we shall require that the garbling process will also be decomposable and will admit certain decomposable security properties. We next formally define the notion of decomposable circuits and decomposable garbling schemes.
Definition 10
(Decomposable Circuit). Let \(C:\{0,1\}^n\rightarrow \{0,1\}\) be a boolean circuit with \(L\) binary gates and W wires. Each gate \(g \in [L]\) has an associated tuple \((f, w_{a}, w_{b}, w_{c})\) where \(f~:~ \{0,1\}^2 \rightarrow \{0,1\}\) is the binary function computed by the gate, \(w_{a}, w_{b} \in [W]\) are the incoming wires, and \(w_{c} \in [W]\) is the outgoing wire. A wire \(w_c\) can be the outgoing wire of at most a single gate, but can be used as an incoming wire to several different gates and therefore this models a circuit with fan-in 2 and unbounded fan-out. We define the predecessor gates of g to be the gates whose outgoing wires are \(w_a,w_b\) (at most 2 of them). We define the successor gates of g to be the gates that have \(w_c\) as an incoming wire. The gates are topologically ordered and labeled by \(1,\dots ,L\) so that if j is a successor of i then \(i<j\). A wire w is an input wire if it is not the outgoing wire of any gate. We assume that the wires \(1,\ldots ,n\) are the input wires. There is a unique output wire w which is not an incoming wire to any gate.
We say that \(C\) is decomposable if there exists a smaller circuit \(C_\mathsf{de}\), called the decomposition circuit, that given a gate label \(g\in [L]\) as input, outputs the associated tuple \(C_\mathsf{de}(g) = (f, w_{a}, w_{b}, w_{c})\).
Definition 11
(Decomposable Garbling). A decomposable garbling scheme consists of a tuple of three deterministic polynomial-time algorithms \((\mathsf {Gar.CirEn},\mathsf {Gar.InpEn},\mathsf {Gar.De})\) that work as follows:
-
\(\widehat{b}_i \leftarrow \mathsf {Gar.InpEn}(i,b;K)\): takes as an input label \(i \in [n]\), a bit \(b\in \{0,1\}\), and secret key \(K\in \{0,1\}^\lambda \), and outputs a garbled input bit \(\widehat{b}_i\).
-
\(\widehat{G}_g \leftarrow \mathsf {Gar.CirEn}(C_\mathsf{de},g;K)\): takes as input a decomposition circuit \(C_\mathsf{de}:\{0,1\}^L\rightarrow \{0,1\}^*\), a gate label \(g\in [L]\), and secret key \(K\in \{0,1\}^\lambda \), and outputs a garbled gate \(\widehat{G}_g\).
-
\(y\leftarrow \mathsf {Gar.De}(\widehat{C},\widehat{b})\): takes as input garbled gates \(\widehat{C}= \left\{ \widehat{G}_g\right\} _{g\in [L]}\), and garbled input bits \(\widehat{b}= \left\{ \widehat{b}_i\right\} _{i\in [n]}\), and outputs \(y\in \{0,1\}^m\).
The scheme should satisfy the following requirements:
-
1.
Correctness: for every decomposable circuit \(C\) with decomposition circuit \(C_\mathsf{de}\) and any input \(b_1,\dots ,b_n\in \{0,1\}^{n}\), the decoding procedure \(\mathsf {Gar.De}\) produces the correct output \(y=C(b_1,\dots ,b_n)\).
-
2.
\((\sigma ,\tau ,\delta )\) -Decomposable Indistinguishability: There are functions \(\sigma (\varPhi ,s,\lambda ),\tau (\varPhi ) \in \mathbb {N}\), \(\delta (\lambda ) \le 1\) such that for any security parameter \(\lambda \), any input \(x\in \{0,1\}^n\), and any two circuits \((C,C')\) that:
-
have the same topology \(\varPhi \), and in particular the same size \(L\) and input-output lengths \((n,m)\),
-
have decomposition circuits \((C_\mathsf{de},C_\mathsf{de}')\) of the same size s
-
and agree on \(x\): \(C(x)=C'(x)\),
there exist hybrid circuits
 , each being of size at most \(\sigma \), as well as (possibly inefficient) hybrid functions
, each being of size at most \(\sigma \), as well as (possibly inefficient) hybrid functions  with the following syntax:
with the following syntax:-
\((K_{\mathsf {pun}}^{(t)},g_{\mathsf {pun}}^{(t)},i_{\mathsf {pun}}^{(t)})\leftarrow \mathsf {Gar.HPunc}^{(t)}(K)\), given a key \(K\in \{0,1\}^\lambda \) and an index \(t\in [\tau ]\), outputs a punctured key \(K_{\mathsf {pun}}^{(t)}\), a gate label \(g_{\mathsf {pun}}^{(t)}\in [L]\), and an input label \(i_{\mathsf {pun}}^{(t)}\in [n]\).
-
\(\widehat{G}_g\leftarrow \mathsf {Gar.HCirEn}^{(t)}(g;K)\), given a gate label \(g\in [L]\), and a (possibly punctured) key \(K\), outputs a fake garbled gate \(\widehat{G}_{g}\).
-
\(\widehat{b}_i \leftarrow \mathsf {Gar.HInpEn}^{(t)}(i,b;K)\), given an input label \(i\in [n]\), and a (possibly punctured) key \(K\), outputs a fake garbled input bit \(\widehat{b}_{i}\).
We require that the following properties hold:
-
(a)
The hybrids transition from C to \(C'\): For any \(K\in \{0,1\}^\lambda \), \(g\in [L]\), \(i\in [n]\), \(b\in \{0,1\}\), we have:
\(\mathsf {Gar.CirEn}(C_\mathsf{de},g;K) = \mathsf {Gar.HCirEn}^{(1)}(g;K),\) \(\mathsf {Gar.InpEn}(i,b;K) = \mathsf {Gar.HInpEn}^{(1)}(i,b;K),\) \(\mathsf {Gar.CirEn}(C_\mathsf{de}',g;K) = \mathsf {Gar.HCirEn}^{(\tau )}(g;K),\) \(\mathsf {Gar.InpEn}(i,b;K) = \mathsf {Gar.HInpEn}^{(\tau )}(i,b;K).\)
-
(b)
Punctured keys preserve functionality: For any \(K\in \{0,1\}^\lambda \), and \(t\in [\tau -1]\), and letting \((K_{\mathsf {pun}}^{(t)},g_{\mathsf {pun}}^{(t)},i_{\mathsf {pun}}^{(t)}) =\mathsf {Gar.HPunc}^{(t)}(K)\), it holds that, for any \(g \ne g_{\mathsf {pun}}^{(t)}\), we have \(\mathsf {Gar.HCirEn}^{(t)}(g;K) = \mathsf {Gar.HCirEn}^{(t)}(g;K_{\mathsf {pun}}^{(t)}) = \mathsf {Gar.HCirEn}^{(t+1)}(g,K),\)
and for any \(i \ne i_{\mathsf {pun}}^{(t)}\) and \(b\in \{0,1\}\), we have \(\mathsf {Gar.HInpEn}^{(t)}(i,b;K) = \mathsf {Gar.HInpEn}^{(t)}(i,b;K_{\mathsf {pun}}^{(t)}) = \mathsf {Gar.HInpEn}^{(t+1)}(i,b;K)\).
-
(c)
Indistinguishability on punctured inputs: For any polysize distinguisher \(\mathcal {D}\), security parameter \(\lambda \in \mathbb {N}\), and circuits \((C,C')\) as above,
$$\begin{aligned}&\Big |\Pr \left[ \mathcal {D}\left( \hat{g}_{\mathsf {pun}}^{(t)},\hat{i}_{\mathsf {pun}}^{(t)},\mathsf {Gar.HPunc}^{(t)}(K)\right) =1\right] - \\&\qquad \qquad \qquad \Pr \left[ \mathcal {D}\left( \hat{g}_{\mathsf {pun}}^{(t+1)},\hat{i}_{\mathsf {pun}}^{(t+1)},\mathsf {Gar.HPunc}^{(t)}(K)\right) =1\right] \Big | \le \delta (\lambda ), \end{aligned}$$where, for \(t \ge 0\) we denote by \(\hat{g}_{\mathsf {pun}}^{(t)}\) the value \(\mathsf {Gar.HCirEn}^{(t)}(g_{\mathsf {pun}}^{(t)};K)\) and by \(\hat{i}_{\mathsf {pun}}^{(t)}\) the value \(\mathsf {Gar.HInpEn}^{(t)}(i_{\mathsf {pun}}^{(t)},x_{i_{\mathsf {pun}}^{(t)}};K)\), with \(x\) being the input on which the two circuits \(C\) and \(C'\) agree on. The probability is over \(K\leftarrow \{0,1\}^\lambda \), and \((K_{\mathsf {pun}}^{(t)},g_{\mathsf {pun}}^{(t)},i_{\mathsf {pun}}^{(t)}) =\mathsf {Gar.HPunc}^{(t)}(K)\).
-
We show that Yao’s garbled circuit scheme, in fact, gives rise to a decomposable garbling scheme where the security loss and size of the hybrid circuits scales with the depth of the garbled circuits.
Theorem 7
Let \(\mathcal {C}= \left\{ \mathcal {C}_{\lambda }\right\} _{\lambda \in \mathbb {N}}\) be a class of boolean circuits where each \(C\in \mathcal {C}_\lambda \) has circuit size at most \(L(\lambda )\), input size at most \(n(\lambda )\), depth at most \(d(\lambda )\), fan-out at most \(\varphi (\lambda )\), and decomposition circuit of size at most \(\varDelta (\lambda )\). Then assuming the existence of \(\delta \)-secure one-way functions, \(\mathcal {C}\) has a decomposable garbling scheme with \((\sigma ,\tau ,\delta )\)-decomposable indistinguishability where the bound on the size of hybrid circuits is \(\sigma = \mathrm {poly}(\lambda , d, \log L, \varphi , \varDelta )\), the number of hybrids is \(\tau = L \cdot 2^{O(d)}\), and the indistinguishability gap is \(\delta ^{\varOmega (1)}\).
The proof is omitted due to the limited space. See the full version [13]. We rely heavily on the ideas of Hemenway et al. [37] which considered an orthogonal question of adaptively secure garbling schemes but (for entirely different reasons) developed ideas that are useful for decomposable garbling.
5 Single-Key Succinct PKFE from SXIO and PKE
This section consists of three subsections. The main part is constructing a weakly succinct PKFE scheme for boolean functions in Sect. 5.1. In Sect. 5.2, we present a transformation from weakly succinct PKFE schemes for boolean functions into ones for non-boolean functions. Lastly, we explain how the pieces come together to give IO from SKFE in Sect. 5.3.
5.1 Weakly Succinct PKFE for Boolean Functions
We now construct a single-key weakly succinct PKFE scheme for the class of boolean functions. The construction is based on succinct IBE, decomposable garbling, and SXIO.
Theorem 8
Let \(\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a family of circuits with a single output bit and let \(n(\lambda ),s(\lambda ),d(\lambda )\) be bounds on their input length, size, and depth (respectively). For any constants \(\beta ,\gamma \) such that \(3\beta< \gamma < 1\), assuming a \(\delta \)-secure, \(\beta \)-compressing SXIO for \(\mathsf {P}/\mathsf {poly}\), there exists a constant \(\alpha \), such that given any \(\delta \)-secure, \(\alpha \)-compressing IBE, and \(\delta \)-secure one-way functions, there exists a \(2^d s \delta \)-secure succinct PKFE for \(\mathcal {C}\) with compression factor \(\gamma \).
Depth Preserving Universal Circuits. To prove the above theorem, we recall the existence of depth preserving universal circuits [23]. Concretely, any family of circuits \(\mathcal {C}\) as considered in Theorem 8 has a uniform family of universal circuits \(\left\{ U_\lambda \right\} _{\lambda \in \mathbb {N}}\) with fan-out \(\lambda \),Footnote 4 depth O(d), and size \(s^3\cdot \mathrm {polylog}(s)\), for some fixed polynomial \(\mathrm {poly}\). Each such circuit takes as input a description \((f_1,\dots ,f_s)\) of a function in \(\mathcal {C}\) and an input \((x_1,\dots ,x_n)\) and outputs f(x). Furthermore, uniformity here means that each circuit has a decomposition circuit of size \(\mathrm {polylog}(s)\).
Ingredients and Notation Used in the Construction
-
We denote by \(U^{(x)}: \{0,1\}^{s} \rightarrow \{0,1\}\) the universal circuit, with \(x \in \{0,1\}^n\) being a hardwired bitstring, such that on input \((f_1,\ldots ,f_s)\), the circuit \(U^{(x)}\) outputs f(x). This circuit has a decomposition circuit of size \(\mathrm {poly}(n,\log (s))\), which we denote by \(U^{(x)}_{\mathsf {de}}\). We also denote by \(L\) the number of gates in the circuit \(U^{(x)}\).
-
Let \(\mathsf {sxi}\mathcal {O}\) be a \(\delta \)-secure, \(\beta \)-compressing SXIO scheme.
-
Let \(\mathsf {IBE}=(\mathsf {IBE}.\mathsf {Setup},\mathsf {IBE}.\mathsf {KeyGen},\mathsf {IBE}.\mathsf {Enc},\mathsf {IBE}.\mathsf {Dec})\) be \(\delta \)-secure, succinct, IBE scheme with \(\alpha \)-compression for the identity space being \(\mathcal {ID}= [s]\times \{0,1\}\).
-
Let \((\mathsf {Gar.CirEn},\mathsf {Gar.InpEn},\mathsf {Gar.De})\) be a decomposable garbling scheme with \((\sigma ,\tau ,\delta )\)-decomposable indistinguishability where \(\tau = s2^{O(d)}\) and \(\sigma = \mathrm {poly}(\lambda ,n,d,\log (s))\). Such schemes are implied by \(\delta \)-secure one-way functions (Theorem 7).
-
Let \(\mathcal {PPRF}= (\mathsf {PRF.Gen}, \mathsf {PRF.Ev},\mathsf {PRF.Punc})\) be a \(\delta \)-secure puncturable PRF. These are implied by \(\delta \)-secure one-way functions [18, 19, 31, 39].
Construction. The scheme consists of the following algorithms.
\(\mathsf {PKFE}.\mathsf {Setup}(1^\lambda )\):
-
Run \((\mathsf {MSK}_{\mathsf {ibe}},\mathsf {MPK}_{\mathsf {ibe}}) \leftarrow \mathsf {IBE}.\mathsf {Setup}(1^\lambda )\).
-
Set \(\mathsf {MSK}= \mathsf {MSK}_{\mathsf {ibe}}\), \(\mathsf {MPK}= \mathsf {MPK}_{\mathsf {ibe}}\).
\(\mathsf {PKFE}.\mathsf {Key}(\mathsf {MSK},f)\):
-
Compute \(\mathsf {SK}_{i,f_i} \leftarrow \mathsf {IBE}.\mathsf {KeyGen}(\mathsf {MSK}_{\mathsf {ibe}},(i,f_i))\) for \(i \in [s]\), where \(f = (f_1,\ldots ,f_s)\).
-
Return \(\mathsf {SK}_{f} =\{\mathsf {SK}_{i,f_i}\}_{i \in [s]}\).
\(\mathsf {PKFE}.\mathsf {Enc}(\mathsf {MPK},x)\):
-
Compute \(U^{(x)}_{\mathsf {de}}\) and pick a garbling key \(K\leftarrow \{0,1\}^\lambda \) and a punctured key \(S\leftarrow \mathsf {PRF.Gen}(1^\lambda )\);
-
Generate an obfuscation
 of the input garbling circuit defined in Fig. 1;
of the input garbling circuit defined in Fig. 1; -
Generate an obfuscation
 of the gate garbling circuit defined in Fig. 2;
of the gate garbling circuit defined in Fig. 2; -
Return
 .
.
\(\mathsf {PKFE}.\mathsf {Dec}(\mathsf {SK}_f,\mathsf {CT}_x)\):
-
For \(i \in [s]\), run
 to obtain an IBE ciphertext, and decrypt the output using \(\mathsf {SK}_{i,f_i}\) to obtain \(\hat{f}_i\).
to obtain an IBE ciphertext, and decrypt the output using \(\mathsf {SK}_{i,f_i}\) to obtain \(\hat{f}_i\). -
For all \(g \in [L]\), run
 , in order to obtain the garbled gate \(\widehat{G}_g\).
, in order to obtain the garbled gate \(\widehat{G}_g\). -
Return \(y\leftarrow \mathsf {Gar.De}(\widehat{C},\hat{f})\), with \(\widehat{C}= \left\{ \widehat{G}_g\right\} _{g\in [L]}\) and \(\hat{f}= \left\{ \hat{f}_i\right\} _{i\in [s]}\).
We omit the proof of correctness, succinctness, and security due to the limited space. See the full version for the complete proof of Theorem 8 [13].
5.2 Weakly Succinct PKFE for Non-Boolean Functions
In this section, we give a transformation from weakly succinct PKFE schemes for boolean functions into ones for non-boolean functions.
Theorem 9
Let \(\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a family of circuits (with multiple output bits) and let \(n(\lambda ),s(\lambda ),d(\lambda )\) be bounds on their input length, size, and depth (respectively). For any constants \(\beta< \gamma < 1\), assuming a \(\beta \)-compressing SXIO for \(\mathsf {P}/\mathsf {poly}\), there exists a constant \(\alpha \), such that given any \(\alpha \)-compressing weakly succinct PKFE for boolean functions of size \(s\cdot \mathrm {polylog}(s)\) and depth O(d), and one-way functions, there exists a succinct PKFE for \(\mathcal {C}\) with compression factor \(\gamma \). If all primitives are \(\delta \)-secure so is the resulting scheme.
The transformation is essentially the same transformation presented in [43, Sect. 4], with the following differences:
-
They use XIO rather than SXIO, which results in a PKFE scheme where only the size of ciphertexts is compressed, whereas the time to encrypt may be large. They then make an extra step, based on LWE, to make encryption efficient. Using SXIO directly as we do, allows avoiding this step.
-
They start from weakly succinct PKFE for boolean functions where the size of ciphertexts is completely independent of the size s of the function class considered. Due to this, they can start from XIO with any compression factor \(\beta <1\). In our notion of weakly succinct, there is dependence on \(s^\alpha \), for some \(\alpha <1\), and we need to make sure that \(\beta \) and \(\alpha \) are appropriately chosen to account for this.
-
As stated, their notion of weak succinctness for PKFE does not explicitly scale with the depth of the function class considered. Eventually, they apply their transformation to function classes in \(\mathbf{NC }^1\), assuming puncturable PRFs in \(\mathbf{NC }^1\) (which exist under LWE). Our succinctness notion allows polynomial dependence on the depth, which should be roughly preserved through the transformation.
The transformation and proof of security are almost identical to the ones in [43] and are omitted due to the limited space. See the full version [13].
5.3 Putting It All Together: From SKFE and PKE to IO
We obtain the following statements from the results proved in this section.
Theorem 10
Let \(\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\} _{\lambda \in \mathbb {N}}\) be a family of circuits (with multiple output bits) and let \(n(\lambda ),s(\lambda ),d(\lambda )\) be bounds on their input length, size, and depth (respectively). Then, for any constant \(\gamma <1\), there exists a constant \(\beta \), such that given any \(\delta \)-secure, \(\beta \)-compressing SXIO for \(\mathsf {P}/\mathsf {poly}\), and \(\delta \)-secure PKE, there exists \(2^d s \delta \)-secure, \(\gamma \)-compressing, weakly succinct PKFE for \(\mathcal {C}\).
Combining the above theorem with the result from Sect. 3, we obtain the following corollary.
Corollary 3
If there exist (1-input) SKFE for \(\mathsf {P}/\mathsf {poly}\) and PKE, both subexponentially-secure, then there exists IO for \(\mathsf {P}/\mathsf {poly}\).
Remark 3 (The security loss)
In order, the known reductions [3, 14] of IO to weakly-succinct PKFE incur a sub-exponential loss. Accordingly, reducing IO to SKFE based on our results incurs a similar loss. However, when restricting attention, to the transformation from SKFE to (weakly-succinct) PKFE, then the loss is \(\mathrm {poly}(2^d,\lambda )\), for circuits of depth d. In particular, for \(\mathbf{NC }^1\), our transformation incurs only polynomial security loss. Such a PKFE for \(\mathbf{NC }^1\), can then be bootstrapped to all polynomial-size circuits using the transformation of [2], and assuming also weak PRFs in \(\mathbf{NC }^1\).
In concurrent work [30, 41], it is shown that weakly-succinct single-key PKFE can then be polynomially reduced to PKFE. In summary, SKFE and PRFs in \(\mathbf{NC }^1\) can be polynomially reduced to PKFE for all polynomial-size circuits.
6 Polynomially-Secure PKE from Secret-Key FE
In this section, we construct PKE from SKFE. Our starting point is Corollary 2 that directly follows from Theorems 3 and 6.
We now show how to construct a PKE scheme from such SXIO.
The Construction. Let \(\left\{ {\mathsf {PRG}}:\{0,1\}^n\rightarrow \{0,1\}^{2n}\right\} _{n\in \mathbb {N}}\) be a length-doubling pseudorandom generator that is \(2^{-n/\log \log n}\)-secure. Let \(\mathsf {sxi}\mathcal {O}\) be a SXIO with compression factor \(\gamma (\lambda )=O(1/\log \log \lambda )\) (and \(\mathrm {poly}(\lambda )\) security) for circuits of size at most \(2^{O((\log \lambda )^\epsilon )}\).
The scheme PKE = \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Dec})\) is defined as follows:
\(\mathsf {KeyGen}(1^\lambda )\):
-
Sample a PRG seed \(s \leftarrow \{0,1\}^{\log \lambda /\gamma (\lambda )}\).
-
Output \(\mathsf {PK}={\mathsf {PRG}}(s)\) and \(\mathsf {SK}=s\).
\(\mathsf {Enc}(\mathsf {PK},x)\):
-
Construct the circuit \(\mathsf {WE}[x,\mathsf {PK}]\) that takes \(s' \in \{0,1\}^{\log \lambda /\gamma (\lambda )}\) as input and outputs x if \(\mathsf {PK}= {\mathsf {PRG}}(s')\) holds and \(\bot \) otherwise.
-
Output \(\mathsf {CT}= \mathsf {sxi}\mathcal {O}(\mathsf {WE}[x,\mathsf {PK}])\)
\(\mathsf {Dec}(\mathsf {SK},\mathsf {CT})\):
-
Compute \(x'= \mathsf {CT}(\mathsf {SK})\).
Proposition 3
PKE is a (polynomially-secure) public-key encryption scheme.
We omit the proof due the limited space. See the full version [13].
Notes
- 1.
The above is a slightly oversimplified account of [43]. They also rely on LWE to deduce the existence of puncturable PRFs in \(\mathbf{NC }^1\) and show their transformation starting from weakly-succinct PKFE for functions in \(\mathbf{NC }^1\). We avoid the reliance on puncturable PRFs in \(\mathbf{NC }^1\) by constructing weakly-succinct PKFE for functions with no depth restriction, at the expense of allowing the complexity of encryption to scale polynomially in the depth. This is still sufficient for [14, Sect. 3.2].
- 2.
Extending this to functions with multibit output is then done, based on SXIO, using a transformation of [43]. Concretely, given an m-bit output function f(x) we consider a new single bit function \(g_f(x,i)\) that returns the ith bit of f(x). The function key is then derived for the boolean function \(g_f\). The new encryption algorithm, for message x, produces an SXIO obfuscation of a circuit that given \(i\in [m]\) uses the old encryption scheme to encrypt (m, i), deriving randomness using a puncturable PRF. The security of the construction is proven as in [43] based on a probabilistic IO argument [22]. (Mild) efficiency of the encryption then follows from the mild efficiency of the SXIO and PKFE with related (constant) compression factors.
- 3.
Their aim was proving adaptive security, which is completely orthogonal to our aim. However, for entirely different reasons, the above goal is useful in both their work and ours.
- 4.
The restriction regarding fan-out is not stated explicitly in [23], but can always be achieved by blowing up the size and depth by a factor of at most O(1).
References
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_28
Ananth, P., Brakerski, Z., Segev, G., Vaikuntanathan, V.: From selective to adaptive security in functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 657–677. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_32
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Indistinguishability obfuscation from functional encryption forsimple functions. Cryptology ePrint Archive, Report 2015/730 (2015). http://eprint.iacr.org/2015/730
Ananth, P., Sahai, A.: Functional encryption for turing machines. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 125–153. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_6
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. In: Guruswami, V. (ed.) 56th FOCS, pp. 191–209. IEEE Computer Society Press, October 2015
Badrinarayanan, S., Gupta, D., Jain, A., Sahai, A.: Multi-input functional encryption for unbounded arity functions. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 27–51. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_2
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (Im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6 (2012)
Bellare, M., Hoang, V.T., Rogaway, P.: Foundations of garbled circuits. In: Yu, T., Danezis, G., Gligor, V.D. (eds.) ACM CCS 2012, pp. 784–796. ACM Press, October 2012
Bellare, M., O’Neill, A.: Semantically-secure functional encryption: possibility results, impossibility results and the quest for a general definition. In: Abdalla, M., Nita-Rotaru, C., Dahab, R. (eds.) CANS 2013. LNCS, vol. 8257, pp. 218–234. Springer, Heidelberg (2013). doi:10.1007/978-3-319-02937-5_12
Bitansky, N., Garg, S., Lin, H., Pass, R., Telang, S.: Succinct randomized encodings and their applications. In: Servedio, R.A., Rubinfeld, R. (eds.) 47th ACM STOC, pp. 439–448. ACM Press, June 2015
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. IACR Cryptology ePrint Archive 2016, 558 (2016)
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: Guruswami, V. (ed.) 56th FOCS, pp. 171–190. IEEE Computer Society Press, October 2015
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_30
Boneh, D., Lewi, K., Raykova, M., Sahai, A., Zhandry, M., Zimmerman, J.: Semantically secure order-revealing encryption: multi-input functional encryption without obfuscation. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 563–594. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_19
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_15
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_29
Brakerski, Z., Komargodski, I., Segev, G.: Multi-input functional encryption in the private-key setting: stronger security from weaker assumptions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 852–880. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_30
Brakerski, Z., Segev, G.: Function-private functional encryption in the private-key setting. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 306–324. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_12
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_19
Cook, S.A., Hoover, H.J.: A depth-universal circuit. SIAM J. Comput. 14(4), 833–839 (1985)
Caro, A., Iovino, V., Jain, A., O’Neill, A., Paneth, O., Persiano, G.: On the achievability of simulation-based security for functional encryption. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 519–535. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_29
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In 54th FOCS, pp. 40–49. IEEE Computer Society Press, October 2013
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_18
Garg, S., Gentry, C., Sahai, A., Waters, B.: Witness encryption and its applications. In Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 467–476. ACM Press, June 2013
Garg, S., Pandey, O., Srinivasan, A.: Revisiting the cryptographic hardness of finding a nash equilibrium. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 579–604. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_20
Garg, S., Pandey, O., Srinivasan, A., Zhandry, M.: Breaking the sub-exponential barrier in obfustopia. Cryptology ePrint Archive, Report 2016/102 (2016). http://eprint.iacr.org/2016/102
Garg, S., Srinivasan, A.: Unifying security notions of functional encryption. IACR Cryptology ePrint Archive 2016:524 (2016)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions (extended abstract). In: 25th FOCS, pp. 464–479. IEEE Computer Society Press, October 1984
Goldwasser, S., Gordon, S.D., Goyal, V., Jain, A., Katz, J., Liu, F.-H., Sahai, A., Shi, E., Zhou, H.-S.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_32
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press, June 2013
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_25
Goyal, V., Jain, A., Koppula, V., Sahai, A.: Functional encryption for randomized functionalities. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 325–351. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_13
Hemenway, B., Jafargholi, Z., Ostrovsky, R., Scafuro, A., Wichs, D.: Adaptively secure garbled circuits from one-way functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 149–178. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53015-3_6
Impagliazzo, R.: A personal view of average-case complexity. In: Proceedings of the Tenth Annual Structure in Complexity Theory Conference, Minneapolis, Minnesota, USA, June 19–22, 1995, pp. 134–147. IEEE Computer Society (1995)
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 13, pp. 669–684. ACM Press, November 2013
Komargodski, I., Segev, G., Yogev, E.: Functional encryption for randomized functionalities in the private-key setting from minimal assumptions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 352–377. Springer, Heidelberg (2015)
Li, B., Micciancio, D.: Compactness vs collusion resistance in functional encryption. IACR Cryptology ePrint Archive 2016:561 (2016)
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_2
Lin, H., Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation with non-trivial efficiency. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9615, pp. 447–462. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49387-8_17
Lin, H., Pass, R., Seth, K., Telang, S.: Output-compressing randomized encodings and applications. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 96–124. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_5
O’Neill, A.: Definitional issues in functional encryption. Cryptology ePrint Archive, Report 2010/556 (2010). http://eprint.iacr.org/2010/556
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N. Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 10, pp. 463–472. ACM Press, October 2010
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_5
Waters, B.: A punctured programming approach to adaptively secure functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 678–697. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_33
Yao, A.C.-C.: Protocols for secure computations (extended abstract). In: 23rd FOCS, pp. 160–164. IEEE Computer Society Press, November 1982
Acknowledgements
We thank Vinod Vaikuntanathan and Hoeteck Wee for valuable discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D. (2016). From Cryptomania to Obfustopia Through Secret-Key Functional Encryption. In: Hirt, M., Smith, A. (eds) Theory of Cryptography. TCC 2016. Lecture Notes in Computer Science(), vol 9986. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53644-5_15
Download citation
DOI: https://doi.org/10.1007/978-3-662-53644-5_15
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53643-8
Online ISBN: 978-3-662-53644-5
eBook Packages: Computer ScienceComputer Science (R0)


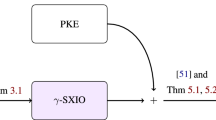
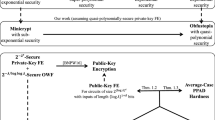

 as the obfuscation.
as the obfuscation. consists of
consists of  for a (plain) public-key encryption scheme.
for a (plain) public-key encryption scheme. takes as input the master secret key
takes as input the master secret key  takes as input the secret key
takes as input the secret key  .
. takes as input the master secret
takes as input the master secret  takes as input the master public key
takes as input the master public key  and a message
and a message  , and outputs a ciphertext c.
, and outputs a ciphertext c. takes as input the secret key
takes as input the secret key  .
. takes as input the master secret
takes as input the master secret  , an identity
, an identity  , and outputs a ciphertext c.
, and outputs a ciphertext c. , each being of size at most
, each being of size at most  with the following syntax:
with the following syntax: of the input garbling circuit defined in Fig.
of the input garbling circuit defined in Fig.  of the gate garbling circuit defined in Fig.
of the gate garbling circuit defined in Fig.  .
. to obtain an IBE ciphertext, and decrypt the output using
to obtain an IBE ciphertext, and decrypt the output using  , in order to obtain the garbled gate
, in order to obtain the garbled gate 

