Automatic selection for general surrogate models

Abstract

In design engineering problems, the use of surrogate models (also called metamodels) instead of expensive simulations have become very popular. Surrogate models include individual models (regression, kriging, neural network...) or a combination of individual models often called aggregation or ensemble. Since different surrogate types with various tunings are available, users often struggle to choose the most suitable one for a given problem. Thus, there is a great interest in automatic selection algorithms. In this paper, we introduce a universal criterion that can be applied to any type of surrogate models. It is composed of three complementary components measuring the quality of general surrogate models: internal accuracy (on design points), predictive performance (cross-validation) and a roughness penalty. Based on this criterion, we propose two automatic selection algorithms. The first selection scheme finds the optimal ensemble of a set of given surrogate models. The second selection scheme further explores the space of surrogate models by using an evolutionary algorithm where each individual is a surrogate model. Finally, the performances of the algorithms are illustrated on 15 classical test functions and compared to different individual surrogate models. The results show the efficiency of our approach. In particular, we observe that the three components of the proposed criterion act all together to improve accuracy and limit over-fitting.

Appendices

Appendix A: Comparison between the proposed PPS parameters and the optimal according to the sum of RMSE

Fig. 24

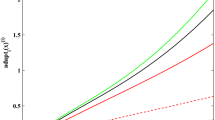
The scaled RMSE for each PPS-optimal ensemble, For each function: Left: using (α,β,γ) = (1,β^⋆,γ^⋆) in light green. Right: using (α,β,γ) = (1,0.5,0.25) in light blue. The function number is as in Table 1

Appendix B: Test functions

The equations and the input parameter space of the functions of Table 1 are defined below:

• 1/ Wing weight function:

  Parameters: S_w ∈ [150, 200], W_fw ∈ [220, 300], A ∈ [6, 10],

  γ ∈ [− 10, 10], q ∈ [16, 45], λ ∈ [0.5, 1], t_c ∈ [0.08, 0.18],

  N_z ∈ [2.5, 6], W_dg ∈ [1700, 2500], W_p ∈ [0.025, 0.08]

  $$\begin{array}{@{}rcl@{}} \text{For } \mathbf{x} &=& (S_{w},W_{fw} A, \gamma, q, \lambda, t_{c}, N_{z}, W_{dg},W_{p} )\\ f_{1}(\mathbf{x}) &=& 0.036 S_{w}^{0.758} W_{fw}^{0.758} \left( \frac{A}{\cos^{2}(\gamma)} \right)^{0.6} q^{0.006} \lambda^{0.04}\\ && \left( \frac{100 t_{c}}{\cos(\gamma)}\right)^{-0.3} (N_{z} W_{dg})^{0.49}+ S_{w} W_{p} \end{array} $$

  (17)

• 2/ Borehole function:

  Parameters: r_w ∈ [0.05, 0.15], r ∈ [100, 50000],

  T_u ∈ [63070, 115600], H_u ∈ [990, 1110], T_l ∈ [63.1, 116],

  H_l ∈ [700, 820], L ∈ [1120, 1680], K_w ∈ [9855, 12045]

  $$\begin{array}{@{}rcl@{}} \text{For } \mathbf{x} &=& (r_{w},r,T_{u},H_{u},T_{l},H_{l},L,K_{w})\\ f_{2}(\mathbf{x}) &=& \frac{2\pi T_{u}(H_{u} - H_{l})}{\ln\left( \frac{r}{r_{w}}\right) \left( 1 + \frac{2L T_{u}}{ln\left( \frac{r}{r_{w}}\right) {r^{2}_{w}} K_{w}} + \frac{T_{u}}{T_{l}}\right)} \end{array} $$

  (18)

• 3/ Dette and Pepelyshev 8-Dim

  Parameters: for all i = 1,…, 8 , x_i ∈ [0, 1]

  $$\begin{array}{@{}rcl@{}} f_{3}(\mathbf{x}) &=& 4(x_{1} - 2 + 8x_{2} - 8{x_{2}^{2}})^{2} + (3-4x_{2})^{2}\\ && + 16 \sqrt{x_{3} + 1} (2x_{3} -1)^{2} + \sum\limits_{i = 4}^{8} i \ln\left( 1 + \sum\limits_{j = 3}^{i} x_{j}\right)\\ \end{array} $$

  (19)

• 4/ Piston simulation function:

  Parameters: M ∈ [30, 60], S ∈ [0.005, 0.020],

  V₀ ∈ [0.002, 0.010], k ∈ [1, 5] × 10³, P₀ ∈ [9, 11] × 10⁴,

  T_a ∈ [290, 296], T₀ ∈ [340, 360]

  $$\begin{array}{@{}rcl@{}} f_{4}(\mathbf{x}) &=& 2 \pi \sqrt{\frac{M}{k+S^{2} \frac{P_{0} V_{0}}{T_{0}} \frac{T_{a}}{V^{2}}}}\\ \text{where } V &=& \frac{S}{2k} \left( \sqrt{A^{2} + 4 k \frac{P_{0} V_{0}}{T_{0}} T_{a}} - A \right)\\ \text{and } A &=& P_{0} S + 19.62 M - \frac{k V_{0}}{S} \end{array} $$

  (20)

• 5/ OTL circuit function:

  Parameters: R_b1 ∈ [50, 150], R_b2 ∈ [25, 70],

  R_f ∈ [0.5, 3], R_c1 ∈ [1.2, 2.5], R_c1 ∈ [0.25, 1.2],

  β ∈ [50, 300]

  $$\begin{array}{@{}rcl@{}} f_{5}(\mathbf{R},\beta) &=& \frac{\left( \frac{12 R_{b2}}{R_{b1} + R_{b2}} + 0.74\right) \beta (R_{c2} + 9)}{\beta(R_{c2} + 9) + R_{f}}\\ && + \frac{11.35 R_{f}}{\beta(R_{c2} + 9) + R_{f}}\\ && + \frac{0.75 R_{f} \beta (R_{c2} + 9)}{ (\beta(R_{c2} + 9) + R_{f}) R_{c1}} \end{array} $$

  (21)

• 6/ Gramacy and Lee (2009) function:

  Parameters: for all i = 1,…, 6 , x_i ∈ [0, 1]

  $$ f_{6}(\mathbf{x}) = \exp[\sin((0.9(x_{1} + 0.48))^{10})] + x_{2}x_{3} +x_{4} $$

  (22)

• 7/ Friedman function:

  Parameters: for all i = 1,…, 5 , x_i ∈ [0, 1]

  $$ f_{7}(\mathbf{x}) = 10 \sin(\pi x_{1} x_{2}) + 20(x_{3} - 0.5)^{2} + 10 x_{4} + 5x_{5} $$

  (23)

• 8/ Dette & Pepelyshev exponential function:

  Parameters: for all i = 1,…, 3 , x_i ∈ [0, 1]

  $$ f_{8}(\mathbf{x}) = 100(e^{-2/x^{1.75}_{1}} + e^{-2/x^{1.5}_{2}} + e^{-2/x^{1.25}_{3}}) $$

  (24)

• 9/ Dette & Pepelyshev curved function:

  Parameters: for all i = 1,…, 3 , x_i ∈ [0, 1]

  $$\begin{array}{@{}rcl@{}} f_{9}(\mathbf{x}) &=& 4(x_{1} -2 + 8x_{2} - 8{x^{2}_{2}})^{2} + (3-4x_{2})^{2}\\ && + 16 \sqrt{x_{3} + 1} (2 x_{3} -1)^{2} \end{array} $$

  (25)

• 10/ Lim non-polynomial function:

  Parameters: x₁,x₂ ∈ [0, 1]

  $$ f_{10}(\mathbf{x}) = \frac{1}{6}[(30 + 5x_{1} \sin(5x_{1})) (4 + \exp(-5x_{2}))-100] $$

  (26)

• 11/ Currin exponential function:

  Parameters: x₁,x₂ ∈ [0, 1]

  $$\begin{array}{@{}rcl@{}} f_{11}(\mathbf{x}) &=& \left[1 - \exp\left( - \frac{1}{2x_{2}}\right)\right]\\ && \times \frac{2300{x_{1}^{3}} + 1900{x_{1}^{2}} + 2092x_{1}+ 60}{100{x_{1}^{3}} + 500{x_{1}^{2}} + 4x_{1} + 20} \end{array} $$

  (27)

• 12/ Franke function:

  Parameters: x₁,x₂ ∈ [0, 1]

  $$\begin{array}{@{}rcl@{}} f_{12}(\mathbf{x}) &=& 0.75 \exp\left( - \frac{(9x_{1} - 2)^{2} +(9x_{2} - 2)^{2}}{4}\right)\\ && + 0.75 \exp\left( - \frac{(9x_{1} + 2)^{2}}{49} - \frac{9x_{2} + 1}{10}\right)\\ && + 0.5 \exp\left( - \frac{(9x_{1} - 7)^{2}}{4} - \frac{(9x_{2} - 3)^{2}}{4}\right)\\ && + 0.2 \exp(- (9x_{1} - 4)^{2} - (9x_{2} - 7)^{2} ) \end{array} $$

  (28)

• 13/ Gramacy and Lee (2008) function:

  Parameters: x₁,x₂ ∈ [− 2, 6]

  $$ f_{13}(\mathbf{x}) = x_{1} \exp(- {x^{2}_{1}} - {x^{2}_{2}}) $$

  (29)

• 14/ Sasena function:

  Parameters: x₁,x₂ ∈ [0.0, 5]

  $$\begin{array}{@{}rcl@{}} f_{14}(\mathbf{x}) &=& 2 + 0.01(x_{2}-{x_{1}^{2}})^{2} + (1-x_{1})^{2}\\ && + 2(2-x_{2})^{2} + 7 \sin(0.5x_{1})\sin(0.7x_{1}x_{2})\\ \end{array} $$

  (30)

• 15/ Gramacy and Lee (2012) function:

  Parameters: x ∈ [0.5, 2.5]

  $$ f_{15}(x) = \frac{\sin(10 \pi x)}{2 x} + (x-1)^{4} $$

  (31)