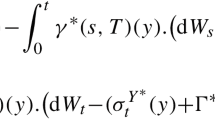Abstract
We develop the HJM framework for forward rates driven by affine processes on the state space of symmetric positive semidefinite matrices. In this setting we find an explicit representation for the long-term yield in terms of the model parameters. This generalises the results of El Karoui et al. (Rev Deriv Res 1(4):351–369, 1997) and Biagini and Härtel (Int J Theor Appl Financ 17(3):1–24, 2012), where the long-term yield is investigated under no-arbitrage assumptions in a HJM setting using Brownian motions and Lévy processes respectively.
Similar content being viewed by others
Notes
For \(\alpha \) and \(\sigma \) we write the shortened version \(\alpha \!\left( s,T\right) := \alpha \!\left( \omega ,s,T\right) \) and \(\sigma \!\left( s,T\right) := \sigma \!\left( \omega ,s,T\right) \).
References
Ahdida, A., Alfonsi, A.: Exact and high order discretization schemes for Wishart processes and their affine extensions. Ann. Appl. Probab. 23(3), 1025–1073 (2013)
Ang, A., Piazzesi, M.: A no-arbitrage vector autoregression of term structure dynamics with macroeconomic and latent variables. J. Monet. Econ. 50(4), 745–787 (2003)
Applebaum, D.: Lévy Processes and Stochastic Calculus, 1st edn. Cambridge University Press, Cambridge (2004)
Bauer, H.: Wahrscheinlichkeitstheorie, 5th edn. Walter de Gruyter, Berlin (2002)
Benabid, A., Bensusan, H., El Karoui, N.: Wishart stochastic volatility: asymptotic smile and numerical framework. HAL Working Paper (2010). HAL: http://hal.archives-ouvertes.fr/docs/00/45/83/71/PDF/ArticleWishart19Feb2010
Biagini, F., Härtel, M.: Behavior of long-term yields in a Lévy term structure. Int. J. Theor. Appl. Financ. 17(3), 1–24 (2014)
Björk, T., Kabanov, Y., Runggaldier, W.: Bond market structure in the presence of marked point processes. Math. Financ. 7(2), 211–223 (1997)
Brigo, D., Mercurio, F.: Interest Rate Models: Theory and Practice, 2nd edn. Springer Finance, Heidelberg (2006)
Bru, M.F.: Wishart processes. J. Theor. Probab. 4(4), 725–751 (1991)
Carmona, R., Tehranchi, M.: Interest Rate Models: An Infinite Dimensional Stochastic Analysis Perspective, 1st edn. Springer Finance, Heidelberg (2006)
Chiarella, C., Kwon, O.K.: Finite dimensional affine realisations of HJM models in terms of forward rates and yields. Rev. Deriv. Res. 6, 129–155 (2003)
Cuchiero, C.: Affine and polynomial processes. PhD Thesis, ETH Zurich (2011)
Cuchiero, C., Filipović, D., Mayerhofer, E., Teichmann, J.: Affine processes on positive semidefinite matrices. Ann. Appl. Probab. 21(2), 397–463 (2011)
Cuchiero, C., Keller-Ressel, M., Mayerhofer, E., Teichmann, J.: Affine processes on symmetric cones. J. Theor. Probab. (2014). doi:10.1007/s10959-014-0580-x
Da Fonseca, J., Grasselli, M.: Riding on the smiles. Quan. Financ. 11(11), 1609–1632 (2011)
Da Fonseca, J., Grasselli, M., Tebaldi, C.: A multifactor volatility Heston model. Quant. Financ. 8(6), 591–604 (2008)
Da Fonseca, J., Gnoatto, A., Grasselli, M.: A flexible matrix Libor model with smiles. J. Econ. Dyn. Control 37, 774–793 (2013)
Da Fonseca, J., Grasselli, M., Ielpo, F.: Estimating the Wishart affine stochastic correlation model using the empirical characteristic function. Stud. Nonlinear Dyn. Econom. 18(3), 253–289 (2013)
Diebold, F., Rudebusch, G.D., Aruoba, S.B.: The macroeconomy and the yield curve: a dynamic latent factor approach. J. Econom. 131(1–2), 309–338 (2006)
Duffie, D., Kan, R.: A yield-factor model of interest rates. Math. Financ. 6(4), 379–406 (1996)
Duffie, D., Filipović, D., Schachermayer, W.: Affine processes and applications in finance. Ann. Appl. Probab. 13(3), 984–1053 (2003)
Dybvig, P.H., Ingersoll, J.E., Ross, S.A.: Long forward and zero-coupon rates can never fall. J. Bus. 69(1), 1–25 (1996)
El Karoui, N., Frachot, A., Geman, H.: A note on the behavior of long zero coupon rates in a no arbitrage framework. Rev. Deriv. Res. 1(4), 351–369 (1997)
European Central Bank: Long-term interest rates for EU member states (2013). ECB: http://www.ecb.int/stats/money/long/html/index.en.html. Accessed 21 Aug 2015
Filipović, D.: Term Structure Models–A Graduate Course, 1st edn. Springer, Berlin (2009)
Georgii, H.-O.: Stochastik, 1st edn. Walter de Gruyter, Berlin (2004)
Gnoatto, A.: The Wishart short-rate model. Int. J. Theor. Appl. Financ. 15(8), 1250056 (2012)
Gnoatto, A., Grasselli, M.: The explicit Laplace transform for the Wishart process. J. Appl. Probab. 51(3), 640–656 (2014)
Goldammer, V., Schmock, U.: Generalization of the Dybvig-Ingersoll-Ross theorem and asymptotic minimality. Math. Financ. 22(1), 185–213 (2012)
Gourieroux, C.: Continuous time Wishart process for stochastic risk. Econom. Rev. 25, 177–217 (2006)
Gourieroux, C., Sufana, R.: Derivative pricing with Wishart multivariate stochastic volatility. J. Bus. Econ. Stat. 28(3), 438–451 (2010)
Grasselli, M., Tebaldi, C.: Solvable affine term structure models. Math. Financ. 18(1), 135–153 (2008)
Gürkaynak, R., Sack, B., Swanson, E.: The sensitivity of long-term interest rates to economic news: evidence and implications for macroeconomic news. Am. Econ. Rev. 95(1), 425–436 (2005)
Hansen, L.P., Scheinkman, J.A.: Pricing growth-rate risk. Financ. Stoch. 16(1), 1–15 (2012)
Härtel, M.: The asymptotic behavior of the term structure of interest rates. PhD Thesis, LMU Munich (2016)
Heath, D., Jarrow, R., Morton, A.: Bond pricing and the term structure of interest rates: a new methodology. Econometrica 60(1), 77–105 (1992)
Hördahl, P., Tristani, O., Vestin, D.: A joint econometric model of macroeconomic and term-structure dynamics. J. Econom. 131(1–2), 405–444 (2006)
Hubalek, F., Klein, I., Teichmann, J.: A general proof of the Dybvig-Ingersoll-Ross-theorem. Math. Financ. 12(4), 447–451 (2002)
Jacod, J., Shiryaev, A.N.: Limit Theorems for Stochastic Processes, 1st edn. Springer, Berlin (2003)
Kardaras, C., Platen, E.: On the Dybvig-Ingersoll-Ross theorem. Math. Financ. 22(4), 729–740 (2012)
Kim, D.H., Wright, J.H.: An arbitrage-free three factor term structure model and the recent behavior of long-term yields and distant-horizon forward rates. Fed. Reserv. Board Financ. Econ. Discuss. Ser. 33, 2005 (2005)
Klenke, A.: Wahrscheinlichkeitstheorie, 1st edn. Springer, Berlin (2006)
Mankiw, N.G., Summers, L.H., Weiss, L.: Do long-term interest rates overreact to short-term interest rates? Brook. Pap. Econ. Activity 1984(1), 223–247 (1984)
Mayerhofer, E.: Affine processes on positive semidefinite \(d \times d\) matrices have jumps of finite variation in dimension \(d > 1\). Stoch. Process. Appl. 122(10), 3445–3459 (2012)
Mayerhofer, E., Pfaffel, O., Stelzer, R.: On strong solutions for positive definite jump-diffusions. Stoch. Process. Appl. 121(9), 2072–2086 (2011)
McCulloch, J.H.: Long forward and zero-coupon rates indeed can never fall. Working Paper # 00(12), Ohio State University (2000)
Muhle-Karbe, J., Pfaffel, O., Stelzer, R.: Option pricing in multivariate stochastic volatility models of OU type. SIAM J. Financ. Math. 3(1), 66–94 (2012)
Pfaffel, O.: Wishart Processes. Student Research project supervised by Claudia Klüppelberg and Robert Stelzer, TU Munich (2008)
Protter, P.: Stochastic Integration and Differential Equations, 2nd edn. Springer, Berlin (2005)
Richter, A.: Explicit solutions to quadratic BSDEs and applications to utility maximization in multivariate affine stochastic volatility models. Stoch. Process. Appl. 124(11), 3578–3611 (2014)
Schulze, K.: Asymptotic maturity behavior of the term structure. Bonn Econ Discussion Papers, University of Bonn (2008)
Shiller, R.J.: The volatility of long-term interest rates and expectations models of the term structure. J. Polit. Econ. 87(6), 1190–1219 (1979)
Yao, Y.: Term structure modeling and asymptotic long rate. Insurance 25, 327–336 (1999)
Yao, Y.: Term structure models: a perspective from the long rate. N. Am. Actuar. J. 3(3), 122–138 (2000)
Acknowledgments
The research leading to these results has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement No. [228087].
Author information
Authors and Affiliations
Corresponding author
Appendix 1
Appendix 1
Here we provide the proofs of Proposition 3.1 and Theorem 3.1. The results follow by applying the Fubini theorem for integrable functions (cf. Theorem 14.16 in Chap. 14 of [42]) and the stochastic Fubini theorem (cf. Theorem 65 in Chap. IV of [49]). For further details on the following computations, we refer to [35].
Proof of Proposition 3.1
Let us introduce for every maturity \(T > 0\) the quantity
for all \(0 \le t \le T\). From the dynamics of the forward rate (3.1) we deduce that for all \(T > 0\)
for all \(0 \le t \le T\). By combining (2.11), (3.3), (5.8), and (3.13), we derive the following identity
Note that in general for \(A, B \in \mathcal {M}_{d}\) with A symmetric, i.e. \(A \in S_{d}\), it holds
Therefore, we get due to \(\sigma \!\left( s,t\right) \in S_{d}\) for all \(s, t \ge 0\) that
Note that for all \(0 \le t \le T\)
With the help of (5.10) and the fact that
we can calculate the quadratic variation of Z for all \(T > 0\) follows
Further, we see that due to Eq. (2.27) of [13] for all \(u \in S_{d}^{+}\) and a process Y on \(S_{d}^{+}\) it holds
where B is defined according to (2.13) and therefore for all \(0\le t\le T\) and \(\alpha = Q^{\top }Q\)
Now, we apply Itô’s formula on \(P\!\left( t,T\right) := \exp \!\left( Z\!\left( t,T\right) \right) \) for every maturity \(T > 0\) (cf. Definition 1.4.2 of [8]) and obtain the following representation, where we use Proposition 1.28 of Chap. II in [39] to combine the measures \(\mu ^{X\!}\!\left( ds,d\xi \right) \) and \(\nu \!\left( ds,d\xi \right) \), since the affine process X has only jumps of finite variation (cf. (2.10)).
Assumption 1 guarantees that all integrals above are finite. \(\square \)
Proof of Theorem 3.1
By using (3.7) we see that the discounted bond price process under \(\mathbb {Q}\) is
for all \(0\le t\le T\). Since \(\frac{P\left( t,T\right) }{\beta _{t}}\), \(t \le T\), has to be a local martingale under \(\mathbb {Q}\), the drift in (5.16) must disappear, i.e. for all \(0\le t\le T\)
It follows for all \(0\le t\le T\) that
\(dt \otimes d\mathbb {P}\)-a.s.
Consequently we get for all \(0\le t\le T\) by Satz 6.28 in [42]
\(dt \otimes d\mathbb {P}\)-a.s.
Hence, \(\frac{P\left( t,T\right) }{\beta _{t}}\), \(t \le T\), is a \(\mathbb {Q}\)-local martingale if and only if equation (3.10) is fulfilled \(dt \otimes d\mathbb {P}\)-a.s. Eq. (3.10) represents the HJM condition on the drift in the affine setting on \(S_{d}^{+}\). Then, the forward rate under \(\mathbb {Q}\) follows a process of the form
where we have used again Proposition 1.28 of Chap. II in [39]. \(\square \)
Rights and permissions
About this article
Cite this article
Biagini, F., Gnoatto, A. & Härtel, M. Long-Term Yield in an Affine HJM Framework on \(S_{d}^{+}\) . Appl Math Optim 77, 405–441 (2018). https://doi.org/10.1007/s00245-016-9379-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-016-9379-8