Abstract
Though the bicycle is a familiar object of everyday life, modeling its full nonlinear three-dimensional dynamics in a closed symbolic form is a difficult issue for classical mechanics. In this article, we address this issue without resorting to the usual simplifications on the bicycle kinematics nor its dynamics. To derive this model, we use a general reduction-based approach in the principal fiber bundle of configurations of the three-dimensional bicycle. This includes a geometrically exact model of the contacts between the wheels and the ground, the explicit calculation of the kernel of constraints, along with the dynamics of the system free of any external forces, and its projection onto the kernel of admissible velocities. The approach takes benefits of the intrinsic formulation of geometric mechanics. Along the path toward the final equations, we show that the exact model of the bicycle dynamics requires to cope with a set of non-symmetric constraints with respect to the structural group of its configuration fiber bundle. The final reduced dynamics are simulated on several examples representative of the bicycle. As expected the constraints imposed by the ground contacts, as well as the energy conservation, are satisfied, while the dynamics can be numerically integrated in real time.






























Similar content being viewed by others
Notes
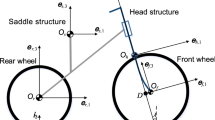
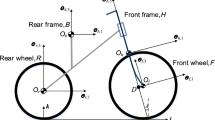
Note that the parameterization of Fig. 2 obeys these conventions.
References
Appell, P.: Traité de mécanique rationnelle. Gauthier-Villars et Cie, Paris (1931)
Astrom, K.J., Klein, R.E., Lennartsson, A.: Bicycle dynamics and control: adapted bicycles for education and research. IEEE Control Syst. 25(4), 26–47 (2005)
Aström, K.J., Murray, R.M.: Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, Cambridge (2010)
Basu-Mandal, P., Chatterjee, A., Papadopoulos, J.: Hands-free circular motions of a benchmark bicycle. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 463(2084), 1983–2003 (2007)
Bloch, A.M.: Nonholonomic Mechanics and Control, Interdisciplinary Applied Mathematics, vol. 24. Springer, New York (2015)
Bloch, A.M., Krishnaprasad, P.S., Marsden, J.E., Murray, R.M.: Nonholonomic mechanical systems with symmetry. Arch. Ration. Mech. Anal. 136(1), 21–99 (1996)
Bourlet, C.: Étude théorique sur la bicyclette. Bull. Soc. Math. Fr. 27, 76–96 (1899)
Boussinesq, J.: Aperçu sur la théorie de la bicyclette. J. Math. Pures Appl. 5, 117–136 (1899)
Boyer, F., Belkhiri, A.: Reduced locomotion dynamics with passive internal dofs: application to nonholonomic and soft robotics. IEEE Trans. Rob. 30(3), 578–592 (2014)
Boyer, F., Belkhiri, A.: Erratum to “Reduced locomotion dynamics with passive internal dofs: application to nonholonomic and soft robotics” [Jun 14 578–592]. IEEE Trans. Rob. 31(3), 805–805 (2015)
Boyer, F., Porez, M.: Multibody system dynamics for bio-inspired locomotion: from geometric structures to computational aspects. Bioinspir. Biomim. 10(2), 1–21 (2015)
Boyer, F., Primault, D.: The Poincaré–Chetayev equations and flexible multibody systems. J. Appl. Math. Mech. 69(6), 925–942 (2005). http://hal.archives-ouvertes.fr/hal-00672477
Campion, G., Bastin, G., D’Andréa-Novel, B.: Structural properties and classification of kinematic and dynamic models of wheeled mobile robots. IEEE Trans. Robot. Autom. 12(1), 47–62 (1996)
Carvallo, E.: Théorie du movement du monocycle part 2: Théorie de la bicyclette. J. l’École Polytech. 6, 1–118 (1901)
Cendra, H., Marsden, J.E., Ratiu, T.S.: Geometric mechanics, lagrangian reduction, and nonholonomic systems. In: Engquist, B., Schmid, W. (eds.) Mathematics Unlimited—2001 and Beyond, pp. 221–273. Springer, Beriln (2001)
Chaplygin, S.: On the theory of motion of nonholonomic systems. The reducing-multiplier theorem. Regul. Chaotic Dyn. 13(4), 369–376 (2008)
Chitta, S., Cheng, P., Frazzoli, E., Kumar, V.: Robotrikke: a novel undulatory locomotion system. In: Proceedings of the 2005 IEEE International Conference on Robotics and Automation (ICRA), pp. 1597–1602 (2005)
Consolini, L., Maggiore, M.: Control of a bicycle using virtual holonomic constraints. Automatica 49(9), 2831–2839 (2013)
Featherstone, R.: Rigid Body Dynamics Algorithms. Springer, Berlin (2008)
Franke, G., Suhr, W., Riess, F.: An advanced model of bicycle dynamics. Eur. J. Phys. 11(2), 116–121 (1990)
Getz, N.H., Marsden, J.E.: Control for an autonomous bicycle. In: Proceedings of 1995 IEEE International Conference on Robotics and Automation, vol. 2, pp. 1397–1402 (1995)
Hertz, H.: Die Prinzipen der Mechanik in neuem Zusammenhange dargestellt. Gesamelte Werke, Band III. Leipzig (1894)
Jones, A.T.: Physics and bicycles. Am. J. Phys. 10(6), 332–333 (1942)
Kelly, S.D., Murray, R.M.: Geometric phases and robotic locomotion. J. Robot. Syst. 12(6), 417–431 (1995)
Klein, F., Sommerfeld, A.: Über die theorie des kreisels. Über die Theorie des Kreisels, by Klein, Felix; Sommerfeld, Arnold. New York: Johnson Reprint Corp., 1965. Bibliotheca mathematica Teubneriana; Bd. 1 4 (1965)
Kooijman, J.D.G., Meijaard, J.P., Papadopoulos, J.M., Ruina, A., Schwab, A.L.: A bicycle can be self-stable without gyroscopic or caster effects. Science 332(6027), 339–342 (2011)
Le Hénaff, Y.: Dynamical stability of the bicycle. Eur. J. Phys. 8(3), 207–210 (1987)
Letov, A.: Stability of an automatically controlled bicycle moving on a horizontal plane. J. Appl. Math. Mech. 23(4), 934–942 (1959)
Lobry, C., Sari, T.: Singular perturbation methods in control theory. Contrle Non Linaire et Applications. Cours du CIMPA, Collection Travaux en Cours, pp. 155–182. Hermann, Paris (2005)
Meijaard, J., Papadopoulos, J.M., Ruina, A., Schwab, A.: Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 463(2084), 1955–1982 (2007)
Morin, P., Samson, C.: Control of nonholonomic mobile robots based on the transverse function approach. IEEE Trans. Robot. 25(5), 1058–1073 (2009)
Ostrowski, J., Burdick, J.: The geometric mechanics of undulatory robotic locomotion. Int. J. Robot. Res. (IJRR) 17(7), 683–701 (1998)
Ostrowski, J., Burdick, J., Lewis, A.D., Murray, R.M.: The mechanics of undulatory locomotion: the mixed kinematic and dynamic case. In: Proceedings of 1995 IEEE International Conference on Robotics and Automation (ICRA), vol. 2, pp. 1945–1951 (1995)
Ostrowski, J., Lewis, A., Murray, R., Burdick, J.: Nonholonomic mechanics and locomotion: the snakeboard example. In: Proceedings of the 1994 IEEE International Conference on Robotics and Automation (ICRA), vol. 3, pp. 2391–2397 (1994)
Ostrowski, J.P.: Computing reduced equations for robotic systems with constraints and symmetries. IEEE Trans. Robot. Autom. 15(1), 111–123 (1999)
Psiaki, M.: Bicycle stability: a mathematical and numerical analysis. Undergradute thesis. Physics Dept., Princeton University, Princeton (1979)
Rankine, W.J.M.: On the dynamical principles of the motion of velocipedes. The Engineer 28(79), 129 (1869)
Timoshenko, S.P., Young, D.H.: Advanced Dynamics. McGraw-Hill, London (1948)
Whipple, F.J.: The stability of the motion of a bicycle. Quarterly Journal of Pure and Applied Mathematics 30(120), 312–348 (1899)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Anthony Bloch.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 26277 KB)
Appendices
Appendix 1: Calculation of the Kernel of Constraints
In this appendix, we calculate \(H = \ker (A,B)\) by inverting symbolically the system that we rewrite in the form \(D=(A,B)(\eta ^\mathrm{T},\dot{r}^\mathrm{T})^\mathrm{T}=0_6\) where D is the \(6\times 1\) vector whose components \(D_i\), \(i=1,2\ldots 6\), form the left-hand side of (38–43). Firstly, \(V_1\), \(V_2\) and \(V_3\) can be extracted from \(D_4\), \(D_5\) and \(D_6\), respectively, as follows:
where we introduced the notations:
After inserting (79) in \(D_3\), one can express \(\varOmega _1\) as:
with:
In a similar way, inserting (77) in \(D_1\) gives:
with:
Inserting (85), (77) and (83) in \(D_2\) allows rewriting \(\varOmega _3\) as:
with:
Now, inserting (87) in (77), (78) and (85) allows us to rewrite them in the following form:
with:
Then, using (92) in (83) gives:
with:
Finally, inserting (96) into (79), we find:
with:
Finally, any vector in the kernel of the constraints can be written in form (62) which require the ordered calculations of (80)–(82), (84), (86), (88), (89), (93), (94), (95), (97), (99).
Appendix 2: Free Bicycle Dynamics
We first start by calculating the acceleration of the four bodies that compose the bicycle in the configuration space \(SE(3)\times S\). This is done by removing all the accelerations \(\dot{\eta }_j\), for \(j\ne 0\) in the recursion on accelerations (64). After straightforward algebra we find:
which need to use the detail expressions of the adjoint map and its time derivative:
and where \({{\mathrm{A}}}_j = (0_3^\mathrm{T},a_j^\mathrm{T})^\mathrm{T}\) is the \((6 \times 1)\) unit vector supporting the joint axis j. Now writing the top row of (63) with k the indexes of all the bodies just after \(\mathcal {B}_{j}\) when descending the structure from \(\mathcal {B}_0\) to its tips, we have for each of the four bodies of the bicycle:
which need the detailed expressions:
where \(m_j 1_{3 \times 3}\) and \(I_{j}\) are the matrices of linear and angular inertia, while \(ms_j = m_j p_{j}(G_j)\) is the vector of first inertia moments that couple linear and angular accelerations, all being related to \({\mathcal {B}_j}\). Then, inserting (107), (106), (105), (101), (102) and (103) into (108) that we identify with the first row of (65), we obtain:
Then introducing (105)–(108) into \(\tau _j = {{\mathrm{A}}}_j^\mathrm{T} f_j\) gives :
that once identified with the second row of (65) gives the expressions below:
Finally, once supplemented with the recursive geometric model \(^{e}g_{j}=\text {}^{e}g_i\text {}^{i}g_{j}(r_j)\) and kinematic one (63-bottom), the above expressions along with (110–113) define all the matrices of the free dynamics, or equivalently, of the left-hand side of (3) and (4).
Rights and permissions
About this article
Cite this article
Boyer, F., Porez, M. & Mauny, J. Reduced Dynamics of the Non-holonomic Whipple Bicycle. J Nonlinear Sci 28, 943–983 (2018). https://doi.org/10.1007/s00332-017-9434-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-017-9434-x