Skip to main content
SpringerLink
Log in

Response of parametrically excited Duffing-van der Pol oscillator with delayed feedback

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

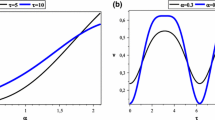
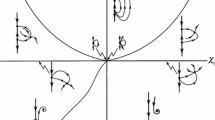
The dynamical behaviour of a parametrically excited Duffing-van der Pol oscillator under linear-plus-nonlinear state feedback control with a time delay is concerned. By means of the method of averaging together with truncation of Taylor expansions, two slow-flow equations on the amplitude and phase of response were derived for the case of principal parametric resonance. It is shown that the stability condition for the trivial solution is only associated with the linear terms in the original systems besides the amplitude and frequency of parametric excitation. And the trivial solution can be stabilized by appreciate choice of gains and time delay in feedback control. Different from the case of the trivial solution, the stability condition for nontrivial solutions is also associated with nonlinear terms besides linear terms in the original system. It is demonstrated that nontrivial steady state responses may lose their stability by saddle-node (SN) or Hopf bifurcation (HB) as parameters vary. The simulations, obtained by numerically integrating the original system, are in good agreement with the analytical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ferdinand Verhulst. Nonlinear Differential Equations and Dynamical Systems[M]. Springer-Verlag, Berlin, 1990.

    Google Scholar 

  2. Jackson E Atlee. Perspectives of Nonlinear Dynamics[M]. Cambridge University Press, New York, 1991.

    Google Scholar 

  3. Guckenheimer J, Holmes P. Nonlinear Oscillation and Bifurcation of Vector Fields[M]. Springer-Verlag, New York, 1993.

    Google Scholar 

  4. Holmes P, Rand D. Phase portraits and bifurcation of the nonlinear oscillator: ẍ + (α + γx 2)ẋ + βx + δx 3 = 0[J]. International Journal of Nonlinear Mechanics, 1980, 15(6):449–458.

    Article  MathSciNet  Google Scholar 

  5. Tsuda Y, Tamura H, Sueoka A, et al. Chaotic behaviour of a nonlinear vibrating system with a retarded argument[J]. JSME International Journal, Series III, 1992, 35(2):259–267.

    Google Scholar 

  6. Szemplinska-Stupnicka, Rudowski J. The coexistence of periodic, almost-periodic and chaotic attractions in the van der Pol-Duffing oscillator[J]. Journal of Sound and Vibration, 1997, 199(2):165–175.

    Article  MathSciNet  Google Scholar 

  7. Maccari Attilio. Approximate solution of a class of nonlinear oscillators in resonance with a periodic excitation[J]. Nonlinear Dynamics, 1998, 15(4):329–343.

    Article  MathSciNet  Google Scholar 

  8. Algaba A, Fernandez-Sanchez E, Freire E, et al. Oscillation-sliding in a modified van der Pol-Duffing electronic oscillator[J]. Journal of Sound and Vibration, 2002, 249(5):899–907.

    Article  MathSciNet  Google Scholar 

  9. Xu J, Chung K W. Effects of time delayed position feedback on a van der Pol-Duffing oscillator[J]. Physica D, 2003, 180(1):17–39.

    Article  MathSciNet  Google Scholar 

  10. Moukam Kakmeni F M, Bowong S, Tchawoua C, et al. Strange attractors and chaos control in a Duffing-van der Pol oscillator with two external periodic forces[J]. Journal of Sound and Vibration, 2004, 277(4/5):783–799.

    Article  MathSciNet  Google Scholar 

  11. Chen Yushu. Bifurcation and Chaos Theory of Nonlinear Vibration Systems[M]. Higher Education Press, Beijing, 1993 (in Chinese).

    Google Scholar 

  12. Fofana M S, Ryba P B. Pramertic stability of nonlinear time delay equations[J]. International Journal of Nonlinear Mechanics, 2004, 39(1):79–91.

    Article  MathSciNet  Google Scholar 

  13. Ji J C, Leung A Y T. Bifurcation control of parametrically excited Duffing system[J]. Nonlinear Dynamics, 2002, 27(4):411–417.

    Article  MathSciNet  Google Scholar 

  14. Hairer E, Norsett S P, Wanner G. Solving Ordinary Differential Equations I: Nonstiff Problems[M]. Springer-Verlag, Berlin, 1987.

    Google Scholar 

  15. Hiroshi Yabuno. Bifurcation control of parametrically excited Duffing system by a combined linear-plus-nonlinear feedback control[J]. Nonlinear Dynamics, 1997, 12(3):263–274.

    Article  MathSciNet  Google Scholar 

  16. Ji J C, Hansen C H. Nonlinear oscillations of a rotor in active magnetic bearings[J]. Journal of Sound and Vibration, 2001, 240(4):599–612.

    Article  Google Scholar 

  17. Ding Qian, Chen Yushu, Ye Min, Leung A Y T. The primary resonance and mode-locking in a certain self-excited system with hysteretic nonlinear[J]. Acta Mechanica Sinica, 2002, 34(1):123–130 (in Chinese).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering, Hebei University of Technology, Tianjin, 300130, P. R. China

    Li Xin-ye Doctor  (李欣业) (Associate Professor)

  2. School of Mechanical Engineering, Tianjin University, Tianjin, 300072, P. R. China

    Chen Yu-shu  (陈予恕) & Wu Zhi-qiang  (吴志强)

  3. Department of Graduate Student, Shandong Institute of Architecture and Engineering, Jinan, 250014, P. R. China

    Song Tao  (宋涛)

Authors
  1. Li Xin-ye Doctor  (李欣业)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chen Yu-shu  (陈予恕)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wu Zhi-qiang  (吴志强)
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Song Tao  (宋涛)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li Xin-ye Doctor  (李欣业).

Additional information

Contributed by CHEN Yu-shu

Project supported by the Scientific Research Foundation for Returned Overseas Chinese Scholar of Ministry of Education, China (No. 2006-331)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, Xy., Chen, Ys., Wu, Zq. et al. Response of parametrically excited Duffing-van der Pol oscillator with delayed feedback. Appl Math Mech 27, 1585–1595 (2006). https://doi.org/10.1007/s10483-006-1201-z

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-006-1201-z

Key words

Chinese Library Classification

2000 Mathematics Subject Classification

Search

Navigation