Hybrid vibration control of a Two-Link Flexible manipulator

Abstract

This research work deals with tip vibration control of a Two-Link Flexible manipulator using hybrid control technique. This technique involves the implementation of unconstrained viscoelastic damping layer on the links in conjunction with active damping using piezoelectric sensors and actuators. Mathematical modelling of the complete system is done using the finite element approach in the inertial frame. Viscoelastic damping is modelled using Kelvin–Voigt elements for which a damping matrix is derived. Active damping is modelled as time-dependent uniformly distributed load applied by the piezoelectric actuator on the flexible link working under feedback control. The angular and linear velocities of the tips of flexible links are used for direct feedback. The unconstrained viscoelastic damping layer effectively reduces the vibrations of the system. The effectiveness of the active control depends upon the relative position of sensors and actuators on the links. The novelty of the work lies in control of torsional and flexural vibrations through the application of passive and active damping methods to the non-inertial frames represented by the manipulator links.

1 Introduction

The vibration control of links of flexible manipulators is a challenging task. Theoretically, the joint torque requirements of flexible manipulators are very less as compared to rigid manipulators but with lower positional accuracy of the end-effector. The accuracy of flexible manipulators decreases due to the vibration of the links. If somehow these vibrations are countered then the power requirements by the robots will reduce apart from achieving positional accuracy. In this paper, the vibration control of flexible links of a Two-Link Flexible planar manipulator having two revolute joints is achieved with the help of hybrid damping method. This method employs passive damping technique using a viscoelastic material (say, rubber) and active damping technique using piezoelectric materials (say, PZT). The phenomenon of viscoelasticity is modelled using Kelvin–Voigt elements. The viscoelastic material is pasted throughout the length of the links while the piezoelectric sensors and actuators are pasted over the links in segmented fashion. In the present work, firstly a brief literature survey is provided which includes the work done by various researchers in the areas of viscoelastic damping and active vibration control. Mathematical modelling of viscoelasticity and active vibration control are described using the finite element approach. Simulation results are discussed for different cases. A brief literature survey was conducted on active and passive damping methods used by various researchers. Firstly, review on viscoelastic damping is provided. Next, a brief study of work done by various authors on active vibration control using piezoelectric materials is provided.

1.1 Review on viscoelastic damping

Zhou et al. [1] have presented a review on various research methods and theoretical models are used to study the mechanics of structures made up of viscoelastic damping materials. The authors give a description of conventional and new methods in this area and also provide information about the advantages, disadvantages and the applicability of various available methods. Grootenhuis [2] has discussed on how to damp the vibrations of structures using viscoelastic damping and also discusses, how to increase the efficacy of viscoelastic damping for both unconstrained and multilayer sandwich constructions. Jones et al. [3] have proposed a method to measure the complex modulus properties of viscoelastic materials attached to thin metal sheets. They have verified their results using a resonance technique. Kapur et al. [4] have analysed a two-layer and three-layer viscoelastically damped beams subjected to shock excitations. The modelling of viscoelasticity is done using a four-element viscoelastic model. The authors have also validated their results experimentally. Xisheng et al. [5] have developed a new method called ‘finite element perturbation method’ to solve the Eigen systems with frequency-dependent stiffness matrix. They have also addressed the issue of optimal design of visco-elastically damped structures with regards to optimal location of constrained damping layers and optimal viscoelastic material selection. Barkanov [6] has studied the transient response of structures with viscoelastic materials using finite element method. The viscoelastic material is represented by complex modulus model. The author has used fast Fourier transform to represent the input signals and transfer functions. The author concluded that the time-domain representation is a correct way to avoid the non-causal effect. Lei et al. [7] have done the dynamic analysis of Euler–Bernoulli beams and Kirchoff plates using non-local damping models that include time and spatial hysteresis effects. The equation of motion presented here is an integro-partial-differential equation. The approximate solutions for eigenvalues and modes are obtained using Galerkin’s method. Lepoittevin and Kress [8] have proposed a method of segmentation to enhance the damping capabilities of constrained layer damping material. In this method, cuts were introduced at suitable locations. Nelder–Mead simplex method was used to find out the optimum position of cuts and damping efficiency was estimated using modal strain energy method. Dutt and Roy [9] have provided the equations of motion of a rotor-shaft system with a viscoelastic rotor using finite elements method. The authors have represented the material constitutive relationship using differential time operator, which, facilitates the generic representation of viscoelasticity by various types of models. Palmeri and Adhikari [10] have presented and validated numerically the state-space form for studying the transverse vibrations of double-beams joined together by viscoelastic core. The authors have used Galerkin’s approach and Lagrange’s equation to present their formulation. According to them, their technique enables one to handle inhomogeneity, different types of boundary conditions and rate-dependent constitutive law for the inner layer for the system. Lei et al. [11] have studied the dynamic characteristics of damped viscoelastic nonlocal beams using Kelvin–Voigt and three-parameter standard viscoelastic models, velocity dependent external damping and nonlocal Euler–Bernoulli beam theory. They developed a transfer function method to obtain the closed-form solution of beams. Hujare and Sahasrabudhe [12] determined the damping performance of different viscoelastic materials using constrained layer damping treatment. The authors have followed ASTM standards during the experimental test. The damping factors have been obtained using half power bandwidth method. Li et al. [13] have presented the dynamic analyses of the system using various damping models. The damping forces are frequency dependent and depend upon the past history of motion. The authors suggested that the damping model may be derived using standard viscoelastic models. They have used both the mode superposition method and Fourier transform method for calculating the dynamic response of the system. Freundlich [14] has obtained the dynamic response of an Euler–Bernoulli simply supported beam subjected to a moving force load using Green’s function. The author has included viscoelastic damping using Kelvin–Voigt model. The governing equations of the system are obtained in the form of fractional derivatives. Ghayesh [15, 16] has studied the effect of various parameters like gradient index, excitation frequency, amplitude of harmonic force and viscoelastic parameters on nonlinear frequency and force responses on materials with viscoelastic properties.

1.2 Review on active damping of vibrations

Benjeddou [17] reviewed the advances and trends in the formulations and applications of finite element modelling of adaptive structural elements. He has tabulated various types of adaptive piezoelectric finite elements used in literature. Cannon and Schmitz [18] have conducted experiments on control of single-link very flexible manipulator with non-collocated sensor-actuator pairs. The authors highlighted the advantages of end-point sensing in controlling such types of systems and time response of the controller for non-collocated arrangement. Sakawa et al. [19] tried to control the rotation angle as well as vibration of a flexible arm clamped on a motor by controlling the motor torque. The authors first derived the governing equations of motion of the system along with the boundary conditions and then developed a feedback control system incorporating dynamic compensator. Experiments were also conducted. Goh and Caughey [20] discussed the theory of active vibration control of large space structures using collocated feedback control. The authors proposed to use position feedback instead of velocity feedback in order to minimize the effect of instability caused by actuator dynamics. Furthermore, the authors showed that position feedback is insensitive to uncertain damping of structures and can well handle unmodelled and uncontrolled modes. Baz and Poh [21] have presented a modified independent modal space control (MIMSC) method for selection of optimal location, control gains and excitation voltage of piezoelectric actuators for active vibration control of a flexible beam. In their analysis, the authors have included the effect of physical parameters of the actuator on elastic and inertial properties of the flexible beam. They have shown that the inclusion of properties of bonding layer reduces vibration amplitudes but at the cost of higher control forces. The authors also demonstrated the effectiveness of MIMSC method in controlling the vibrations of flexible beams having large degrees of freedom with a very small number of actuators. Tzou and Wan [22] tried to maintain a precise trajectory of a flexible robot with the help of passive viscoelastic actuator which is directly attached to the robot. Flexible links are analysed with the help of ‘finite element’ approach. Again in the year 1991, Tzou [23] presented an active micro-position feedback control technique using piezoelectric actuators. He first prepared a mathematical model of active vibration control and then verified the results through experiments. He achieved the active position control by varying the feedback gains. Lesieutre and Lee [24] presented a ‘finite element’ for planar beams with active constrained layer (ACL) damping treatments. This element based upon non-shear locking phenomenon includes frequency-dependent viscoelastic model and segmented constraining layers that facilitate multiple inputs and improved performance. The viscoelastic model is implemented using anelastic displacement fields (ADF) method. The authors concluded that a segmented ACL is more robust than the continuous treatment. This arrangement facilitates damping of modes at least up to the number of independent patches by control action. Aldraihem and Wetherhold [25] have proposed a shear-deformable beam theory to model the coupled bending and twisting vibration in laminated beams. They have considered two types of coupling—mass coupling and stiffness coupling. The active control of the beam was studied on two different types of piezoelectric layers viz. lead zirconate titanate (PZT) and PZT/epoxy piezoelectric composite (PZT/Ep). After modal cost and controllability analyses, the authors concluded that PZT/Ep provided the best bending-twisting actuation for vibration damping. Xu and Koko [26] developed a general scheme of analysing/designing actively controlled smart structures with piezoelectric sensors and actuators. The authors used feedback control law in the controller. They showed that locations of piezoelectric sensors and actuators might have significant influence on the performance of the system. Sun et al. [27] proposed a hybrid control algorithm to control the rotation of a flexible beam while suppressing the vibrations of the beam. The authors used PD feedback control for controlling beam rotation and PZT actuator control was used for suppressing the vibrations of the beam. The actuator placement was done based upon the mode shape functions and the stability of the control system was analysed using virtual joint model. Qiu et al. [28] carried out studies on active vibration control of a cantilever beam with non-collocated arrangement of acceleration sensor and piezoelectric patch actuator. The authors tried to reduce the problems of phase hysteresis and time delay by using proportional feedback control algorithm and sliding mode control algorithm. First two vibration modes are controlled. The performance of the control system is checked through experiments. Mirzaee et al. [29] dealt with maneuver control and vibration suppression of a two-link flexible arm with embedded piezoelectric sensors and actuators. The authors obtained the governing equations of motion of the system using extended Hamilton’s principle and assumed modes method. The control system is based upon variable structure control employed for rigid motion control and Lyapunov control for vibration suppression of the links. The application of viscoelastic and active damping methods lie in control of vibrations of flexible structures. These structures possess geometric nonlinearities and exhibit nonlinear dynamics. The efficacy of damping methods described earlier can be increased by first understanding the behaviour of flexible structures. Various work are available in the literature that describe the nonlinear dynamics [30, 31] of flexible beams and plates. These make use of Hamilton’s principle along with modified couple stress theory [32,33,34] and strain gradient elasticity theory [35]. Researchers have used Galerkin’s method to discretize the governing equations of motion. In many cases, it has been observed that these structures exhibit size-dependent dynamic behaviour [36,37,38,39,40]. It is found from the literature that the dynamics of such systems is significantly affected by material gradient index [41, 42].

From the above literature survey, it is found that viscoelastic damping is due to the phenomenon of shear strain within the viscoelastic materials. The physical properties of these materials are frequency dependent. These materials can be applied on the structure either in a constrained or unconstrained manner. Once applied, they become an integral part of the structure and provide some fixed damping behaviour. On the other hand, in active vibration control methods, piezoelectric sensors and actuators are applied on the structure at suitable locations. From the survey, it is found that researchers have used either the position feedback or velocity feedback while designing the control system using piezo ceramics. The primary steps in active vibration control are: modelling of the smart structure, accurate positioning of sensors and actuators, determination of optimal feedback gain and performance evaluation of controller design [43]. Yavuz et al. [44] have tried to control the residual vibrations of a single-link flexible composite manipulator using trapezoidal and triangular velocity profiles for motion commands, both through simulation and experiment. The authors conclude that by proper selection of motion parameters—acceleration time, constant time and deceleration time, the residual vibrations (vibrations after stopping) of the manipulator can be controlled within specified limits.

In the present work, velocity feedback is used for active vibration control. Besides that, unconstrained viscoelastic damping treatment is also applied. Thus, hybrid damping approach is followed to contain the vibrations of the flexible links. A host of the researchers have used the approach of modal sensor and modal actuator [45] for active vibration control but in this paper, the vibration control is achieved by using direct feedback of velocity variables. Modal approach is not considered here, because the eigen values of the manipulator are configuration-dependent which changes with time.

2 Mathematical modelling

Firstly, mathematical model of the Two-link Flexible manipulator will be described in brief. Then, modelling for viscoelastic damping and active vibration control will be shown. The governing equations of the manipulator are found in the inertial frame. The links of the manipulator represent non-inertial frames and passive and active damping materials are applied over these links. The effects of passive and active vibration controls are also studied with respect to the inertial frame of Ref. [46].

2.1 Mathematical model of the Two-link Flexible manipulator

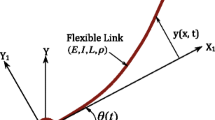
The governing equations of the two-link flexible planar manipulator are provided by [47] using Lagrangian dynamics along with the assumed modes method (AMM). The mathematical model presented there considers only the flexural vibrations of the flexible links. Figure 1 shows a Two-Link Flexible manipulator undergoing both bending and torsional deformations along with rigid revolutions at the joints.

Fig. 1

Dynamic analysis of Two-Link Flexible manipulator undergoing both bending and torsional deformations

The detailed explanation of Fig. 1 and derivation of the mathematical model for Two-Link Flexible manipulator are explained in “Appendix” provided at the last. In the present work, finite element method (FEM) is used to model the vibratory motions of the flexible links instead of AMM. Both the flexural and torsional vibrations are dealt with in the present work. This involves division of flexible links into some finite number of elements and finding the inertia and stiffness matrices that govern the dynamics of the system under consideration. Figure 2 shows the discretization of flexible links using two Space-frame elements [48].

Fig. 2

Dynamics modelling of a Two-Link Flexible manipulator using Space-frame finite elements

A ‘space-frame element’ has two nodes with each node having six degrees of freedom: three translational (Q_6i-5, Q_6i-4 and Q_6i-3) and three rotational (Q_6i-2, Q_6i-1 and Q_6i) (refer to Fig. 2). The complete equation of motion of the flexible manipulator is given by Eq. (1a). The symbols have their usual meanings.

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {M_{rr} } & {M_{rf} } \\ {M_{fr} } & {M_{ff} } \\ \end{array} } \right]_{{\left( {n + N} \right) X \left( {n + N} \right)}} \left\{ {\begin{array}{*{20}c} {\ddot{q}_{r} } \\ {\ddot{q}_{f} } \\ \end{array} } \right\}_{{\left( {n + N} \right) X 1}} + \left[ {\begin{array}{*{20}c} {C_{rr} } & 0 \\ 0 & {C_{ff} } \\ \end{array} } \right]_{{\left( {n + N} \right) X \left( {n + N} \right)}} \left\{ {\begin{array}{*{20}c} {\dot{q}_{r} } \\ {\dot{q}_{f} } \\ \end{array} } \right\}_{{\left( {n + N} \right) X \left( {n + N} \right)}} \\ & + \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & {K_{ff} } \\ \end{array} } \right]_{{\left( {n + N} \right) X \left( {n + N} \right)}} \left\{ {\begin{array}{*{20}c} {q_{r} } \\ {q_{f} } \\ \end{array} } \right\}_{{\left( {n + N} \right) X \left( {n + N} \right)}} + \left[ {\begin{array}{*{20}c} H \\ 0 \\ \end{array} } \right]_{{\left( {n + N} \right) X 1}} + \left[ {\begin{array}{*{20}c} G \\ 0 \\ \end{array} } \right]_{{\left( {n + N} \right) X 1}} = \left\{ {\begin{array}{*{20}c} {F_{r} } \\ {F_{f} } \\ \end{array} } \right\}_{{\left( {n + N} \right) X 1}} \\ \end{aligned}$$

(1a)

In Eq. (1a), subscripts—r and f stand for rigid and flexible respectively. N represents the rigid degrees of freedom present in the system and n represents the flexible degrees of freedom obtained from finite element formulation. In Eq. (1a), the first term in left hand side represents inertia torque; the second term represents damping and gyroscopic torque; the third term represents restoring torque; the fourth term represents centrifugal and Coriolis’ torque and the fifth term represents the gravity torque. The term on the right hand side represents the external torque. For the present case, since there are two flexible links, we have N = 2. Hence, M_rr consists of two diagonal elements—M₁₁ and M₂₂. M_rf and M_fr represent the coupling between rigid and flexible motions. It is seen that

$$M_{fr} = M_{rf}^{'}$$

(1b)

2.2 Mathematical modelling for hybrid vibration control

The hybrid vibration control used in the present work involves the mathematical modelling of three systems, viz., the smart beam, the feedback control system and the viscoelastic damping. The smart beam involves the application of sensor-actuator pair on the beam at suitable locations. The relative position of sensor and actuator can be varied. The feedback control system involves the use of ‘proportional-derivative’ controller. The viscoelastic damping is modelled using Kelvin–Voigt models. Finite element method is used for modelling the smart beam and viscoelastic damping matrix.

2.2.1 The smart beam

Figure 3 shows a smart beam having a pair of piezo-sensor and piezo-actuator applied on it. From the figure, it can be seen that the voltage generated by the sensor is fed back to the actuator. The actuator applies a time-varying uniformly distributed load, p(t) on the beam where it is pasted.

Fig. 3

Schematic diagram for active vibration control of a smart beam/link

The mathematical modelling of piezo-sensors and actuators are provided by Preumont [45]. The piezo-sensor can be modelled either as a current amplifier or a charge amplifier. In this paper, the piezo-sensor is modelled as a current amplifier. The voltage generated by the piezo-sensor is given by Eq. (2) as follows.

$$v_{s} \left( t \right) = - R_{f} E_{p} h d_{31} \mathop \int \limits_{a}^{b} \dot{w}^{''} b_{p} \left( x \right)dx$$

(2)

where R_f = piezo resistance, w represents the deflection of any point on the beam and wʹ represents the slope at that point. In Eq. (2), dot (.) represents differentiation w.r.t. time, i.e. $\frac{d}{dt}$ while dash (ʹ) represents differentiation w.r.t. space, i.e., $\frac{d}{dx}$. Again, in the same equation, b_p(x) = width of the piezo-sensor, a and b represent the initial and final coordinates of the points on the beam/link between which the piezo-sensor is located. These coordinates are measured along the beam axis, such that, ‘(b–a)’ represents the length L_p of the piezo-sensor.

If b_p(x) = constant, then

$$v_{s} \left( t \right) = - R_{f} E_{p} h d_{31} b_{p} \left[ {\dot{w}^{'} \left( b \right) - \dot{w}^{'} \left( a \right)} \right]$$

(3a)

If b_pʹʹ(x) = constant, then

$$v_{s} \left( t \right) = - R_{f} E_{p} h d_{31} .\left[ {b_{p} \left( x \right)\left\{ {\dot{w}^{'} \left( b \right) - \dot{w}^{'} \left( a \right)} \right\} - b_{p}^{'} \left( x \right).\left\{ {\dot{w}\left( b \right) - \dot{w}\left( a \right)} \right\}} \right]$$

(3b)

where $\dot{w}^{'} \left( b \right)$ = rate of change of slope at point b, $\dot{w}^{'} \left( a \right)$ = rate of change of slope w.r.t. time at point a on the beam, $\dot{w}\left( b \right)$ = rate of change of deflection at point b and $\dot{w}\left( a \right)$ = rate of change of deflection at point a on the beam.

The equation of motion for the beam with piezo-actuator is given by Eq. (4) as follows.

$$m\ddot{w} + \left( {EIw^{\prime\prime}} \right)^{''} = - E_{p} d_{31} v_{a} \left( t \right)b_{p}^{''} \left( x \right)h$$

(4)

In Eq. (4), m = mass per unit length of the beam, EI = flexural rigidity of the beam, E_p = Young’s modulus of the piezo-ceramic, h = thickness of the beam, w = deflection of the beam, v_a = voltage applied at the actuator and d₃₁ = piezoelectric constant. Equation (4) is valid only when the thickness of the piezo-ceramic is negligible in comparison to the beam thickness. In the present case, these piezoelectric sensors and actuators are pasted on the links of the Two-link Flexible manipulator for achieving active vibration control of the links (Fig. 5). The beam equation—Eq. (4) may also be written as:

$$m\ddot{w} + \left( {EIw^{\prime\prime}} \right)^{''} = K_{a} v_{a} \left( t \right)$$

(4a)

$${\text{where}},\;K_{a} = - E_{p} d_{31} b_{p}^{''} \left( x \right)h = piezo - actuator constant.$$

(4b)

From Fig. 3, we can write

$$v_{a} \left( t \right) = K_{G} v_{s} \left( t \right)$$

(5)

Thus, Eq. (4) gets modified to:

$$m\ddot{w} + \left( {EIw^{\prime\prime}} \right)^{''} = K_{G} K_{a} v_{s} \left( t \right) = f\left( t \right)$$

(6a)

where f(t) = time-dependent force applied by piezo-actuator on the beam.

This force is converted into a time-varying uniformly distributed load using the following equation.

$$p\left( t \right) = \frac{f\left( t \right)}{{L_{p} }}$$

(6b)

where L_p = length of the piezo-actuator = (b–a). This uniformly distributed load ‘p(t)’ is used to formulate the load vector in Eq. (11) obtained by finite element formulation. The expression for ‘p(t)’ is found out as follows.

$$p\left( t \right) = \frac{{ - K_{a} K_{G} R_{f} E_{p} hd_{31} }}{2}\left[ {\begin{array}{*{20}l} {b_{p}^{'} \left( x \right)} \hfill & { - b_{p}^{'} \left( x \right)} \hfill & { - b_{p}^{'} \left( x \right)} \hfill & {b_{p}^{'} \left( x \right)} \hfill \\ {\frac{{L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill & {\frac{{ - L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill & {\frac{{ - L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill & {\frac{{L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill \\ {b_{p}^{'} \left( x \right)} \hfill & { - b_{p}^{'} \left( x \right)} \hfill & { - b_{p}^{'} \left( x \right)} \hfill & {b_{p}^{'} \left( x \right)} \hfill \\ {\frac{{ - L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill & {\frac{{L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill & {\frac{{ L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill & {\frac{{ - L_{p} }}{6}b_{p}^{'} \left( x \right)} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{q}_{3} } \\ {\dot{q}_{4} } \\ {\begin{array}{*{20}c} {\dot{q}_{5} } \\ {\dot{q}_{6} } \\ \end{array} } \\ \end{array} } \right\}$$

(6c)

A feedback control system based upon proportional-cum-derivative (PD) control [49] is used for tip vibration control. In the present work, ‘finite element approach’ is used for achieving the active vibration control of the links of the Two-link Flexible manipulator. Figure 4 shows the schematic diagram of the set-up of the flexible manipulator with piezo-sensors and piezo-actuators pasted on the links. In the figure, four finite elements per link are used for modelling the system. The links of the flexible manipulator are modelled using ‘Frame element’. A ‘frame element’ has two nodes: each node having three degrees of freedom. Therefore in Fig. 4, there are total twenty seven degrees of freedom which correspond to the flexible motion of the links. Besides that, there are two rigid degrees of freedom, viz., θ₁ and θ₂ also. The first three degrees of freedom at ‘node 1’ are considered to be fixed. Thus, the flexible manipulator shown in the figure has net twenty six degrees of freedom. Damping is introduced into the system by using Kelvin–Voigt viscoelastic damping model. It is assumed that the viscoelastic materials are pasted throughout the links.

Fig. 4

Diagram showing the relative placements of sensors and actuators on the flexible links of the Two-Link Flexible manipulator. (In the figure, S₁ Sensor on Link-1; S₂ Sensor on Link-2; A₁ Actuator on Link-1 and A₂ Actuator on Link-2.)

In Fig. 4, the encircled numbers represent the number of ‘finite element’ while the non-circled numbers represent the node numbers. At any node i, there are three degrees of freedom and represented by—q_3i-2, q_3i-1 and q_3i. First two degrees of freedom represent translation along X- and Y-axes respectively while the third degree of freedom represents rotation about Z-axis which is perpendicular to the X–Y plane. For active control of vibration of the links, the sensors and actuators are arranged in some specific fashion on the links. Table 1 gives details about the relative positions of sensors and actuators pasted on the flexible links.

Table 1 Table describing the relative positions of sensors and actuators placed on the flexible links

From Table 1, it can be found that the sensors and actuators can be arranged in two ways on the links, viz., collocated and non-collocated. The sensed degrees of freedom and the controlled degrees of freedom will be the same in collocated arrangement while they will be different in non-collocated arrangement. The equation of motion for the Two-link Flexible manipulator having both rigid and elastic motions of the links is given by Eq. (1a). For the present case, since there are two flexible links, we have N = 2. Hence, M_rr will be a square matrix of order 2. C_rr represents joint damping square matrix of order 2 and K_rr represents joint stiffness square matrix of order 2. M_ff, C_ff and K_ff represent mass, damping and stiffness matrices for elastic motion of the links. The terms with subscripts—‘rf’ and ‘fr’ represent the coupling between rigid and elastic motions. In the present case, C_rr and K_rr are taken as null matrices and the terms—C_rf, C_fr, K_rf and K_fr are taken as zero. The mass matrix M_ff is formulated by assembling the mass matrices of flexible links, viscoelastic materials and piezoelectric materials. The piezoelectric materials are applied in segmented fashion (Fig. 4). The damping matrix C_ff is due to the presence of viscoelastic damping. The stiffness matrix K_ff is formulated by assembling the stiffness matrices of flexible links, viscoelastic materials and piezoelectric materials.

2.2.2 Formulation of mass, damping and stiffness matrices

Mass and stiffness matrices for a frame element are given as under [48]. These are provided in Eqs. (7) and (9).

Elemental mass matrix is given as:

$$\varvec{m}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\varvec{m}_{{\bf 11}}^{\varvec{e}} } & {\varvec{m}_{{\bf 12}}^{\varvec{e}} } \\ {\varvec{m}_{{\bf 21}}^{\varvec{e}} } & {\varvec{m}_{{\bf 22}}^{\varvec{e}} } \\ \end{array} } \right]$$

(7a)

$$\varvec{m}_{{\bf 11}}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {2a} & 0 & 0 \\ 0 & {156b} & {22l_{e} b} \\ 0 & {22l_{e} b} & {4l_{e}^{2} b} \\ \end{array} } \right];\varvec{m}_{{\bf 12}}^{\varvec{e}} = \varvec{m}_{{\bf 21}}^{\varvec{e}} \varvec{ } = \left[ {\begin{array}{*{20}c} a & 0 & 0 \\ 0 & {54b} & { - 13l_{e} b} \\ 0 & {13l_{e} b} & { - 3l_{e}^{2} b} \\ \end{array} } \right];$$

$$\varvec{m}_{{\bf 22}}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {2a} & 0 & 0 \\ 0 & {156b} & { - 22l_{e} b} \\ 0 & { - 22l_{e} b} & {4l_{e}^{2} b} \\ \end{array} } \right]$$

where $a = \frac{{\rho A_{e} l_{e} }}{6};b = \frac{{\rho A_{e} l_{e} }}{420}$; ρ = density of the material; A_e = area of cross-section of the element; l_e = length of the element

$${\text{Global}}\;{\text{mass}}\;{\text{matrix}},\quad \varvec{m}_{\varvec{G}}^{\varvec{e}} = \varvec{ L}_{pf}^{\varvec{T}} \varvec{m}^{\varvec{e}} \varvec{L}_{pf}$$

(7b)

$${\text{where}}\quad \varvec{L}_{pf} = \left[ {\begin{array}{*{20}c} {\varvec{\lambda}_{pf} } & 0 \\ 0 & {\varvec{\lambda}_{pf} } \\ \end{array} } \right]$$

(8a)

is the transformation matrix that converts the motion in non-inertial frame (the flexible links) to the inertial frame (frame X–Y). The superscript ‘T’ stands for ‘transpose’. In Eq. (8a),

$$\varvec{\lambda}_{pf} = \left[ {\begin{array}{*{20}c} {\cos \theta_{1} } & {\sin \theta_{1} } & 0 \\ { - \sin \theta_{1} } & {\cos \theta_{1} } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\quad {\text{for}}\;{\text{Link-1}},\;{\text{and}}$$

(8b)

$$\varvec{\lambda}_{pf} = \left[ {\begin{array}{*{20}c} {\cos \left( {\theta_{1} + \theta_{2} } \right)} & {\sin \left( {\theta_{1} + \theta_{2} } \right)} & 0 \\ { - \sin \left( {\theta_{1} + \theta_{2} } \right)} & {\cos \left( {\theta_{1} + \theta_{2} } \right)} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]\quad {\text{for}}\;{\text{Link-2}}.$$

(8c)

Elemental stiffness matrix is given as:

$$\varvec{k}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\varvec{k}_{11}^{\varvec{e}} } & {\varvec{k}_{12}^{\varvec{e}} } \\ {\varvec{k}_{21}^{\varvec{e}} } & {\varvec{k}_{22}^{\varvec{e}} } \\ \end{array} } \right]$$

(9a)

$$\varvec{k}_{11}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{EA_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{12EI_{e} }}{{l_{e}^{3} }}} & {\frac{{6EI_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{6EI_{e} }}{{l_{e}^{2} }}} & {\frac{{4EI_{e} }}{{l_{e} }}} \\ \end{array} } \right];\;\varvec{k}_{12}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{ - EA_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{ - 12EI_{e} }}{{l_{e}^{3} }}} & {\frac{{6EI_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{ - 6EI_{e} }}{{l_{e}^{2} }}} & {\frac{{2EI_{e} }}{{l_{e} }}} \\ \end{array} } \right];$$

$$\varvec{k}_{21}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{ - EA_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{ - 12EI_{e} }}{{l_{e}^{3} }}} & {\frac{{ - 6EI_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{6EI_{e} }}{{l_{e}^{2} }}} & {\frac{{2EI_{e} }}{{l_{e} }}} \\ \end{array} } \right];\;\varvec{k}_{22}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{EA_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{12EI_{e} }}{{l_{e}^{3} }}} & {\frac{{ - 6EI_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{ - 6EI_{e} }}{{l_{e}^{2} }}} & {\frac{{4EI_{e} }}{{l_{e} }}} \\ \end{array} } \right];$$

where E = Young’s modulus of elasticity of the material; I_e = area moment of inertia of the element

$${\text{Global}}\;{\text{stiffness}}\;{\text{matrix}},\varvec{k}_{\varvec{G}}^{\varvec{e}} = \varvec{ L}_{pf}^{\varvec{T}} \varvec{k}^{\varvec{e}} \varvec{L}_{pf}$$

(9b)

Mass matrix of flexible link: In Eq. (7), density (ρ) of steel is taken.

Mass matrix of viscoelastic material: In Eq. (7), density (ρ) of a viscoelastic material (rubber) is taken.

Mass matrix of piezoelectric material: For this, density (ρ) of piezo-ceramic is used in Eq. (7).

The stiffness matrices are also formulated in similar fashion. The right hand side of Eq. (1a) is represented by following expressions (Eqs. 10 and 11).

$$F_{r} = \left\{ {\begin{array}{*{20}c} {\tau_{1} } \\ {\tau_{2} } \\ \end{array} } \right\}\;{\text{and}}\;F_{f} = Load\;vector\;containing\;loads\;acting\;on\;Flexible\;Links$$

(10)

where τ₁ and τ₂ are torques applied at joint 1 and joint 2 respectively and F_f is formed by assembling the elemental load vectors which is given as follows:

$$\varvec{f}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} 0 & {\frac{{pl_{e} }}{2}} & {\begin{array}{*{20}c} {\frac{{pl_{e}^{2} }}{12}} & 0 & {\begin{array}{*{20}c} {\frac{{pl_{e} }}{2}} & { - \frac{{pl_{e}^{2} }}{12}} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]^{T} ;$$

(11a)

p = p(t) =time-dependent distributed load (Fig. 3).

$${\text{Global}}\;{\text{load}}\;{\text{vector}},\;\varvec{f}_{\varvec{G}}^{\varvec{e}} = \varvec{ L}_{pf}^{\varvec{T}} \varvec{f}^{\varvec{e}}$$

(11b)

Now, for the Kelvin–Voigt element used for modelling the phenomenon of viscoelasticity, the stored energy and rate of dissipation in differential form are given as follows [50]:

$$Stored\; energy, dU_{e} = \mathop \int \limits_{0}^{A} \frac{1}{2}\sigma^{T} \epsilon\, dx\,dA$$

(12)

$$Rate \;of\; dissipation, d\phi_{e} = \mathop \int \limits_{0}^{A} \eta \left({D\epsilon} \right)^{2} \,dx \,dA$$

(13)

In Eqs. (12) and (13), σ = stress within the viscoelastic element of length dx and area dA, ϵ = strain within the viscoelastic element, η = dynamic viscosity of the viscoelastic material and A = total cross-sectional area of the viscoelastic patch pasted on the flexible link. Using Eqs. (12) and (13) and the principle of minimum potential energy used for finite element formulation [48], the stiffness matrix for viscoelastic material can be formulated as given in Eq. (9). Damping matrix, c^e for the viscoelastic material was derived and is as follows (Eq. 14).

$$\varvec{c}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\varvec{c}_{11}^{\varvec{e}} } & {\varvec{c}_{12}^{\varvec{e}} } \\ {\varvec{c}_{21}^{\varvec{e}} } & {\varvec{c}_{22}^{\varvec{e}} } \\ \end{array} } \right]$$

(14a)

$$\varvec{c}_{11}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{\eta A_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{12\eta I_{e} }}{{l_{e}^{3} }}} & {\frac{{6\eta I_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{6\eta I_{e} }}{{l_{e}^{2} }}} & {\frac{{4\eta I_{e} }}{{l_{e} }}} \\ \end{array} } \right] ;\;\varvec{c}_{12}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{ - \eta A_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{ - 12\eta I_{e} }}{{l_{e}^{3} }}} & {\frac{{6\eta I_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{ - 6\eta I_{e} }}{{l_{e}^{2} }}} & {\frac{{2\eta I_{e} }}{{l_{e} }}} \\ \end{array} } \right];$$

$$\varvec{c}_{21}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{ - \eta A_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{ - 12\eta I_{e} }}{{l_{e}^{3} }}} & {\frac{{ - 6\eta I_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{6\eta I_{e} }}{{l_{e}^{2} }}} & {\frac{{2\eta I_{e} }}{{l_{e} }}} \\ \end{array} } \right];\;\varvec{c}_{22}^{\varvec{e}} = \left[ {\begin{array}{*{20}c} {\frac{{\eta A_{e} }}{{l_{e} }}} & 0 & 0 \\ 0 & {\frac{{12\eta I_{e} }}{{l_{e}^{3} }}} & {\frac{{ - 6\eta I_{e} }}{{l_{e}^{2} }}} \\ 0 & {\frac{{ - 6\eta I_{e} }}{{l_{e}^{2} }}} & {\frac{{4\eta I_{e} }}{{l_{e} }}} \\ \end{array} } \right];$$

$${\text{Global}}\;{\text{damping}}\;{\text{matrix}},\;\varvec{c}_{\varvec{G}}^{\varvec{e}} = \varvec{ L}_{pf}^{\varvec{T}} \varvec{c}^{\varvec{e}} \varvec{L}_{pf}$$

(14b)

2.3 Active vibration control of torsional vibrations

In this section, mathematical models for piezo-sensor and piezo-actuator in torsion will be presented based upon the theory of piezo-actuation provided by Preumont [45]. Using torsion equation we can write:

$$\tau = \frac{Tr}{J}\;{\text{and}}\;T = GJ\frac{\partial \phi }{\partial x} = GJ\phi^{\prime }$$

(15a)

$${\text{Thus}},\tau = Gr\phi^{\prime } = G\gamma$$

(15b)

In above equations, $\tau$ = shear stress, T = twisting torque, J = polar moment of inertia, G = modulus of rigidity, $\phi$ = twist, $\gamma$ = shear strain and r = radius (refer to Fig. 5). Taking the torsional piezo-sensor as current amplifier, the voltage, v generated by it can be expressed as:

$$v = Rd_{24} G_{p} r\mathop \int \limits_{a}^{b} b_{p} \left( x \right)\dot{\phi }^{'} \left( x \right)\cdot dx$$

(16a)

where R = resistance of piezo-sensor, d₂₄ = piezoelectric constant, G_p= modulus of rigidity of piezo-sensor and b_p = width of piezo-sensor. If b_p(x) = b_p = constant then,

Fig. 5

Development of mathematical model of torsional piezo-actuator

$$v = Rd_{24} G_{p} rb_{p} \left[ {\dot{\phi }^{'} \left( b \right) - \dot{\phi }'\left( a \right)} \right]$$

(16b)

For torsional piezo-actuator we can write,

$$T = \int \left({2E_{44} \epsilon_{23} - \frac{{d_{24} v}}{{b_{p}}}E_{44}} \right)r \cdot dA = GJ\phi^{\prime} - \frac{{d_{24} vE_{44}}}{{b_{p}}}\int r \cdot dA$$

(17)

where E₄₄ = Young’s modulus of piezo-actuator, $\epsilon_{23}$ = shear strain in piezo-actuator and A = area of cross-section of piezo-actuator.

From Fig. 5 we can write,

$$\int r \cdot dA = A\sqrt {\left( {0.5h + h_{p} } \right)^{2} + 0.25b_{p}^{2} }$$

(18)

where A = h_pL_p, h = beam thickness, h_p = thickness of piezo-actuator and L_p = length of piezo-actuator. Using above equation, we can write:

$$T = GJ\phi^{\prime} - \frac{{d_{24} vE_{44} h_{p} L_{p} }}{{b_{p} }}.\frac{{b_{p} }}{2}.\left[ {1 + \left( {\frac{{0.5h + h_{p} }}{{0.5b_{p} }}} \right)^{2} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$

(19)

For (0.5 h + h_p) ≪ b_p, $\left( {\frac{{0.5h + h_{p} }}{{0.5b_{p} }}} \right)^{2} \ll 1$

$${\text{So}},T = GJ\phi^{\prime} - \frac{1}{2}\left( {d_{24} vE_{44} h_{p} L_{p} } \right)$$

(20a)

Now, inertia torque is represented as:

$$I_{m} \ddot{\phi } = - T$$

(20b)

Therefore we get,

$$I_{m} \ddot{\phi } + GJ\phi^{\prime} = \frac{1}{2}\left( {d_{24} vE_{44} h_{p} L_{p} } \right)$$

(21a)

where I_m = mass moment of inertia of beam. It is known that shear stress is always complimentary. So, in order to control the torsional vibrations, two piezo-actuators should be attached on the opposite faces of the beam at the same location. Thus, above equation will get modified as follows.

$$I_{m} \ddot{\phi } + GJ\phi^{\prime} = \left( {d_{24} vE_{44} h_{p} L_{p} } \right)$$

(21b)

Equation (21) is used to find out torsional moments during finite element formulation. Referring to Fig. 3, if q_aT and q_bT are assumed to be the torsional degrees of freedom at nodes 2 and 3 respectively then the load vector, f_T(t) during finite element formulation will be given as follows.

$$f_{T} \left( t \right) = \left( {d_{24} vE_{44} h_{p} L_{p} } \right)\left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & { - \,1} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\dot{q}_{aT} } \\ {\dot{q}_{bT} } \\ \end{array} } \right\}$$

(21c)

Equations (11) and (21c) are to be assembled together to formulate the load vector for Space-frame element. The results using Space-frame element are shown in Fig. 22.

2.4 Validation of mathematical model of Two-Link Flexible manipulator

The natural frequencies of the Two-Link Flexible manipulator using FEM program is validated for different manipulator configurations from the work of Karagulle [51]. Table 2 gives the physical parameters of the flexible manipulator used for validation. Table 3 gives the natural frequencies at different manipulator configurations.

Table 2 Physical parameters of Two-Link Flexible manipulator used for validation [51]

From Table 3, it can be seen that the natural frequencies obtained through simulation in the present work matches fairly well with the natural frequencies obtained by Karagulle et al. [51] through experiment. The percentage difference lies between ± 1.5%. Thus, mathematical model of the Two-Link Flexible manipulator is validated.

Table 3 First mode natural frequencies of Two-Link Flexible manipulator at different configurations

2.5 Validation of mathematical model of active damping using piezoceramics

The validation of the mathematical model used for active vibration control in this paper is done for single flexible link using the results of Sun et al. [52]. The vibration control of the single flexible link as well as the control of hub angle is achieved by using PZT actuator and ‘proportional-derivative’ controller. Table 4 shows the system parameters used for validation of results.

Table 4 System parameters for validation for single flexible link [52]

Four piezoelectric actuators are applied at two locations on the link: two near the hub and two at the tip. The hub angle and tip responses are provided in Figs. 6, 7 and 8. The values of PD gains are: K_p = 100 and K_v = 100. The flexible link is initially displaced by 0.1 rad.

Fig. 6

Variation of desired hub angle and actual hub angle with time for Single Link Flexible manipulator

Fig. 7

a Time response of the deflection of tip of Single Link Flexible manipulator along X-direction [52], b time response of the deflection of tip of Single Link Flexible manipulator along X-direction (p_x) as obtained by Sun et al. [52]

Fig. 8

a Time response of the deflection of tip of Single Link Flexible manipulator along Y-direction, b time response of the deflection of tip of Single Link Flexible manipulator along Y-direction (p_y) as obtained by Sun et al. [52]

Figure 6 compares between the joint response of the hub of the Single Link Flexible manipulator for the present case and that obtained by Sun et al. It takes some time for the actual hub angle to match with the desired hub angle. This response matches fairly well with the response obtained by Sun et al. [52]. Figures 7a and 8a show the tip responses obtained from the present work while Figs. 7b and 8b show tip responses obtained by Sun et al.

Figures 7 and 8 show the time responses of the tip of the Single Link Flexible manipulator. These responses match fairly well with the time responses obtained by Sun et al. [52]. From above figures, it can be concluded that the mathematical model used in this paper works fairly well for the tip vibration control of flexible manipulator system.

3 Results using viscoelastic, active and hybrid damping

In this section, simulation results obtained from the mathematical model described in previous section are shown. Firstly, the results are obtained for viscoelastic and active damping cases separately. After that, both types of damping are combined, i.e., hybrid damping is used. The results are discussed for all these three cases. Table 5 enlists the physical and simulation parameters used during simulation.

Table 5 Parameters table for simulation of Two-link Flexible manipulator

3.1 Results using viscoelastic damping

Kelvin–Voigt elements are taken to model the viscoelastic material (rubber). One finite element per link is used in this case. Hence, total number of ‘finite elements’ used is 2. Figures 9, 10, 11 and 12 show the comparison of tip responses of the second flexible link between viscoelastically damped and undamped cases. The viscoelastic damping is achieved by using 1000 Kelvin–Voigt (K–V) elements.

Fig. 9

Comparison of slope rates (rate of change of slope) of tip of second flexible link of Two-Link Flexible manipulator between viscoelastically damped and undamped cases

Fig. 10

a FFT of slope rate of tip-2 of Two Link Flexible manipulator (undamped case), b FFT of slope rate of tip-2 of Two Link Flexible manipulator (damped case)

Fig. 11

Comparison of slopes of tip of second flexible link of Two-Link Flexible manipulator between viscoelastically damped and undamped cases

Fig. 12

Comparison of velocity of tip of second flexible link of Two-Link Flexible manipulator between viscoelastically damped and undamped cases

Figure 9 shows the rate of change of slope, i.e., slope rate of end point (tip) of second flexible link both in the presence and absence of viscoelastic damping. The response shown here corresponds to the time rate of change of degree of freedom—q_3i shown in Fig. 4. The undamped case exhibits high amplitude of vibration. For the damped case, the response exhibits higher harmonics initially which get reduced with time. Besides that, an overall reduction can be seen in the amplitude of damped response with time. At t = 0.05 s, there is sudden change in the value of excitation torque (Table 5), so there is an increase in the amplitude of vibrations in both undamped and damped cases at that moment. The FFT of undamped and damped responses are provided in Fig. 10a, b below respectively.

From Fig. 10a, b, it can be observed that in undamped case, the higher harmonic is predominant. The vibration response of the tip can be explained by the dominant higher mode. On the other hand, in damped case multiple numbers of modes are present. Contribution of all these modes is to be taken care of for interpreting the vibration response of the tip. But, remarkable fact is that in undamped case the magnitude of vibration is very high when compared to the magnitude of vibration in damped case. Thus, it can be said that viscoelastic damping decreases the magnitude of tip vibration of two-link flexible manipulator significantly but at the same time it increases the contribution of higher modes in the vibration response. Furthermore, it can also be observed from the FFT curves that viscoelastically damped structures vibrate at frequencies different from the original frequencies of the structure. Following figures compare between the tip slope and tip velocity of the flexible manipulator for undamped and damped cases.

Figure 11 shows comparison between the damped and undamped responses of slope of tip of second flexible link. This corresponds to the degree of freedom—q_3i shown in Fig. 4. The undamped response shows high amplitude of vibration while the damped case exhibits lower amplitude.

In Fig. 10, the velocity of tip of second flexible link for damped and undamped cases are compared. The tip velocity is represented by degree of freedom: q_3i-1 in Fig. 4. From Fig. 12, it is clear that due to the presence of viscoelastic damping, the amplitude of vibration decreases. Above results show that use of unconstrained viscoelastic layer decreases the amplitude of vibrations of the tip of the flexible manipulator effectively. It can also be seen that due to the presence of unconstrained viscoelastic layer, the frequencies of the actual undamped system gets changed.

3.2 Results using active damping (using piezo patches)

In this section, simulation results obtained for active damping using piezoelectric sensors and actuators are presented. Firstly, results are obtained by varying the relative position of sensors and actuators, and thereafter the effect of proportional and derivative gains is studied.

3.2.1 Results based upon relative placements of piezo-sensors and piezo-actuators on links

Four finite elements per link are used. Hence, total number of finite elements used is eight. The relative placements of piezo-sensors and piezo-actuators can be understood using Table 1. Figures 13 and 14 show the comparison of tip responses of Link-2 of Two-Link Flexible manipulator for undamped and actively damped cases for the collocated arrangement of piezo-sensors and piezo-actuators.

Fig. 13

Comparison of slope rates (rate of change of slopes) of tip of second flexible link of Two-Link Flexible manipulator between undamped and actively damped cases for collocated arrangement

Fig. 14

Comparison of velocities of tip of second flexible link of Two-Link Flexible manipulator between undamped and actively damped cases for collocated arrangement

Figure 13 shows comparison of rate of change of slope (angular velocity) of tip of second flexible link between undamped and actively damped cases for collocated arrangement. From the figure, it is clear that there is considerable reduction in amplitude of vibration due to the active control.

In Fig. 14, the velocities of tip of second flexible link for undamped case and actively damped case are compared with each other. Collocated arrangement of sensor-actuator pair is taken. There is a decrease in the higher harmonics and amplitude of vibrations is also less due to the presence of active damping. From Figs. 13 and 14 both, it can be seen that the natural frequencies of the original system get altered due to the presence of sensors and actuators on the flexible links. Figures 15 and 16 show the comparison of the tip responses of second flexible link between collocated and non-collocated arrangement of sensors and actuators.

Fig. 15

Comparison of slope rates (rate of change of slopes) of tip of second flexible link of Two-Link Flexible manipulator for collocated and non-collocated sensor-actuator pairs

Fig. 16

Comparison of linear velocities of tip of second flexible link of Two-Link Flexible manipulator for collocated and non-collocated sensor-actuator pairs

In Fig. 15, slope rates of tip of second flexible link are compared together. It can be seen that the collocated arrangement gives better response than the non-collocated arrangement.

Figure 16 shows comparison between the tip velocities of second flexible link for collocated and non-collocated arrangements of sensors and actuators. The results are similar as obtained in Fig. 15. In collocated arrangement, the actuator is applied at the same position where sensor is applied. Thus, the correct vibration sensed by sensor can be used to provide the exact damping force by the actuator. On the other hand, in non-collocated arrangement, the sensor and actuator are at different locations. As a result, there will always be an error between the sensed variable and the controlled variable. Thus, collocated arrangement is the best from the point of view of vibration control. Preumont [45] has described that it is always better to use collocated arrangement whenever possible because this arrangement achieves robust control. On the other hand, the non-collocated arrangement makes the system—non-minimum phase, i.e., the system has zeros in right half of the s-plane. As a result, instability of the system increases. This property of being non-minimum phase does not cause any problem when the right half plane zeros lie well outside the bandwidth of the closed-loop control system. This can be done by using high damping along with non-collocated arrangement.

3.2.2 Results based upon different values of PD gains used during active control of vibrations

Following results (Figs. 17, 18) are obtained for active vibration control using piezo-actuators after selecting different values of proportional and derivative gains (K_p and K_v respectively).

Fig. 17

Comparison of slope rates (rate of change of slopes) of tip of second flexible link of Two-Link Flexible manipulator at different values of PD gains

Fig. 18

Comparison of linear velocities of tip of second flexible link of Two-Link Flexible manipulator at different values of PD gains

Figures 13 and 17 are to be looked upon together. From Fig. 13 it can be interpreted that by using PD gains, there is a decrease in the vibration of the tip of the flexible manipulator. But from Fig. 17, it is found that the vibration of tip is lower at fewer values of PD gains than that at high values of PD gains. This can be understood from the classical control theory where, on increasing the derivative gain, overshoot increases. In Fig. 17, K_p1 and K_p2 are the proportional gains used for Flexible Link-1 while K_v1 and K_v2 are the derivative gains used for Flexible Link-2.

In Fig. 18, the linear velocities of tip of second flexible link are compared with each other at different values of PD gains. The results are similar as in Fig. 17. From Figs. 13, 17 and 18 it can be interpreted that PD gains help in reducing the tip vibrations of the flexible manipulator but these gains must be selected properly. For the present case, the low values of gains give better results.

3.3 Results using hybrid damping

Here, in this case, both active damping and viscoelastic damping are used. The PD gains used are: K_p = 4 and K_v = 4 for both the links while Kelvin–Voigt elements are taken to incorporate viscoelastic damping. Figures 19, 20 and 21 show the tip responses of second flexible link under the influence of hybrid damping.

Fig. 19

Comparison of slope rates (rate of change of slopes) of tip of second flexible link of Two-Link Flexible manipulator between active damping control and hybrid damping control

Fig. 20

Comparison of slopes of tip of second flexible link of Two-Link Flexible manipulator between active damping control and hybrid damping control

Fig. 21

Comparison of bending rates of tip of second flexible link of Two-Link Flexible manipulator between active damping control and hybrid damping control

From above results, it can be concluded that hybrid damping is better than the active damping. While using high values of PD gains during active control, it becomes necessary to use passive damping so that the amplitude of vibration remains within permissible limits. The results on torsional deformation of tip of second flexible link are shown in Fig. 22. The physical parameters provided in Table 5 are used for simulation. The torsional deformation of tip corresponds to the degree of freedom: Q_6i-2 shown in Fig. 2. Space-frame elements are used for obtaining the following results. Due to the presence of torsional vibrations, the Two-link Flexible manipulator does not remain planar. Figure 22a, b compare the torsional deformations of tip between undamped and damped cases.

Fig. 22

Comparison of torsional deformations of tip of second flexible link of Two-Link Flexible manipulator between active damping case and undamped case

From Fig. 22, it can be observed that, the response of ‘actively damped case’ is better than the response of ‘undamped case’. The values of PD gains used are: K_p = 2 and K_v = 2.8. The torsional vibrations are reduced by using active control.

3.4 Comments on eigen values

During simulation, it is found that the natural frequencies of the original flexible manipulator change due to the application of viscoelastic and piezoelectric materials for the purpose of vibration control. Table 6 shows the change in natural frequencies of the Two-Link Flexible manipulator due to the presence of viscoelastic and piezoelectric layers on the flexible links. The physical parameters are the same as provided in Table 5.

Table 6 Change in natural frequencies of the Two-Link Flexible manipulator due to the presence of viscoelastic and piezoelectric layers

The frequencies in Table 6 are found out at the manipulator configuration: θ₁ = 0° and θ₂ = 0°. The viscoelastic layers are applied throughout the length of the links. Only one Kelvin–Voigt element is considered here. The piezoelectric layers are applied in collocated fashion (Table 1 and Fig. 4). While using active control (using piezoelectric layers), the values of PD gains used are: K_p = 2 and K_v = 2.8. Change in the value of K_p changes the natural frequencies of the system. Eight finite elements are used to find out these frequencies except in the second column. The columns under the heading—‘Undamped System’ form the basis of convergence study. By using more number of finite elements, accurate frequencies of the system are captured but at the cost of high simulation time.

4 Conclusions

The present work describes the tip vibration control of a Two-Link Flexible manipulator using passive viscoelastic damping, active damping and hybrid damping techniques. The passive damping is achieved by pasting an unconstrained viscoelastic layer on the flexible links. With the help of finite element modelling, the damping matrix for viscoelastic material is derived. Active damping is achieved using piezoceramic patches. The piezo-sensors and piezo-actuators are pasted at specific locations on the links. But in this paper, this concept of modal controller cannot be directly used because the manipulator system is an inertia-variant system due to which its Eigen values change with time. The piezoelectric sensor senses the vibration of the flexible link on which it is pasted and sends velocity feedback (angular velocity and linear velocity) and position feedback to the piezo-actuator. Based upon this feedback, the piezo-actuator applies a time-dependant turning moments on the portion of flexible link where it is pasted. A proportional-derivative based feedback controller is designed for obtaining the positional accuracy of the flexible manipulator. The results show that the presence of viscoelastic damping effectively reduces the amplitude of vibration of flexible links but at the same time it increases the presence of higher modes of vibration.

During active vibration control, the relative placement of sensors and actuators play a significant role. It is found that collocated control is more effective than non-collocated control in curbing the vibrations.

When both viscoelastic damping and active damping are used together, better results are obtained. Thus, it is advisable to use hybrid damping for vibration control of the flexible manipulator where lower values of controller gains can be used to produce the same effect. Also, the passive viscoelastic material is very effective for higher frequency components of vibration.

The mathematical model described in this paper is validated both for a single flexible link manipulator and two-link flexible manipulator. Another novelty of the present work lies in control of both torsional and flexural vibrations through the application of passive and active damping methods to the non-inertial frames represented by the manipulator links.

The key findings of this paper can be highlighted as follows:

• 1. The presence of viscoelastic damping material alters the original frequencies of vibration of the system. This is true for actively damped case also. The damped response is composed of multiple frequencies but with very less magnitude. On the other hand, the undamped response consists of one dominant frequency. This may be either the lower mode or any of the higher modes.

• 2. The control forces applied by the piezo-actuators are modeled as distributed load p(t) on the flexible links. This load is expressed in matrix form so that it can be used during finite element formulation.

• 3. A hypothesis for control of torsional vibrations using piezo-actuators is presented.

Appendix

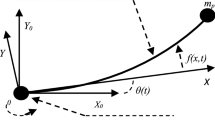
In Fig. 1, plane X–Y is the plane of bending while plane Y–Z is the plane of torsion. X–Y-Z is the reference/ground frame while X₁–Y₁–Z₁ and X₂–Y₂–Z₂ are the local frames attached to Link-1 and Link-2 respectively. Axis X₁ is aligned along the un-deformed neutral axis (N.A.) of Link-1 while axis X₂ is aligned along the un-deformed neutral axis of Link-2. The origins of these local frames are located at Joint-1 and Joint-2 respectively. Joint-1 is given a rigid rotation of θ₁ and Joint-2 is given a rigid rotation of θ₂. The position of any point on Link-1 with respect to ground is given by:

$$\left\{ {p_{1} } \right\} = \left[ {T_{1} } \right]\left[ {T_{1T} } \right]\left\{ {r_{1T} } \right\} + \left[ {T_{1} } \right]\left\{ {r_{1} } \right\}$$

(22)

Similarly, the position of any point on Link-2 with respect to ground is given by:

$$\left\{ {p_{2} } \right\} = \left[ {T_{1} } \right]\left\{ {r_{1}^{*} } \right\} + \left[ {T_{1} } \right]\left[ {T_{1T}^{*} } \right]\left\{ {r_{1T}^{*} } \right\} + \left[ {T_{A}^{*} } \right]\left[ {T_{1} } \right]\left[ {T_{2} } \right]\left\{ {r_{2} } \right\} + \left[ {T_{1} } \right]\left[ {T_{2} } \right]\left[ {T_{2T} } \right]\left\{ {r_{2T} } \right\}$$

(23)

In above expressions,

$$T_{1} = \left[ {\begin{array}{*{20}c} {\cos \theta_{1} } & {\begin{array}{*{20}c} { - \sin \theta_{1} } & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {\sin \theta_{1} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { {\text{cos}}\theta_{1} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right];\quad T_{2} = \left[ {\begin{array}{*{20}c} {\cos \theta_{2} } & {\begin{array}{*{20}c} { - \sin \theta_{2} } & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {\sin \theta_{2} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} { {\text{cos}}\theta_{2} } \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right];\left\{ {r_{1} } \right\} = \left\{ {\begin{array}{*{20}c} {x_{1} } \\ {\begin{array}{*{20}c} {w_{1} \left( {x_{1} ,t} \right)} \\ 0 \\ \end{array} } \\ \end{array} } \right\};$$

$$\left\{ {r_{1}^{*} } \right\} = \left\{ {\begin{array}{*{20}c} {L_{1} } \\ {\begin{array}{*{20}c} {w_{1} \left( {L_{1} ,t} \right)} \\ 0 \\ \end{array} } \\ \end{array} } \right\};\left\{ {r_{2} } \right\} = \left\{ {\begin{array}{*{20}c} {x_{2} } \\ {\begin{array}{*{20}c} {w_{2} \left( {x_{2} ,t} \right)} \\ 0 \\ \end{array} } \\ \end{array} } \right\};\quad T_{A}^{*} = \left[ {\begin{array}{*{20}c} {\cos \left( {w_{1}^{*'} } \right)} & {\begin{array}{*{20}c} { - \sin \left( {w_{1}^{*'} } \right)} & 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {\sin \left( {w_{1}^{*'} } \right)} \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\cos \left( {w_{1}^{*'} } \right)} \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} { 0} \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right];$$

$$\left\{ {r_{iT} } \right\} = \left\{ {\begin{array}{*{20}c} 0 & {b_{i} \phi_{i} } & {b_{i} } \\ \end{array} } \right\}^{\prime } ;\quad \left\{ {r_{iT}^{*} } \right\} = \left\{ {\begin{array}{*{20}c} 0 & {b_{i} \phi_{i}^{*} } & {b_{i} } \\ \end{array} } \right\}^{'} ;\quad \left\{ g \right\}^{'} = \left\{ {\begin{array}{*{20}c} 0 & g & 0 \\ \end{array} } \right\};$$

$$\left[ {T_{iT} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{i} } & { - \sin \phi_{i} } \\ 0 & {\sin \phi_{i} } & {\cos \phi_{i} } \\ \end{array} } \right];\left[ {T_{iT}^{*} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi_{i}^{*} } & { - \sin \phi_{i}^{*} } \\ 0 & {\sin \phi_{i}^{*} } & {\cos \phi_{i}^{*} } \\ \end{array} } \right];$$

(24)

• L₁ and L₂ = lengths of Link-1and Link-2 respectively,

• θ₁ and θ₂ = joint rotations (rigid) of Joint-1and Joint-2 respectively,

• x₁ and x₂ = distances measured along un-deformed Link-1 and Link-2 axes, i.e. X₁ and X₂ respectively,

• w₁(x₁, t) and w₂(x₂, t) = elastic displacements of Link-1 and Link-2 respectively undergoing bending vibrations

• $w_{1}^{*'}$ = bending angle at end point of Link-1 = $\frac{{dw_{1}^{*} }}{{dx_{1} }}$

• {r₁} = position coordinates of any point on Link-1 w.r.t to un-deformed Link-1axis i.e., X₁ in plane X₁-Y₁

• {r₂} = position coordinates of any point on Link-2 w.r.t to un-deformed Link-2 axis i.e., X₂ in plane X₂–Y₂

• {r ^*₁ } = position coordinates of end point of Link-1 w.r.t. un-deformed beam-1 axis X₁ in plane X₁–Y₁

• {r_iT} = position coordinates of any point on Link-i in plane Y_i–Z_i

• ϕ_i = ϕ_i(x_i, t) = torsional deformation of any point on Link-i

• ϕ ^*_i  = ϕ_i(L_i, t) = torsional displacement of end point of Link-i; i represents the link number (i = 1 and 2)

The total kinetic energy of the manipulator system is given by:

$$K.E. = \frac{1}{2}\rho_{1} A_{1} \mathop \int \limits_{0}^{{L_{1} }} \left\{ {\dot{p}_{1} } \right\}^{'} \left\{ {\dot{p}_{1} } \right\}dx_{1} + \frac{1}{2}\rho_{2} A_{2} \mathop \int \limits_{0}^{{L_{2} }} \left\{ {\dot{p}_{2} } \right\}^{'} \left\{ {\dot{p}_{2} } \right\}dx_{2}$$

(25)

Total potential energy of the manipulator system is given by:

$$\begin{aligned} P.E. & = \frac{{E_{1} I_{1} }}{2}\mathop \int \limits_{0}^{{L_{1} }} \left( {\frac{{\partial^{2} w_{1}^{2} }}{{\partial x_{1}^{2} }}} \right)^{2} dx_{1} + \frac{{G_{1} J_{1} }}{2}\mathop \int \limits_{0}^{{L_{1} }} \left( {\frac{{\partial \phi_{1} }}{{\partial x_{1} }}} \right)^{2} dx_{1} + \rho_{1} A_{1} \mathop \int \limits_{0}^{{L_{1} }} \left\{ g \right\}^{\prime } \left\{ {p_{1} } \right\}dx_{1} \\ & \quad + \frac{{E_{2} I_{2} }}{2}\mathop \int \limits_{0}^{{L_{2} }} \left( {\frac{{\partial^{2} w_{2}^{2} }}{{\partial x_{2}^{2} }}} \right)^{2} dx_{2} + \frac{{G_{2} J_{2} }}{2} \mathop \int \limits_{0}^{{L_{2} }} \left( {\frac{{\partial \phi_{2} }}{{\partial x_{2} }}} \right)^{2} dx_{2} + \rho_{2} A_{2} \mathop \int \limits_{0}^{{L_{2} }} \left\{ g \right\}^{\prime } \left\{ {p_{2} } \right\}dx_{2} \\ \end{aligned}$$

(26)

In Eq. (26), J₁ and J₂ are the polar moment of inertias of Link-1 and Link-2 respectively. The joint torques can be obtained using Lagrangian dynamics as follows:

$$\frac{d}{dt}\left( {\frac{{\partial {\mathcal{L}}}}{{\partial \dot{q}}}} \right) - \frac{{\partial {\mathcal{L}}}}{\partial q} = F$$

(27)

In above expression, ${\mathcal{L}}$ represents Lagrangian of the system and is obtained by taking the difference of total kinetic energy and total potential energy of the system; q represents generalized coordinates and F represents generalized torque/force.

$$q = \left\{ {\begin{array}{*{20}c} {\theta_{1} } & {\theta_{2} } & {\begin{array}{*{20}c} {w_{1} } & {w_{1}^{*} } & {\begin{array}{*{20}c} {w_{2} } & {w_{2}^{*} } & {\begin{array}{*{20}c} {\phi_{1} } & {\phi_{1}^{*} } & {\begin{array}{*{20}c} {\phi_{2} } & {\phi_{2}^{*} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{'}$$

(28a)

$$F = \left\{ {\begin{array}{*{20}c} {\tau_{1} } & {\tau_{2} } & {\begin{array}{*{20}c} 0 & 0 & {\begin{array}{*{20}c} 0 & 0 & {\begin{array}{*{20}c} 0 & 0 & {\begin{array}{*{20}c} 0 & 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right\}^{'}$$

(28b)

where $\tau_{1}$ and $\tau_{2}$ are the external torques applied at joint-1 and joint-2 respectively. Some typical simulation results based on the mathematical model described above is presented below. Table 7 describes the physical and simulation parameters used for a Two-Link Flexible manipulator used by Habib and Korayem [53].

Table 7 Physical and simulation parameters for Two-Link Flexible manipulator [53]

The simulation results are shown in Figs. 23, 24, 25, 26, 27 and 28. The natural frequencies and the general nature of response level matches with the predictions by Habib and Korayem [53].

Fig. 23

Torque applied at Joint-1

Fig. 24

Torque applied at Joint-2

Fig. 25

Comparison of Joint-1 response between present work and Habib and Korayem’s work [53]

Fig. 26

Comparison of Joint-2 response between present work and Habib and Korayem’s work [53]

Fig. 27

Tip deflection of Link-2 as obtained in the present case (undamped case)

Fig. 28

Tip deflection of Link-2 as obtained by Habib [53]

From above results, it can be concluded that the joint responses (Figs. 25, 26) for the present work and that found in the literature match fairly well. Furthermore, the tip responses in both the cases exhibit same frequency of 44 Hz (Figs. 27, 28). Thus, the mathematical model of Two-Link Flexible manipulator described in the present work gets validated.