Abstract
We study corrections to the Grimus–Stockinger theorem dealing with the large-distance asymptotic behavior of the external wave-packet modified neutrino propagator within the framework of a field-theoretical description of the neutrino-oscillation phenomenon. The possibility is discussed that these corrections, responsible for breakdown of the classical inverse-square law (ISL), can lead to measurable effects at small but macroscopic distances accessible in the SBL (anti)neutrino experiments and in particular can provide an explanation of the well-known reactor antineutrino anomaly.
Similar content being viewed by others
Notes
It is assumed implicitly that the function Φ along with its first to third derivatives are absolutely integrable and, moreover, that Φ is a rotation-invariant function; the latter property will be implied from here on. It is also pertinent to note that, as can be seen from the subsequent calculations, the remainder term in Eq. (3) is actually
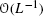 , not
, not 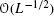 .
.More accurately,
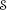 and
and 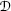 are the supports of the products of the one-particle distribution functions f
a
(p
a
,x
a
) of the in-particles a, expressed in terms of the most probable momenta p
a
and spatial coordinates, x
a
, of the centers of the external wave packets. It is supposed for simplicity that the functions f
a
are time-independent during the detection period, the devices
are the supports of the products of the one-particle distribution functions f
a
(p
a
,x
a
) of the in-particles a, expressed in terms of the most probable momenta p
a
and spatial coordinates, x
a
, of the centers of the external wave packets. It is supposed for simplicity that the functions f
a
are time-independent during the detection period, the devices 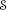 and
and 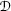 are finite and mutually disjoint within the space domain, and their effective spatial dimensions are small compared to the mean distance between them but very large compared to the effective dimensions (\({\sim}\sigma_{\varkappa}^{-1}\)) of all in and out wave packets moving inside
are finite and mutually disjoint within the space domain, and their effective spatial dimensions are small compared to the mean distance between them but very large compared to the effective dimensions (\({\sim}\sigma_{\varkappa}^{-1}\)) of all in and out wave packets moving inside 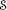 and
and 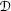 (see Ref. [30] for more details).
(see Ref. [30] for more details).As is shown in Ref. [30], the factor
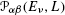 is not really the probability since it does not in general satisfy the unitarity relation. However, this fact is not essential in the context of the present study and this quantity can be referred to as the probability.
is not really the probability since it does not in general satisfy the unitarity relation. However, this fact is not essential in the context of the present study and this quantity can be referred to as the probability.A simple example of such a function at v∈supp(h) is
$$h(v) = \exp \bigl\{ 4- (1-a\eta+a|v| )^{-2} \bigl[1- (1-a\eta +a|v| )^2 \bigr]^{-1} \bigr\} , $$where \(a=(1-1/\sqrt{2})/(\eta-\delta)>0\).
We do not discuss the legitimacy of this interchange.
A more definitive estimate is not feasible for the moment, considering that the function σ eff varies within wide limits over the phase spaces of the nuclear fission (\(\overline{\nu}_{e}\)-produced) processes in the power reactor and the inverse β-decay reaction in the detector.
References
C. Giunti, C.W. Kim, Fundamentals of Neutrino Physics and Astrophysics (Oxford University Press, London, 2007)
C. Giunti, C.W. Kim, J.A. Lee, U.W. Lee, Phys. Rev. D 48, 4310 (1993). arXiv:hep-ph/9305276 [hep-ph]
W. Grimus, P. Stockinger, Phys. Rev. D 54, 3414 (1996). arXiv:hep-ph/9603430
S. Mohanty, arXiv:hep-ph/9706328 (1997)
C. Giunti, C.W. Kim, U.W. Lee, Phys. Lett. B 421, 237 (1998). arXiv:hep-ph/9709494
J.E. Campagne, Phys. Lett. B 400, 135 (1997)
K. Kiers, N. Weiss, Phys. Rev. D 57, 3091 (1998). arXiv:hep-ph/9710289
M. Zrałek, Acta Phys. Pol. B 29, 3925 (1998). arXiv:hep-ph/9810543
A. Ioannisian, A. Pilaftsis, Phys. Rev. D 59, 053003 (1999). arXiv:hep-ph/9809503
W. Grimus, P. Stockinger, S. Mohanty, Phys. Rev. D 59, 013011 (1999). arXiv:hep-ph/9807442
W. Grimus, S. Mohanty, P. Stockinger, arXiv:hep-ph/9909341 (1999)
W. Grimus, S. Mohanty, P. Stockinger, Phys. Rev. D 61, 033001 (2000). arXiv:hep-ph/9904285
C.Y. Cardall, D.J.H. Chung, Phys. Rev. D 60, 073012 (1999). arXiv:hep-ph/9904291
C.Y. Cardall, Phys. Rev. D 61, 073006 (2000). arXiv:hep-ph/9909332
M. Beuthe, arXiv:hep-ph/0010054 (2000)
M. Beuthe, Phys. Rep. 375, 105 (2003). arXiv:hep-ph/0109119
M. Beuthe, Phys. Rev. D 66, 013003 (2002). arXiv:hep-ph/0202068
C. Giunti, J. High Energy Phys. 11, 017 (2002). arXiv:hep-ph/0205014
M. Garbutt, B.H.J. McKellar, arXiv:hep-ph/0308111 (2003)
A. Asahara, K. Ishikawa, T. Shimomura, T. Yabuki, Prog. Theor. Phys. 113, 385 (2005). arXiv:hep-ph/0406141
A.D. Dolgov, O.V. Lychkovskiy, A.A. Mamonov, L.B. Okun, M.V. Rotaev, M.G. Schepkin, Nucl. Phys. B 729, 79 (2005). arXiv:hep-ph/0505251
C.C. Nishi, Phys. Rev. D 73, 053013 (2006). arXiv:hep-ph/0506109
E. Akhmedov, J. Kopp, M. Lindner, J. High Energy Phys. 05, 005 (2008). arXiv:0802.2513 [hep-ph]
V.A. Naumov, D.V. Naumov, Russ. Phys. J. 53, 549 (2010)
J. Kopp, J. High Energy Phys. 06, 049 (2009). arXiv:0904.4346 [hep-ph]
E. Akhmedov, A. Smirnov, Yad. Fiz. 72, 1417 (2009). arXiv:0905.1903 [hep-ph]
B.D. Keister, W.N. Polyzou, Phys. Scr. 81, 055102 (2010). arXiv:0908.1404 [hep-ph]
A.E. Bernardini, M.M. Guzzo, C.C. Nishi, Fortschr. Phys. 59, 372 (2011). arXiv:1004.0734 [hep-ph]
C. Anastopoulos, N. Savvidou, arXiv:1005.4307 [quant-ph] (2010)
D.V. Naumov, V.A. Naumov, J. Phys. G 37, 105014 (2010). arXiv:1008.0306v2 [hep-ph]
E. Akhmedov, A. Smirnov, Found. Phys. 41, 1279 (2011). arXiv:1008.2077 [hep-ph]
E. Akhmedov, J. Kopp, J. High Energy Phys. 04, 008 (2010). arXiv:1001.4815 [hep-ph]
T.R. Morris, J. Phys. G 39, 045010 (2012). arXiv:1110.3266 [hep-ph]
E. Akhmedov, D. Hernandez, A. Smirnov, J. High Energy Phys. 04, 052 (2012). arXiv:1201.4128 [hep-ph]
E. Akhmedov, A. Wilhelm, J. High Energy Phys. 01, 165 (2013). arXiv:1205.6231 [hep-ph]
S.E. Korenblit, D.V. Taychenachev, arXiv:1304.5192 [hep-th] (2013)
C. Giunti, M. Laveder, Phys. Rev. C 83, 065504 (2011). arXiv:1006.3244 [hep-ph]
G. Mention, M. Fechner, Th. Lasserre, Th.A. Mueller, D. Lhuillier et al., Phys. Rev. D 83, 073006 (2011). arXiv:1101.2755 [hep-ex]
Th.A. Mueller, D. Lhuillier, M. Fallot, A. Letourneau, S. Cormon et al., Phys. Rev. C 83, 054615 (2011). arXiv:1101.2663 [hep-ex]
P. Huber, Phys. Rev. C 84, 024617 (2011). arXiv:1106.0687 [hep-ph]
M.V. Fedoryuk, Metod Perevala (Nauka, Moscow, 1977)
P. Anselmann et al. (GALLEX Collaboration), Phys. Lett. B 342, 440 (1995)
W. Hampel et al. (GALLEX Collaboration), Phys. Lett. B 420, 114 (1998)
F. Kaether, W. Hampel, G. Heusser, J. Kiko, T. Kirsten, Phys. Lett. B 685, 47 (2010). arXiv:1001.2731 [hep-ex]
J.N. Abdurashitov, V.N. Gavrin, S.V. Girin, V.V. Gorbachev, T.V. Ibragimova et al., Phys. Rev. Lett. 77, 4708 (1996)
J.N. Abdurashitov et al. (SAGE Collaboration), Phys. Rev. C 59, 2246 (1999). arXiv:hep-ph/9803418
J.N. Abdurashitov, V.N. Gavrin, S.V. Girin, V.V. Gorbachev, P.P. Gurkina et al., Phys. Rev. C 73, 045805 (2006). arXiv:nucl-ex/0512041
Th. Lasserre, J. Phys. Conf. Ser. 375, 042042 (2012)
Th. Lasserre, in PoS (EPS-HEP2011) (2011), p. 100
G. Mention, J. Phys. Conf. Ser. 408, 012025 (2013)
C. Zhang, X. Qian, P. Vogel, Phys. Rev. D 87, 073018 (2013). arXiv:1303.0900 [nucl-ex]
J.M. Conrad, C.M. Ignarra, G. Karagiorgi, M.H. Shaevitz, J. Spitz, Adv. High Energy Phys. 2013, 163897 (2013). arXiv:1207.4765 [hep-ex]
C. Giunti, M. Laveder, Y.F. Li, Q.Y. Liu, H.W. Long, Phys. Rev. D 86, 113014 (2012). arXiv:1210.5715 [hep-ph]
S.K. Kang, Y.D. Kim, Y. Ko, K. Siyeon, arXiv:1303.6173 [hep-ph] (2013)
J. Kopp, P.A.N. Machado, M. Maltoni, T. Schwetz, J. High Energy Phys. 05, 050 (2013). arXiv:1303.3011v2 [hep-ph]
C. Giunti, Acta Phys. Pol. B, Proc. Suppl. 6, 667 (2013)
K.N. Abazajian, M.A. Acero, S.K. Agarwalla, A.A. Aguilar-Arevalo, C.H. Albright et al., arXiv:1204.5379 [hep-ph] (2012)
J. Hamann, S. Hannestad, G.G. Raffelt, Y.Y.Y. Wong, J. Cosmol. Astropart. Phys. 09, 034 (2011). arXiv:1108.4136 [astro-ph.CO]
A. Mirizzi, G. Mangano, N. Saviano, E. Borriello, C. Giunti et al., arXiv:1303.5368 [astro-ph.CO] (2013)
F.P. An et al. (Daya Bay Collaboration), Phys. Rev. Lett. 108, 171803 (2012). arXiv:1203.1669 [hep-ex]
F.P. An et al. (Daya Bay Collaboration), Chin. Phys. C 37, 011001 (2013). arXiv:1210.6327 [hep-ex]
J.K. Ahn et al. (RENO Collaboration), Phys. Rev. Lett. 108, 191802 (2012). arXiv:1204.0626 [hep-ex]
A. Palazzo, arXiv:1308.5880 [hep-ph] (2013)
C. Giunti, M. Laveder, Y.F. Li, H.W. Long, arXiv:1308.5288 [hep-ph] (2013)
A. Esmaili, E. Kemp, O.L.G. Peres, Z. Tabrizi, arXiv:1308.6218 [hep-ph] (2013)
H. Furuta, Y. Fukuda, T. Hara, T. Haruna, N. Ishihara et al., Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 662, 90 (2012). arXiv:1108.2910 [hep-ex]
D.A. Dwyer, K.M. Heeger, B.R. Littlejohn, P. Vogel, arXiv:1109.6036 [hep-ex] (2011)
J. Spitz, Phys. Rev. D 85, 093020 (2012). arXiv:1203.6050 [hep-ph]
A.S. Cucoanes (Nucifer Collaboration), J. Phys. Conf. Ser. 375, 042063 (2012)
A.V. Derbin, A.S. Kayunov, V.N. Muratova, arXiv:1204.2449 [hep-ph] (2012)
A.P. Serebrov, V.G. Zinoviev, A.K. Fomin, U.E. Loginov, M.S. Onegin et al., arXiv:1205.2955 [hep-ph] (2012)
V. Belov, V. Brudanin, M. Danilov, V. Egorov, M. Fomina et al., J. Instrum. 08, P05018 (2013). arXiv:1304.3696 [physics.ins-det]
M. Elnimr, I. Stancu, M. Yeh, R. Svoboda, M.J. Wetstein, F.G. Garcia, B. Osmanov, H. Ray, R. Tayloe, J. Boissevain et al., arXiv:1307.7097 [physics.ins-det] (2013)
O. Yasuda, J. High Energy Phys. 09, 036 (2011). arXiv:1107.4766 [hep-ph]
J. Gaffiot, Nucl. Phys. B, Proc. Suppl. 237–238, 326 (2013)
Acknowledgements
This work was supported by the Federal Target Program “Scientific and Scientific-Pedagogical Personnel of the Innovative Russia” under Contract No. 14.U02.21.0913 The authors would like to thank Z.G. Berezhiani, S.E. Korenblit, and especially D.V. Naumov (who was the active partner in the early stages of this research) for very useful suggestions, comments and criticisms.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Inverse overlap tensors
The higher order corrections are rather involved but, within the CRGP model for the external wave packets, they are constructed from the spatial components of inverse overlap tensors \(\widetilde{\Re}_{s}^{\mu\nu}\) and \(\widetilde{\Re}_{d}^{\mu\nu}\) defined by Eqs. (35). Here we write down the explicit expressions for these components. It is proved that for arbitrary lepton number violating processes
(where I s and I d denote the sets of incoming wave packets in the source and detector vertices, respectively; and, similarly, F s and F d denote the sets of outgoing wave packets which include charged leptons) the components of the inverse overlap tensors can be written as

where

the symbols  and
and  denote the sets of the in and out packets in the source and detector vertices, respectively; u
a
=p
a
/m
a
=(Γ
a
,u
a
) and Γ
a
are the (most probable) 4-velocity and Lorentz factor of the packet a, respectively. It can be verified that the determinant |ℜ
s,d
| is invariant and \(\widetilde{\Re}_{s,d}^{\mu \nu}\) transforms as a tensor under Lorentz transformations. Note that the above formulas were derived without taking into account the energy-momentum conservation.
denote the sets of the in and out packets in the source and detector vertices, respectively; u
a
=p
a
/m
a
=(Γ
a
,u
a
) and Γ
a
are the (most probable) 4-velocity and Lorentz factor of the packet a, respectively. It can be verified that the determinant |ℜ
s,d
| is invariant and \(\widetilde{\Re}_{s,d}^{\mu \nu}\) transforms as a tensor under Lorentz transformations. Note that the above formulas were derived without taking into account the energy-momentum conservation.
As the simplest illustration, we consider here the particular case: the two-particle decay a→ℓ+ν ∗ in the source, where ℓ is a charged lepton and ν ∗ is a virtual (anti)neutrino with definite mass. In this case
This simple expression can also be used for estimations of the inverse overlap tensors for more involved reactions and decays in the case of strong hierarchy between the momentum spreads σ ϰ . Let us mention, in passing, that the inequality \(\mathfrak{C}_{1}<0\) (see Sect. 4) holds over the whole phase space of the two-particle decay into real (on-shell) neutrino, assuming exact energy-momentum conservation. The corresponding contribution to the inverse-squared effective momentum spread (37) is then given by the following expression:
in which
\(E^{\pm}_{\nu} = E_{\nu}^{\star}\varGamma_{a}(1\pm|\mathbf{v}_{a}|)\) are the kinematic boundaries of E ν , \(E_{\nu}^{\star}= (m_{a}^{2}-m_{\ell}^{2} )/(2m_{a})\) is the neutrino energy in the rest frame of the decaying particle a, and v a is the velocity of a. The neutrino mass has been neglected in derivation. The kinematic factor K varies within wide limits at relativistic energies but vanishes when the particle a is at rest. For the median neutrino energy, \(E_{\nu}=\overline{E}_{\nu}= (E^{+}_{\nu}+E^{-}_{\nu} )/2=E_{\nu}^{\star}\varGamma_{a}\),
Appendix B: Effective neutrino wave packet
Here we consider some kind of dualism between the propagator and effective wave-packet approaches. Namely we show that in the asymptotic regime L→∞, the generalized neutrino Green function (1) can be represented as a product of outgoing and incoming effective wave functions of the on-mass-shell neutrino. Below, we use the results of Ref. [30] (obtained within the CRGP model) but with a different and—as we believe—more adequate interpretation which, in particular, allows us to get another look at the corrections to the GS asymptotic.
Let us consider the factor
originated in the full amplitude after applying the GS theorem 1 to Eq. (1) and using the saddle-point integration in variable q 0 [30]. Here
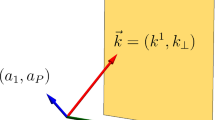
p ν =(E ν ,p ν ) is the mean neutrino 4-momentum (p ν ≈E ν l in the ultrarelativistic case) and \(P_{\pm}=\tfrac{1}{2}(1\pm\gamma_{5})\) are the chiral projectors involved into the Standard Model amplitude. The 4-vector X=(X 0,X)=X d −X s is the difference between the so-called impact points X s and X d which determine the coordinates of the space-time overlap regions of the external wave packets in the source and detector vertices; note that X=L=L l and X 0=T (see Ref. [30] for more details). The function \(\mathfrak{D}\), which can be treated as the uncertainty of the virtual neutrino energy, is defined by

where \(q_{0}^{\text{st}} \approx E_{\nu}\) is the stationary point. So, in the first approximation the function \(\mathfrak{D}\) does not depend on the neutrino mass and in the coordinate frame where l=(0,0,1) is determined by the 00, 03 and 33 components of the inverse overlap tensors. By applying the identity
in which u(p ν ) is the usual Dirac bispinor for a free ultrarelativistic left-handed neutrino, we can rewrite Eq. (B.1) as follows:
where
and
Let us now compare the function ψ y (p ν ,x) with the wave function

describing a generic fermion wave packet |p,s,y〉 in the coordinate representation (here Ψ(x) is the free fermion field and s is the spin projection). Within the CRGP approximation, valid under the conditions

We see therefore that the spinor multiplier \(\psi_{X_{d}}(\mathbf {p}_{\nu },X_{s}-X_{d})\) in Eq. (B.4) can be interpreted as the wave function describing the wave packet of a real (on-shell) neutrino incoming to the detector, while the multiplier \(\psi_{X_{s}}^{\dagger}(\mathbf {p}_{\nu },X_{d}-X_{s})/|\mathbf {X}_{d}-\mathbf {X}_{s}|\) can naturally be treated as the spherical wave function of the same neutrino packet escaping the source. From this interpretation it in particular follows that the effective neutrino momentum spread, \(\sigma_{\nu} = m\mathfrak{D}/E_{\nu}\), is not a constant but an invariant function of the neutrino energy as well as of the mean momenta, masses, and momentum spreads of the external wave packets; due to the factor m/E ν it is extremely small in all realistic situations. The main distinctive feature of the effective neutrino wave packet from the conventional quantum-mechanical wave packets is that it depends on both the source and detector variables. Therefore the duality under discussion should not be understood in a literal sense.
The case becomes even more complicated when one takes into account the higher-order corrections to the GS asymptotics. These corrections yield an additional factor
with the complex-valued coefficient functions a k dependent on the contributions from both the source and detector. Except for very special or trivial cases (when, i.g., one of the contributions is negligible) the functions a k cannot be factorized to the product of the source and detector dependent multipliers. Therefore, if the spacing between the impact points is short the incoming and outgoing neutrino wave packets are not yet separated from each other as it is the case at the asymptotically large distances. In other words, the duality between the propagator and wave-packet treatments is destroyed at short distances and such a case cannot be adequately described in terms of the asymptotically free in and out neutrino wave packets.
Considering now that the modulus-squared full amplitude incorporates the factors \(|\varXi_{X_{s}}|^{2}\) and \(|\varXi_{X_{d}}|^{2}\) which represent (up to a normalization) the probability densities to obtain the in and out neutrino wave packets near the corresponding impact points in the source and detector, we conclude that the factor |Σ|2 affects both these densities or, to put this another way, at relatively short distances between the impact points the factor |Σ|2 changes the probabilities of neutrino production and detection.
It is important to note that, in contrast with the function \(\mathfrak {D}\), the coefficient functions a k include the components \(\widetilde{\Re}_{s,d}^{11}\) and \(\widetilde{\Re }_{s,d}^{22}\) transversal with respect to the neutrino momentum direction l=(0,0,1) (see Eq. (37) as the simplest example). These components are not suppressed by the Lorentz factor E ν /m and thus the ISL violation effect can be large even for massless neutrinos.
Rights and permissions
About this article
Cite this article
Naumov, V.A., Shkirmanov, D.S. Extended Grimus–Stockinger theorem and inverse-square law violation in quantum field theory. Eur. Phys. J. C 73, 2627 (2013). https://doi.org/10.1140/epjc/s10052-013-2627-z
Received:
Revised:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-013-2627-z



 , not
, not 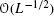 .
.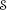 and
and 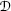 are the supports of the products of the one-particle distribution functions f
a
(p
a
,x
a
) of the in-particles a, expressed in terms of the most probable momenta p
a
and spatial coordinates, x
a
, of the centers of the external wave packets. It is supposed for simplicity that the functions f
a
are time-independent during the detection period, the devices
are the supports of the products of the one-particle distribution functions f
a
(p
a
,x
a
) of the in-particles a, expressed in terms of the most probable momenta p
a
and spatial coordinates, x
a
, of the centers of the external wave packets. It is supposed for simplicity that the functions f
a
are time-independent during the detection period, the devices 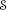 and
and 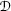 are finite and mutually disjoint within the space domain, and their effective spatial dimensions are small compared to the mean distance between them but very large compared to the effective dimensions (
are finite and mutually disjoint within the space domain, and their effective spatial dimensions are small compared to the mean distance between them but very large compared to the effective dimensions (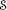 and
and 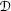 (see Ref. [
(see Ref. [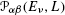 is not really the probability since it does not in general satisfy the unitarity relation. However, this fact is not essential in the context of the present study and this quantity can be referred to as the probability.
is not really the probability since it does not in general satisfy the unitarity relation. However, this fact is not essential in the context of the present study and this quantity can be referred to as the probability.