Abstract
We define Morse functions and prove the basic results (existence and genericity, Morse lemma …)
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The main advantage of this proof is that it gives a slightly more general result than the Morse lemma: near a critical point, a function can be written as the sum of a constant, a quadratic form of rank k≤n and a function in the remaining n−k variables whose partial derivatives of orders 1 and 2 are all zero at the point in question.
- 2.
The definitions “narrow passage between two mountains” or “depression forming a passage between two mountain summits” found in dictionaries are not much more precise.
- 3.
If f is a function of two arguments (u,v)∈U×V⊂E×F, then we let (D 1 f)(u,v) denote the linear map
$$(D_1f)_{(u,v)}:E\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}$$that is the partial differential of f with respect to the first variable. The analogue holds for (D 2 f)(u,v).
References
Laudenbach, F.: Topologie différentielle (1992). Cours à l’École Polytechnique
Milnor, J.: Morse Theory. Princeton University Press, Princeton (1963)
Author information
Authors and Affiliations
Exercises
Exercises
Exercise 1
Let U be an open subset of R
n and let \(f:U\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) be a  function. Let V be an open subset of R
n and let \(\varphi:V\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow}U\) be a diffeomorphism. Compute (d
2(f∘φ))
y
(for y∈V).
function. Let V be an open subset of R
n and let \(\varphi:V\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow}U\) be a diffeomorphism. Compute (d
2(f∘φ))
y
(for y∈V).
Let M be a manifold and let \(g:M\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) be a function. Show that the bilinear form (d 2 g) x is well defined on the vector subspace
Exercise 2
The cotangent vector bundle T ⋆ V of the manifold V is endowed with its natural manifold structure (recalled in Appendix A). Verify that we can see the differential df of a function \(f:V\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) as a section
of the cotangent vector bundle (which is an embedding of V in T ⋆ V).
What are the critical points of f in this terminology? Show that the point a is a nondegenerate critical point of f if and only if the submanifold df(V) is transverse to the zero section at the point in question.
Prove that a nondegenerate critical point of a function is isolated (without using the Morse lemma!).
Exercise 3
(Monkey Saddle)
We consider the function
Study the critical point (0,0). Is it nondegenerate? Draw a few regular level sets of the function f as well as its graph.
Exercise 4
If \(f:V\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) and \(g:W\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) are Morse functions, then \(f+g:V\times W\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) is also a Morse function whose critical points are the pairs of critical points of f and g.
Exercise 5
(On the Complex Projective Space)
By passing to the quotient, the function on C n+1−{0} defined by
induces a function on the complex projective space P n(C), which we still denote by f.
Verify that this is a Morse function whose critical points are the points [1,0,…,0] (of index 0), [0,1,0,…,0] (of index 2) and so on up to [0,…,0,1] (of index 2n).
Readers eager to know where this function may well have come from (from [54], of course, but before that?) can turn to Remark 2.1.12.
Exercise 6
(On the sphere and on the real projective plane)
With essentially the same formula, let us now consider the function
and the resulting function \(g:\mathbf{P}^{2}(\mathbf{R})\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) on the real projective plane that follows from it by passing to the quotient. Verify that f (and therefore g) is a Morse function and show that it has six critical points (and therefore that g has three):
-
Two points of index 0, the points (±1,0,0), at level 0
-
Two points of index 1, the points (0,±1,0), at level 1
-
Two points of index 2, the points (0,0,±1), at level 2.
Figure 1.7 shows a few level sets of this function on the sphere. The critical level set containing the two points of index 1 consists of the two circles defined by intersecting the sphere with the planes z=±x.
Exercise 7
In a square, draw the level sets of the height function on the “inner tube” torus (the answer is somewhere in this book).
Exercise 8
(A projective quadric)
We consider the “quadric” Q in P 3(C) defined by the equation
Show that Q is a compact submanifold of the manifold P 3(C) of (real) dimension 4.
Let us write z j =x j +iy j (for 0≤j≤3) and z=x+iy for z∈C 4, with x,y∈R 4. We fix two real numbers λ and μ and, for z∈C 4, we set
Verify that for \(\left \vert u\right \vert =1\), we have
and deduce from it that \(\widetilde {f}\) defines a function
Suppose that the real numbers λ and μ occurring in the definition of f satisfy 0<λ<μ. Let g be the restriction of f to Q. Show that g is a Morse function that has a local minimum, a local maximum and two critical points of index 2.
Exercise 9
In this exercise, we propose a different proof of the existence of numerous Morse functions on a manifold, and more precisely of Theorem 1.2.5:
-
(1)
Using, for example, Exercise 2, show that the set of Morse functions on the compact manifold V is open for the
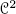 topology, and therefore also for the
topology, and therefore also for the 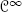 topology.
topology. -
(2)
Let a∈V and let U be the open set of a chart centered at a. We let
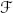 denote the space of differentials of the functions defined on U (or of exact 1-forms) , seen as a subset of
denote the space of differentials of the functions defined on U (or of exact 1-forms) , seen as a subset of 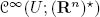 (for every x∈U, (df)
x
is a linear functional on R
n). Note that
(for every x∈U, (df)
x
is a linear functional on R
n). Note that 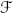 is not an open subset. Let α be a plateau function with support in U and value 1 on a compact neighborhood K of a. For
is not an open subset. Let α be a plateau function with support in U and value 1 on a compact neighborhood K of a. For 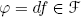 , we let $$\begin{aligned} F:U\times(\mathbf{R}^n)^\star&\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\\ (x, A)&\mathchoice{\longmapsto}{\mapsto}{\mapsto}{\mapsto}f(x)+\alpha(x)A\cdot x. \end{aligned}$$
, we let $$\begin{aligned} F:U\times(\mathbf{R}^n)^\star&\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\\ (x, A)&\mathchoice{\longmapsto}{\mapsto}{\mapsto}{\mapsto}f(x)+\alpha(x)A\cdot x. \end{aligned}$$ComputeFootnote 3 (D 1 F)(x,A) for x∈K and show that F is a submersion
$$K\times(\mathbf{R}^n)^\star \mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow}(\mathbf{R}^n)^\star.$$Show that
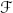 is locally transversal to \(\left \{0\right \}\) (in the sense of Subsection A.3.c).
is locally transversal to \(\left \{0\right \}\) (in the sense of Subsection A.3.c). -
(3)
Show that every point a of V admits a compact neighborhood K such that the set of functions \(f:V\mathchoice{\longrightarrow}{\rightarrow}{\rightarrow}{\rightarrow} \mathbf{R}\) whose critical points in K are nondegenerate is dense in
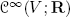 .
. -
(4)
Deduce a proof of Theorem 1.2.5 from this.
Rights and permissions
Copyright information
© 2014 Springer-Verlag London
About this chapter
Cite this chapter
Audin, M., Damian, M. (2014). Morse Functions. In: Morse Theory and Floer Homology. Universitext. Springer, London. https://doi.org/10.1007/978-1-4471-5496-9_1
Download citation
DOI: https://doi.org/10.1007/978-1-4471-5496-9_1
Publisher Name: Springer, London
Print ISBN: 978-1-4471-5495-2
Online ISBN: 978-1-4471-5496-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



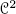 topology, and therefore also for the
topology, and therefore also for the 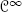 topology.
topology.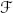 denote the space of differentials of the functions defined on U (or of exact 1-forms) , seen as a subset of
denote the space of differentials of the functions defined on U (or of exact 1-forms) , seen as a subset of 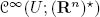 (for every x∈U, (df)
x
is a linear functional on R
n). Note that
(for every x∈U, (df)
x
is a linear functional on R
n). Note that 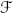 is not an open subset. Let α be a plateau function with support in U and value 1 on a compact neighborhood K of a. For
is not an open subset. Let α be a plateau function with support in U and value 1 on a compact neighborhood K of a. For 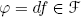 , we let
, we let 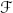 is locally transversal to
is locally transversal to 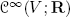 .
.